Вестник Военного инновационного технополиса «ЭРА», 2023, T. 4, № 2, стр. 190-201
Современные подходы к построению систем распознавания образов комбинированного типа на основе искусственных нейронных сетей
В. Е. Дементьев 1, С. Х. Киреев 2, И. А. Кулешов 1, *
1 ПАО “Интелтех”
Санкт-Петербург, Россия
2 Военно-научный комитет Главного управления связи ВС РФ
Санкт-Петербург, Россия
* E-mail: dem-vlad@rambler.ru
Поступила в редакцию 06.07.2023
После доработки 06.07.2023
Принята к публикации 05.10.2023
Аннотация
Проведен анализ современных подходов к построению систем распознавания объектов комбинированного типа. Описаны математическая постановка задачи анализа и формализация подходов практической реализации с использованием аппарата сверточных нейронных сетей. Описание применяемых алгоритмов и методов для поиска и классификации признаков объектов сделано в аспекте использования глубокого обучения. Проведены сравнительный анализ и моделирование нейросетевых алгоритмов для решения задачи классификации и поиска объектов на изображениях. Приведены значения показателей обучения и реализации нейросетевых моделей различной архитектуры с разными значениями параметров обучения на известных наборах данных. Исследованы параметры точности, достоверности и полноты идентификации объекта, зависящие от используемых архитектур нейронной сети.
ВВЕДЕНИЕ
Системы распознавания и классификации объектов широко применяются в различных сферах жизнедеятельности [1–13]. Как правило, кривая технологического развития идет по пути комплексирования используемых методов с целью повышения качества функционирования, а также получения некоего синергетического эффекта. Современная практика говорит о том, что больший эффект позволяют получить комбинированные системы распознавания образов, поскольку охватывают больший круг задач. Поскольку в настоящий момент имеется достаточно богатый опыт внедрения интеллектуальных подходов в различных областях, логичным было использование и внедрение таких решений и для систем распознавания образов.
Применение систем интеллектуализации позволяет охватить круг сложноформализуемых задач, для которых разработка математической модели либо затруднена, либо вообще невозможна [14, 15]. Поскольку технологический процесс совершенствования объектов постоянно усложняется, то и задача разработки адекватных математических моделей становится сложно реализуемой. Это приводит к тому, что для разработки систем распознавания образов [19–30] все чаще применяются методы управления сложными объектами [16, 17], использующие контроль параметров, а не состояний.
Усложнение объектов, увеличение числа анализируемых признаков приводят к усложнению аппаратно-программных средств автоматизированной обработки информации [19, 24, 26, 27]. Динамика изменения характеристик объектов распознавания и наличие значительного количества помех и искажений при их анализе негативно влияют на точность и достоверность итогового результата [19, 26]. Это существенно затрудняет решение задачи автоматизации обработки информации и управления [27]. Наиболее эффективное решение связано с применением интеллектуальных методов и подходов, разработкой адекватных алгоритмов обработки данных и увеличения требуемых вычислительных мощностей [19, 25–27].
Как правило, процесс распознавания объектов состоит из двух этапов. На первом решается задача обнаружения (идентификации) объекта, принадлежащего известному для интеллектуальной системы набору классов. На втором этапе выполняется непосредственно классификация идентифицированного объекта в зависимости от его принадлежности какому-то классу из известных. Процесс может выполняться как последовательно, так и параллельно. Наибольшие затруднения связаны с частой изменчивостью получаемых для распознавания изображений объектов. На точность и достоверность распознавания влияет множество факторов, к которым можно отнести расположение в пространстве, окрас и форму объекта, время суток (освещение) и множество других. Известна практика применения подходов распознавания: алгоритмы адаптивного усиления [1], алгоритмы на основе гистограмм градиентов [2, 3] и информации о цвете [4], высокую эффективность при распознавании лиц показали алгоритмы каскадных классификаторов на основе метода Виолы–Джонса [5, 6], алгоритмы контурного анализа [7] и ряд других.
Решения на базе сетей Хопфилда позволяют распознавать объекты с использованием ассоциативной памяти, устанавливающей взаимосвязи между векторами входных данных. Известны два типа ассоциативной памяти: автоассоциативная (взаимозависимость входных векторов характерна для одного и того же вектора) и гетероассоциативная (взаимозависимостью характеризуются два различных вектора). Ассоциативная память запоминает и восстанавливает эталонные образы [28]. Сеть Хопфилда является полносвязной нейронной сетью с симметричной матрицей связей. Для обучения сетей Хопфилда часто используют метод Хебба и правило проекции.
Генеративным вариантом сети Хопфида является машина Больцмана, которая для обучения использует алгоритм имитации отжига. Главным ее достоинством является возможность обучаться внутренним представлениям и решать сложные комбинаторные задачи.
Современные интеллектуальные методы решения задачи классификации используют предварительное выделение признаков (Feature Engineering), а также глубокие сверточные нейронные сети, реализующие последовательный анализ в режиме скользящего окна [8]. Наиболее перспективным с точки зрения достоверности и точности классификации является применение Regional Convolutional Neural Networks (R-CNN) или регионных (областных) глубоких сверточных нейронных сетей, позволяющих одновременно выполнять как поиск объектов, так и их классификацию [9–11].
В отличие от рассмотренных ранее они предназначены непосредственно для идентификации известных объектов и в своей основе имеют специальные алгоритмы предобработки – region-proposal-function, выявляющие на изображении его отдельные участки, содержащие потенциально идентифицируемые объекты. Это позволяет добиться требуемой точности идентификации при существенном сокращении не только используемых вычислительных мощностей, но и временных затрат на расчеты. К известным примерам реализации такого подхода можно отнести, например, [12, 13].
Важной особенностью рекурентных сетей является то, что они получают данные не только с предыдущего слоя сети, но и от собственного выхода с предыдущего прохода очередной эпохи, что существенно ужесточает требования к порядку предоставления данных.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Как было отмечено ранее, идентификация объектов распознавания происходит путем анализа его характеристик – признаков, общая сумма которых составляет его образ, который может быть описан как
где Р – образ объекта, описываемый набором признаков x1–xn.Отметим, что достоверность и точность идентификации объекта зависят не только от количества признаков, которое распознала нейросеть, но и от их информативности, поскольку необходимо учитывать значение энтропии наряду с вероятностью распознавания. На практике для решения подобной задачи применяются многопараметрические системы распознавания, в которых объект представляется совокупностью признаков, имеющих разную природу возникновения, что обусловливает применение различных подходов при регистрации входных параметров и повышает достоверность выходных данных. В этом случае математическая модель объекта распознавания будет иметь вид
(2)
$\left\{ \begin{gathered} \begin{array}{*{20}{c}} {{{P}_{1}} = \left\{ {{{x}_{{11}}},{{x}_{{12}}},...,{{x}_{{1n}}}} \right\}} \\ {{{P}_{2}} = \left\{ {{{x}_{{21}}},{{x}_{{22}}},...,{{x}_{{2n}}}} \right\}} \\ {...............................} \end{array} \hfill \\ {{P}_{k}} = \left\{ {{{x}_{{k1}}},{{x}_{{k2}}},...,{{x}_{{kn}}}} \right\}, \hfill \\ \end{gathered} \right.$Приведенное описание может существенно повысить точность и достоверность пространства признаков идентифицируемого объекта. Необходимо учитывать и тот факт, что, например, для сетей Хопфилда существует определенное требование, заключающееся в том, что матрица весовых коэффициентов должна быть квадратной, ее диагональные элементы равны нулю (${{W}_{{ij}}}$ = 0), а связи симметричны (${{W}_{{ij}}} = {{W}_{{ji}}}$).
Для сравнения в работе рассмотрены различные структуры сверточных нейронных сетей, применяемые в комбинированных системах распознавания образов. К ним относятся: сети Хопфилда, R-CNN с оригинальным алгоритмом region-proposal function, Fast R-CNN, Faster R-CNN [9–11]. При проведении исследований использовали набор данных COCO (насчитывающий 330 000 изображений размером 640 × 507 пикселей разбитых на 80 классов) [29], содержащий также пояснения, в которых имеются координаты объекта, класс, к которому он принадлежит, ссылку на него и дополнительную информацию. Для обучения и тестирования сетей анализировалось 6000 случайных изображений.
Модель R-CNN. Распознавание объектов с использованием модели R-CNN [9] выполняется в несколько этапов.
Этап 1. Генерация области анализа (region proposals), предположительно содержащей целевые объекты (обычно до 2000 возможных областей), с использованием различных алгоритмов (например, Edge Boxes или Selective search), позволяющих снизить вычислительную сложность идентификации объектов. Как правило, вначале выполняется анализ детектором исходного изображения (изображений) в разных масштабах со сдвигом окна идентификации и в результате формируется набор целевых областей прямоугольной формы, потенциально содержащих объект.
Алгоритм Edge Boxes [30] генерирует области анализа в форме прямоугольной рамки, ограничивающей объект. Границы области обеспечивают описательное информативное представление исходного изображения. Число образов, ограниченных контурами и полностью находящихся внутри ограничивающего прямоугольника, характеризует значение вероятности нахождения объекта в данном прямоугольнике. Итоговое число контуров объектов распознавания получается путем исключения из общего числа тех контуров, которые выходят за границы прямоугольной рамки, т.е. содержат замкнутые или почти замкнутые линии.
Алгоритм селективного поиска (selective search) [31] использует стратификационную выборку схожих областей, выстраиваемую в соответствии с цветом, текстурой, фоном, размером, формой и графом. Для графов максимумом выбирается интенсивность пикселя, а в качестве ребра берут пару соседних пикселей. Весом ребра выступает разница между интенсивностями пикселей вершин ребра, которая в дальнейшем используется для классификации элементов распознаваемых объектов. После предварительной группировки похожих областей изображения вычисляется новое значение сходства объектов до тех пор, пока вся выделенная область анализа не станет единым объектом. Интенсивность пикселей является главным фактором, учитываемым при распознавании объектов в ходе анализа.
Этап 2. Формируется набор признаков исходного изображения. Проводится масштабирование сгруппированных областей анализа в соответствии с архитектурой сверточной нейронной сети (CNN) таким образом, что каждая область преобразуется в квадрат 227 × 227 пикселей. До начала процесса форматирования граница области анализа расширяется на 16 пикселей и вместе с основным квадратом объекта подается на вход CNN. На выходе CNN формируется 4096-мерный вектор признаков для каждой области анализа.
Этап 3. Используется метод опорных векторов (SVM) для классификации объектов из каждой области анализа на основе полученного вектора признаков. Для этого применяется алгоритм Non-Maximum Suppression, учитывающий для определения контура только локальные максимумы пикселей.
Алгоритм region-proposal-function R-CNN имеет архитектуру, похожую на алгоритм, рассмотренный в [9], но отличается лучшими характеристиками в плане оперативности и оптимальности.
Этап 1. Генерация множества областей анализа, потенциально включающих в себя объект распознавания. Преобразование исходного изображения к черно-белому или серому. Определяются значения, выступающие в качестве констант по масштабу и соотношению сторон. На этом этапе для поиска прямоугольных областей анализа перекрытие соседних ограничивающих прямоугольников задается как значение параметра α, а порог, согласно которому кандидаты будут удаляться, как значение параметра β. Для генерации областей интереса используется модификация алгоритма Edge Boxes.
Этап 2. Определяется область анализа в виде ограничивающего прямоугольника, в которой с использованием весов контуров объектов внутри него вычисляется их общее число. Находятся координаты пикселей этих контуров для дальнейшего определения соприкасающихся контуров как между собой, так и с граничным прямоугольником. Веса контуров, выходящих за границы области анализа, в оценку не включаются, полученная оценка нормируется относительно области анализа и записывается в массив по убыванию, что позволяет отбросить минимальные значения весов контуров распознаваемых объектов.
Этап 3. Классификация объектов распознавания для каждой области анализа. Для выделенного прямоугольника из области анализа поочередно сравниваются пересекающиеся с ним, вычисляются перекрывающиеся площади и определяется пороговое значение. Если пороговое значение больше β, то прямоугольник отбрасывается. Затем полученный массив передается на CNN, определяющую класс объекта или фона.
Рассмотренный алгоритм не обладает необходимой оперативностью вследствие того, что создается достаточно большое число областей для анализа (прямоугольников) и возникает необходимость хранения большого количества данных.
Модель Fast R-CNN
Этап 1. Генерация областей анализа, в которых потенциально могут находиться объекты распознавания.
Этап 2. Формируется карта признаков исходного объекта, для чего на вход CNN подается полное исходное изображение, но при этом последний слой сети (max-pool) заменяется на слой (RoI pooling) [10]. Координаты области анализа модифицируются в координаты карты признаков, получается требуемый вектор признаков с фиксированной разметкой, представляющий собой матрицу признаков объекта.
Этап 3. Выполняется уточнение границ области интереса при помощи регрессионной модели (Bounding Box Regression). Полученные области интереса и полученные векторы признаков подаются на вход двум новым полностью связным слоям. Первый из этих слоев используется для уточнения границ прямоугольника, а второй – для классификации объекта, расположенного внутри этого прямоугольника (этап 4). Для уточнения ограничивающего прямоугольника регрессионная модель обучается корректировать прогнозируемую ограничивающую рамку с использованием функций CNN.
Этап 4. Классификация объектов распознавания в области анализа, для чего применяется слой softmax, имеющий K + 1 выходов (K – количество классов объектов), учитывающая наличие фона на исходном изображении. Этапы 3 и 4 выполняются параллельно.
Модель Faster R-CNN. В отличие от Fast R-CNN в Faster R-CNN для генерации областей анализа используется специальная сеть Region Proposal Network (RPN).
Этап 1. Формирование карты признаков на основе исходного изображения с помощью CNN.
Этап 2. Генерация областей анализа, потенциально содержащих объект, формирование карты признаков на основе применения и ее обработка скользящим окном 3 × 3 RPN. В итоге формируется массив из девяти областей анализа, имеющих один и тот же центр, но различного размера и параметров. Для каждой области анализа выделяется вектор признаков и пороговое значение, на основе которого принимается решение о соответствии объекту распознавания.
Этап 3. Преобразование вектора признаков области анализа исходного изображения в вектор признаков заданной размерности с помощью слоя RoI pooling.
Этап 4. Уточнение границ области анализа и значения вектора признаков при помощи двух полносвязных слоев регрессионной модели (Bounding Box Regression). Первый слой уточняет границы прямоугольника, второй – классифицирует объект распознавания внутри области анализа (этап 5).
Этап 5. Классификация объектов в областях анализа, для чего применяется слой softmax, имеющий K + 1 выходов (K – количество классов объектов), учитывающая наличие фона на исходном изображении. Этапы 4 и 5 выполняются параллельно.
Сеть Хопфилда. При обучении сети Хопфилда по правилу Хебба входные векторы транспонируются в векторы $\overline {{{x}_{k}}} $, где k – номер анализируемого объекта. Для одного обучающего вектора $x$ значения весов вычисляются по формуле
где N – количество элементов во входном векторе, W – матрица весовых коэффициентов сети размером N × N, X – матрица, составленная из обучающих векторов размером N × p (p – общее количество обучающих векторов).В основе другого метода обучения сети Хопфилда – метода проекций – используется операция псевдоинверсии матрицы
где ${{X}^{ + }}$ – операция псевдоинверсии применительно к матрице X.В результате распознавания образов сеть стремится к устойчивому состоянию, при котором функция энергии сети достигает минимального значения – аттрактора. Множество аттракторов представляют память сети Хопфилда. Сеть является устойчивой, если изменение выхода сети становится меньше с каждой итерацией, пока выход не окажется постоянным.
Для доказательства устойчивости сети Хопфилда используется функция, зависящая от состояния сети и называемая функцией энергии:
(5)
$E(Y) = - \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{w}_{{ij}}}{{y}_{i}}{{y}_{j}}} + \sum\limits_{j = 1}^n {{{\Theta }_{j}}{{y}_{j}}} } .$Однако при обучении сети Хопфилда возникают ситуации, когда устойчивое состояние сети достигнуто, но сгенерированное решение не является верным. Такое явление называется ложным распознаванием или локальным минимумом сети. Для устойчивой сети любое изменение состояния нейрона либо уменьшит энергию сети, либо оставит неизменной.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В ходе исследования проведено сравнение по различным показателям четырех типов нейронных сетей на предмет точности и достоверности распознавания объектов. В качестве набора данных для сравнения использовали набор данных COCO (насчитывающий 330 000 изображений размером 640 × 507 пикселей разбитых на 80 классов) [29]. Отметим, что информативность признаков объектов распознавания в рамках данной работы не рассматривали, но она является важным параметром, влияющим на качество и итоговое значение результата. В качестве основных показателей для оценки использовали [32, 33]:
– доля правильных ответов алгоритма (accuracy);
– точность (precision);
– полнота (recall);
– среднее гармоническое точности и полноты (precision и recall) – F-мера;
– площадь под кривой ошибок (AUC-ROC и AUC-PR);
– логистическая функция потерь (Logistic Loss).
Доля правильных ответов алгоритма (accuracy) относится к классу наиболее простых и понятных, однако редко используемых метрик, так как наименее информативна при решении задач с неравными классами, а также никоим образом не оценивает предсказательную точность сети:
Для оценки качества работы сети на каждом из классов по отдельности применяются метрики точность (precision) и полнота (recall):
Точность (precision) интерпретируется как доля объектов, идентифицированных классификатором корректными (положительными) и при этом действительно ими являющимися, а полнота (recall) показывает, какую долю объектов положительного класса из всех признаков положительного класса нашел алгоритм.
Как правило, для оптимизации гиперпараметров алгоритма применяется метрика F-мера как среднее гармоническое precision и recall:
(9)
${{F}_{\alpha }}\left( {1 + {{\alpha }^{2}}} \right) * \frac{{precision*recall}}{{\left( {{{\alpha }^{2}} * precision} \right) + recall}}.$В данном случае α определяет вес точности в метрике, при α = 1 это среднее гармоническое (с множителем 2, чтобы в случае precision = 1 и recall = = 1 иметь ${{F}_{1}}$ = 1). F-мера достигает максимума при полноте и точности, равных единице, и стремится к нулю, если любой из аргументов также стремится к нулю.
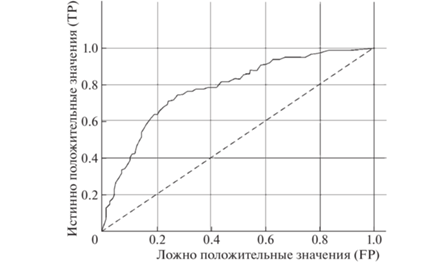
Одной из метрик, позволяющей оценить ИНС в целом, не привязываясь к конкретному порогу, является метрика – площадь под кривой ошибок (AUC-ROC). Данная кривая представляет собой линию от (0.0) до (1.1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR):
TPR – это полнота, а FPR показывает, какую долю из признаков протоколов negative класса алгоритм предсказал неверно. Тогда, если сеть не делает ошибок (FPR = 0, TPR = 1), площадь под кривой будет равна единице; в противном случае, при случайной вероятности классов, AUC-ROC → → 0.5, а TP = FP. На рис. 1 показано соответствие выбора объекта в определенной точке и соответствующего значения порога. Чем больше площадь под кривой, тем выше качество алгоритма, кроме этого, важное значение имеет крутизна кривой, в идеале (при TPR → max и FPR → min) кривая должна стремиться к точке (0,1).Важным достоинством метрики AUC-ROC является устойчивость к несбалансированным классам признаков, т.е. случайно выбранный объект, относящийся к классу positive, имеет вероятность ранжирования выше, чем случайный объект, относящийся к классу negative.
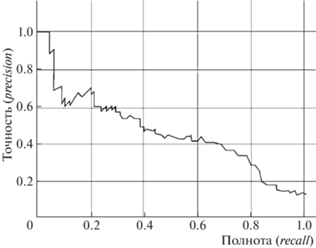
Метрики Precision и recall также используют для построения кривой и аналогично AUC-ROC находят площадь под ней (рис. 2).
Для решения задач классификации допустимо использование логистической функции потерь.
(12)
$\log loss = - \frac{1}{l}\sum\limits_{i - 1}^l {\left( {{{y}_{i}}\log \left( {{{{\tilde {y}}}_{i}}} \right) + \left( {1 - {{y}_{i}}} \right)\log \left( {1 - {{{\tilde {y}}}_{i}}} \right)} \right)} ,$Как правило, минимизация логистической функции представляет собой задачу максимизации доли правильных ответов сети (accuracy) за счет применения достаточно большого регрессионного коэффициента за неверные предсказания.
Наглядно подобная ситуация при неверном ответе и уверенной классификации показана на рис. 3, исходя из которого можно сделать вывод, что ошибка на одном признаке дает существенное ухудшение итоговой ошибки на выборке (чем ближе к нулю ответ алгоритма, тем выше значение ошибки и круче растет кривая). Следовательно, данная метрика не всегда точно отражает результаты оценки и для нашей модели применяться не будет. Рис. 6
Для оценки алгоритмов проведены испытания с использованием известного набора данных C-OCO. В качестве метрик для оценки использовали точность (precision), полноту (recall) и среднее гармоническое точности и полноты (precision и recall) – F-мера. Результаты представлены в табл. 1. На рис. 4, 5 показаны расчетные значения точности, полноты и F-меры для различных вариантов CNN. Рис. 7
Таблица 1.
Расчетные значения точности, полноты и F-меры
| Номер п/п | Сети Хопфилда | R-CNN | ||||
|---|---|---|---|---|---|---|
| precision | recall | F-мера | precision | recall | F-мера | |
| 1 | 0.88 | 0.9 | 0.89 | 0.89 | 0.8 | 0.84 |
| 2 | 0.91 | 1 | 0.95 | 0.92 | 0.95 | 0.93 |
| 3 | 0.81 | 0.9 | 0.85 | 0.8 | 0.88 | 0.84 |
| 4 | 0.8 | 0.94 | 0.86 | 0.8 | 0.94 | 0.86 |
| 5 | 0.93 | 0.9 | 0.91 | 0.94 | 0.85 | 0.89 |
| 6 | 0.92 | 1 | 0.96 | 0.92 | 1 | 0.96 |
| 7 | 0.91 | 1 | 0.95 | 0.91 | 1 | 0.95 |
| 8 | 0.94 | 0.88 | 0.91 | 0.94 | 0.83 | 0.88 |
| 9 | 0.97 | 0.9 | 0.93 | 1 | 0.88 | 0.94 |
| 10 | 0.85 | 0.94 | 0.89 | 0.85 | 0.94 | 0.89 |
| 11 | 0.83 | 0.84 | 0.83 | 0.83 | 0.83 | 0.83 |
| 12 | 0.9 | 0.95 | 0.92 | 0.9 | 0.9 | 0.9 |
| 13 | 0.66 | 0.88 | 0.75 | 0.7 | 0.88 | 0.78 |
| 14 | 0.9 | 0.93 | 0.91 | 0.95 | 0.9 | 0.92 |
| 15 | 0.83 | 1 | 0.91 | 0.83 | 0.95 | 0.89 |
| 16 | 0.83 | 1 | 0.91 | 0.83 | 1 | 0.91 |
| 17 | 0.83 | 0.9 | 0.86 | 0.83 | 0.9 | 0.86 |
| 18 | 0.88 | 0.89 | 0.88 | 0.88 | 0.89 | 0.88 |
| 19 | 0.94 | 0.88 | 0.91 | 0.94 | 0.88 | 0.91 |
| 20 | 0.9 | 0.93 | 0.91 | 0.9 | 0.93 | 0.91 |
| 21 | 0.88 | 0.95 | 0.91 | 0.88 | 0.95 | 0.91 |
| 22 | 0.87 | 0.94 | 0.9 | 0.87 | 0.94 | 0.9 |
| 23 | 0.94 | 0.95 | 0.94 | 0.94 | 0.95 | 0.94 |
| 24 | 0.9 | 0.88 | 0.89 | 0.9 | 0.88 | 0.89 |
| 25 | 0.85 | 0.88 | 0.86 | 0.88 | 0.8 | 0.84 |
| 26 | 0.78 | 0.88 | 0.83 | 0.8 | 0.88 | 0.84 |
| 27 | 0.85 | 0.93 | 0.89 | 0.83 | 0.93 | 0.88 |
| 28 | 0.85 | 0.95 | 0.9 | 0.8 | 0.95 | 0.87 |
| 29 | 0.85 | 0.94 | 0.89 | 0.7 | 0.94 | 0.8 |
| 30 | 0.94 | 0.9 | 0.92 | 0.94 | 0.88 | 0.91 |
| 31 | 0.89 | 0.95 | 0.92 | 0.89 | 0.88 | 0.88 |
| 32 | 0.85 | 0.93 | 0.89 | 0.85 | 0.93 | 0.89 |
| 33 | 0.86 | 1 | 0.92 | 0.86 | 1 | 0.92 |
| 34 | 0.8 | 0.92 | 0.86 | 0.8 | 0.9 | 0.85 |
| 35 | 0.97 | 0.95 | 0.96 | 1 | 0.95 | 0.97 |
| Итого | 0.87 | 0.93 | 0.9 | 0.87 | 0.91 | 0.89 |
| 36 | 0.89 | 0.8 | 0.84 | 0.89 | 0.89 | 0.89 |
| 37 | 0.92 | 0.95 | 0.93 | 0.92 | 0.95 | 0.93 |
| 38 | 0.8 | 0.88 | 0.84 | 0.85 | 0.9 | 0.87 |
| 39 | 0.8 | 0.94 | 0.86 | 0.84 | 0.94 | 0.89 |
| 40 | 0.94 | 0.85 | 0.89 | 0.94 | 0.88 | 0.91 |
| 41 | 0.92 | 1 | 0.96 | 0.92 | 1 | 0.96 |
| 42 | 0.91 | 1 | 0.95 | 0.91 | 1 | 0.95 |
| 43 | 0.94 | 0.83 | 0.88 | 0.94 | 0.83 | 0.88 |
| 44 | 1 | 0.88 | 0.94 | 1 | 0.88 | 0.94 |
| 45 | 0.85 | 0.94 | 0.89 | 0.85 | 0.94 | 0.89 |
| 46 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 |
| 47 | 0.9 | 0.9 | 0.9 | 0.93 | 0.96 | 0.94 |
| 48 | 0.7 | 0.88 | 0.78 | 0.83 | 0.92 | 0.87 |
| 49 | 0.95 | 0.9 | 0.92 | 0.95 | 0.93 | 0.94 |
| 50 | 0.83 | 0.95 | 0.89 | 0.88 | 0.95 | 0.91 |
| 51 | 0.83 | 1 | 0.91 | 0.84 | 1 | 0.91 |
| 52 | 0.83 | 0.9 | 0.86 | 0.85 | 0.9 | 0.87 |
| 53 | 0.88 | 0.89 | 0.88 | 0.9 | 0.93 | 0.91 |
| 54 | 0.94 | 0.88 | 0.91 | 0.94 | 0.9 | 0.92 |
| 55 | 0.9 | 0.93 | 0.91 | 0.92 | 0.93 | 0.92 |
| 56 | 0.88 | 0.95 | 0.91 | 0.89 | 0.95 | 0.92 |
| 57 | 0.87 | 0.94 | 0.9 | 0.88 | 0.94 | 0.91 |
| 58 | 0.94 | 0.95 | 0.94 | 0.94 | 0.95 | 0.94 |
| 59 | 0.9 | 0.88 | 0.89 | 0.92 | 0.9 | 0.91 |
| 60 | 0.88 | 0.8 | 0.84 | 0.88 | 0.9 | 0.89 |
| 61 | 0.8 | 0.88 | 0.84 | 0.84 | 0.95 | 0.89 |
| 62 | 0.83 | 0.93 | 0.88 | 0.88 | 0.93 | 0.9 |
| 63 | 0.8 | 0.95 | 0.87 | 0.83 | 0.95 | 0.89 |
| 64 | 0.7 | 0.94 | 0.8 | 0.79 | 0.94 | 0.86 |
| 65 | 0.94 | 0.88 | 0.91 | 0.95 | 0.9 | 0.92 |
| 66 | 0.89 | 0.88 | 0.88 | 0.9 | 0.9 | 0.9 |
| 67 | 0.85 | 0.93 | 0.89 | 0.9 | 0.95 | 0.92 |
| 68 | 0.86 | 1 | 0.92 | 0.89 | 1 | 0.94 |
| 69 | 0.8 | 0.9 | 0.85 | 0.88 | 0.94 | 0.91 |
| 70 | 1 | 0.95 | 0.97 | 1 | 0.95 | 0.97 |
| Итого | 0.87 | 0.91 | 0.89 | 0.89 | 0.93 | 0.91 |
ЗАКЛЮЧЕНИЕ
Рассмотрен сравнительный анализ алгоритмов сверточных искусственных нейронных сетей для применения в комбинированных системах распознавания образов. Для анализа использовались модели нейронных сетей Хопфилда, R‑CNN, Fast R-CNN, Faster R-CNN. Исходя из представленных результатов можно сделать вывод, что использование предложенного подхода к генерации областей анализа повышает точность и достоверность получаемых результатов поиска объекта на изображении. Тестирование работы модификаций различных моделей R-CNN показывает, что модель Faster R-CNN и сеть Хопфилда существенно превосходят по показателям точности (precision), полноты (recall) и среднего гармонического точности и полноты (precision и recall) – F-меры другие модели из-за использования в качестве алгоритма генерации областей анализа специальной сети формирования соответствующих предложений. Однако сеть Хопфилда проигрывает по показателю точности (precision). В целом полученные результаты моделирования и тестирования приведенных моделей свидетельствуют о высокой точности классификации и полноте обнаружения объектов на изображении для всех рассмотренных алгоритмов. Рис. 8
Список литературы
Бутенко В.В. // Молодой ученый. 2015. № 4. С. 52.
Борисов Е.О. О задаче поиска объекта на изображении. Часть 2. Применение методов машинного обучения. http://mechanoid.kiev.ua/cv-image-detector2.html
Dalal N., Triggs B. // IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA. 2005. № 1. P. 886.
Артемов А.А., Кавалеров М.В., Кузнецов Г.С. // Вестник ПНИПУ. Электротехника, информационные технологии, системы управления. 2011. № 5.
Акимов А.В., Сирота А.А. // Компьютерная оптика. 2016. № 6. С. 899.
Viola P., Jones M. // Int. J. Comp. Vis. 2004. № 57 (2). P. 137.
Нгуен Т.Т. // Известия Томского политехнического университета. 2010. № 5. С. 122.
R-CNN, Fast R-CNN, Faster R-CNN, YOLO–Object Detection Algorithms. https://towardsdatascience.com/r-cnn-fast-r-cnnfaster-r-cnn-yolo-object-detection-algorithms-36d53571365e
Girshick R., Darrell J., Malik T. // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2015. № 38.
Girshick R. // International Conference on Computer Vision (ICC). 2015.
Girshick R., Shaoqing R., Kaiming H. // Neural Information Processing Systems (NIPS). 2015.
Mask R-CNN: архитектура современной нейронной сети для сегментации объектов на изображениях. https://habr.com/ru/post/421299
Wang Y., Wang C., Zhan H. et al. // Remote Sens. 2019. № 11. P. 531.
Leigh W., Purvis R., Ragusa J.M. // Decis. Support Syst. 2002. V. 32. P. 361.
Wen Q., Yang Z., Song Y., Jia P. // Expert Syst. Appl. 2010. V. 37. P. 1015.
Liu Y.Y., Barabasi A.L. // Rev. Mod. Phys. 2016. V. 88. № 3. P. 58. https://doi.org/10.1103/RevModPhys.88.035006
Vamvoudakis K., Jagannathan S. Control of complex systems. Elsevier Inc., 2016. 762 p. https://doi.org/10.1016/C2015-0-02422-4
Simankov V.S., Lutsenko E.V. Adaptivnoe upravlenie slozhnymi sistemami na osnove teorii raspoznavaniya obrazov [Adaptive control of complex systems by patterns recognition theory]. Krasnodar. 1999. P. 318.
Shingo M., Hirasawa K. // Proceedings of the 13th annual conference companion on Genetic and evolutionary computation (GECCO'11). ACM, Dublin, Ireland. 2011. P. 1659.
Garcia-Pedrajas N., Ortiz-Boyer D. // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2006. V. 28. P. 1001.
Popovici E.C., Stancu L.A., Guta O.G. et al. // 10th International Conference on Communications (COMM). 2014. P. 91. https://doi.org/10.1109/ ICComm.2014.6866686
Platt J.C., Christiani N., Shawe-Taylor J. // Proc. Neural Information Processing Systems (NIPS '99). 1999. P. 547.
Anand R., Mehrotra K.G., Mohan C.K., Ranka S. // IEEE Trans. Neural Networks. 1995. V. 6. P. 117.
Dietterich T.G., Bakiri G. // J. Artif. Intell. Res. 1995. V. 2. P. 263.
Rifkin R., Klautau A. // J. Mach. Learn. Res. 2004. V. 5. P. 101.
Allwein E.L., Schapire R.E., Singer Y. // J. Mach. Learn. Res. 2000. V. 1. P. 113.
Bezdek J.C. // J. Intell. Fuzzy Syst. 1993. V. I (1). P. l.
Павлова А.И., Бобрикова К.А. // Siberian J. Life Sci. Agriculture. 2016. № 5 (77). P. 134. https://doi.org/10.12731/wsD-2016-5-7
Microsoft COCO: Common Objects in Context. http://cocodataset.org/#home
Zitnick C., Dollár P. // Comput. Vis. 2014. P. 391.
Sande J., Gevers K., Smeulders T. // Int. J. Comput. Vis. 2013. № 104. P. 154.
Чулков А.А., Дементьев В.Е. // Защита информации. Инсайд. 2021. № 1 (97). С. 62.
Чулков А.А., Дементьев В.Е. // Защита информации. Инсайд. 2021. № 2 (98) С. 68.
Дополнительные материалы отсутствуют.
Инструменты
Вестник Военного инновационного технополиса «ЭРА»