Теплофизика высоких температур, 2021, T. 59, № 2, стр. 221-230
Моделирование стационарных ударных волн в пористой меди методом сглаженных частиц (SPH)
С. А. Мурзов 1, 2, *, А. Н. Паршиков 1, 2, С. А. Дьячков 1, 2, М. С. Егорова 1, 2, С. А. Медин 1, В. В. Жаховский 1, 2
1 ФГБУН Объединенный институт высоких температур РАН (ОИВТ РАН)
Москва, Россия
2 ФГУП “Всероссийский научно-исследовательский институт автоматики
им. Н.Л. Духова” (ФГУП “ВНИИА”)
Москва, Россия
* E-mail: murzovs@gmail.com
Поступила в редакцию 30.12.2019
После доработки 10.08.2020
Принята к публикации 22.12.2020
Аннотация
В работе рассчитываются параметры ударной адиабаты пористого материала в мезоскопической постановке с помощью разработанного метода подвижного окна наблюдения. Пористый материал представляется в виде каркаса из сплошного вещества, заполняющего пространство между порами, механические свойства и ударная адиабата которого зачастую хорошо известны. Суть метода состоит в следующем: несжатое вещество втекает в расчетную область с постоянной скоростью, а скорость вытекания из области подбирается итерациями так, чтобы фронт волны установился неподвижным относительно окна, так как для расчета ударных адиабат необходимо достижение стационарного режима распространения ударной волны. Моделирование ударных волн выполнено как в стандартной постановке с неподвижным поршнем (методом обращенного движения), так и в системе подвижного окна наблюдения. Продемонстрировано, что после достижения стационарного режима волновые профили, полученные обоими методами, идентичны. В качестве примера рассчитаны ударные адиабаты пористой меди, которые хорошо воспроизводят экспериментальные данные для разной пористости. Предлагаемый мезоскопический метод расчета отклика пористых материалов на ударное сжатие в подвижном окне открывает возможность прямого расчета искомых ударных адиабат при пористости материалов, ранее не исследованных экспериментально.
ВВЕДЕНИЕ
Моделирование сверхзвуковых скачков, таких как стационарные ударные волны (УВ) или волны детонации (ДВ), распространяющихся с постоянной скоростью в среде, может потребовать больших вычислительных затрат, так как переход в стационарный режим распространения может занять значительное время, потому что требуется рассматривать образцы достаточно большой протяженности при моделировании в системе координат неподвижного образца или неподвижного поршня [1].
Мезоскопическое моделирование УВ [1–4] в системе координат неподвижного образца или неподвижного поршня, как схематически изображено на рис. 1, приводит к увеличению затрачиваемого вычислительного времени пропорционально квадрату длины пробега УВ (при постепенной подаче несжатого материала в расчетную область перед фронтом УВ), так как УВ распространяется по все большей области материала и расчетное время, затрачиваемое на шаг моделирования, растет пропорционально длине пробега УВ. При этом ударная волна в веществе с мезоструктурой в виде пор, гранул или смеси из разных веществ приводит к появлению зоны осцилляции напряжений за фронтом УВ. В работе [1] исследовано ударное сжатие пористого алюминия методом обращенного движения, где показана необходимость увеличения времени расчета для исследования стационарности УВ с ростом пористости и снижением амплитуды воздействия. Работа авторов [2] представляет первые попытки учитывать влияние неоднородностей, пор и ансамблей пор в трехмерном гидродинамическом моделировании. К настоящему времени мезоскопическое моделирование ударных волн в пористых материалах проводится в том числе методом молекулярной динамики [3] на нанометровом масштабе пор. Мезоскопическое моделирование распространения ударной волны по реагирующему материалу с переходом ударной волны в детонационную [4] может поставить отдельные задачи для крупномасштабного моделирования, где характерные времена термически активированных реакций разложения при схлопывании пор и длина пробега до детонации могут различаться на несколько порядков.
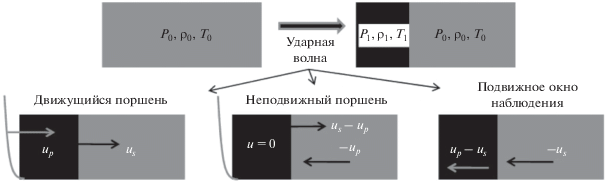
Рис. 1.
Различные системы координат в моделировании ударной волны; up и us полагаются в системе отсчета покоящейся мишени.
В организации входных и выходных границ в расчете методом сглаженных частиц в гидродинамике (SPH) имеется три доминирующих подхода. Первый из них представлен работами [5–8], где предлагается задавать границы слоями пограничных частиц, размещаемыми за проницаемыми границами. Положение этих частиц меняется в соответствии с их скоростью. Так, пограничная частица, переходя через границу входного условия, становится реальной расчетной. И наоборот, реальная частица, переходящая границу выходного условия, становится пограничной и затем удаляется по мере удаления от этой границы. В работе [5] введены неотражающие граничные условия входа и выхода, где несколько слоев частиц вблизи границ получают свое состояние на основе оценки значений инвариантов Римана для частиц из расчетной области и условия нулевых инвариантов Римана, соответствующих акустическим волнам, распространяющимся внутрь области от границ. Данные граничные условия применимы в том числе для дозвукового режима распространения течения и способны моделировать вытекание вещества из расчетной области.
Второй подход [9] является обобщением полуаналитических граничных условий с использованием искусственно введенных сегментов (отрезков), описывающих границу [10]. Так, новые частицы у входной границы появляются на месте точек-частиц контакта двух соседних сегментов в соответствии с дифференциальным уравнением изменения массы по времени, определяющим плотность потока массы. Удаление частиц на выходе происходит с поглощением массы точками-частицами. Третий подход реализует зеркальные отражения частиц за границы [11–13], при этом отражение частиц происходит лишь по координате. В настоящей работе используется подход, наиболее близкий к представленным в [5, 6], так как он является самым простым для реализации из трех рассмотренных.
Моделирование в подвижном окне наблюдения позволяет достигнуть истинно стационарного состояния ударной волны в пористом материале. В работе [14] был предложен метод молекулярно-динамического моделирования в подвижной системе координат, привязанной к фронту УВ. В этом методе фронт УВ покоится в расчетной области, а несжатое вещество втекает в него с постоянной скоростью, равной по модулю скорости движения УВ. Для получения эквивалентной ударной волны в системе координат неподвижной жесткой стенки (рис. 1) необходимо произвести моделирование столкновения образца при начальной скорости −up о неподвижную жесткую стенку. В результате столкновения со стенкой вещество останавливается и в нем формируется УВ, распространяющаяся со скоростью us – up.
В настоящей работе этот метод модифицирован для целей гидродинамического моделирования стационарных УВ с помощью параллельного кода [15], использующего бессеточный контактный метод сглаженных частиц (contact smoothed particle hydrodynamics – CSPH) [16, 17]. Метод CSPH является модификацией метода SPH, где скорости и напряжения в точке контакта SPH-частиц определяются из решения задачи Римана.
При стандартном моделировании отклика пористого материала на ударное воздействие этот материал, как правило, представляется сплошной средой, поэтому требуется знание ударной адиабаты такой среды. В наиболее интересной с точки зрения практики области невысоких нагрузок значительный вклад в реакцию материала на воздействие будут вносить его прочностные характеристики. Рассчитать ударную адиабату для этой области воздействий, пользуясь лишь знанием уравнения состояния сплошного вещества, не представляется возможным. Экспериментальное же определение ударной адиабаты требует затрат на создание и испытание реальных образцов, что не всегда возможно, если речь идет о предполагаемом, а не об уже существующем материале. В предлагаемой работе вычисляются ударные адиабаты пористой меди для разных пористостей в мезоскопическом моделировании с использованием известных механических свойств и ударной адиабаты сплошной меди.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СРЕДЫ
Модель формулируется в приближении сплошной среды, в котором используются законы сохранения массы, импульса и энергии, дополненные материальными уравнениями, описывающими механический отклик среды на деформацию [18]:
Для определения девиатора напряжений в упругой среде используется закон Гука
Тензор девиаторной части скорости деформации
Уравнение состояния меди задано в форме Ми–Грюнайзена:
где e – удельная внутренняя энергия; Γ – параметр Грюнайзена; в качестве опорных кривых давления и внутренней энергии используются их величины на ударной адиабате:При плотности вещества ρ выше начальной ρ0 (x = ρ0/ρ < 1) состояние вещества описывается ударной адиабатой вида us = ca + saup, где us – скорость ударной волны, up – скорость вещества, ca, sa – коэффициенты. При плотности вещества ниже начальной (x > 1) использовалась линейно-упругая кривая давления с согласованным модулем объемного сжатия:
При моделировании ударных волн в стандартной постановке с неподвижным поршнем материал рассматривался как сжимаемая жидкость, уравнение состояния для которой задано в форме Ми–Грюнайзена. Константы вещества приведены в таблице (модель 1).
Параметры среды, используемые в моделировании
| ρ0, г/см3 | Γ | сa, км/с | sa | G, ГПа | Y, ГПа | |
|---|---|---|---|---|---|---|
| Модель 1 | 8.924 | 1.7 | 3.91 | 1.51 | 0 | 0 |
| Модель 2 | 8.96 | 1.7 | 4.184 | 1.4205 | 43 | 0.35 |
Для моделирования в подвижной системе координат используется модель 2, константы которой соответствуют результатам молекулярно-динамического моделирования меди. Аппроксимация ударной адиабаты получена в моделировании монокристаллической меди методом [14]. Модель упругопластического течения использует условия на цилиндре текучести Мизеса, ограничивая величину интенсивности напряжений
соответствующим масштабированием компонент девиатора напряжений где Y – предел текучести.МЕТОД ПОЛУЧЕНИЯ СТАЦИОНАРНОЙ УДАРНОЙ ВОЛНЫ
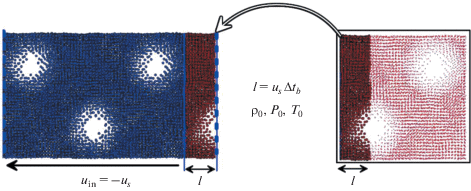
Моделирование в подвижной системе координат имеет целью получение стационарного режима распространения УВ, при котором ударный фронт остается неподвижным относительно расчетной области (окна наблюдения). Расчетная область моделирования, схематически изображенная на рис. 2, состоит из зон подачи вещества через правую границу окна, ударного сжатия и выхода вещества из расчетной области с последующим удалением вещества на левой границе окна. Детали алгоритма обсуждаются ниже на примере моделирования методом сглаженных частиц. При моделировании CSPH методом стационарной УВ в окне наблюдения происходит создание потока новых частиц на входе в окно и удаление такого же потока частиц при выходе из окна. Таким образом, расчет производится с конечным количеством частиц и может производиться неограниченно долго, в отличие от расчетов в неподвижной системе координат, где требуется включать в расчет все новые и новые частицы, переходящие через ударный фронт в связи с пробегом УВ по образцу. Помимо этого очевидного преимущества, моделирование в подвижном окне дает возможность расчета с более мелким размером SPH-частиц, что особенно важно для УВ в пористых материалах, так как ширина фронта волны в пористом материале значительно больше, чем в сплошном веществе, а из-за колебаний давления при коллапсе пор необходима постановка зоны выхода вещества и границы удаления на значительных расстояниях. Относительная величина колебаний давления во фронте УВ растет с увеличением пористости образца и уменьшается с ростом скорости УВ, что необходимо учитывать при моделировании. Поэтому моделирование первоначально проводится для сильной УВ, а затем полученное течение используется для получения УВ с меньшим давлением путем перезапуска расчета с преобразованными скоростями частиц. Программная реализация метода подвижного окна выполнена в виде модуля для параллельного программного комплекса CSPH&VD3, разрабатываемого во ФГУП “ВНИИА им. Н.Л. Духова” авторами [15].
Рис. 2.
Схема расчетной области при моделировании ударной волны в подвижном окне методом сглаженных частиц.

В начальный момент времени расчетная область подготавливается в виде прямоугольного параллелепипеда. Область плотно заполняется SPH-частицами по узлам гранецентрированной кубической (ГЦК) решетки. После этого запускается алгоритм “встряхивания” частиц [19] для достижения упаковки, близкой к жидкой, в которой дальний кристаллический порядок отсутствует. Подготовка “жидкой” упаковки состоит в воздействии на частицы случайных объемных сил, способствующих встряхиванию частиц, с постепенным затуханием их амплитуды, а также во введении сил трения для полной остановки частиц. Затем в образце вырезаются поры требуемого размера.
РАСЧЕТНАЯ ОБЛАСТЬ И ГРАНИЧНЫЕ УСЛОВИЯ В ПОДВИЖНОМ ОКНЕ
Поперечные размеры образца составляют Ly × × Lz = 20 × 20 мкм2, вдоль этих направлений заданы периодические граничные условия. Длина образца вдоль оси X составляла Lx ≈ 0.57 мм. Начальный размер SPH-частиц равен 1/$\sqrt 2 $ мкм, что соответствует 20 периодам ГЦК-решетки в поперечном направлении расчетной области. Сферические поры создаются в узлах другой ГЦК-решетки, причем ось X является направлением [100] решетки. В одной кубической ячейке размерами 20 × 20 × 20 мкм3 располагаются четыре поры с координатами центров (–5, 5, 5), (–5, –5, 5), (‒5, 5, –5), (–5, –5, –5) в микрометрах, которые отсчитываются от центра ячейки при выборе осей вдоль ее ребер. Решетка пор имеет период, равный поперечному размеру расчетной области, а радиус пор составляет rp = 4.9854 мкм и соответствует пористости $m = {{L_{z}^{3}} \mathord{\left/ {\vphantom {{L_{z}^{3}} {\left( {L_{z}^{3} - 4 \times {{4\pi r_{p}^{3}} \mathord{\left/ {\vphantom {{4\pi r_{p}^{3}} 3}} \right. \kern-0em} 3}} \right)}}} \right. \kern-0em} {\left( {L_{z}^{3} - 4 \times {{4\pi r_{p}^{3}} \mathord{\left/ {\vphantom {{4\pi r_{p}^{3}} 3}} \right. \kern-0em} 3}} \right)}} = 1.35.$
SPH-частицы удаляются после пересечения плоскости с фиксированной координатой x = xl левой границы окна. Приграничными считаются частицы внутри расчетной области вблизи плоскости удаления, а именно, частицы с координатами x < xl + d0, где d0 – ширина зоны выхода. В этой зоне вместо системы уравнений гидродинамики решается лишь уравнение движения для координат приграничных частиц, при этом их скорости одинаковы и равны отрицательной скорости выхода uout → up – us, а поперечные компоненты скорости полагаются равными нулю. Все остальные, а именно, плотность, энергия и другие термодинамические величины, остаются неизменными и равными последним своим значениям перед попаданием в зону выхода. Здесь и далее сохраняются для скорости поршня up и скорости УВ us их обычные положительные значения, измеренные в системе координат неподвижного несжатого вещества. Для создания ударно-волнового сжатия в веществе необходим механизм передачи давления от частиц изнутри приграничной зоны к частицам вне ее, который реализуется посредством их взаимодействия, что естественным образом создает УВ при соответствующей разнице массовых скоростей, давления и плотности между этими частицами. При этом межчастичным взаимодействиям запрещено менять состояние приграничных частиц.
Граница подачи вещества имеет переменное положение, которое может варьироваться в ходе расчета на величину в несколько слоев SPH-частиц. Это связано с программной реализацией CSPH&VD3, где вставка нового слоя возможна лишь в момент обновления списка соседних частиц. Обновление списка соседей происходит через небольшое число шагов интегрирования Δtb (около 10), но переменный шаг по времени в гидродинамическом моделировании приводит к тому, что правая граница, двигаясь с постоянной скоростью us, проходит разное расстояние за одинаковое число шагов интегрирования. Положение границы равномерно смещается в отрицательном направлении оси X, но скачком изменяет свое положение в положительном направлении при вставке новых слоев SPH-частиц. Поэтому граница вблизи подачи вещества характеризуется дискретностью своего положения. Для такой послойной подачи подготовка малого образца с порами производится до начала моделирования. При этом используется образец с поперечными размерами Ly × Lz, равными поперечному размеру исходного образца, и такого же размера вдоль оси X. В данном образце укладывается ровно один период вышеописанной ГЦК-решетки сферических пор, а подготовка образца проводится подобно основному образцу. Из данного образца формируется структура из набора связных списков. Каждый связный список хранит в себе положения SPH-частиц, находящихся в одном слое ГЦК-решетки вдоль оси X. Таким образом, в момент подачи вещества определяются номера связных списков из данного набора и происходит последовательная вставка всех частиц из этих слоев. Вдоль оси X задано периодическое граничное условие, т.е. после последнего слоя подается первый слой.
На схеме рис. 3 показана зона входа частиц в расчетную область. Новые наборы слоев частиц изображены темно-красным цветом, синим – частицы, уже участвующие в расчете, а оставшиеся красные частицы будут вставляться по мере освобождения места вблизи правой границы образца. Положение вставляемого слоя учитывает положение последнего вставленного слоя. Когда вставка из вещества доходит до конца красного образца, то слои начинают вставляться, начиная с первого, т.е. процесс периодически повторяется. Частицы в зоне входа вещества имеют координаты x > xr – di, где di – ширина зоны входа, xr – правая граница расчетной области. Границы зоны входа показаны синими пунктирными линиями на рис. 3. Частицы внутри зоны входа движутся равномерно и прямолинейно вплоть до попадания в зону расчета межчастичного взаимодействия, при этом массовая скорость всех частиц направлена вдоль оси X и равна скорости входа uin = −us. Отметим еще раз, что скорость входа является фиксированной на протяжении всего времени моделирования и равна скорости УВ в стационарном режиме, а скорость выхода является переменной контролируемой величиной, которая требует подстройки для достижения стационарности ударного фронта. Значение скорости выхода изменяется таким образом, чтобы стабилизировать ударный фронт в желаемом положении внутри подвижного окна.
ПОЛУЧЕНИЕ СТАЦИОНАРНОГО УДАРНОГО ФРОНТА
Пусть в начальный момент времени в окне задан образец с определенной мезоскопической структурой, имеющий среднюю начальную плотность ρ00 и состоящий из N0 частиц. Если в системе распространяется УВ и сжатое вещество обладает большей плотностью, то при достижении стационарного режима следует ожидать увеличения полного числа SPH-частиц Nf относительно начального числа, т.е. Nf > N0. Условие стационарности требует такого положения ударного фронта, при котором количество частиц равно Nf и ударный фронт неподвижен. Однако в случае высокой пористости возможен аномальный ход ударной адиабаты, когда плотность за ударным фронтом уменьшается, и тогда Nf < N0. В этом случае вместо числа частиц предпочтительнее иметь дело со средним давлением в окне наблюдения
Если целевой величиной является среднее давление, то
Опишем итерационный алгоритм обратной связи для подбора массовой скорости uout на выходе из окна, а также технику проведения такого расчета на примере сплошного образца. Цель этого алгоритма состоит в нахождении неизвестной скорости up, при которой ударный фронт стабилизируется при uout = up – us.
Для этого будем управлять скоростью выхода в зависимости от числа частиц или среднего давления с помощью простой управляющей функции
Выбранная зависимость является убывающей функцией, что необходимо, чтобы гарантировать сходимость алгоритма к uout = up – us при некотором ω *. Чтобы в стационарном режиме получить ω = 1, заранее неизвестный подгоночный параметр скорости β должен стать равным по модулю скорости выхода. С целью достижения β → –(up – us) введем корректирующее уравнение для изменения параметра β за одну итерацию:
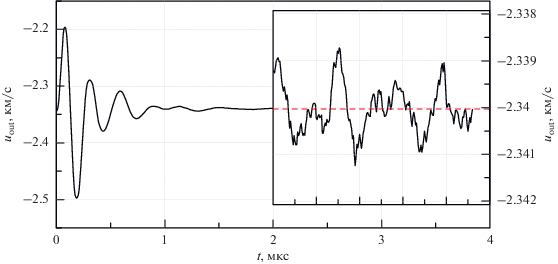
В дополнение к описанному алгоритму для ускорения выхода ударного фронта на стационарное положение используется объемная сила для всех частиц с давлением выше некоторого порогового P > P *, пропорциональная отклонению массовой скорости SPH-частицы от uout. Данная сила отключается автоматически, если система приближается к стационарному положению |ω − 1| < ε (ε = 0.03), однако при отклонении от стационарного значения включается режим “грубой” настройки скорости выхода каждый раз, когда система оказывается достаточно отклонена от стационарного состояния. На рис. 4 представлен пример сходимости скорости выхода на стационарное значение uout = −2.34 км/с. При этом уровень шума скорости выхода в стационарном режиме составляет приблизительно 0.05%. Поэтому ошибка расчета давления УВ также равна 0.05% при фиксированной начальной плотности и скорости УВ, так как $P = {{\rho }_{{00}}}{{u}_{s}}{{u}_{p}}.$
СРАВНЕНИЕ ВОЛНОВЫХ ПРОФИЛЕЙ, ПОЛУЧЕННЫХ В ПОДВИЖНОМ ОКНЕ И В СИСТЕМЕ НЕПОДВИЖНОГО ЖЕСТКОГО ПОРШНЯ
Проведем сравнение результатов моделирования УВ в подвижном окне и при нагружении материала жестким поршнем (случай неподвижного поршня соответствует удару образца о жесткую стенку). Для задания граничного условия на жестком поршне используется взаимодействие SPH-частиц с их зеркальными образами, которые получаются отражением нормальной компоненты скорости частиц и их положения относительно плоскости жесткого поршня [20]. Задание граничного условия в подвижном окне предполагает фиксированную скорость входа, при этом стационарная скорость выхода вещества из расчетной области определяет скорость натекания вещества на поршень. Для точного определения скорости в УВ необходимо получить стационарный режим, поэтому сначала проводилось моделирование в подвижном окне, и затем вычислялась скорость натекания вещества. Далее проводилось моделирование УВ в точно таком же образце с неподвижной жесткой стенкой.
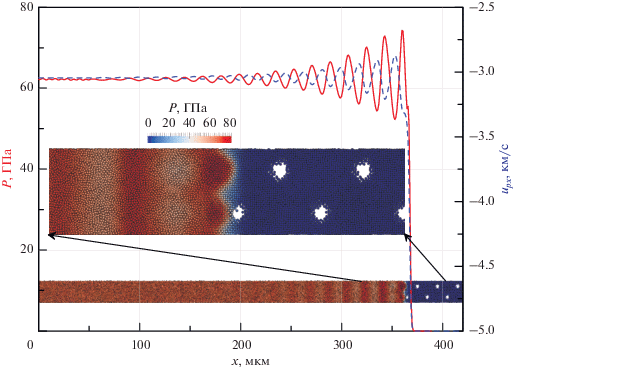
На рис. 5 красными линиями представлены профили плотности, массовой скорости, давления и девиаторов напряжений, полученные в подвижной системе координат. Скорость ударной волны us = 3.5 км/с равна (с противоположным знаком) скорости входа вещества us = –uin в расчетную область. В результате моделирования получена стационарная скорость выхода uout = = −2.34 км/с, откуда вычисляется массовая скорость за фронтом ударной волны up = us + uout = = 1.16 км/с относительно покоящегося несжатого образца.
Рис. 5.
Профили стационарных УВ одинаковых амплитуд, полученных при моделировании упругопластической пористой меди методом подвижного окна (красные линии) и в системе неподвижного поршня (черный пунктир); профили: (а) – плотности (1) и скорости (2) течения, (б) – давления (3) и девиатора напряжений (4).
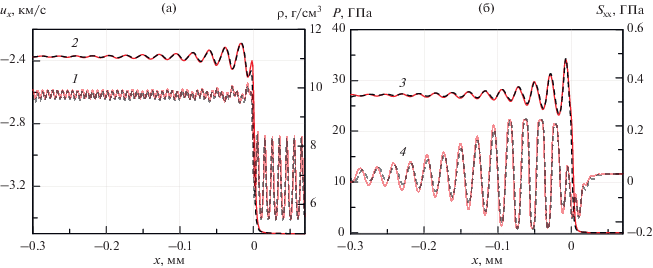
Для получения эквивалентной ударной волны в системе координат неподвижной жесткой стенки (рис. 1) необходимо произвести моделирование столкновения образца меди с начальной скоростью вдоль оси X Ux = −up с неподвижной жесткой стенкой. В результате столкновения вещество останавливается и образуется УВ, распространяющаяся со скоростью Us = us – up. На рис. 6 черные пунктирные линии показывают соответствующие величины плотности и напряжений, а также профиль преобразованной массовой скорости, полученный из исходного профиля скорости вычитанием скорости УВ в данной системе координат ${{\dot {U}}_{x}}$ = Ux – Us. Наблюдается согласие в полученных профилях, что означает эквивалентность в возможности задания граничного условия для создания ударных волн в системе координат неподвижного ударного фронта.
Рис. 6.
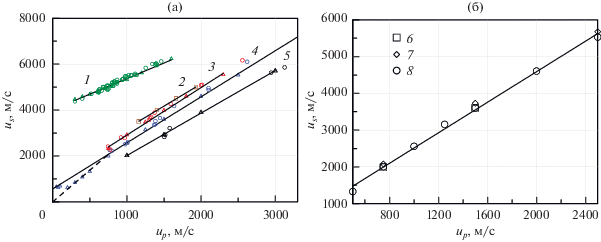
Расчетные ударные адиабаты (а) пористой меди (треугольники – неподвижная жесткая стенка, квадраты – подвижное окно) сравниваются с экспериментальными данными [21] (окружности) при различных начальных плотностях: 1 – 8.924 г/см3, 2 – 6.637, 3 – 6.3, 4 – 5.7, 5 – 4.5; прямые сплошные линии – линейная аппроксимация us(up), пунктирная линия – расчет по (2); (б) – сравнение ударных адиабат пористой меди при плотности 5.7 г/см3 для различных размеров пор и начальных размеров SPH-частиц в микрометрах соответственно: 6 – 142.5 и 5; 7 – 28.5 и 1; 8 – 28.5 и 0.5.
Отметим, что плотность SPH-частиц имеет периодический характер, что связано с явным заданием мезоскопической структуры и периодичностью геометрии пор. При этом сохраняющиеся осцилляции плотности за областью релаксации давления являются результатом неоднородной плотности SPH-частиц, вызванной неоднородным прогревом частиц, вовлеченных в процессе схлопывания пор. Показанные на рис. 5 профили подобраны таким образом, чтобы распространяющаяся УВ была в одинаковой фазе в обеих системах отсчета, что позволило сопоставить профили явно.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ УДАРНЫХ ВОЛН В ПОРИСТОЙ МЕДИ
Гидродинамическая постановка. Моделирование ударного нагружения пористой меди производится в приближении сжимаемой жидкости для SPH-частиц меди с использованием модели 1 и метода обращенного движения в системе неподвижной жесткой стенки. Исходный образец готовится с явным заданием мезоскопической структуры пор с размерами, соответствующими заданной пористости. Для моделирования распространения ударной волны в пористой меди использовалась структура, состоящая из последовательности кубов с парой пор, имеющих центр на главной диагонали, как описано в [22]. Размеры образцов составляли 1036 × 80 × 80 мкм3.
Результаты проведенного моделирования для меди с различной пористостью хорошо согласуются с экспериментальными ударными адиабатами в имеющемся диапазоне экспериментальных данных. Также проведено моделирование ударного нагружения пористой структуры при низких скоростях воздействия и начальной плотности образца 5.7 г/см3.
Ударная адиабата сплошного вещества и ударная адиабата, полученная в CSPH-расчетах, представлены на рис. 6a. Результаты масштабирования при пропорциональном увеличении линейных размеров системы без изменения числа SPH-частиц показаны на рис. 6б. На этом же рисунке показан результат моделирования с более мелким размером SPH-частиц при фиксированной геометрии пор, что показывает сходимость полученных результатов по размеру SPH-частиц. На рис. 6а представлено сравнение с экспериментальными данными из [21], где черными линиями показана линейная аппроксимация полученных в моделировании ударных адиабат при различной пористости. Представленные данные находятся в пределах погрешности экспериментальных ударных адиабат в рассматриваемом диапазоне. Однако для моделирования сильных УВ в материалах с большей пористостью необходимо применять модель сплошного вещества для более высоких плотностей энергии [23].
В моделировании УВ с начальной плотностью 5.7 г/см3 в области малых значений амплитуды УВ наблюдается отклонение от линейной зависимости us от up, которая характерна для высоких скоростей удара up > 750 м/с. Данная часть кривой может быть приближенно описана процессом полного схлопывания вакуумированных пор при пренебрежимо малом скачке давления. Если допустить, что коллапс пор происходит без сопротивления и нагрева, то плотность вещества за ударной волной можно оценить величиной плотности сплошной меди ρ0. Тогда закон сохранения массы на ударном скачке записывается в виде
где ρ00 – начальная плотность пористого материала, ρ1 – плотность вещества в ударной волне. В приближении ρ1 ≈ ρ0 [24, 25]:(2)
${{u}_{s}} = {{{{\rho }_{0}}{{u}_{p}}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}{{u}_{p}}} {({{\rho }_{0}} - {{\rho }_{{00}}})}}} \right. \kern-0em} {({{\rho }_{0}} - {{\rho }_{{00}}})}}.$Оценка с использованием уравнения (2) показана пунктирной линией на рис. 5a для исходной плотности 5.7 г/см3. При скорости удара up < 200 м/с скорость ударной волны выходит на постоянное значение, при этом из-за низких амплитуд давления сжатия повышается относительная амплитуда осцилляций давления на фронте, в результате чего снижается точность определения скорости фронта и давления на фронте.
Упругопластическая постановка. При экспериментальном определении отклика материала на ударное сжатие измеряется напряжение в сжатом материале, которое зависит от режима упругопластического деформирования. В мезоскопическом моделировании пористого материала предлагается учесть прочностные свойства каркаса сплошного материала, которые дают отдельный вклад в наблюдаемое напряженное состояние. Следует отметить, что данный эффект особенно важен для определения ударной адиабаты при такой амплитуде воздействия на материал, когда давление в УВ сравнимо с девиаторной частью напряжений. В используемой упругопластической модели величина девиаторов напряжений ограничена условием на цилиндре Мизеса, радиус которого по порядку величины равен пределу текучести Y, что может служить оценкой амплитуд ударных волн, где ударная адиабата пористого материала определяется прочностными эффектами в сплошной меди. Рассмотренный диапазон напряжений ударного сжатия имеет пластический характер. Получены стационарные ударные волны в пористой меди с использованием упругопластической модели вещества для SPH-частиц. Использовалось подвижное окно с вышеописанной методикой установления стационарного ударного фронта. Моделирование проводилось, начиная со скорости ударной волны us = –uin = 5 км/с. Выбор функции скорости выхода uout частиц из окна позволяет изменить темп перехода УВ на стационарный режим. В начальный период времени по среде должна пойти УВ большей амплитуды, чем ожидается в стационарном режиме, чтобы иметь и большую скорость распространения, чем скорость подачи вещества. Начальное значение скорости выхода uout для старта расчета (при t = 0) оценено из известных ударных адиабат для пористой меди. В частности, использовалась ударная адиабата меди с начальной плотностью ρ00 = = 6.3 г/см3. Плотность сплошной меди для используемого уравнения состояния ρ0 = 8.96 г/см3, что для пористости m = 1.35 составляет ρ00 ≈ ≈ 6.637 г/см3. Полагая линейной поправку на изменение массовой скорости up в УВ при малом изменении пористости для фиксированной скорости ударной волны us, можно положить up(ρ00 = = 6.637) ≈ 6.3/6.637up(ρ00 = 6.3). Полученные профили скорости и давления имеют осциллирующий характер за фронтом стационарной УВ (рис. 7), причем колебания находятся практически в противофазе, что объясняется адиабатическим изменением внутренней энергии волнами сжатия и разрежения, возникших после коллапса пор за фронтом УВ. Приход ударного фронта к поре приводит к высокой скорости схлопывания пор, что может вызвать кумулятивный эффект и ускорение струй вещества, которые тормозятся при ударе о внутреннюю поверхность поры, вызывая пики давления в профиле. Стоит отметить, что амплитуда колебаний затухает с расстоянием от фронта, и этому способствуют различные механизмы диссипации механической энергии в тепло: процессы многократного сжатия и разгрузки и схемные эффекты метода SPH. Ширина окна выбиралась достаточно большой, чтобы исключить воздействие выходного граничного условия на процесс затухания колебаний давления, и гарантирует установление стационарного режима распространения УВ.
ЗАКЛЮЧЕНИЕ
Мезоскопическое моделирование ударной волны в пористом материале позволяет наблюдать процессы прохождения волны и схлопывания пор, используя только свойства сплошного вещества. Получены стационарные УВ в пористой меди с использованием метода подвижного окна, в котором применяются два граничных условия: фиксированная скорость входа и адаптивная скорость выхода вещества из расчетной области. При этом алгоритм корректировки скорости выхода частиц из расчетной области работает таким образом, чтобы ударный фронт приобрел нулевую скорость в окне и установился в заданном положении расчетной области. Показано, что волновые профили УВ равных амплитуд совпадают при моделировании методами неподвижного поршня и подвижного окна. Полученные фронты стационарных ударных волн имеют осциллирующий характер, что наблюдается при больших скоростях распространения УВ. Представленные ударные адиабаты хорошо согласуются с экспериментальными данными, что позволяет получать ударные адиабаты пористых материалов, для которых нет экспериментальных данных по их ударному нагружению.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-19-00697).
Список литературы
Медин С.А., Паршиков А.Н. Мезомеханическое моделирование ударного сжатия пористого алюминия // Матем. моделирование. 2014. Т. 26. № 1. С. 42.
Mader C.L., Kershner J.D. The Three-dimenional Hydrodynamic Hotspot Model. Tech. Rep. Los Alamos National Laboratory, Los Alamos, NM, USA, 1981. LA-UR-85-742.
Zhao F.P., Wu H., Luo S.-N. Microstructure Effects on Shock Response of Cu Nanofoams // J. Appl. Phys. 2013. V. 114. P. 073501.
Mi X., Michael L., Nikiforakis N., Higgins A.J. Meso-resolved Simulations of Shock-to-detonation Transition in Nitromethane with Air-filled Cavities // J. Appl. Phys. 2019. V. 125. P. 245901.
Lastiwka M., Basa M., Quinlan N.J. Permeable and Non-reflecting Boundary Conditions in SPH // Int. J. Numer. Meth. Fluids. 2009. V. 61. Iss. 7. P. 709.
Federico I., Marrone S., Colagrossi A., Aristodemo F., Antuono M. Simulating 2D Open-channel Flows Through an SPH Model // Europ. J. Mech., B: Fluids. 2012. V. 34. P. 35.
Sun P.-N., Colagrossi A., Zhang A. Numerical Simulation of the Self-propulsive Motion of a Fishlike Swimming Foil Using the δ+-SPH Model // Theor. Appl. Mech. Lett. 2018. V. 8. Iss. 2. P. 115.
Alvarado-Rodriguez C., Klapp J., Sigalotti L., Dominguez J., Sanchez E. Nonreflecting Outlet Boundary Conditions for Incompressible Flows Using SPH // Comp. Fluids. 2017. V. 159. P. 177.
Ferrand M., Joly A., Kassiotis C., Violeau D., Leroy A., Morel F.-X., Rogers B.D. Unsteady Open Boundaries for SPH Using Semi-analytical Conditions and Riemann Solver in 2D // Comput. Phys. Commun. 2016. V. 210. P. 29.
Ferrand M., Laurence D.R., Rogers B.D., Violeau D., Kassiotis C. Unified Semi-analytical Wall Boundary Conditions for Inviscid, Laminar or Turbulent Flows in the Meshless SPH Method // Int. J. Numer. Meth. Fluids. 2012. V. 71. Iss. 4. P. 446.
Hirschler M., Kunz P., Huber M., Hahn F., Nieken U. Open Boundary Conditions for ISPH and Their Application to Micro-flow // J. Comput. Phys. 2016. V. 307. P. 614.
Kunz P., Hirschler M., Huber M., Nieken U. Inflow/Outflow with Dirichlet Boundary Conditions for Pressure in ISPH // J. Comp. Phys. 2016. V. 326. P. 171.
Monteleone A., Monteforte M., Napoli E. Inflow/Outflow Pressure Boundary Conditions for Smoothed Particle Hydrodynamics Simulations of Incompressible Flows // Comput. Fluids. 2017. V. 159. P. 9.
Zhakhovskii V.V., Zybin S.V., Nishihara K., Anisimov S.I. Shock Wave Structure in Lennard-Jones Crystal via Molecular Dynamics // Phys. Rev. Lett. 1999. V. 83. P. 1175.
Egorova M.S., Dyachkov S.A., Parshikov A.N., Zhakhovsky V.V. SPH Modeling Using Dynamic Domain Decomposition and Load Balancing Displacement of Voronoi Subdomains // Comput. Phys. Commun. 2019. V. 234. P. 112.
Parshikov A.N., Medin S.A. Smoothed Particle Hydrodynamics Using Interparticle Contact Algorithms // J. Comput. Phys. 2002. V. 180. P. 358.
Медин С.А., Паршиков А.Н. Развитие метода SPH и его применение в задачах гидродинамики конденсированных сред // ТВТ. 2010. Т. 48. № 6. С. 973.
Олдер Б., Фернбах С., Ротенберг М. Вычислительные методы в гидродинамике / Под ред. Ротенберга М. М.: Мир, 1967. 385 с.
Dyachkov S.A., Parshikov A.N., Zhakhovsky V.V. SPH Simulation of Boron Carbide Under Shock Compression with Different Failure Models // J. Phys.: Conf. Ser. 2017. V. 815. P. 012012.
Takeda H., Miyama S.M., Sekiya M. Numerical Simulation of Viscous Flow by Smoothed Particle Hydrodynamics // Prog. Theor. Phys. 1994. V. 92. № 5. P. 939.
Marsh S.P. LASL Shock Hugoniot Data. Los Alamos, NM, USA: Los Alamos National Laboratory, 1980. 658 p.
Murzov S.A., Dyachkov S.A., Egorova M.S., Parshikov A.N., Zhakhovsky V.V. Multiscale Smoothed Particle Hydrodynamics Simulation of Detonation Initiation // J. Phys. Conf. Ser. 2019. V. 1147. P. 012041.
Трунин Р.Ф., Медведев А.Б., Фунтиков А.И., Подурец М.А., Симаков Г.В., Севастьянов А.Г. Ударное сжатие пористых железа, меди и вольфрама и их уравнение состояния в области терапаскальных давлений // ЖЭТФ. 1989. Т. 95. № 2. С. 631.
Wilkinson S.D., Braithwaite M., Nikiforakis N., Michael L. A Complete Equation of State for Non-ideal Condensed Phase Explosives // J. Appl. Phys. 2017. V. 122. P. 225112.
Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. Практ. пособ. М.: Физматлит, 2008. 656 с.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур