Теплоэнергетика, 2022, № 8, стр. 39-49

ВЫВОД УРАВНЕНИЙ

Рассматривается стационарное течение несжимаемой среды – жидкого металла. Течение и теплообмен можно описать следующей системой дифференциальных уравнений сохранения в векторном виде:

где ρ, p, μ, λ и ${{c}_{p}}$ ‒ плотность, давление, динамический коэффициент вязкости, теплопроводность и теплоемкость среды (в данном случае жидкого металла); f ‒ вектор массовых сил (в данной задаче сила плавучести).

В уравнении (3) не учитывается вязкая диссипация. В уравнениях (1)‒(3) дифференцирование по координатам представляется как оператор $\nabla ,$ дивергенция вектора скорости V ‒ как скалярное произведение $\nabla \cdot {\mathbf{V}},$ градиент скалярного поля температуры – как $\nabla T.$ Очевидно, что для сплошной среды векторная запись уравнений является наиболее общей и справедлива в любой системе координат.

Задачу течения в прямой трубе удобнее всего решать в цилиндрической системе в координатах (r₀, φ₀, z₀). В ЦСК базис e_0i (i = 1, 2, 3) является ортогональным, поэтому систему уравнений, используя коэффициенты Ламе, можно записать в хорошо известном тензорном виде [14]. В кольцевой системе базис тоже ортогональный, координаты также выражаются тройкой чисел (r, φ, z), но длина базисного вектора ${{{\mathbf{e}}}_{z}}$ зависит от координат (r, φ), что обусловливает кривизну продольных координатных линий. Модуль базисного вектора рассчитывается по формуле

где R ‒ радиус кольцевой закрутки трубы (см. рис. 1).

Для сокращения записи формул вводится следующий параметр:

Для дальнейшего изложения следует ввести некоторые понятия из векторного анализа [6, 7]:

прямой и обратный базисы; обратный базис eⁱ находится через прямой e_i: ${{{\mathbf{e}}}^{i}} = {{\left( {{{{\mathbf{e}}}_{j}} \cdot {{{\mathbf{e}}}_{k}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\mathbf{e}}}_{j}} \cdot {{{\mathbf{e}}}_{k}}} \right)} {\left[ {{{{\mathbf{e}}}_{i}} \cdot \left( {{{{\mathbf{e}}}_{j}} \cdot {{{\mathbf{e}}}_{k}}} \right)} \right]}}} \right. \kern-0em} {\left[ {{{{\mathbf{e}}}_{i}} \cdot \left( {{{{\mathbf{e}}}_{j}} \cdot {{{\mathbf{e}}}_{k}}} \right)} \right]}},$ где индексы (i, j, k) в результате циклической перестановки принимают значения (1, 2, 3);

ковариантные и контравариантные компоненты [6] соответствуют верхним и нижним индексам соответственно, так что ковариантный базис – это e_i, а контравариантный, обратный ему, – eⁱ; вектор r раскладывается по координатам прямого и обратного базисов: ${\mathbf{r}} = {{x}^{i}}{{{\mathbf{e}}}_{i}} = {{x}_{i}}{{{\mathbf{e}}}^{i}},$ xⁱ = (r, φ, z).

Свойства системы координат представляются как скалярное произведение базисных векторов и выражаются метрическим тензором g_ij. Для ковариантного базиса в винтовой системе координат

Определитель матрицы метрического тензора имеет вид

Тензор g_ij превращается в метрический тензор для ЦСК, если R устремить к бесконечности (соответственно A устремится к единице).

Для обратного (контравариантного) метрического тензора справедливы формулы:

Скалярное произведение векторов прямого и обратного базисов по определению равно единичному (шаровому) тензору: $g_{j}^{i} = ({{{\mathbf{e}}}^{i}} \cdot {{{\mathbf{e}}}_{j}}) = {{\delta }_{{ij}}}$ (0 при $i \ne j$ и 1 при $i = j$).

Обычно рассматривают контравариантные компоненты вектора скорости как результат разложения по векторам прямого базиса: V = V  ⁱeⁱ, V = (V ^r, V ^φ, V ^z).

На практике используются “физические” компоненты вектора V = V*ⁱ, которые имеют одинаковую размерность ‒ метр в секунду: V = (V*^r, V*^φ, V*^z) [2]. Связь с “физическими” компонентами осуществляется через диагональные члены метрического тензора g_ij (по $i$ не суммировать!):

Частная производная вектора по координате в криволинейном базисе выражается следующей формулой:

После разложения производной вектора по контравариантным компонентам получается следующий тензор:

Здесь введены символы Кристоффеля второго порядка [6, 7], которые определяют разложение производной базисного вектора по базису:

Символы Кристоффеля $\Gamma _{{jk}}^{i}$ можно рассчитать по формулам [6]:

В КСК символы Кристоффеля имеют следующий вид:

Уравнения сохранения (1)–(3) в тензорном виде [6]:

Член в уравнении (2), связанный с вязкостью $\nabla \cdot \mu \nabla {\mathbf{V}},$ определяется через тензор производных от компонент вектора скорости $V_{{,k}}^{i},$ если взять ковариантную производную от тензора по правилу, заимствованному из [6]:

Контравариантные компоненты объемных сил находятся согласно соотношениям ${{f}^{i}} = {\mathbf{f}}{{{\text{e}}}^{j}}.$

Далее рассматривается преобразование системы уравнений (9)–(11) в КСК. Для “физических” компонент вектора скорости V = (V*^r, V*^φ, V*^z) нужно будет учесть представление (6). Далее в формулах слагаемых индекс “*” будет опущен. В уравнениях можно выделить два вида членов: слагаемые, не связанные с закруткой потока, такие же, как и в ЦСК, и добавочные слагаемые, в которые входит радиус закрутки R или параметр А. Уравнение неразрывности (9) по виду остается точно таким же, как и в ЦСК, с добавлением слагаемого:

В левой конвективной части трех уравнений для проекций импульса (10) появятся следующие члены:

при $i = 1$

при $i = 2$

при $i = 3$

В этих выражениях первые слагаемые связаны с изменением модуля базисного вектора ${{{\mathbf{e}}}_{z}},$ а вторые представляют собой добавочные компоненты инерционных сил, возникающие в кольцевой системе координат, ‒ компоненты центробежной и кориолисовой сил.

Для градиента давления добавочный член в правой части уравнения (10) имеет вид при $i = 1$

В уравнении сохранения энергии (11) в левой конвективной части добавится только одно слагаемое

Дополнения (14)–(18) вносят наиболее существенный вклад в уравнения (9)‒(11).

Далее приводятся добавочные члены в уравнениях движения (10) в КСК для компонент силы вязкости $\mu {{g}^{{km}}}{{\left( {V_{{,m}}^{i}} \right)}_{{,k}}}$ (коэффициент μ внесен под знак производной для последующего перехода к осредненным уравнениям с вводом коэффициента турбулентной вязкости – уравнениям Рейнольдса):

при $i = 1$

при $i = 2$

при $i = 3$

В уравнении сохранения энергии (11) справа появляются новые слагаемые

При учете турбулентности с использованием двухпараметрической модели, например k‒ε [15], в кольцевой системе координат также появятся дополнительные слагаемые, которыми нужно дополнить уравнения в ЦСК. Поскольку уравнения сохранения для скалярных величин k и ε похожи на уравнения сохранения энергии (энтальпии) (11), то и добавочные члены можно записать в виде, аналогичном (18) и (22). Таким образом, в левой конвективной части уравнений для f = {k, ε} добавится только по одному слагаемому

а в правых частях уравнений появятся новые слагаемые

Дополнительными слагаемыми, входящими в члены и связанными с генерацией или порождением турбулентности, предлагается пренебречь: они составляют не более 1/R².

ЧИСЛЕННЫЙ РАСЧЕТ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

В этом разделе в качестве примера представлены результаты численного решения поставленной задачи в КСК. Радиусы поворота трубы выбраны достаточно большими R = {5d, 10d, 20d, 40d, 80d}, где d ‒ внутренний радиус трубы, толщина стенки δ = 0.0025d.

Уравнения (9)–(11) приводились к безразмерному виду и для осредненных переменных имели вид:

уравнение движения

уравнение энергии

Здесь p* ‒ динамическое давление, отнесенное к масштабу $\rho V_{0}^{2};$ ${{V}_{0}}$ ‒ средняя по сечению канала скорость теплоносителя; $\operatorname{Re} = {{{{V}_{0}}d} \mathord{\left/ {\vphantom {{{{V}_{0}}d} \nu }} \right. \kern-0em} \nu }$ ‒ число Рейнольдса; $\nu $ ‒ кинематический коэффициент вязкости; Gr_q = g βq_сd⁴/(λν²) ‒ число Грасгофа; g – ускорение свободного падения; β ‒ коэффициент термического расширения; Pr = µρc_p/λ ‒ число Прандтля; Pr_t = ε_t/ε_q ‒ турбулентное число Прандтля; ε_t ‒ коэффициент турбулентной вязкости; ε_q ‒ коэффициент турбулентного переноса тепла; $\Theta = {{\left( {T - {{T}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {T - {{T}_{0}}} \right)} {\left( {{{{{q}_{{\text{c}}}}d} \mathord{\left/ {\vphantom {{{{q}_{{\text{c}}}}d} \lambda }} \right. \kern-0em} \lambda }} \right)}}} \right. \kern-0em} {\left( {{{{{q}_{{\text{c}}}}d} \mathord{\left/ {\vphantom {{{{q}_{{\text{c}}}}d} \lambda }} \right. \kern-0em} \lambda }} \right)}}$ ‒ безразмерная разность температур; g* = g/g ‒ безразмерный вектор ускорения свободного падения; T ‒ температура жидкости; T₀ ‒ температура на входе в трубу.

Масштаб для координат r и z принимался равным внутреннему диаметру трубы d = 2r₀. Компоненты вектора скорости V относились к V₀. На входе в трубу профиль скорости считался единичным: |V| = 1. На выходе из канала обеспечивалось условие постоянства расхода. Тепловой поток на внутренней стороне стенки в безразмерном виде задавался выражением $q_{{\text{с}}}^{ * } = {1 \mathord{\left/ {\vphantom {1 {\operatorname{Pe} {{{({{\partial \Theta } \mathord{\left/ {\vphantom {{\partial \Theta } {\partial R}}} \right. \kern-0em} {\partial R}})}}_{{\text{с}}}}}}} \right. \kern-0em} {\operatorname{Pe} {{{({{\partial \Theta } \mathord{\left/ {\vphantom {{\partial \Theta } {\partial R}}} \right. \kern-0em} {\partial R}})}}_{{\text{с}}}}}} = - {1 \mathord{\left/ {\vphantom {1 {\operatorname{Pe} }}} \right. \kern-0em} {\operatorname{Pe} }}$ (Pe ‒ число Пекле). Участку обогрева 50d предшествовал участок гидродинамической стабилизации 20d. Турбулентное число Прандтля принималось равным Pr_t = 1. Уравнения (23) и (24) записаны с учетом упрощений и допущений, справедливых как для ртути, так и для других жидких металлов.

При численном решении задачи расчетная сетка имела размеры ${{N}_{r}} \times {{N}_{\varphi }} \times {{N}_{z}} = 50 \times 50 \times 450$ и вблизи стенок сгущалась (N_i – число ячеек по соответствующей координате).

Система уравнений (23), (24) с учетом уравнения неразрывности (1) решалась в пакете численного моделирования процессов гидродинамики и тепломассообмена ANES20XE [15]. Коэффициент турбулентной вязкости ${{\varepsilon }_{t}}$ вводился разными способами: алгебраическим ‒ ε_t рассчитывался по формулам Рейхардта [7], либо двумя уравнениями для k‒ε-модели с пристенными функциями [15]. Первый упрощенный способ для моделирования турбулентности оправдал себя при численных расчетах течения жидкого металла (ртути) в прямых трубах и каналах некруглого сечения [16, 17]. Следует отметить, что результаты расчетов с использованием разных способов учета турбулентности различаются незначительно. Далее приведены некоторые результаты расчетов, в которых применялась k‒ε-модель.

В серии расчетов кроме турбулентности учитывалось также влияние сил плавучести, возникающих при свободной конвекции. Вектор силы плавучести в уравнениях (10) определяется компонентами $\left( { - \sin \varphi \frac{{{{{\operatorname{Gr} }}_{q}}}}{{{{{\operatorname{Re} }}^{2}}}}\Theta ,\,\, - \cos \varphi \frac{{{{{\operatorname{Gr} }}_{q}}}}{{{{{\operatorname{Re} }}^{2}}}}\Theta ,\,\,0} \right).$ В расчете принималось, что ${{\operatorname{Gr} }_{q}} = \{ 0,1,2,4\} \times {{10}^{8}}.$ Поля безразмерной разности температур Θ были пересчитаны относительно среднемассовой температуры $\bar {T}$ в данном сечении:

Как уже упоминалось ранее, представленная методика расчета на основе системы дифференциальных уравнений в ЦСК путем добавления дополнительных слагаемых, возникающих в новой криволинейной системе координат, проверена на другой подобной задаче винтовой формы в ВСК в [13]. Правильность формул для добавочных слагаемых в настоящей задаче, решаемой в КСК, может быть подтверждена следующими рассуждениями. Авторами экспериментально и численно была решена задача течения и теплоотдачи в горизонтальной прямой трубе с однородным обогревом (q_c = const) с учетом термогравитационной конвекции [16]. В результате воздействия сил плавучести возникали вторичные течения в виде двух симметричных продольных вихрей. Численный расчет проводился в ЦСК с использованием аналогичных (23)‒(24) уравнений и граничных условий применяемых моделей турбулентности.

Совпадение результатов расчета с опытными данными, полученными для течения ртути в трубе в идентичных расчету условиях, очень хорошее. В изогнутой трубе в КСК добавляются инерционные силы и приводят к тому же результату, что и действие термогравитационной конвекции: появлению вторичных продольных вихревых структур. Таким образом, центробежная сила по характеру действия на гидродинамику подобна действию гравитации в неизотермическом потоке. Поэтому результаты расчетов для КСК, представленные далее, вполне правдоподобны как качественно, так и количественно (по порядку величины).

Что касается сложности и громоздкости формул добавочных слагаемых для диффузионных членов, то их вклад существенен в очень “кривых” трубах, где R близок к d. На практике труб с такой кривизной не встречается. Когда R ≈ (5‒10)d и выше, вклад большинства этих слагаемых оказывается малым (кратен 1/R) или ничтожно малым. В частности, V  ^r и V  ^φ много меньше V  ^z, слагаемые с ${\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}}$ заметны только на начальном термическом участке, который для турбулентных течений не превышает 15d. А вот вклад дополнительных инерционных сил и градиента давления здесь определяющий.

На рис. 2 показаны результаты, полученные для сечения трубы, удаленного от входа на 30d. Полагается, что труба закручена в змеевик с минимально возможным шагом. Понятно, что в змеевике, строго говоря, базис не ортогональный. Однако если шаг змеевика мал по сравнению с радиусом закрутки, приближенно можно рассматривать задачу как течение в незамкнутой кольцевой трубе. Учитываемые дополнительные слагаемые вводились в расчет системы дифференциальных уравнений в виде функций источниковых членов.

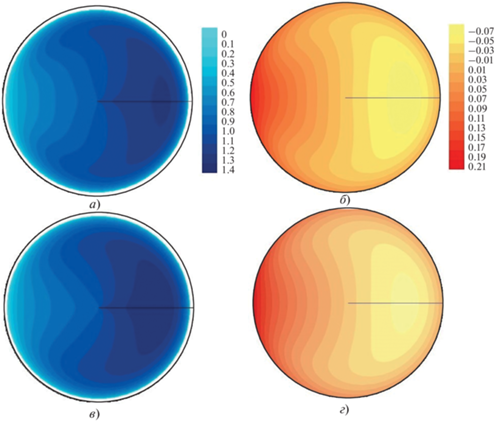
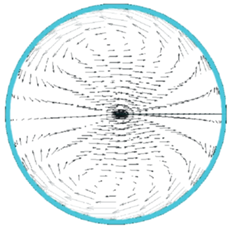
Изотахи и изотермы на рис. 2 в сечении трубы, удаленном от входа в зону обогрева на расстояние $z = 30d,$ показывают, что симметрия течения сильно нарушается как для R = 5d, так и для R = 10d. Причина заключается в воздействии центробежной силы, которая проявляется в плоскости закрутки и прижимает поток к периферийной стороне кольцевой трубы. При этом, как показано на рис. 3, в плоскости трубы возникают вторичные течения.

При наложении термогравитационной (свободной) конвекции картина полей скорости и температуры еще более усложняется (рис. 4), симметрия в горизонтальной плоскости при этом нарушается. Кольцевой поворот лежит в горизонтальной плоскости: добавляются силы плавучести, которые на основное течение накладывают еще два вторичных вихря, лежащих в поперечном сечении трубы. Поэтому минимумы и максимумы скорости и температуры смещаются по часовой стрелке.

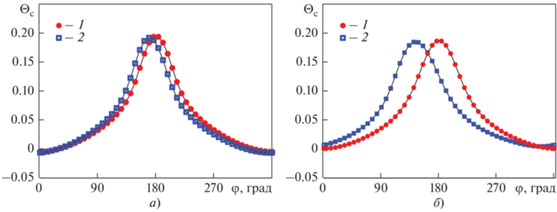
Распределение температуры стенки Θ_c = = ${{\left( {{{T}_{{\text{с}}}} - \overline T } \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{{\text{с}}}} - \overline T } \right)} {\left( {{{{{q}_{{\text{c}}}}d} \mathord{\left/ {\vphantom {{{{q}_{{\text{c}}}}d} \lambda }} \right. \kern-0em} \lambda }} \right)}}} \right. \kern-0em} {\left( {{{{{q}_{{\text{c}}}}d} \mathord{\left/ {\vphantom {{{{q}_{{\text{c}}}}d} \lambda }} \right. \kern-0em} \lambda }} \right)}}$ при кольцевой закрутке потока (в отсутствие сил плавучести) становится неоднородным с появлением локальных минимума и максимума при φ = 0 и φ = 180° соответственно (рис. 5, а). Наличие термогравитационной конвекции ($\,{{\operatorname{Gr} }_{q}} = 2 \times {{10}^{8}}$) приводит к смещению минимума и максимума к нижней (φ = 270°) и верхней (φ = 90°) образующим трубы (рис. 5, б).

Расчет кольцевых каналов разной формы требует изменения только одного параметра ‒ радиуса поворота R, что позволяет на одной и той же сетке получить целое семейство решений. Графики на рис. 6 иллюстрируют, как уменьшается эффект закрутки с увеличением радиуса поворота R.

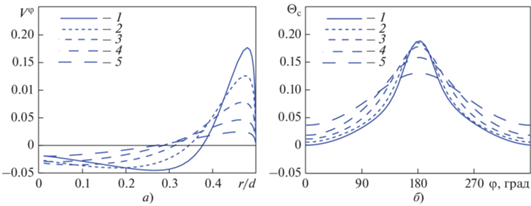
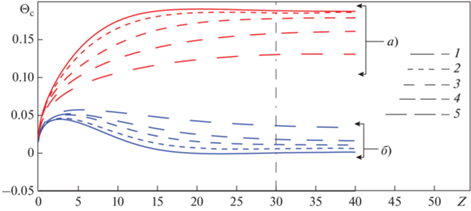
Распределения безразмерной разности температур Θ_с при φ = 0 и φ = 180° для разных радиусов закрутки показаны на рис. 7. Эти данные позволяют судить о длине начального термического участка, где происходит перестройка профилей скорости и температуры, и участке стабилизации. На рис. 7 вертикальной штрихпунктирной линией отмечено сечение $z = 30d,$ в котором построены поля – распределения скорости и температуры в сечении трубы, представленные на рис. 2‒6.

Таким образом, теплоотдача в закрученных трубах, усложненная воздействием смешанной турбулентной конвекции, определяется не средними значениями коэффициентов теплоотдачи (числами Нуссельта), а локальными. Поэтому рассматривать надо в первую очередь максимальную и минимальную температуры стенки в поперечном сечении трубы (рис. 8).

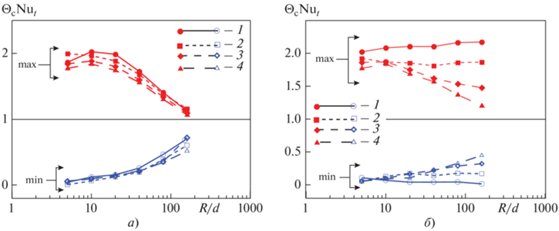
На рис. 8 показаны максимальные и минимальные значения относительной разности температур стенки и среднемассовой в безразмерном виде ${{\Theta }_{{\text{с}}}}$ Nu_t в зависимости от безразмерного радиуса поворота ${R \mathord{\left/ {\vphantom {R d}} \right. \kern-0em} d}.$ Фактически ${{\Theta }_{{\text{c}}}}{\text{N}}{{{\text{u}}}_{t}} = {{\left( {{{T}_{{\text{с}}}} - \overline T } \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{{\text{с}}}} - \overline T } \right)} {\left( {{{T}_{{{\text{с,}}t}}} - \overline T } \right)}}} \right. \kern-0em} {\left( {{{T}_{{{\text{с,}}t}}} - \overline T } \right)}},$ где Nu_t определяется по зависимости Лайона [18], соответствующей теплоотдаче для стабилизированного турбулентного теплообмена в трубе:

Как видно на рис. 8, а, при увеличении R максимальные и минимальные значения безразмерной температуры стенки асимптотически приближаются к единице, а максимальной разницы достигают в диапазоне R/d от 5 до 20. При этом максимальное значение безразмерного комплекса составляет примерно 2.0. Это означает, что максимальная разность температуры стенки и среднемассовой примерно в 2 раза превышает среднее по периметру трубы значение, а минимальная приближается к нулю, т.е. равна среднемассовой. Наблюдается расслоение точек по числам Рейнольдса, но оно незначительно. При наложении свободной конвекции картина усложняется (см. рис. 8, б). Разности между максимальным и минимальным значениями безразмерной температуры при Re = 10 000 и увеличении R сохраняются на уровне 2.0, т.е. разность температур при наложении двух факторов: закрутки потока и наличия свободной конвекции ‒ по-прежнему не превышает 2.0, но при больших R уже определяется только силами плавучести.

В несколько ином виде результаты, показанные на рис. 8, представлены на рис. 9. Здесь даны максимальные и минимальные значения ${{\Theta }_{{\text{с}}}}$ в зависимости от числа Пекле (или Рейнольдса) в сопоставлении с функцией обратного числа Нуссельта 1/Nu_t, определенного по формуле Лайона.

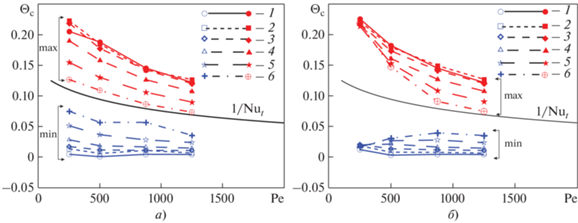
На рис. 9, а видно, что максимальное и минимальное значения ${{\Theta }_{{\text{с}}}}$ асимптотически приближаются к 1/Nu_t при увеличении как радиуса поворота, так и числа Пекле. Вид аналогичных кривых при наличии свободной конвекции несколько отличается (см. рис. 9, б) от такового на рис. 9, а.

Следует отметить еще раз, что наличие поворота трубы приводит к появлению горячего пятна, где температура стенки значительно выше средней по сечению и выше значений, рассчитанных для прямой трубы. А наблюдаемая неоднородность в распределении температуры стенки ‒ следствие как закрутки потока, так и влияния свободной конвекции ‒ является важным фактором, влияющим на теплообмен в трубах. Этот фактор требуется учитывать как в теплогидравлических, так и в прочностных расчетах. Появление дополнительных напряжений, гидравлических вместе с термическими, может привести к деформации и усталостному разрушению термонагруженных стенок труб, используемых в теплообменных устройствах.

ВЫВОДЫ

1. Система дифференциальных уравнений, записанная в тензорном виде для криволинейной системы координат, позволила определить все члены, необходимые для расчета характеристик гидродинамики и теплообмена в жидкометаллической среде: давление, компоненты вектора скорости и температуры.

2. Преимущество предложенной методики заключается в простоте описания геометрической формы расчетной области, поскольку появляется возможность использовать структурированную расчетную сетку, упрощается задание граничных условий – границы расчетной области проходят по координатным поверхностям. Изменение формы расчетной области определяется только одним параметром – радиусом кольцевой закрутки трубы. При этом вид выводимых результатов расчетов становится более удобным для анализа и последующей обработки. Для учета турбулентности можно применить разные модели: алгебраические, хорошо зарекомендовавшие себя в прямых каналах с жидкометаллической средой, или параметрические с двумя и более уравнениями. Все это позволяет существенно экономить вычислительные ресурсы, сокращает время расчета и способствует получению более точных результатов.

3. В данной методике за основу берется система дифференциальных уравнений в цилиндрической системе координат и дополняется членами, которые отражают закрутку продольной оси трубы в кольцевой системе координат. Основным параметром является радиус закрутки трубы. При этом геометрическая форма пространства расчетной области при переходе к кольцевой системе координат остается такой же, как и для цилиндрической системы координат.

4. Выполненные с применением предлагаемой методики параметрические расчеты показывают принципиальные границы совместного влияния радиуса кольцевой закрутки и смешанной конвекции при течении жидкого металла.