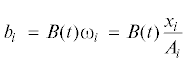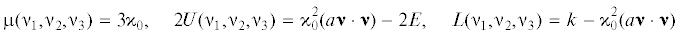Прикладная математика и механика, 2023, T. 87, № 6, стр. 901-914

Кинематическое истолкование движения твердого тела в новом решении уравнений Гриоли

Г. В. Горр^1, *

¹ Математический институт им. В.А. Стеклова РАН
Москва, Россия

Поступила в редакцию 25.05.2023
После доработки 23.08.2023
Принята к публикации 25.09.2023

EDN: HWKSFN
DOI: 10.31857/S0032823523060048

Аннотация

В статье получено новое решение уравнений Гриоли задачи о движении твердого тела, имеющего неподвижную точку, под действием потенциальных и гироскопических сил. С использованием модифицированного метода Пуансо, предложенного автором статьи, показано, что движение тела в построенном решении представляется качением без скольжения эллипсоида инерции тела по неподвижной в пространстве плоскости. Данный результат можно отнести к аналогу результата Пуансо, полученному в истолковании движения тела в решении Эйлера.

Ключевые слова: решение уравнений Гриоли, кинематическое истолкование, модифицированный метод Пуансо

1. Введение. В динамике твердого тела, имеющего неподвижную точку, большое значение имеют геометрические исследования свойств движения тела. Известным примером истолкования движения тела в задаче о движении тяжелого твердого тела является результат Л. Пуансо [1], который доказал, что движение тела в классическом решении Л. Эйлера можно представить качением без скольжения эллипсоида инерции тела по неподвижной в пространстве плоскости. Большой вклад в исследование движения тяжелого твердого тела внесли Д. Сильвестр [2], который интерпретировал движение тела качением центральной поверхности второго порядка по одной из ее касательных плоскостей, неподвижной в пространстве; Д. Мак-Куллаг [3], изучавший движение гирационного эллипсоида в решении Эйлера, и другие [4–9]. Обзор классических результатов, полученных в кинематическом истолковании движения тела, имеющего неподвижную точку, представлен в учебнике по теоретической механике [10], в монографиях [11, 12], в которых особое внимание уделено уравнениям П.В. Харла-мова [13], описывающим уравнения неподвижного годографа вектора угловой скорости. Благодаря применению этих уравнений получено геометрическое истолкование движения тела во многих решениях уравнений Эйлера–Пуассона и их обобщений на случай, когда учитываются движения несомых тел (систем, называемых гиростатом). В статье [9] Н.Е. Жуковский отмечал большое значение геометрического истолкования в теоретической механике. В статье [14] предложен модифицированный метод Пуансо, который основан на рассмотрении свойств вектора, который коллинеарен вектору угловой скорости. Показано [15], что в одном из решений [16], полученном в задаче о движении твердого тела в потенциальном силовом поле, движение тела представляется качением без скольжения эллипсоида инерции тела по неподвижной в пространстве плоскости.

Данная статья посвящена изучению уравнений Гриоли [17], которые являются наиболее общими уравнениями движения тела под действием потенциальных и гироскопических сил, допускающими три первых интеграла. Частный вариант этих уравнений в другой постановке рассматривал Х.М. Яхья [18, 19]. В статье [20] показана эквивалентность уравнений Д. Гриоли и Х.М. Яхьи. Для доказательства данного утверждения применялся метод инвариантных соотношений (ИС) построения частных решений уравнений динамики твердого тела [21]. При этом рассматривались три линейных ИС для компонент момента количества движения и применялись методы решения обратных задач механики и метод ИС [22], который имеет отличие от метода [21]. Следует отметить и уравнения М.П. Харламова [23], полученные в исследовании движений механических систем под действием гироскопических сил. Они также являются частной формой уравнений Гриоли.

В данной статье рассмотрены три линейных ИС по компонентам момента количества движения тела, правые части которых зависят от компонент единичного вектора оси симметрии силовых полей. Используя метод решения обратных задач, находится потенциальная функция и функция, характеризующая гироскопические силы. Третья функция, входящая в правые части уравнений Гриоли, не содержится в первых интегралах данных уравнений и она равна дивергенции вектора момента количества движения. Далее полагается, что конец вспомогательного вектора, введенного в модифицированном методе Пуансо [14], принадлежит эллипсоиду инерции тела в неподвижной точке, а градиент к эллипсоиду ортогонален неподвижной в пространстве плоскости. Это требование на структуру заданных ИС дает возможность выразить компоненты вектора момента количества движения через линейные функции от первой и второй компонент вектора оси симметрии силовых полей и произвольную дифференцируемую функцию от третьей компоненты указанного вектора. Таким образом, в статье найдено новое решение уравнений Гриоли и установлено, что движение можно представить качением без скольжения эллипсоида инерции по неподвижной в пространстве плоскости. Полученный в статье результат дополняет исследования [15, 24, 25], увеличивая число случаев в динамике твердого тела, которые являются аналогом истолкования Пуансо [14].

2. Постановка задачи. Рассмотрим задачу о движении твердого тела, имеющего неподвижную точку, под действием потенциальных и гироскопических сил, которая описывается дифференциальными уравнениями Гриоли [17]:

(2.1)

${\mathbf{\dot {x}}} = {\mathbf{x}} \times a{\mathbf{x}} + \mu {\text{(}}{{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}{\text{)(}}{\mathbf{\nu }} \times a{\mathbf{x}}{\text{)}} + \frac{{\partial L{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}}}{{\partial {\mathbf{\nu }}}} \times a{\mathbf{x}} + \frac{{\partial U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})}}{{\partial {\mathbf{\nu }}}} \times {\mathbf{\nu }}$

(2.2)

${\mathbf{\dot {\nu }}} = {\text{(}}{\mathbf{\nu }} \times a{\mathbf{x}}{\text{)}}$

В уравнениях (2.1), (2.2) введены обозначения: ${\mathbf{x}} = (x_{1}^{{}},x_{2}^{{}},x_{3}^{{}})$ – вектор момента количества движения; ${\mathbf{\nu }} = (\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ – единичный вектор оси симметрии силовых полей; $a = \operatorname{diag} \left( {\frac{1}{{{{A}_{1}}}},\frac{1}{{{{A}_{2}}}},\frac{1}{{{{A}_{3}}}}} \right)$ (${{A}_{1}},{{A}_{2}},{{A}_{3}}$ – главные моменты инерции) – матрица гирационного тензора; $\mu {\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}$, $L{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}$, $U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}$ – дифференцируемые функции от $\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}$; $\frac{{\partial L{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}}}{{\partial {\mathbf{\nu }}}} = \overline {{\text{grad}}} \,L{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}$, $\frac{{\partial U{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}}}{{\partial {\mathbf{\nu }}}}$ = $\overline {\operatorname{grad} } \,U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$; точка над ${\mathbf{x}}$ и ${\mathbf{\nu }}$ обозначает относительную производную по времени $t$. Уравнения (2.1), (2.2) имеют первые интегралы

(2.3)

$a{\mathbf{x}} \cdot {\mathbf{x}} - 2U{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}} = {\text{2}}E,\quad {\mathbf{x}} \cdot {\mathbf{\nu }} + L{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}} = k;\quad {\mathbf{\nu }} \cdot {\mathbf{\nu }} = 1,$

где E и $k$ – произвольные постоянные.

В монографии [22] на основании применения метода решения обратной задачи механики исследованы условия существования инвариантных соотношений (ИС):

(2.4)

$x_{1}^{{}} = g_{1}^{{}}{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{),}}\quad x_{2}^{{}} = g_{2}^{{}}{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{),}}\quad x_{3}^{{}} = g_{3}^{{}}{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{),}}$

где $g_{i}^{{}}{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}$ ${\text{(}}i = \overline {1,3} {\text{)}}$ – дифференцируемые функции от $\nu _{i}^{{}}$ ${\text{(}}i = \overline {1,3} {\text{)}}$. Показано, что если функции $U{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}$, $L{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}$ находить из первых интегралов (2.3), то уравнения (2.1), (2.2) допускают ИС (2.4) при выполнении равенства

(2.5)

$\mu {\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}} = \frac{{\partial g_{1}^{{}}{\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}}}}{{\partial \nu _{1}^{{}}}} + \frac{{\partial g_{2}^{{}}{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}}}{{\partial \nu _{2}^{{}}}} + \frac{{\partial g_{3}^{{}}{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}}}{{\partial \nu _{3}^{{}}}}$

В данной статье применен модифицированный метод Пуансо, установленный в [14]. Согласно этому методу, вектору угловой скорости ${\mathbf{\omega }} = a{\mathbf{x}}$ сопоставим в соответствие вектор ${\mathbf{b}}{\text{(}}t{\text{)}}$:

(2.6)

${\mathbf{b}}{\text{(}}t{\text{)}} = B{\text{(}}t{\text{)}}{\mathbf{\omega }}{\text{(}}t{\text{)}}\quad \left( {B{\text{(}}t{\text{)}} \in {{C}^{1}}} \right)$

Введем главную подвижную систему координат $Oxyz$ с единичными векторами ${\mathbf{i}}_{1}^{{}},\,{\mathbf{i}}_{2}^{{}},\,{\mathbf{i}}_{3}^{{}}$. Неподвижную систему координат обозначим через $O\xi \eta \zeta $, а ее единичные векторы – через ${\mathbf{v}}_{1}^{{}}{\text{,}}{\mathbf{v}}_{2}^{{}},{\mathbf{v}}_{3}^{{}} = {\mathbf{\nu }}$.

Запишем ${\mathbf{b}}{\text{(}}t{\text{)}}$, ${\mathbf{\omega }}{\text{(}}t{\text{)}}$:

(2.7)

${\mathbf{b}}{\text{(}}t{\text{)}} = b_{1}^{{}}{\mathbf{i}}_{1}^{{}} + b_{2}^{{}}{\mathbf{i}}_{2}^{{}} + b_{3}^{{}}{\mathbf{i}}_{3}^{{}},\quad {\mathbf{\omega }}{\text{(}}t{\text{)}} = \frac{1}{{{{A}_{1}}}}x_{1}^{{}}{\mathbf{i}}_{1}^{{}} + \frac{1}{{{{A}_{2}}}}x_{2}^{{}}{\mathbf{i}}_{2}^{{}} + \frac{1}{{{{A}_{3}}}}x_{3}^{{}}{\mathbf{i}}_{3}^{{}}$

Эллипсоид инерции тела описывается уравнением

(2.8)

$\Phi (x,y,z) = {{A}_{1}}x_{{}}^{2} + {{A}_{2}}y_{{}}^{2} + {{A}_{3}}z_{{}}^{2} - \sigma _{0}^{2} = 0\quad \left( {\sigma _{0}^{2} = \operatorname{const} } \right)$

Касательная плоскость к поверхности (2.8) ортогональна вектору

(2.9)

$\overline {\operatorname{grad} } \,\Phi (x,y,z) = {{A}_{1}}x{\mathbf{i}}_{1}^{{}} + {{A}_{2}}y{\mathbf{i}}_{2}^{{}} + {{A}_{3}}z{\mathbf{i}}_{3}^{{}}$

Отметим, что в равенствах (2.7) $b_{i}^{{}}$, $x_{i}^{{}}$ ${\text{(}}i = \overline {1,3} {\text{)}}$ зависят от $t$.

Постановка задачи. Определить условия на функции (2.4), $B{\text{(}}t{\text{)}}$, при выполнении которых компоненты вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ удовлетворяют уравнениям

(2.10)

$A_{1}^{{}}b_{1}^{2} + A_{2}^{{}}b_{2}^{2} + A_{3}^{{}}b_{3}^{2} = \sigma _{0}^{2}{\kern 1pt} $

(2.11)

${\mathbf{b}}{\text{(}}t{\text{)}} \cdot {\mathbf{\nu }}{\text{(}}t{\text{)}} = {{k}_{0}}$

(2.12)

$\overline {{\text{grad}}} \,\Phi {\text{(}}b_{1}^{{}},b_{2}^{{}},b_{3}^{{}}{\text{)}} = {{A}_{1}}{{b}_{1}}{\mathbf{i}}_{1}^{{}} + {{A}_{2}}b_{2}^{{}}{\mathbf{i}}_{2}^{{}} + {{A}_{3}}b_{3}^{{}}{\mathbf{i}}_{2}^{{}} = \beta {\text{(}}t{\text{)}}{\mathbf{\nu }}$

Поясним механическую трактовку условий (2.10)–(2.12). Равенство (2.10) характеризует свойство того, что конец вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ принадлежит эллипсоиду инерции. Равенство (2.11) означает, что неподвижный годограф вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ является плоской кривой. Равенство (2.12) определяет свойство того, что касательная плоскость к эллипсоиду инерции при некоторых условиях на $\sigma _{0}^{{}}{\kern 1pt} $, $k_{0}^{{}}{\kern 1pt} $ и функцию $\beta {\text{(}}t{\text{)}}$ совпадает с плоскостью (2.11). Следовательно, ставится задача о нахождении решения уравнений (2.1), (2.2), для которого имеет место аналог истолкования движения тела, полученного Пуансо в решении Эйлера. В отличие от подхода Пуансо, при данном подходе концы вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ принадлежат эллипсоиду инерции, а в методе Л. Пуансо эллипсоиду инерции принадлежат концы вектора ${\mathbf{\omega }}{\text{(}}t{\text{)}}$.

Отметим, что для применения метода ИС [22] в интегрировании системы уравнений (2.1), (2.2) используется уравнение (2.2), которое в скалярной форме состоит из уравнений

(2.13)

$\dot {\nu }_{1}^{{}} = \omega _{3}^{{}}\nu _{2}^{{}} - \omega _{2}^{{}}\nu _{3}^{{}},\quad \dot {\nu }_{2}^{{}} = \omega _{1}^{{}}\nu _{3}^{{}} - \omega _{3}^{{}}\nu _{1}^{{}},\quad \dot {\nu }_{3}^{{}} = \omega _{2}^{{}}\nu _{1}^{{}} - \omega _{1}^{{}}\nu _{2}^{{}},$

где

(2.14)

$\omega _{i}^{{}} = \frac{1}{{{{A}_{i}}}}g_{i}^{{}}{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}$

3. Исследование уравнений (2.13). Введем углы Эйлера $\theta {\text{,}}\varphi {\text{,}}\psi $ [10]:

(3.1)

$\theta = \arccos \nu _{3}^{{}},\quad \varphi = {\text{arctg}}\frac{{\nu _{1}^{{}}}}{{\nu _{2}^{{}}}},\quad \dot {\psi } = \frac{{\omega _{1}^{{}}\nu _{1}^{{}} + \omega _{2}^{{}}\nu _{2}^{{}}}}{{1 - \nu _{3}^{2}}}$

Поскольку предполагается, что уравнения (2.1), (2.2) проинтегрированы, то по формулам (3.1) можно найти углы $\theta ,\varphi ,\psi $. Следовательно, подвижный базис ${\mathbf{i}}_{1}^{{}},\,{\mathbf{i}}_{2}^{{}},\,{\mathbf{i}}_{3}^{{}}$ в неподвижном базисе ${\mathbf{v}}_{1}^{{}},{\mathbf{v}}_{2}^{{}},{\mathbf{v}}_{3}^{{}}$ получим с помощью переменных $\theta ,\varphi ,\psi $. Рассмотрим уравнение (2.12), используя в силу (2.6) значения ${{b}_{i}}$:

(3.2)

и углы Эйлера $\theta ,\varphi ,\psi $ в матрице, определяющей связь между подвижной и неподвижной системами координат, получим

$\overline {{\text{grad}}} \,\Phi = B{\text{(}}t{\text{)}}(x_{1}^{{}}{\mathbf{i}}_{1}^{{}} + x_{2}^{{}}{\mathbf{i}}_{2}^{{}} + x_{3}^{{}}{\mathbf{i}}_{3}^{{}}) = $

$ = B{\text{(}}t{\text{)}}\left\{ {[{\text{(cos}}\varphi \cos \psi - \sin \varphi \sin \psi \cos \theta )x_{1}^{{}} - } \right.$

$ - \;(\sin \varphi \cos \psi + \cos \varphi \sin \psi \cos \theta )x_{2}^{{}} + x_{3}^{{}}\sin \psi \sin \theta ]{\mathbf{v}}_{1}^{{}} + $

$ + \;[(\cos \varphi \sin \psi + \sin \varphi \cos \psi \cos \theta )x_{1}^{{}} - (\sin \varphi \sin \psi - \cos \varphi \cos \psi \cos \theta )x_{2}^{{}} - $

(3.3)

$ - \;\left. {x_{3}^{{}}\cos \psi \sin \theta ]{\mathbf{v}}_{2}^{{}} + (x_{1}^{{}}\sin \varphi \sin \theta + x_{2}^{{}}\cos \varphi \sin \theta + x_{3}^{{}}\cos \theta ){\mathbf{\nu }}} \right\} = \beta {\text{(}}t{\text{)}}{\mathbf{\nu }}$

Равенство (3.3) выполняется, если имеют место соотношения

(3.4)

$x_{1}^{{}} = \frac{{\nu _{1}^{{}}x_{3}^{{}}}}{{\nu _{3}^{{}}}},\quad x_{2}^{{}} = \frac{{\nu _{2}^{{}}x_{3}^{{}}}}{{\nu _{3}^{{}}}},$

которые записаны с учетом выражений $\nu _{1}^{{}} = \sin \theta \sin \varphi $, $\nu _{2}^{{}} = \sin \theta \cos \varphi $, $\nu _{3}^{{}} = \cos \theta $. В качестве независимой функции $x_{3}^{{}}$ в формулах (2.4), (3.4) примем $x_{3}^{{}} = g{\text{(}}\nu _{3}^{{}})$, где $g{\text{(}}\nu _{3}^{{}})$ – дифференцируемая функция от $\nu _{3}^{{}}$. Тогда ИС (2.4) с учетом (3.4) запишем в виде

(3.5)

$x_{1}^{{}} = \frac{{\nu _{1}^{{}}g{\text{(}}\nu _{3}^{{}})}}{{\nu _{3}^{{}}}},\quad x_{2}^{{}} = \frac{{\nu _{2}^{{}}g{\text{(}}\nu _{3}^{{}})}}{{\nu _{3}^{{}}}},\quad x_{3}^{{}} = g{\text{(}}\nu _{3}^{{}})\quad \left( {{\mathbf{x}} = \frac{{g{\text{(}}{{\nu }_{3}})}}{{\nu _{3}^{{}}}}{\mathbf{\nu }}} \right)$

На основании (3.5) равенство (3.3) упрощается:

(3.6)

$\overline {{\text{grad}}} \,\Phi = \frac{{B{\text{(}}\nu _{3}^{{}})g{\text{(}}\nu _{3}^{{}})}}{{\nu _{3}^{{}}}}{\mathbf{\nu }}$

Таким образом, при записи (3.6) в качестве вспомогательной переменной выбрана переменная $\nu _{3}^{{}}$. Из (3.5), (3.6) следует значение функции $\beta {\text{(}}t{\text{)}}$:

$\beta {\text{(}}t{\text{)}} = \frac{{B{\text{(}}\nu _{3}^{{}}(t))g{\text{(}}\nu _{3}^{{}}(t))}}{{\nu _{3}^{{}}(t)}}$

Пусть γ – множество решений уравнений (2.13), в которых $\omega _{i}^{{}}$ в силу (2.14), (3.5) имеют вид

(3.7)

$\omega _{1}^{{}} = \frac{{\nu _{1}^{{}}g{\text{(}}\nu _{3}^{{}})}}{{A_{1}^{{}}\nu _{3}^{{}}}},\quad \omega _{2}^{{}} = \frac{{\nu _{2}^{{}}g{\text{(}}\nu _{3}^{{}})}}{{A_{2}^{{}}\nu _{3}^{{}}}},\quad \omega _{3}^{{}} = \frac{{g{\text{(}}\nu _{3}^{{}})}}{{A_{3}^{{}}}}$

Запишем уравнения (2.13), принимая во внимание равенства (3.7):

(3.8)

$\dot {\nu }_{1}^{{}} = \frac{{g{\text{(}}\nu _{3}^{{}})(A_{2}^{{}} - A_{3}^{{}})\nu _{2}^{{}}\nu _{3}^{{}}}}{{\nu _{3}^{{}}A_{2}^{{}}A_{3}^{{}}}},\quad \dot {\nu }_{2}^{{}} = \frac{{g{\text{(}}\nu _{3}^{{}})(A_{3}^{{}} - A_{1}^{{}})\nu _{3}^{{}}\nu _{1}^{{}}}}{{\nu _{3}^{{}}A_{3}^{{}}A_{1}^{{}}}},\quad \dot {\nu }_{3}^{{}} = \frac{{g{\text{(}}\nu _{3}^{{}})(A_{1}^{{}} - A_{2}^{{}})\nu _{1}^{{}}\nu _{2}^{{}}}}{{\nu _{3}^{{}}A_{1}^{{}}A_{2}^{{}}}}$

Таким образом, множество ${{\gamma }}$ определяется соотношениями

(3.9)

$\nu _{i}^{{}} = \nu _{i}^{{}}(t),$

которые описывают решение системы (3.8). Отметим, что в уравнениях $g{\text{(}}\nu _{3}^{{}})$ – произвольная дифференцируемая функция от $\nu _{3}^{{}}$; функции $L(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ и $U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ на ИС (3.7) найдем, используя первые интегралы (2.3):

(3.10)

$L(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = k - \frac{{g(\nu _{3}^{{}})}}{{\nu _{3}^{{}}}}\left( {\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2}} \right)$

(3.11)

$2U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = \frac{{g_{{}}^{2}(\nu _{3}^{{}})}}{{\nu _{3}^{2}{{A}_{1}}{{A}_{2}}{{A}_{3}}}}\left( {{{A}_{2}}{{A}_{3}}\nu _{1}^{2} + {{A}_{1}}{{A}_{3}}\nu _{2}^{2} + {{A}_{1}}{{A}_{2}}\nu _{3}^{2}} \right) - 2E$

В монографии [22] показано, что в функции (3.10) при нахождении $\overline {\operatorname{grad} } \,L(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ нельзя выражение $\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2}$ заменять единицей, так как в противном случае из уравнений (2.1), (2.2) не следует условие (2.5) (ниже будет приведен пример этого свойства).

Из векторного представления ${\mathbf{x}}$ из (3.5) следует, что вектор ${\mathbf{x}}$ коллинеарен вектору ${\mathbf{\nu }}$, а переменность его модуля зависит от функции $g({{\nu }_{3}}):{{\nu }_{3}}$. Данное свойство возможно и в задаче о движении тяжелого твердого тела, несущего ротор, то есть в задаче о движении гиростата [26] под действием силы тяжести. Из формул (3.10), (3.11) следует, что функции $L(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$, $U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ имеют сингулярный вид. Такого вида функции рассматривали ранее [27–29] и другие (см. монографию [30]) без объяснения применения результатов в каких-либо силовых полях, так как они решали математические проблемы существования соответствующих решений уравнений динамики твердого тела. Объяснение применимости сингулярных функций $L(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$, $U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ дано в статьях [31, 32] при рассмотрении задач квантовой механики.

В дальнейшем целесообразно рассматривать два варианта ИС (3.7). В первом варианте (см. (3.5)) полагаем, что $g{\text{(}}{{\nu }_{3}})$ – произвольная дифференцируемая функция ${{\nu }_{3}}$; во втором варианте предполагаем, что она определяется из уравнения $\mu (\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = 0$. Во втором случае из условия (2.5) получим

(3.12)

$g(\nu _{3}^{{}}) = \frac{{g_{0}^{{}}}}{{\nu _{3}^{2}}}$

На примере (3.12) покажем, что в формуле (3.10) нельзя заменять выражение $\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2}$ единицей. При выполнении условия (3.12) ИС (3.5) таковы:

(3.13)

$x_{1}^{{}} = \frac{{\nu _{1}^{{}}}}{{\nu _{3}^{3}}}g_{0}^{{}},\quad x_{2}^{{}} = \frac{{\nu _{2}^{{}}}}{{\nu _{3}^{3}}}g_{0}^{{}},\quad x_{3}^{{}} = \frac{1}{{\nu _{3}^{2}}}g_{0}^{{}}\quad \left( {{\mathbf{x}} = \frac{{{{g}_{0}}}}{{\nu _{3}^{3}}}{\mathbf{\nu }}} \right)$

Для наглядности проведенных преобразований запишем динамические уравнения, которые следуют из (2.1), в случае (3.13). Используя функции $L(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$, $U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ из (3.10), (3.11) при значении $g{\text{(}}\nu _{3}^{{}})$ из (3.12), установим следующие уравнения:

(3.14)

$\begin{gathered} {{{\dot {x}}}_{1}} = \frac{{g_{0}^{2}\nu _{2}^{{}}}}{{{{A}_{1}}{{A}_{2}}{{A}_{3}}\nu _{3}^{7}}}\left[ {{{A}_{1}}({{A}_{2}} - {{A}_{3}})\nu _{3}^{2} - 3{{A}_{3}}({{A}_{1}} - {{A}_{2}})\nu _{1}^{2}} \right] \\ {{{\dot {x}}}_{2}} = \frac{{g_{0}^{2}\nu _{1}^{{}}}}{{{{A}_{1}}{{A}_{2}}{{A}_{3}}\nu _{3}^{7}}}\left[ {{{A}_{2}}({{A}_{3}} - {{A}_{1}})\nu _{3}^{2} - 3{{A}_{3}}({{A}_{1}} - {{A}_{2}})\nu _{2}^{2}} \right] \\ {{{\dot {x}}}_{3}} = \frac{{2g_{0}^{2}\nu _{1}^{{}}\nu _{2}^{{}}}}{{{{A}_{1}}{{A}_{2}}\nu _{3}^{6}}}({{A}_{2}} - {{A}_{1}}) \\ \end{gathered} $

Если в левые части системы (3.14) подставить значения (3.13) и воспользоваться уравнениями Пуассона (3.8) при условии (3.12):

(3.15)

$\dot {\nu }_{1}^{{}} = \frac{{g_{0}^{{}}(A_{2}^{{}} - A_{3}^{{}})\nu _{2}^{{}}\nu _{3}^{{}}}}{{\nu _{3}^{3}A_{2}^{{}}A_{3}^{{}}}},\quad \dot {\nu }_{2}^{{}} = \frac{{g_{0}^{{}}(A_{3}^{{}} - A_{1}^{{}})\nu _{3}^{{}}\nu _{1}^{{}}}}{{\nu _{3}^{3}A_{3}^{{}}A_{1}^{{}}}},\quad \dot {\nu }_{3}^{{}} = \frac{{g_{0}^{{}}(A_{1}^{{}} - A_{2}^{{}})\nu _{1}^{{}}\nu _{2}^{{}}}}{{\nu _{3}^{3}A_{1}^{{}}A_{2}^{{}}}},$

то получим тождества. Таким образом, данные свойства нельзя получить в случае, если в выражении (3.10) применять геометрический интеграл $\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2}$ = 1.

4. Интегрирование уравнений Пуассона (3.8), (3.15). Поскольку уравнения (3.8) имеют два первых интеграла

(4.1)

$\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2} = 1,\quad {{A}_{2}}{{A}_{3}}\nu _{1}^{2} + {{A}_{1}}{{A}_{3}}\nu _{2}^{2} + {{A}_{1}}{{A}_{2}}\nu _{3}^{2} = c_{0}^{2},$

то интегрирование уравнений (3.8) сводится к квадратурам. Из (4.1) определим функции $\nu _{1}^{{\text{2}}}{\text{(}}\nu _{3}^{{}})$, $\nu _{2}^{{\text{2}}}{\text{(}}\nu _{3}^{{}})$:

(4.2)

$\nu _{1}^{2} = \frac{{A_{1}^{{}}(A_{3}^{{}} - A_{2}^{{}})\nu _{3}^{2} + c_{0}^{2} - A_{1}^{{}}A_{3}^{{}}}}{{A_{3}^{{}}(A_{2}^{{}} - A_{1}^{{}})}},\quad \nu _{2}^{2} = \frac{{A_{2}^{{}}(A_{1}^{{}} - A_{3}^{{}})\nu _{3}^{2} + A_{2}^{{}}A_{3}^{{}} - c_{0}^{2}}}{{A_{3}^{{}}(A_{2}^{{}} - A_{1}^{{}})}}$

Без ограничения общности полагаем, что главные моменты инерции удовлетворяют неравенствам

(4.3)

$A_{1}^{{}} < A_{2}^{{}} < A_{3}^{{}}$

Тогда, в силу (4.3), имеют место условия

$\alpha _{0}^{{}} = \frac{{A_{1}^{{}}(A_{3}^{{}} - A_{2}^{{}})}}{{A_{3}^{{}}(A_{2}^{{}} - A_{1}^{{}})}} > 0,\quad \beta _{0}^{{}} = \frac{{A_{2}^{{}}(A_{3}^{{}} - A_{1}^{{}})}}{{A_{3}^{{}}(A_{2}^{{}} - A_{1}^{{}})}} > 0$

Запишем соотношения (4.2) в виде

(4.4)

$\nu _{1}^{2} = {{\alpha }_{0}}(\nu _{3}^{2} - {{\alpha }_{1}}),\quad \nu _{2}^{2} = {{\beta }_{0}}( - \nu _{3}^{2} + {{\beta }_{1}}),$

где

(4.5)

${{\alpha }_{1}} = - \frac{{A_{1}^{{}}A_{3}^{{}} - c_{0}^{2}}}{{A_{1}^{{}}(A_{3}^{{}} - A_{2}^{{}})}},\quad {{\beta }_{1}} = \frac{{A_{2}^{{}}A_{3}^{{}} - c_{0}^{2}}}{{A_{2}^{{}}(A_{3}^{{}} - A_{1}^{{}})}}$

Для примера действительности функций (4.4) положим, что параметр $c_{0}^{2}$ удовлетворяет условию

(4.6)

$A_{1}^{{}}A_{3}^{{}} < c_{0}^{2} < A_{2}^{{}}A_{3}^{{}}$

Тогда переменная $\nu _{3}^{{}}$ изменяется на множестве

(4.7)

$\nu _{3}^{{}} \in \left\{ {\left[ { - \sqrt {{{\beta }_{1}}} , - \sqrt {{{\alpha }_{1}}} } \right] \cup \left[ {\sqrt {{{\alpha }_{1}}} ,\sqrt {{{\beta }_{1}}} } \right]} \right\},$

где, в силу (4.6), $\alpha _{1}^{2} < \beta _{1}^{2} < 1$, то есть множество (4.7) содержится во множестве [–1; 1], причем $\nu _{3}^{{}} \ne 0$. Зависимость $\nu _{3}^{{}}{\text{(}}t)$ находим из третьего уравнения системы (3.8) путем обращения интеграла

(4.8)

$\int\limits_{{v}_{3}^{{(0)}}}^{{{{v}}_{3}}} {\frac{{{v}_{3}^{{}}d{v}_{3}^{{}}}}{{g({v}_{3}^{{}})\sqrt {\left( {\nu _{3}^{2} - {{\alpha }_{1}}} \right)\left( { - \nu _{3}^{2} + {{\beta }_{1}}} \right)} }} = \frac{{(A_{1}^{{}} - A_{2}^{{}})}}{{A_{1}^{{}}A_{2}^{{}}}}\sqrt {\alpha _{0}^{{}}\beta _{0}^{{}}} (t - t_{0}^{{}})} $

В случае (3.12) для вычисления интеграла можно ввести новую переменную $u = \nu _{3}^{2}$. Следовательно, интеграл (4.8) примет вид

(4.9)

$\int\limits_{{{u}_{0}}}^u {\frac{{udu}}{{g_{0}^{{}}\sqrt {{\text{(}}u - {{\alpha }_{1}})({{\beta }_{1}} - u)} }} = \frac{{2(A_{1}^{{}} - A_{2}^{{}})}}{{A_{1}^{{}}A_{2}^{{}}}}\sqrt {\alpha _{0}^{{}}\beta _{0}^{{}}} (t - t_{0}^{{}})} $

Очевидно, что интеграл в левой части (4.9) вычисляется в элементарных функциях.

5. Исследование уравнений (2.10), (2.11). Подставим в уравнения (2.10), (2.11) значения (3.2), в которых $x_{i}^{{}}$ ${\text{(}}i = \overline {1,3} {\text{)}}$ имеют вид (3.5):

(5.1)

$\frac{{{{B}^{2}}{\text{(}}\nu _{3}^{{}})g_{{}}^{{\text{2}}}{\text{(}}\nu _{3}^{{}})}}{{{{A}_{1}}{{A}_{2}}{{A}_{3}}\nu _{3}^{2}}}{{F}_{1}}(\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}} = \sigma _{0}^{2}$

(5.2)

$\frac{{B{\text{(}}\nu _{3}^{{}})g{\text{(}}\nu _{3}^{{}}){{F}_{1}}(\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}}}{{{{A}_{1}}{{A}_{2}}{{A}_{3}}\nu _{3}^{{}}}} = k_{0}^{{}},$

где функция ${{F}_{1}}(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})$ такова:

(5.3)

${{F}_{1}}(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = {{A}_{2}}{{A}_{3}}\nu _{1}^{2} + {{A}_{3}}{{A}_{1}}\nu _{2}^{2} + {{A}_{1}}{{A}_{2}}\nu _{3}^{2}$

Поскольку уравнения (5.1), (5.2) рассматриваются на многообразии, которое характеризует кривую γ, то, в силу (4.1) (первого интеграла уравнений (3.8)), ${{F}_{1}}(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = c_{0}^{2}$. Внесем это значение в равенства (5.1), (5.2):

(5.4)

$B{\text{(}}\nu _{3}^{{}})g{\text{(}}\nu _{3}^{{}}) = \frac{{\sigma _{0}^{{}}\sqrt {{{A}_{1}}{{A}_{2}}{{A}_{3}}} }}{{c_{0}^{{}}}}\nu _{3}^{{}}$

(5.5)

$B{\text{(}}\nu _{3}^{{}})g{\text{(}}\nu _{3}^{{}}) = \frac{{k_{0}^{{}}{{A}_{1}}{{A}_{2}}{{A}_{3}}}}{{c_{0}^{2}}}\nu _{3}^{{}}$

Из соотношений (5.4), (5.5) получим условие

(5.6)

$\sigma _{0}^{{}} = \frac{{k_{0}^{{}}\sqrt {{{A}_{1}}{{A}_{2}}{{A}_{3}}} }}{{c_{0}^{2}}}$

При выполнении равенства (5.6) уравнения (5.4), (5.5) аналитически эквивалентны. Данное свойство, в силу (2.10), (2.11), является весьма примечательным. Геометрическая трактовка его такова: если конец вектора ${\mathbf{b}}$ принадлежит эллипсоиду инерции тела, то проекция ${\mathbf{b}}$ на вектор ${\mathbf{\nu }}$ (неподвижный в пространстве) постоянна и наоборот. Если в (5.4) $B{\text{(}}\nu _{3}^{{}}) = B_{0}^{{}}$ (это значение можно принять за единицу), то на эллипсоиде инерции тела лежит конец вектора ${\mathbf{\omega }}$. Такое свойство имеет место и в решении Эйлера. При $B{\text{(}}\nu _{3}^{{}}) = 1$ из (5.4) следует равенство

(5.7)

$g{\text{(}}\nu _{3}^{{}}) = {{\varkappa }_{0}}\nu _{3}^{{}}\quad \left( {{{\varkappa }_{0}} = \frac{{\sigma _{0}^{{}}\sqrt {{{A}_{1}}{{A}_{2}}{{A}_{3}}} }}{{c_{0}^{{}}}}} \right)$

Используя $g{\text{(}}\nu _{3}^{{}})$ из (5.7), запишем ИС (3.5) в векторной форме:

(5.8)

${\mathbf{x}} = {{\varkappa }_{0}}{\mathbf{\nu }}$

В силу (5.8) вектор ${\mathbf{x}}$ не только постоянен по величине, но и неподвижен в пространстве. Это означает, что при $B{\text{(}}\nu _{3}^{{}}) = 1$ для уравнений (2.1), (2.2) имеет место случай Эйлера, который полностью изучен в учебниках по теоретической механике (см., например, [10]). Здесь представляет интерес применение метода решения обратных задач механики, который позволил из уравнений Гриоли получить уравнения Эйлера. Запишем только основные формулы при ${{x}_{i}} = {{\varkappa }_{0}}{{\nu }_{i}}$:

(5.9)

(5.10)

$\frac{{\partial U(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})}}{{\partial {\mathbf{\nu }}}} \times {\mathbf{\nu }} = \varkappa _{0}^{2}(a{\mathbf{x}} \times {\mathbf{\nu }}),\quad \frac{{\partial L(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})}}{{\partial {\mathbf{\nu }}}} \times a{\mathbf{x}} = - 2\varkappa _{0}^{2}({\mathbf{\nu }} \times a{\mathbf{x}})$

Подстановка величин из (5.9), (5.10) в уравнение (2.1) дает уравнение

(5.11)

${\mathbf{\dot {x}}} = {\mathbf{x}} \times a{\mathbf{x}},$

которое характеризует решение Эйлера. Таким образом, при $B = 1$ имеем: ${\mathbf{b}}{\text{(}}t{\text{)}} = {\mathbf{\omega }}{\text{(}}t{\text{)}}$, то есть годограф вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ совпадает с годографом вектора ${\mathbf{\omega }}$.

Покажем, что при $B{\text{(}}\nu _{3}^{{}}{\text{)}}\; \ne 1$ годограф вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ существенно отличается от годографа вектора ${\mathbf{\omega }}{\text{(}}t{\text{)}}$. Запишем (5.4), приняв обозначение $\varepsilon _{0}^{{}} = \frac{{\sigma _{0}^{{}}\sqrt {{{A}_{1}}{{A}_{2}}{{A}_{3}}} }}{{c_{0}^{{}}}}$:

(5.12)

$B(\nu _{3}^{{}}) = \frac{{\varepsilon _{0}^{{}}\nu _{3}^{{}}}}{{g(\nu _{3}^{{}})}}$

Покажем, что вектор $A{\mathbf{b}}{\text{(}}t{\text{)}}$ коллинеарен вектору ${\mathbf{\nu }}$. В силу равенства ${\mathbf{b}}{\text{(}}t{\text{)}} = B{\text{(}}\nu _{3}^{{}}{\text{)}}{\mathbf{\omega }}$ для вектора $A{\mathbf{b}}{\text{(}}t{\text{)}}$ получим значение: $A{\mathbf{b}}{\text{(}}t{\text{)}}$ = $B{\text{(}}\nu _{3}^{{}}{\text{)}}A{\mathbf{\omega }}$ = $B{\text{(}}\nu _{3}^{{}}{\text{)}}{\mathbf{x}}$, где вектор ${\mathbf{x}}$ указан в (3.5). На основании (3.5), (5.12) получим:

(5.13)

$A{\mathbf{b}}{\text{(}}t{\text{)}} = \varepsilon _{0}^{{}}{\mathbf{\nu }},$

то есть в неподвижном пространстве вектор (5.13) постоянен. Очевидно, что для вектора ${\mathbf{x}} = A{\mathbf{\omega }}$ это свойство не выполняется (см. (3.5)). Использование равенства (5.13) при кинематическом истолковании недостаточно, так как это не позволяет качественно исследовать годографы векторов ${\mathbf{b}}{\text{(}}t{\text{)}}$ и ${\mathbf{\omega }}{\text{(}}t{\text{)}}$ и выполнить их сравнительный анализ. Поскольку при произвольной функции ${\text{g(}}\nu _{3}^{{}}{\text{)}}$ получить конкретный результат невозможно, то в дальнейшем полагаем $\mu {\text{(}}\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}{\text{)}} = {\text{0}}$ (см. [22]).

6. Случай $\mu (\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = 0$. Рассмотрим случай $\mu (\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = 0$, который характеризуется равенством (3.12). Компоненты вектора момента количества движения в подвижной системе координат имеют вид (3.13), компоненты вектора ${\mathbf{\omega }}$ в подвижной системе координат определены соотношениями

(6.1)

$\omega _{1}^{{}} = \frac{{g_{0}^{{}}\nu _{1}^{{}}}}{{A_{1}^{{}}\nu _{3}^{3}}},\quad \omega _{2}^{{}} = \frac{{g_{0}^{{}}\nu _{2}^{{}}}}{{A_{2}^{{}}\nu _{3}^{3}}},\quad \omega _{3}^{{}} = \frac{{g_{0}^{{}}}}{{A_{3}^{{}}\nu _{3}^{2}}}$

Для нахождения компонент вектора ${\mathbf{b}}{\text{(}}t{\text{)}} = B{\text{(}}\nu _{3}^{{}}{\text{)}}{\mathbf{\omega }}$ обратимся к уравнению (5.4). Так как $g(\nu _{3}^{{}}) = \frac{{g_{0}^{{}}}}{{\nu _{3}^{2}}}$, то из (5.4) следует

(6.2)

$B{\text{(}}\nu _{3}^{{}}) = d_{0}^{{}}\nu _{3}^{3},$

где

$d_{0}^{{}} = \frac{{\sigma _{0}^{{}}\sqrt {{{A}_{1}}{{A}_{2}}{{A}_{3}}} }}{{g_{0}^{{}}c_{0}^{{}}}}$

Для применения комплексного подхода в истолковании движения тела запишем выражения для углов Эйлера из (3.7) с учетом (6.1):

(6.3)

$\theta = \arccos {{\nu }_{3}},\quad \varphi = {\text{arctg}}\frac{{\sqrt {{{\alpha }_{0}}(\nu _{3}^{2} - {{\alpha }_{1}})} }}{{\sqrt {{{\beta }_{0}}(\beta _{1}^{{}} - \nu _{3}^{2})} }}$

(6.4)

$\psi (\nu _{3}^{{}}) = \frac{1}{{A_{3}^{{}}(A_{1}^{{}} - A_{2}^{{}})\sqrt {{{\alpha }_{0}}{{\beta }_{0}}} }}\int\limits_{\nu _{3}^{{(0)}}}^{\nu _{3}^{{}}} {\frac{{\left( {c_{0}^{2} - A_{1}^{{}}A_{2}^{{}}\nu _{3}^{2}} \right)d\nu _{3}^{{}}}}{{\left( {1 - \nu _{3}^{2}} \right)\sqrt {\left( {\nu _{3}^{2} - {{\alpha }_{1}}} \right)\left( {{{\beta }_{1}} - \nu _{3}^{2}} \right)} }}} ,$

где вспомогательная переменная $\nu _{3}^{{}}$ определяется из (4.8):

(6.5)

$\int\limits_{\nu _{3}^{{(0)}}}^{\nu _{3}^{{}}} {\frac{{\nu _{3}^{3}\;d\nu _{3}^{{}}}}{{\sqrt {\left( {\nu _{3}^{2} - {{\alpha }_{1}}} \right)\left( {{{\beta }_{1}} - \nu _{3}^{2}} \right)} }}} = \frac{{{{g}_{0}}(A_{1}^{{}} - A_{2}^{{}})\sqrt {{{\alpha }_{0}}{{\beta }_{0}}} }}{{A_{1}^{{}}A_{2}^{{}}}}(t - t_{0}^{{}}) = \tau $

Введем обозначение

$H(\nu _{3}^{{}}) = - \frac{1}{4}\left[ {({{\alpha }_{1}} + {{\beta }_{1}})\arcsin \frac{{{{\alpha }_{1}} + {{\beta }_{1}} - 2\nu _{3}^{2}}}{{{{\beta }_{1}} - {{\alpha }_{1}}}} + 2\sqrt {\left( {\nu _{3}^{2} - {{\alpha }_{1}}} \right)\left( {{{\beta }_{1}} - \nu _{3}^{2}} \right)} } \right]$

Тогда из формулы (6.5) следует

(6.6)

$H\left( {\nu _{3}^{{(0)}}} \right) - H(\nu _{3}^{{}}) = \tau \quad \left( {\nu _{3}^{{(0)}} = \nu _{3}^{{}}(0)} \right)$

Очевидно, что найти явную зависимость $\nu _{3}^{{}}(\tau )$ из (6.6) невозможно. Поэтому исследование соотношений (6.3)–(6.5) целесообразно провести, не обращаясь к (6.6). Положим, без ограничения общности, что $\nu _{3}^{2}$ изменяется на отрезке

(6.7)

${{\alpha }_{1}} \leqslant \nu _{3}^{2} \leqslant {{\beta }_{1}}$

При таком подходе следует учитывать, что радикалы $\sqrt {\nu _{3}^{2} - {{\alpha }_{1}}} $, $\sqrt {{{\beta }_{1}} - \nu _{3}^{2}} $ изменяют свои знаки при переходе через граничные значения ${{\alpha }_{1}}$, ${{\beta }_{1}}$. Это свойство вытекает из формулы (6.5): ${{\left. {\frac{{d{{\nu }_{3}}}}{{dt}}} \right|}_{{\nu _{3}^{{(0)}}}}} > 0$ в начальный момент ($\nu _{3}^{{(0)}} = \nu _{3}^{{}}(t_{0}^{{}})$) и в силу периодического изменения переменной $\nu _{3}^{2}$ на отрезке (6.7) указанные радикалы изменяют свои знаки. Данный подход необходимо применять при построении подвижного и неподвижного годографов вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$, а также при истолковании движения тела на основании качения без скольжения эллипсоида инерции тела (2.10) по плоскости (2.11).

Для исследования подвижного годографа вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ обратимся к формулам (6.1), (6.2). С учетом равенств $\omega _{i}^{{}} = \frac{{b_{i}^{{}}}}{{d_{0}^{{}}\nu _{3}^{3}}}$ ${\text{(}}i = \overline {1,3} {\text{)}}$ из (6.1) найдем

(6.8)

$\nu _{i}^{{}} = \frac{{A_{i}^{{}}b_{i}^{{}}}}{{\lambda _{0}^{{}}}}\quad {\text{(}}\lambda _{0}^{{}} = g_{0}^{{}}d_{0}^{{}}{\text{)}}$

Подставим $\nu _{i}^{{}}$ из (6.8) в геометрический интеграл $\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2} = 1$. Тогда получим уравнение

(6.9)

$A_{1}^{2}b_{1}^{2} + A_{2}^{2}b_{2}^{2}\, + A_{3}^{2}b_{3}^{2} = \lambda _{0}^{2}$

Рассмотрим линейную комбинацию уравнений (2.10) и (6.9):

(6.10)

$A_{1}^{{}}\left( {\lambda _{0}^{2} - \sigma _{0}^{2}A_{1}^{{}}} \right)b_{1}^{2} + A_{2}^{{}}\left( {\lambda _{0}^{2} - \sigma _{0}^{2}A_{2}^{{}}} \right)b_{2}^{2} + A_{3}^{{}}\left( {\lambda _{0}^{2} - \sigma _{0}^{2}A_{3}^{{}}} \right)b_{3}^{2} = 0$

Следовательно, в качестве подвижного годографа вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ можно рассматривать линию пересечения эллипсоида (2.10) и конуса (6.10).

В задачах кинематического истолкования движения твердого тела важную роль играет формула [14]

(6.11)

${\text{tg(}}\alpha {\text{(}}t{\text{)}} - \psi {\text{(}}t{\text{))}} = \frac{{({\mathbf{\omega }}{\text{(}}t{\text{)}} \times {\mathbf{\nu }}{\text{(}}t{\text{))}} \cdot ({\mathbf{\nu }}{\text{(}}t{\text{)}} \times {\mathbf{i}}_{3}^{{}})}}{{{\mathbf{i}}_{3}^{{}} \cdot ({\mathbf{\omega }}{\text{(}}t{\text{)}} \times {\mathbf{\nu }}{\text{(}}t{\text{))}}}},$

где $\alpha $ – полярный угол уравнений неподвижного годографа. Поскольку функция $\psi {\text{(}}t{\text{)}}$ известна (см. (6.4)), то при замене ${\mathbf{\omega }}$ на ${\mathbf{b}}$ в (6.11) найдем полярный угол уравнений неподвижного годографа вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$. Однако, этот подход приводит к значительным вычислительным трудностям. Его можно использовать в комплексном подходе [33] истолкования движения тела; для этого необходимо использовать формулы (6.3)–(6.5). В результате движение тела можно описать с помощью улов Эйлера: $\theta = \theta {\text{(}}\nu _{3}^{{}}{\text{)}}$, $\varphi = \varphi {\text{(}}\nu _{3}^{{}}{\text{)}}$, $\psi = \psi {\text{(}}\nu _{3}^{{}}{\text{)}}$.

Преобразуем уравнения [13] с помощью замены ${\mathbf{\omega }} = \frac{1}{{B{\text{(}}\nu _{3}^{{}}{\text{)}}}}{\mathbf{b}}$:

(6.12)

$b_{\xi }^{{}} = b_{\rho }^{{}}\cos \alpha ,\quad b_{\eta }^{{}} = b_{\rho }^{{}}\sin \alpha ,\quad b_{\zeta }^{{}} = {\mathbf{b}} \cdot {\mathbf{\nu }},$

где

(6.13)

$b_{\rho }^{2} = b_{{}}^{2} - b_{\zeta }^{2},\quad \dot {\alpha } = \frac{1}{{b_{\rho }^{2}}}\left[ {{\mathbf{\dot {b}}} \cdot ({\mathbf{\nu }} \times {\mathbf{b}})} \right]$

На основании равенств (6.8), уравнений (3.15), соотношения (2.11), из равенств (6.12), (6.13) получим

(6.14)

$b_{\zeta }^{{}}(\nu _{3}^{{}}) = k_{0}^{{}} = \frac{{\sigma _{0}^{2}}}{{{{\lambda }_{0}}}},\quad b_{\rho }^{2}(\nu _{3}^{{}}) = \frac{{\lambda _{0}^{2}}}{{A_{1}^{2}A_{2}^{2}A_{3}^{2}}}F_{2}^{{}}(\nu _{3}^{{}})$

(6.15)

$\dot {\alpha } = - \frac{{g_{0}^{{}}F_{3}^{{}}(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})}}{{\nu _{3}^{3}F_{2}^{{}}(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}})}}$

(6.16)

$\begin{gathered} F_{2}^{{}}(\nu _{3}^{{}}) = A_{1}^{{}}A_{2}^{{}}(A_{3}^{{}} - A_{1}^{{}})(A_{3}^{{}} - A_{2}^{{}})\nu _{3}^{2} - A_{3}^{2}A_{1}^{{}}A_{2}^{{}} + A_{3}^{{}}(A_{1}^{{}} + A_{2}^{{}})c_{0}^{2} - c_{0}^{4} \\ F_{3}^{{}}(\nu _{1}^{{}},\nu _{2}^{{}},\nu _{3}^{{}}) = A_{1}^{{}}{{(A_{3}^{{}} - A_{2}^{{}})}^{2}}\nu _{2}^{2}\nu _{3}^{2} + A_{2}^{{}}{{(A_{1}^{{}} - A_{3}^{{}})}^{2}}\nu _{3}^{2}\nu _{1}^{2} + A_{3}^{{}}{{(A_{2}^{{}} - A_{1}^{{}})}^{2}}\nu _{1}^{2}\nu _{2}^{2} \\ \end{gathered} $

Построение подвижного годографа (уравнения (6.9), (6.10)) и неподвижного годографа (уравнения (6.14), (6.15)), в силу (4.7), достаточно проводить при $\nu _{3}^{{}} \in \left[ {\sqrt {{{\alpha }_{1}}} ,\sqrt {{{\beta }_{1}}} } \right]$. При таком подходе радикалы $\sqrt {\nu _{3}^{2} - {{\alpha }_{1}}} $, $\sqrt {{{\beta }_{1}} - \nu _{3}^{2}} $ после нулевых значений в силу

$\frac{{d\nu _{3}^{{}}}}{{d\tau }} = \sqrt {\left( {\nu _{3}^{2} - {{\alpha }_{1}}} \right)\left( {{{\beta }_{1}} - \nu _{3}^{2}} \right)} \quad \left( {{{{\left( {\nu _{3}^{{(0)}}} \right)}}^{2}} - {{\alpha }_{1}} \ne 0,\;{{{\left( {\nu _{3}^{{(0)}}} \right)}}^{2}} - {{\beta }_{1}} \ne 0} \right)$

изменяют свой знак. При этом полагаем ${{\left. {\frac{{d{{\nu }_{3}}}}{{d\tau }}} \right|}_{{\tau = 0}}} > 0$. Свойство проекции неподвижного годографа установить достаточно просто: эта кривая расположена в кольце с радиусами

${{R}_{1}} = {{\left| {b_{\rho }^{{}}(\nu _{3}^{{}})} \right|}_{{{{\alpha }_{1}}}}},\quad {{R}_{2}} = {{\left| {b_{\rho }^{{}}(\nu _{3}^{{}})} \right|}_{{{{\beta }_{1}}}}}$

и касается указанных окружностей. В силу формулы (6.15) и свойств функций (6.16) при $g_{0}^{{}} > 0$ угол $\alpha {\text{(}}t{\text{)}}$ убывает, при $g_{0}^{{}} < 0$ угол $\alpha {\text{(}}t{\text{)}}$ возрастает.

Для сопоставления подвижных годографов векторов ${\mathbf{b}}{\text{(}}t{\text{)}}$ и ${\mathbf{\omega }}{\text{(}}t{\text{)}}$ запишем годограф ${\mathbf{\omega }}{\text{(}}t{\text{)}}$ как линию пересечения поверхностей

(6.17)

$A_{1}^{2}\left( {c_{0}^{2} - A_{2}^{{}}A_{3}^{{}}} \right)\omega _{1}^{2} + A_{2}^{2}\left( {c_{0}^{2} - A_{1}^{{}}A_{3}^{{}}} \right)\omega _{2}^{2} + A_{3}^{2}\left( {c_{0}^{2} - A_{1}^{{}}A_{2}^{{}}} \right)\omega _{3}^{2} = 0$

(6.18)

$A_{{1`}}^{{}}\omega _{1}^{2} + A_{2}^{{}}\omega _{2}^{2} + A_{3}^{{}}\omega _{3}^{2} - \frac{{c_{0}^{2}A_{3}^{2}}}{{g_{0}^{{}}A_{1}^{{}}A_{2}^{{}}}}\omega _{3}^{3} = 0$

Из уравнений (6.9), (6.10) следует, что подвижный годограф вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ является линией пересечения поверхностей второго порядка, а из уравнений (6.17), (6.18) – подвижный годограф вектора ${\mathbf{\omega }}{\text{(}}t{\text{)}}$ является линией пересечения поверхности второго порядка (6.17) (конуса) и поверхности третьего порядка (6.18). Следовательно, полодии ${\mathbf{b}}{\text{(}}t{\text{)}}$ отличаются от полодии ${\mathbf{\omega }}{\text{(}}t{\text{)}}$ в случае Эйлера.

На основании формулы

(6.19)

${\mathbf{x}}({v}_{3}^{{}}) = \frac{{g_{0}^{{}}}}{{{{\nu }}_{3}^{3}}}{\mathbf{\nu }}$

устанавливаем уравнения подвижного годографа ${\mathbf{x}}$:

(6.20)

$\begin{gathered} x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = \frac{{A_{3}^{{}}}}{{{{g}_{0}}}}x_{3}^{3} \\ x_{1}^{2}\left( {c_{0}^{2} - A_{2}^{{}}A_{3}^{{}}} \right) + x_{2}^{2}\left( {c_{0}^{2} - A_{1}^{{}}A_{3}^{{}}} \right) + x_{3}^{2}\left( {c_{0}^{2} - A_{1}^{{}}A_{2}^{{}}} \right) = 0 \\ \end{gathered} $

Из (6.20) следует, что подвижный годограф в данном случае (линия пересечения поверхностей второго и третьего порядка) не совпадает по своему типу с подвижным годографом ${\mathbf{x}}{\text{(}}t{\text{)}}$ в случае Эйлера. Таким образом, несмотря на различные типы полодий и герполодий, построение их не вызывает затруднений, поскольку все аналитические формулы в статье выписаны.

ЗАКЛЮЧЕНИЕ

1. В статье для кинематического истолкования движения тела применен модифицированный метод Пуансо, предложенный автором статьи.

2. Получено новое решение уравнений Гриоли задачи о движении тела под действием потенциальных и гироскопических сил. Кинематическое истолкование движения тела в данном решении характеризуется движением без скольжения эллипсоида инерции по неподвижной в пространстве плоскости.

3. Отличие истолкования движения тела, полученного в данной статье, от истолкования в случае Эйлера состоит в том, что в первом подходе эллипсоид инерции содержит полодию вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$, а в случае Эйлера он содержит полодию вектора угловой скорости ${\mathbf{\omega }}{\text{(}}t{\text{)}}$. Подвижный годограф ${\mathbf{\omega }}{\text{(}}t{\text{)}}$ в решении Эйлера – линия пересечения поверхностей второго порядка. Аналогичным свойством обладает и подвижный годограф вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$, но в статье подвижный годограф вектора ${\mathbf{\omega }}{\text{(}}t{\text{)}}$ – линия пересечения поверхностей второго и третьего порядка.

Исследование выполнено за счет гранта Российского научного фонда № 19-71-30012.

Список литературы

Poinsot L. Thèorie nouvelle de la rotation des corps // J. Math. Pures et Appl. 1851. Bd. 1. № 16. P. 289–336.
Sylvester J.J. On the motion of a rigid body acted on by no external forces // Philos. Trans. Roy. Soc. London. 1866. V. 156. P. 757–780.
Mac-Cullagh J. On the rotation of a solid body // Proc. Roy. Irish Acad. 1840–1844. V. 2. P. 542–545; 1845–1847. V. 3. P. 370–371.
Darboux G. Sur la theorie de Poinsot et sur des mouvements correspondants a la meme polhodie // C. R. Acad. Sci. 1885. V. 101. P. 1555–1561.
Darboux G. Sur le mouvement d’un corps pesant de revolution fixe par un point de son axe // J. Math. Pures et Appl. 1885. V. 1. P. 403–430.
Jacobi C.G.J. Sur la rotation d’un corps de rèvolution grave autour d’un point quelconque de son axe // in: Gesammelte Werke. Berlin: G. Reimer, 1882. B. 2. S. 493–510.
Hess W. Über das Problem der Rotation // Math. Ann. 1882. V. 20. S. 461–470.
Hess W. Ūber des Jacobische Theorem von der Ersetzbarkeit einer Lagrangeschen Rotation durch zwei Poinsotische Rotation // Z. Math. Phys. 1888. V. 33. P. 292–305.
Жуковский Н.Е. Геометрическая интерпретация рассмотренного С.В. Ковалевской случая движения тяжелого твердого тела около неподвижной точки // в: Собр. соч.: В 7 т. М.; Л.: Гостехиздат, 1948. Т. 1. С. 294–339.
Суслов Г.К. Теоретическая механика. М.: Гостехиздат, 1946. 655 с.
Горр Г.В., Кудряшова Л.В., Степанова Л.А. Классические задачи динамики твердого тела. Развитие и современное состояние. Киев: Наукова думка, 1978. 296 с.
Гашененко И.Н., Горр Г.В., Ковалев А.М. Классические задачи динамики твердого тела. Киев: Наукова думка, 2012. 401 с.
Харламов П.В. Кинематическое истолкование движения тела, имеющего неподвижную точку // ПММ. 1964. Т. 28. Вып. 3. С. 502–507.
Горр Г.В. Об одном подходе в применении теоремы Пуансо кинематического истолкования движения тела с неподвижной точкой // Мех. тверд. тела. 2012. Вып. 42. С. 26–36.
Горр Г.В. Об одном аналоге истолкования Пуансо решения Эйлера в задаче о движении твердого тела в потенциальном поле сил // ПММ. 2020. Т. 84. Вып. 1. С. 20–32.
Горр Г.В. О трех инвариантных соотношениях уравнений движения тела в потенциальном поле сил // ПММ. 2020. Т. 84. Вып. 1. С. 20–32.
Grioli G. Questioni di dinamica del corpo rigido // Atti. Accad. Naz. Lincei, Rend. Cl. Sci. Fis. Mat. e Natur. 1963. V. 35. f. 1–2. P. 35–39.
Yehia H.M. New generalizations of all the known integrable problems in rigid–body dynamics // J. Phys. A.: Math. Gen. 1999. V. 32. P. 7565–7580.
Yehia H.M. Equivalent mechanical systems with cyclic coordinates and new in-tegrable problems // Int. J. Non-Linear Mech. 2001. V. 36. P. 89–105.
Горр Г.В. Об одном классе решений уравнений динамики твердого тела под действием потенциальных и гироскопических сил // ПММ. 2018. Т. 82. Вып. 5. С. 547–558.
Леви-Чивита Т., Амальди У. Курс теоретической механики: в 2 т. М.: Изд-во иностр. литер, 1951. Т. 2, ч. 2: Динамика систем с конечным числом степеней свободы. 555 с.
Горр Г.В. Инвариантные соотношения уравнений динамики твердого тела (теория, результаты, комментарии). М.; Ижевск: Ин-т компьютерных исслед., 2017. 424 с.
Харламов М.П. Симметрия в системах с гироскопическими силами // Мех. тверд. тела. 1983. Вып. 15. С. 87–93.
Гашененко И.Н. Кинематическое представление по Пуансо движения тела в случае Гесса // Мех. тверд. тела. 2010. Вып. 40. С. 12–20.
Маркеев А.П. О геометрической интерпретации Пуансо движения твердого тела в случае Эйлера // Пробл. мех. управл. движ. Нелин. дин. системы. Межвузовский сборник научных трудов. Пермь 1981. С. 123–131.
Горр Г.В. Об одном подходе в исследовании движения гиростата с переменным гиростатическим моментом // Вестн. Удмурт. Ун-та. Матем. Мех. Компьют. науки. 2021. Т. 31. Вып. 1. С. 1–14.
Горячев Д.Н. Новые случаи интегрируемости динамических уравнений Эйлера // Варшав. унив. Изв. 1916. кн. 3. С. 1–13.
Горячев Д.Н. Новые случаи движения твердого тела вокруг неподвижной точки // Варшав. унив. Изв. 1915. кн. 3. С. 1–11.
Yehia H.M. New integrable problems in the dynamics of rigid bodies with Kovalevskaya configuration. I – The case of axisymmetric forces // Mech. Res. Com. 1996. V. 23. № 5. P. 423–437.
Борисов А.В., Мамаев И.С. Динамика твердого тела. Ижевск: НИЦ “Регулярная и хаотическая динамика”. 2001. 384 с.
Комаров И.В., Кузнецов В.Б. Обобщенный гиростат Горячева–Чаплыгина в квантовой механике // Диф. геом., группы Ли и мех. 1987. Зап. Науч. Сем. ЛОМИ НАН СССР. 1987. Т. 9. С. 134–141.
Комаров И.В., Кузнецов В.Б. Квазиклассическое квантование волчка Ковалевской // ТМФ. 1987. Т. 73. № 3. С. 335–347.
Gorr G.V. A Complex approach to the interpretation of the motion of a solid with a fixed point // Mech. Solids. 2021. V. 56. № 6. P. 932–946.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал