Прикладная математика и механика, 2020, T. 84, № 4, стр. 442-454

Исследование ограниченной задачи трех тел, притягивающихся по закону Ньютона, в случае, когда массы двух основных тел равны, началось более ста лет назад [1, 2]. Основные результаты [1, 2] изложены в монографиях [3, 4]. В последние десятилетия этой задаче уделялось очень большое внимание. Особенно много исследований появилось после публикации статьи [5], в которой рассматривался случай эллиптической ограниченной задачи, и было показано существование таких движений, в которых отклонение тела пренебрежимо малой массы от центра масс основных гравитирующих тел может принимать сколь угодно большие значения, но не имеет предела при неограниченном возрастании времени (осциллирующие движения). К настоящему времени довольно подробно исследована задача о существовании, устойчивости и бифуркациях периодических движений в круговой и эллиптической задачах, проведен анализ возможности хаотизации движения, даны обобщения классической задачи на случай, учитывающий световое давление, а также на случай, когда количество точек конечных масс больше двух. Большая библиография упомянутых исследований содержится в публикациях [6–14].

В статье численно-аналитическими методами исследуется задача о существовании и устойчивости прямолинейных движений третьего тела с периодом, кратным периоду обращения двух основных притягивающих тел по их эллиптическим орбитам малого эксцентриситета.

1. Введение. Рассмотрим три тела (материальные точки) ${{P}_{1}}$, ${{P}_{2}}$ и P₃, движущиеся под действием гравитационного притяжения по закону Ньютона. Считаем, что точки ${{P}_{1}}$ и ${{P}_{2}}$ имеют равные массы, а масса точки P₃ пренебрежимо мала. Движение точек ${{P}_{1}}$ и ${{P}_{2}}$ определяется из задачи двух тел (материальных точек). Будем предполагать, что орбита точки ${{P}_{2}}$ в ее движении относительно ${{P}_{1}}$ является эллипсом с эксцентриситетом $e$. Через $X,Y,Z$ обозначим координаты точки ${{P}_{3}}$ в системе координат $OXYZ$ с началом в центре масс тел ${{P}_{1}}$ и ${{P}_{2}}$ и осью $OX$, направленной по прямой ${{P}_{1}}{{P}_{2}}$ в сторону точки ${{P}_{2}}$, направление кратчайшего поворота оси $OX$ к оси $OY$совпадает с направлением вращения точки ${{P}_{2}}$ относительно ${{P}_{1}}$. Пусть $r$ – расстояние между точками ${{P}_{1}}$ и ${{P}_{2}}$. Если ввести координаты Нехвилла $x = X{\text{/}}r$, $y = Y{\text{/}}r$, $z = Z{\text{/}}r$ и в качестве независимой переменной принять истинную аномалию $\nu $ в эллиптическом движении точки ${{P}_{2}}$, то диференциальные уравнения движения точки ${{P}_{3}}$ можно записать [15, 16] в форме уравнений Лагранжа второго рода с функцией $L$ вида

где точкой обозначено дифференцирование по $\nu $, а

Введя обобщенные импульсы

уравнения движения можно записать в форме канонических уравений с функцией Гамильтона вида

Уравнения движения допускают решения, в которых $x = y = {{p}_{x}} = {{p}_{y}} = 0$, а изменение переменных $z$, ${{p}_{z}}$ описывается уравнениями с функцией Гамильтона

Для этих частных решений точка ${{P}_{3}}$ во все время движения остается на прямой $x = y = 0$, проходящей через центр масс точек ${{P}_{1}}$ и ${{P}_{2}}$ и перпендикулярной плоскости, в которых расположены орбиты этих точек.

В случае, когда орбиты точек ${{P}_{1}}$ и ${{P}_{2}}$ – окружности ($e = 0$), упомянутые прямолинейные траектории точки ${{P}_{3}}$ описываются уравнениями

которым соответствует функция Гамильтона

Система уравнений (1.2) является интегрируемой и довольно подробно изучена [1–4, 6]. Она допускает интеграл энергии

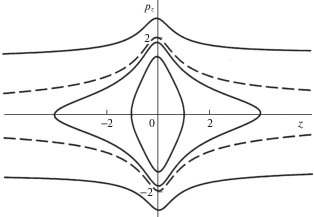
Фазовый портрет системы показан на рис. 1. При $h = - 2$ точка ${{P}_{3}}$ находится в положении равновесия $z = 0$; при $ - 2 < h < 0$ – совершает периодические колебания в окрестности этого равновесия. При этом $ - {{z}_{{\max }}} < z < {{z}_{{\max }}}$, где ${{z}_{{\max }}}$ – максимальное отклонение точки ${{P}_{3}}$ от положения равновесия,

Если ${{\varphi }_{{\max }}}$ – максимальное значение угла между отрезками ${{P}_{3}}{{P}_{2}}$ и ${{P}_{1}}{{P}_{2}}$ при колебаниях точки ${{P}_{3}}$, то $k = \sin ({{\varphi }_{{\max }}}{\text{/}}2)$. Постоянная $h$ интеграла (1.4) может быть выражена через параметр $k$:

При $h \geqslant 0$ движения точки ${{P}_{3}}$ являются неограниченными. Значению $h = 0$ на рис. 1 отвечают сепаратрисы. Они задаются уравнениями

Кривые (1.7) изображены на рис. 1 штриховыми линиями. Они разделяют области неограниченных движений точки ${{P}_{3}}$ по прямой от области, отвечающей колебательному характеру ее движения.

Колебания точки ${{P}_{3}}$ удобно описывать в переменных действие-угол $I,w$. Переменная $I$ равняется поделенной на $2\pi $ площади, заключенной внутри фазовой траектории. Вычисления показывают, что переменная $I$ может быть выражена через параметр $k$ при помощи полных эллиптических интегралов 1-го, 2-го и 3-го родов:

Здесь и далее используются общепринятые обозначения теории эллиптических интегралов и функций [17–19].

Функция $I(k)$ имеет обратную функцию, так как $\partial I{\text{/}}\partial k \ne 0$. Действительно, используя известные [18] правила дифференцирования полных эллиптических интегралов, из выражения (1.8) можно получить

Но при выполнении ограничений (1.5) на параметр $k$ справедливы неравенства $\Pi (2{{k}^{2}},k) > 0$ и $2E(k) > K(k)$. Поэтому $\partial I{\text{/}}\partial k > 0$.

Функция (1.3) зависит только от переменной $I$:

где $k = k(I)$ – функция, обратная к функции (1.8). Для частоты колебаний имеем выражение

В переменных действие-угол $I,\;w$ уравнения движения (1.2) записываются в виде

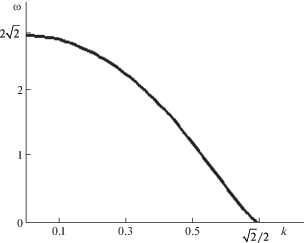
Для частоты (1.11) справедливо неравенство $0 < \omega < 2\sqrt 2 $. В рассматриваемом интервале $0 < k < \sqrt 2 {\text{/}}2$ функция $\omega (k)$ является монотонно убывающей. Для малых колебаний в окрестности равновесия $(0 < k \ll 1)$

а в окрестности сепаратрис (1.7) (когда $0 < 1 - 2{{k}^{2}} \ll 1$)

График функции $\omega (k)$ представлен на рис. 2.

Для дальнейшего отметим, что функция (1.10) удовлетворяет условию невырожденности ${{\partial }^{2}}{{H}_{0}}{\text{/}}\partial {{I}^{2}} \ne 0$. В самом деле, вычисления показывают, что

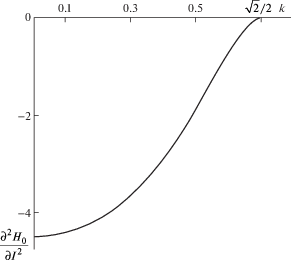
В интервале $0 < k < \sqrt 2 {\text{/}}2$ величина ${{\partial }^{2}}{{H}_{0}}{\text{/}}\partial {{I}^{2}}$ отрицательна и монотонно возрастает. Для малых колебаний справедлива оценка

а вблизи сепаратрис

График функции ${{\partial }^{2}}{{H}_{0}}{\text{/}}\partial {{I}^{2}}$показан на рис. 3.

Далее рассматривается случай, когда орбиты точек ${{P}_{1}}$ и ${{P}_{2}}$ близки к круговым $(0 < e \ll 1)$. Решается задача о существовании и устойчивости периодических движений точки ${{P}_{3}}$ вдоль прямой $x = y = 0$ с периодом, кратным периоду обращения точек ${{P}_{1}}$ и ${{P}_{2}}$ по их орбитам. Для периодических орбит, лежащих в малой окрестности сепаратрис, аналогичная задача рассматривалась в [13, 14].

2. Субгармонические колебания. Пусть орбиты точек ${{P}_{1}}$ и ${{P}_{2}}$ близки к круговым. При малых значениях $e$ функция Гамильтона (1.1) записывается в виде

где ${{H}_{0}}$ – функция (1.3), а

Пусть значение $I = {{I}_{0}}$ переменной действие таково, что частота (1.11) прямолинейных колебаний точки ${{P}_{3}}$ в случае круговых орбит точек ${{P}_{1}}$ и ${{P}_{2}}$ будет рациональным числом $n{\text{/}}m$, где $n$ и $m$ – взаимно простые натуральные числа. Из (1.12) тогда следует, что

т.е. в невозмущенной системе с функцией Гамильтона ${{H}_{0}}$ колебания точки ${{P}_{3}}$ будут периодическими с периодом $2\pi m{\text{/}}n$. Следуя [20], рассмотрим задачу о существовании и устойчивости периодических движений в возмущенной системе с функцией Гамильтона (2.1).

2.1. Общая схема исследования. Невозмущенная система является невырожденной (см. (1.13) и рис. 3). Пусть ${{H}_{1}}(I,w,\nu )$ – функция (2.2), записанная в переменных $I,w$, отвечающих движению с функцией Гамильтона ${{H}_{0}}$. Через $\left\langle {{{H}_{1}}} \right\rangle $ обозначим ее среднее значение на невозмущенном движении (2.3):

Величина (2.4) – функция от ${{I}_{0}}$ и ${{w}_{0}}$. Пусть существует ${{w}_{0}}$ такое, что

и при этом тогда [20] существует $2\pi m$-периодическое движение полной системы с функцией Гамильтона (2.1), которое аналитично по $e$ и при $e$ = 0 переходит в движение (2.3) невозмущенной системы.

Вопрос об устойчивости этого $2\pi m$-периодического движения решается рассмотрением величин

на невозмущенном движении (2.3). Согласно [20], при ${{\chi }_{1}} < 0$ периодическое движение неустойчиво, а при ${{\chi }_{1}} > 0$ устойчиво в первом (линейном) приближении. В [21] при помощи КАМ-теории [22] показано , что если ${{\chi }_{1}} > 0$ и при этом ${{\chi }_{2}} \ne 0$, то периодическое движение устойчиво по Ляпунову (не только в первом приближении, но и в строгой нелинейной постановке задачи).

2.2. О численном способе построения замены z, ${{p}_{z}} \to I$, w. Для реализации описанной схемы исследования необходимо предварительно получить каноническое преобразование z, ${{p}_{z}} \to I$, w, приводящее функцию Гамильтона ${{H}_{0}}$ к виду (1.10). Следуя [23], укажем как это можно сделать численным способом в общем случае автономной гамильтоновой системы с одной степенью свободы, а не только в нашей конкретной задаче.

Пусть в системе с функцией Гамильтона $H(q,p)$ в некотором интервале изменения постоянной $h$ интеграла энергии $H(q,p) = h$ движение имеет периодический характер и описывается формулами (через $t$ обозначается независимая переменная)

Пусть $I$ – переменная действие, а $h(I)$ – функция $H(q,p)$, записанная в переменных действие-угол $I,w$. Тогда каноническое преобразование $q,p \to I,w$ может быть записано в виде

Для доказательства достаточно убедиться, что скобка Пуассона $(q{\text{*}},p{\text{*}})$ функций (2.9) по переменным $w,I$ равна единице. Действительно, учитывая тождества $H(q{\text{*}},p{\text{*}}) = h$ и

можно показать, что

В рассматриваемой задаче, когда $H$– это функция ${{H}_{0}}$ из (1.3), замена переменных $z,{{p}_{z}} \to I,w$ задается получаемыми из (1.2) и (1.12) дифференциальными уравнениями

Будем полагать, что (см. рис. 1)

Функции $z$ и ${{p}_{z}}$ будут соответственно нечетной и четной функциями $w$. Зависимость этих функций от $I$ проявляется через параметр $k$, который при численном интегрировании уравнений (2.10) , (2.11) считается заданной величиной.

2.3. О существовании и устойчивости прямолинейных субгармонических колебаний точки ${{P}_{3}}$ и их устойчивости. Если в формуле (2.4) перейти к интегрированию по переменной $w$, определяемой вторым из равенств (2.3), то для среднего значения функции (2.2) получим следующее выражение:

Очевидно, что при $n \ne 1$ величина (2.12) тождественно равняется нулю. Следовательно, при анализе субгармонических колебаний, существование которых можно установить уже в первом приближении по $e$, надо в невозмущенном движении (2.3) положить n = 1. Поэтому далее значение частоты невозмущенного движения задается равенством

в котором $m$ – натуральное число $(m = 1,2,...)$. Соответствующие этим частотам периоды колебаний точки ${{P}_{3}}$ и ее максимальное отклонение ${{z}_{{\max }}}$ от положения равновесия $z = 0$ монотонно возрастают с ростом $m$. При $m = 1$ период колебаний точки ${{P}_{3}}$ равен периоду обращения точек ${{P}_{1}}$ и ${{P}_{2}}$ по их орбитам, а максимальное отклонение точки ${{P}_{3}}$ от положения равновесия приблизительно равно расстоянию между точками ${{P}_{1}}$ и ${{P}_{2}}$ (${{z}_{{\max }}} = 1.044$), а при $m = 100$ период колебаний в сто раз больше периода обращения точек ${{P}_{1}}$ и ${{P}_{2}}$, при этом ${{z}_{{\max }}} = 27.115$.

В излагаемом численно-аналитическом исследовании мы ограничимся значениями $m$, не превосходящими 100.

Заметим, что функция $G(z)$ под знаком интеграла в выражении (2.12) – четная $\pi $-периодическая функция $w$. Положив в (2.12) $n = 1$ и учтя это замечание, находим следующее выражение для среднего значения функции ${{H}_{1}}$:

где коэффициент ${{a}_{m}}$ равен нулю, если $m$ – нечетное число, а при $m$ четном

Для нахождения коэффициентов (2.15) численным способом рассмотрим вспомогательную функцию ${{\varphi }_{m}}(w)$, определяемую дифференциальным уравнением

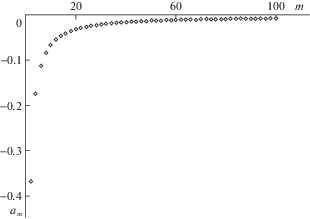
с начальным условием ${{\varphi }_{m}}(0) = 0$. Проинтегрировав это уравнение совместно с уравнениями (2.10), (2.11) (в которых $\omega = 1{\text{/}}m$) от $w = 0$ до $w = 2\pi $, получим ${{a}_{m}} = {{\varphi }_{m}}(2\pi )$.

Вычисления показали, что для всех рассмотренных четных $m$ (от $m = 2$ до $m = 100$) коэффициент ${{a}_{m}}$ отрицателен. График функции ${{a}_{m}}$ показан на рис. 4.

Поскольку величина ${{a}_{m}}$ отлична от нуля, то получаемое из (2.5) и (2.14) уравнение для порождающих значений ${{w}_{0}}$ эквивалентно уравнению $\sin m{{w}_{0}} = 0$, которое на промежутке $[0,2\pi )$ имеет $2m$ корней

При этих значениях ${{w}_{0}}$ для левой части соотношения (2.6) получаем выражение

а величины ${{\chi }_{1}}$ и ${{\chi }_{2}}$ из (2.7) будут такими:

Так как величины ${{a}_{m}}$ и ${{\partial }^{2}}{{H}_{0}}{\text{/}}\partial {{I}^{2}}$ отрицательны, то (см. раздел 2.1) при достаточно малых эксцентриситетах $e$ значения ${{w}_{0}}$ из (2.17) порождают $2m$ периодических решений $z{\text{*}}\left( \nu \right)$, $p_{z}^{*}(\nu )$ уравнений с функцией Гамильтона (2.1) периода $2\pi m$ по $\nu $. Эти периодические решения соответствуют двум различным $2\pi m$-периодическим движениям точки ${{P}_{3}}$. Одно из них отвечает четным, а другое нечетным значениям $s$. Первое движение неустойчиво (для него ${{\chi }_{1}} < 0$), а второе устойчиво по Ляпунову (для него ${{\chi }_{1}} > 0$, ${{\chi }_{2}} \ne 0$). Движения, отвечающие оставшимся $(2m - 2)$-м решениям получаются из этих двух сдвигом начальной фазы ${{w}_{0}}$ на величину, кратную $2\pi {\text{/}}m$.

2.4. О неустойчивости прямолинейных субгармонических колебаний по отношению к пространственным возмущениям. Для исследования устойчивости периодических движений $z{\text{*}}\left( \nu \right)$, $p_{z}^{*}(\nu )$ точки ${{P}_{3}}$ вдоль прямой $x = y = 0$ положим

и рассмотрим линеаризованные уравнения возмущенного движения. Им соответствует квадратичная относительно ${{q}_{j}}$, ${{p}_{j}}$ $(j = 1,2,3)$ функция Гамильтона где $\Gamma _{2}^{{(2)}}$ и $\Gamma _{2}^{{(3)}}$ – квадратичные формы относительно ${{q}_{i}}$, ${{p}_{i}}$ $(i = 1,2)$ и ${{q}_{3}}$, ${{p}_{3}}$ соответственно. Коэффициенты квадратичных форм $2\pi m$-периодичны по $\nu $.

Возмущенное движение для пространственных переменных ${{q}_{i}}$, ${{p}_{i}}$ $(i = 1,2)$ отделяется от движений для возмущений, оставляющих точку ${{P}_{3}}$ на прямолинейной траектории. Устойчивость по отношению к этим возмущениям исследована выше. Поэтому будем рассматривать линейные уравнения возмущенного движения, отвечающие пространственным возмущениям ${{q}_{i}}$, ${{p}_{i}}$ $(i = 1,2)$.

Характеристическое уравнение матрицы Х$(\nu )$ фундаментальных решений системы с функцией Гамильтона $\Gamma _{2}^{{(2)}}$, вычисленной при $\nu = 2\pi m$, как и для всякой линейной гамильтоновой системы с периодическими коэффициентами [24], будет возвратным:

где коэффициент ${{c}_{1}}$ равен следу матрицы Х$(2\pi m)$, а ${{c}_{2}}$ – сумма всех ее главных миноров второго порядка. Коэффициенты ${{c}_{1}}$ и ${{c}_{2}}$ – аналитические функции эксцентриситета $e$ $(0 < e \ll 1)$.

Если уравнение (2.20) имеет хотя бы один корень, модуль которого больше единицы, то исследуемое периодическое движение неустойчиво. Причем не только в линейном приближении, но и в строгом нелинейном смысле [24]. В изучаемой задаче для всех $2\pi m$-периодических движений $(m = 2,4,...,100)$ реализуется как раз этот случай. Чтобы убедиться в этом, достаточно, ввиду аналитичности коэффициентов ${{c}_{1}}$ и ${{c}_{2}}$ по $e$, проверить, что уравнение (2.20) имеет корень, по модулю больший единицы, при нулевом значении эксцентриситета.

При $e = 0$ имеем такую функцию Гамильтона, отвечающую линеаризованным уравнениям движения:

К каноническим уравнениям, отвечающим этой функции Гамльтона, надо еще добавить уравнения (1.2) для $z{\text{*}}\left( \nu \right)$, $p_{z}^{*}(\nu )$ с начальными условиями $z{\text{*}}\left( 0 \right) = 0$, $p_{z}^{*}(0)$ = $2\sqrt 2 k$ (где для заданного $m$ величина $k$ находится из соотношения (2.13)).

Задав $m$ $(m = 2,4,...{\text{ }}100)$ и проинтегрировав от $\nu = 0$ до $\nu = 2\pi m$ систему уравнений для нахождения $z{\text{*}}\left( \nu \right)$, $p_{z}^{*}(\nu )$ и элементов матрицы ${{x}_{{ij}}}(\nu )$ фундаментальных решений, получим величины ${{c}_{1}}$ и ${{c}_{2}}$. Корни уравнения (2.20) выражаются через ${{c}_{1}}$ и ${{c}_{2}}$ по формулам

Вычисления показали, что для каждого $m = 2,4,...{\text{ }},100$ среди корней (2.22) есть корень, модуль которого больше единицы. Например, при $m = 2$ (когда $\omega = 1{\text{/}}2$, $k = 0.608$, $h = - 0.522$, ${{c}_{1}} = 18.500$, ${{c}_{2}} = 78.575$) таких корней даже два:

При остальных $m$ $(m = 4,...{\text{ }},100)$ два из корней (2.22) вещественны и два комплексно сопряженные. При наибольшем из рассмотренных $m$ ($m = 100$, $\omega = 1{\text{/}}100$, $k = 0.701$, $h = - 0.037$, ${{c}_{1}} = 6.218$, ${{c}_{2}} = - 9.683$) корни таковы:

Заключение. Рассмотрены $2\pi m$-периодические прямолинейные движения точки ${{P}_{3}}$, которые обнаруживаются уже при анализе первого приближения по $e$. Оказалось, что для этих движений $m$ – четное число. Рассмотрение четных значений $m$ от $m = 2$ до $m = 100$ показало, что для возмущений, не уводящих точку ${{P}_{3}}$ с прямой, $m$ движений устойчивы по Ляпунову и $m$ движений неустойчивы. Если же возмущения имеют общий пространственный характер, то все $m$ пар $2\pi m$-периодических движений ($m = 2,4,...{\text{ }},100$) неустойчивы.

Для решения задачи о существовании субгармонических колебаний периода $2\pi m$ ($m$ = 1, 2, …) можно использовать иные подходы, отличные от примененных выше. Задача о существовании таких движений, обладающих теми или иными свойствами симметрии, исследовалась ранее [8] при помощи специального алгоритма, разработанного для обратимых систем. Существование симметричных субгармонических колебаний для сколь угодно больших $m$ [11] устанавливается при помощи анализа функции Мельникова [25].

Многие вопросы о субгармонических колебаниях точки ${{P}_{3}}$ требуют дополнительного исследования. Например, анализ более высоких приближений по $e$ позволил бы рассмотреть другие типы субгармонических движений. Несомненный интерес представляет также задача о численном продолжении субгармонических колебаний на значения $e$, не являющиеся малыми [8].

Работа выполнена за счет гранта Российского научного фонда (проект № 19-11-00116) в Московском авиационном институте (Национальном исследовательском университете) и в Институте проблем механики им. А.Ю. Ишлинского РАН.