Прикладная математика и механика, 2019, T. 83, № 3, стр. 393-402

Для цилиндра в неограниченном циркуляционном потоке идеальной несжимаемой жидкости с монотонно убывающей завихренностью была обнаружена сдвиговая неустойчивость [1], отвечающая за появление ветровых волн на воде [2], и неустойчивость различных сложных вихревый течений [3]. Бесконечный цилиндр в циркуляционном потоке идеальной несжимаемой жидкости – простейшая двумерная система, в которой реализуется сдвиговая неустойчивость. Для проведения экспериментальных исследований по выявлению такой неустойчивости необходимо рассмотреть случай ограниченной области течения. Было показано [4], что в этом случае в системе существует еще один тип неустойчивости, который реализуется в течении с постоянной завихренностью (в том числе и при нулевой завихренности) и связан именно с ограниченностью области течения. Был проведен анализ ограниченной задачи в линейном приближении и построен лагранжиан для потенциального течения [4]. Изучение обнаруженной неустойчивости течения в ограниченной области с постоянной завихренностью в нелинейном приближении – основная задача данной работы. Рассматриваемое среднее течение – известное течение Куэтта между вращающимися цилиндрами в вязкой жидкости, анализу, устойчивости которого посвящено большое количество исследований [5]. Исследовалась устойчивость системы из двух незакрепленных цилиндров в невязком потенциальном потоке между ними [6]. При анализе устойчивости твердого тела в идеальной жидкости получен обобщенный критерий устойчивости в линейном приближении [7, 8].

Для решения задачи в нелинейном приближении удобно использовать подход Лагранжа, который обладает рядом преимуществ. Найденная функция Лагранжа системы позволяет сразу сделать вывод об устойчивости или неустойчивости системы, не прибегая к решению дисперсионного уравнения.

Впервые уравнения Лагранжа для движения твердого тела в потенциальном потоке жидкости с однозначным потенциалом были применены Томсоном и Тэтом [9] и обоснованы Кирхгофом [10]. Для движения торообразных твердых тел в многосвязной области, занятой жидкостью, потенциал скорости может быть неоднозначным. Для этого случая Томсон [11] вывел новый вид функции Лагранжа, в котором по аналогии с методом Рауса исключения циклической координаты, добавлены произведения циркуляций и расходов через перегородки твердых тел. Эта идея далее была развита Жуковским [12] и его последователями [13, 14] для исследования динамики твердого тела с полостями, заполненными жидкостью.

В рассматриваемой задаче жидкость заполняет зазор между двумя круговыми цилиндрами, вставленными один в другой. Если расстояние между осями цилиндров не меняется, а течение потенциально, то для построения функции Лагранжа можно применять подход Томсона [11] и Жуковского [12]. Таким путем можно вычислить силу, действующую на внутренний цилиндр (задача Чизотти [15]). Однако в рассматриваемом здесь случае расстояние между осями цилиндров меняется и, кроме того, необходимо учитывать постоянную завихренность.

Для получения функции Лагранжа используется ее более общий вид, выведенный ранее [16], на основе которого для произвольного движения внутреннего цилиндра предложен алгоритм определения функции Лагранжа в виде разложения в ряд по малому смещению оси внутреннего цилиндра. Из найденной функции Лагранжа получено условие устойчивости и силы, действующей на цилиндр, в точной нелинейной постановке. Проведено сравнение результатов для частного случая циркуляционного обтекания внутреннего неподвижного цилиндра. Найденное выражение для силы совпадает с точным аналитическим выражением, полученным Чизотти [16]. Решение в линейном приближении полностью совпадает с полученным ранее решением [4].

Использование подхода Лагранжа во многих задачах механики жидкости также позволяет выявлять интегральные характеристики течений [17]. Проводимое ниже исследование представляет интерес как в связи с разделением двух неустойчивостей (сдвиговой и возникающей из-за ограниченности области течения) в эксперименте, так и в связи с развитием подхода Лагранжа в механике жидкости. Рассматриваемая неустойчивость имеет невязкую природу. Вязкий механизм неустойчивости системы, исследовался П.Л. Капицей [18] и были даны оценки вязких сил.

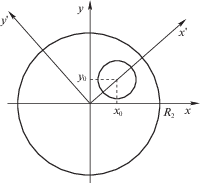
1. Постановка задачи. Рассматривается система, состоящая из двух вставленных один в другой цилиндров: внешний цилиндр радиуса ${{R}_{2}}$ жестко закреплен, внутренний цилиндр радиуса ${{R}_{1}}$ подвижный. В положении равновесия цилиндры коаксиальны. Область между ними заполнена несжимаемой идеальной жидкостью, поле скорости которой имеет циркуляцию, постоянную завихренность и удовлетворяет условиям непротекания на обоих цилиндрах.

Положение подвижного внутреннего цилиндра удобно описывать с помощью координат центра его поперечного сечения ${{x}_{0}}$, ${{y}_{0}}$ (рис. 1), ${{\dot {x}}_{0}}$ и ${{\dot {y}}_{0}}$ – компоненты вектора скорости его движения. В рамках плоской задачи требуется получить уравнения динамики внутреннего цилиндра с учетом гидродинамических сил и решить задачу устойчивости коаксиального стационарного течения при смещениях внутреннего цилиндра.

2. Метод решения. Метод решения задачи заключается в построении функции Лагранжа $L({{x}_{0}},{{y}_{0}},{{\dot {x}}_{0}},{{\dot {y}}_{0}})$, с помощью которой уравнения динамики цилиндра запишутся в лагранжевой форме

Если течение потенциально (${\mathbf{v}} = \nabla \Phi $) и потенциал $\Phi $ – однозначная функция, то функция Лагранжа равна кинетической энергии жидкости [15]: $L = {{\rho }_{0}}\int_S {\frac{{{{{\mathbf{v}}}^{2}}}}{2}dxdy} $, где ${{\rho }_{0}}$ – плотность жидкости, а $S$ – область, занятая жидкостью.

Если двусвязная полость внутри твердого тела заполнена жидкостью, течение которой имеет циркуляцию $\Gamma $, то потенциал $\Phi $ – неоднозначная функция.

В рассматриваемом случае полость ограничена двумя окружностями (рис. 1). При обходе контура сечения внутреннего цилиндра потенциал изменяется на величину $\Gamma $, тогда меняется вид функции Лагранжа: к ней добавляется полученное Томсоном [11] слагаемое

где $P$ – перегородка, искусственно вводимая в многосвязных областях [15], $\chi $ – относительный поток жидкости через воображаемую перегородку $P$, ${\mathbf{v}}{\text{*}}$ – скорость точек системы координат, скрепленной с твердым телом (так называемая переносная скорость [19]), а ${{{\mathbf{v}}}_{0}}$ и ${\mathbf{\Omega }}$ – поступательная скорость движения и угловая скорость твердого тела, соответственно. Было показано [16], что добавочное слагаемое (2.1) и функцию Лагранжа можно записать в виде

Эта формула для функции Лагранжа была распространена [16, 20] на общий случай, в котором течение имеет циркуляцию $\Gamma $ и постоянную завихренность $\omega ,$ а граница полости деформируется. При этом в качестве скорости ${\mathbf{v}}{\text{*}}$ принимается скорость воображаемой несжимаемой среды. Значение ${\mathbf{v}}{\text{*}}$ на границе совпадает со скоростью точек границы, а внутри области $S$ значение ${\mathbf{v}}{\text{*}}$ однозначно определяется положением границы. По аналогии с понятием переносной скорости, как распределения скорости точек системы координат, скрепленной с твердым телом, введено понятие скорости воображаемой несжимаемой среды, скрепленной с границей области течения [16]. Формула (2.2) распространяет обобщенную формулу Томсона для функции Лагранжа на случай течений с постоянной завихренностью в произвольной полости с деформируемой границей.

3. Нахождение скорости ${\mathbf{v}}{\text{*}}$. Скорость ${\mathbf{v}}{\text{*}}$ может быть найдена с помощью функции ${\mathbf{X}}({{x}_{0}},{{y}_{0}},{\mathbf{X}}{\text{*}})$ отображения фиксированной области ${\mathbf{X}}* \in \tilde {S}$ на область течения ${\mathbf{X}} \in S$ с якобианом преобразования равным единице (${\text{det}}\left\| {\partial X{\text{/}}\partial X{\text{*}}} \right\|$ = 1), и находится как производная сложной функции:

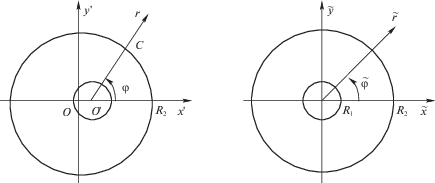
Преобразование ${\mathbf{X}}({{x}_{0}},{{y}_{0}},{\mathbf{X}}*)$, сохраняющее площадь, строится так. В физической области $S$ введем полярные координаты $r$, $\varphi $ с центром, совпадающим с центром круга радиуса ${{R}_{1}}$ (левая часть рис. 2). Воображаемая область $\tilde {S}$ – кольцо, ограниченное двумя концентрическими окружностями с теми же радиусами ${{R}_{1}}$ и ${{R}_{2}}$ (правая часть рис. 2). Введем полярные координаты $\tilde {r}$, $\tilde {\varphi }$ с центром, совпадающим с центром концентрических окружностей. Преобразование координат $r,\varphi \to \tilde {r},\tilde {\varphi }$, сохраняющее площадь (с единичным якобианом) $rdrd\varphi = \tilde {r}d\tilde {r}d\tilde {\varphi }$, удобно строить в переменных $\rho ,\varphi \to \tilde {\rho },\tilde {\varphi }$:

Тогда условие сохранения площади элементарной площадки имеет вид $d\rho d\varphi = d\tilde {\rho }d\tilde {\varphi }$.

Введем производящую функцию отображения $F(\varphi ,\tilde {\rho }) = (\varphi + \Phi (\varphi ))\tilde {\rho }$. Тогда отображение, сохраняющее площадь, находится из уравнений (см. [21])

Используя уравнение (3.3) и значения $\rho $ и $\tilde {\rho }$ на границе внутреннего цилиндра, получим уравнение для функции $\Phi (\varphi )$

Его решение имеет вид

Формулы (3.2)–(3.4) определяют отображение области течения (рис. 2 слева) на концентрическое кольцо ${{R}_{1}} < \tilde {r} < {{R}_{2}}$ (рис. 2 справа). Декартовы компоненты скорости ${\mathbf{v}}{\text{*}}$ согласно равенству (3.1) имеют вид

Зависимости $r(\tilde {r},\tilde {\varphi })$ и $\varphi (\tilde {r},\tilde {\varphi })$ определяются с помощью соотношений (3.2)–(3.4). По формулам (3.5) компоненты скорости вычисляются точно.

4. Нахождение потенциального поля скорости. Для вычисления функции Лагранжа (2.1) необходимо найти поле скорости ${\mathbf{v}}$. Для начала рассмотрим более простой случай потенциального среднего течения. Удобно перейти к комплексным переменным. Так, ось внутреннего цилиндра смещена в точку ${{z}_{0}} = {{x}_{0}} + i{{y}_{0}}$ (рис. 1), а комплексный вектор скорости жидкости между двумя цилиндрами на комплексной плоскости z = $x + iy$ можно записать в виде

где ${{W}_{\Gamma }}$ – комплексный потенциал чисто циркуляционного течения, $W$ – комплексный потенциал бесциркуляционного течения.

С помощью преобразования поворота $z = \frac{{{{z}_{0}}}}{{{{r}_{0}}}}z{\text{'}}$ можно перейти из исходной системы координат $z = x + iy$ в систему координат $z{\text{'}} = x{\text{'}} + iy{\text{'}}$, в которой внутренний цилиндр оказывается смещен только по оси $Ox{\text{'}}$ на величину ${{r}_{0}} = \sqrt {x_{0}^{2} + y_{0}^{2}} $. Координаты этих систем связаны зависимостями

В системе $z{\text{'}} = x{\text{'}} + iy{\text{'}}$ комплексную скорость жидкости можно переписать в виде

Рассмотрим циркуляционную и бесциркуляционную части по отдельности.

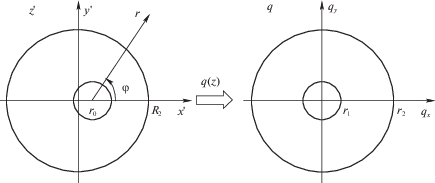
Циркуляционное течение. Рассмотрим циркуляционное течение вокруг смещенного цилиндра. Потенциал $W_{\Gamma }^{'}$ определяется с помощью конформного отображения комплексной плоскости $z{\text{'}}$ действительного течения на плоскость $q$ (рис. 3).

Введем обозначения

Отображение области между сечениями цилиндров на кольцо ${{r}_{1}} < \left| q \right| < {{r}_{2}}$ можно осуществить с помощью дробно-линейного преобразования

Комплексный потенциал циркуляционного течения имеет вид

Кинетическая энергия жидкости в кольце приводится к интегралу по границе

Нормаль является внешней по отношению к области, занятой жидкостью. Производная функции тока по нормали к внешней окружности равна скорости жидкости с обратным знаком: ${{\left. {\partial \Psi {\text{/}}\partial n} \right|}_{{{{C}_{2}}}}}$ = $ - {v}$, а производная по нормали к внутренней окружности равна скорости жидкости: ${{\left. {\partial \Psi {\text{/}}\partial n} \right|}_{{{{C}_{1}}}}}$ = ${v}$. Соответствующие интегралы равны циркуляции с выбранным знаком. Таким образом, для кинетической энергии получаем выражение

Поскольку рассматривается чисто циркуляционное течение, в котором внутренний цилиндр неподвижен, скорость ${\mathbf{v}}* = 0$. Функция Лагранжа согласно второму равенству (2.2) равна кинетической энергии с обратным знаком: L = $\frac{1}{2}\Gamma ({{\Psi }_{2}} - {{\Psi }_{1}})$.

Сила, действующая на цилиндр со стороны циркуляционного потока, вычисляется по формуле Лагранжа $F = \partial L{\text{/}}\partial {{r}_{0}}$. Выполнив дифференцирование, для силы получим выражение

Чизотти было получено точное выражение для силы. Оно приведено в монографии Ламба [15]. Если устранить небольшую опечатку, то это выражение тождественно приведенному выше, что убедительно подтверждает достоверность метода Лагранжа и приведенного точного выражения функции Лагранжа для чисто циркуляционного течения.

Потенциальное течение. При отсутствии завихренности и циркуляции потенциал течения можно представить в виде

где $\dot {x}_{0}^{'}$ и $\dot {y}_{0}^{'}$ – компоненты скорости движения внутреннего цилиндра в системе координат $x{\text{'}}$, $y{\text{'}}$. Потенциалы ${{W}_{x}}$ и ${{W}_{y}}$ можно записать в виде рядов Лорана

Из них можно получить все коэффициенты ${{A}_{k}}$ и ${{B}_{k}}$ в виде рядов по степеням ${{r}_{0}}$. С точностью до $O(r_{0}^{3})$ найдем

Такой порядок точности достаточен для определения условий устойчивости.

5. Постоянная завихренность. Для учета постоянной завихренности удобно перейти в систему координат $z_{\omega }^{'} = x_{\omega }^{'} + iy_{\omega }^{'}$, вращающуюся с угловой скоростью $\omega $: $z{\text{'}} = z_{\omega }^{'}{{e}^{{i\omega t}}}$. В системах $z{\text{'}}$ и $z_{\omega }^{'}$ комплексные координаты центра поперечного сечения внутреннего цилиндра и его скорость в начальный момент времени связаны между собой:

Для декартовых компонент центра поперечного сечения имеем

и для компонент скорости

Во вращающейся системе координат $z_{\omega }^{'}$ течение имеет комплексный потенциал

При возвращении в исходную систему скорости центра $\dot {x}_{{\omega 0}}^{'}$, $\dot {y}_{{\omega 0}}^{'}$ нужно заменить на $\dot {x}_{0}^{'}$, $\dot {y}_{0}^{'} - \omega {{r}_{0}}$. Тогда в разд. 4

Таким образом, комплексный вектор скорости (4.1) представляется в следующем окончательном виде:

Величины $W_{\Gamma }^{'}$, ${{W}_{x}}$ и ${{W}_{y}}$ определены формулами (4.3)–(4.5).

6. Разложения для лагранжиана. Лагранжиан (2.1) удобно вычислять, перейдя к полярным координатам на плоскости $\tilde {r}$, $\tilde {\varphi }$, изображенной на рис. 2 справа. Имеем выражение

Подставляя в него скорость течения (5.1), используя связь координат (3.3), выражение для скорости ${\mathbf{v}}{\text{*}}$ (3.5) и обозначения (4.2), получим

Введем обозначения

С помощью замены

найдем с точностью до членов, квадратичных по координатам и скоростям, функцию Лагранжа в координатах ${{x}_{0}}$, ${{y}_{0}}$

Для того, чтобы получить функцию Лагранжа всей системы, необходимо добавить к найденному выражению кинетическую энергию движения цилиндра, т.е.

В полученной функции Лагранжа присутствуют линейные по скоростям слагаемые (гироскопические члены). Для того чтобы избавиться от них, перейдем во вращающуюся систему координат

В новых координатах функция Лагранжа имеет вид

где $T$ – квадратичная форма по скоростям, функция $\Pi $ не зависит от скоростей.

Вычисленная с этой точностью функция Лагранжа соответствует динамическим уравнениям линейной теории [4]. В нелинейном приближении следует учесть члены порядка четвертых степеней по ${{x}_{0}}$, ${{y}_{0}}$. К функции Лагрнажа (6.1) добавится слагаемое

Нелинейный член в потенциале оказывается отрицательным, что ведет к неустойчивости системы в случае, если линейный член обращается в нуль.

7. Анализ устойчивости. В линейном приближении, согласно равенству (6.1), потенциальная энергия оказывается положительной, а система по теореме Лагранжа – устойчивой при

Если $M > {{M}_{*}}$ система оказывается неустойчивой. Этот вывод совпадает с результатом анализа устойчивости в линейном приближении [4].

Решение задачи устойчивости при $M = {{M}_{*}}$, требует учета высших степеней по ${{X}_{0}}$, ${{Y}_{0}}$ (6.2); в результате потенциальная энергия отрицательна:

Таким образом, задача устойчивости полностью решена: при $M < {{M}_{*}}$ стационарная точка ${{X}_{0}} = 0$, ${{Y}_{0}} = 0$ устойчива; при $M \geqslant {{M}_{*}}$ – неустойчива.

Параметры $\Gamma $ и $\omega $ в рамках модели идеальной жидкости остаются произвольными числами. Рассматриваемое среднее течение с постоянной завихренностью между двумя цилиндрами удовлетворяет как уравнениям Эйлера, так и уравнениям Навье–Стокса. Таким образом, параметры $\Gamma $ и $\omega $ можно связать с угловыми скоростями вращения цилиндров ${{\omega }_{1}}$ и ${{\omega }_{2}}$, определяющими течения Куэтта в вязкой жидкости. Угловая компонента скорости течения Куэтта имеет вид

Для нее в принятых обозначениях имеем

Таким образом, параметры $\omega $ и $\Gamma $ выражены через угловые скорости цилиндров ${{\omega }_{1}}$ и ${{\omega }_{2}}$.

Условие устойчивости, выраженное через угловые скорости вращения цилиндров ${{\omega }_{1}}$ и ${{\omega }_{2}}$, примет вид

При $M \geqslant {{M}_{*}}$ равновесие неустойчиво.

Исследование выполнено за счет гранта Российского научного фонда (19-19-00373).