Проблемы машиностроения и надежности машин, 2023, № 2, стр. 71-81

Установление закономерности повышения износостойкости модифицированного радиального подшипника скольжения

Д. У. Хасьянова^1, *, М. А. Мукутадзе^2, **

¹ Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

² Ростовский государственный университет путей сообщения
Ростов-на-Дону, Россия

^* E-mail: dinara.khasyanova@mail.ru
^** E-mail: murman1963@yandex.ru

Поступила в редакцию 16.01.2022
После доработки 17.10.2022
Принята к публикации 20.10.2022

EDN: ASKRNH
DOI: 10.31857/S0235711923010066

Полный текст (PDF)

Аннотация

Для повышения ресурса и уровня надежности в статье рассмотрен радиальный подшипник скольжения с металлическим покрытием поверхности вала и адаптированным к условиям трения опорным профилем подшипниковой втулки. Теоретическое исследование проведено с использованием общеизвестных уравнений движения микрополярной жидкости для “тонкого слоя”, уравнения неразрывности и уравнения, описывающего радиус расплавленного контура вала с учетом формулы скорости диссипации механической энергии. Найдено точное автомодельное и асимптотическое решение с учетом и без учета расплава покрытия, а также при учете зависимости вязкости смазочного материала и расплава покрытия, обладающих при ламинарном режиме течения микрополярными реологическими свойствами, от давления. Экспериментальное исследование модифицированного подшипника скольжения проведено на модернизированной машине трения модели ИИ 5018.

Ключевые слова: гидродинамический режим, повышение износостойкости, уровень надежности, металлическое покрытие, адаптированный профиль, фаз эволюции трибосистемы, расплавы покрытия

Вопросы надежности машин всегда были актуальны для промышленности, а повышение их ресурса – важной задачей, имеющей большое экономическое значение. Для повышения эффективности производства и производительности труда возникает необходимость решения проблемы надежности вновь создаваемых и эксплуатируемых машин на этапе проектирования машин, когда принимаются принципиальные решения о конструктивном исполнении деталей и их сопряжений, применяемых материалах и технологиях, обеспечивающих требуемый уровень надежности. В этой связи данное исследование является актуальным, поскольку затрагивает проблемы прогнозирования и обеспечения показателей надежности одного из самых распространенных сопряжений деталей машин в технике – подшипника скольжения. При этом подшипники скольжения определяют безотказность работы машин и механизмов, а их ресурс лимитирует состояние (износом) рабочих поверхностей – поверхностей трения.

Отказы подшипников скольжения машин и технологического оборудования приводят к их полной остановке, прекращению производственных процессов, значительным временным и финансовым затратам. В связи с этим прогнозирование ресурса подшипников скольжения является актуальной проблемой как на этапе проектирования, так и на этапе эксплуатации машин и механизмов, что требует развития моделей отказов, методов расчета ресурса подшипников скольжения на основе физики процессов с учетом конструктивных, эксплуатационных и режимных факторов.

Разработке расчетной модели радиальных подшипников скольжения с металлическим покрытием посвящено значительное количество работ [1–5]. Однако процесс смазывания на расплавах покрытий не является самоподдерживающимся процессом. Для обеспечения самоподдерживающегося процесса смазывания подшипников скольжения возникает необходимость не только в наличии покрытия на одной из контактных поверхностей, но и постоянного наличия смазочного материала, которое можно обеспечить при постоянной подаче смазочного материала или пористым покрытием на другой контактной поверхности [6–15], а также нестандартным опорным профилем.

В предлагаемой статье приводится расчетная модель радиального подшипника скольжения с нестандартным опорным профилем подшипниковой втулки и покрытием поверхности вала с учетом зависимости вязкости смазочного материала и расплава покрытия, обладающая микрополярными реологическими свойствами в зависимости от давления при ламинарном режиме течения. Визуализация разработанных теоретических расчетных моделей и оценка их точности, выполненная на основе сравнения результатов их численного анализа и триботехнических параметров, рассчитанных по адекватным регрессионным моделям, полученным экспериментально, доказали их высокую эффективность, точность (в пределах 9–13%) и применимость во всем исследованном диапазоне размеров и нагрузочных скоростных режимов. Параллельный анализ уровня температуры в контактной области и величины коэффициента трения в процессе работы при постепенном прекращении подачи смазочного материала позволил установить последовательность фаз перехода от смазывания маслом к смазыванию металлическим расплавом при сохранении гидродинамического режима.

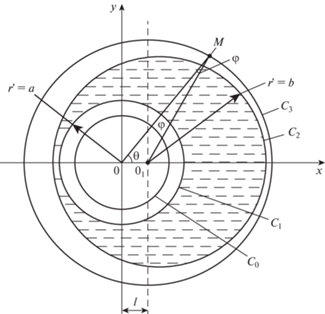
Постановка задачи. Рассматривается установившееся течение несжимаемой жидкости и расплава покрытия в рабочем зазоре, обладающее микрополярными реологическими свойствами. Подшипник с некруговым профилем опорной поверхности неподвижен, а вал при наличии легкоплавкого покрытия на его поверхности вращается со скоростью Ω. В полярной системе координат (рис. 1) $r{\kern 1pt} '$, θ с полюсом в центре вала уравнения контуров вала с легкоплавким покрытием С₁, вала с расплавленным контуром поверхности С₀, подшипниковой втулки некруговым профилем опорной поверхности С₂ и подшипниковой втулки запишутся в виде

(1)

$\begin{gathered} {{C}_{1}}:r{\kern 1pt} ' = {{r}_{0}},\quad {{C}_{0}}:r{\kern 1pt} ' = {{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right), \\ {{С}_{2}}:r{\kern 1pt} ' = {{r}_{1}}\left( {1 + H} \right) - a{\kern 1pt} '\sin \omega \theta ,\quad {{С}_{3}}:r{\kern 1pt} ' = {{r}_{1}}\left( {1 + H} \right), \\ \end{gathered} $

где $H = \varepsilon \cos \theta - \frac{1}{2}{{\varepsilon }^{2}}{{\sin }^{2}}\theta + ...$, $\varepsilon = \frac{e}{{{{r}_{0}}}}$, ${{r}_{0}}$ – радиус вала с легкоплавким покрытием; r₁ – радиус подшипниковой втулки; е – эксцентриситет; ε – относительный эксцентриситет; $\lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)$ – функция, определяющая профиль расплавленного контура покрытия вала; a′ и ω – амплитуда возмущения и параметр адаптированного профиля втулки соответственно.

Рис. 1.

Расчетная модель.

Полагаем, что вязкостные характеристики зависят от давления по закону

(2)

$\mu {\kern 1pt} ' = {{\mu }_{0}}{{e}^{{\tilde {\alpha }p'}}},\quad \kappa {\kern 1pt} ' = {{\kappa }_{0}}{{e}^{{\tilde {\alpha }p'}}},\quad \gamma {\kern 1pt} ' = {{\gamma }_{0}}{{e}^{{\tilde {\alpha }p'}}},$

где μ' – коэффициент динамической вязкости смазочного материала; $\kappa {\kern 1pt} '$, $\gamma {\kern 1pt} '$ – коэффициенты вязкости микрополярного смазочного материала; ${{\mu }_{0}}$ – характерная вязкость ньютоновского смазочного материала; $p{\kern 1pt} '$ – гидродинамическое давление в смазочном слое; $\tilde {\alpha }$ – экспериментальная постоянная величина; ${{\kappa }_{0}}$, ${{\gamma }_{0}}$ – характерная вязкость микрополярного смазочного материала.

Исходными базовыми уравнениями с учетом (2) являются безразмерные уравнения: движения несжимаемой микрополярной жидкости для “тонкого слоя”, уравнение неразрывности и уравнение, описывающее профиль расплавленного контура покрытия поверхности вала с учетом скорости диссипации механической энергии с соответствующими граничными условиями

(3)

$\begin{gathered} \frac{{{{\partial }^{2}}u}}{{\partial {{r}^{2}}}} + {{N}^{2}}\frac{{\partial {v}}}{{\partial r}} = {{e}^{{ - \alpha p}}}\frac{{dp}}{{d\theta }};\quad \frac{{{{\partial }^{2}}{v}}}{{\partial {{r}^{2}}}} = \frac{{v}}{{{{N}_{1}}}} + \frac{1}{{{{N}_{1}}}}\frac{{du}}{{dr}};\quad \frac{{\partial u}}{{\partial \theta }} + \frac{{\partial {v}}}{{\partial r}} = 0; \\ - \frac{{d\Phi \left( \theta \right)}}{{d\theta }} = K{{e}^{{ - \alpha p}}}\int\limits_{ - \Phi \left( \theta \right)}^{h\left( \theta \right)} {{{{\left( {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right)}}^{2}}} dr, \\ \end{gathered} $

где ${{u}_{0}} = 0$, ${v} = 0$, ${v} = 0$ при $r = 1 + \eta \cos \theta - {{\eta }_{1}}\sin \omega \theta = h\left( \theta \right)$;

(4)

$u = 1,\quad {v} = 0,\quad {v} = 1\quad {\text{при}}\quad r = {{r}_{0}} - \Phi \left( \theta \right);\quad p\left( 0 \right) = p\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}},$

где $K = \frac{{\left( {2{{\mu }_{0}} + \kappa {}_{0}} \right)\Omega \left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right)}}{{L{\kern 1pt} '{\kern 1pt} \delta }}$; $\Phi \left( \theta \right) = \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)$; $\eta = \frac{e}{\delta }$; ${{\eta }_{1}} = \frac{{a{\kern 1pt} '}}{\delta }$.

Переход к безразмерным переменным реализован на основе следующих формул:

$r{\kern 1pt} ' = \left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right) + \delta r;\quad \delta = {{r}_{1}} - \left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right);\quad {{{v}}_{{r'}}} = \Omega \delta u,$

(5)

$\begin{gathered} {{{v}}_{\theta }} = \Omega {v}\left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right);\quad p{\kern 1pt} ' = p{\kern 1pt} *{\kern 1pt} p;\quad p{\kern 1pt} * = \frac{{\left( {2{{\mu }_{0}} + {{\kappa }_{0}}} \right)\Omega {{{\left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right)}}^{2}}}}{{2\delta {}^{2}}}; \\ {v}{\kern 1pt} ' = {v},\quad \mu {\kern 1pt} ' = {{\mu }_{0}}\mu ,\quad \kappa {\kern 1pt} ' = {{\kappa }_{0}}\kappa ,\quad \gamma {\kern 1pt} ' = {{\gamma }_{0}}\gamma , \\ \end{gathered} $

${{N}^{2}} = \frac{{{{\kappa }_{0}}}}{{2{{\mu }_{0}} + {{\kappa }_{0}}}};\quad {{N}_{1}} = \frac{{2{{\mu }_{0}}{{l}^{2}}}}{{{{\delta }^{2}}{{\kappa }_{0}}}};\quad {{l}^{2}} = \frac{{{{\gamma }_{0}}}}{{4{{\mu }_{0}}}}.$

Введя обозначение $z = {{e}^{{ - \alpha p}}}$ и учитывая, что зазор мал и ${v} = 0$, осредним второе уравнение системы (3) по толщине смазочного слоя, в результате получим

(6)

$\begin{gathered} \frac{{{{\partial }^{2}}u}}{{\partial {{r}^{2}}}} + \frac{{{{N}^{2}}}}{{2{{N}_{1}}h}}\left( {2r - h} \right) = - \frac{1}{{{\alpha }}}\frac{{dz}}{{d\theta }};\quad \frac{{\partial u}}{{\partial r}} + \frac{{\partial {v}}}{{\partial \theta }} = 0;\quad {v} = \frac{1}{{2{{N}_{1}}h}}\left( {{{r}^{2}} - rh} \right); \\ z\frac{{d\Phi \left( \theta \right)}}{{d\theta }} = - K\int\limits_{ - \Phi \left( \theta \right)}^{h\left( \theta \right)} {{{{\left( {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right)}}^{2}}} dr, \\ \end{gathered} $

с соответствующими граничными условиями

(7)

$\begin{gathered} {v} = 0,\quad u = 0\quad {\text{при}}\quad r = 1 + \eta \cos \theta - {{\eta }_{1}}\sin \omega \theta ; \\ {v} = 0,\quad u = 1\quad {\text{при}}\quad r = 0 - \Phi \left( \theta \right);\quad z\left( 0 \right) = z\left( {2\pi } \right) = {{e}^{{ - \alpha \frac{{{{p}_{g}}}}{{p*}}}}}. \\ \end{gathered} $

Асимптотическое решение системы дифференциальных уравнений (6) с учетом (7) ищем по параметру K, характеризующему расплав покрытия

${v}\left( {r,\theta } \right) = {{{v}}_{0}}\left( {r,\theta } \right) + K{{{v}}_{1}}\left( {r,\theta } \right) + {{K}^{2}}{{{v}}_{2}}\left( {r,\theta } \right) + \ldots ,$

(8)

$\begin{gathered} u\left( {r,\theta } \right) = {{u}_{0}}\left( {r,\theta } \right) + K{{u}_{1}}\left( {r,\theta } \right) + {{K}^{2}}{{u}_{2}}\left( {r,\theta } \right) + \ldots , \\ \Phi \left( \theta \right) = - K{{\Phi }_{1}}\left( \theta \right) - {{K}^{2}}{{\Phi }_{2}}\left( \theta \right) - {{K}^{3}}{{\Phi }_{3}}\left( \theta \right) - \ldots , \\ \end{gathered} $

$p\left( \theta \right) = {{p}_{0}}\left( \theta \right) + K{{p}_{1}}\left( \theta \right) + {{K}^{2}}{{p}_{2}}\left( \theta \right) + {{K}^{3}}{{p}_{3}}\left( \theta \right) \ldots .$

Тогда уравнения (6)–(7) примут вид:

– для нулевого приближения

(9)

$\frac{{{{\partial }^{2}}{{u}_{0}}}}{{\partial {{r}^{2}}}} + \frac{{{{N}^{2}}}}{{2{{N}_{1}}h}}\left( {2r - h} \right) = - \frac{1}{\alpha }\frac{{d{{z}_{0}}}}{{d\theta }},\quad \frac{{\partial {{{v}}_{0}}}}{{\partial r}} + \frac{{\partial {{u}_{0}}}}{{\partial \theta }} = 0,$

с граничными условиями

(10)

$\begin{gathered} {{{v}}_{0}} = 0,\quad {{u}_{0}} = 0,\quad {{{v}}_{0}} = 0\quad {\text{при}}\quad r = 1 + \eta \cos \theta - {{\eta }_{1}}\sin \omega \theta , \\ {{{v}}_{0}} = 0,\quad {{u}_{0}} = 1,\quad {{{v}}_{0}} = 0\quad {\text{при}}\quad r = 0 - \Phi \left( \theta \right);\quad {{z}_{0}}\left( 0 \right) = {{z}_{0}}\left( {2\pi } \right) = {{e}^{{ - \alpha \frac{{{{p}_{g}}}}{{p*}}}}}; \\ \end{gathered} $

– для первого приближения

(11)

$\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{r}^{2}}}} = - \frac{1}{\alpha }\frac{{d{{z}_{1}}}}{{d\theta }},\quad \frac{{\partial {{{v}}_{1}}}}{{\partial r}} + \frac{{\partial {{u}_{1}}}}{{\partial \theta }} = 0,\quad {{z}_{0}}\frac{{d{{\Phi }_{1}}\left( \theta \right)}}{{d\theta }} = - K\int\limits_{\tilde {\Phi }}^{h\left( \theta \right)} {{{{\left( {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right)}}^{2}}dr} ,$

с граничными условиями

(12)

$\begin{gathered} {{{v}}_{1}} = {{\left. {\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial r}}} \right)} \right|}_{{r = 0}}} \cdot \tilde {\Phi };\quad {{u}_{1}} = {{\left. {\left( {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right)} \right|}_{{r = 0}}} \cdot \tilde {\Phi }, \\ {{{v}}_{1}} = 0,\quad {{u}_{1}} = 0\quad {{{v}}_{1}} = 0\quad {\text{при}}\quad r = h\left( \theta \right) + \tilde {\Phi }, \\ {{z}_{1}}\left( 0 \right) = {{z}_{1}}\left( {2\pi } \right) = 0,\quad \Phi \left( 0 \right) = \Phi \left( {2\pi } \right) = h_{0}^{*}. \\ \end{gathered} $

Точное автомодельное решение задачи для нулевого и первого приближения будем искать по известному методу [9, 10]. В результате для поля скоростей и давления получим следующие аналитические выражения:

– для нулевого приближения

(13)

$\begin{gathered} \tilde {\psi }_{0}^{'}\left( \xi \right) = \frac{{{{{\tilde {С}}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right), \\ {{{\tilde {u}}}_{0}} = {{{\tilde {С}}}_{1}}\frac{{{{\xi }^{2}}}}{2} - \frac{{{{N}^{2}}}}{{2{{N}_{1}}}}\left( {\frac{{{{\xi }^{3}}}}{3} - \frac{{{{\xi }^{2}}}}{2}} \right) - \left( {\frac{{{{N}^{2}}}}{{12{{N}_{1}}}} + \frac{{{{{\tilde {С}}}_{1}}}}{2} + 1} \right)\xi + 1,\quad {{{\tilde {C}}}_{1}} = 6, \\ {{z}_{0}} = - 6\alpha \left( {\eta \sin \theta + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos \omega \theta - 1} \right) - \frac{{{{\eta }_{1}}\theta }}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right) + {{e}^{{ - \alpha \frac{{{{p}_{g}}}}{{p*}}}}}; \\ \end{gathered} $

– для первого приближения

(14)

$\begin{gathered} \tilde {\psi }_{1}^{'}\left( \xi \right) = \frac{{{{{\tilde {\tilde {С}}}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right),\quad {{{\tilde {u}}}_{1}}\left( \xi \right) = {{{\tilde {\tilde {С}}}}_{1}}\frac{{{{\xi }^{2}}}}{2} - \left( {\frac{{{{{\tilde {\tilde {С}}}}_{1}}}}{2} + M} \right)\xi + M,\quad {{{\tilde {\tilde {C}}}}_{1}} = 6M, \\ {{z}_{1}} = - 6M\alpha \frac{{\left( {\tilde {\eta }\sin \theta + \frac{{{{{\tilde {\eta }}}_{1}}}}{\omega }\left( {\cos \omega \theta - 1} \right) - \frac{{{{{\tilde {\eta }}}_{1}}\theta }}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right)}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}}, \\ \end{gathered} $

где $\tilde {\eta } = \frac{\eta }{{1 + \tilde {\Phi }}}$; ${{\tilde {\eta }}_{1}} = \frac{{{{\eta }_{1}}}}{{1 + \tilde {\Phi }}}$; ${{\Phi }_{1}}\left( \theta \right) = \frac{1}{{\mathop {\sup {{z}_{0}}}\limits_{\theta \in \left[ {0;2\pi } \right]} }}\left( {\theta - \eta \sin \theta - \frac{{{{\eta }_{1}}}}{\omega }\cos \omega \theta } \right)\left( {1 - \frac{{{{N}^{4}}}}{{720N_{1}^{2}}}} \right) + h_{0}^{*}$.

Применяя разложение в ряд Тейлора для функции ${{e}^{{ - \alpha p}}}$ и ${{e}^{{ - \alpha \frac{{{{p}_{g}}}}{{p*}}}}}$, получим

(15)

$p = \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}} - 6\left( {A + KMB} \right)\left( {1 + \alpha \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}} \right)}}^{2}}} \right),$

где

$A = - \left[ {\eta \sin \theta - \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos \omega \theta - 1} \right) + \frac{{{{\eta }_{1}}\theta }}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right];$

$B = \frac{{\tilde {\eta }\sin \theta + \frac{{{{{\tilde {\eta }}}_{1}}}}{\omega }\left( {\cos \omega \theta - 1} \right) - \frac{{{{{\tilde {\eta }}}_{1}}\theta }}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}}.$

С учетом (9), (11) и (15) для составляющей вектора поддерживающей силы и силы трения получим

${{R}_{y}} = p{\kern 1pt} *{\kern 1pt} {{r}_{0}}\int\limits_0^{2\pi } {\left( {p--\frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}} \right)\sin \theta } d\theta = \frac{{6\left( {2{{\mu }_{0}} + {{\kappa }_{0}}} \right)\Omega r_{0}^{3}}}{{{{\delta }^{2}}}}\left( {1 + \alpha \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}} \right)}}^{2}}} \right) \times $

$ \times \;\left[ {\eta \pi + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right) - KM\left( {\frac{{\tilde {\eta }\pi + \frac{{{{{\tilde {\eta }}}_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right)}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}}} \right)} \right],$

(16)

${{L}_{{тр}}} = \mu \int\limits_0^{2\pi } {\left[ {{{{\left. {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right|}}_{{r = 0}}} + K{{{\left. {\frac{{\partial {{u}_{1}}}}{{\partial r}}} \right|}}_{{r = 0}}}} \right]d\theta = \left( {2{{\mu }_{0}} + {{\kappa }_{0}}} \right)\left( {1 - \alpha p + \frac{{{{\alpha }^{2}}{{p}^{2}}}}{2}} \right) \times } $

$ \times \;\left[ { - 2\pi + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right) + \frac{{{{N}^{2}}}}{{4{{N}_{1}}}}\left( {2\pi + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right)} \right) + } \right.$

$\left. {^{{^{{^{{^{{}}}}}}}} + \;\tilde {\Phi }K\left( {2\pi - \frac{{2{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right)} \right)} \right].$

В результате численного анализа построены зависимости (рис. 2).

Рис. 2.

Влияние параметра ω, характеризующего адаптированный профиль, и параметра α, характеризующего зависимость вязкости от давления, на величину: (а) – несущей способности и (б) – силы трения.

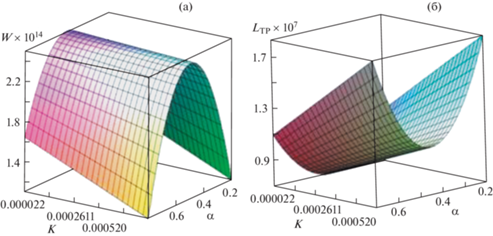
Экспериментальное исследование. Для подтверждения выводов, сделанных на основе теоретических результатов, а также для проверки эффективности сделанных рекомендаций проведено экспериментальное исследование.

При изготовлении образцов и проведении экспериментальных исследований использовался ряд материалов, марки и состав которых приведены в табл. 1.

Таблица 1.

Применяемые материалы

№ п/п	Наименование	Марка	Состав	ГОСТ
1	Сталь	Сталь 45	С – 0.42–0.50%	1050-84
2	Бронза	Бр АЖ 9-4	Al – 9%, Fe – 4%	1628-78
3	Cплав Вуда	Cплав Вуда	Bi – 50%; Pb – 25% Sn – 12.5%; Co – 12%	10928-90
4	Медь порошковая	МП-1	Сu – 99.5%	4960-75
5	Авиационное масло	МС-20	по ГОСТ	21743-76
6	Турбинное масло	Тп-22С	по ГОСТ	101821-2001

Исходные данные для экспериментальных полнофакторных исследований приведены в табл. 2.

Таблица 2.

План полнофакторных экспериментальных исследований типа 2²

№ п/п	Переменные факторы		Величина переменных факторов
№ п/п	наименование	размер- ность	нижний уровень	верхний уровень	нулевой уровень	интервал варьиров
1	Контактная нагрузка	МПа	0.5	3.5	2.0	1.5
2	Скорость	м/с	1.0	2.0	1.5	0.5

Наименее трудоемкой и наиболее эффективной статистической методикой является применение стандартных оптимальных полнофакторных двухуровневых экспериментальных планов типа 2^к, позволяющее получить адекватные регрессионные модели для инженерных расчетов.

Схема экспериментальных исследований включала следующие этапы: 1 – работа в режиме гидродинамического смазывания; 2 – прекращение подачи жидкого смазочного материала смазывания; 3 – работа до полного расхода расплава или разрушения легкоплавкого покрытия.

При этом на компьютере постоянно фиксировалась величина коэффициента трения f, а предварительно устанавливалась несущая способность подшипника.

Наличие пленки жидкого смазочного материала имело место только на первом, начальном, этапе при смазывании маслом. Затем на втором, конечном, этапе подача смазочного материала прекращалась, и с ростом температуры подшипник смазывался металлическим расплавом. Гидродинамический режим смазывания сохранялся постоянно.

Примеры типичных осциллограмм изменений коэффициента трения и температуры в процессе работы исследуемой трибосистемы приведены на рис. 3, 4 .

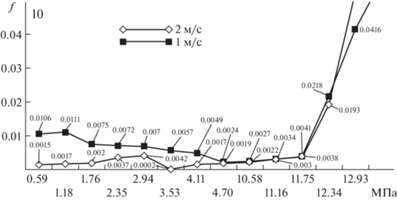
Рис. 3.

Осциллограмма изменений коэффициента трения, снятая в процессе испытаний модели радиального подшипника на машине трения с легкоплавким покрытием из сплава Вуда.

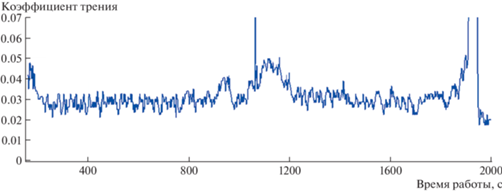
Рис. 4.

Осциллограмма изменения температуры при испытаниях радиальных подшипников (машина трения ИИ 5018).

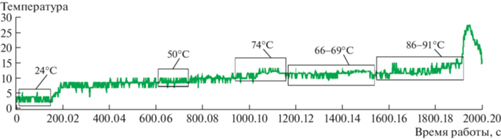
На приведенных осцилограммах можно отметить первоначальный незначительный рост температуры при смазывании маслом (гидродинамический режим) и более интенсивный – с прекращением его подачи. Затем температура растет до плавления покрытия (68°С), потом снижается в связи со смазыванием расплавом (гидродинамический режим) и растет до 91°С, а затем благодаря утечкам расплава и его расходу резко повышается.

Точки на рис. 4 выбраны из фиксированной на компьютере осциллограммы через каждые 150 с. Осциллограмма получена на машине трения при смазывании авиационным маслом марки МС-20.

Схема перехода трибосистемы на смазывание расплавом представлена на рис. 5. Общий анализ осциллограмм изменений коэффициента трения и температуры контактной зоны испытываемых образцов радиальных и упорных подшипников скольжения позволил установить последовательность и выделить общие фазы исследуемого процесса гидродинамического смазывания металлическим расплавом в следующем виде.

Рис. 5.

Фазы эволюции трибосистемы: 1 – приработка; 2 – прекращение подачи смазочного материала; 3 – сухая приработка покрытия; 4 – уменьшение смазывания; 5 – смазывание расплавом; 6 – разрушение покрытия.

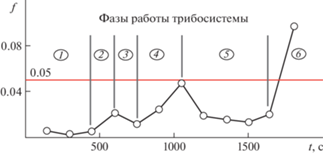
Более подробно фазы эволюции трибосистемы (рис. 5): 1 – исходная работа в режиме гидродинамического смазывания жидким смазочным материалом; 2 – прекращение подачи жидкого смазочного материала, переход к “голодному” смазыванию, рост коэффициента трения и температуры; 3 – приработка контактной поверхности покрытия в условиях дефицита смазочного материала и некоторое снижение коэффициента трения; 4 – сухое трение, практически без смазочного материала, и дальнейший рост коэффициента трения и контактной температуры; 5 – плавление легкоплавкого металлического покрытия (сплав Вуда) и смазывание расплавом в гидродинамическом режиме; 6 – вытеснение расплава из зоны трения, резкий рост коэффициента трения.

Таким образом, установлены последовательные этапы механизма смазывания подшипников скольжения металлическими расплавами. Это может быть использовано как некоторая компенсация аварийного прекращения подачи смазочного материала, а также как определенный ограничитель температуры трибосистемы.

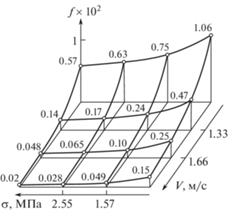
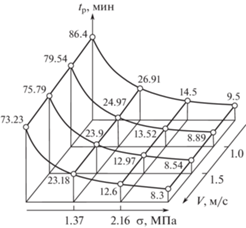
К основным эксплуатационным характеристикам исследуемых подшипников скольжения относятся их нагрузочная способность и коэффициенты трения в исследуемом диапазоне нагрузочно-скоростных режимов. Знание несущей способности позволяет ограничить нагрузку в области исследований для определения коэффициента трения (рис. 6–8 ).

Рис. 6.

Несущая способность исследуемых трибосистем.

Рис. 7.

Влияние нагрузочно-скоростных режимов на коэффициент трения подшипников.

Рис. 8.

Влияние нагрузочно-скоростных режимов на ресурс подшипников.

В табл. 3 приведены результаты верификации расчетных моделей, полученных теоретически, путем их сравнения с данными экспериментальных исследований.

Таблица 3.

Сравнение расчетных и экспериментальных коэффициентов трения при смазывании расплавом

№ п/п	Исходный смазочный материал	Режимы нагружения		Коэффициент трения, f		Погреш-ность, %
№ п/п	Исходный смазочный материал	σ, МПа	V, м/с	эксперимент	расчет	Погреш-ность, %
1	МС-20	4.0	0.5	0.0270	0.0280	3–5
2	Тп-22С + + 5% Сu (вес)	4.0	0.5	0.0344	0.03270
3		2.0	0.5	0.0318	0.03080
4		4.0	2.0	0.0475	0.04860
5		2.0	2.0	0.0437	0.04221

Величины коэффициентов трения (табл. 3), с высокой достоверностью подтверждают наличие стабильного гидродинамического режима смазывания в условиях проведенного эксперимента и удовлетворительную сходимость результатов эксперимента с итогами теоретических исследований. Наибольшая невязка сравниваемых величин не превышает 5%.

Выводы. 1. Оценка комплексного влияния гидродинамического давления на реологию микрополярных смазочных материалов (минерального масла и легкоплавкого металлического расплава) при получении расчетных моделей подшипников скольжения обеспечила повышение точности расчетов основных параметров трибосистем (коэффициента трения и несущей способности) на 8–11%. 2. Визуализация разработанных теоретически расчетных моделей и оценка их точности, выполненная на основе сравнения результатов их численного анализа и триботехнических параметров, рассчитанных по адекватным регрессионным моделям, полученных экспериментально, доказала их высокую эффективность, точность (в пределах 9–13%) и применимость во всем исследованном диапазоне размеров и нагрузочно-скоростных режимов (d = 10–100 мм; V = 0.5–11 м/с; σ = 8–11 МПа). 3. Параллельный анализ уровня температуры в контактной области и величины коэффициента трения в процессе работы подшипника с легкоплавким металлическим покрытием при постепенном прекращении подачи жидкого смазочного материала в рабочую зону позволил установить последовательность фаз перехода от смазывания минеральным маслом к смазыванию металлическим расплавом при сохранении гидродинамического режима.

Список литературы

Akhverdiev K. S., Mukutadze A.M. Damper with porous anisotropic ring // Mechanical Engineering Research. 2016. V. 6. № 2. P. 1.
Mukutadze M.A., Khasyanova D.U. Optimization of the supporting surface of a slider bearing according to the load-carrying capacity taking into account the lubricant viscosity depending on pressure and temperature // J. of Machinery Manufacture and Reliability. 2018. V. 47. № 4. P. 356.
Opatskikh A. Ferromagnetic lubricants in a bearing with a porous coating of a base ring // Key Engineering Materials. 2022. T. 909 KEM. C. 123.
Kharlamov P. Application of elastic-dissipative characteristics of the friction contact monitoring for the study of tribological processes in the system “railway track-rolling stock” // Lecture Notes in Networks and Systems. 2022. T. 403 LNNS. C. 510.
Куманин С.В. Устойчивый режим работы клиновидной опоры скольжения повышенной несущей способности, работающей на сжимаемом смазочном материале и на собственном расплаве // Инженерный вестник Дона. 2022. № 6 (90). С. 766.
Ильичев В.Ю. Разработка методики определения характеристик упорных подшипников скольжения // Научные известия. 2022. № 26. С. 142.
Кохановский В.А., Поляков В.Н. Опорный профиль трибосистем скольжения // Вестник машиностроения. 2021. № 3. С. 53.
Ахвердиев К.С., Болгова Е.А., Лагунова Е.О., Куманин С.В. Гидродинамический расчет клиновидной системы “ползун-направляющая”, работающей на сжимаемом смазочном материале в условиях наличия расплава на поверхности направляющей // Омский научный вестник. 2021. № 2 (176). С. 10.
Ахвердиев К.С., Болгова Е.А. Клиновидная опора скольжения с податливой опорной поверхностью, работающая на сжимаемом материале в условиях наличия расплава на поверхности направляющей // Вестник Ростовского государственного университета путей сообщения. 2021. № 2 (82). С. 8.
Ахвердиев К.С., Василенко В.В., Лагунова Е.О. Расчетная модель упорного подшипника с плавким покрытием ползуна и пористым покрытием направляющей // Вестник Ростовского государственного университета путей сообщения. 2021. № 3 (83). С. 8.
Bagrova V.N., Kolobov I.A. Ways to improve wear resistance and damping properties of radial bearings taking into account inertial forces // B cбopникe: J. of Physics: Conf. Series. “Int. Conf. on Automatics and Energy, ICAE-2021”. 2021. C. 012105.
Задорожная Н.С. Спектральная краевая задача колебаний невязкой жидкости бесконечной электропроводности // В сборнике: Сборник научных трудов “Транспорт: наука, образование, производство”. Труды Международной научно-практической конференции. 2020. С. 226.
Ахвердиев К.С., Лагунова Е.О. Математическая модель вязкоупругого смазочного материала // В сборнике: Сборник научных трудов “Транспорт: наука, образование, производство”. Труды Международной научно-практической конференции. 2020. С. 177.
Ахвердиев К.С., Лагунова Е.О., Солоп К.С. Расчетная модель упорного подшипника скольжения на основе нелинейного реологического уравнения Максвелла с учетом существования предельного напряжения сдвига // Вестник Ростовского государственного университета путей сообщения. 2015. № 4 (60). С. 129.
Ахвердиев К.С., Колесников И.В., Митрофанов С.В., Копотун Б.Е. Метод гидродинамического расчета упорного подшипника с учетом зависимости вязкости слоистой смазочной жидкости от температуры // Инженерный вестник Дона. 2015. № 3 (37). С. 141.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал