1. На главную
  2. Электронные версии
  3. Журнал общей биологии
  4. T. 83, № 5, 2022

Журнал общей биологии, 2022, T. 83, № 5, стр. 380-388

Морфологическое разнообразие икосаэдрических вирусов

Ю. Л. Войтеховский *

Геологический институт ФИЦ КНЦ РАН
184209 Апатиты, Ферсмана, 14, Россия

* E-mail: woyt@geoksc.apatity.ru

Поступила в редакцию 01.07.2022
После доработки 28.07.2022
Принята к публикации 16.08.2022

Полный текст (PDF)

Аннотация

Статья посвящена морфологическому разнообразию икосаэдрических вирусов – отдельным капсидам и структуре многообразия в целом. Показано, что фиксация капсидов триангуляционными числами не различает изомеров. Описание капсидов с точечными группами симметрии Ih (с плоскостями симметрии) и I (без них) детализировано. В их многообразии выделены серии подобия, попарно связанные переходами к дуальным капсидам. В рамках общебиологической проблематики серии подобия интерпретированы как гомологические ряды, дуальные переходы между ними – как рефрены. Определено понятие капсидов-генераторов, порождающих гомологические ряды и рефрены и не сводимых к более простым формам. Высказаны гипотезы о том, что базовыми формами икосаэдрических вирусов могут быть не только икосаэдр и дуальный к нему додекаэдр, но все формы икосаэдро-додекаэдрической системы и их комбинации, а гомологические ряды и рефрены икосаэдрических вирусов могут указывать на их филогенетическое родство.

Мир вирусов весьма разнообразен. Как особая, пограничная форма жизни они поражают широтой экспансии в клетки живых и растительных организмов, а также бактерий. Проявляя вне клетки хозяина лишь признаки биополимеров, в клетке они показывают признаки живого – имея генетический материал (ДНК, РНК, иногда то и другое), копируют себя путем самосборки из тела хозяина и эволюционируют (мутируют) под влиянием внешних агентов. Не имея клеточного строения как фундаментального свойства живой материи, вирусы обладают рациональной конструкцией – свернутые в клубки (закономерна ли свертка – неизвестно) ДНК, РНК (или обе) упакованы в капсиды из белковых глобул, иногда еще и в липидные оболочки. Форма вирусов варьирует от спиральной, икосаэдрической и продолговатой до более сложной комплексной. Их высокая эргономичность доказывается тем, что все элементы конструкций использованы природой на разных уровнях иерархии неорганической и органической материи. Во всех формах, так или иначе, усматривается симметрия, подсказывающая математический аппарат описания.

Продолжающаяся пандемия COVID-19 заставила представителей разных наук говорить об икосаэдрических вирусах. Проблема их места в природе (Жданов и др., 2012) из теоретической быстро перешла в практическую. Сейчас важно объединить усилия в исследовании этих совершенных механизмов, уничтожающих наш биологический вид. В части таксономии икосаэдрических вирусов далее мы базируемся на хорошо известном положении. “Номенклатура и классификация вирусов – трудная область вирусологии… Группировка может быть основана на морфологических и физиологических критериях. Идеал, к которому мы стремимся – это создать такую классификацию, которая отражала бы эволюционные и филогенетические взаимоотношения организмов, а также обеспечивала бы удобную и рациональную систему номенклатуры” (Лурия и др., 1981, с. 18–23). Форма капсида по-прежнему остается важным классификационным признаком, несмотря на смещение акцентов в детальное исследование генома (International Committee…, 2020).

Форма минеральных и биологических объектов – всегда компромисс между внутренним императивом (у первых – кристаллическая решетка, у вторых – генотип) и условиями среды. Для икосаэдрических вирусов хотелось бы иметь такую морфологическую классификацию, которая вскрывала бы их филогенетическое родство. Кристаллография биологических структур впервые и мощно заявила о себе расшифровкой ДНК и РНК Уотсоном и Криком в 1953 г. (Нобелевская премия 1962 г.). Но они занимались и сферическими вирусами (Crick, Watson, 1956). Экспонируя тени, отбрасываемые вирусами в рентгеновских лучах, они увидели их полигональные контуры и догадались о полиэдрических формах. Вскоре для капсидов был подобран и базовый полиэдр – икосаэдр. Мы постараемся показать, что в уточнении существующей классификации и номенклатуры икосаэдрических капсидов, а также в более глубоком понимании внутренних связей в их многообразии помощь может оказать кристаллография. Ввиду гетерогенности популяций вирусов оговоримся, что в целом нами рассматриваются их идеальные модели. О плеоморфизме коронавирусов коротко сказано в конце статьи.

ПРИНЦИПЫ МОРФОЛОГИЧЕСКОЙ КЛАССИФИКАЦИИ И НОМЕНКЛАТУРЫ КАПСИДОВ ИКОСАЭДРИЧЕСКИХ ВИРУСОВ

Принципы строения капсидов икосаэдрических вирусов из капсомеров (субъединиц, сферических белковых глобул) и их классификация предложены в статье Каспара и Клуга (Caspar, Klug, 1962). Всякий капсид построен из 20 равносторонних треугольных граней – фрагментов плоской сетки, образованной глобулами по принципу плотнейшей шаровой упаковки (рис. 1а). Если линии глобул параллельны ребрам икосаэдра, то капсиды имеют плоскости симметрии, а их точечная группа симметрии (т. г. с.) обозначается Ih11.

Рис. 1.

а – аденовирус с т. г. с. Ih (по: Рис, Стернберг, 2002). б – разворот треугольной грани капсида с т. г. с. I относительно ряда глобул (горизонтальная ось h).

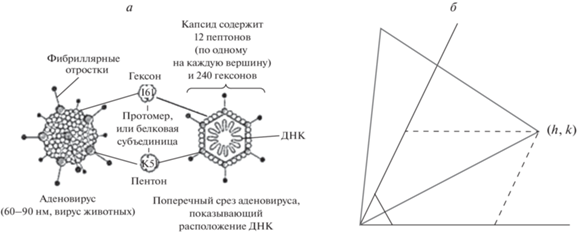
Линии глобул не всегда параллельны ребрами икосаэдра, что и создавало проблему отыскания общей формулы для их числа в капсиде (рис. 1б). Такие капсиды не имеют плоскостей симметрии, а их т. г. с. обозначается I. В статье Каспара и Клуга (Caspar, Klug, 1962) анонсирована формула для “триангуляционных чисел”: Т = Рf 2, где Р = h2 + + hk + k2, h ≥ k ≥ 0 – любые пары целых чисел без общих делителей (h > 0, так как h = 0 влечет k = 0, что противоречит смыслу триангуляционного числа как площади грани капсида); f = 1, 2, 3…; (h, k) – координаты вершины грани в косоугольной (60°) системе координат, согласованной с плотнейшей упаковкой глобул. Ее вывод впервые дан в статье Шмальца с соавт. (Schmalz et al., 1988) и сводится к отысканию площади грани капсида по теореме косинусов. При этом за элементарный принимается треугольник, в который вписана одна глобула.

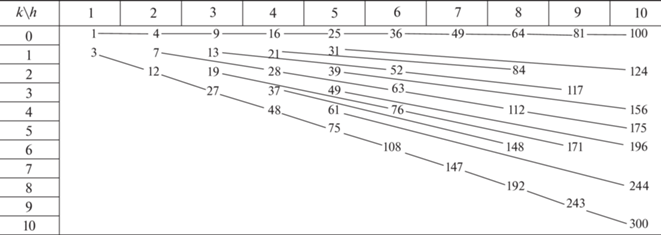
Сегодня в основу описания икосаэдрических капсидов положены именно триангуляционные числа, сведенные в классификационную таблицу (табл. 1). В этом есть известное удобство. Число глобул в капсиде равно М = 10Т + 2. Они образуют морфологические субъединицы: 12 пентамеров и 10(Т – 1) гексамеров. При этом Т = (m – 1)2, где m – число глобул на ребре грани капсида с т. г. с. Ih (верхняя строка табл. 1), 20Т – число элементарных треугольников на любом капсиде (Костюченко, Месянжинов, 2002; Rux et al., 2003; Simpson et al., 2003; Гнутова, 2011). Для многих вирусов эти характеристики известны: бактериофаг φX174: Т = 1, M = 12, m = 2, (h, k) = (1, 0); вирус желтой мозаики турнепса: Т = 3, M = 32, (h, k) = = (1, 1); вирус полиомы: Т = 4, M = 42, m = 3, (h, k) = (2, 0); паповавирус: Т = 7, М = 72, (h, k) = = (2, 1); реовирус: Т = 9, M = 92, m = 4, (h, k) = (3, 0); ротавирус: Т = 13, М = 132, (h, k) = (3, 1); вирусы герпеса и ветряной оспы: Т = 16, M = 162, m = 5, (h, k) = (4, 0); аденовирус и вирус собачьего гепатита: Т = 25, M = 252, m = 6, (h, k) = (5, 0); радужный вирус: Т = 81, M = 812, m = 10, (h, k) = (9, 0) и др. (Вайнштейн, Киселев, 1964; Мэтьюз, 1973). Триангуляционные числа сверены с международной базой данных (https://ictv.global/report).

Таблица 1.  

Триангуляционные числа

k\h 1 2 3 4 5 6 7 8 9 10
0 1 4 9 16 25 36 49 64 81 100
1 3 7 13 21 31 43 57 73 91 111
2   12 19 28 39 52 67 84 103 124
3     27 37 49 63 79 97 117 139
4       48 61 76 93 112 133 156
5      75 91 109 129 151 175
6   108 127 148 171 196
7     147 169 193 219
8       192 217 244
9         243 271
10           300

Примечание: выделены капсиды-изомеры, во врезке – коронавирус SARS-CoV-2.

Табл. 1 открыта в бесконечность, но для вирусов должна иметь естественное ограничение. Для гигантских икосаэдрических вирусов указывают размер 600 нм (Xiao et al., 2005; Claverie et al., 2006; Raoult et al., 2007; Van Etten, 2011; Forterre, Gaïa, 2016), что примерно в 6 раз больше вируса полиомы с (h, k) = (2, 0). Следовательно, они находятся заведомо за пределами табл. 1. Анализ таблицы обнаруживает вирусы-изомеры с одинаковым триангуляционным числом. Для Т = 49 их можно различить по симметрии: капсид (h, k) = (7, 0) имеет т. г. с. Ih, капсид (5, 3) – т. г. с. I. Но для Т = 91 оба капсида (9, 1) и (6, 5) имеют т. г. с. I. Это говорит о недостаточности описания капсидов триангуляционными числами и т. г. с. В то же время символ (h, k) (рис. 1б) фиксирует структуру капсида однозначно. Его и следует использовать в номенклатуре икосаэдрических вирусов. Как будет показано далее, дело не только в однозначности описания.

СЕРИИ ПОДОБИЯ И ДУАЛЬНЫЕ ПЕРЕХОДЫ

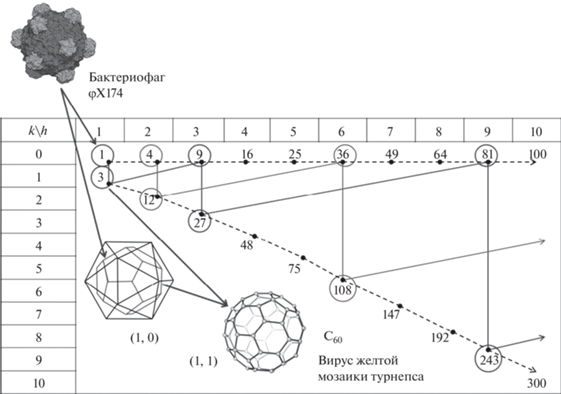
В статье Каспара и Клуга (Caspar, Klug, 1962, p. 15) предложено деление икосаэдрических капсидов на три серии (табл. 1 ). Первая (верхняя строка табл. 1 ) порождена простейшим капсидом (1, 0) – икосаэдром, в вершинах которого расположены белковые глобулы. Он отвечает бактериофагу φX174. Остальные капсиды серии, все с т. г. с. Ih, получаются увеличением грани икосаэдра с помощью коэффициентов подобия f = 2, 3, 4… при той же ориентировке относительно плотнейшей упаковки глобул (рис. 1б). Эту серию подобия логично обозначить (h, k) = (1, 0). Судя по публикациям (к сожалению, даются не снимки высокого разрешения, а раскрашенные модели), коронавирус SARS-CoV-2 имеет капсид (2, 0), Т = 4, аналогичный вирусу полиомы (табл. 1 , врезка). (Еще одна, неожиданная модель рассмотрена в конце статьи). Это второй капсид в серии. Далее следуют: реовирус (3, 0), вирус герпеса и ветряной оспы (4, 0), аденовирус и вирус собачьего гепатита (5, 0), радужный вирус (9, 0).

Вторая серия подобия (диагональ табл. 1 ) порождается капсидом (1, 1) – додекаэдром, над гранями которого построены пентагональные пирамиды. Капсиды этой серии тоже имеют т. г. с. Ih. Остальные капсиды в табл. 1 имеют т. г. с. I. Судя по тому, что в статье Каспара и Клуга (Caspar, Klug, 1962) они названы “skew classes” (скошенные классы), каждый капсид (h, k) означает отдельный класс. Но преобразованием подобия любой такой капсид тоже порождает бесконечную серию. А все их многообразие состоит из серий подобия (лучей), начинающихся с (h, k), у которых h и k не имеют общих делителей (табл. 2).

Таблица 2.  

Серии подобия

Примечание: серии с началом (h, k) при h > 5 не показаны, так как уже второй член серии находится вне таблицы.

Табл. 1 и 2 содержат и другие связи. Капсид (1, 1) получается из (1, 0) как усеченный икосаэдр из додекаэдра – дуальным переходом22 и последующим отсечением всех вершин. То есть капсиды бактериофага φX174 и вируса желтой мозаики турнепса соотносятся, как додекаэдр и усеченный икосаэдр, т.е. нобелевский фуллерен С60. Следующие отсюда биоминеральные аналогии рассмотрены в нескольких статьях (Voytekhovsky, 2015; Voytekhovsky, Stepenshchikov, 2016).

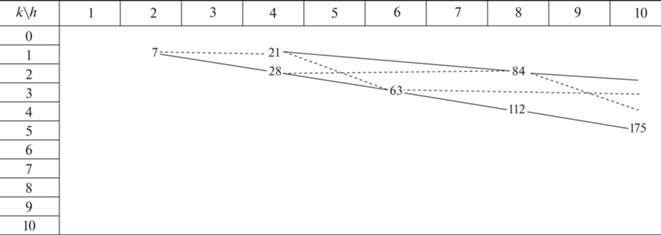
Как выразить алгебраически дуальный переход? На целочисленной треугольной решетке (рис. 1) ребра (h1, k1) и (h2, k2) любых двух капсидов выражаются друг через друга линейно: (h1, k1) → (h2, k2) = (ah1 + bk1, ch1 + dk1). В статье Войтеховского (Voytekhovsky, 2016) показано, что дуальный переход утраивает триангуляционное число. Из условия Т2 = 3Т1 найдено, что для любого (h1, k1) оно разрешимо лишь в случае: (h1, k1) → (h1 + 2k1, h1 – k1). Легко убедиться в переходах между верхней строкой и диагональю табл. 1 : (f, 0) → (f, f) → → (3f, 0) → (3f, 3f)… Серии подобия (1, 0) и (1, 1), казавшиеся раздельными, дуальным переходом объединяются (рис. 2, зигзаги 16–48–…, 25–75– …, 49–147–… и др. опущены). Ничто не мешает соединить в пары и серии подобия (лучи), образованные “skew” капсидами. В табл. 3 показано объединение серий, порожденных капсидами (2, 1) и (4, 1).

Рис. 2.

Объединение серий (1, 0) и (1, 1).

Таблица 3.  

Объединение серий (2, 1) и (4, 1)

Легко видеть, что каждый капсид принадлежит некоторой серии подобия и некоторому зигзагу, связывающему ее с дуальной серией. В начале дуальных серий стоит капсид, названный нами генератором (h, k). Его критерий: h и k взаимно просты, (h – k) не делится на 3 (табл. 4). От любого капсида переход к генератору выполняется пошаговым алгоритмом: (h, k) → [(h + 2k)/3, (h – k)/3]. Заметим, что изомеры существуют и среди генераторов. Простейшие – это (9, 1) и (6, 5) с Т = 91 и т. г. с. I (табл. 1 ).

Таблица 4.  

Триангуляционные числа генераторов

k\h 1 2 3 4 5 6 7 8 9 10
0 1                  
1   7 13   31 43   73 91  
2     19       67   103  
3       37 49   79 97   139
4      61       133  
5   91 109   151  
6     127      
7       169 193  
8         217  
9           271
10            

Примечание: выделены генераторы-изомеры.

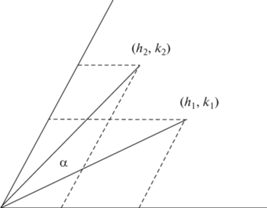
ОБЩЕЕ ПРЕОБРАЗОВАНИЕ КАПСИДА

Между икосаэдрическими капсидами есть еще более глубокая связь. А именно, можно найти их общее преобразование друг в друга: (h1, k1) → (h2, k2). По сути, задача состоит в повороте вектора (h1, k1), образующего угол α1 с осью h, до вектора (h2, k2), образующего угол α2 с осью h, и растяжении/сжатии (рис. 3). В ортогональной декартовой системе координат преобразование имеет вид:

$\left( {{{x}_{2}},{{y}_{2}}} \right) = \left( {{{x}_{1}},{{y}_{1}}} \right)\left( {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha } \\ { - \sin \alpha }&{\cos \alpha } \end{array}} \right)\left( {\begin{array}{*{20}{c}} t&0 \\ 0&t \end{array}} \right),$
где α = α2 – α1, коэффициент растяжения t = (T2/T1)1/2. Переход к косоугольной (60°) системе координат: x1 = $T_{1}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{\kern 1pt} $cosα1, y1 = $T_{1}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{\kern 1pt} $sinα1, x2 = $T_{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{\kern 1pt} $cosα2, y2 = = $T_{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{\kern 1pt} $sinα2. Выражая тригонометрические функции через стороны треугольников (рис. 3), после преобразований получим:

$\begin{gathered} \left( {2{{h}_{2}} + {{k}_{2}},\sqrt 3 {{k}_{2}}} \right) = \\ = \left( {2{{h}_{1}} + {{k}_{1}},\sqrt 3 {{k}_{1}}} \right)\left( {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha } \\ { - \sin \alpha }&{\cos \alpha } \end{array}} \right)\sqrt {{{{{T}_{2}}} \mathord{\left/ {\vphantom {{{{T}_{2}}} {{{T}_{1}}}}} \right. \kern-0em} {{{T}_{1}}}}} . \\ \end{gathered} $
Рис. 3.

Общее преобразование капсида.

Зная (h1, k1) и (h2, k2), находим коэффициент растяжения (T2/T1)1/2 и угол 0 ≤ α ≤ 60°.

Частные случаи следуют из этого уравнения. Для преобразований подобия (h1, k1) → (h2, k2) = = (f h1, f k1) подстановкой получим единичную матрицу поворота: cos α = 1, sin α = 0, т.е. α = 0. Действительно, серии подобия объединяют капсиды с одинаково ориентированными гранями. Для дуальных переходов (h1, k1) → (h2, k2) = (h1 + 2k1, h1 – k1) решение имеет вид: α = arc sin [1/2 – 3k1 × × (h1 + k1)/2T1]. При k1 = 0 (верхняя строка табл. 1 ): α = 30°, при k1 = h1 (диагональ табл. 1 ): α = –30° – в обоих случаях коэффициент растяжения равен $\sqrt 3 $. Последовательные дуальные переходы отличаются знаком поворота.

ПРОСТЫЕ ФОРМЫ ИКОСАЭДРИЧЕСКОЙ СИСТЕМЫ

Кристаллографический взгляд на икосаэдрические капсиды позволяет допустить, что ситуация может быть сложнее. Икосаэдр и додекаэдр (он особенно ощущается при дуальных переходах между сериями подобия) – лишь две простые формы33 в икосаэдрических т. г. с. Ih и I. Почему икосаэдр использован вирусами в качестве формы капсида? Вероятно, при данной длине цепочки ДНК/РНК для строительства почти сферической оболочки нужно минимальное количество материала (белковых глобул) и, возможно, времени. А еще потому, что кодирование высокосимметричной формы проще, чем низкосимметричной. (Хотя мы еще плохо понимаем, как это происходит в геноме). И если вирусы прибегают к развороту плотнейшей упаковки белковых глобул относительно ребер икосаэдра, почему не допустить, что они используют все простые формы, разрешенные в т. г. с. Ih и I, и даже их комбинации? Некоторые из них заведомо сферичнее, чем икосаэдр и додекаэдр (рис. 4). Одна из форм – ромбический триаконтаэдр – уже зафиксирована (Pimonov et al., 2019). Не за горами и остальные. И для них придется создать таблицы аналогов триангуляционных чисел. Отдадим должное классикам кристаллографии (Федоров, 1915; Доливо-Добровольский, 1924), державшим все простые формы т. г. с. Ih и I в поле зрения, несмотря на то, что в решетчатых трансляционных структурах классической кристаллографии они запрещены. Пришло время – и в расширенной кристаллографии квазисферических полиэдрических оболочек они пригодились.

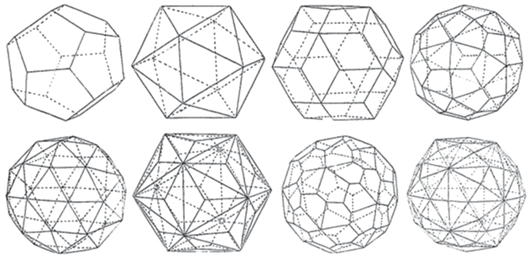
Рис. 4.

Простые формы в т. г. с. Ih и I, в скобках – число граней. Верхний ряд: додекаэдр (12), икосаэдр (20), триаконтаэдр (30), тетрагонтриикосаэдр (60). Нижний ряд: тригонпентадодекаэдр (60), тригонтриикосаэдр (60), пентагонтриикосаэдр (60, общая форма в т. г. с. I), гексаикосаэдр (120, общая форма в т. г. с. Ih).

Отметим еще один подход к описанию капсидов, а именно – коронавирусов. В статье Косцио с соавт. (Coscio et al., 2020) отмечено, что им свойственен плеоморфизм. Соглашаясь с правилами организации капсидов икосаэдрических вирусов (Crick, Watson, 1956; Caspar, Klug, 1962), авторы погружают его во “всеобъемлющий принцип дизайна” (Wolynes, 1996), согласно которому большая конструкция должна строиться из мелких с помощью операций симметрии. В биологических структурах тем самым экономится геном. Целесообразность видится в использовании максимально высоких т. г. с. Таких две – кубо-октаэдрическая (реализуемая в кристаллах трех из пяти видов симметрии кубической сингонии) и икосаэдро-додекаэдрическая (разрешенная для квазикристаллов, в природе найденная однажды и требующая подтверждения; реализуемая в капсидах икосаэдрических вирусов, скелетах радиолярий и других биологических объектах).

Для капсидов коронавирусов указанные авторы неожиданно выбирают первый вариант и называют эту модель “усеченный октаэдр”. На первый взгляд, такая форма недостаточна сферична. Зато, как утверждают авторы, она удобна для прилегающих изнутри протеиновых димеров и тетрамеров. Если модель верна хотя бы для некоторых видов коронавирусов, то для систематики таких капсидов придется ввести коэффициент К “глубины срезания вершин октаэдра гранями куба”, например, в виде отношения площадей граней этих простых форм. Далее следует установить углы, образуемые линиями белковых глобул с ребрами кубо-октаэдра, и для каждого К вывести аналоги триангуляционных чисел. Задача интересная, но все же новая модель сначала требует подтверждения.

ОБСУЖДЕНИЕ

В науках о природе идеалом естественной системы в смысле А.А. Любищева (1923) считается периодическая таблица химических элементов Д.И. Менделеева. Ее уникальность состоит в том, что она сочетает в себе структуру (химические элементы строго упорядочены по заряду ядра, “минимальный” элемент – водород № 1, “максимальный” элемент на сегодня – оганесон № 118) и классификацию на периоды (по числу электронных оболочек) и группы (по сходству электронных конфигураций на валентных оболочках). Поэтому положение элемента в таблице очень много говорит о его свойствах.

Но система (таблица) икосаэдрических капсидов еще более совершенна. Символ (h, k) однозначно определяет его строение, в том числе т. г. с., принадлежность к той или иной серии подобия и ее дуальную серию. Уже очевидна важная роль генераторов (1, 0), (2, 1), (3, 1) и (3, 2), покрывающих сериями подобия и дуальными сериями большую часть известного многообразия капсидов. К ним следует присмотреться хотя бы ради поиска способов разрушения этих совершенных оболочек. По-видимому, не лишена смысла следующая гипотеза. Если капсиды отражают филогенетическое родство икосаэдрических вирусов, то филогенетические линии хотя бы фрагментарно должны вкладываться в серии подобия и/или дуальные серии.

В логике устройства системы икосаэдрических капсидов угадывается мысль С.В. Мейена (2007а, с. 209): “Зная законы композиции, мы можем наметить пределы разнообразия отдельных форм и структур, заготовить необходимое и достаточное количество классификационных ячеек. Если же отдельные ячейки окажутся пустыми, мы будем целеустремленно искать отвечающие им объекты” или, добавим, искать причины запрета. О сходном пишет Г.Ю. Любарский (2011, с. 30), обсуждая концепцию биологического разнообразия: “Всевозможных зависимостей между разными показателями бесконечное количество. Среди них особо ценятся те, которые обозначают какую-то простую связь показателей, и при этом дают важную закономерность изучаемого разнообразия, “раскалывают” его, так что становится понятно, как это огромное разнообразие устроено”.

В контексте общебиологической проблематики и терминологии интересно обсудить, чему соответствуют серии подобия и дуальные серии. По-видимому, первые вполне отвечают гомологическим рядам Н.И. Вавилова, хотя последний термин употребляется в разных контекстах. “Столь же проблематичны и многоплановы современные представления о гомологии структур: диапазон ее трактовок варьирует между признанием полной объективности и полной субъективности 〈…〉. В первом случае 〈…〉 подразумевается некий тип отношений между структурами, аналогичный родству между организмами 〈…〉. Во втором случае 〈…〉 гомология нередко отождествляется со сходством: структуры гомологичны, если их сходство (подобие) существенно в некотором фиксированном контексте” (Павлинов, 2011, с. 91). Наше понимание гомологии отвечает второму варианту, пока не доказано филогенетическое родство икосаэдрических вирусов в сериях подобия и дуальных сериях.

Дуальные переходы (зигзаги) в парах гомологичных серий подобия хочется связать с рефренами С.В. Мейена. “Члены рефрена сходны нетривиально. Это сходство сохраняется при условии сравнения с помощью (закона изменения – Ю.В.). Рефрен – это такое множество объектов, принадлежащих разным таксонам (разным сериям подобия – Ю.В.), которые могут быть сделаны неотличимыми посредством одного и того же преобразования (“изменения И”) (перехода (h, k) → (h + 2k, h – k) – Ю.В.). 〈…〉 Ряды Н.И. Вавилова – наиболее известный случай проявления рефрена. При введении понятия рефрена я специально подчеркивал, что самое интересное и важное в рядах Вавилова – не повторность отдельных форм от ряда к ряду, а одинаковая упорядоченность обоих рядов, т.е. инвариантность изменений в рядах” (Мейен, 2007б, с. 308).

Аналогичного взгляда на рефрены придерживается и Ю.В. Чайковский (2016, с. 32): “Первичным материалом и понятием диатропики служит ряд, а основными свойствами разнообразия являются параллелизм (сходство рядов) и комбинативность. Огромное разнообразие явлений создается не количеством элементов, а количеством их комбинаций. Мысль эта есть уже у Хэйла, затем у многих, а после Мейена можно сказать, что она проявляется в рефренах. Рефрен – это (в моем понимании) ряд направленных параллельных рядов. Самый простой пример: строки периодической таблицы – это ряды, а вся таблица – это рефрен”. Уточним лишь, что в нашем случае рефрены создаются зигзагами дуальных переходов между гомологичными сериями подобия.

ВЫВОДЫ

Все сказанное обосновывает следующие основные выводы и задачи дальнейших исследований:

Номенклатуру икосаэдрического капсида следует строить на символе (h, k) его грани, фиксирующем ее ориентацию относительно плотнейшей упаковки белковых глобул.

Систематика капсидов в первом приближении по т. г. с. Ih и I логична. Класс Ih состоит из дуальных серий подобия (1, 0) и (1, 1), связанных переходом (h, k) → (h + 2k, h – k).

Класс I также состоит из дуальных серий подобия, порождаемых генераторами (h, k), узнаваемыми по критерию: h и k взаимно просты, (h – k) не делится на 3. Поиск генератора выполняется пошаговым алгоритмом (h, k) → [(h + 2k)/3, (h – k)/3].

Коронавирус SARS-CoV-2, по-видимому, имеет капсид (2, 0), т. г. с. Ih, Т = 4, аналогичный вирусу полиомы, второй в серии подобия, порождаемой генератором (1, 0) – капсидом бактериофага φX174. Модель “усеченного октаэдра” требует подтверждения.

Найдено общее преобразование икосаэдрических капсидов (h1, k1) → (h2, k2). Это уникальный случай биологического (пограничного) многообразия, для которого получен столь общий результат, даже если он имеет чисто теоретическое значение.

Представляют интерес вопросы: о частоте встречаемости икосаэдрических вирусов в классах Ih и I, их различных видов (h, k), изомеров и генераторов; о естественных границах многообразия. Все эти задачи имеют аналоги в кристаллографии ввиду разной встречаемости пространственных групп симметрии в минералах.

Наконец, фундаментален вопрос, имеют ли гомологические ряды подобия и рефрены (дуальные серии) икосаэдрических капсидов филогенетическую подоплеку.

Список литературы

  1. Вайнштейн Б.К., Киселев Н.А., 1964. Строение вирусов // Основы молекулярной биологии. Вирусология и иммунология. Проблемы общей вирусологии, структура и биосинтез антител. М.: Наука. С. 7–48.

  2. Гнутова Р.В., 2011. Современные тенденции в таксономии и номенклатуре вирусов // Успехи соврем. биологии. Т. 131. № 6. С. 563–577.

  3. Доливо-Добровольский В.В., 1924. Исследование додекаэдро-икосаэдрической системы // Зап. РМО. № 1. С. 169–181.

  4. Жданов В.М., Львов Д.К., Забережный А.Д., 2012. Место вирусов в биосфере // Вопросы вирусологии. № S1. С. 21–32.

  5. Костюченко В.А., Месянжинов В.В., 2002. Архитектура сферических вирусов // Успехи биол. химии. Т. 42. С. 177–192.

  6. Лурия С., Дорнелл Дж., Балтимор Д., Кэмпбелл Э., 1981. Общая вирусология. М.: Мир. 680 с.

  7. Любарский Г.Ю., 2011. Рамочная концепция для теории биологического разнообразия // Зоол. исследования. № 10. С. 5–44.

  8. Любищев А.А., 1923. О форме естественной системы организмов // Изв. Биол. НИИ при Перм. ун-те. Т. 2. № 3. С. 99–110.

  9. Мейен С.В., 2007а. Морфология растений в номотетическом аспекте // In memoriam. С.В. Мейен: палеоботаник, эволюционист, мыслитель. М.: ГЕОС. С. 162–222.

  10. Мейен С.В., 2007б. Заметки о теоретической биологии // In memoriam. С.В. Мейен: палеоботаник, эволюционист, мыслитель. М.: ГЕОС. С. 294–318.

  11. Мэтьюз Р., 1973. Вирусы растений. М.: Мир. 600 с.

  12. Павлинов И.Я., 2011. Как возможно выстраивать таксономическую теорию // Зоол. исследования. № 10. С. 45–100.

  13. Рис Э., Стернберг М., 2002. Введение в молекулярную биологию: от клеток к атомам. М.: Мир. 142 с.

  14. Федоров Е.С., 1915. Практикум по основным отделам кристаллографии. Петроград: Эконом. типо-лит. 20 с.

  15. Чайковский Ю.В., 2016. Заключительные мысли. М.: Т-во науч. изд. КМК. 175 с.

  16. Caspar D.L.D., Klug A., 1962. Physical principles in the construction of regular viruses // Cold Spring Harb. Symp. Quant. Biol. V. 27. P. 1–24.

  17. Claverie J., Ogata H., Audic S., Abergel C., Suhre K., Fournier P., 2006. Mimivirus and the emerging concept of ‘giant’ virus // Virus Res. V. 117. P. 133–144.

  18. Coscio F., Nadra A.D., Ferreiro D.U., 2020. A structural model for the coronavirus nucleocapsid // arXiv. https://doi.org/10.48550/arXiv.2005.12165

  19. Crick F.H.C., Watson J.D., 1956. The structure of small viruses // Nature. V. 177. P. 473–475.

  20. Forterre P., Gaïa M., 2016. Giant viruses and the origin of modern eukaryotes // Curr. Opin. Microbiol. V. 31. P. 44–49.

  21. International Committee on Taxonomy of Viruses Executive Committee, 2020. The new scope of virus taxonomy: partitioning the virosphere into 15 hierarchical ranks // Nat. Microbiol. V. 5. P. 668–674.

  22. Pimonov V.V., Konevtsova O.V., Rochal S.B., 2019. Anomalous small viral shells and simplest polyhedra with icosahedral symmetry: the rhombic triacontahedron case // Acta Cryst. A. V. 75. P. 135–141.

  23. Raoult D., La Scola B., Birtles R., 2007. The discovery and characterization of Mimivirus, the largest known virus and putative pneumonia agent // Clin. Infect. Dis. V. 45. P. 95–102.

  24. Rux J., Kuser P., Burnett R., 2003. Structural and phylogenetic analysis of Adenovirus hexons by use of high-resolution X-ray crystallographic, molecular modeling, and sequence-based methods // J. Virol. V. 77. P. 9553–9566.

  25. Schmalz T.G., Seitz W.A., Klein D.J., Hite G.E., 1988. Elemental carbon cages // J. Am. Chem. Soc. V. 110. № 4. P. 1113–1127.

  26. Simpson A.A., Nandhagopal N., Van Etten J.L., Rossmann M.G., 2003. Structural analyses of Phycodnaviridae and Iridoviridae // Acta Cryst. D. V. 59. P. 2053–2059.

  27. Van Etten J., 2011. Giant viruses // Am. Sci. V. 99. № 4. P. 304–311.

  28. Voytekhovsky Yu.L., 2015. Biomineral analogues in ontogeny and phylogeny // Paleontol. J. V. 49. № 14. P. 1691–1697.

  29. Voytekhovsky Yu.L., 2016. Homological series of icosahedral viruses and fullerenes // Paleontol. J. V. 50. № 13. P. 1505–1509.

  30. Voytekhovsky Yu.L., Stepenshchikov D.G., 2016. Fullerene transformations as analogues of radiolarian skeleton microevolution // Paleontol. J. V. 50. № 13. P. 1544–1548.

  31. Wolynes P.G., 1996. Symmetry and the energy landscapes of biomolecules // Proc. Natl. Acad. Sci. USA. V. 93. P. 14249–14255.

  32. Xiao C., Chipman P.R., Battisti A.J., Bowman V.D., Renesto P. et al., 2005. Cryo-electron microscopy of the giant Mimivirus // J. Mol. Biol. V. 353. P. 493–496.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал общей биологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал