1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 66, № 2, 2021

Журнал неорганической химии, 2021, T. 66, № 2, стр. 204-219

Cпектроскопия ЯМР – универсальный метод исследования структуры и магнитных свойств комплексов парамагнитных лантанидов в растворах (обзор)

Ю. Г. Горбунова a, b, *, А. Г. Мартынов b, К. П. Бирин b, А. Ю. Цивадзе a, b

a Институт общей и неорганической химии им. Н.С. Курнакова РАН
119991 Москва, Ленинский пр-т, 31, Россия

b Институт физической химии и электрохимии РАН им. А.Н. Фрумкина
119071 Москва, Ленинский пр-т, 31, корп. 4, Россия

* E-mail: yulia@igic.ras.ru

Поступила в редакцию 10.08.2020
После доработки 19.08.2020
Принята к публикации 25.08.2020

Полный текст (PDF)

Аннотация

Координационные соединения лантанидов привлекают все большее внимание исследователей благодаря уникальным физико-химическим (в том числе оптическим и магнитным) свойствам. При этом тонкая настройка свойств функциональных материалов на их основе возможна за счет управления структурой комплексов. В данном обзоре на примере серий соединений парамагнитных лантанидов с тетрапиррольными лигандами рассмотрено применение спектроскопии ЯМР для решения сложной задачи идентификации парамагнитных комплексов лантанидов, а также для установления корреляции между строением координационной сферы ионов лантанидов и магнитными характеристиками комплексов. Показано, как анализ лантанид-индуцированных сдвигов и скоростей лантанид-индуцированной релаксации в сериях изоструктурных соединений способствует выявлению спектрально-структурных корреляций, которые с привлечением рентгеноструктурных и расчетных данных позволяют не только устанавливать структуру соединения в растворе, но и проводить первичную оценку возможности использования комплексов в качестве мономолекулярных магнитов.

Ключевые слова: лантанид-индуцированный сдвиг, лантанид-индуцированная релаксация, фталоцианины, порфирины, спектрально-структурные корреляции, магнитные материалы

ВВЕДЕНИЕ

Уникальные свойства ионов лантанидов с частично заполненными 4f-подуровнями обусловливают широкое применение координационных соединений на их основе в качестве релаксационных агентов для магнитно-резонансной томографии, парамагнитных и люминесцентных меток для изучения биологических объектов [1–5 ]. Среди новых высокотехнологичных областей применения комплексов лантанидов особое внимание привлекает создание мономолекулярных материалов для хранения больших объемов информации и разработки технологий квантовых вычислений [6–9], катализаторов для полимеризации диенов и циклических эфиров [10], а также редокс-активных материалов для элементов записи и хранения информации [11–13]. Кроме того, в последнее время все большее внимание уделяется гибридным органо-неорганическим соединениям, когда комплексы лантанидов вводятся либо на поверхность/в объем неорганической матрицы [14], либо, наоборот, функциональные органические молекулы встраиваются в неорганические лантанидсодержащие матрицы [15]. Особого внимания заслуживает относительно новый класс соединений – слоистые гидроксиды лантанидов, особенностью которых является возможность изменения их состава в широких пределах при изменении основного структурного мотива. Так, за счет анионного обмена с органическими лигандами возможно получение уникальных люминесцентных материалов [16–19], сенсоров и препаратов для биомедицинских приложений, в том числе тераностики [20], а также катализаторов и фотокатализаторов [21–24]. Недавно было показано, что комбинирование наночастиц диоксида церия с фталоцианинами позволяет контролировать процесс генерации синглетного кислорода фотосенсибилизатором [25, 26].

Такой широкий диапазон применения координационных соединений лантанидов обусловлен их специфической 4f-электронной конфигурацией и разнообразием координационных чисел. Все это в совокупности со значительным уменьшением атомных и ионных размеров лантанидов в ряду от La к Lu (так называемое лантанидное сжатие) позволяет тонко варьировать геометрию и электронную структуру комплексов на их основе. В свою очередь, корреляция между строением комплексов лантанидов и функциональными характеристиками материалов на их основе определяет важность разработки подходов к определению их структуры при совместном применении спектральных и структурных методов для создания материалов с заданными свойствами.

Комплементарное применение структурных методов в сочетании со спектроскопией ЯМР для исследования парамагнитных комплексов лантанидов позволяет решать две взаимосвязанные задачи. С одной стороны, знание структуры, полученной на основе рентгеноструктурного анализа (РСА) или квантово-химического моделирования, позволяет интерпретировать спектры ЯМР парамагнитных комплексов и определять тем самым характеристики, важные для дизайна, например, магнитных материалов [27, 28]. С другой стороны, анализ спектров ЯМР позволяет изучать особенности геометрической структуры и электронного строения комплексов в растворе [29–31]. Данные методы применимы также к исследованию внутримолекулярной динамики конформационно-подвижных соединений – макроциклов, полидентатных лигандов, биомолекул и т.п. [32–35].

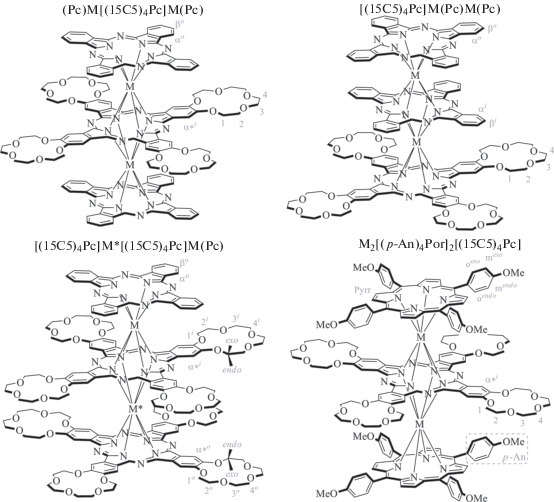
В представленном обзоре подробно описан подход к решению обеих задач с применением спектрально-структурного анализа на примере работ авторов по исследованию сэндвичевых трехпалубных комплексов лантанидов с тетрапиррольными лигандами (рис. 1) – перспективных компонентов новых супрамолекулярных оптоэлектронных и магнитных материалов [36–38].

Рис. 1.

Строение гетеролептических краун-замещенных трехпалубных комплексов РЗЭ(III) с обозначением протонов, использованным для отнесения спектров ЯМР.

ПРИМЕНЕНИЕ МЕТОДА ЯМР ДЛЯ ИЗУЧЕНИЯ КОМПЛЕКСОВ ЛАНТАНИДОВ

Характерной особенностью комплексов парамагнитных лантанидов является наличие в их спектрах ЯМР сигналов резонанса, существенно смещенных относительно их положения в спектрах диамагнитных аналогов. Наблюдаемые лантанид-индуцированные сдвиги (ЛИС, $\Delta \delta _{k}^{{{\text{Ln}}}},$ уравнение (1), где M – диамагнитный ион РЗЭ – La3+, Lu3+ или Y3+) могут быть как положительными, так и отрицательными в зависимости от природы лантанида в составе комплекса и взаимного расположения рассматриваемого атома и иона лантанида [39].

Кроме того, наличие парамагнитных ионов в таких комплексах приводит к лантанид-индуцированному увеличению скорости релаксации (ЛИР), что еще больше усложняет задачу анализа спектров ЯМР комплексов лантанидов. Так, ускорение релаксации в комплексах лантанидов приводит к уширению сигналов в спектрах соединений, пропорциональному времени поперечной релаксации ${{T}_{2}}.$ При этом пропадает расщепление сигналов, которое позволяет выделить группы спиново-связанных протонов, а в предельном случае уширение приводит к полному исчезновению сигналов в спектре. Кроме того, применение двумерных методик с переносом поляризации становится практически невозможным в силу низкой эффективности такого переноса в условиях быстрой продольной релаксации ядер ${{T}_{1}}.$

Тем не менее задача исследования комплексов парамагнитных лантанидов методом спектроскопии ЯМР может быть решена на основании функциональных зависимостей ЛИС и ЛИР от геометрических характеристик, определяющих взаимное расположение рассматриваемого атома и иона лантанида.

ЛИС протона Hk определяется как суперпозиция контактной ($\Delta \delta _{k}^{{{\text{con}}}},$ уравнение (2)) и дипольной ($\Delta \delta _{k}^{{{\text{dip}}}},$ уравнение (3)) составляющих, передающихся через систему связей и пространство соответственно:

(1)
$\Delta \delta _{k}^{{{\text{Ln}}}} = \delta _{k}^{{{\text{Ln}}}} - \delta _{k}^{{\text{M}}} = \Delta \delta _{k}^{{{\text{con}}}} + \Delta \delta _{k}^{{{\text{dip}}}},$
(2)
$\Delta \delta _{k}^{{{\text{con}}}} = {{F}_{k}}{{\left\langle {{{S}_{Z}}} \right\rangle }^{{{\text{Ln}}}}},$
(3)
$\Delta \delta _{k}^{{{\text{dip}}}} = \frac{{\chi _{{ax}}^{{{\text{Ln}}}}}}{{12\pi }}{{G}_{k}},\,\,\,\,{{G}_{k}} = \frac{{3{{{\cos }}^{2}}{{\theta }_{k}} - 1}}{{r_{k}^{3}}}.$

Коэффициент ${{F}_{k}}$ в уравнении (2) характеризует величину контактной составляющей ЛИС, возникающей благодаря делокализации спиновой плотности в молекуле комплекса по системе химических связей в результате взаимодействия Ферми. Данное взаимодействие быстро затухает с увеличением количества связей между ионом лантанида и рассматриваемым протоном. Величина ${{\left\langle {{{S}_{Z}}} \right\rangle }^{{{\text{Ln}}}}}$ является расчетной табулированной характеристикой магнитных свойств ионов лантанидов [40, 41].

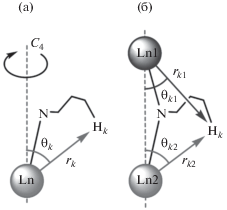
Коэффициент ${{G}_{k}}$ в уравнении (3) характеризует дипольную составляющую ЛИС, связанную с взаимодействием рассматриваемого k-го ядра с парамагнитным центром через пространство: ${{\theta }_{k}}$ – азимут относительно главной оси симметрии молекулы, ${{r}_{k}}$ – расстояние от k-го протона до иона Ln3+ (рис. 2a), $\chi _{{ax}}^{{{\text{Ln}}}}$ – аксиальная анизотропия тензора магнитной восприимчивости. В случае биядерных комплексов, содержащих два иона лантанидов, величина $\Delta \delta _{k}^{{{\text{dip}}}}$ является аддитивной и определяется индивидуальными вкладами от каждого иона (рис. 2б, уравнение (4)). Таким образом, входящая в выражение для дипольного вклада ЛИС величина ${{G}_{k}}$ несет информацию о геометрических характеристиках молекулы комплекса в растворе, в то время как $\chi _{{{\text{ax}}}}^{{{\text{Ln}}}}$ характеризует магнетохимические свойства комплекса.

(4)
$\Delta \delta _{k}^{{{\text{dip}}}} = \frac{{\chi _{{{\text{ax}}}}^{{{\text{Ln1}}}}}}{{12\pi }}\left[ {\frac{{3{{{\cos }}^{2}}{{\theta }_{{k1}}} - 1}}{{r_{{k1}}^{3}}}} \right] + \frac{{\chi _{{{\text{ax}}}}^{{{\text{Ln2}}}}}}{{12\pi }}\left[ {\frac{{3{{{\cos }}^{2}}{{\theta }_{{k2}}} - 1}}{{r_{{k2}}^{3}}}} \right].$
Рис. 2.

Определение параметров, входящих в уравнение (3) и определяющих величину дипольного вклада ЛИС в случае моно- (а) и биядерных (б) комплексов.

Разделение ЛИС на контактную и дипольную составляющие основано на использовании приближенного представления дипольного вклада в виде произведения параметра кристаллического поля $A_{2}^{0}$ как характеристики рассматриваемого комплекса и табулированной расчетной константы Блини ${{D}^{{{\text{Ln}}}}}$ как характеристики иона лантанида [42]. Дальнейшей трансформацией уравнения (5) могут быть получены различные линейные формы, применение которых для серий изоструктурных комплексов с различными лантанидами позволяет исследовать поведение коэффициентов ${{F}_{k}},$ $A_{2}^{0}$ и ${{G}_{k}}$ по мере увеличения числа f-электронов и уменьшения ионных радиусов лантанидов [39, 43].

(5)
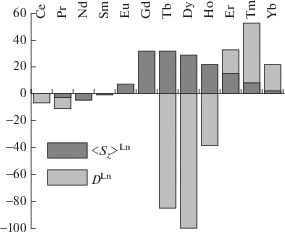
$\Delta \delta _{k}^{{{\text{Ln}}}} = {{F}_{k}}{{\left\langle {{{S}_{z}}} \right\rangle }^{{{\text{Ln}}}}} + A_{2}^{0}{{D}^{{{\text{Ln}}}}}{{G}_{k}}.$

Многочисленные примеры применения такого подхода к анализу сэндвичевых комплексов с парамагнитными лантанидами свидетельствуют о пренебрежимо малом вкладе контактной составляющей в величину ЛИС [44–49], поскольку величина $\Delta \delta _{k}^{{{\text{con}}}}$ быстро уменьшается с увеличением числа связей между ионом лантанида и рассматриваемым протоном. Такое поведение ЛИС также связано со спецификой изменения термов ${{\left\langle {{{S}_{Z}}} \right\rangle }^{{{\text{Ln}}}}}$ и ${{D}^{{{\text{Ln}}}}}$ в ряду лантанидов (рис. 3).

Рис 3.

Изменение термов ${{\left\langle {{{S}_{Z}}} \right\rangle }^{{{\text{Ln}}}}}$ и ${{D}^{{{\text{Ln}}}}}$ в ряду лантанидов [40–42].

Благодаря преимущественно дипольной природе ЛИС становится возможным прямое сопоставление структурных характеристик, найденных с помощью рентгеноструктурного анализа или квантово-химического моделирования с данными, полученными из анализа спектров ЯМР.

Другим подходом спектрально-структурного изучения комплексов лантанидов методом ЯМР является исследование времен релаксации ядер [43]. ЛИР является функцией парамагнитных характеристик ядра и $r_{k}^{6},$ где ${{r}_{k}}$ – расстояние от парамагнитного лантанида до изучаемого ядра k. Таким образом, информация об уменьшении времени релаксации позволяет выполнить отнесение сигналов в спектре по данным о строении соединения, а также уточнить межъядерные расстояния внутри соединения в растворе. Время продольной релаксации ${{T}_{1}}$ может быть измерено с помощью стандартной двухимпульсной последовательности. Время поперечной релаксации ${{T}_{2}}$ определяется из соотношения $\Delta {{\nu }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\left( {{\pi }{{T}_{2}}} \right)}^{{ - 1}}},$ где $\Delta {{\nu }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – полуширина сигнала.

Выявление парамагнитного ускорения релаксации ${{T}_{1}}$ возможно при наличии данных о времени релаксации изоструктурного комплекса диамагнитного лантанида. В этом случае наблюдаемая скорость релаксации определяется как

(6)
$\frac{1}{{T_{1}^{{{\text{exp}}}}}} = \frac{1}{{T_{1}^{{{\text{dia}}}}}} + \frac{1}{{T_{1}^{{{\text{para}}}}}}.$

В этом выражении $T_{1}^{{{\text{exp}}}}$ – наблюдаемое время релаксации ядра, $T_{1}^{{{\text{dia}}}}$ – время релаксации ядра в диамагнитном реперном комплексе, ${1 \mathord{\left/ {\vphantom {1 {T_{1}^{{{\text{para}}}}}}} \right. \kern-0em} {T_{1}^{{{\text{para}}}}}}$ – парамагнитный вклад в скорость релаксации. Вычисленные из приведенного соотношения ${1 \mathord{\left/ {\vphantom {1 {T_{1}^{{{\text{para}}}}}}} \right. \kern-0em} {T_{1}^{{{\text{para}}}}}}$ являются прямой характеристикой расстояния лантанид–ядро. Для пары ядер k и l в соединении справедливо соотношение (7), которое позволяет проводить отнесение сигналов резонанса на основе структурных моделей и уточнять геометрические параметры структуры соединения:

(7)
$\frac{{T_{{1k}}^{{{\text{para}}}}}}{{T_{{1l}}^{{{\text{para}}}}}} = {{\left( {\frac{{{{r}_{k}}}}{{{{r}_{l}}}}} \right)}^{6}}.$

В случае соединений, содержащих два парамагнитных центра, анализ усложняется в силу их взаимного влияния на каждый рассматриваемый протон. Таким образом, наблюдаемая скорость релаксации определяется тремя вкладами: диамагнитным и двумя парамагнитными:

(8)
$\frac{1}{{T_{1}^{{{\text{exp}}}}}} = \frac{1}{{T_{1}^{{{\text{dia}}}}}} + \frac{1}{{T_{1}^{{{\text{para(Ln1)}}}}}} + \frac{1}{{T_{1}^{{{\text{para(Ln2)}}}}}}.$

В связи с тем, что парамагнитное ускорение релаксации быстро спадает с удалением ядра от парамагнитного центра, а также с учетом симметричного строения изучаемых комплексов для наиболее точного определения отклонений межатомных расстояний в расчетной геометрической модели от реальных значений следует использовать данные о парамагнитном ускорении, определяемом ближайшим к ядру лантанидом. Для анализа расстояний Hi ↔ Ln внутри комплекса необходимо разложить суммарное парамагнитное ускорение релаксации на парамагнитные вклады, определяемые влиянием каждого из лантанидов. С учетом соотношения ${1 \mathord{\left/ {\vphantom {1 {T_{1}^{{{\text{para}}}}}}} \right. \kern-0em} {T_{1}^{{{\text{para}}}}}} \sim {{r}^{{ - 6}}}$ для любого протона системы Hk:

(9)
$T_{1}^{{{\text{para(Ln1)}}}} = T_{1}^{{{\text{para}}}} + T_{1}^{{{\text{para}}}}{{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}^{6}}.$

Точное определение расстояний по данным времен релаксации требует разложения парамагнитного ускорения на вклады, определяемые различными механизмами релаксации. Кроме того, необходима информация о ряде параметров ядра лантанида, зависящих от его окружения. Эта информация отсутствует в литературе для комплексов лантанидов с тетрапиррольными лигандами, однако возможна верификация расчетной структурной модели на основании отношений расстояний и парамагнитных ускорений релаксации. Для двух протонов k и l комплекса должно выполняться равенство:

(10)
$\frac{{{{r}_{1}}({{{\text{H}}}_{k}})}}{{{{r}_{1}}({{{\text{H}}}_{l}})}} = {{\left[ {\frac{{T_{1}^{{{\text{para(Ln1)}}}}({{{\text{H}}}_{k}})}}{{T_{1}^{{{\text{para(Ln1)}}}}({{{\text{H}}}_{l}})}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}.$

Приведенное соотношение позволяет экспериментально определить соотношение расстояний Ln ↔ Hk для любой пары протонов комплекса, а также для модельной структуры. Соотношение экспериментальной и рассчитанной величин может служить характеристикой точности модели.

Структурно-спектральные характеристики гетеролептических краун-замещенных трехпалубных фталоцианинатов лантанидов

В данном разделе рассмотрено применение метода ЯМР-спектроскопии для изучения двух серий изомерных комплексов, содержащих два незамещенных фталоцианиновых лиганда (Рс) и один тетра-15-краун-5-замещенный лиганд [(15С5)4Рс] в терминальном или центральном положении – [(15C5)4Pc]M(Pc)M(Pc) [46, 50] и (Pc)M[(15C5)4Pc]M(Pc) [51, 52], а также ряд комплексов с двумя соседними замещенными лигандами – [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) (рис. 1). Для последнего семейства комплексов были получены как гомо- (M* = M [51, 52]), так и гетероядерные (M* ≠ M [49, 53, 54]) производные. В качестве металлов-комплексообразователей использовали лантаниды(III) Nd, Sm, Eu, Tb, Dy, Ho, Er, Tm, Yb, в качестве диамагнитного репера – Y. Интерес к исследованию данных комплексов обусловлен их способностью к супрамолекулярной сборке [37, 38, 55], что позволяет рассматривать их как перспективные компоненты функциональных магнитных материалов [56] и молекулярных переключателей с управляемыми свойствами [57].

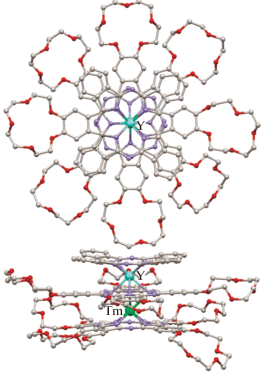
Для различных типов обсуждаемых комплексов были выращены монокристаллы, структура которых расшифрована рентгеноструктурным методом [49, 51], что позволило установить единообразие строения координационных полиэдров ионов лантанидов вне зависимости от количества и расположения краун-эфирных заместителей. Координационные полиэдры ионов металлов представляют собой искаженные тетрагональные антипризмы, образованные развернутыми под углом ~45° тетрапиррольными лигандами. Связи ионов металлов с изоиндольными атомами азота, образованные терминальными лигандами, систематически короче на ~0.3 Å по сравнению со связями от ионов M3+ до атомов Niso мостиковых внутренних лигандов. Расстояния между фталоцианиновыми лигандами составляют 2.9–3.1 Å, расстояния между металлоцентрами – 3.43–3.53 Å. Для примера на рис. 4 показана структура комплекса [(15C5)4Pc]Y[(15C5)4Pc]Tm(Pc) [49].

Рис. 4.

Структура гетероядерного комплекса [(15C5)4Pc]Tm[(15C5)4Pc]Y(Pc), вид сверху и сбоку. Атомы водорода и сольватные молекулы растворителей не показаны [49].

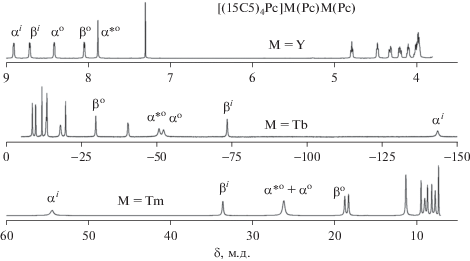
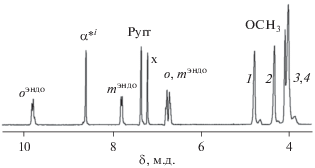
Для всех трех серий соединений были получены спектры 1H ЯМР растворов в CDCl3. Сдвиги для комплекса каждого парамагнитного лантанида индивидуальны и характеризуются его природой. На рис. 5 приведены примеры спектров изоструктурных комплексов [(15C5)4Pc]M(Pc)M(Pc) со спектральными диапазонами, характеристичными для ионов лантанидов с максимальными положительными (Tm3+) и отрицательными (Tb3+) ЛИС в тетрапиррольном окружении. В то же время спектр комплекса иттрия имеет типичный для диамагнитных соединений вид.

Рис. 5.

Примеры спектров 1H ЯМР комплексов [(15C5)4Pc]M(Pc)M(Pc), где M = Y, Tb, Tm [50, 55], с отнесением сигналов резонанса ароматических протонов. Обозначения протонов даны на рис. 1.

В табл. 1 и 2 приведены химические сдвиги сигналов резонанса протонов в спектрах ЯМР изомерных гомоядерных комплексов (Pc)M[(15C5)4Pc]M(Pc) и [(15C5)4Pc]M(Pc)M(Pc) в CDCl3. Из этих данных видно, что в гомоядерных комплексах сигналы резонанса всех протонов претерпевают смещение либо в слабое (M = = Eu, Er, Tm, Yb), либо в сильное поле (Nd, Sm, Tb, Dy, Ho) относительно их положения в спектре диамагнитного комплекса иттрия. Во всех случаях величина этого смещения уменьшается с увеличением расстояния между протоном и ионами Ln3+.

Таблица 1.  

Положение сигналов резонанса (δ, м.д.) в спектрах 1H ЯМР гомоядерных комплексов (Pc)M[(15C5)4Pc]M(Pc) [51, 52] в CDCl3. Обозначения протонов приведены на рис. 1

H Nd Sm Eu Tb Dy Ho Er Tm Yb Y
αo 6.46 8.02 9.72 –50.47 –21.51 –2.13 21.77 25.1 10.38 8.58
βo 6.69 7.56 8.39 –30.07 –11.57 0.8 15.61 17.76 8.93 7.92
α*i 1.49 6.59 11.92 –154.76 –74 –21.96 44.23 53.58 13 8.25
1-CH2 2.37 4.42 6.62 –67.6 –31.59 –8.51 20.81 23.4 7.34 5.13
2-CH2 3.07 4.29 5.68 –35.27 –15.37 –2.58 13.58 15.99 5.9 4.67
3-CH2 3.29 4.06 4.96 –21.68 –8.7 –0.41 10.07 11.64 5.11 4.31
4-CH2 3.35 4.06 4.85 –19.23 –7.46 –0.01 9.45 10.89 4.98 4.26
Таблица 2.  

Положение сигналов резонанса (δ, м.д.) в спектрах 1H ЯМР гомоядерных комплексов [(15C5)4Pc]M(Pc)M(Pc) [46, 50] в CDCl3. Обозначения протонов приведены на рис. 1

H Nd Sm Eu Tb Dy Er Tm Y
αo 6.23 7.87 9.80 –53.27 –24.00 22.17 26.14 8.44
βo 6.76 7.72 8.70 –31.67 –12.78 15.41 18.70 8.09
α*i 2.48 7.39 13.13 –148.51 –72.05 45.10 54.40 8.97
β*i 4.99 7.85 11.37 –76.35 –34.37 28.86 33.56 8.71
α*o 5.51 7.30 9.27 –54.81 –24.00 22.64 26.14 7.86

Указанная выше возможность пренебрежения контактной составляющей ЛИС позволяет рассматривать ЛИС как величину, пропорциональную аксиальной анизотропии тензора магнитной восприимчивости $\chi _{{ax}}^{{{\text{Ln}}}}$ иона Ln3+ и геометрическому параметру ${{G}_{k}},$ аддитивному в случае биядерных комплексов (рис. 2б, уравнение (4)). В случае несимметричных гомоядерных трис-фталоцианинатов [(15C5)4Pc]M[(15C5)4Pc]M(Pc) ионы лантанидов оказываются в неэквивалентном координационном окружении – гомо- и гетеролептическом, что приводит к разнице в величинах $\chi _{{ax}}^{{{\text{Ln1}}}}$ и $\chi _{{ax}}^{{{\text{Ln2}}}}$ [49], однако в первом приближении этим различием можно пренебречь из-за близости электронных свойств незамещенных и краун-замещенных лигандов. Аналогичное приближение используется для анализа спектров комплексов [(15C5)4Pc]M(Pc)M(Pc) [46].

Таким образом, с использованием указанного приближения отношения ЛИС для различных пар протонов Hk и Hl можно с достаточной точностью описать отношением соответствующих геометрических факторов – ${{R}_{{kl}}}.$ Подставив в уравнение (11) выражения для ЛИС из уравнения (1), получим уравнение (12), согласно которому можно оценить положение сигналов резонанса в спектрах парамагнитных комплексов $\delta _{k}^{{{\text{Ln}}}}$ исходя из положения соответствующих сигналов в спектре ЯМР диамагнитного комплекса $\delta _{k}^{Y}$ и отношений ${{R}_{{kl}}}$ для соответствующих пар протонов, которые могут быть найдены из рентгеноструктурных данных или данных квантово-химического моделирования [44, 48]:

(11)
$\frac{{\Delta \delta _{k}^{{{\text{Ln}}}}}}{{\Delta \delta _{l}^{{{\text{Ln}}}}}} \approx \frac{{\Delta \delta _{k}^{{{\text{dip}}}}}}{{\Delta \delta _{l}^{{{\text{dip}}}}}} = {{R}_{{kl}}},\,\,\,\,{{R}_{{kl}}} = \frac{{{{G}_{k}}}}{{{{G}_{l}}}},$
(12)
$\delta _{k}^{{{\text{Ln}}}} = \delta _{k}^{Y} + \Delta \delta _{l}^{{{\text{Ln}}}}{{R}_{{kl}}}.$

Применение уравнения (12) позволяет объяснить особенность спектров ЯМР изомерных гетероядерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [M*, M] по сравнению с гомоядерными аналогами. В спектрах комплексов [Ln*, Y] и [Y*, Ln] наблюдаются сигналы резонанса, смещенные как в сильное, так и в слабое поле относительно их положения в спектре комплекса [Y*, Y], тогда как в спектрах гомоядерных комплекcов [Ln*, Ln] величина ЛИС имеет одинаковый знак для всех протонов (табл. 3).

Таблица 3.  

Положение сигналов резонанса (δ, м.д.) в спектрах 1H ЯМР гомо- и гетероядерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [M*, M] в CDCl3 [49, 51, 53]. Обозначения протонов приведены на рис. 1

Параметр [Tb*, Tb] [Tb*, Y] [Y*, Tb] [Y*, Y]
αo –56.34 24.82 –71.45 8.58
βo –34.72 9.19 –34.22 8.02
α*i –157.94 –70.67 –71.45 8.27
α*o –56.34 –71.09 23.86 7.95
экзо-1i –36.99 –19.67 –42.05 5.19
эндо-1i –36.25 –29.76 –28.04 5.19
экзо-1o –33.84 –22.30 9.18 4.79
эндо-1o –17.78 –33.77 0.08 4.44

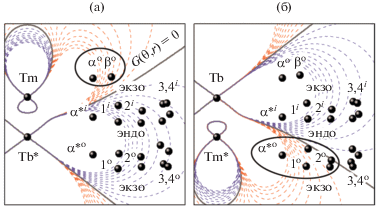
Такое поведение гетероядерных комплексов обусловлено нелинейностью функции ${{G}_{k}},$ из-за которой вокруг иона Ln3+ образуются области как с отрицательными, так и с положительными знаками ${{G}_{k}}$ (рис. 6). Так, в случае комплексов [Tb*, Y] в области с ${{\theta }_{k}} > 0$ оказываются ароматические протоны терминального незамещенного фталоцианинового лиганда αo и βo (рис. 6a), тогда как в случае изомерного комплекса [Y*, Tb] в эту область попадают протоны замещенного лиганда – ароматические протоны α*o и экзопротоны первой метиленовой группы краун-эфирных заместителей (рис. 6б).

Рис. 6.

Контурные карты функции $G(\theta ,r)$ для гетероядерных комплексов [Ln*, Y] (a) и [Y*, Ln] (б) и гомоядерных комплексов [Ln*, Ln] (в) [49]. Координаты протонов получены усреднением данных РСА для комплекса [Tm*, Y]. Овалами отмечены протоны, попадающие в область противоположного знака функции $G(\theta ,r)$ по сравнению с большинством протонов молекул. Обозначения протонов даны на рис. 1.

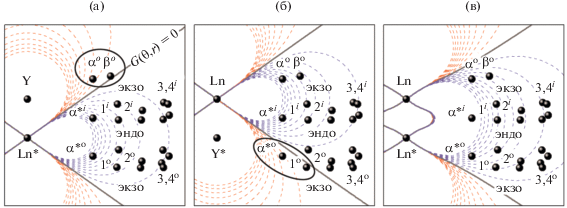
В спектрах гомоядерных комплексов функции ${{G}_{k}}$ суммируются для обоих ионов лантанидов и все протоны находятся в знакопостоянной области с ${{\theta }_{k}} < 0$ (рис. 6в). Наблюдаемое согласие между величинами ${{G}_{k}},$ рассчитанными из данных РСА и 1H ЯМР, свидетельствует об изоструктурности комплексов в кристалле и в растворе, благодаря чему данные РСА являются адекватной моделью для интерпретации спектров ЯМР трис-фталоцианинатов лантанидов.

Наличие данных РСА для исследованных комплексов позволяет определить величину входящей в уравнение (12) важной характеристики магнитных свойств комплексов – аксиальной анизотропии тензора магнитной восприимчивости $\chi _{{ax}}^{{{\text{Ln}}}}.$ Знак данной величины определяет знаки ЛИС протонов, попадающих в области с различными знаками ${{G}_{k}}.$

С помощью метода наименьших квадратов были найдены угловые коэффициенты зависимости величин ЛИС протонов от соответствующих им значений функции ${{G}_{k}},$ рассчитанных исходя из рентгеноструктурных данных (рис. 7). Проведение такого анализа для серий гетероядерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [Ln*, Y] и [Y*, Ln] показало, что в комплексах [Y*, Ln] с гетеролептическим окружением ионов Ln3+ $\chi _{{ax}}^{{{\text{Ln}}}}$ выше, чем в изомерных комплексах [Ln*, Y] с гомолептическим окружением иона Ln3+ (табл. 4).

Рис. 7.

Определение аксиальной анизотропии $\chi _{{{\text{ax}}}}^{{{\text{Tb}}}}$ регрессионным методом на основании данных ЯМР и РСА для гетероядерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [M*, M] [49].

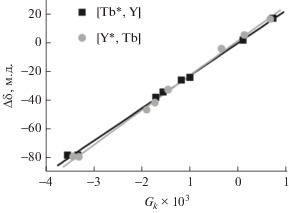
Таблица 4.  

Аксиальная анизотропия тензора магнитной восприимчивости в комплексах [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [M*, M] по данным спектроскопии 1H ЯМР и РСА [49]

Ln [Ln*, Y] $\chi _{{ax}}^{{{\text{Ln}}}}$, м–3 [Y*, Ln] $\chi _{{ax}}^{{{\text{Ln}}}}$, м–3
Nd 3.42 × 10–32 3.55 × 10–32
Eu –2.06 × 10–32 –2.22 × 10–32
Tb 8.41 × 10–31 8.98 × 10–31
Dy 4.30 × 10–31 4.92 × 10–31
Er –1.90 × 10–31 –2.17 × 10–31
Tm –2.39 × 10–31 –2.57 × 10–31
Yb –2.77 × 10–32 –2.95 × 10–32

Определение величин $\chi _{{ax}}^{{{\text{Ln}}}}$ позволило с помощью уравнения (4) интерпретировать особенности спектрального поведения гетероядерных комплексов, содержащих два различных парамагнитных ядра. Это было сделано на примере пары изомерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc), содержащих ионы Tb3+ и Tm3+.

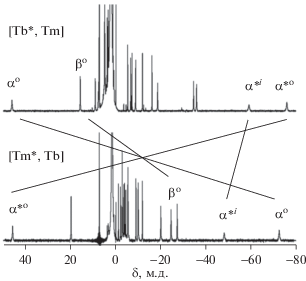
Поскольку величина $\chi _{{ax}}^{{{\text{Tb}}}}$ в 3.5 раза больше $\chi _{{ax}}^{{{\text{Tm}}}},$ именно влияние иона тербия доминирует в проявлении совокупного $\Delta \delta _{k}^{{{\text{dip}}}}.$ Однако из-за того, что эти ионы характеризуются противоположными по знаку величинами $\chi _{{ax}}^{{{\text{Ln}}}},$ границы, в которых величина дипольной составляющей является знакопостоянной, деформируются – области с $\Delta \delta _{k}^{{{\text{dip}}}} < 0$ сокращаются, а области с $\Delta \delta _{k}^{{{\text{dip}}}} > 0$ увеличиваются (рис. 8). В результате спектральный диапазон, в котором наблюдаются сигналы резонанса комплексов, содержащих ионы Tb3+ и Tm3+ расширяется до 130 м.д. (рис. 9) по сравнению с комплексами, содержащими ионы Tb3+ и Y3+ (95 м.д., табл. 3).

Рис. 8.

Контурные карты функции $G(\theta ,r)$ для изомерных гетероядерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [Tb*, Tm] и [Tm*, Tb]. Координаты протонов получены усреднением данных РСА для комплекса [Tm*, Y]. Овалами отмечены протоны, попадающие в область положительных значений ЛИС, по сравнению с большинством протонов молекул [49]. Обозначения протонов даны на рис. 1.

Рис. 9.

Спектры 1H ЯМР изомерных гетероядерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [Tb*, Tm] и [Tm*, Tb] в CDCl3 [49]. Обозначения протонов даны на рис. 1.

Структурно-спектральные характеристики гетеролептических порфиринато-фталоцианинатов лантанидов

Описанный подход применим к другим классам гетеролептических трехпалубных комплексов, например к гетеролептическим порфиринато-фталоцианинатам, для которых пренебрежение разницей в анизотропии $\chi _{{ax}}^{{{\text{Ln}}}}$ для ионов металлов в окружении Por/Pc или Pc/Pc даже в случае гомоядерных комплексов не корректно [58]. Для спектрального анализа таких соединений были разработаны селективные методы получения гетеролептических трехпалубных комплексов, содержащих тетра(15-краун-5)фталоцианин и мезо-арилзамещенные порфирины с заданным расположением металлоцентров и тетрапиррольных лигандов [59–63]. Этот класс соединений был подробно изучен на примере симметричных гетеролептических трехпалубных комплексов, содержащих центральный тетра(15-краун-5)фталоцианиновый и терминальные тетра-мезо(4-метоксифенил)порфириновыe лиганды – Ln2[(p-An)4Por]2[(15C5)4Pc], где Ln = La(III), Ce(III), Pr(III), Nd(III), Sm(III) и Eu(III). Спектр 1H ЯМР диамагнитного комплекса лантана представлен на рис. 10.

Рис. 10.

Спектры 1Н ЯМР комплекса Ln2[(p-An)4Por]2[(15C5)4Pc] в CDCl3 с отнесением сигналов резонанса ароматических протонов [48]. Обозначения протонов даны на рис. 1.

Как описано выше, для надежного отнесения сигналов в спектрах гетеролептических комплексов парамагнитных лантанидов необходима структурная информация о молекуле. Однако для данного класса соединений не удалось вырастить монокристаллы, в связи с этим нами был разработан подход, позволяющий построить расчетную модель их строения. Расчет геометрии сложных макроциклических структур квантово-химическими методами, например DFT, с достаточной точностью требует большой вычислительной мощности и длительного времени, поэтому нами был разработан упрощенный метод, позволяющий получить геометрические параметры протонов, определяемые их расположением относительно парамагнитного центра. Для получения пространственной модели строения молекулы оказались пригодны методы молекулярной механики и молекулярной динамики, такие как MM+ и AMBER98. В качестве модели был выбран комплекс церия с центральным октаметоксифталоцианиновым и терминальными тетра-мезо(4-метоксифенил)порфириновыми лигандами. Для этого соединения был выполнен расчет геометрии и полученные результаты сопоставлены с данными рентгеноструктурного анализа для родственных комплексов [64]. На основе найденной расчетной структуры был проведен анализ ЛИС сигналов резонанса протонов.

В рассматриваемых комплексах ЛИС сигналов ароматических протонов фталоцианинового лиганда и пиррольных протонов порфирина, отдаленных от ионов лантанидов на пять и четыре связи соответственно, могут иметь существенный контактный вклад, в то время как остальные протоны удалены от парамагнитного центра на большее число связей, что позволяет построить первичный анализ спектров серии соединений на допущении о преимущественно дипольной природе ЛИС. Для этого с использованием уравнения (4) были вычислены значения геометрических параметров Gk для каждого из типов протонов молекулы (табл. 5). В последнем столбце приведены значения суммарных геометрических функций Gk, нормированные на геометрический параметр ароматического протона фталоцианиновой палубы.

Таблица 5.

Геометрические параметры ароматических протонов модельного комплекса Ln2[(p-An)4Por]2[(15C5)4Pc] [48]

Hk Ln1 Ln2 $\begin{gathered} \sum {{{G}_{k}} = } \\ = {{G}_{{k1}}} + {{G}_{{k2}}} \\ \end{gathered} $ $\frac{{\sum {{{G}_{k}}} }}{{\sum {G(\alpha {\kern 1pt} {{*}^{i}})} }}$
θk1, град rk1, Å Gk1 × 103 θk1, град rk1, Å Gk1 × 103
oэндо 93.61 5.19 –7.06 57.51 6.14 –0.58 –7.64 1.05
oэкзо 49.22 5.86 1.39 30.77 8.68 1.86 3.25 –0.45
mэндо 89.50 7.52 –2.35 63.85 8.38 –0.71 –3.06 0.42
mэкзо 58.19 8.02 –0.32 40.95 10.40 0.63 0.31 –0.04
Pyrr 70.68 5.39 –4.28 43.25 7.43 1.44 –2.84 0.39
α*i 108.17 5.79 –3.65 71.83 5.79 –3.65 –7.29 1.00

Сигнал ароматического протона наиболее удобен для анализа сигналов в спектрах и ЛИС, так как его отнесение выполнено с хорошей точностью для всех трехпалубных гетеролептических комплексов. Из этого рассмотрения становится ясно, что два протона молекулы попадают в область магнитного воздействия лантанида, противоположную по знаку и, как следствие, направлению ЛИС большей части протонов системы. Это внешние орто- и мета-протоны мезо-заместителя порфириновой палубы, причем величины ЛИС этих протонов отличаются на порядок. Абсолютное значение геометрического параметра мета-протона мало по сравнению с параметрами остальных протонов молекулы, и его теоретически ожидаемый ЛИС также мал. Следует отметить, что самым высоким значением ${{G}_{k}}$ характеризуется не протон фталоцианиновой палубы, эффективно взаимодействующий с обоими парамагнитными центрами, а внутренний орто-протон мезо-заместителя, ЛИС которого определяется преимущественно одним лантанидом.

Графическое представление взаимного расположения протонов и парамагнитных металлоцентров в молекуле трехпалубного комплекса приведено на рис. 11. Схема представляет собой сечение молекулы по оси Ln–Ln. В каждой точке пространства вычислено значение $G(\theta ,r)$ и определено геометрическое место точек с $G(\theta ,r) = 0,$ что является границей, при пересечении которой знак $G(\theta ,r)$ изменяется на противоположный.

Рис. 11.

Контурные карты функции $G(\theta ,r)$ для комплексов Ln2[(p-An)4Por]2[(15C5)4Pc], координаты атомов получены на основании расчета методом MM+ [48]. Овалами отмечены протоны, попадающие в область противоположного знака функции $G(\theta ,r)$ по сравнению с большинством протонов молекул. Обозначения протонов даны на рис. 1.

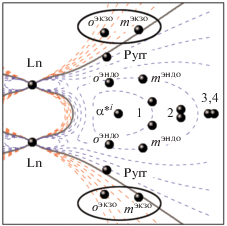
Нулевая огибающая этой системы нелинейна и по мере удаления от системы двух лантанидов стремится к углу наклона 54.7° по отношению к оси Ln–Ln, характерному для одноядерных комплексов [44]. Однако в пределах молекулы этот угол больше, что объясняет размещение протонов комплекса в областях разного знака ЛИС. Бóльшая часть протонов молекулы комплекса находится в зоне ЛИС одного знака, однако внешние орто- и мета-протоны мезо-анизильных заместителей порфириновой палубы попадают в область противоположного знака. Важно отметить, что пиррольные протоны порфириновых палуб находятся близко к нулевой линии, что позволяет предположить их малый дипольный ЛИС несмотря на близкое расположение к металлоцентрам.

Полученные численные значения геометрических параметров и их графическое представление позволили выполнить отнесение сигналов в спектрах комплексов парамагнитных лантанидов. Для этого было найдено такое соответствие сигналов в спектре диамагнитного комплекса лантана и комплексов парамагнитных лантанидов, при котором отношение ${{\Delta \delta ({{{\text{H}}}_{k}})} \mathord{\left/ {\vphantom {{\Delta \delta ({{{\text{H}}}_{k}})} {\Delta \delta ({\alpha }{{{\text{*}}}^{i}})}}} \right. \kern-0em} {\Delta \delta ({\alpha }{{{\text{*}}}^{i}})}}$ близко к вычисленному ${{G({{{\text{H}}}_{k}})} \mathord{\left/ {\vphantom {{G({{{\text{H}}}_{k}})} {G({\alpha }{{{\text{*}}}^{i}})}}} \right. \kern-0em} {G({\alpha }{{{\text{*}}}^{i}})}}.$ На рис. 12 приведены примеры отнесения сигналов для комплексов европия и неодима, сдвигающих сигналы в область слабых и сильных полей соответственно. В табл. 6 приведены численные значения химических сдвигов сигналов резонанса протонов молекулы и относительные ЛИС для полученной серии комплексов парамагнитных лантанидов. Анализ спектров серии комплексов лантанидов позволил выполнить точное отнесение сигналов протонов мезо-арильных заместителей, которое невозможно выполнить другими методами.

Рис. 12.

Отнесение сигналов в спектрах 1H ЯМР трехпалубных комплексов Ln2[(p-An)4Por]2[(15C5)4Pc] в CDCl3, где Ln = La, Ce, Eu [48].

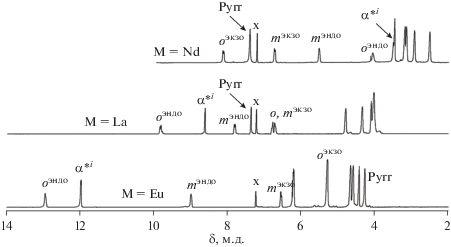
Таблица 6.  

Положение сигналов резонанса (δ, м.д.) в спектрах 1H ЯМР трехпалубных комплексов Ln2[(p-An)4Por]2[(15C5)4Pc] [48]. Относительные значения $\Delta \delta _{k}^{{{\text{rel}}}}$ соответствуют отношениям ЛИС рассматриваемых протонов к ЛИС ароматических протонов фталоцианинового лиганда α*

Параметр La Ce Pr Nd Sm Eu
δk δk $\Delta \delta _{k}^{{{\text{rel}}}}$ δk $\Delta \delta _{k}^{{{\text{rel}}}}$ δk $\Delta \delta _{k}^{{{\text{rel}}}}$ δk $\Delta \delta _{k}^{{{\text{rel}}}}$ δk $\Delta \delta _{k}^{{{\text{rel}}}}$
1-CH2 4.83 –0.35 0.46 1.30 0.45 2.57 0.44 4.22 0.46 6.23 0.42
2-CH2 4.38 1.32 0.27 2.27 0.27 2.99 0.27 4.01 0.28 5.32 0.28
3-CH2 4.06 2.12 0.17 2.73 0.17 3.20 0.17 3.85 0.16 4.68 0.18
4-CH2 4.06 2.28 0.16 2.83 0.16 3.25 0.16 3.85 0.16 4.61 0.16
oэндо 9.84 –2.64 1.12 1.13 1.12 4.12 1.12 8.16 1.26 13.00 0.94
oэкзо 6.75 10.08 –0.30 9.04 –0.30 8.17 –0.28 7.16 –0.31 5.32 –0.43
mэндо 7.85 2.75 0.46 4.33 0.45 5.57 0.45 6.94 0.68 9.01 0.35
mэкзо 6.80 6.67 0.01 6.74 0.01 6.77 0.01 6.73 0.05 6.57 –0.07
α*i 8.65 –2.53 1.00 0.89 1.00 3.55 1.00 7.32 1.00 12.01 1.00
Pyrr 7.40 3.15 0.38 5.81 0.20 7.45 –0.01 6.60 0.60 4.30 –0.92
OMe 4.14 2.77 0.12 3.19 0.12 3.52 0.12 3.94 0.15 4.45 0.09

Величины относительного ЛИС протонов молекулы, нормированные на величину ЛИС ароматического протона фталоцианинового лиганда, совпадают качественно и близки количественно к рассчитанным на основе параметризованной модели комплекса (табл. 6). Однако при детальном рассмотрении полученного массива данных обнаруживаются некоторые отклонения наблюдаемых соотношений от расчетных.

Так, ЛИС внешнего мета-протона мезо-заместителя отличается от рассчитанного как по знаку (для комплексов Ce, Pr, Nd), так и по абсолютной величине. Это отклонение объясняется сравнительно малой величиной ЛИС, сравнимой с уширением сигнала при уменьшении времени поперечной релаксации ${{T}_{2}},$ что снижает точность ее определения. Отклонения относительных ЛИС сигналов протонов комплекса самария определяются уменьшением точности определения ЛИС в связи с малыми величинами ${{\left\langle {{{S}_{Z}}} \right\rangle }^{{{\text{Sm}}}}}$ и ${{D}^{{{\text{Sm}}}}}$ и, как следствие, малыми ЛИС. Выполненное отнесение сигналов в спектрах трехпалубных комплексов согласуется с данными о скорости релаксации протонов (табл. 7).

Таблица 7.

Экспериментальное время продольной релаксации протонов трехпалубных комплексов Ln2[(p-An)4Por]2[(15C5)4Pc] [48]

Параметр La Nd Eu
  $1/T_{1}^{{{\text{exp}}}}$, с–1 $1/T_{1}^{{{\text{exp}}}}$, с–1 $1/T_{1}^{{{\text{para}}}}$, с–1 $1/T_{1}^{{{\text{exp}}}}$, с–1 $1/T_{1}^{{{\text{para}}}}$, с–1
1-CH2 5.88 9.39 3.51 7.87 1.99
2-CH2 5.88 7.85 1.97 6.45 0.57
3-CH2 4.00 5.47 1.47 4.76 0.76
4-CH2 4.00 5.38 1.38 4.76 0.76
oэндо 2.22 48.78 46.56 11.11 8.89
oэкзо 1.67 13.95 12.28 6.45 4.78
mэндо 1.67 5.21 3.55 2.86 1.19
mэкзо 1.67 4.08 2.42 2.86 1.19
α*i 3.13 16.61 13.49 11.11 7.99
Pyrr 1.25 23.09 21.84 7.87 6.62
OMe 1.96 3.09 1.13 2.27 0.31

Имея данные о временах релаксации протонов диамагнитного репера – комплекса лантана, можно выделить диамагнитный и парамагнитный вклады экспериментально наблюдаемой скорости релаксации. Учитывая, что ${1 \mathord{\left/ {\vphantom {1 {T_{1}^{{{\text{para}}}}}}} \right. \kern-0em} {T_{1}^{{{\text{para}}}}}} \sim {{r}^{{ - 6}}}$ (r – расстояние от протона до парамагнитного центра), парамагнитный вклад в скорость релаксации быстро уменьшается с удалением рассматриваемого протона от иона лантанида, и, таким образом, данные о временах релаксации предоставляют дополнительные сведения для верификации расчетной модели структуры комплекса. Однако следует отметить, что даже малая ошибка в определении расстояний в расчетной модели комплекса существенно влияет на результаты анализа за счет шестой степени отношения расстояний. В целом данные парамагнитного ускорения релаксации согласуются с определенными расстояниями и подтверждают выполненное отнесение сигналов.

Сравнение параметров модели и полученных релаксационных данных для трехпалубных гетеролептических комплексов неодима и европия показало, что ошибка расчетных величин для протонов мезо-заместителей порфириновых палуб находится в интервале 1–5%, что подтверждает корректность описания геометрии всего ряда полученных комплексов с помощью полученной оптимизированной структурной модели. Необходимо отметить, что данное уточнение невозможно для краун-эфирных заместителей молекулы из-за большого набора их конформаций без возможности определить наиболее выгодную. Отношения, включающие параметры пиррольного и фталоцианинового протонов молекулы, демонстрируют существенно бóльшую ошибку. Это может определяться их близостью к парамагнитному центру и существенным вкладом контактного механизма ускорения релаксации аналогично ЛИС.

Магнетохимические свойства гетеролептических фталоцианинатов РЗЭ

Для серии комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – гомоядерного [Tb*, Tb] и изомерных гетероядерных [Tb*, Y] и [Y*, Tb] – были исследованы магнетохимические свойства с использованием ac-магнитометрии [54].

Для гомоядерного комплекса при нулевом постоянном внешнем магнитном поле в интервале температур 1.9–28 K наблюдались зависимости действительной (χ') и мнимой (χ'') компонент магнитной восприимчивости от частоты осциллирующего магнитного поля, что свидетельствовало о наличии медленной магнитной релаксации. В случае гетероядерных комплексов медленную магнитную релаксацию можно было наблюдать только при наложении постоянного внешнего магнитного поля напряженностью 1.5 кЭ.

Такое различие в поведении гомо- и гетероядерных комплексов обусловлено реализацией механизма квантового туннелирования в случае гетероядерных комплексов в отсутствие внешнего магнитного поля. Реализация этого механизма обусловлена искажением координационных полиэдров ионов тербия от правильной квадратной антипризмы за счет разницы в длинах связей с атомами азота терминальных и внутреннего лигандов (рис. 4). В случае гомоядерного комплекса благодаря близости расположения ионов Tb3+ между ними реализуется ферромагнитное взаимодействие, эффективно подавляющее квантовое туннелирование [65, 66]. Наличие такого взаимодействия в гомоядерном комплексе было подтверждено измерением магнитной восприимчивости комплексов [M*, M].

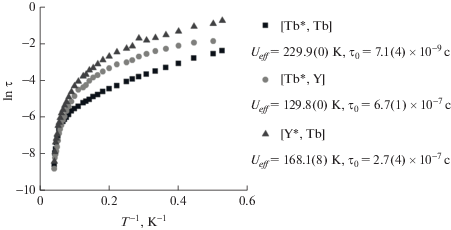
С использованием обобщенной модели Дебая были определены времена релаксации намагниченности τ при разных температурах. С помощью уравнения Аррениуса были найдены высоты энергетического барьера перемагничивания Ueff и времена релаксации τ0 (рис. 13). Полученные данные свидетельствуют о том, что в гетероядерных комплексах более высокий барьер Ueff наблюдается у комплекса c ионом тербия, находящимся между [(15C5)4Pc] и (Pc). Следует отметить, что для этого же комплекса характерно более высокое значение аксиальной анизотропии $\chi _{{ax}}^{{Tb}},$ найденное по данным спектроскопии 1H ЯМР и РСА (табл. 4). Подобное усиление SMM-свойств с ростом анизотропии было отмечено в работах М. Ямашиты [67, 68]. Таким образом, найденные корреляции между величиной барьера и координационным окружением ионов Tb3+ в трехпалубных комплексах могут быть использованы для направленного получения комплексов с улучшенными магнитными характеристиками.

Рис. 13.

Зависимость времени релаксации намагниченности от 1/Т, значения барьера перемагничивания и времени τ0, найденные по уравнению Аррениуса для гомо- и гетероядерных комплексов [(15C5)4Pc]M*[(15C5)4Pc]M(Pc) – [Tb*, Tb], [Tb*, Y] и [Y*, Tb] [54].

В то время как особенности магнитного поведения, в том числе явление молекулярного магнетизма, могут быть полноценно изучены лишь с использованием dc- и ac-магнитометрии, спектроскопия ЯМР как существенно более доступный метод может дать ценную первичную информацию о магнитных свойствах комплексов и способствовать выявлению новых корреляций для получения молекулярных магнетиков с улучшенными характеристиками.

Список литературы

  1. Harnden A.C., Parker D., Rogers N.J. // Coord. Chem. Rev. 2019. V. 383. P. 30. https://doi.org/10.1016/j.ccr.2018.12.012

  2. Staszak K., Wieszczycka K., Marturano V. et al. // Coord. Chem. Rev. 2019. V. 397. P. 76. https://doi.org/10.1016/j.ccr.2019.06.017

  3. Kaczmarek M. // J. Lumin. 2020. V. 222. P. 117174. https://doi.org/10.1016/j.jlumin.2020.117174

  4. Zairov R.R., Yagodin A.V., Khrizanforov M. et al. // J. Nanoparticle Res. 2019. V. 21. № 1. P. 12. https://doi.org/10.1007/s11051-018-4455-4

  5. Ning Y., Zhu M., Zhang J.-L. // Coord. Chem. Rev. 2019. V. 399. P. 213028. https://doi.org/10.1016/j.ccr.2019.213028

  6. Wang H., Wang B.W., Bian Y. et al. // Coord. Chem. Rev. 2016. V. 306. № P1. P. 195. https://doi.org/10.1016/j.ccr.2015.07.004

  7. Cador O., Le Guennic B., Pointillart F. // Inorg. Chem. Front. 2019. V. 6. № 12. P. 3398. https://doi.org/10.1039/c9qi00875f

  8. Lan Y., Klyatskaya S., Ruben M. // Bis(phthalocyaninato) Lanthanide(III) Complexes - from Molecular Magnetism to Spintronic Devices / Eds. Layfield R.A., Murugesu M. Lanthanides Actinides Mol. Magn., Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015: pp. 223–292. https://doi.org/10.1002/9783527673476.ch8

  9. Harriman K.L.M., Errulat D., Murugesu M. // Trends Chem. 2019. V. 1. № 4. P. 425. https://doi.org/10.1016/j.trechm.2019.04.005

  10. Lyubov D.M., Tolpygin A.O., Trifonov A.A. // Coord. Chem. Rev. 2019. V. 392. P. 83. https://doi.org/10.1016/j.ccr.2019.04.013

  11. MacDonald M.R., Bates J.E., Ziller J.W. et al. // J. Am. Chem. Soc. 2013. V. 135. № 26. P. 9857. https://doi.org/10.1021/ja403753j

  12. Fedushkin I.L., Maslova O.V., Morozov A.G. et al. // Angew. Chem. Int. Ed. 2012. V. 51. № 42. P. 10584. https://doi.org/10.1002/anie.201204452

  13. Shokurov A.V., Kutsybala D.S., Martynov A.G. et al. // Langmuir. 2020. V. 36. № 6. P. 1423. https://doi.org/10.1021/acs.langmuir.9b03403

  14. Kaczmarek A.M., Van Der Voort P. // Materials. 2020. V. 13. № 3. P. 566. https://doi.org/10.3390/ma13030566

  15. Yapryntsev A.D., Baranchikov A.E., Ivanov V.K. // Russ. Chem. Rev. 2020. V. 89. № 6. P. 629. https://doi.org/10.1070/RCR4920

  16. Yorov K.E., Kottsov S.Y., Baranchikov A.E. et al. // J. Sol-Gel Sci. Technol. 2019. V. 92. № 2. P. 304. https://doi.org/10.1007/s10971-019-04958-9

  17. Yapryntsev A., Abdusatorov B., Yakushev I. et al. // Dalton Trans. 2019. V. 48. № 18. P. 6111. https://doi.org/10.1039/C9DT00390H

  18. Yapryntsev A.D., Baranchikov A.E., Skogareva L.S. et al. // CrystEngComm. 2015. V. 17. № 13. P. 2667. https://doi.org/10.1039/C4CE02303J

  19. Xiang Y., Yu X.-F., He D.-F. et al. // Adv. Funct. Mater. 2011. V. 21. № 22. P. 4388. https://doi.org/10.1002/adfm.201101808

  20. Yapryntsev A.D., Bykov A.Y., Baranchikov A.E. et al. // Inorg. Chem. 2017. V. 56. № 6. P. 3421. https://doi.org/10.1021/acs.inorgchem.6b02948

  21. Gándara F., Puebla E.G., Iglesias M. et al. // Chem. Mater. 2009. V. 21. № 4. P. 655. https://doi.org/10.1021/cm8029517

  22. Demel J., Kubát P., Millange F. et al. // Inorg. Chem. 2013. V. 52. № 5. P. 2779. https://doi.org/10.1021/ic400182u

  23. Wang X., Chen W., Song Y.-F. // Eur. J. Inorg. Chem. 2014. V. 2014. № 17. P. 2779. https://doi.org/10.1002/ejic.201400122

  24. Sokolov M.R., Enakieva Y.Y., Yapryntsev A.D. et al. // Adv. Funct. Mater. 2020. V. 30. № 27. P. 2000681. https://doi.org/10.1002/adfm.202000681

  25. Shekunova T.O., Lapkina L.A., Shcherbakov A.B. et al. // J. Photochem. Photobiol., A. Chem. 2019. V. 382. P. 111925. https://doi.org/10.1016/j.jphotochem.2019.111925

  26. Lapkina L.A., Gorbunova Y.G., Gil D.O. et al. // J. Porphyrins Phthalocyanines. 2013. V. 17. № 06n07. P. 564. https://doi.org/10.1142/S1088424613500648

  27. Hiller M., Krieg S., Ishikawa N. et al. // Inorg. Chem. 2017. V. 56. № 24. P. 15285. https://doi.org/10.1021/acs.inorgchem.7b02704

  28. Santria A., Fuyuhiro A., Fukuda T. et al. // Dalton Trans. 2019. V. 48. № 22. P. 7685. https://doi.org/10.1039/C9DT00915A

  29. Joss D., Häussinger D. // Prog. Nucl. Magn. Reson. Spectrosc. 2019. V. 114–115. P. 284. https://doi.org/10.1016/j.pnmrs.2019.08.002

  30. Babailov S.P. // Prog. Nucl. Magn. Reson. Spectrosc. 2008. V. 52. № 1. P. 1. https://doi.org/10.1016/j.pnmrs.2007.04.002

  31. Geraldes C.F.G.C., Zhang S., Sherry A.D. // Inorg. Chim. Acta 2004. V. 357. № 2. P. 381. https://doi.org/10.1016/j.ica.2003.03.001

  32. Babailov S.P., Coutsolelos A.G., Dikiy A. et al. // Eur. J. Inorg. Chem. 2001. V. 2001. № 1. P. 303. https://doi.org/10.1002/1099-0682(20011)2001:1<303::AID-EJIC303>3.0.CO;2-Y

  33. Babailov S.P. // Inorg. Chem. 2012. V. 51. № 3. P. 1427. https://doi.org/10.1021/ic201662q

  34. Babailov S.P., Stabnikov P.A., Zapolotsky E.N. et al. // Inorg. Chem. 2013. V. 52. № 9. P. 5564. https://doi.org/10.1021/ic400525r

  35. Birin K.P., Gorbunova Y.G., Tsivadze A.Y. // Dalton Trans. 2011. V. 40. № 43. P. 11474. https://doi.org/10.1039/c1dt11231g

  36. Горбунова Ю.Г., Лапкина Л.А., Мартынов А.Г. и др. // Коорд. химия. 2004. V. 30. № 4. P. 263. https://doi.org/10.1023/B:RUCO.0000022799.63314.fc

  37. Gorbunova Y.G., Martynov A.G., Tsivadze A.Y. // Crown-Substituted Phthalocyanines: From Synthesis Towards Materials, in: K.M. Kadish, K.M. Smith, R. Guilard (Eds.), Handbook of Porphyrin Science, World Scientific Publishing, 2012: pp. 271–388 https://doi.org/10.1142/9789814397605_0015

  38. Martynov A.G., Gorbunova Y.G., Tsivadze A.Y. // Russ. J. Inorg. Chem. 2014. V. 59. № 14. P. 1635. https://doi.org/10.1134/S0036023614140046

  39. Piguet C., Geraldes C.F.G.C. // Paramagnetic NMR Lanthanide Induced Shifts for Extracting Solution Structures, in: K.A. Gschneidner, J.-C.G. Bünzli, V.K. Pecharsky (Eds.), Handbook on the Physics and Chemistry of Rare Earths, Elsevier Science B.V., 2003: pp. 353–463 https://doi.org/10.1016/S0168-1273(02)33005-8

  40. Golding R., Halton M. // Aust. J. Chem. 1972. V. 25. № 12. P. 2577. https://doi.org/10.1071/CH9722577

  41. Pinkerton A.A.A., Rossier M., Spiliadis S. et al. // J. Magn. Reson. 1985. V. 64. № 3. P. 420. https://doi.org/10.1016/0022-2364(85)90104-0

  42. Bleaney B. // J. Magn. Reson. 1972. V. 8. № 1. P. 91. https://doi.org/10.1016/0022-2364(72)90027-3

  43. Peters J.A., Huskens J., Raber D.J. // Prog. Nucl. Magn. Reson. Spectrosc. 1996. V. 28. № 3–4. P. 283. https://doi.org/10.1016/0079-6565(95)01026-2

  44. Ishikawa N., Iino T., Kaizu Y. // J. Phys. Chem. A. 2003. V. 107. № 39. P. 7879. https://doi.org/10.1021/jp034971n

  45. Arnold D.P., Jiang J. // J. Phys. Chem. A. 2001. V. 105. № 32. P. 7525. https://doi.org/10.1021/jp0105847

  46. Martynov A.G., Gorbunova Y.G. // Polyhedron. 2010. V. 29. № 1. P. 391. https://doi.org/10.1016/j.poly.2009.06.009

  47. Martynov A.G., Gorbunova Y.G., Tsivadze A.Y. // Dalton Trans. 2011. V. 40. № 27. P. 7165. https://doi.org/10.1039/c1dt10455a

  48. Birin K.P., Gorbunova Y.G., Tsivadze A.Y. // Magn. Reson. Chem. 2010. V. 48. № 7. P. 505. https://doi.org/10.1002/mrc.2612

  49. Polovkova M.A., Martynov A.G., Birin K.P. et al. // Inorg. Chem. 2016. V. 55. № 18. P. 9258. https://doi.org/10.1021/acs.inorgchem.6b01292

  50. Martynov A.G., Zubareva O.V., Gorbunova Y.G. et al. // Inorg. Chim. Acta. 2009. V. 362. № 1. P. 11. https://doi.org/10.1016/j.ica.2008.01.008

  51. Martynov A.G., Zubareva O.V., Gorbunova Y.G. et al. // Eur. J. Inorg. Chem. 2007. № 30. P. 4800. https://doi.org/10.1002/ejic.200700489

  52. Мартынов А.Г., Сафонова Е.А., Горбунова Ю.Г. и др. // Журн. неорган. химии. 2010. Т. 55. № 3. С. 389.

  53. Цивадзе А.Ю., Мартынов А.Г., Половкова М.А. и др. // Изв. АН. Сер. химическая. 2011. № 11. P. 2216.

  54. Holmberg R.J., Polovkova M.A., Martynov A.G. et al. // Dalton Trans. 2016. V. 45. № 22. P. 9320. https://doi.org/10.1039/C6DT00777E

  55. Martynov A.G., Polovkova M.A., Berezhnoy G.S. et al. // Inorg. Chem. 2020. V. 59. № 13. P. 9424. https://doi.org/10.1021/acs.inorgchem.0c01346

  56. Horii Y., Kishiue S., Damjanović M. et al. // Chem. Eur. J. 2018. V. 24. № 17. P. 4320. https://doi.org/10.1002/chem.201705378

  57. Martynov A.G., Safonova E.A., Tsivadze A.Y. et al. // Coord. Chem. Rev. 2019. V. 387. P. 325. https://doi.org/10.1016/j.crr.2019.02.004

  58. Sakaue S., Fuyuhiro A., Fukuda T. et al. // Chem. Commun. 2012. V. 48. № 43. P. 5337. https://doi.org/10.1039/c2cc31125a

  59. Birin K.P., Gorbunova Y.G., Tsivadze A.Y. // Dalton Trans. 2011. V. 40. № 43. P. 11539. https://doi.org/10.1039/c1dt11141h

  60. Birin K.P., Gorbunova Y.G., Tsivadze A.Y. // Dalton Trans. 2012. P. 23. https://doi.org/10.1039/c2dt30841j

  61. Birin K.P., Poddubnaya A.I., Gorbunova Y.G. et al. // Macroheterocycles. 2017. V. 10. № 4–5. P. 514. https://doi.org/10.6060/mhc171258b

  62. Birin K.P., Gorbunova Y.G., Tsivadze A.Y. et al. // J. Porphyrins Phthalocyanines. 2009. V. 13. № 2. P. 283. https://doi.org/10.1142/S1088424609000358

  63. Birin K.P., Kamarova K.A., Gorbunova Y.G. et al. // Prot. Met. 2013. V. 49. № 2. P. 173. https://doi.org/10.1134/S2070205113020032

  64. Sun X., Li R., Wang D. et al. // Eur. J. Inorg. Chem. 2004. № 19. P. 3806. https://doi.org/10.1002/ejic.200400289

  65. Ishikawa N., Iino T., Kaizu Y. // J. Am. Chem. Soc. 2002. V. 124. № 38. P. 11440. https://doi.org/10.1021/ja027119n

  66. Katoh K., Kajiwara T., Nakano M. et al. // Chem. Eur. J. 2011. V. 17. № 1. P. 117. https://doi.org/10.1002/chem.201002026

  67. Katoh K., Breedlove B.K., Yamashita M. // Chem. Sci. 2016. V. 7. P. 4329. https://doi.org/10.1039/C5SC04669F

  68. Morita T., Damjanović M., Katoh K. et al. // J. Am. Chem. Soc. 2018. V. 140. № 8. P. 2995. https://doi.org/10.1021/jacs.7b12667

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал