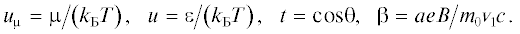Микроэлектроника, 2022, T. 51, № 3, стр. 218-229

Влияние анизотропии изоэнергетической поверхности на электропроводность и постоянную Холла для тонкой полупроводниковой пленки

П. А. Кузнецов^a, С. Б. Московский^a, Д. Н. Романов^a, *

^a Ярославский государственный университет им. П.Г. Демидова
150003 Ярославль, ул. Советская, 14, Россия

Поступила в редакцию 09.07.2021
После доработки 27.07.2021
Принята к публикации 15.09.2021

EDN: YKLDTC
DOI: 10.31857/S0544126922020065

Аннотация

Решена кинетическая задача о расчете электропроводности и постоянной Холла для тонкой полупроводниковой пленки. В качестве граничных условий для функции распределения носителей заряда используется модель диффузных граничных условий. Изоэнергетическая поверхность материала пленки – эллипсоид вращения. Предполагается, что в объеме полупроводника доминирует рассеяние на атомах примеси и на дислокациях электронов (дырок). Проведен анализ электропроводности и постоянной Холла тонкой пленки в зависимости от эффективной массы.

Ключевые слова: кинетическое уравнение, функция распределения, тонкая пленка, электропроводность, постоянная Холла

1. ВВЕДЕНИЕ

Известно, что электропроводность тонких пленок отличается от электропроводности макроскопических образцов [1]. Различие, в частности, объясняется ограничением длины свободного пробега носителей заряда границей образца и, как следствие, увеличением вклада поверхностного рассеяния электронов (дырок) по сравнению с объемным рассеянием. В результате, поверхностное рассеяние начинает оказывать значительное влияние на кинетические коэффициенты (классический размерный эффект). Классический размерный эффект приводит к увеличению удельного сопротивления и постоянной Холла тонких пленок. Влияние механизма поверхностного рассеяния и шероховатости поверхности на электрическое сопротивление пленок до сих пор изучается.

Метод расчета электропроводности и постоянной Холла тонкой металлической пленки со сферически поверхностью Ферми подробно описан в классической работе Зондхеймера [2]. Электропроводность полупроводниковой тонкой пленки с изотропной зонной структурой была рассчитана в работе [3]. Влияние граничных условий на высокочастотную электропроводность тонкого проводящего слоя в продольном магнитном поле с учетом диффузно-зеркальных граничных условий рассмотрено в работе [4].

Электронные свойства полупроводников определяются относительно небольшим числом электронов, перенесенных в зону проводимости, и дырок, образующихся в валентной зоне. Почти все электроны находятся на уровнях, близких к минимуму зоны проводимости, в то время как дырки сосредоточены вблизи максимума валентной зоны (долины). Если долина не находится в центре зоны Бриллюэна, то возникает несколько одинаковых долин, по крайней мере две. Поверхности постоянной энергии вблизи экстремумов имеют форму эллипсоида и обычно определяются путем указания направлений главных осей эллипсоидов, значений трех “эффективных масс” и положений эллипсоидов в импульсном пространстве. Эллипсоиды соответствуют анизотропному закону дисперсии энергии носителей заряда, который проявляется в зависимости электропроводности от направления напряженности электрического поля.

Примерами материалов с эллипсоидальными поверхностями постоянной энергии являются такие типичные полупроводники, как кремний и германий. В данных полупроводниках минимум энергии не расположен в центре зоны Бриллюэна. Зона проводимости кремния имеет шесть симметрично расположенных минимумов энергии в направлении [100]; зона проводимости германия обладает 8 минимумами энергии, расположенными на границах зоны Бриллюэна в направлении [111]. Изоэнергетические поверхности вблизи этих минимумов имеют вид эллипсоидов вращения.

В случае кремния [5] главные оси всех шести эллипсоидов энергии параллельны осям прямоугольной координатной системы, совпадающим с ребрами куба элементарной ячейки, поэтому удельная электропроводность равна

${{\sigma }} = 2\frac{{{{e}^{2}}{{n}^{{\left( i \right)}}}}}{{{{m}_{\parallel }}}}\left\langle {{\tau }} \right\rangle + 4\frac{{{{e}^{2}}{{n}^{{\left( i \right)}}}}}{{{{m}_{ \bot }}}}\left\langle {{\tau }} \right\rangle = \frac{{{{e}^{2}}n}}{{m{\kern 1pt} '}}\left\langle {{\tau }} \right\rangle ,$

где концентрация электронов $n = {{N}_{с}}{{n}^{{\left( i \right)}}} = 6{{n}^{{\left( i \right)}}}$ (${{N}_{с}}$ – число эквивалентных минимумов, ${{n}^{{\left( i \right)}}}$ – число электронов в одном эллипсоиде, $i$ – номер эллипсоида), $m{\kern 1pt} ' = {{3{{m}_{\parallel }}{{m}_{ \bot }}} \mathord{\left/ {\vphantom {{3{{m}_{\parallel }}{{m}_{ \bot }}} {\left( {{{m}_{ \bot }} + 2{{m}_{\parallel }}} \right)}}} \right. \kern-0em} {\left( {{{m}_{ \bot }} + 2{{m}_{\parallel }}} \right)}}$ – вспомогательная эффективная масса.

В работе [6] рассмотрено влияние примеси на электропроводность и эффект Холла в монокристаллах n-Ge, легированных Sb, La, Nd, Pr. Снижение подвижности объясняется нарушением кристаллической структуры и образованием комплексов электрически пассивных примесей.

В рамках теории перколяции [7] было объяснено снижение электропроводности нанокристаллических пленок кремния при толщине слоя от $150$ до $20~\,\,{\text{нм}}$. Проводимость пленок нанокристаллического кремния (Si) зависит от направления тока, что позволяет управлять токами утечки через легирующие барьерные структуры.

Экспериментальное исследование изменения электропроводности пленок SOI от толщины пленок Si в диапазоне от $3$ до $66~\,\,{\text{нм}}$ было проведено в работе [8]. Сопротивление пленки резко возрастало с уменьшением толщины пленки Si в области $4.5\,\,~{\text{нм}}$, что может существенно влиять на ширину проводящих путей (т.е. нанопроволок), необходимых для соединения элементов схемы.

В настоящей работе рассчитана электропроводность и постоянная Холла полупроводниковой монокристаллической пленки в случае эллипсоидальной изоэнергетической поверхности полупроводника. Использована модель диффузных граничных условий для функции распределения.

2. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим тонкую полупроводниковую бесконечную пленку толщиной a. Предполагаем, что газ свободных носителей заряда является невырожденным. Пленка помещена в переменное продольное электрическое поле и в поперечное стационарное магнитное поле. Индукция магнитного поля ${\mathbf{B}}$ направлена вдоль оси $Z$, а напряженность внешнего электрического поля ${\mathbf{E}}~$ вдоль оси $X$ (рис. 1a). Сила, действующая на электроны (дырки), имеет вид:

(1)

${\mathbf{F}} = e\left( {{\mathbf{E}} + {{{\mathbf{E}}}_{H}}} \right) + \frac{e}{c}\left[ {{\mathbf{v}} \times {\mathbf{B}}} \right],$

где $c$ – скорость света, $e$ и ${\mathbf{v}}$ – соответственно, заряд и скорость свободного электрона (дырки), ${{{\mathbf{E}}}_{H}}$ – напряженность электрического поля, обусловленная эффектом Холла.

Рис. 1.

Тонкая полупроводниковая пленка в скрещенных полях (a); изоэнергетическая поверхность полупроводника (б).

Однородное периодическое во времени внешнее электрическое поле меняется по гармоническому закону:

(2)

$E = {{E}_{{0x}}}{\text{exp}}\left( { - i{{\omega }}t} \right).$

Соответственно ${{{\mathbf{E}}}_{H}}$ имеет аналогичный вид:

(3)

${{E}_{H}} = {{E}_{{0y}}}{\text{exp}}\left( { - i{{\omega }}t} \right),$

где ${{E}_{{0x}}}$ – амплитуда напряженности внешнего электрического поля, ${{E}_{{0y}}}$ – амплитуда напряженности электрического поля ${{{\mathbf{E}}}_{H}}$, ${{\omega }}$ – частота внешнего электрического поля, приложенного к пленке.

Изоэнергетические поверхности полупроводника в импульсном пространстве (рис. 1б) вблизи экстремума энергии проводников представляют собой эллипсоиды вращения (например, у кремния и германия [5]). Рассмотрим случай, когда ось вращения изоэнергетического эллипсоида параллельна оси ${{p}_{x}}$, вдоль которой направлен вектор напряженности внешнего электрического поля ${\mathbf{E}}$. В этом случае зависимость энергии ε и импульса ${\mathbf{p}}$ носителя заряда от проекций скоростей ${{v}_{x}},~{{v}_{y}},~{{v}_{z}}$ будет иметь вид [5]:

(4)

$\varepsilon = \frac{{{{m}_{\parallel }}v_{x}^{2}}}{2} + \frac{{{{m}_{ \bot }}\left( {v_{y}^{2} + v_{z}^{2}} \right)}}{2},~~$

(5)

${\mathbf{p}} = \left( {{{m}_{\parallel }}{{v}_{x}},~{{m}_{ \bot }}{{v}_{y}},~{{m}_{ \bot }}{{v}_{z}}} \right),~$

где ${{m}_{\parallel }}$ – продольная эффективная масса (масса вдоль оси ${{p}_{x}}$); ${{m}_{ \bot }}$ – поперечная эффективная масса (масса вдоль осей ${{p}_{y}}$ и ${{p}_{z}}$).

Расчет электропроводности и постоянной Холла тонкой пленки проведем в рамках кинетической теории. Квантовые размерные эффекты не учитываются, поскольку предполагается выполнение следующих условий [5]:

(6)

$~a \gg {{{{\lambda }}}_{{{\text{Б}} \bot }}},~\,\,\,\,eE{{{{\lambda }}}_{{{\text{Б}}\parallel }}} \ll {{\varepsilon }_{{{\text{кин}}}}},~\,\,\,\,\hbar {{\Omega }} \ll {{\varepsilon }_{{{\text{кин}}}}},$

(7)

${{\lambda }_{{{\text{Б}} \bot ,\parallel }}} = \frac{{2{{\pi }}\hbar }}{{\sqrt {2{{m}_{{ \bot ,\parallel }}}{{\varepsilon }_{{{\text{кин}}}}}} }},\,\,\,\,~\Omega = \frac{{eB}}{{c\sqrt {{{m}_{ \bot }}{{m}_{\parallel }}} }},\,\,\,\,~{{\varepsilon }_{{{\text{кин}}}}} = \frac{3}{2}{{k}_{{\text{Б}}}}T,~$

где ${{\lambda }_{{\text{Б}}}}$ – длина волны де Бройля, ${{\varepsilon }_{{{\text{кин}}}}}$ – кинетическая энергия свободных носителей заряда в невырожденном полупроводнике, $\hbar $ – постоянная Планка, ${{k}_{{\text{Б}}}}$ – постоянная Больцмана, $T$ – температура. При комнатной температуре пренебречь квантовыми размерными эффектами можно для кремния при $a \gg 140\,\,~{\text{нм}},$ $~{{E}_{{ext}}} \ll 6.0 \times {{10}^{5}}\,{{\text{В}} \mathord{\left/ {\vphantom {{\text{В}} {\text{м}}}} \right. \kern-0em} {\text{м}}},$ $~B \ll $ $~ \ll 140~\,\,{\text{Тл}}$; для германия $a \gg 22\,\,~{\text{нм}},$ $~E \ll 7.8 \times $ $~ \times \,\,{{10}^{5}}\,{{\,{\text{В}}} \mathord{\left/ {\vphantom {{\,{\text{В}}} {\text{м}}}} \right. \kern-0em} {\text{м}}},$ $~B \ll 120\,\,~{\text{Тл}}$.

Кинетическое уравнение для носителей заряда в кристалле под действием внешних сил имеет вид [9]:

(8)

$\frac{{\partial f}}{{\partial t}} + {\mathbf{v}}\frac{{\partial f}}{{\partial {\mathbf{r}}}} + {\mathbf{F}}\frac{{\partial f}}{{\partial {\mathbf{p}}}} = {\text{St}}\left( f \right),~$

где ${\mathbf{v}}$ и ${\mathbf{r}}$ – вектор скорости и радиус-вектор электронов (дырок); ${\mathbf{F}}$ – сила, действующая на носители заряда со стороны внешних полей (1)–(3); ${\text{St}}\left( f \right)$ – интеграл столкновения; $f$ – неравновесная функция распределения. Неравновесную функцию распределения $f$ представим в виде двух составляющих: равновесной функции распределения Ферми–Дирака ${{f}_{0}}$ и неравновесной поправки ${{f}_{1}},$ возникающей под действием внешних полей $\left[ {10} \right]$:

(9)

$~f\left( {z,{\mathbf{v}}} \right) = {{f}_{0}}\left( \varepsilon \right) + {{f}_{1}}\left( {z,{\mathbf{v}}} \right){{{\text{e}}}^{{ - i{{\omega }}t}}},~$

(10)

${{f}_{0}} = {\text{exp}}\left\{ {\frac{{{{\mu }} - \varepsilon }}{{{{k}_{{\text{Б}}}}T}}} \right\},~$

(11)

${{f}_{1}}\left( {z,{\mathbf{v}}} \right) = - \frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }}\left[ {{{p}_{x}}{{\psi }_{x}}\left( {{{v}_{z}},z} \right) + {{p}_{y}}{{\psi }_{y}}\left( {{{v}_{z}},z} \right)} \right],$

где ${{f}_{0}}$ – функция распределения Ферми–Дирака для невырожденного газа свободных носителей заряда [1], ${{f}_{1}}$ – неравновесная поправка, ${{\psi }_{x}}\left( {{{v}_{z}},z} \right)$ и ${{\psi }_{y}}\left( {{{v}_{z}},z} \right)$ – неизвестные функции, ${{\mu }}$ – химический потенциал.

Предполагаем, что частота ${{\omega }}$ много меньше частоты плазменного резонанса ${{{{\omega }}}_{p}}$ в полупроводниковой пленке (в кремнии и германии данная частота лежит в среднем инфракрасном диапазоне ${{{{\omega }}}_{p}} \approx 4.1 \times {{10}^{{13}}}\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ и ${{{{\omega }}}_{p}} \approx 6.2 \times {{10}^{{13}}}\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ соответственно при концентрации донорной примеси $n = {{10}^{{17}}}\,\,{\text{с}}{{{\text{м}}}^{{ - 3}}}$ и при комнатной температуре). В этом случае равновесная функция распределения (8) будет локальной, то есть не зависящей от пространственных координат. Основным ограничением на частоту является пренебрежение токами поляризации [11]:

(12)

${{\omega }} \ll {{{{\omega }}}_{k}} = {{2{{\sigma }}} \mathord{\left/ {\vphantom {{2{{\sigma }}} \varepsilon }} \right. \kern-0em} \varepsilon },~$

где ${{\sigma }}$ – удельная электропроводность, ε – диэлектрическая проницаемость. Таким образом, для кремния и германия частота ${{\omega }_{k}}$ лежит в дальнем инфракрасном диапазоне (для Si${{{{\omega }}}_{k}} \approx 9.6 \times {{10}^{{12}}}\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ и для Ge${{{{\omega }}}_{k}} \approx 7.0 \times {{10}^{{12}}}\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ при концентрации донорной примеси $n = {{10}^{{17}}}\,\,{\text{с}}{{{\text{м}}}^{{ - 3}}}$ и при комнатной температуре). Толщина пленки много меньше глубины скин-слоя δ (скин-эффект не учитывается):

(13)

${{\delta }} = \frac{c}{{\sqrt {2{{\pi \sigma \mu \omega }}} }},$

где ${{\mu }}$ – магнитная проницаемость (в данной статье рассматриваются немагнитные полупроводники с ${{\mu }} = 1$). В этом случае удельная электропроводность при комнатной температуре должна быть меньше $~2.8 \times {{10}^{5}}\,\,{\text{О}}{{{\text{м}}}^{{ - 1}}} \cdot {{{\text{м}}}^{{ - 1}}}$ для кремния и $2.2 \times {{10}^{5}}\,\,{\text{О}}{{{\text{м}}}^{{ - 1}}} \cdot {{{\text{м}}}^{{ - 1}}}$ для германия, что соответствует концентрациям меньшим ${{10}^{{21}}}\,\,{\text{с}}{{{\text{м}}}^{{ - 3}}}$, то есть справедливо вплоть до вырожденного газа. Глубина скин-слоя ${{\delta }}$ (13) определяется при максимально возможной частоте, определяемой условием (12) (для кремния ${{\omega }} \ll 9.6 \times {{10}^{{12}}}\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ и ${{{{\omega }}}_{{{\text{max}}}}} = $ $ = 9.6 \times {{10}^{{11}}}\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$, для германия ω $ \ll $ 7.0 × 10¹² рад/с и ${{{{\omega }}}_{{{\text{max}}}}} = 7.0 \times {{10}^{{11}}}\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$) и равна ${{\delta }} = 41\,\,~{\text{мкм}}$ для кремния и ${{\delta }} = 48~\,\,{\text{мкм}}$ для германия.

В случае упругого рассеяния (рассеяние на атомах примеси и на дислокациях является упругим [5]), когда энергия носителей заряда не меняется, можно воспользоваться приближением времени релаксации для интеграла столкновений [9]

(14)

${\text{St}}\left( f \right) = - \frac{{f - {{f}_{0}}}}{\tau }.~$

Предполагаем, что время релаксации ${{\tau }}$ не зависит от скорости носителей заряда. Такое приближение справедливо, если рассеяние носителей заряда на ионах примеси проявляется значительно слабее, чем рассеяние на нейтральных атомах примеси [5]. В анизотропном проводнике время релаксации перестает быть скаляром и становится тензором. Однако, во многих случаях и при сложной зонной структуре можно считать время релаксации носителя заряда скаляром, зависящим от его энергии [5]. В данной работе мы ограничимся таким приближением.

Кинетическое уравнение (8) с учетом (1)–(5), (9) в линейном по внешнему полю приближении и в приближении времени релаксации (14) имеет вид:

(15)

$\nu {{f}_{1}} + {{v}_{z}}\frac{{\partial {{f}_{1}}}}{{\partial z}} + e\left( {{{E}_{{0x}}}{{v}_{x}} + {{E}_{{0y}}}{{v}_{y}}} \right)\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }} + \frac{{eB}}{c}\left( {{{v}_{y}}\frac{{\partial {{f}_{1}}}}{{\partial {{p}_{x}}}} - {{v}_{x}}\frac{{\partial {{f}_{1}}}}{{\partial {{p}_{y}}}}} \right) = 0,$

где $\nu = {{\tau }^{{ - 1}}} - i\omega $ – комплексная частота рассеяния.

Для однозначного определения неравновесной функции распределения $f$ (9)–(11) из уравнения (15) необходимо задать для нее граничные условия. В качестве таковых используем модель диффузного отражения носителей заряда от верхней и нижней границ пленки [2]:

(16)

$\left\{ {\begin{array}{*{20}{c}} {f_{1}^{ + }\left( {0,{{v}_{x}},{{v}_{y}},{{v}_{z}}} \right) = 0,} \\ {f_{1}^{ - }\left( {a, - {{v}_{x}},{{v}_{y}},{{v}_{z}}} \right) = 0,} \end{array}} \right.~~$

где $f_{1}^{ + }$ и $f_{1}^{ - }$ – малые отклонения от равновесной функции распределения Ферми–Дирака электронов (дырок) соответственно с положительной и отрицательной проекциями скорости на ось $X$.

Плотность тока ${\mathbf{j}}$ определяется следующим образом:

(17)

${\mathbf{j}} = en{\mathbf{v}} = e\int {{\mathbf{v}}{{f}_{1}}\frac{{2{{d}^{3}}p}}{{{{h}^{3}}}}} ,~$

где h – постоянная Планка; концентрация носителей заряда n имеет вид:

(18)

$n = \int {{{f}_{0}}\frac{{2{{d}^{3}}p}}{{{{h}^{3}}}}} .~$

В выражениях (17)–(18) суммирование заменено интегрированием, так как компоненты квазиимпульса вектора ${\mathbf{p}}$ в пределе одной зоны (зоны проводимости или валентной зоны) пробегают почти непрерывную последовательность значений. Данное приближение справедливо вследствие пренебрежения квантовыми размерными эффектами.

3. РЕШЕНИЕ КИНЕТИЧЕСКОГО УРАВНЕНИЯ

Подставляя $~{{f}_{1}}$(11) в уравнение (15) и приравнивая коэффициенты при ${{p}_{x}}$ и ${{p}_{y}}$, получим систему дифференциальных уравнений на функции ${{\psi }_{x}}\left( {{{v}_{z}},z} \right)$ и ${{\psi }_{y}}\left( {{{v}_{z}},z} \right)$ с учетом (4), (5)

(19)

$\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {{\psi }_{x}}}}{{\partial z}} = - \frac{\nu }{{{{v}_{z}}}}{{\psi }_{x}} + \frac{{eB}}{{{{m}_{\parallel }}c{{v}_{z}}}}{{\psi }_{y}} + \frac{{e{{E}_{{0x}}}}}{{{{m}_{\parallel }}{{v}_{z}}}},} \\ {\frac{{\partial {{\psi }_{y}}}}{{\partial z}} = - \frac{{eB}}{{{{m}_{ \bot }}c{{v}_{z}}}}{{\psi }_{x}} - \frac{{{\nu }}}{{{{v}_{z}}}}{{\psi }_{y}} + \frac{{e{{E}_{{0y}}}}}{{{{m}_{ \bot }}{{v}_{z}}}}.} \end{array}} \right.~$

Выражение для неравновесной поправки ${{f}_{1}}$ (11) с учетом решения системы дифференциальных уравнений (19) и граничных условий (16) будет иметь следующий вид:

(20)

${{f}_{1}} = \left\{ {\begin{array}{*{20}{c}} {f_{1}^{ + },\,\,\,~\,{{v}_{z}} > 0,} \\ {f_{1}^{ - },\,\,\,\,~{{v}_{z}} < 0,} \end{array}} \right.~$

(21)

$\begin{gathered} f_{1}^{ + } = \frac{{ce}}{{2{{k}_{{\text{Б}}}}T}}{\text{exp}}\left( {\frac{{{{\mu }} - \varepsilon }}{{{{k}_{Б}}T}}} \right)\left( {{{A}_{1}}\left( { - i, - i,1,1,1,0} \right) + {{A}_{1}}\left( {i,i,1, - 1, - 1,0} \right) + } \right. \\ \left. { + \,\,\frac{{2\left[ {Be\left\{ {{{E}_{{0y}}}{{m}_{\parallel }}{{v}_{x}} - {{E}_{{0x}}}{{m}_{ \bot }}{{v}_{y}}} \right\} + c{{m}_{ \bot }}{{m}_{\parallel }}\left\{ {{{E}_{{0x}}}{{v}_{x}} + {{E}_{{0y}}}{{v}_{y}}} \right\}{{\nu }}} \right]}}{{{{B}^{2}}{{e}^{2}} + {{c}^{2}}{{m}_{ \bot }}{{m}_{\parallel }}{{{{\nu }}}^{2}}}}} \right), \\ \end{gathered} $

(22)

$\begin{gathered} f_{1}^{ - } = \frac{{ce}}{{2{{k}_{{\text{Б}}}}T}}{\text{exp}}\left( {\frac{{{{\mu }} - \varepsilon }}{{{{k}_{{\text{Б}}}}T}}} \right)\left( {{{A}_{1}}\left( { - i, - i,1,1,1,a} \right) + {{A}_{1}}\left( {i,i,1, - 1, - 1,a} \right) + } \right. \\ \left. { + \,\,\frac{{2\left[ {Be\left\{ {{{E}_{{0y}}}{{m}_{\parallel }}{{v}_{x}} - {{E}_{{0x}}}{{m}_{ \bot }}{{v}_{y}}} \right\} + c{{m}_{ \bot }}{{m}_{\parallel }}\left\{ {{{E}_{{0x}}}{{v}_{x}} + {{E}_{{0y}}}{{v}_{y}}} \right\}\nu } \right]}}{{{{B}^{2}}{{e}^{2}} + {{c}^{2}}{{m}_{ \bot }}{{m}_{\parallel }}{{{{\nu }}}^{2}}}}} \right),~ \\ \end{gathered} $

(23)

$\begin{gathered} {{A}_{1}}\left( {{{a}_{1}},{{a}_{2}},{{a}_{3}},{{a}_{4}},{{a}_{5}},{{a}_{6}}} \right) = \frac{{\left[ {{{E}_{{0x}}}\sqrt {{{m}_{ \bot }}} + {{a}_{1}}{{E}_{{0y}}}\sqrt {{{m}_{\parallel }}} } \right]\left( {{{a}_{2}}\sqrt {{{m}_{\parallel }}} {{v}_{x}} + {{a}_{3}}\sqrt {{{m}_{ \bot }}} {{v}_{y}}} \right)}}{{Be + {{a}_{4}}ic\sqrt {{{m}_{ \bot }}{{m}_{\parallel }}} {{\nu }}}} \times \\ \times \,\,{\text{exp}}\left[ { - \frac{{\left( {z - {{a}_{6}}} \right)\nu }}{{{{v}_{z}}}} + \frac{{{{a}_{5}}i\left( {z - {{a}_{6}}} \right)Be}}{{c{{v}_{z}}\sqrt {{{m}_{ \bot }}{{m}_{\parallel }}} }}} \right].~~ \\ \end{gathered} $

4. РАСЧЕТ ЭЛЕКТРОПРОВОДНОСТИ И ПОСТОЯННОЙ ХОЛЛА

Проекции скорости электронов (дырок) можно выразить в параметрическом виде через сферические координаты с учетом (4):

(24)

$\left\{ \begin{gathered} {{v}_{x}} = \sqrt {{{2\varepsilon } \mathord{\left/ {\vphantom {{2\varepsilon } {{{m}_{\parallel }}}}} \right. \kern-0em} {{{m}_{\parallel }}}}} \sin {\kern 1pt} \theta \cos {\kern 1pt} \varphi , \hfill \\ {{v}_{y}} = \sqrt {{{2\varepsilon } \mathord{\left/ {\vphantom {{2\varepsilon } {{{m}_{ \bot }}}}} \right. \kern-0em} {{{m}_{ \bot }}}}} \sin {\kern 1pt} \theta \sin {\kern 1pt} \varphi , \hfill \\ {{v}_{z}} = \sqrt {{{2\varepsilon } \mathord{\left/ {\vphantom {{2\varepsilon } {{{m}_{ \bot }}}}} \right. \kern-0em} {{{m}_{ \bot }}}}} \cos {\kern 1pt} \theta , \hfill \\ \end{gathered} \right.$

где $0 \leqslant {{\theta }} \leqslant {{\pi }}$ и $0 \leqslant {{\varphi }} \leqslant 2{{\pi }}$ – параметры.

В дальнейших расчетах плотности тока (17) и концентрации (18) удобно перейди от координат в импульсном пространстве $\left( {{{p}_{x}},{{p}_{y}},{{p}_{z}}} \right)$ к новым координатам $\left( {\varepsilon ,{{\theta }},{{\varphi }}} \right)$, тогда определитель Якоби из формул (5), (23) имеет вид

(25)

$I = \frac{{\partial \left( {{{p}_{x}},{{p}_{y}},{{p}_{z}}} \right)}}{{\partial \left( {\varepsilon ,{{\theta }},{{\varphi }}} \right)}} = {{m}_{ \bot }}\sqrt {2{{m}_{\parallel }}\varepsilon } {\text{sin}}{\kern 1pt} {{\theta }}.{\text{\;\;}}$

Концентрация носителей заряда (15) с учетом выражений (8), (22) равна

(26)

$n = 2{{m}_{ \bot }}\sqrt {{{m}_{\parallel }}} {{\left( {\frac{{2{{\pi }}{{k}_{{\text{Б}}}}T}}{{{{h}^{2}}}}} \right)}^{{3/2}}}\left( {\frac{{{\mu }}}{{{{k}_{{\text{Б}}}}T}}} \right).~$

Введем безразмерные параметры:

(27)

${{m}_{0}} = \sqrt[3]{{m_{ \bot }^{2}{{m}_{\parallel }}}},\,\,\,\,~{{k}_{ \bot }} = {{{{m}_{ \bot }}} \mathord{\left/ {\vphantom {{{{m}_{ \bot }}} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}},\,\,\,\,~{{k}_{\parallel }} = {{{{m}_{\parallel }}} \mathord{\left/ {\vphantom {{{{m}_{\parallel }}} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}},~$

(28)

${{x}_{0}} = {a \mathord{\left/ {\vphantom {a \lambda }} \right. \kern-0em} \lambda },\,\,\,\,~{{y}_{0}} = {{a\omega } \mathord{\left/ {\vphantom {{a\omega } {{{v}_{1}}}}} \right. \kern-0em} {{{v}_{1}}}},\,\,\,\,~{{z}_{0}} = {{x}_{0}} - i{{y}_{0}} = {{a\nu } \mathord{\left/ {\vphantom {{a\nu } {{{v}_{1}}}}} \right. \kern-0em} {{{v}_{1}}}},$

(29)

Здесь ${{k}_{\parallel }},~{{k}_{ \bot }}$ – продольная и поперечная эффективные массы соответственно; ${{x}_{0}}$ – безразмерная толщина пленки; ${{\lambda }} = {{v}_{1}}{{\tau }}$ – длина свободного пробега электронов (дырок); ${{y}_{0}}$ – безразмерная частота внешнего электрического поля; ${{\beta }}$ – безразмерная индукция магнитного поля.

Отдельно стоит отметить взаимосвязь безразмерных эффективных масс: поскольку ${{m}_{0}} = \sqrt[3]{{m_{ \bot }^{2}{{m}_{\parallel }}}}$, то $k_{ \bot }^{2}{{k}_{\parallel }} = 1$, поэтому ${{k}_{\parallel }} = {1 \mathord{\left/ {\vphantom {1 {k_{ \bot }^{2}}}} \right. \kern-0em} {k_{ \bot }^{2}}}$. Также при изменении безразмерных эффективных масс предполагается постоянство концентрации свободных носителей заряда (26), следовательно, $m_{ \bot }^{2}{{m}_{\parallel }} = {\text{const}},~$ ${{m}_{0}} = {\text{const}}$, а ${{k}_{ \bot }} \propto {{m}_{ \bot }},~$ $~{{k}_{\parallel }} \propto {{m}_{\parallel }}$.

При нормировке ${{z}_{0}}$ использовалась характерная скорость носителей заряда ${{v}_{1}}$, которая вводилась следующим образом [12]:

(30)

$nv_{1}^{2} = \frac{5}{3}\int {{{v}^{2}}{{f}_{0}}\frac{{2{{d}^{3}}p}}{{{{h}^{3}}}}} ,\,\,\,\,~{{\tilde {v}}_{1}} = \sqrt {\frac{{{{m}_{0}}}}{{2{{k}_{{\text{Б}}}}T}}} {{v}_{1}},$

(31)

${{\tilde {v}}_{1}} = \sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} {\kern 1pt} .~$

В экспериментальных условиях обычно находят усредненный по толщине пленки ток:

(32)

$\left\langle {{{j}_{x}}} \right\rangle = \frac{1}{a}\mathop \smallint \limits_0^a {{j}_{x}}dz,\,\,\,\,~\left\langle {~{{j}_{y}}} \right\rangle = \frac{1}{a}\mathop \smallint \limits_0^a {{j}_{y}}dz.~~$

Удельная проводимость находится из локального закона Ома:

(33)

${{\sigma }_{x}} = {{\left. {\frac{{{{j}_{x}}}}{{{{E}_{x}}}}} \right|}_{{{{j}_{y}} = 0}}}.~~$

Постоянная Холла определяется формулой:

(34)

${{A}_{H}} = {{\left. {\frac{{{{E}_{y}}}}{{B{{j}_{x}}}}} \right|}_{{{{j}_{y}} = 0}}}.~$

Выражения (33) и (34) рассчитываются при условии, что поперечный ток равен нулю $\left( {{{j}_{y}} = 0} \right)$.

Опуская промежуточные вычисления, получим выражения для удельной электропроводности (33) и постоянной Холла (34) с учетом (17), (20)–(32):

(35)

${{\sigma }_{x}}\left( {{{x}_{0}},{{y}_{0}},{{k}_{ \bot }},{{\beta }}} \right) = {{\sigma }_{0}}\Sigma \left( {{{x}_{0}},{{y}_{0}},{{k}_{ \bot }},{{\beta }}} \right),\,\,\,\,~{{\sigma }_{0}} = {{n{{e}^{2}}\tau } \mathord{\left/ {\vphantom {{n{{e}^{2}}\tau } {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}},$

(36)

${{A}_{H}}\left( {{{x}_{0}},{{y}_{0}},{{k}_{ \bot }},{{\beta }}} \right) = {{A}_{{H,0}}}{{R}_{H}}\left( {{{x}_{0}},{{y}_{0}},{{k}_{ \bot }},\beta } \right),\,\,\,\,~{{A}_{{H,0}}} = {1 \mathord{\left/ {\vphantom {1 {\left( {nec} \right)}}} \right. \kern-0em} {\left( {nec} \right)}},$

(37)

$\Sigma = {{x}_{0}}k_{ \bot }^{2}\frac{{{{{\left( {{{z}_{0}} - {{A}_{2}}{{a}_{s}}} \right)}}^{2}} + {{{\left( {\beta - {{A}_{2}}{{b}_{s}}} \right)}}^{2}}}}{{{{z}_{0}}\left( {z_{0}^{2} + k_{ \bot }^{{2/3}}{{\beta }^{2}}} \right) + {{A}_{2}}\left[ {{{a}_{s}}\left( {{{k}_{ \bot }}{{\beta }^{2}} - z_{0}^{2}} \right) - 2{{b}_{s}}k_{ \bot }^{{ - 1/3}}\beta {{z}_{0}}} \right]}},$

(38)

${{R}_{H}} = \frac{1}{\beta }\frac{{\beta \left( {z_{0}^{2} + {{k}_{ \bot }}{{{{\beta }}}^{2}}} \right) + {{A}_{2}}\left[ {{{b}_{s}}k_{ \bot }^{{ - 1/2}}\left( {z_{0}^{2} - {{k}_{ \bot }}{{\beta }^{2}}} \right) - 2{{a}_{s}}\beta {{z}_{0}}} \right]}}{{{{{\left( {{{z}_{0}} - {{A}_{2}}{{a}_{s}}} \right)}}^{2}} + {{{\left( {\beta - {{A}_{2}}{{b}_{s}}} \right)}}^{2}}}}.~$

(39)

${{a}_{s}} = \mathop \smallint \limits_0^\infty \mathop \smallint \limits_0^1 {{u}^{2}}{{e}^{{ - u}}}x\left( {1 - {{x}^{2}}} \right)\left( {1 - {\text{exp}}\left( { - \frac{{{{z}_{0}}}}{{x\sqrt u }}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right){\text{cos}}\left( {\frac{{{\beta }}}{{x\sqrt u }}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right)} \right)dxdu,$

(40)

${{b}_{s}} = \mathop \smallint \limits_0^\infty \mathop \smallint \limits_0^1 {{u}^{2}}{{e}^{{ - u}}}x\left( {1 - {{x}^{2}}} \right){\text{exp}}\left( { - \frac{{{{z}_{0}}}}{{x\sqrt u }}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right){\text{sin}}\left( {\frac{{{\beta }}}{{x\sqrt u }}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right)dxdu,~~$

(41)

${{A}_{2}} = \sqrt {\frac{{24}}{{5\left( {2 + k_{ \bot }^{3}} \right){{\pi }}}}{\kern 1pt} } .~~$

Здесь ${{{{\sigma }}}_{0}}$ – статическая электропроводность, ${{\Sigma }}$ – безразмерная удельная электропроводность, ${{A}_{{H,0}}}$ – постоянная Холла в случае толстой пленки (классический случай), ${{R}_{H}}$ – безразмерная постоянная Холла.

Проведем замену переменных во внутреннем интеграле выражения (39) $y = x\sqrt u $:

$\begin{gathered} {{a}_{s}} = \mathop \smallint \limits_0^\infty \mathop \smallint \limits_0^1 {{u}^{2}}{{e}^{{ - u}}}x\left( {1 - {{x}^{2}}} \right)\left( {1 - {\text{exp}}\left( { - \frac{{{{z}_{0}}}}{{x\sqrt u }}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right){\text{cos}}\left( {\frac{{{\beta }}}{{x\sqrt u }}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right)} \right)dxdu = \\ = \mathop \smallint \limits_0^\infty \mathop \smallint \limits_0^{\sqrt u } y{{e}^{{ - u}}}\left( {u - {{y}^{2}}} \right)\left( {1 - {\text{exp}}\left( { - \frac{{{{z}_{0}}}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right){\text{cos}}\left( {\frac{{{\beta }}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right)} \right)dydu. \\ \end{gathered} $

Меняя местами знаки интегрирования и вычисляя интеграл по переменной $u$, получаем

(42)

$\begin{gathered} {{a}_{s}} = \mathop \smallint \limits_0^\infty \mathop \smallint \limits_{{{y}^{2}}}^\infty y{{e}^{{ - u}}}\left( {u - {{y}^{2}}} \right)\left( {1 - {\text{exp}}\left( { - \frac{{{{z}_{0}}}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right){\text{cos}}\left( {\frac{{{\beta }}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right)} \right)dudy = \\ = \mathop \smallint \limits_0^\infty y{{e}^{{ - {{y}^{2}}}}}\left( {1 - {\text{exp}}\left( { - \frac{{{{z}_{0}}}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right){\text{cos}}\left( {\frac{{{\beta }}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right)} \right)dy.~ \\ \end{gathered} $

Аналогично для коэффициента ${{b}_{s}}$ (40)

(43)

${{b}_{s}} = \mathop \smallint \limits_0^\infty y{{e}^{{ - {{y}^{2}}}}}{\text{exp}}\left( { - \frac{{{{z}_{0}}}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right){\text{sin}}\left( {\frac{{{\beta }}}{y}\sqrt {\frac{5}{6}\left( {k_{ \bot }^{2} + \frac{2}{{{{k}_{ \bot }}}}} \right)} } \right)dy.$

5. ПРЕДЕЛЬНЫЕ СЛУЧАИ

1. Случай толстой пленки $\left( {{{x}_{0}} \gg 1} \right)$ или высоких частот $\left( {{{y}_{0}} \gg 1} \right)$.

Если $\left| {{{z}_{0}}} \right| \gg 1$, то в выражении (42), (43) экспоненты быстро затухают, в итоге получаем ${{a}_{s}} = 0.5$, ${{b}_{s}} = 0.$ Подставляя ${{a}_{s}}$и ${{b}_{s}}$ в выражения (34)–(38), получаем

(44)

${{\Sigma }} = \frac{{{{x}_{0}}}}{{{{z}_{0}}}}k_{ \bot }^{2},\,\,\,\,~{{R}_{H}} = 1.$

Удельная проводимость и постоянная Холла (44) в этом случае соответствуют классическим результатам (соответственно формула Друде и формула для постоянной Холла в макроскопическом образце).

2. Случай сферической изоэнергетической поверхности $\left( {{{k}_{ \bot }} = 1} \right)$.

Безразмерная электропроводность (37), (41) будет иметь вид

(45)

${{\Sigma }} = {{x}_{0}}\frac{{{{{\left( {{{z}_{0}} - \sqrt {\frac{8}{{5{{\pi }}}}} {{a}_{s}}} \right)}}^{2}} + {{{\left( {{{\beta }} - \sqrt {\frac{8}{{5{{\pi }}}}} {{b}_{s}}} \right)}}^{2}}}}{{{{z}_{0}}\left( {z_{0}^{2} + {{{{\beta }}}^{2}}} \right) + \sqrt {\frac{8}{{5{{\pi }}}}} \left[ {{{a}_{s}}\left( {{{{{\beta }}}^{2}} - z_{0}^{2}} \right) - 2{{b}_{s}}{{\beta }}{{z}_{0}}} \right]}},~~$

(46)

${{R}_{H}} = \frac{1}{{{\beta }}}\frac{{{{\beta }}\left( {z_{0}^{2} + {{{{\beta }}}^{2}}} \right) + \sqrt {\frac{8}{{5{{\pi }}}}} \left[ {{{b}_{s}}\left( {z_{0}^{2} - {{{{\beta }}}^{2}}} \right) - 2{{a}_{s}}{{\beta }}{{z}_{0}}} \right]}}{{{{{\left( {{{z}_{0}} - \sqrt {\frac{8}{{5{{\pi }}}}} {{a}_{s}}} \right)}}^{2}} + {{{\left( {{{\beta }} - \sqrt {\frac{8}{{5{{\pi }}}}} {{b}_{s}}} \right)}}^{2}}}}.~~$

Полученное выражения (45), (46) соответствует электропроводности тонкой металлической пленки в случае сферической поверхности Ферми [3].

6. АНАЛИЗ РЕЗУЛЬТАТОВ

Прежде, чем исследовать зависимости безразмерной электропроводности и постоянной Холла (37), (38), (42), (43), определим в каких диапазонах изменяются безразмерные параметры (27)–(29) на примере кремния и германия.

Для кремния и германия безразмерная поперечная эффективная масса равна ${{k}_{ \bot }} = 0.59$ и ${{k}_{ \bot }} = 0.37$ соответственно (27). Вследствие пренебрежения квантовыми размерными эффектами (6), (7) и скин-эффектом (13) толщина пленки a должна находиться в пределах ${{{{\lambda }}}_{{{\text{Б}} \bot }}} \ll a \ll \delta $. Диапазон частот внешнего поля ограничен условием (12). Допустимые значения магнитной индукции определяются из (6), (7). В табл. 1 и 2 представлены значения размерных и безразмерных величин.

Таблица 1.

Параметры для пленок ${\text{Si}}$ и ${\text{Ge}}$

Полупроводник	${{a}_{{{\text{min}}}}},~\,\,{\text{нм}}$	${{a}_{{{\text{max}}}}},\,\,~{\text{мкм}}$	${{{{\omega }}}_{{{\text{max}}}}},\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$	${{B}_{{{\text{max}}}}},{\text{Тл}}$
Si	$140$	$4.1$	$9.6 \times {{10}^{{11}}}$	$14$
Ge	$220$	$4.8$	$7.0 \times {{10}^{{11}}}$	$12$

Таблица 2.

Безразмерные параметры для пленок ${\text{Si}}$ и ${\text{Ge}}$

Полупроводник	${{x}_{{{\text{0min}}}}}$	${{x}_{{{\text{0max}}}}}$	${{y}_{{{\text{0max}}}}}$		${{{{\beta }}}_{{{\text{max}}}}}$
Полупроводник	${{x}_{{{\text{0min}}}}}$	${{x}_{{{\text{0max}}}}}$	${{x}_{{{\text{0min}}}}}$	${{x}_{{{\text{0max}}}}}$	${{x}_{{{\text{0min}}}}}$	${{x}_{{{\text{0max}}}}}$
Si	0.07	1200	0.46	1.3	3.7	100
Ge	0.9	1400	0.35	7.6	4.8	100

Классический размерный эффект наблюдается при ${{x}_{0}} < 10$ [25 ] .Осцилляции в зависимости электропроводности от индукции магнитного поля наблюдаются в интервале: $0.1 < {{\beta }} < 10$ [2].

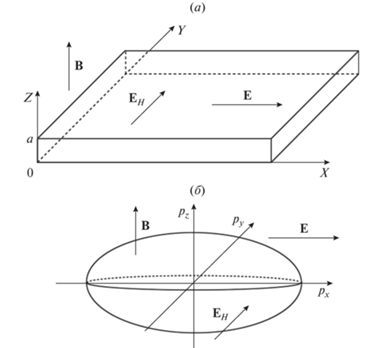
На рис. 2 показана зависимость модуля безразмерной электропроводности ${{\Sigma \;}}$ от безразмерной толщины ${{x}_{0}}$ тонкого полупроводникового слоя. С увеличением толщины слоя вклад диффузного рассеяния на поверхностях по сравнению с объемным рассеянием снижается, что приводит к росту средней проекции скорости вдоль внешнего электрического поля и, как следствие, к росту удельной электропроводности. Локальный максимум наблюдается при ${{x}_{0}} = {{y}_{0}}$.

Рис. 2.

Зависимость модуля безразмерной электропроводности ${{\Sigma \;}}$ от безразмерной толщины ${{x}_{0}}$ при ${{y}_{0}} = 0.2$, ${{\beta }} = 0.1$. Кривые 1 – ${{k}_{ \bot }} = 0.37;$ 2 – ${{k}_{ \bot }} = 0.59;$ 3 – ${{k}_{ \bot }} = 1$.

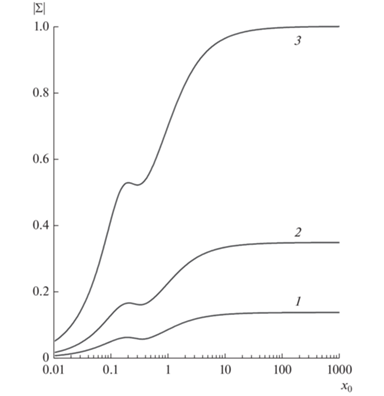
На рис. 3 изображена зависимость аргумента безразмерной электропроводности ${{\Sigma }}$ от безразмерной толщины ${{x}_{0}}$ тонкого полупроводникового слоя. Минимум аргумента обусловлен таким искривлением траектории электронов (дырок), при котором средняя проекция импульса носителей заряда на внешнее электрического поле стремится к минимальному значению, а при некоторых значениях эффективной массы может принимать отрицательные значения.

Рис. 3.

Зависимость аргумента безразмерной электропроводности ${{\Sigma }}$ от безразмерной толщины ${{x}_{0}}$ при ${{y}_{0}} = 0.2$, ${{\beta }} = 0.1$. (Обозначения кривых см. подпись к рис. 2.)

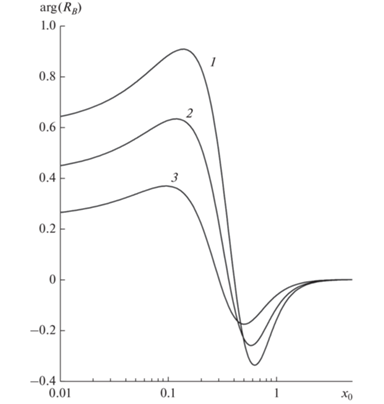
На рис. 4 и 5 представлена зависимость модуля и аргумента постоянной Холла ${{R}_{B}}$ от безразмерной толщины ${{x}_{0}}$ тонкого полупроводникового слоя. Максимум модуля постоянной Холла возникает вследствие максимального значения проекции импульса электронов (дырок) на направление, перпендикулярное скрещенным полям. Данный максимум наблюдается при ${{x}_{0}} = {{{{y}_{0}}} \mathord{\left/ {\vphantom {{{{y}_{0}}} {\sqrt {{{k}_{ \bot }}} }}} \right. \kern-0em} {\sqrt {{{k}_{ \bot }}} }}$. При больших толщинах на рис. 2–рис. 5 наблюдается макроскопическая асимптотика (44).

Рис. 4.

Зависимость модуля безразмерной постоянной Холла ${{R}_{B}}$ от безразмерной толщины ${{x}_{0}}$ при ${{y}_{0}} = 0.2$, ${{\beta }} = 0.1$. (Обозначения кривых см. подпись к рис. 2.)

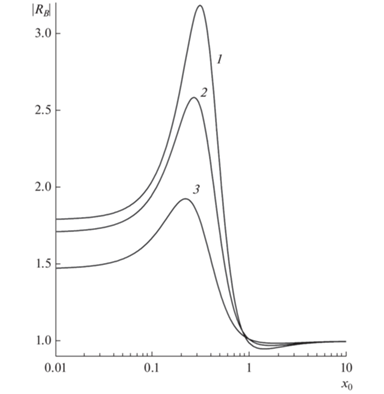
Рис. 5.

Зависимость аргумента безразмерной постоянной Холла ${{R}_{B}}$ от безразмерной толщины ${{x}_{0}}$ при ${{y}_{0}} = 0.2$, ${{\beta }} = 0.1$. (Обозначения кривых см. подпись к рис. 2.)

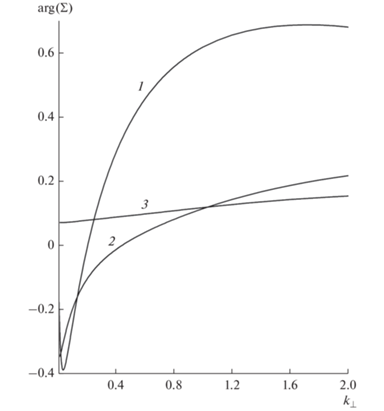
На рис. 6 и 7 показана зависимость модуля и аргумента безразмерной электропроводности ${{\Sigma }}$ от безразмерной поперечной эффективной массы ${{k}_{ \bot }}$. С увеличением поперечной эффективной массы скорость в направлении к границам пленки уменьшается, следовательно, снижается вклад поверхностного рассеяния по сравнению с объемным рассеянием, то есть возрастает проводимость как по модулю, так и по аргументу.

Рис. 6.

Зависимость модуля безразмерной электропроводности ${{\Sigma }}$ от безразмерной поперечной эффективной массы ${{k}_{ \bot }}$ при ${{y}_{0}} = 0.2$, ${{\beta }} = 0.1$. Кривые 1 – ${{x}_{0}} = 0.1$, 2 – ${{x}_{0}} = 0.5$, 3 – ${{x}_{0}} = 1$.

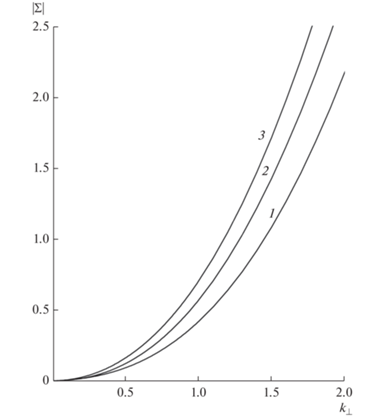
Рис. 7.

Зависимость аргумента безразмерной электропроводности ${{\Sigma }}$ от безразмерной поперечной эффективной массы ${{k}_{ \bot }}$ при ${{y}_{0}} = 0.2$, ${{\beta }} = 0.1$. (Обозначения кривых см. подпись к рис. 6.)

ЗАКЛЮЧЕНИЕ

В рамках кинетической теории исследовано влияние анизотропии изоэнергетической поверхности на электропроводность и постоянную Холла тонкой полупроводниковой пленки. Представлены предельные переходы к ранее известным результатами в случаях толстой пленки и сферической изоэнергетической поверхности. Показано, что модуль электропроводности возрастает при увеличении поперечной эффективной массы. По положениям максимума в зависимостях модулей электропроводности и постоянной Холла от толщины можно определить частоты внешнего электрического поля и поперечную эффективную массу.

Список литературы

Абрикосов А.А. Основы теории металлов. М.: Наука. 1987, 520 с.
Sondheimer E.H. The mean free path of electrons in metals // Adv. Phys. 2001. V. 50. № 6. P. 499–537.
Кузнецова И.А., Романов Д.Н., Савенко О.В., Юшканов А.А. Расчет высокочастотной электропроводности тонкого полупроводникового слоя в случае различных коэффициентов зеркальности его поверхностей // Микроэлектроника. 2017. Т. 46. № 4. С. 275–283.
Кузнецов П.А., Савенко О.В., Юшканов А.А. Высокочастотный магнетотранспорт в тонком металлическом слое с варьируемыми коэффициентами зеркальности границ // ЖТФ. 2020. Т. 90. № 12. С. 2002–2012.
Ансельм А.И. Введение в теорию полупроводников. М.: Наука, 1978. 615 с.
Гайдар Г.П., Гайворонская Е.Ю. Эффект Холла в германии, легированном разными примесями // ЭОМ. 2017. Т. 53. № 2. С. 70–74.
Голубев В.Г., Морозова Л.Е., Певцов А.Б., Феоктистов Н.А. Проводимость тонких нанокристаллических пленок кремния // ФТП. 1999. Т. 33. № 1. С. 75–78.
MacHale J., Meaney F., Kennedy N., Eaton L., Mirabelli G., White M., Thomas K., Pelucchi E., Petersen D.H., Lin R., Petkov N., Connolly J., Hatem C., Gity F., Ansari L., Long B., Duffy R. Exploring conductivity in ex-situ doped Si thin films as thickness approaches 5 nm // J. Appl. Phys. 2019. V. 125. P. 225709.
Ландау Л.Д. Теоретическая физика. Том X. Физическая кинетика. М.: Наука. 1979. С. 22.
Аскеров Б.М. Электронные явления переноса в полупроводниках. М.: Наука. 1985. С. 208.
Ландау Л.Д. Теоретическая физика. Том VIII. Электродинамика сплошных сред. М.: Наука. 1982. С. 279.
Kuznetsova I.A., Romanov D.N., Savenko O.V. Electrical conductivity of a thin film in the case of an arbitrarily oriented ellipsoidal isoenergetic surface of a conductor // Phys. Scr. 2021. V. 96. P. 045803.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал