Известия РАН. Механика жидкости и газа, 2023, № 2, стр. 33-45

ЭВОЛЮЦИЯ ПОТОКА ВЯЗКОЙ ЭЛЕКТРОПРОВОДНОЙ ЖИДКОСТИ НА ВРАЩАЮЩЕЙСЯ СТЕНКЕ ПРИ НАЛИЧИИ МАГНИТНОГО ПОЛЯ С УЧЕТОМ ИНДУКЦИОННОГО И ДИФФУЗИОННОГО ЭФФЕКТОВ

А. А. Гурченков^*

Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия

^* E-mail: Challenge2005@mail.ru

Поступила в редакцию 21.06.2022
После доработки 30.09.2022
Принята к публикации 11.10.2022

EDN: NTGGUV
DOI: 10.31857/S0568528122600709

Аннотация

Изучается эволюция течения вязкой электропроводной жидкости на вращающейся пластине в присутствии магнитного поля. Представлено аналитическое решение трехмерных нестационарных уравнений магнитной гидродинамики. При этом используется полное уравнение магнитной индукции, т.е. учитывается как индукционный эффект, так и диссипация энергии вследствие протекания электрических токов. Жидкость вместе с ограничивающей плоскостью вращается как одно целое с постоянной угловой скоростью вокруг неперпендикулярного к плоскости направления. Неустановившийся поток индуцирован внезапно начинающимися колебаниями стенки и приложенным магнитным полем, направленным перпендикулярно плоскости. Определены поле скоростей и индуцированное магнитное поле в потоке вязкой электропроводной жидкости, заполняющей полупространство, ограниченное плоской стенкой. Рассматривается ряд частных случаев движения стенки. На основании полученных результатов исследуются отдельные структуры пограничных слоев у стенки.

Ключевые слова: уравнения магнитной гидродинамики, электропроводная жидкость, нормальные колебания, пограничные слои

В магнитной гидродинамике характер взаимодействия проводящей жидкости и магнитного поля определяется магнитным числом Рейнольдса, который представляет собой отношение инерционных сил к силам, обеспечивающим диффузию магнитного поля в проводящей жидкости. По величине магнитного числа Рейнольдса (Re_m) процессы в магнитной гидродинамике делятся на три класса – это процессы с малой (${\text{R}}{{{\text{e}}}_{m}} \ll 1$), умеренной (${\text{R}}{{{\text{e}}}_{m}}\sim 1$) и большой (${\text{R}}{{{\text{e}}}_{m}} \gg 1$) проводимостью. Случай малой проводимости реализуется, в частности, в лабораторных установках с жидкими металлами и низкотемпературной плазмой, при этом магнитное поле мало изменяется и можно считать, что оно задано извне. Движущаяся в этом поле проводящая жидкость индуцирует электрический ток, который, создавая силу Лоренца, влияет на движение жидкости, тем самым создает МГД-эффекты. В противоположном случае, т.е. в случае большой проводимости среды или при ее больших размерах (условие выполняется для астрофизических объектов, а также для горячей плазмы термоядерных устройств) можно пренебречь диффузией магнитного поля. Это случай гидродинамического приближения, когда перенос преобладает над диффузией. В общем третьем случае изменение магнитного поля складывается из его переноса движущимся проводящим веществом и диффузией относительно этого вещества – при этом необходимо использовать полное уравнение индукции. Данное исследование обобщает предыдущие результаты [1–6]. Так, в работе [1] изучалось нестационарное движение вязкой жидкости, ограниченной перемещающейся плоской стенкой в отсутствие магнитного поля. В [2] рассматривался неустановившийся поток вязкой несжимаемой жидкости на вращающейся пластине в отсутствие вдува (отсоса) среды и магнитного поля. Показано, что один из двух пограничных слоев, формирующихся на стенке, неограниченно растет при наличии резонанса ω = 2Ω (ω – частота колебаний стенки, 2Ω – удвоенная частота вращения системы стенка-жидкость). Кроме того, решение зависит от порядка операций в двойном предельном переходе $t \to \infty $ , ω $ \to $ 2Ω , где t – время. Установившееся решение уравнений Навье–Стокса при наличии вдува (отсоса) среды рассмотрено в [3]. Нестационарный поток вязкой несжимаемой жидкости на пористой пластине при наличии вдува (отсоса) среды изучался в [4]. Одна из последних работ [5] посвящена изучению течения электропроводной жидкости между параллельными стенками с изолирующими свойствами в постоянном магнитном поле, но жидкость предполагается идеальной, а течение жидкости стационарным. В работе [6] рассмотрен нестационарный поток вязкой несжимаемой электропроводной жидкости на вращающейся пластине. Задача рассмотрена в магнитно-гидродинамическом приближении, т.е. для случая бесконечно большой проводимости жидкости. Большое число работ посвящено численным исследованиям задач. Так, в работах [7–10] представлены численные исследования задачи о течении сжимаемого газа около пластины с движущейся против потока поверхностью и в приближении пограничного слоя рассмотрена затопленная незакрученная струя вязкой несжимаемой жидкости, вытекающая из отверстия. Обсуждаются неустойчивые периодические по времени и устойчивые стационарные решения данной задачи. В [11] предложена математическая модель, основанная на системе дифференциальных уравнений неоднородной многокомпонентной механики жидкости. Метод позволяет в единой постановке анализировать динамику и тонкую структуру обтекания препятствий в широком диапазоне параметров течения. В [12] обсуждается теория электромагнитной гидродинамики, которая в полном объеме в гидродинамическом приближении учитывает электро-ионную структуру плазмы, в том числе инерцию электронов и ионов и их взаимодействие. В [13] приведен анализ быстрого прямого атомно-молекулярного, механического с потоком или волнообразного с групповой скоростью и медленного диффузионного переноса энергии. Обсуждаются различные типы неустойчивостей в механике жидкостей и газов. В работе [14] методом математического моделирования исследуется закрученное течение со свободной поверхностью с возникающей на ней воронкой. Методами видеорегистрации в [15] прослежена эволюция картины распределения вещества капли чернил, свободно падающей на взволнованную поверхность жидкости. Методами теории сингулярных возмущений в линейном и слабо нелинейном приближениях в [16] рассмотрена задача генерации пучков периодических внутренних волн в вязкой экспоненциально стратифицированной жидкости полосой, колеблющейся вдоль наклонной плоскости. В [17] выполнены исследования гидродинамики и теплообмена при опускном течении жидкого металла в прямоугольном канале с соотношением сторон примерно 3/1 в компланарном магнитном поле (МП) при условии неоднородного (одностороннего) обогрева канала. В настоящей работе представлено исследование нестационарного потока вязкой электропроводной жидкости на вращающейся пластине при наличии магнитного поля с использованием полного уравнения магнитной индукции. Поток индуцирован продольными колебаниями пластины.

1. АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ МАГНИТНОЙ ГИДРОДИНАМИКИ

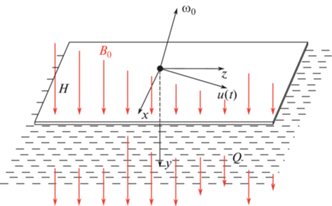
Рассмотрим движение вязкой электропроводной несжимаемой жидкости в полупространстве, ограниченном плоской стенкой, которая вращается вместе со стенкой как одно целое с угловой скоростью ${{\omega }_{0}} = {\text{const}}$, причем вектор ${{\omega }_{0}}$ образует с этой плоскостью угол $\beta $ ($0 < \beta < \pi {\text{/}}2{\text{\;}})$. Бесконечная пластина H ограничивает полупространство Q, заполненное несжимаемой жидкостью плотности $\rho $, кинематической вязкости $\nu $ и магнитной проницаемости $\mu $. Жидкость находится в поле массовых сил с потенциалом $U$.

Свяжем с пластиной декартову систему координат $Oxyz$ с ортами $~{{{\mathbf{e}}}_{x}}$, ${{{\mathbf{e}}}_{y}}$, ${{{\mathbf{e}}}_{z}}$ так, что плоскость $Oxz$ совпадает с пластиной, а ось $Oy$ направлена перпендикулярно пластине внутрь жидкости. Схематично постановка задачи представлена на рис. 1.

Рис. 1.

Схематичное представление геометрии задачи.

В момент времени $t > 0$ пластина начинает двигаться в продольном направлении со скоростью ${\mathbf{u}}\left( t \right)$ и в этот момент включается однородное магнитное поле с индукцией B₀, которое направлено перпендикулярно пластине, т.е. ${{{\mathbf{B}}}_{0}} = {{B}_{0}}{{{\mathbf{e}}}_{y}}$.

Уравнения движения жидкости в системе координат $Oxyz$, вращающейся с угловой скоростью ω₀ имеют вид:

(1.1)

$\left\{ \begin{gathered} {{\omega }_{0}} \times {{\omega }_{0}} \times {\mathbf{r}} + 2{{\omega }_{0}} \times {\mathbf{v}} + \frac{{\partial {\mathbf{v}}}}{{\partial t}} + \left( {{\mathbf{v}}\nabla } \right){\mathbf{v}} = - \frac{1}{\rho }\nabla P + \nabla U + {{\nu }}\Delta {\mathbf{v}} + \frac{1}{{\rho \mu }}{\text{rot}}{\mathbf{B}} \times {\mathbf{B}} \hfill \\ {\text{div}}{\mathbf{v}} = 0{\text{;}}\quad {\mathbf{r}} \in Q \hfill \\ \frac{{\partial {\mathbf{B}}}}{{\partial t}} = {\text{rot}}\left( {{\mathbf{v}} \times {\mathbf{B}}} \right) + {{{{\nu }}}_{m}}~\Delta {\mathbf{B}} \hfill \\ {\text{div}}{\mathbf{B}} = 0;\quad {\mathbf{r}} \in Q \hfill \\ \end{gathered} \right.$

Граничные и начальные условия:

${\mathbf{v}}\left( {{\mathbf{r}},t} \right) = {\mathbf{u}}\left( t \right),\quad ~{\mathbf{r}} \in H,\quad t > 0$

$\left| {{\mathbf{v}}\left( {{\mathbf{r}},t} \right)} \right| \to 0,\quad \left| {\mathbf{r}} \right| \to \infty ,\quad t > 0,\quad {\mathbf{v}}\left( {{\mathbf{r}},0} \right) = 0,\quad {\mathbf{r}} \in Q$

${\mathbf{B}}\left( {{\mathbf{r}},t} \right) = {{{\mathbf{B}}}_{0}} = {\text{const,}}\quad {\mathbf{r}} \in H,\quad t > 0$

${\mathbf{B}}\left( {{\mathbf{r}},0} \right) = 0,\quad {\mathbf{r}} \in Q$

Здесь $t$ – время, r – радиус-вектор относительно полюса 0, ${\mathbf{v}}$ – скорость жидкости, $P$ – давление, ${{{{\nu }}}_{m}}$ – магнитная вязкость.

Решение системы (1.1), удовлетворяющее начальным и граничным условиям, ищем в виде

(1.2)

$\left\{ \begin{gathered} {\mathbf{v}} = {{{v}}_{x}}\left( {y,t} \right){{{\mathbf{e}}}_{{\mathbf{x}}}} + {{{v}}_{z}}\left( {y,t} \right){{{\mathbf{e}}}_{{\mathbf{z}}}} \hfill \\ {\mathbf{B}} = {{B}_{x}}\left( {y,t} \right){{{\mathbf{e}}}_{{\mathbf{x}}}} + {{B}_{0}}{{{\mathbf{e}}}_{{\mathbf{y}}}} + {{B}_{z}}\left( {y,t} \right){{{\mathbf{e}}}_{{\mathbf{z}}}} \hfill \\ P = \frac{\rho }{2}{{\left( {{{\omega }_{0}} \times {\mathbf{r}}} \right)}^{2}} + \rho U + \rho q\left( {y,t} \right) \hfill \\ \end{gathered} \right.$

где q – новая функция давления.

Тогда система (1.1) распадается на подсистемы:

(1.3)

$\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {{{v}}_{x}}}}{{\partial t}} + 2{{\omega }_{0}}{{{\mathbf{e}}}_{{\mathbf{y}}}} \cdot {{{v}}_{z}} = \nu \frac{{{{\partial }^{2}}{{{v}}_{x}}}}{{\partial {{y}^{2}}}} + \frac{1}{{\mu \rho }}{{B}_{0}}\frac{{\partial {{B}_{x}}}}{{\partial y}}} \\ {\frac{{\partial {{{v}}_{z}}}}{{\partial t}} - 2{{\omega }_{0}}{{{\mathbf{e}}}_{{\mathbf{y}}}} \cdot {{{v}}_{x}} = \nu \frac{{{{\partial }^{2}}{{{v}}_{z}}}}{{\partial {{y}^{2}}}} + \frac{1}{{\mu \rho }}{{B}_{0}}\frac{{\partial {{B}_{z}}}}{{\partial y}}} \end{array}} \right.$

(1.4)

$\left\{ {\frac{{\partial q}}{{\partial y}} = 2} \right.{\mathbf{v}}({{\omega }_{0}} \times {{{\mathbf{e}}}_{y}}) - \left( {{{B}_{z}}\frac{{\partial {{B}_{z}}}}{{\partial y}} + {{B}_{x}}\frac{{\partial {{B}_{x}}}}{{\partial y}}} \right)\frac{1}{{\mu \rho }}$

(1.5)

$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{{\partial {{B}_{x}}}}{{\partial t}} = {{B}_{0}}\frac{{\partial {{{v}}_{x}}}}{{\partial y}} + {{\nu }_{m}}\frac{{{{\partial }^{2}}{{B}_{x}}}}{{\partial {{y}^{2}}}}} \end{array}} \\ {~\frac{{\partial {{B}_{z}}}}{{\partial t}} = {{B}_{0}}\frac{{\partial {{{v}}_{z}}}}{{\partial y}} + {{\nu }_{m}}\frac{{{{\partial }^{2}}{{B}_{z}}}}{{\partial {{y}^{2}}}}} \end{array}$

Обозначим ${{\omega }_{y}} = {{\omega }_{0}}{{{\mathbf{e}}}_{{\mathbf{y}}}} = {{\Omega }}$ и введем комплексную структуру

$\begin{gathered} {\hat {v}} = {{{v}}_{x}}\left( {y,t} \right) + i{{{v}}_{z}}\left( {y,t} \right)~,\quad \hat {u}\left( t \right) = {{u}_{x}} + i{{u}_{z}} \\ \hat {B} = {{B}_{x}}\left( {y,t} \right) + i~{{B}_{z}}\left( {y,t} \right) \\ \end{gathered} $

Тогда система уравнений примет вид

(1.6)

$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\hat {v}}}}{{\partial t}} - i2\Omega {\hat {v}} = \nu \frac{{{{\partial }^{2}}{\hat {v}}}}{{\partial {{y}^{2}}}} + \frac{{{{B}_{0}}}}{{\mu \rho }}\frac{{\partial{ \hat {B}}}}{{\partial y}}} \\ {\frac{{\partial{ \hat {B}}}}{{\partial t}} = {{B}_{0}}\frac{{\partial {\hat {v}}}}{{\partial y}} + ~{{\nu }_{m}}\frac{{{{\partial }^{2}}\hat {B}}}{{\partial {{y}^{2}}}}} \end{array}} \right.$

Граничные и начальные условия

$y = 0,\quad t > 0;\quad {\hat {v}}\left( {y,t} \right) = \hat {u}\left( t \right),\quad \hat {B}\left( {y,t} \right) = 0~~$

$y \to \infty ;\quad \left| {{\hat {v}}\left( {y,t} \right)} \right| \to 0,\quad \left| {\hat {B}\left( {y,t} \right)} \right| \to 0$

$t = 0,\quad y > 0;\quad {\hat {v}}\left( {y,0} \right) = 0,\quad \hat {B}\left( {y,0} \right) = 0$

Исключая магнитную индукцию из уравнений (1.6), получаем

(1.7)

$\frac{{{{\partial }^{2}}{\hat {v}}\left( {y,t} \right)}}{{\partial {{t}^{2}}}} - \frac{\partial }{{\partial t}}\left[ {\left( {\nu + {{\nu }_{m}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} + i2{{\Omega }}} \right]{\hat {v}}\left( {y,t} \right) - \left( {\frac{{B_{0}^{2}}}{{\mu \rho }} - i2{{\Omega }}{{\nu }_{m}}} \right)\frac{{{{\partial }^{2}}{\hat {v}}\left( {y,t} \right)}}{{\partial {{y}^{2}}}} + \nu {{\nu }_{m}}\frac{{{{\partial }^{4}}{\hat {v}}\left( {y,t} \right)}}{{\partial {{y}^{4}}}} = 0$

$y = 0,~\quad t > 0;\quad {\hat {v}}\left( {y,t} \right) = \hat {u}\left( t \right)$

$y \to \infty ;\quad \left| {{\hat {v}}\left( {y,t} \right)} \right| \to 0~$

$t = 0,\quad y > 0;\quad {\hat {v}}\left( {y,t} \right) = 0$

Решение уравнения (1.7) найдем с помощью синус-преобразования Фурье, которое введем формулой [18]

${\tilde {v}}\left( {\lambda ,t} \right) = \sqrt {\frac{2}{\pi }} \mathop \smallint \limits_0^\infty {\hat {v}}\left( {y,t} \right)\sin \lambda ydy~$

Дифференциальное уравнение (1.7) принимает вид

(1.8)

$\begin{gathered} \frac{{{{\partial }^{2}}{\tilde {v}}\left( {\lambda ,t} \right)}}{{\partial {{t}^{2}}}} + \left[ {{{\lambda }^{2}}\left( {\nu + {{\nu }_{m}}} \right) - i2{{\Omega }}} \right]\frac{{\partial {\tilde {v}}\left( {\lambda ,t} \right)}}{{\partial t}} + \left( {{{\lambda }^{4}}\nu {{\nu }_{m}} + \frac{{B_{0}^{2}}}{{\mu \rho }}{{\lambda }^{2}} - i2{{\Omega }}{{\nu }_{m}}{{\lambda }^{2}}} \right){\tilde {v}}\left( {\lambda ,t} \right) = \\ \, = \sqrt {\frac{2}{\pi }} \left[ {\lambda \left( {\nu + {{\nu }_{m}}} \right)u_{t}^{'} + \lambda u\left( {\frac{{B_{0}^{2}}}{{\mu \rho }} - i2{{\Omega }}{{\nu }_{m}} + {{\lambda }^{2}}\nu {{\nu }_{m}}} \right)} \right] = \mu \left( {\lambda ,t} \right)~ \\ {\tilde {v}}\left( {\lambda ,~0} \right) = 0\quad {{{{\tilde {v}}}}_{t}}\left( {\lambda ,~0} \right) = 0 \\ \end{gathered} $

Здесь $\mu \left( {\lambda ,t} \right) = \lambda \sqrt {\frac{2}{\pi }} \left[ {\left( {\nu + {{\nu }_{m}}} \right)u_{t}^{'} + u\left( {\frac{{B_{0}^{2}}}{{\mu \rho }} - i2{{\Omega }}{{\nu }_{m}} + {{\lambda }^{2}}\nu {{\nu }_{m}}} \right)} \right]$

Граничное условие учтено автоматически.

Характеристическое уравнение (1.8) и его корни

${{q}^{2}} + [{{\lambda }^{2}}\left( {\nu + {{\nu }_{m}}} \right) - i2{{\Omega }}]q + \left( {{{\lambda }^{4}}\nu {{\nu }_{m}} + \frac{{B_{0}^{2}}}{{\mu \rho }}{{\lambda }^{2}} - i2{{\Omega }}{{\nu }_{m}}{{\lambda }^{2}}} \right) = 0$

${{q}_{{1,2}}} = - \frac{1}{2}[{{\lambda }^{2}}\left( {\nu + {{\nu }_{m}}} \right) - i2{{\Omega }}] \pm \frac{1}{2}\sqrt {{{{[{{\lambda }^{2}}\left( {\nu - {{\nu }_{m}}} \right) - i2\Omega ]}}^{2}} - 4{{\lambda }^{2}}\left( {\frac{{B_{0}^{2}}}{{\mu \rho }}} \right)} = \sigma \pm \omega $

$\sigma = - \frac{1}{2}[{{\lambda }^{2}}\left( {\nu + {{\nu }_{m}}} \right) - i2{{\Omega }}]~$

${{\omega }^{2}} = \frac{1}{4}\left[ {{{{[{{\lambda }^{2}}\left( {\nu - {{\nu }_{m}}} \right) - i2\Omega ]}}^{2}} - 4{{\lambda }^{2}}\left( {\frac{{B_{0}^{2}}}{{\mu \rho }}} \right)} \right]$

Решение неоднородного уравнения (1.8) имеет вид

$\tilde {V}\left( {\lambda ,~t} \right) = {{c}_{1}}{\text{exp}}\left( {{{q}_{1}}t} \right) + {{c}_{2}}\exp \left( {{{q}_{2}}t} \right),$

где c₁, c₂ находятся по методу Лагранжа вариации произвольных постоянных

$\left\{ {\begin{array}{*{20}{l}} {c_{1}^{'}{\text{exp}}\left( {{{q}_{1}}t} \right) + c_{2}^{'}\exp \left( {{{q}_{2}}t} \right) = 0} \\ {c_{1}^{'}\exp \left( {{{q}_{1}}t} \right) + c_{2}^{'}{{q}_{2}}\exp \left( {{{q}_{2}}t} \right) = \mu \left( {\lambda ,t} \right)} \end{array}} \right.$

${{c}_{1}}\left( t \right) = {{\tilde {c}}_{1}} + \mathop \smallint \limits_0^t \frac{{\mu \left( {\lambda ,\tau } \right)\exp \left( { - {{q}_{1}}t} \right)}}{{{{q}_{1}} - {{q}_{2}}}}d\tau ,\quad {{c}_{2}}\left( t \right) = {{\tilde {c}}_{2}} - \mathop \smallint \limits_0^t \frac{{\mu \left( {\lambda ,\tau } \right)\exp \left( { - {{q}_{2}}t} \right)}}{{{{q}_{1}} - {{q}_{2}}}}d\tau $

Наконец

(1.9)

$\begin{gathered} ~\tilde {V}\left( {\lambda ,~t} \right) = {{{\tilde {c}}}_{1}}\exp \left( {{{q}_{1}}t} \right) + {{{\tilde {c}}}_{2}}\exp \left( {{{q}_{2}}t} \right) + \\ + \frac{1}{{{{q}_{1}} - {{q}_{2}}}}\mathop \smallint \limits_0^t \mu \left( {\lambda ,\tau } \right)\left( {{\text{exp}}\left( {{{q}_{1}}\left( {t - \tau } \right)} \right) - {\text{exp}}\left( {{{q}_{2}}\left( {t - \tau } \right)} \right)} \right)d\tau \\ \end{gathered} $

Удовлетворяя начальным условиям, получаем

(1.10)

$\tilde {V}\left( {\lambda ,~t} \right) = \frac{1}{\omega }\mathop \smallint \limits_0^t \mu \left( {\lambda ,\tau } \right){\text{exp}}\left( {\sigma \left( {t - \tau } \right)} \right){\text{sh}}\omega \left( {t - \tau } \right)d\tau $

Для нахождения $\hat {V}\left( {y,~t} \right)~~~$применим обратное синус-преобразование Фурье [19]

$\hat {V}\left( {y,~t} \right) = \sqrt {\frac{2}{\pi }} \mathop \smallint \limits_0^\infty \tilde {V}\left( {\lambda ,~t} \right)\sin \lambda yd\lambda $

Тогда получим

(1.11)

$\begin{gathered} \hat {V}(y,t) = \frac{2}{\pi }\int\limits_0^\infty {\frac{\lambda }{\omega }\int\limits_0^t {\left[ {({v} + {{{v}}_{m}})u_{t}^{'} + u\left( {\frac{{B_{0}^{2}}}{{\mu \rho }} - i2\Omega {{{v}}_{m}} + {{\lambda }^{2}}{v}{{{v}}_{m}}} \right)} \right]} } \exp (\sigma (t - \tau )){\text{sh}}\omega (t - \tau )d\tau \sin \lambda yd\lambda \\ \hat {V}(y,t) = \frac{2}{\pi }\int\limits_0^t {\left[ {({v} + {{{v}}_{m}})u_{t}^{'} + u\left( {\frac{{B_{0}^{2}}}{{\mu \rho }} - i2\Omega {{{v}}_{m}} + {{\lambda }^{2}}{v}{{{v}}_{m}}} \right)} \right]\int\limits_0^\infty {\frac{{\lambda \sin \lambda y}}{\omega }\exp (\sigma (t - \tau )){\text{sh}}\omega (t - \tau )d\lambda d\tau } } \\ \end{gathered} $

Вектор касательных напряжений, действующий со стороны жидкости на стенку, определяется выражением [1]

$\hat {F} = \rho \nu {{\left. {\frac{{\partial{ \hat {V}}}}{{\partial y}}} \right|}_{{y = 0}}}$

Подставляя скорость $\hat {V}\left( {y,~t} \right)$ из (1.11), получаем

(1.12)

$\hat {F} = \rho \nu \frac{2}{\pi }\mathop \smallint \limits_0^t \left\{ {\left[ {\left( {\nu + {{\nu }_{m}}} \right)u_{t}^{'} + u\left( {\frac{{B_{0}^{2}}}{{\mu \rho }} - i2{{\Omega }}{{\nu }_{m}} + {{\lambda }^{2}}\nu {{\nu }_{m}}} \right)} \right]~~\mathop \smallint \limits_0^\infty \frac{{{{\lambda }^{2}}}}{\omega }{\text{exp}}\left( {\sigma \left( {t - \tau } \right)} \right){\text{sh}}\omega \left( {t - \tau } \right)} \right\}d\lambda d\tau {\text{\;}}$

Полученные соотношения полностью решают задачу.

2. ПОЛЕ СКОРОСТЕЙ, ИНДУЦИРОВАННОЕ ДВИЖЕНИЕМ СТЕНКИ

Пусть плоскость H начинает двигаться в продольном направлении со скоростью u(t) = = u(0)expλt, λ = α + iω. Рассмотрим “нормальные” колебания вязкой электропроводной жидкости в полупространстве, ограниченном плоскостью Н, т.е. будем изучать класс движений, в котором все временные факторы зависят от времени посредством множителя expλt. Тогда система уравнений (1.5) принимает вид

(2.1)

$\left\{ {\begin{array}{*{20}{l}} {\lambda \hat {V} - ~i2\Omega \hat {V} = \nu \frac{{{{\partial }^{2}}\hat {V}}}{{\partial {{y}^{2}}}} + \frac{{{{B}_{0}}}}{{\mu \rho }}\frac{{\partial{ \hat {B}}}}{{\partial y}}} \\ {\lambda \hat {B} = {{B}_{0}}\frac{{\partial{ \hat {V}}}}{{\partial y}} + {{\nu }_{m}}\frac{{{{\partial }^{2}}\hat {B}}}{{\partial {{y}^{2}}}}} \end{array}} \right.$

Граничные и начальные условия

$y = 0,\quad t > 0{\text{:}}\quad \hat {V}\left( {y;t} \right) = \hat {u}\left( 0 \right);\quad \hat {B}(y;t){\text{ }} = 0$

$y \to \infty {\text{:}}\quad \hat {V}\left( {y;t} \right) \to 0,\quad \hat {B}(y;t) \to 0$

$t = 0;\quad y > 0;\quad \hat {V}\left( {y;0} \right) = 0,\quad \hat {B}(y;0) = 0$

Исключая из (2.1) магнитную индукцию, для функции $~\hat {V}\left( y \right)$ получаем обыкновенное дифференциальное уравнение

(2.2)

$\nu {{\nu }_{m}}\frac{{{{d}^{4}}\hat {V}}}{{d{{y}^{4}}}} - \left[ {\lambda (\nu + {{\nu }_{m}}) + \frac{{B_{0}^{2}}}{{\mu \rho }} - i2\Omega {{\nu }_{m}}} \right]~\frac{{{{d}^{2}}\hat {V}}}{{d{{y}^{2}}}} + \lambda (\lambda - i2\Omega )\hat {V} = 0$

и граничные условия

(2.3)

$y = 0,\quad \hat {V}(0) = \hat {u}(0);\quad y \to \infty ;\quad \hat {V}\left( y \right) \to ~0$

Характеристическое уравнение (2.2) имеет вид

(2.4)

$\nu {{\nu }_{m}}{{x}^{4}} - \left( {\lambda \left( {\nu + {{\nu }_{m}}} \right) + \frac{{B_{0}^{2}}}{{\mu \rho }} - i2\Omega {{\nu }_{m}}} \right){{x}^{2}} + \lambda (\lambda - i2\Omega ) = 0$

Введем обозначение

$G = \frac{1}{{2\nu {{\nu }_{m}}}}\left( {\lambda \left( {\nu + {{\nu }_{m}}} \right) + \frac{{B_{0}^{2}}}{{\mu \rho }} - i2\Omega {{\nu }_{m}}} \right)$

Корни уравнения (2.4)

$~{{x}_{j}} = \pm \sqrt {G \pm \sqrt {{{G}^{2}} - \frac{{\lambda \left( {\lambda - i2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} } ,\quad \overline {j = 1,4} $

Решение уравнения (2.2) запишется в виде

(2.5)

$\hat {V}\left( y \right) = {{\Sigma }_{j}}{{C}_{j}}~{\text{exp}}{{x}_{j}}y~~$

где C_j подлежат определению из граничных условий (2.3). Запишем магнитную индукцию, найденную по полю скоростей, так

(2.6)

$\hat {B}(y) = \frac{{\mu \rho }}{{{{B}_{0}}}}(\lambda - i2\Omega )\mathop \sum \limits_{j = 1}^4 {{C}_{j}}\frac{1}{{{{x}_{j}}}}\exp {{x}_{j}}y - \frac{{\mu \rho }}{{{{B}_{0}}}}\nu \mathop \sum \limits_{j = 1}^4 {{C}_{j}}{{x}_{j}}\exp {{x}_{j}}y$

Из условий ограниченности решения на бесконечности надо положить константы C₃ и C₄ равными нулю, так как им соответствуют корни x₃ и x₄, имеющие перед радикалом знак плюс. Удовлетворяя граничным условиям (2.3), получаем систему алгебраических уравнений для определения ${{C}_{j}},$ (j = 1, 2)

(2.7)

$\left\{ \begin{gathered} {{C}_{1}} + {{C}_{2}} = \hat {u}(0) \hfill \\ (\lambda - i2\Omega )\left( {\frac{{{{C}_{1}}}}{{{{x}_{1}}}} + \frac{{{{C}_{2}}}}{{{{x}_{2}}}}} \right) - {v}({{C}_{1}}{{x}_{1}} + {{C}_{2}}{{x}_{2}}) = 0 \hfill \\ \end{gathered} \right.$

Заметим, что корни x_j можно представить в следующем виде:

${{x}_{1}} = - \sqrt {G + \sqrt {{{G}^{2}} - \frac{{\lambda \left( {\lambda - i2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} } = ~~ - (m + n)$

(2.8)

${{x}_{2}} = - \sqrt {G - \sqrt {{{G}^{2}} - \frac{{\lambda \left( {\lambda - i2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} } = - (m - n)$

$m = \frac{1}{{\sqrt 2 }}\sqrt {G + \sqrt {\frac{{\lambda \left( {\lambda - i2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} } ,\quad n = \frac{1}{{\sqrt 2 }}\sqrt {G - \sqrt {\frac{{\lambda \left( {\lambda - i2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} } .$

С учетом этого замечания и обозначений

${{d}_{1}} = \frac{{\lambda - i2\Omega }}{{{{x}_{1}}}} - \nu {{x}_{{1~}}},\quad {{d}_{2}} = \frac{{\lambda - i2\Omega }}{{{{x}_{2}}}} - \nu {{x}_{2}}$

система уравнений (2.7) перепишется в виде

$\left\{ {\begin{array}{*{20}{c}} {{{C}_{1}} + {{C}_{2}} = \hat {u}\left( 0 \right)} \\ {{{d}_{1}}{{C}_{1}} + {{d}_{2}}{{C}_{2}} = 0~} \end{array}} \right.\quad \Delta = {{d}_{2}} - {{d}_{1}} = - 2n\left( {\nu + \sqrt {\frac{{\nu {{\nu }_{m}}\left( {\lambda - i2\Omega } \right)}}{{{\lambda }}}} } \right)$

Определяя C₁ и C₂, находим поле скоростей жидкости в форме

(2.9)

$\hat {V}(y,t) = \frac{{\hat {u}(0)}}{\Delta }\exp ( - \alpha t)({{d}_{2}}\exp ( - (m + n)y) - {{d}_{1}}\exp ( - (m - n)y))\exp (iwt)$

3. СТРУКТУРА ПОГРАНИЧНЫХ СЛОЕВ

Рассмотрим более подробно выражение для поля скоростей (2.9).

В выражение для m и n входит величина G, которую представим в виде

(3.1)

$\begin{gathered} G = \frac{{B_{0}^{2} - \mu \rho \alpha \left( {\nu + {{\nu }_{m}}} \right)}}{{2\mu \rho \nu {{\nu }_{m}}}} + i\frac{{\omega \nu + {{\nu }_{m}}\left( {\omega - 2\Omega } \right)}}{{2\nu {{\nu }_{m}}}} = C + iD \\ C = \frac{{B_{0}^{2} - \mu \rho \alpha \left( {\nu + {{\nu }_{m}}} \right)}}{{2\mu \rho \nu {{\nu }_{m}}}},\quad D = \frac{{\omega \nu + {{\nu }_{m}}\left( {\omega - 2\Omega } \right)}}{{2\nu {{\nu }_{m}}}} \\ \end{gathered} $

Величину $\sqrt {\lambda \left( {\lambda - i2\Omega } \right){\text{/}}\nu {{\nu }_{m}}} $ представим в виде суммы:

$\sqrt {\frac{{\lambda \left( {\lambda - i2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} = \sqrt {\frac{{{{\alpha }^{2}} - \omega \left( {\omega - 2\Omega } \right)}}{{\nu {{\nu }_{m}}}} + i\frac{{\left( { - 2\alpha } \right)\left( {\omega - \Omega } \right)}}{{\nu {{\nu }_{m}}}}} = A + iB$

(3.2)

$A = \frac{1}{{\sqrt 2 }}{{\left[ {\sqrt {{{{\left( {\frac{{{{\alpha }^{2}} - \omega \left( {\omega - 2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} \right)}}^{2}} + \frac{{4{{\alpha }^{2}}{{{\left( {\omega - \Omega } \right)}}^{2}}}}{{{{{\left( {\nu {{\nu }_{m}}} \right)}}^{2}}}}} + \frac{{{{\alpha }^{2}} - \omega \left( {\omega - 2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} \right]}^{{1/2}}}$

(3.3)

$B = \frac{1}{{\sqrt 2 }}{{\left[ {\sqrt {{{{\left( {\frac{{{{\alpha }^{2}} - \omega \left( {\omega - 2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} \right)}}^{2}} + \frac{{4{{\alpha }^{2}}{{{\left( {\omega - \Omega } \right)}}^{2}}}}{{{{{\left( {\nu {{\nu }_{m}}} \right)}}^{2}}}}} - \frac{{{{\alpha }^{2}} - \omega \left( {\omega - 2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} \right]}^{{1/2}}}$

(3.4)

$m = \frac{1}{{\sqrt 2 }}\sqrt {C + A + i\left( {D + B} \right)} = \frac{1}{{\sqrt 2 }}\left( {{{A}_{1}} + i{{B}_{1}}} \right)$

(3.5)

$n = \frac{1}{{\sqrt 2 }}\sqrt {C - A + i\left( {D - B} \right)} = \frac{1}{{\sqrt 2 }}\left( {{{A}_{2}} + i{{B}_{2}}} \right)$

(3.6)

${{A}_{1}} = \frac{1}{{\sqrt 2 }}{{\left( {\sqrt {{{{\left( {C + A} \right)}}^{2}} + {{{\left( {D + B} \right)}}^{2}}} ~\, + \,C + A} \right)}^{{1/2}}}$

(3.7)

${{B}_{1}} = \frac{1}{{\sqrt 2 }}{{\left( {\sqrt {{{{\left( {C + A} \right)}}^{2}} + {{{\left( {D + B} \right)}}^{2}}} - C - A} \right)}^{{1/2}}}$

(3.8)

${{A}_{2}} = \frac{1}{{\sqrt 2 }}{{\left( {\sqrt {{{{\left( {C - A} \right)}}^{2}} + {{{\left( {D - B} \right)}}^{2}}} ~\, + \,C - A} \right)}^{{1/2}}}$

(3.9)

${{B}_{2}} = \frac{1}{{\sqrt 2 }}{{\left( {\sqrt {{{{\left( {C - A} \right)}}^{2}} + {{{\left( {D - B} \right)}}^{2}}} - C + A} \right)}^{{1/2}}}$

С помощью равенств (3.4)–(3.9) поле скоростей жидкости представим в виде суперпозиции плоских волн, которая имеет вид

(3.10)

$\widehat {~V}\left( {y,t} \right) = {{M}_{1}}{\text{exp}}i\left( {\omega t - {{k}_{1}}y} \right) + {{M}_{{2~}}}{\text{exp}}i\left( {\omega t + {{k}_{1}}y} \right)$

${{M}_{1}} = \frac{{\hat {u}(0)}}{\Delta }{{d}_{2}}\exp \left( { - \alpha t - \frac{y}{{{{\delta }_{1}}}}} \right),\quad {{M}_{2}} = \frac{{\hat {u}(0)}}{\Delta }{{d}_{1}}\exp \left( { - \alpha t + \frac{y}{{{{\delta }_{2}}}}} \right).$

Первая из этих волн излучается стенкой в полупространство, заполненное вязкой электропроводной жидкостью. Эта волна распространяется вдоль оси у с фазовой скоростью ${{V}_{f}} = \omega {\text{/}}{{k}_{1}}$ и затухает на расстоянии ${{\delta }_{1}}$ от стенки – это толщина пограничного слоя, которая определяется выражением $~{{\delta }_{1}} = \sqrt 2 {\text{/}}({{A}_{1}} + {{A}_{2}})$. Волновое число ${{k}_{1}} = ({{В}_{1}} + {{В}_{2}}){\text{/}}\sqrt 2 $. Вторая волна имеет ту же структуру, при этом волновое число и величина пограничного слоя имеют вид: ${{k}_{2}} = ({{В}_{1}} - {{В}_{2}}){\text{/}}\sqrt 2 $ δ₂ = = $\sqrt 2 {\text{/}}({{A}_{1}} + {{A}_{2}})$. Вторая волна набегает на стенку из бесконечности со скоростью ${{V}_{f}} = \omega {\text{/}}{{k}_{2}}$. Фазовые скорости этих волн различны и зависят от частоты, т.е. среда обладает дисперсией. Групповые скорости этих волн также различны. Они зависят от коэффициентов затухания и вращения стенки, магнитной индукции и параметров жидкости. Амплитуды этих волн зависят от величины проекции угловой скорости на ось у, параметров движения стенки, магнитной индукции и параметров жидкости.

Выберем индукцию магнитного поля $B_{0}^{2} = \mu \rho \alpha \left( {\nu + {{\nu }_{m}}} \right)~$ и введем безразмерные переменную и параметры: $Y = \omega {\text{/}}\alpha $ и $S = 2\Omega {\text{/}}\alpha $, $\gamma = \nu {\text{/}}{{\nu }_{m}}$. В этом случае безразмерные волновые числа принимают вид:

$~{{k}_{{1,2}}} \times 2\sqrt {\frac{{2\nu }}{\alpha }} = {{(\sqrt {{{A}^{2}} + {{{\left( {D + B} \right)}}^{2}}} - A)}^{{\frac{1}{2}}}} \pm {{(\sqrt {{{A}^{2}} + {{{\left( {D - B} \right)}}^{2}}} + A)}^{{\frac{1}{2}}}}$

$\frac{2}{{{{\delta }_{{1,2}}}}} \times \sqrt {\frac{{2\nu }}{\alpha }} = {{(\sqrt {{{A}^{2}} + {{{\left( {D + B} \right)}}^{2}}} + A)}^{{\frac{1}{2}}}} \pm {{(\sqrt {{{A}^{2}} + {{{\left( {D - B} \right)}}^{2}}} - A)}^{{\frac{1}{2}}}}~$

$A = \sqrt \gamma {{\left( {\sqrt {{{{(1 - {{Y}^{2}} + Ys)}}^{2}} + {{{\left( {2Y - s} \right)}}^{2}}} + (1 - {{Y}^{2}} + Ys)} \right)}^{{\frac{1}{2}}}}$

$D + B = \frac{{\left( {\gamma + 1} \right)Y - s}}{{\sqrt 2 }} + \sqrt \gamma {{\left( {\sqrt {{{{(1 - {{Y}^{2}} + Ys)}}^{2}} + {{{\left( {2Y - s} \right)}}^{2}}} - (1 - {{Y}^{2}} + Ys)} \right)}^{{\frac{1}{2}}}}$

$D - B = \frac{{\left( {\gamma + 1} \right)Y - s}}{{\sqrt 2 }} - \sqrt \gamma {{\left( {\sqrt {{{{(1 - {{Y}^{2}} + Ys)}}^{2}} + {{{\left( {2Y - s} \right)}}^{2}}} - (1 - {{Y}^{2}} + Ys)} \right)}^{{\frac{1}{2}}}}$

Параметр γ, введенный выше, представляет отношение вязкостей, кинематической и магнитной, т.е. отношение магнитного числа Рейнольдса к числу Рейнольдса, связанного с вязкостью жидкости. На следующих рисунках представлено поведение волновых чисел и групповых скоростей в зависимости от частоты колебаний стенки для случая, когда изменение магнитного поля в равной мере обеспечивается его переносом движущимся проводящим веществом и диффузией магнитного поля относительно этого вещества. Анализ зависимостей волновых чисел k(ω) показал, что это комплексное число, действительная часть которого определяет зависимость фазовой скорости волны от частоты, а мнимая часть – зависимость коэффициента затухания амплитуды волны от частоты. Дисперсия связана с внутренними свойствами материальной среды, обычно выделяются частотная дисперсия, при которой поляризация в диспергирующей среде зависит от значений поля в предшествующие моменты времени (память), и пространственная дисперсия, когда поляризация в данной точке зависит от значений поля в некоторой области. Кроме того, анализ зависимостей волновых чисел ${{k}_{{1,2}}}$, ${{\delta }_{{1,2}}}$ от Y при определенном выборе магнитной индукции показал, что существуют особые точки нестационарной задачи, в которых волновые числа имеют угловые точки, в которых соответствующие производные не существуют.

Так, на рис. 2 представлены графики зависимости волновых чисел ${{k}_{1}}$ и ${{k}_{2}}$ от Y (частота ω при фиксированных s (s = 2) и значении параметра $\gamma = \nu {\text{/}}{{\nu }_{m}} = 1$). На интервале 0 < Y < 1 волновое число ${{k}_{1}}$ монотонно убывает, в то время как ${{k}_{2}}$ остается постоянным. При Y > 1 волновые числа монотонно возрастают. Отметим, что при Y = 1 оба волновых числа имеют угловую точку, в которой не существует производная dk/dω.

Рис. 2.

Зависимость волновых чисел ${{k}_{1}}$, ${{k}_{2}}$ от частоты Y: $\gamma $ = 1.

На рис. 3 показана зависимость величин пограничных слоев δ₁, δ₂ от Y при значении параметра $\gamma $ = 1. На интервале 0 < Y < 1 эти функции ведут себя диаметрально противоположно. Так, функция δ₁(Y) монотонно возрастает до значения 0.5 при Y = 1 и затем монотонно убывает, асимптотически приближаясь к величине 0.2. Функция δ₂(Y) при 0 < Y < 1 монотонно убывает от значений 1.3 до 0.5 в точке Y = 1 и стремится к значению 0.2 как и функция δ₁(Y). Обе функции при Y = 1 имеют угловые точки.

Рис. 3.

Зависимость величин пограничных слоев δ₁, δ₂ от частоты Y: $\gamma $ = 1.

На рис. 4 представлен характер зависимости волновых пакетов от Y (частота ω при фиксированных s (s = 2) и значении параметра $\gamma = \nu {\text{/}}{{\nu }_{m}} = 1$. Скорость волнового пакета ${{V}_{{g1}}}$, излучаемого колеблющейся стенкой, носит сложный характер. На интервале 0 < Y < 1 скорость монотонно убывает от отрицательных значений –2 до значения – 4.75, что свидетельствует о наличии аномальной дисперсии среды. В особой точке Y = 1 скорость ${{V}_{{g1}}}$ имеет скачок, равный |6.75|, изменяясь от –4.75 до +2. Далее в этой точке скорость падает до 1 и остается постоянной при увеличении частоты. Скорость ${{V}_{{g2}}}$ (скорость набегающей волны) имеет еще более сложный характер. В интервале 0 < Y < 1 существует особая точка Y = 0.6, в которой скорость терпит бесконечный разрыв, изменяясь от +$\infty $ слева от 0.6 до –$\infty $ справа от 0.6. Далее скорость ${{V}_{{g2}}}$, оставаясь отрицательной, возрастает до значения – 4.75 при Y = 1. Это вторая особая точка ${{V}_{{g2}}}$, в которой она терпит конечный скачок, величина которого по модулю равна |6.75|, и, достигнув значения 2, терпит еще скачок, опустившись до значения ${{V}_{{g2}}}$ = 1. Это значение остается постоянным при увеличении частоты колебаний стенки.

Рис. 4.

Зависимость волновых пакетов ${{V}_{{g1}}}$, ${{V}_{{g2}}}$, от частоты Y: $\gamma $ = 1.

Рассмотрим гармонические колебания стенки $\hat {u}\left( t \right) = \hat {u}\left( 0 \right){\text{exp}}\left( {i\omega t} \right)$.

В этом случае

$\alpha = 0,\quad А = ~~0,\quad С = {\text{ }}0$

$D = \frac{{\omega \nu + {{\nu }_{m}}\left( { - 2\Omega } \right)}}{{2\nu {{\nu }_{m}}}},\quad B = \sqrt {\frac{{\omega \left( {{{\omega }} - i2\Omega } \right)}}{{\nu {{\nu }_{m}}}}} $

Волновые числа первой волны

${{k}_{1}} = \frac{{\sqrt {D + B} }}{2} + \frac{{\sqrt {D - B} }}{2},\quad {{\delta }_{1}} = {{\left( {\frac{{\sqrt {D + B} }}{2} + \frac{{\sqrt {D - B} }}{2}} \right)}^{{ - 1}}}$

Волновые числа второй волны

${{k}_{2}} = \frac{{\sqrt {D + B} }}{2} - \frac{{\sqrt {D - B} }}{2},\quad {{\delta }_{2}} = {{\left( {\frac{{\sqrt {D + B} }}{2} - \frac{{\sqrt {D - B} }}{2}} \right)}^{{ - 1}}}$

Рассмотрим случай резонанса ω = 2Ω. Тогда D = $\Omega {\text{/}}{{\nu }_{m}}$, B = 0.

Волновые числа первой волны ${{\delta }_{1}} = \sqrt {{{\nu }_{m}}{\text{/}}\Omega } ~$, ${{k}_{1}} = \sqrt {\Omega {\text{/}}{{\nu }_{m}}} $ зависят только от магнитной вязкости жидкости и проекции угловой скорости вращения системы стенка-жидкость на нормаль к стенке и не зависят от вязкости жидкости.

Для второй волны δ₂ = $\infty $, ${{k}_{2}}$ = 0, т.е. набегающая волна отсутствует, и пограничный слой заполняет все полупространство.

4. О СОПОСТАВЛЕНИИ РЕШЕНИЙ УРАВНЕНИЙ МАГНИТНОЙ ГИДРОДИНАМИКИ С ПОЛНЫМ УРАВНЕНИЕМ МАГНИТНОЙ ИНДУКЦИИ С РЕШЕНИЕМ В ГИДРОДИНАМИЧЕСКОМ ПРИБЛИЖЕНИИ

Представляет интерес сравнить решение уравнений гидродинамики с использованием полного уравнения магнитной индукции, представленное в данной работе, с решением этой задачи в гидродинамическом приближении, которое опубликовано в [6]. Формулы для волновых чисел и групповых скоростей, выражающие функциональную зависимость от частоты колебаний стенки, полученные в данной работе, содержат параметр $~\gamma $ = $\nu {\text{/}}{{\nu }_{m}}$ – отношение кинематической вязкости к магнитной вязкости и, который вообще говоря, может меняться в широких пределах. Поэтому графики соответствующих функций должны сильно отличаться. Кроме того, выбранное магнитное поле $~B_{0}^{2} = \mu \rho \alpha (\nu + {{\nu }_{m}})$ = $\nu $(1 + $1{\text{/}}\gamma $) зависит от параметра $\gamma $ и совпадает с полем работы [6] только при γ = 1. Поэтому для корректности сопоставления графиков волновых чисел и волновых пакетов как функции частоты колебаний стенки с соответствующими графиками работы [6] было выбрано значение параметра $\gamma = 1$. Сопоставление результатов показало, что графики волновых чисел и волновых пакетов существенно отличаются. Особенно сильно отличие проявляется при сопоставлении графиков волновых пактов. В [6] волна, излучаемая стенкой, имеет скорость ${{V}_{{g1}}}$, которая монотонно возрастает с ростом частоты Y. В представленной работе скорость излучаемой стенкой волны имеет сложный характер. На интервале 0 < Y < 1 скорость монотонно убывает от отрицательных значений –2 до значения –4.75, что свидетельствует о наличии аномальной дисперсии среды. В особой точке Y = 1 скорость ${{V}_{{g1}}}$ имеет скачок, равный |6.75|, изменяясь от –4.75 до +2. Далее в этой точке скорость падает до 1 и остается постоянной при увеличении частоты. Скорость волны, набегающей на стенку в [6], имеет две угловые точки при Y = 0.5 и Y = 0.55 и далее с ростом частоты монотонно возрастает. В данной работе скорость ${{V}_{{g2}}}$ (скорость набегающей волны) имеет еще более сложный характер. В интервале 0 < Y < 1 существует особая точка Y = 0.6, в которой скорость терпит бесконечный разрыв, изменяясь от +$\infty $ слева от Y = 0.6 до –$\infty $ справа от Y = 0.6. Далее скорость ${{V}_{{g2}}}$, оставаясь отрицательной, возрастает до значения – 4.75 при Y = 1. Это вторая особая точка ${{V}_{{g2}}}$, в которой она терпит конечный скачок, величина которого по модулю равна |6.75|, и, достигнув значения 2, терпит еще скачок, опустившись до значения ${{V}_{{g2}}}$ = 1. Это значение остается постоянным при увеличении частоты колебаний стенки. Из сопоставления решений становится ясно, как диссипативный член в уравнении индукции перестраивает картину течения вязкой электропроводной жидкости. Представляет интерес оценить влияние изменения параметра $\gamma $ на картину течения жидкости. Численный анализ для $\gamma $= 5 представлен на рис. 5, 6, 7 .

Рис. 5.

Зависимость волновых чисел ${{k}_{1}}$, ${{k}_{2}}$ от частоты Y: $\gamma $ = 5.

Рис. 6.

Зависимость величин пограничных слоев δ₁, δ₂ от частоты Y: $\gamma $ = 5.

Рис. 7.

Зависимость волновых пакетов ${{V}_{{g1}}}$, ${{V}_{{g2}}}$, от частоты Y: $\gamma $ = 5.

На рис. 5 представлена зависимость волновых чисел ${{k}_{1}}$ и ${{k}_{2}}$ как функции частоты Y. Они монотонно возрастают с увеличением частоты, причем k₁ растет, начиная с ${{k}_{1}}$(0) = 3.5, а k₂ с отрицательных значений ${{k}_{{2~}}}\left( 0 \right) - 2.7$ с угловой точкой при Y = 1, при этом Y(1) = –2.2. На рис. 6 показаны графики функций ${{\delta }_{1}}\left( Y \right)$ и ${{\delta }_{2}}\left( Y \right)$. Волновое число δ₁ возрастает от значения ${{\delta }_{1}}\left( 0 \right) = 0.25$ с максимумом δ₁(0.5) = 0.34 и затем монотонно убывает до 0.1. Волновое число δ₂ (набегающая волна) убывает с ${{\delta }_{2}}\left( 0 \right)$ = 0.63 до значения δ₂(0.5) = 0.34 – угловая точка и затем резко возрастает до δ₂(1) = 0.45 – угловая точка и затем монотонно убывает до 0.1. Графики групповых скоростей представлены на рис. 7. Скорость волнового пакета, излучаемого стенкой, ${{V}_{{g1}}}$, имеет бесконечный разрыв в точке Y = 0.15, причем скорость падает от отрицательных значений ${{V}_{{g1}}}$(0) = $ - $5.5 до –$\infty $, затем скачком возрастает до +$\infty $ и резко убывает на интервале 0.5 < Y < 1 до значения ${{V}_{{g1}}}$(1) = 1 и, опустившись до значения 0.7, остается постоянной с ростом частоты. Скорость набегающей волны ${{V}_{{g2}}}$ возрастает от ${{V}_{{g1}}}$(0) = 1 до +$\infty $ на интервале 0 < Y < 1. В точке Y = 1 скорость скачком падает до ${{V}_{{g1}}}$(1) = 0.7 и остается постоянной с ростом частоты. Проведенный анализ показывает, как диффузионный член в уравнении индукции меняет картину течения электропроводной жидкости. Кроме того, изменяя величины вкладов в изменение магнитного поля от переноса движущимся проводящим веществом и диффузией относительно этого вещества, можно наблюдать, как меняются волновые числа набегающих на стенку и излучаемых стенкой волн.

ЗАКЛЮЧЕНИЕ

Проведен анализ задачи неустановившегося течения вязкой электропроводной несжимаемой жидкости в плоско-параллельной конфигурации. Найдены точные решения трехмерных нестационарных уравнений магнитной гидродинамики. В отличие от гидродинамического приближения здесь используется полное уравнение магнитной индукции. При этом никаких ограничений на характер движения пластины не накладывается. Определены поле скоростей в потоке и векторы касательных напряжений, действующие из жидкости на стенку. Для случая “нормальных” колебаний пластины поле скоростей вязкой электропроводной жидкости представлено в виде суперпозиции двух волн, распространяющихся вдоль оси у навстречу друг другу. Волна, излучаемая стенкой, распространяется с фазовой скоростью ${{V}_{{f1}}}$ = $\omega {\text{/}}{{k}_{1}}$ и затухает на расстоянии δ₁ от стенки. Вторая волна набегает на стенку из бесконечности со скоростью ${{V}_{{f2}}}$ = = $\omega {\text{/}}{{k}_{2}}$ и затухает на расстоянии δ₂. При этом волновые числа зависят от частоты, т.е. среда обладает дисперсией. Анализ зависимости групповых скоростей ${{V}_{{g1}}}$ и ${{V}_{{g2}}}$ от Y (частота ω при фиксированных s = 2 и $\gamma = 1$) показал, что существуют особые точки нестационарной задачи, в которых волновые пакеты терпят конечные и бесконечные разрывы, принимая как положительные, так и отрицательные значения, что свидетельствует о наличии аномальной дисперсии. Для случая незатухающих колебаний стенки рассмотрен случай резонанса и исследована структура пограничных слоев, примыкающих к стенке. Показано, что в этом случае существует только волна, излучаемая стенкой, причем волновые числа этой волны зависят только от магнитной вязкости электропроводной среды и проекции угловой скорости на ось у и не зависят от кинематической вязкости. Волна, набегающая на стенку, отсутствует, и пограничный слой заполняет все полупространство. Математическая процедура интегрирования системы дифференциальных уравнений рассматриваемой задачи может быть использована при исследовании более сложных задач. Кроме того, полученные результаты могут быть использованы для учета силовых воздействий при движении жидкости в каналах различной формы, а также в задачах фильтрации и при моделировании различных физических явлений в движущейся жидкости.

Список литературы

Слезкин Н.А. Динамика вязкой несжимаемой жидкости. М.: Гостехиздат, 1955. 520 с.
Thornley Cl. On Stokes and Rayleigh layers in a rotating system // Quan J. Mech and Appl. Math. 1968. V. 21. № 4. P. 451–461.
Gupta A.S. Ekman Layer on a Porous Plate // J. Phys. of Fluid. 1971. V. 15. № 5. P. 930–941.
Гурченков А.А., Яламов Ю.И. Нестационарный поток на пористой пластине при наличии вдува (отсоса) среды // ПМТФ. 1980. № 4. С. 66–69.
Холодова Е.С. Диссертация на соискание ученой степени доктора физ.-мат наук, С-Петербургский государственный университет. С-Петербург, 2019. 451 с.
Гурченков А.А. Нестационарный поток вязкой несжимаемой электропроводной жидкости на вращающейся пластине. // ПММ. 2021. Т. 5–6. С. 770–778.
Гайфуллин А.М., Накрохин С.А. Обтекание сжимаемым газом пластины с движущейся против потока поверхностью // Изв. РАН. МЖГ. 2021. № 1. С. 47–51.
Гайфуллин А.М., Жвик В.В. Связь дальней асимптотики струи с профилем скорости в отверстии // Доклады РАН. Физика, технические науки. 2020. Т. 495. С. 50–53.
Гайфуллин А.М., Жвик В.В. Нелокальный закон сохранения в свободной затопленной струе // ЖВМиМФ. 2021. Т. 61. № 10. С. 1646–165б.
Dimitrieva N.F. Stratified Flow Structure near the Horizontal Wedge // Fluid Dynamics. 2019. V. 54. № 7. P. 940–947. https://doi.org/10.1134/S0032823519030111
Dimitrieva N.F. Calculation of nonuniform fluid flows in a gravity field // In Proc. Topical Problems of Fluid Mechanics, ed. D. Šimurda, T. Bodnár, Prague, 2020. P. 48–55. https://doi.org/10.14311/TPFM.2020.007
Гавриков М.Б. Двухжидкостная электромагнитная гидродинамика : [монография] / Гавриков М.Б. Ин-т прикладной математики им. М.В. Келдыша. М.: КРАСАНД, 2018. 583 с.
Chashechkin Yu D. Differential fluid mechanics – basis of the theory of flows with combustion // J. Phys.: Conf. Ser. 2021. V. 1891. P. 0112023. https://doi.org/10.1088/1742- 6596/1891/1/012023
Ермаков М.К. Моделирование вихревого течения с воронкой на основе матричного метода. 12-я Междунар. конф. – школа молодых ученых “Волны и вихри в сложных средах” М. 01–03 декабря 2021 г.
Чашечкин Ю.Д. Эволюция тонкоструктурного распределение вещества свободно падающей капли в смешивающихся жидкостях // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 3. С. 67–77.
Chashechkin Yuli D. Conventional partial and new complete solutions of the fundamental equations of fluid mechanics in the problem of periodic internal waves with accompanying ligaments generation // Mathematics. 2021. V. 9. № 586. https://doi.org/10.3390/math9060586
Поддубный И.И., Разуванов Н.Г. Исследование гидродинамики и теплообмена при опускном течении жидкого металла в канале прямоугольного сечения в компланарном магнитном поле // Теплоэнергетика. 2016. № 2. С. 13–21.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. М.: Наука, 1981. 632 с.
Корн Г., Корн Т. Справочник по математики для научных работников и инженеров М.: Наука, 1978. 832 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал