Известия РАН. Механика жидкости и газа, 2023, № 2, стр. 46-54

ЭФФЕКТИВНЫЙ ТЕНЗОР ЯДЕР РЕЛАКСАЦИИ СЛОИСТОЙ СРЕДЫ, СОСТОЯЩЕЙ ИЗ ВЯЗКОУПРУГОГО МАТЕРИАЛА И ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

В. В. Шумилова^a, *

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

Поступила в редакцию 23.06.2022
После доработки 11.10.2022
Принята к публикации 11.10.2022

EDN: NSTBGN
DOI: 10.31857/S0568528122600424

Аннотация

Выведены явные формулы для расчета компонентов эффективного тензора ядер релаксации двухфазной слоистой среды с периодической микроструктурой. Первая фаза такой среды состоит из изотропного вязкоупругого материала, а вторая фаза – из вязкой несжимаемой жидкости. Установлено, в частности, что компоненты указанного тензора зависят от объемной доли жидкости внутри ячейки периодичности и не зависят от числа слоев и расстояний между ними.

Ключевые слова: вязкая несжимаемая жидкость, вязкоупругость, тензор ядер релаксации, эффективная среда

Одним из основных направлений механики гетерогенных сред является исследование динамических свойств двухфазных микронеоднородных сред, состоящих из твердого материала и жидкости. Важной частью этого исследования является определение эффективных динамических характеристик с помощью известных физико-механических параметров фаз исходных сред и их геометрического распределения.

Строго обоснованные эффективные (усредненные) модели для двухфазных сред, состоящих из твердого материала и вязкой жидкости, были построены в [1–6]. В частности, было установлено, что эффективные среды представляют собой однородные вязкоупругие материалы, обладающие как вязкостью, так и памятью. Таким образом, если твердая фаза состоит из упругого материала или вязкоупругого материала Кельвина–Фойгта, то соответствующая эффективная среда приобретает такое свойство, которым не обладают по отдельности ни твердая, ни жидкая фаза исходной среды. Эффект появления памяти при изучении макроскопического поведения суспензии, состоящей из упругих сферических частиц в ньютоновской вязкой среде, был также обнаружен Р. Кристенсеном [7].

Среди множества геометрических моделей двухфазных сред особый интерес представляют слоистые среды. Это связано с тем, что для таких сред часто удается найти явные формулы для расчета их эффективных характеристик по известным толщине и параметрам слоев (см., например, [5, 6, 8, 9]). Стоит также отметить, что наличие таких формул дает возможность решать не только прямые, но и обратные задачи по определению толщины и параметров слоев на основе экспериментальных данных.

В данной статье выводятся формулы для нахождения компонентов эффективного тензора ядер релаксации двухфазной плоскослоистой среды с периодической микроструктурой. В качестве первой фазы рассматривается изотропный вязкоупругий материал, а в качестве второй фазы – вязкая несжимаемая жидкость. Предполагается, что число жидких слоев внутри ячейки периодичности равно $M$ ($M \geqslant 1$), а их суммарная объемная доля равна h ($0 < h < 1$). Для вывода искомых формул решаются вспомогательные стационарные и эволюционные задачи на единичном кубе. Доказывается, в частности, что компоненты эффективного тензора ядер релаксации зависят от h и не зависят от числа слоев и расстояний между ними внутри ячейки периодичности. Точно такой же результат был получен в [9] для двухфазных слоистых вязкоупругих материалов (в этом случае h обозначает долю одной из вязкоупругих фаз).

1. ИСХОДНАЯ И УСРЕДНЕННАЯ МОДЕЛИ СЛОИСТОЙ СРЕДЫ

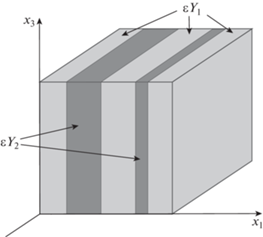
Пусть $\Omega $ – ограниченная область в пространстве ${{\mathbb{R}}^{3}}$ с гладкой границей $\partial \Omega $, заполненная двухфазной средой с периодической структурой. В качестве ячейки периодичности рассмотрим куб ${{Y}_{\varepsilon }} = \varepsilon Y$, где $Y{{ = (0,1)}^{3}}$ – единичный куб, а величина $\varepsilon $ много меньше линейных размеров области $\Omega $. Предполагаем, что ячейка ${{Y}_{\varepsilon }}$ содержит M ($M \geqslant 1$) слоев вязкой несжимаемой жидкости и M + 1 слоев изотропного вязкоупругого материала, параллельных плоскости $O{{x}_{2}}{{x}_{3}}$. Для более ясного представления о внутренней структуре ячейки ${{Y}_{\varepsilon }}$ введем обозначения

${{Y}_{1}} = \bigcup\limits_{m = 0}^M ({{h}_{{2m}}},{{h}_{{2m + 1}}}) \times {{(0,1)}^{2}},\quad {{Y}_{2}} = \bigcup\limits_{m = 1}^M ({{h}_{{2m - 1}}},{{h}_{{2m}}}) \times {{(0,1)}^{2}}$

$\Gamma = \partial {{Y}_{1}} \cap \partial {{Y}_{2}} = \bigcup\limits_{m = 1}^{2M} \{ {{h}_{m}}\} \times {{(0,1)}^{2}}$

где $0 = {{h}_{0}} < {{h}_{1}} < {{h}_{2}} < ... < {{h}_{{2M}}} < {{h}_{{2M + 1}}} = 1$. Будем считать, что множество $\varepsilon {{Y}_{1}}$ представляет собой вязкоупругую часть, а множество $\varepsilon {{Y}_{2}}$ – жидкую часть ячейки ${{Y}_{\varepsilon }}$ (рис. 1). Объединение всех вязкоупругих и жидких слоев области $\Omega $ обозначим соответственно через ${{\Omega }_{{1\varepsilon }}}$ и ${{\Omega }_{{2\varepsilon }}}$, а суммарную объемную долю жидкости внутри ${{Y}_{\varepsilon }}$ – через h:

$h = \frac{{{\text{|}}\varepsilon {{Y}_{2}}{\text{|}}}}{{{\text{|}}{{Y}_{\varepsilon }}{\text{|}}}} = \frac{{{\text{|}}{{Y}_{2}}{\text{|}}}}{{{\text{|}}Y{\text{|}}}} = \sum\limits_{m = 1}^M ({{h}_{{2m}}} - {{h}_{{2m - 1}}})$

Рис. 1.

Ячейка периодичности ${{Y}_{\varepsilon }}$ при M = 2.

Определяющие соотношения, связывающие компоненты тензоров напряжений и малых деформаций в вязкоупругой фазе ${{\Omega }_{{1\varepsilon }}}$, записываются в виде

(1.1)

$\sigma _{{ij}}^{\varepsilon } = {{\Gamma }_{{ijkh}}}(t) * {{e}_{{kh}}}({{{\mathbf{u}}}^{\varepsilon }})$

В развернутой форме

$\sigma _{{ij}}^{\varepsilon } = {{a}_{{ijkh}}}{{e}_{{kh}}}({{{\mathbf{u}}}^{\varepsilon }}) + {{b}_{{ijkh}}}{{e}_{{kh}}}\left( {\frac{{\partial {{{\mathbf{u}}}^{\varepsilon }}}}{{\partial t}}} \right) - {{d}_{{ijkh}}}(t) * {{e}_{{kh}}}({{{\mathbf{u}}}^{\varepsilon }})$

Здесь ${{{\mathbf{u}}}^{\varepsilon }}(x,t)$ – вектор перемещений; ${{e}_{{kh}}}({{{\mathbf{u}}}^{\varepsilon }}) = e_{{kh}}^{x}({{{\mathbf{u}}}^{\varepsilon }}) = (\partial u_{k}^{\varepsilon }{\text{/}}\partial {{x}_{h}} + \partial u_{h}^{\varepsilon }{\text{/}}\partial {{x}_{k}}){\text{/}}2$ – компоненты тензора малых деформаций; $\sigma _{{ij}}^{\varepsilon }$ – компоненты тензора напряжений; символ $ * $ – операция свертки по переменной t; $\Gamma (t)$ – тензор ядер релаксации: $\Gamma (t) = \delta (t)a + \delta {\kern 1pt} '(t)b - d(t)$; $\delta (t)$ – дельта-функция Дирака; a, b и $d(t)$ – тензоры модулей упругости, коэффициентов вязкости и регулярных частей ядер релаксации соответственно. Отметим, что в (1.1), как везде ниже, предполагается суммирование по повторяющимся индексам, а индексы $i,\;j,\;k,\;h$ принимают значения от 1 до 3.

Компоненты тензоров a, b и $d(t)$ заданы в виде

${{a}_{{ijkh}}} = \lambda {{\delta }_{{ij}}}{{\delta }_{{kh}}} + \mu ({{\delta }_{{ik}}}{{\delta }_{{jh}}} + {{\delta }_{{ih}}}{{\delta }_{{jk}}})$

${{b}_{{ijkh}}} = \zeta {{\delta }_{{ij}}}{{\delta }_{{kh}}} + {{\eta }_{1}}({{\delta }_{{ik}}}{{\delta }_{{jh}}} + {{\delta }_{{ih}}}{{\delta }_{{jk}}})$

${{d}_{{ijkh}}}(t) = \left( {{{G}_{1}}(t) - \frac{1}{3}G(t)} \right){{\delta }_{{ij}}}{{\delta }_{{kh}}} + \frac{1}{2}G(t)({{\delta }_{{ik}}}{{\delta }_{{jh}}} + {{\delta }_{{ih}}}{{\delta }_{{jk}}})$

где $\lambda $ и $\mu $ – параметры Ламе; $\zeta $ и ${{\eta }_{1}}$ – коэффициенты вязкости; ${{\delta }_{{ij}}}$ – символ Кронекера; $G(t)$ и ${{G}_{1}}(t)$ – регулярные части ядер сдвиговой и объемной релаксации [10]. Кроме того, предполагается, что

${{G}_{1}}(t) = {{k}_{1}}G(t),\quad G(t) = \sum\limits_{n = 1}^N {{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}},\quad \sum\limits_{n = 1}^N \frac{{{{{v}}_{n}}}}{{{{\gamma }_{n}}}} \leqslant K$

где ${{k}_{1}} \in {{\mathbb{R}}^{ + }} \cup \{ 0\} $; ${{{v}}_{n}}$, ${{\gamma }_{n}} \in {{\mathbb{R}}^{ + }}$ ($n = 1,...,N)$; ${{\gamma }_{i}} < {{\gamma }_{j}}$ при $i < j$; $K = 2\mu $ при ${{k}_{1}} = 0$ и K = min{2μ, $(\lambda + 2\mu {\text{/}}3){\text{/}}{{k}_{1}}\} $ при ${{k}_{1}} > 0$ [11].

Определяющие соотношения в жидкой фазе ${{\Omega }_{{2\varepsilon }}}$ записываются в виде

$\sigma _{{ij}}^{\varepsilon } = - {{\delta }_{{ij}}}{{p}^{\varepsilon }} + 2{{\eta }_{2}}{{e}_{{ij}}}\left( {\frac{{\partial {{{\mathbf{u}}}^{\varepsilon }}}}{{\partial t}}} \right)$

где ${{p}^{\varepsilon }}(x,t)$ – давление, а ${{\eta }_{2}}$ – динамический коэффициент вязкости жидкости.

Математическая модель, описывающая колебания двухфазной среды в области $\Omega $, имеет вид

(1.2)

$\begin{array}{*{20}{c}} {{{\rho }_{s}}\frac{{{{\partial }^{2}}u_{i}^{\varepsilon }}}{{\partial {{t}^{2}}}} = \frac{{\partial \sigma _{{ij}}^{\varepsilon }}}{{\partial {{x}_{j}}}} + {{f}_{i}}(x,t),\quad x \in {{\Omega }_{{s\varepsilon }}},\quad s = 1,2} \\ {{\text{div}}{\kern 1pt} \frac{{\partial {{{\mathbf{u}}}^{\varepsilon }}}}{{\partial t}} = 0,\quad x \in {{\Omega }_{{2\varepsilon }}},\quad [{{{\mathbf{u}}}^{\varepsilon }}]{\kern 1pt} {{{\text{|}}}_{{{{S}_{\varepsilon }}}}} = 0,\quad [{{\sigma }_{{i1}}}]{\kern 1pt} {{{\text{|}}}_{{{{S}_{\varepsilon }}}}} = 0} \\ {{{{\mathbf{u}}}^{\varepsilon }}(x,t){{{\text{|}}}_{{\partial \Omega }}} = 0,\quad {{{\mathbf{u}}}^{\varepsilon }}(x,0) = \frac{{\partial {{{\mathbf{u}}}^{\varepsilon }}}}{{\partial t}}(x,0) = 0} \end{array}$

где ${{\rho }_{s}} = {\text{const}} > 0$ – плотность среды в ${{\Omega }_{{s\varepsilon }}}$, ${{f}_{i}}(x,t)$ – компоненты вектора объемной силы, $[g]{{{\text{|}}}_{{{{S}_{\varepsilon }}}}}$ – скачок функции g при переходе через границы слоев ${{S}_{\varepsilon }} = \partial {{\Omega }_{{1\varepsilon }}} \cap \partial {{\Omega }_{{2\varepsilon }}}$.

Используя результаты [4], можно выписать усредненную модель, соответствующую исходной модели (1.2) и построенную при $\varepsilon \to 0$. Она имеет вид

(1.3)

$\begin{gathered} \rho \frac{{{{\partial }^{2}}{{u}_{i}}}}{{\partial {{t}^{2}}}} = \frac{{\partial {{\sigma }_{{ij}}}}}{{\partial {{x}_{j}}}} + {{f}_{i}}(x,t),\quad x \in \Omega \\ {{{\mathbf{u}}}^{\varepsilon }}(x,0) = \frac{{\partial {{{\mathbf{u}}}^{\varepsilon }}}}{{\partial t}}(x,0) = 0 \\ \end{gathered} $

Эта модель описывает колебания однородного вязкоупругого материала с постоянной плотностью $\rho = {{\rho }_{1}}(1 - h) + {{\rho }_{2}}h$ и определяющими соотношениями:

${{\sigma }_{{ij}}} = \Gamma _{{ijkh}}^{0}(t) * {{e}_{{kh}}}({\mathbf{u}}),\quad {{\Gamma }^{0}}(t) = \delta (t)\alpha + \delta {\kern 1pt} '(t)\beta - g(t)$

Здесь $\alpha $ и $\beta $ – постоянные тензоры модулей упругости и коэффициентов вязкости, а $g(t)$ – тензор регулярных частей ядер релаксации эффективной среды. Компоненты этих тензоров находятся по формулам

(1.4)

${{\alpha }_{{ijkh}}} = (1 - h){{a}_{{ijkh}}} + \int\limits_{{{Y}_{1}}} ({{b}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{D}}}^{{kh}}}) + {{a}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{Z}}}^{{kh}}}))dy + \int\limits_{{{Y}_{2}}} (2{{\eta }_{2}}e_{{ij}}^{y}({{{\mathbf{D}}}^{{kh}}}) - {{\delta }_{{ij}}}{{A}^{{kh}}})dy$

(1.5)

${{\beta }_{{ijkh}}} = (1 - h){{b}_{{ijkh}}} + {{\eta }_{2}}h({{\delta }_{{ik}}}{{\delta }_{{jh}}} + {{\delta }_{{ih}}}{{\delta }_{{jk}}}) + \int\limits_{{{Y}_{1}}} {{b}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{Z}}}^{{kh}}})dy + \int\limits_{{{Y}_{2}}} (2{{\eta }_{2}}e_{{ij}}^{y}({{{\mathbf{Z}}}^{{kh}}}) - {{\delta }_{{ij}}}{{B}^{{kh}}})dy$

(1.6)

$\begin{gathered} {{g}_{{ijkh}}}(t) = (1 - h){{d}_{{ijkh}}}(t) + \int\limits_{{{Y}_{1}}} ({{d}_{{ijlm}}}(t)e_{{lm}}^{y}({{{\mathbf{Z}}}^{{kh}}}) + {{d}_{{ijlm}}}(t) * e_{{lm}}^{y}({{{\mathbf{W}}}^{{kh}}}))dy - \\ \, - \int\limits_{{{Y}_{1}}} \left( {{{a}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{W}}}^{{kh}}}) + {{b}_{{ijlm}}}e_{{lm}}^{y}\left( {\frac{{\partial {{{\mathbf{W}}}^{{kh}}}}}{{\partial t}}} \right)} \right)dy - \int\limits_{{{Y}_{2}}} \left( {2{{\eta }_{2}}e_{{ij}}^{y}\left( {\frac{{\partial {{{\mathbf{W}}}^{{kh}}}}}{{\partial t}}} \right) - {{\delta }_{{ij}}}{{S}^{{kh}}}} \right)dy \\ \end{gathered} $

Здесь $\{ {{{\mathbf{Z}}}^{{kh}}}(y),{{B}^{{kh}}}(y)\} $, $\{ {{{\mathbf{D}}}^{{kh}}}(y),{{A}^{{kh}}}(y)\} $, $\{ {{{\mathbf{W}}}^{{kh}}}(y,t),{{S}^{{kh}}}(y,t)\} $ – Y-периодические решения задач:

(1.7)

$\begin{array}{*{20}{c}} {\frac{\partial }{{\partial {{y}_{j}}}}(\sigma _{{ij}}^{{(1)}}({{{\mathbf{Z}}}^{{kh}}},{{B}^{{kh}}})) = 0,\quad y \in Y,\quad {\text{div}}{\kern 1pt} {{{\mathbf{Z}}}^{{kh}}} = - {{\delta }_{{kh}}},\quad y \in {{Y}_{2}}} \\ {\int\limits_Y {{{\mathbf{Z}}}^{{kh}}}dy = 0,\quad [{{{\mathbf{Z}}}^{{kh}}}]{\kern 1pt} {{{\text{|}}}_{\Gamma }} = 0,\quad [\sigma _{{i1}}^{{(1)}}({{{\mathbf{Z}}}^{{kh}}},{{B}^{{kh}}})]{\kern 1pt} {{{\text{|}}}_{\Gamma }} = 0} \end{array}$

(1.8)

$\begin{array}{*{20}{c}} {\frac{\partial }{{\partial {{y}_{j}}}}(\sigma _{{ij}}^{{(2)}}({{{\mathbf{D}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{A}^{{kh}}})) = 0,\quad y \in Y,\quad {\text{div}}{\kern 1pt} {{{\mathbf{D}}}^{{kh}}} = 0,\quad y \in {{Y}_{2}}} \\ {\int\limits_Y {{{\mathbf{D}}}^{{kh}}}dy = 0,\quad [{{{\mathbf{D}}}^{{kh}}}]{\kern 1pt} {{{\text{|}}}_{\Gamma }} = 0,\quad [\sigma _{{i1}}^{{(2)}}({{{\mathbf{D}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{A}^{{kh}}})]{\kern 1pt} {{{\text{|}}}_{\Gamma }} = 0} \end{array}$

(1.9)

$\begin{array}{*{20}{c}} {\frac{\partial }{{\partial {{y}_{j}}}}(\sigma _{{ij}}^{{(3)}}({{{\mathbf{W}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{S}^{{kh}}})) = 0,\quad y \in Y,\quad {\text{di}}{{{\text{v}}}_{y}}{{{\mathbf{W}}}^{{kh}}} = 0,\quad y \in {{Y}_{2}}} \\ {\int\limits_Y {{{\mathbf{W}}}^{{kh}}}dy = 0,\quad {{{\mathbf{W}}}^{{kh}}}(y,0) = {{{\mathbf{D}}}^{{kh}}}(y),\quad y \in Y} \\ {[{{{\mathbf{W}}}^{{kh}}}]{\kern 1pt} {{{\text{|}}}_{\Gamma }} = 0,\quad [\sigma _{{i1}}^{{(3)}}({{{\mathbf{W}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{S}^{{kh}}})]{\kern 1pt} {{{\text{|}}}_{\Gamma }} = 0} \end{array}$

соответственно. Здесь введены обозначения:

$\sigma _{{ij}}^{{(1)}}({{{\mathbf{Z}}}^{{kh}}},{{B}^{{kh}}}) = {{b}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{Z}}}^{{kh}}}) + {{b}_{{ijkh}}},\quad y \in {{Y}_{1}}$

$\sigma _{{ij}}^{{(1)}}({{{\mathbf{Z}}}^{{kh}}},{{B}^{{kh}}}) = 2{{\eta }_{2}}e_{{ij}}^{y}({{{\mathbf{Z}}}^{{kh}}}) + {{\eta }_{2}}({{\delta }_{{ik}}}{{\delta }_{{jh}}} + {{\delta }_{{ih}}}{{\delta }_{{jk}}}) - {{\delta }_{{ij}}}{{B}^{{kh}}},\quad y \in {{Y}_{2}}$

$\sigma _{{ij}}^{{(2)}}({{{\mathbf{D}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{A}^{{kh}}}) = {{b}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{D}}}^{{kh}}}) + {{a}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{Z}}}^{{kh}}}) + {{a}_{{ijkh}}},\quad y \in {{Y}_{1}}$

$\sigma _{{ij}}^{{(2)}}({{{\mathbf{D}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{A}^{{kh}}}) = 2{{\eta }_{2}}e_{{ij}}^{y}({{{\mathbf{D}}}^{{kh}}}) - {{\delta }_{{ij}}}{{A}^{{kh}}},\quad y \in {{Y}_{2}}$

$\begin{gathered} \sigma _{{ij}}^{{(3)}}({{{\mathbf{W}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{S}^{{kh}}}) = {{a}_{{ijlm}}}e_{{lm}}^{y}({{{\mathbf{W}}}^{{kh}}}) + {{b}_{{ijlm}}}e_{{lm}}^{y}\left( {\frac{{\partial {{{\mathbf{W}}}^{{kh}}}}}{{\partial t}}} \right) - {{d}_{{ijlm}}}(t) * e_{{lm}}^{y}({{{\mathbf{W}}}^{{kh}}}) - \\ \, - {{d}_{{ijlm}}}(t)e_{{lm}}^{y}({{{\mathbf{Z}}}^{{kh}}}) - {{d}_{{ijkh}}}(t),\quad y \in {{Y}_{1}} \\ \end{gathered} $

$\sigma _{{ij}}^{{(3)}}({{{\mathbf{W}}}^{{kh}}},{{{\mathbf{Z}}}^{{kh}}},{{S}^{{kh}}}) = 2{{\eta }_{2}}e_{{ij}}^{y}\left( {\frac{{\partial {{{\mathbf{W}}}^{{kh}}}}}{{\partial t}}} \right) - {{\delta }_{{ij}}}{{S}^{{kh}}},\quad y \in {{Y}_{2}}$

Нетрудно убедиться, что

${{{\mathbf{Z}}}^{{kh}}}(y) = {{{\mathbf{Z}}}^{{hk}}}(y),\quad {{{\mathbf{D}}}^{{kh}}}(y) = {{{\mathbf{D}}}^{{hk}}}(y),\quad {{{\mathbf{W}}}^{{kh}}}(y,t) = {{{\mathbf{W}}}^{{hk}}}(y,t)$

${{B}^{{kh}}}(y) = {{B}^{{hk}}}(y),\quad {{A}^{{kh}}}(y) = {{A}^{{hk}}}(y),\quad {{S}^{{kh}}}(y,t) = {{S}^{{hk}}}(y,t)$

поэтому для нахождения компонентов эффективного тензора ядер релаксации ${{\Gamma }^{0}}(t)$ достаточно знать решения вспомогательных задач (1.7)–(1.9) при $k \leqslant h$.

2. РЕШЕНИЯ ВСПОМОГАТЕЛЬНЫХ ЗАДАЧ НА ЕДИНИЧНОМ КУБЕ

Будем искать решение задачи (1.7) при $k = h = 1$ в виде

${{{\mathbf{Z}}}^{{11}}}(y) = (z({{y}_{1}}),0,0),\quad {{B}^{{11}}}(y) = {{B}_{1}} = {\text{const}}$

где $z({{y}_{1}})$ – кусочно-линейная функция

$z({{y}_{1}}) = {{A}_{m}}{{y}_{1}} + {{C}_{m}},\quad {{y}_{1}} \in ({{h}_{{m - 1}}},{{h}_{m}}),\quad m = 1,...,2M + 1$

Из (1.7) и условия Y-периодичности решения ${{{\mathbf{Z}}}^{{11}}}(y)$ следует, что функция $z({{y}_{1}})$ и постоянная ${{B}_{1}}$ должны удовлетворять условиям

(2.1)

$z(0) = z(1),\quad \int\limits_0^1 z({{y}_{1}})d{{y}_{1}} = 0,\quad [z]{\kern 1pt} {{{\text{|}}}_{{{{y}_{1}} = {{h}_{m}}}}} = 0,\quad m = 1,...,2M$

(2.2)

${{\left. {\left( {{{b}_{{i111}}} + {{b}_{{i111}}}\frac{{dz}}{{d{{y}_{1}}}}} \right)} \right|}_{{{{h}_{{2n - 1}}} - 0}}} = {{\left. {\left( {2{{\eta }_{2}}\frac{{dz}}{{d{{y}_{1}}}} + 2{{\delta }_{{i1}}}{{\eta }_{2}} - {{\delta }_{{i1}}}{{B}_{1}}} \right)} \right|}_{{{{h}_{{2n - 1}}} + 0}}}$

(2.3)

${{\left. {\left( {{{b}_{{i111}}} + {{b}_{{i111}}}\frac{{dz}}{{d{{y}_{1}}}}} \right)} \right|}_{{{{h}_{{2n}}} + 0}}} = {{\left. {\left( {2{{\eta }_{2}}\frac{{dz}}{{d{{y}_{1}}}} + 2{{\delta }_{{i1}}}{{\eta }_{2}} - {{\delta }_{{i1}}}{{B}_{1}}} \right)} \right|}_{{{{h}_{{2n}}} - 0}}}$

(2.4)

$\frac{{dz}}{{d{{y}_{1}}}} = - 1,\quad {{y}_{1}} \in ({{h}_{{2n - 1}}},{{h}_{{2n}}}),\quad n = 1,...,M$

Из (2.2)–(2.4) сразу находим

(2.5)

$\begin{gathered} {{A}_{1}} = {{A}_{2}} = ... = {{A}_{{2M + 1}}},\quad {{A}_{2}} = {{A}_{4}} = ... = {{A}_{{2M}}} = - 1 \\ {{B}_{1}} = - {{b}_{1}}(1 + {{A}_{1}}),\quad {{b}_{1}} = {{b}_{{1111}}} = \zeta + 2{{\eta }_{1}} \\ \end{gathered} $

Далее, граничные условия в (2.1) приводят к равенствам

${{A}_{m}}{{h}_{m}} + {{C}_{m}} = {{A}_{{m + 1}}}{{h}_{m}} + {{C}_{{m + 1}}},\quad m = 1,...,2M$

которые ввиду (2.5) можно переписать в виде

${{C}_{{2m + 1}}} - {{C}_{{2m}}} + ({{A}_{1}} + 1){{h}_{{2m}}} = 0,\quad m = 1,...,M$

${{C}_{{2m}}} - {{C}_{{2m - 1}}} - ({{A}_{1}} + 1){{h}_{{2m - 1}}} = 0,\quad m = 1,...,M$

Складывая эти равенства при всех $m = 1,...,M$ и учитывая, что в силу условия 1-периодичности функции $z({{y}_{1}})$

(2.6)

${{C}_{1}} = {{A}_{1}} + {{C}_{{2M + 1}}}$

находим

${{A}_{1}} = \frac{h}{{1 - h}},\quad {{B}_{1}} = - \frac{{{{b}_{1}}}}{{1 - h}}$

Таким образом,

${{C}_{m}} = {{C}_{{m + 1}}} + \frac{{{{{( - 1)}}^{m}}{{h}_{m}}}}{{1 - h}},\quad m = 1,...,2M$

Откуда получим

(2.7)

${{C}_{m}} = {{C}_{{2M + 1}}} + \frac{1}{{1 - h}}\sum\limits_{k = m}^{2M} {{( - 1)}^{k}}{{h}_{k}} = {{C}_{1}} - \frac{1}{{1 - h}}\left( {h - \sum\limits_{k = m}^{2M} {{{( - 1)}}^{k}}{{h}_{k}}} \right),\quad m = 1,...,2M$

С другой стороны, из второго условия в (2.1) имеем

(2.8)

$\frac{h}{{1 - h}}\sum\limits_{m = 0}^M (h_{{2m + 1}}^{2} - h_{{2m}}^{2}) - \sum\limits_{m = 1}^M (h_{{2m}}^{2} - h_{{2m - 1}}^{2}) + 2\sum\limits_{m = 1}^{2M + 1} {{C}_{m}}({{h}_{m}} - {{h}_{{m - 1}}}) = 0$

Так как

$\frac{h}{{1 - h}}\sum\limits_{m = 0}^M (h_{{2m + 1}}^{2} - h_{{2m}}^{2}) - \sum\limits_{m = 1}^M (h_{{2m}}^{2} - h_{{2m - 1}}^{2}) = \frac{1}{{1 - h}}\left( {h - \sum\limits_{m = 1}^{2M} {{{( - 1)}}^{m}}h_{m}^{2}} \right)$

$\begin{gathered} \sum\limits_{m = 1}^{2M + 1} {{C}_{m}}({{h}_{m}} - {{h}_{{m - 1}}}) = {{C}_{1}} + \frac{1}{{1 - h}}\left( { - h + \sum\limits_{m = 1}^{2M} ({{h}_{m}} - {{h}_{{m - 1}}})\sum\limits_{k = m}^{2M} {{{( - 1)}}^{k}}{{h}_{k}}} \right) = \\ \, = {{C}_{1}} + \frac{1}{{1 - h}}\left( { - h + \sum\limits_{m = 1}^{2M} {{{( - 1)}}^{m}}h_{m}^{2}} \right) \\ \end{gathered} $

то из (2.6)–(2.8) получаем

${{C}_{1}} = \frac{1}{{2(1 - h)}}\left( {h - \sum\limits_{m = 1}^{2M} {{{( - 1)}}^{m}}h_{m}^{2}} \right)$

${{C}_{m}} = \frac{1}{{2(1 - h)}}\left( { - h - \sum\limits_{m = 1}^{2M} {{{( - 1)}}^{m}}h_{m}^{2} + 2\sum\limits_{k = m}^{2M} {{{( - 1)}}^{k}}{{h}_{k}}} \right)$

${{C}_{{2M + 1}}} = - \frac{1}{{2(1 - h)}}\left( {h + \sum\limits_{m = 1}^{2M} {{{( - 1)}}^{m}}h_{m}^{2}} \right)$

Аналогично находятся решения задач (1.7) при остальных значениях k и h. В окончательном виде при $k \leqslant h$ они имеют вид

${{{\mathbf{Z}}}^{{11}}}(y) = {{{\mathbf{Z}}}^{{22}}}(y) = {{{\mathbf{Z}}}^{{33}}}(y) = (z({{y}_{1}}),0,0),\quad {{{\mathbf{Z}}}^{{23}}}(y) = (0,0,0)$

${{{\mathbf{Z}}}^{{12}}}(y) = (0,{{c}_{1}}z({{y}_{1}}),0),\quad {{{\mathbf{Z}}}^{{13}}}(y) = (0,0,{{c}_{1}}z({{y}_{1}})),\quad {{B}^{{11}}}(y) = - \frac{{{{b}_{1}}}}{{1 - h}}$

${{B}^{{12}}}(y) = {{B}^{{13}}}(y) = {{B}^{{23}}}(y) = 0,\quad {{B}^{{22}}}(y) = {{B}^{{33}}}(y) = - 2{{\eta }_{2}} - \frac{{\zeta + 2{{\eta }_{1}}h}}{{1 - h}}$

${{c}_{1}} = \frac{{(1 - h)({{\eta }_{2}} - {{\eta }_{1}})}}{{{{\eta }_{{12}}}}},\quad {{\eta }_{{12}}} = {{\eta }_{1}}h + {{\eta }_{2}}(1 - h)$

Подставляя найденные решения ${{{\mathbf{Z}}}^{{kh}}}(y)$ в (1.8) и повторяя предыдущие рассуждения, находим решения задач (1.8) при $k \leqslant h$:

${{{\mathbf{D}}}^{{11}}}(y) = {{{\mathbf{D}}}^{{22}}}(y) = {{{\mathbf{D}}}^{{33}}}(y) = {{{\mathbf{D}}}^{{23}}}(y) = (0,0,0),\quad {{{\mathbf{D}}}^{{12}}}(y) = (0,{{c}_{2}}z({{y}_{1}}),0)$

${{{\mathbf{D}}}^{{13}}}(y) = (0,0,{{c}_{2}}z({{y}_{1}})),\quad {{A}^{{11}}}(y) = - \frac{{{{a}_{1}}}}{{1 - h}},\quad {{A}^{{12}}}(y) = {{A}^{{13}}}(y) = {{A}^{{23}}}(y) = 0$

${{A}^{{22}}}(y) = {{A}^{{33}}}(y) = - \frac{{\lambda + 2\mu h}}{{1 - h}},\quad {{a}_{1}} = {{a}_{{1111}}} = \lambda + 2\mu ,\quad {{c}_{2}} = - \frac{{\mu {{\eta }_{2}}(1 - h)}}{{\eta _{{12}}^{2}}}$

Подставляя, в свою очередь, ${{{\mathbf{Z}}}^{{kh}}}(y)$ и ${{{\mathbf{D}}}^{{kh}}}(y)$ в (1.9), нетрудно убедиться, что

${{{\mathbf{W}}}^{{11}}}(y,t) = {{{\mathbf{W}}}^{{22}}}(y,t) = {{{\mathbf{W}}}^{{33}}}(y,t) = {{{\mathbf{W}}}^{{23}}}(y,t) = (0,0,0)$

${{S}^{{11}}}(y,t) = \frac{1}{{1 - h}}\left( {{{k}_{1}} + \frac{2}{3}} \right)\sum\limits_{n = 1}^N {{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}},\quad {{S}^{{23}}}(y,t) = 0$

${{S}^{{22}}}(y,t) = {{S}^{{33}}}(y,t) = \frac{1}{{1 - h}}\left( {{{k}_{1}} + h - \frac{1}{3}} \right)\sum\limits_{n = 1}^N {{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}}$

Нам остается найти решения задач (1.9) при k = 1, $h = 2$ и при k = 1, $h = 3$. Будем искать ${{{\mathbf{W}}}^{{12}}}(y,t)$ и ${{{\mathbf{W}}}^{{13}}}(y,t)$ в виде

${{{\mathbf{W}}}^{{12}}}(y,t) = (0,p(t)z({{y}_{1}}),0),\quad {{{\mathbf{W}}}^{{13}}}(y,t) = (0,0,p(t)z({{y}_{1}})),\quad p(0) = {{c}_{2}}$

Из граничных условий задачи (1.9) следует, что ${{S}^{{12}}}(y,t) = {{S}^{{13}}}(y,t) = 0$, а функция p(t) удовлетворяет интегро-дифференциальному уравнению

(2.9)

${{\eta }_{{12}}}\frac{{dp}}{{dt}} - \frac{h}{2}G(t) * p(t) + \mu hp(t) = \frac{{{{\eta }_{2}}(1 - h)}}{{2{{\eta }_{{12}}}}}G(t)$

Покажем, что решение p(t) этого уравнения, удовлетворяющее начальному условию $p(0) = {{c}_{2}}$, имеет вид

(2.10)

$p(t) = \sum\limits_{k = 1}^{N + 1} {{p}_{k}}{{e}^{{ - {{\xi }_{k}}t}}}$

где ${{\xi }_{1}}$, …, ${{\xi }_{{N + 1}}}$ – корни рационального уравнения, а ${{p}_{1}}$, …, ${{p}_{{N + 1}}}$ – решение линейной системы уравнений. Действительно, подставляя (2.10) в (2.9), получаем

(2.11)

$\begin{gathered} \sum\limits_{k = 1}^{N + 1} {{A}_{k}}{{p}_{k}}{{e}^{{ - {{\xi }_{k}}t}}} + \frac{1}{2}\sum\limits_{n = 1}^N {{B}_{n}}{{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}} = 0 \\ {{A}_{k}} = {{\eta }_{{12}}}{{\xi }_{k}} - \mu h - \frac{h}{2}\sum\limits_{n = 1}^N \frac{{{{{v}}_{n}}}}{{{{\xi }_{k}} - {{\gamma }_{n}}}},\quad {{B}_{n}} = \sum\limits_{k = 1}^{N + 1} \frac{{h{{p}_{k}}}}{{{{\xi }_{k}} - {{\gamma }_{n}}}} + \frac{{{{\eta }_{2}}(1 - h)}}{{{{\eta }_{{12}}}}} \\ \end{gathered} $

Ясно, что равенство (2.11) выполняется только тогда, когда ${{A}_{k}} = 0$ и ${{B}_{n}} = 0$ для всех k = 1, ..., $N + 1$ и $n = 1,...,N$. Отсюда следует, что ${{\xi }_{1}}$, …, ${{\xi }_{{N + 1}}}$ – корни уравнения

(2.12)

${{\eta }_{{12}}}\xi - \mu h = \frac{h}{2}\sum\limits_{n = 1}^N \frac{{{{{v}}_{n}}}}{{\xi - {{\gamma }_{n}}}}$

Величины ${{p}_{1}}$, …, ${{p}_{{N + 1}}}$ – решение системы $N + 1$ линейных уравнений

$\sum\limits_{k = 1}^{N + 1} {{p}_{k}} = - \frac{{\mu {{\eta }_{2}}(1 - h)}}{{\eta _{{12}}^{2}}},\quad \sum\limits_{k = 1}^{N + 1} \frac{{{{p}_{k}}}}{{{{\xi }_{k}} - {{\gamma }_{n}}}} + \frac{{{{\eta }_{2}}(1 - h)}}{{{{\eta }_{{12}}}h}} = 0,\quad n = 1,...,N$

Отметим, что корни уравнения (2.12) – положительны и различны, поэтому без ограничения общности можно считать, что $0 < {{\xi }_{1}} < ... < {{\xi }_{{M + 1}}}$.

3. ЭФФЕКТИВНЫЙ ТЕНЗОР ЯДЕР РЕЛАКСАЦИИ

Перейдем к выводу формул для вычисления компонентов эффективного тензора ${{\Gamma }^{0}}(t)$ с помощью найденных выше решений вспомогательных задач (1.7)–(1.9). Перед этим следует отметить, что компоненты эффективного тензора удовлетворяют классическим условиям симметрии, т.е. $\Gamma _{{ijkh}}^{0}(t) = \Gamma _{{jikh}}^{0}(t) = \Gamma _{{ijhk}}^{0}(t) = \Gamma _{{hkij}}^{0}(t)$. Нетрудно также убедиться, что $\Gamma _{{ijkh}}^{0}(t) = 0$ как только δ_ijδ_kh + + ${{\delta }_{{ik}}}{{\delta }_{{jh}}} + {{\delta }_{{ih}}}{{\delta }_{{jk}}} = 0$. Более того, эффективная среда является трансверсально изотропной, т.е. выполнены соотношения

$\Gamma _{{2222}}^{0}(t) = \Gamma _{{3333}}^{0}(t),\quad \Gamma _{{1122}}^{0}(t) = \Gamma _{{1133}}^{0}(t),\quad \Gamma _{{1212}}^{0}(t) = \Gamma _{{1313}}^{0}(t)$

$\Gamma _{{2222}}^{0}(t) - \Gamma _{{2233}}^{0}(t) = 2\Gamma _{{2323}}^{0}(t)$

Таким образом, нам достаточно вывести формулы для компонентов тензоров α, β и $g(t)$ с индексами {1111}, {2222}, {1122}, {1212}, {2323}.

Полагая $i = j = k = h = 1$ и подставляя решения задач (1.7)–(1.9) в формулы (1.4)–(1.6), последовательно находим

${{\alpha }_{{1111}}} = {{a}_{1}}(1 - h) + \frac{{{{a}_{1}}h}}{{1 - h}}\sum\limits_{m = 0}^M \int\limits_{{{h}_{{2m}}}}^{{{h}_{{2m + 1}}}} d{{y}_{1}} + \frac{{{{a}_{1}}}}{{1 - h}}\sum\limits_{m = 1}^M \int\limits_{{{h}_{{2m - 1}}}}^{{{h}_{{2m}}}} d{{y}_{1}} = \frac{{\lambda + 2\mu }}{{1 - h}}$

${{\beta }_{{1111}}} = {{b}_{1}}(1 - h) + 2{{\eta }_{2}}h + \frac{{{{b}_{1}}h}}{{1 - h}}\sum\limits_{m = 0}^M \int\limits_{{{h}_{{2m}}}}^{{{h}_{{2m + 1}}}} d{{y}_{1}} + \left( { - 2{{\eta }_{2}} + \frac{{{{b}_{1}}}}{{1 - h}}} \right)\sum\limits_{m = 1}^M \int\limits_{{{h}_{{2m - 1}}}}^{{{h}_{{2m}}}} d{{y}_{1}} = \frac{{\zeta + 2{{\eta }_{1}}}}{{1 - h}}$

${{g}_{{1111}}}(t) = (1 - h){{d}_{{1111}}}(t) + \frac{{h{{d}_{{1111}}}(t)}}{{1 - h}}\sum\limits_{m = 0}^M \int\limits_{{{h}_{{2m}}}}^{{{h}_{{2m + 1}}}} d{{y}_{1}} + \frac{{G(t)}}{{1 - h}}\left( {{{k}_{1}} + \frac{2}{3}} \right)\sum\limits_{m = 1}^M \int\limits_{{{h}_{{2m - 1}}}}^{{{h}_{{2m}}}} d{{y}_{1}} = \frac{1}{{1 - h}}\left( {{{k}_{1}} + \frac{2}{3}} \right)\sum\limits_{n = 1}^N {{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}}$

Аналогично выводятся формулы для остальных искомых компонентов тензоров $\alpha $, $\beta $ и $g(t)$. В окончательном виде они записываются в виде

${{\alpha }_{{2222}}} = \frac{{\lambda + 2\mu (1 - 2h + 2{{h}^{2}})}}{{1 - h}},\quad {{\alpha }_{{1212}}} = \frac{{\mu \eta _{2}^{2}(1 - h)}}{{\eta _{{12}}^{2}}}$

${{\alpha }_{{1122}}} = \frac{{\lambda + 2\mu h}}{{1 - h}},\quad {{\alpha }_{{2323}}} = (1 - h)\mu ,\quad {{\beta }_{{1212}}} = \frac{{{{\eta }_{1}}{{\eta }_{2}}}}{{{{\eta }_{{12}}}}},\quad {{\beta }_{{1122}}} = \frac{{\zeta + 2{{\eta }_{1}}h}}{{1 - h}}$

${{\beta }_{{2222}}} = 4{{\eta }_{2}}h + \frac{{\zeta + 2{{\eta }_{1}}(1 - 2h + 2{{h}^{2}})}}{{1 - h}},\quad {{\beta }_{{2323}}} = {{\eta }_{1}}(1 - h) + {{\eta }_{2}}h$

${{g}_{{2222}}}(t) = \frac{1}{{1 - h}}\left( {{{k}_{1}} - 2h(1 - h) + \frac{2}{3}} \right)\sum\limits_{n = 1}^N {{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}}$

${{g}_{{1122}}}(t) = \frac{1}{{1 - h}}\left( {{{k}_{1}} + h - \frac{1}{3}} \right)\sum\limits_{n = 1}^N {{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}},\quad {{g}_{{1212}}}(t) = - {{\eta }_{2}}\sum\limits_{k = 1}^{N + 1} {{\xi }_{k}}{{p}_{k}}{{e}^{{ - {{\xi }_{k}}t}}}$

${{g}_{{2323}}}(t) = \frac{{1 - h}}{2}\sum\limits_{n = 1}^N {{{v}}_{n}}{{e}^{{ - {{\gamma }_{n}}t}}}$

Анализ полученных формул показывает, что компоненты тензора ${{\Gamma }^{0}}(t)$ не зависят от числа вязкоупругих и жидких слоев внутри ячейки периодичности ${{Y}_{\varepsilon }}$. Для их вычисления требуется знать лишь объемную долю $h$ жидкости внутри ${{Y}_{\varepsilon }}$, тензор ядер релаксации $\Gamma (t)$ вязкоупругих слоев и динамическую вязкость ${{\eta }_{2}}$ жидкости. С другой стороны, так как $\rho = {{\rho }_{1}}(1 - h) + {{\rho }_{2}}h$, то эффективная плотность $\rho $ также не зависит от числа M. Это означает, что коэффициенты и ядра сверток эффективных уравнений акустики (3) не зависят от общего числа слоев внутри ${{Y}_{\varepsilon }}$ и расстояний между ними. С этой точки зрения среда, для которой ячейка ${{Y}_{\varepsilon }}$ состоит из двух или более жидких слоев с их суммарной толщиной $\varepsilon h$, эквивалентна среде (с такими же характеристиками фаз), для которой ${{Y}_{\varepsilon }}$ состоит из одного жидкого слоя толщины $\varepsilon h$.

Используя результаты [3–5] и следуя приведенной выше схеме решения вспомогательных задач, аналогичным образом можно вывести явные формулы для расчета компонентов тензора ${{\Gamma }^{0}}(t)$ в случаях, когда: 1) $b \ne 0$, $d(t) = 0$; 2) $b = 0$, $d(t) \ne 0$; 3) $b = 0$, $d(t) = 0$. Заметим, что первый случай соответствует среде, состоящей из жидкости и вязкоупругого материала Кельвина–Фойгта, а третий случай – среде, состоящей из жидкости и упругого материала.

Во всех трех случаях компоненты тензоров $\alpha $ и $\beta $ вычисляются по тем же формулам, что и выше. Отметим, что если $b = 0$, то $\zeta = {{\eta }_{1}} = 0$ и, следовательно, ${{\beta }_{{1111}}} = {{\beta }_{{1122}}} = {{\beta }_{{1212}}} = 0$, ${{\beta }_{{2222}}} = 4{{\eta }_{2}}h$, ${{\beta }_{{2323}}} = {{\eta }_{2}}h$.

Во втором случае компоненты тензора $g(t)$ также вычисляются по формулам, выведенным нами для общего случая $b \ne 0$, $d(t) \ne 0$. В первом и третьем случаях все компоненты тензора $g(t)$ равны нулю, кроме следующих:

${{g}_{{1m1m}}}(t) = {{g}_{{m11m}}}(t) = {{g}_{{1mm1}}}(t) = \frac{{h(1 - h){{\mu }^{2}}\eta _{2}^{2}}}{{\eta _{{12}}^{3}}}\exp \left( { - \frac{{\mu ht}}{{{{\eta }_{{12}}}}}} \right),\quad m = 2,3$

Отметим, что утверждение о независимости эффективных уравнений акустики от числа слоев исходной среды внутри ячейки периодичности остается верным для всех трех перечисленных выше случаев твердой фазы.

ЗАКЛЮЧЕНИЕ

Рассмотрена математическая модель колебаний многослойной среды, состоящей из чередующихся слоев изотропного вязкоупругого материала и вязкой несжимаемой жидкости. С помощью соответствующей усредненной модели показано, что эффективный тензор ядер релаксации слоистой среды имеет три аддитивные составляющие: одну регулярную $g(t)$ и две сингулярные $\delta (t)\alpha $ и $\delta {\kern 1pt} '(t)\beta $, где $\alpha $, $\beta $ и $g(t)$ – эффективные тензоры модулей упругости, коэффициентов вязкости и регулярных частей ядер релаксации соответственно. Найдены периодические решения вспомогательных задач на единичном кубе и с их помощью выведены явные формулы для вычисления компонентов тензоров $\alpha $, $\beta $, $g(t)$. Показано, что для применения этих формул требуется знать лишь объемную долю жидкости внутри ячейки периодичности, тензор ядер релаксации вязкоупругих слоев и динамическую вязкость жидкости. Полученные формулы позволяют решать не только прямые, но и обратные задачи, к числу которых относится, например, задача по определению доли жидкости внутри взятого образца слоистой среды при известных параметрах ее фаз и по имеющимся экспериментальным данным.

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А20-120011690138-6).

Список литературы

Санчес-Паленсия Э. Неоднородные среды и теория колебаний. М.: Мир, 1984. 472 с.
Sanchez-Hubert J. Asymptotic study of the macroscopic behavior of a solid-liquid mixture // Math. Methods Appl. Sci. 1980. № 2. P. 1–18.
Gilbert R.P., Mikelić A. Homogenizing the acoustic properties of the seabed: Part I // Nonlinear Analysis. 2000. V. 40. № 1. P. 185–212.
Шамаев А.С., Шумилова В.В. Усреднение уравнений акустики для пористого вязкоупругого материала с долговременной памятью, заполненного вязкой жидкостью // Диф. уравнения. 2012. Т. 48. № 8. С. 1174–1186.
Шамаев А.С., Шумилова В.В. Спектр одномерных колебаний в комбинированной слоистой среде, состоящей из вязкоупругого материала и вязкой сжимаемой жидкости // Изв. РАН. МЖГ. 2013. № 1. С. 17–25.
Shumilova V.V. Spectrum of one-dimensional vibrations of a layered medium consisting of a Kelvin–Voigt material and a viscous incompressible fluid // Журн. СФУ. Сер. Матем. и физ. 2013. Т. 6. № 3. С. 349–356.
Кристенсен Р. Введение в механику композитов. М.: Мир, 1982. 336 с.
Победря Б.Е. Механика композиционных материалов. М.: МГУ, 1984. 336 с.
Shumilova V.V. Homogenization of the system of acoustic equations for layered viscoelastic media // J. Math. Sci. 2022. V. 261. № 3. P. 488–501.
Ильюшин А.А., Победря Б.Е. Основы математической теории термовязкоупругости. М.: Наука, 1970. 280 с.
Шамаев А.С., Шумилова В.В. О спектре одномерных колебаний композита, состоящего из слоев упругого и вязкоупругого материалов // Сиб. журн. индустр. матем. 2012. Т. 15. № 4. С. 124–134.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал