1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2023

Известия РАН. Механика жидкости и газа, 2023, № 1, стр. 31-40

ВЗАИМОДЕЙСТВИЕ СВЕРХЗВУКОВОГО ЗВЕЗДНОГО ВЕТРА С НАБЕГАЮЩИМ ПОТОКОМ МЕЖЗВЕЗДНОЙ СРЕДЫ: ВЛИЯНИЕ АЗИМУТАЛЬНОГО МАГНИТНОГО ПОЛЯ ЗВЕЗДЫ

С. Д. Корольков a, b, *, В. В. Измоденов a, b, **

a МГУ им. М.В. Ломоносова, Московский центр фундаментальной и прикладной математики
Москва, Россия

b Институт космических исследований РАН
Москва, Россия

* E-mail: korolkov.msu@mail.ru
** E-mail: izmod@iki.rssi.ru

Поступила в редакцию 09.10.2022
После доработки 11.10.2022
Принята к публикации 11.10.2022

Полный текст (PDF)

Аннотация

Рассматривается задача о взаимодействии гиперзвукового звездного ветра с окружающей межзвездной средой. Среды считаются полностью ионизованными и описываются в рамках идеальной магнитогидродинамики. Новизна работы заключается в учете магнитного поля звезды. При определенных параметрах течения магнитное поле качественным образом изменяет форму астропаузы – тангенциального разрыва, отделяющего звездный ветер от межзвездной среды. Вместо классической параболоидальной формы астропауза приобретает трубчатую (или цилиндрическую) форму. Показано, что трубчатая форма имеет место для медленно движущихся звезд или, в системе координат звезды, для набегающих потоков с числом Маха (M∞) меньше критического. При достижении критического числа Маха ($M_{\infty }^{*}$) потоком происходит бифуркация режима течения и форма астропаузы изменяется с трубчатой на классическую. Для звезд с сильным магнитным полем бифуркация происходит при бóльших числах Маха, чем для звезд со слабым магнитным полем. Также показано, что при M∞ = 1 происходит еще одна качественная перестройка течения, при которой форма астропаузы не меняется, но образуются головная ударная волна и диск Маха.

Ключевые слова: звездный ветер, межзвездная среда, астропауза

Звездный ветер – поток плазмы, истекающей из верхней части атмосферы звезды в межзвездную среду. Если принять во внимание движение самой звезды, то в связанной с ней системе координат межзвездная среда набегает на звезду и взаимодействует со звездным ветром. При этом возникает задача о взаимодействии двух потоков. Первая модель взаимодействия солнечного ветра с межзвездной средой в предположении потенциального и несжимаемого течения (${{M}_{\infty }} \ll 1$) была предложена в работе [1]. В этом решении найдена форма гелиопаузы (астропаузы в случае других звезд) – тангенциального разрыва, отделяющего солнечный ветер от межзвездной среды. В частности, было показано, что гелиопауза имеет форму параболоида, т.е. открыта в хвостовой области (см. рис. 1в). Модель обтекания солнечного ветра сверхзвуковым потоком была предложена в работе [2], солнечный ветер также предполагался сверхзвуковым. В этом случае (см. рис. 1г) головная область взаимодействия состоит из 1) внутренней ударной волны (TS), на которой испытывает торможение сверхзвуковой звездный ветер, 2) астропаузы (HP) и 3) головной ударной волны (BS), на которой замедляется сверхзвуковой набегающий поток. Позже структура такого течения была изучена численно (см., например, [3, 4]).

Рис. 1.

Схематичное представление картины течения в случаях: неподвижной межзвездной среды (а), слабого набегающего потока при ${{M}_{\infty }} < M_{\infty }^{*}$ (б), сильного дозвукового набегающего потока ${{M}_{\infty }} > M_{\infty }^{*}$ (в) и сверхзвукового набегающего потока ${{M}_{\infty }} > 1$ (г).

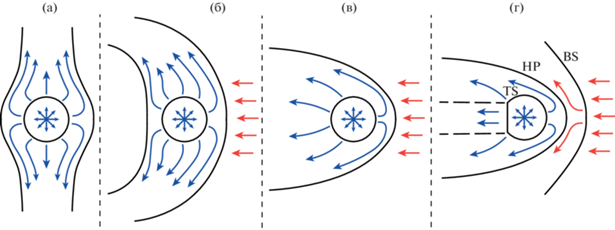
Рис. 2.

Изолинии плотности и линии тока приведены по результатам расчетов для различных значений числа Маха ${{M}_{\infty }}$ в двух плоскостях (экваториальной $XOY$ и полярной $XOZ$), ${{M}_{A}} = 12,\;\chi = 2$, оси в безразмерных координатах. Номер расчета–число Маха: (1) – 0.1, (2) – 0.25, (3) – 0.3, (4) – 0.35, (5) – 0.5, (6) – 0.9, (7) – 1.6, (8) – 2.2.

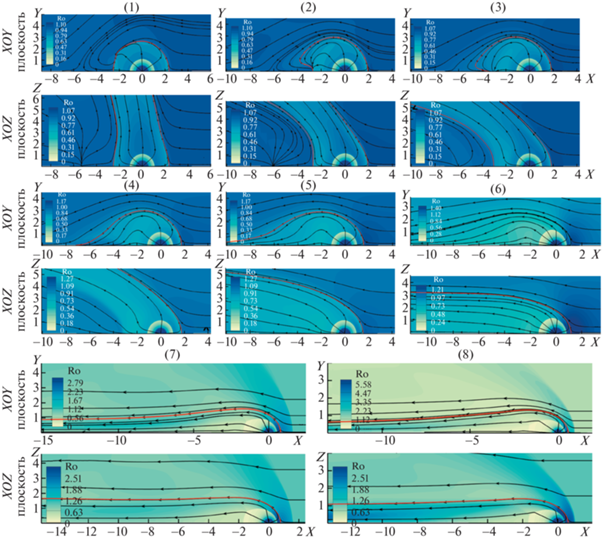
Рис. 3.

Распределение модуля скорости (в логарифмическом масштабе) вдоль оси x для расчетов с различными значениями числа Маха ${{M}_{\infty }}$ набегающего потока. ${{M}_{A}} = 12,\;\chi = 2$.

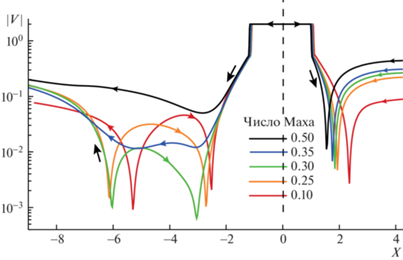
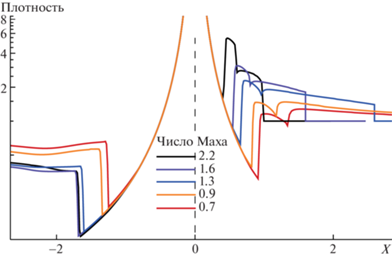
Рис. 4.

Распределение плотности вдоль оси X для различных значений ${{M}_{\infty }}$ набегающего потока в логарифмическом масштабе, ${{M}_{A}} = 12,\;\chi = 2$.

В настоящее время модели взаимодействия солнечного ветра с межзвездной средой достаточно сложны и учитывают большой набор физических эффектов. Однако основное влияние на картину течения оказывают три из них: 1) проникновение нейтральных атомов водорода в гелиосферу с последующей резонансной перезарядкой, 2) межзвездное магнитное поле и 3) магнитное поле звезды.

Первый эффект был открыт в 70-х годах прошлого столетия и связан с экспериментами по рассеянному Лайман-альфа излучению в околосолнечном пространстве, подтверждающими проникновение атомов водорода (H) из локальной межзвездной среды в гиперзвуковой солнечный ветер (см., например, [5, 6]). Как выяснилось в дальнейшем, влияние нейтральных атомов H заключается в достаточно эффективном процессе резонансной перезарядки (см. [7]), при котором происходит обмен электроном между атомом водорода и протоном плазмы. Перезарядка сопровождается обменом импульса и энергии между нейтральной и заряженной компонентой. Численное моделирование (см. газодинамические модели: [3, 8–10] и кинетико-газодинамические модели: [4, 11, 12]) подтвердило существенное влияние перезарядки на глобальную картину течения. Однако такой процесс изменяет лишь положение поверхностей разрывов, не изменяя их форму. Качественно картина течения остается прежней.

Влияние межзвездного магнитного поля на гелиопаузу впервые было изучено в работе [13] в осесимметричном случае (${{{\mathbf{V}}}_{\infty }}\parallel {{{\mathbf{B}}}_{\infty }}$). Позже трехмерные магнитогидродинамические расчеты показали (см. [14–16]), что межзвездное магнитное поле, направленное под углом по отношению к направлению движения межзвездной среды, приводит к асимметрии гелиосферы. При этом топологическая форма гелиопаузы осталась прежней.

Вопрос о влиянии магнитного поля Солнца на форму гелиопаузы в настоящий момент остается открытым. Из-за наличия азимутальной компоненты у магнитного поля звезды, течение звездного ветра может распадаться на два потока, направленных к полюсам звезды (см. работы [17] и рис. 1а,б). Такое поведение было подтверждено расчетами в работах ([18, 19]), хотя и противоречит результатам, в работах [20–23].

Качественно влияние звездного магнитного поля на течение может быть проиллюстрировано с помощью оценки величины магнитной силы ${{{\mathbf{F}}}_{{mag}}} = \left( {[\nabla \times {\mathbf{B}}] \times {\mathbf{B}}} \right){\text{/}}(4\pi )$ в области за внутренней ударной волной (TS) на примере задачи истечения гиперзвукового звездного ветра в покоящуюся среду с противодавлением. В этом случае течение состоит из сверхзвуковой и дозвуковой областей, которые отделяются друг от друга ударной волной. Расстояние до ударной волны определяется формулой: ${{R}_{{TS}}} \sim \sqrt {{{{\dot {M}}}_{ \odot }}{{V}_{0}}{\text{/}}(4\pi {{p}_{\infty }})} $, где ${{\dot {M}}_{ \odot }}$ – скорость потери массы звезды, V0 – терминальная скорость сверхзвукового звездного ветра, ${{p}_{\infty }}$ – давление межзвездного газа. В сверхзвуковой области течения (при $R < {{R}_{{TS}}}$) можно написать точное решение для гиперзвукового источника: $V \sim {{V}_{0}}$, $\rho \sim 1{\text{/}}{{R}^{2}}$ и $p \sim 1{\text{/}}{{R}^{{2\gamma }}}$, где R – расстояние до звезды. В дозвуковой области течения ($R > {{R}_{{TS}}}$) газ можно приближенно рассматривать как несжимаемый и получить следующее решение: $V \sim 1{\text{/}}{{R}^{2}}$, $\rho \sim {{\rho }_{\infty }}$ и $p \sim {{p}_{\infty }}$. Далее в предположении, что магнитное поле не влияет на течение плазмы, можно решить уравнение вмороженности магнитного поля $\nabla \times [{\mathbf{V}} \times {\mathbf{B}}] = 0$ и, предполагая параллельность магнитного поля вектору скорости звездного ветра на поверхности звезды, получить следующее решение для магнитных полей в сверхзвуковой области:

(1)
$R < {{R}_{{TS}}}:{{B}_{R}} \sim 1{\text{/}}{{R}^{2}},\quad {{B}_{\phi }} \sim (1{\text{/}}R)\sin \theta ,\quad {{B}_{\theta }} = 0$

Приведенное выше решение для $R < {{R}_{{TS}}}$ было получено в работе [24]. Это решение было продолжено за ударную волну:

(2)
$R > {{R}_{{TS}}}:\quad {{B}_{R}} \sim 1{\text{/}}{{R}^{2}},\quad {{B}_{\phi }} \sim R\sin \theta ,\quad {{B}_{\theta }} = 0$

Здесь $\theta $ – полярный угол, отсчитываемый от оси вращения звезды (оси z), ϕ – азимутальный угол.

Из продемонстрированного решения видно, что за ударной волной плазменное $\beta = 8\pi p{\text{/}}{{B}^{2}}$ уменьшается с расстоянием, что в итоге приведет к сильному влиянию магнитных полей на течение плазмы. Магнитная сила ${{{\mathbf{F}}}_{{mag}}}$ имеет главную составляющую в $r$ – направлении (в цилиндрической ($z$, $r$, $\phi $) системе координат, где ось $z$ – ось вращения звезды): ${{F}_{{mag,r}}} \sim - 2r$ для магнитного поля (2), поэтому магнитное поле отклоняет звездный ветер от исходного радиального направления к оси $z$. Таким образом, за ударной волной формируются две струи, направленные по оси вращения звезды, что приводит к трубчатой форме астропаузы. Задача истечения намагниченного звездного ветра в покоящуюся межзвездную среду подробно исследована в работах [25, 26], схематическая картина такого течения представлена на рис. 1а.

В случае наличия набегающего потока межзвездной среды цилиндрообразный тангенциальный разрыв (астропауза) будет изгибаться по направлению набегающего потока (см. рис. 1б). Исследование такого течения представляет как теоретический, так и практический интерес. Для различных звезд скорость их движения относительно межзвездной среды, а также величины индукции магнитного поля могут принимать довольно широкий диапазон значений. Так как число наблюдаемых астросфер в настоящее время неуклонно растет, то можно ожидать, что астросферы с трубчатой структурой тангенциального разрыва будут открыты в ближайшем будущем.

Структура работы следующая: в разд. 1 изложены постановка задачи в безразмерном виде, граничные условия и численный метод решения, в разд. 2 представлены и обсуждаются основные результаты и, наконец, в разд. 2 подводятся итоги проделанной работы и задается направление будущих исследований.

1. ПОСТАНОВКА ЗАДАЧИ

Целью настоящей работы является исследование влияния азимутального магнитного поля звезды на глобальную структуру астросферы в приближении идеальной магнитной гидродинамики. Для обособленного изучения влияния магнитного поля звезды здесь пренебрегается влиянием нейтральной компоненты и магнитного поля в межзвездной среде, а также другими физическими процессами в астросферах. Звезда считается сферически-симметричным гиперзвуковым точечным источником с заданными массовым расходом ${{\dot {M}}_{ \odot }}$, терминальной скоростью ${{V}_{0}}$ и напряженностью магнитного поля ${{B}_{E}}$ на 1 а.е. Звездный ветер и межзвездная среда считаются полностью ионизованной водородной плазмой с уравнением состояния $p = 2{{n}_{p}}{{k}_{B}}T$, где ${{n}_{p}}$ – концентрация протонов, ${{k}_{B}}$ – постоянная Больцмана, T – температура плазмы. Отношение удельных теплоемкостей $\gamma $ принимается постоянным и равным 5/3. Азимутальная составляющая магнитного поля звезды на внутренней границе считается решением спирали Паркера:

(3)
${{B}_{\varphi }} = {{B}_{E}}\left( {\frac{{{{R}_{E}}}}{R}} \right){\text{sin}}\theta $

Индексом “E” здесь и далее обозначаются параметры на 1 а.е.

Радиальной составляющей магнитного поля в граничных условиях также пренебрегается (ввиду убывания пропорционально квадрату расстояния). В межзвездной среде считаются заданными все параметры потока: скорость ${{V}_{\infty }}$, плотность ${{\rho }_{\infty }}$ и давление ${{p}_{\infty }}$.

Сформулируем задачу в безразмерном виде. Для этого примем: 1) ${{\rho }_{\infty }}$ за характерную плотность; 2) ${{a}_{\infty }} = \sqrt {\gamma {{p}_{\infty }}{\text{/}}{{\rho }_{\infty }}} $ за характерную скорость; 3) ${{R}_{*}} = \sqrt {{{V}_{0}}{{{\dot {M}}}_{ \odot }}{\text{/}}(4\pi \gamma {{p}_{\infty }})} $ за характерное расстояние, пропорциональное расстоянию до внешней ударной волны, полученному из аналитического стационарного решения задачи о взаимодействии ненамагниченного сферически-симметричного звездного ветра с покоящейся межзвездной средой (см. [1]). Мы не выбрали ${{V}_{\infty }}$ в качестве характерной скорости для возможности рассмотрения предельного случая ${{V}_{\infty }} = 0$.

Таким образом, поставленная задача будет зависеть от 4 безразмерных параметров: 1) газодинамического числа Маха в локальной межзвездной среде (${{M}_{\infty }} = {{V}_{\infty }}{\text{/}}\sqrt {\gamma {{p}_{\infty }}{\text{/}}{{\rho }_{\infty }}} $); 2) альфвеновского числа Маха в звездном ветре (${{M}_{A}} = {{V}_{0}}\sqrt {4\pi {{\rho }_{E}}} {\text{/}}{{B}_{E}}$), фактически задающего напряженность магнитного поля звезды; 3) параметра $\gamma $, который в данной работе считается постоянным и равным 5/3 для одноатомного газа и 4) числа $\chi = {{V}_{0}}{\text{/}}{{a}_{\infty }}$ – отношение терминальной скорости источника к скорости звука набегающего потока.

Запишем стационарную систему уравнений идеальной магнитной гидродинамики, сохраняющую свой вид при указанном обезразмеривании:

(4)
${\text{div}}(\rho V) = 0$
(5)
${\text{div}}\left[ {\rho VV + \left( {p + \frac{{{{B}^{2}}}}{{8\pi }}} \right) \cdot \widehat I - \frac{{BB}}{{4\pi }}} \right] = 0$
(6)
${\text{div}}\left[ {\left( {e + p + \frac{{{{B}^{2}}}}{{8\pi }}} \right)V - \frac{{({\mathbf{V}} \cdot {\mathbf{B}})}}{{4\pi }}{\mathbf{B}}} \right] = 0$
(7)
${\text{div}}({\mathbf{BV}} - {\mathbf{VB}}) = 0,\quad {\text{div}}({\mathbf{B}}) = 0$
(8)
$e = \frac{p}{{(\gamma - 1)}} + \rho \frac{{{{V}^{2}}}}{2} + \frac{{{{B}^{2}}}}{{8\pi }}$

Здесь e – полная энергия единицы объема газа, B – вектор индукции магнитного поля, ab –тензорное произведение двух векторов a и b, I – единичный тензор, ’·’ – скалярное произведение.

Используя систему уравнений (4–7), легко показать, что параметр $\chi $ является несущественным для рассматриваемой стационарной задачи (см. [27]), так как имея решение с конкретным ${{\chi }_{1}}$, можно произвести перенормировку решения в звездном ветре (до HP) и получить новое решение, соответствующее параметру ${{\chi }_{2}}$ следующим образом:

(9)
$\begin{gathered} {{\rho }_{2}}({\mathbf{r}}) = \frac{{\chi _{1}^{2}}}{{\chi _{2}^{2}}}{{\rho }_{1}}({\mathbf{r}}),\quad {{{\mathbf{V}}}_{2}}({\mathbf{r}}) = \frac{{{{\chi }_{2}}}}{{{{\chi }_{1}}}}{{{\mathbf{V}}}_{1}}({\mathbf{r}}) \\ {{p}_{2}}({\mathbf{r}}) = {{p}_{1}}({\mathbf{r}}),\quad {{{\mathbf{B}}}_{2}}({\mathbf{r}}) = {{{\mathbf{B}}}_{1}}({\mathbf{r}}) \\ \end{gathered} $

Функции ${{\rho }_{2}}({\mathbf{r}})$, ${{{\mathbf{V}}}_{2}}({\mathbf{r}})$, ${{p}_{2}}({\mathbf{r}})$, ${{{\mathbf{B}}}_{2}}({\mathbf{r}})$ удовлетворяют: 1) дифференциальным уравнениям (4)–(7); 2) условиям Ренкина–Гюгонио на разрывах; 3) балансу давления и условиям $({\mathbf{V}} \cdot {\mathbf{n}}) = 0$, $({\mathbf{B}} \cdot {\mathbf{n}}) = 0$ на тангенциальном разрыве, где n – нормаль к поверхности разрыва; 4) внутреннему граничному условию ${{V}_{0}} = {{\chi }_{2}}{{a}_{\infty }}$. Следовательно, есть только два безразмерных параметра, определяющих решение задачи (не считая $\gamma $, изменение которого может представлять только теоретический интерес, неприменимый к астрофизическим приложениям).

1.1. Граничные условия

Для завершения постановки задачи осталось сформулировать граничные условия в безразмерном виде. В численных расчетах необходимо ставить внутренние граничные условия на определенном безразмерном расстоянии ${{\hat {R}}_{{in}}}$ от звезды. В проведенных расчетах использовалось ${{\hat {R}}_{{in}}} = 0,07$. В безразмерном виде граничными условиями на ${{\hat {R}}_{{in}}}$ являются:

${{\hat {V}}_{{in}}} = \chi ,\quad {{\hat {\rho }}_{{in}}} = \frac{1}{{{{\chi }^{2}}\hat {R}_{{in}}^{2}}},\quad {{\hat {B}}_{{in}}} = \frac{{\sqrt {4\pi } }}{{{{{\hat {R}}}_{{in}}}{{M}_{A}}}}$

Граничные условия в набегающем потоке следующие:

${{\hat {V}}_{\infty }} = {{M}_{\infty }},\;\;{{\hat {\rho }}_{\infty }} = 1,\;\;{{\hat {p}}_{\infty }} = 1$

Для безразмерных параметров в случае Солнечной системы имеем: ${{M}_{\infty }} = 2$, ${{M}_{A}} = 12.9$, $\chi = 32.2$. Характерное расстояние ${{R}_{*}} = 394.5$ а.е.

1.2. Метод расчета

Решение стационарных уравнений (4)–(7) находится методом установления по времени. Используется метод контрольных объемов с решением задачи о распаде произвольного разрыва на границе (см. [28]) и нахождением потоков массы, импульса и энергии через границу ячейки для применения интегральных законов сохранения. Решение задачи о распаде произвольного разрыва в рамках идеальной магнитной гидродинамики находится приближенно методом “HLLC” (см., например, [29]). Для обеспечения равенства нулю дивергенции магнитного поля (которая может возникать вследствие: 1) неправильных начальных условий для магнитных полей и 2) неточности численного решения МГД-задачи о распаде произвольного разрыва) была использована схема очистки потока от дивергенции, предложенная в работе [30].

Вычисления производились на адаптивной декартовой сетке с возможностью увеличения разрешения в нужных областях течения. Для точного определения положения астропаузы использовался метод конвективного переноса индикатора Q (см., например, [31]): вместе с системой (4)–(7) решается уравнение:

$\frac{{\partial \rho Q}}{{\partial t}} + {\text{div}}(V\rho Q) = 0$
с граничными условиями Q = 1 в источнике и Q = 100 в набегающем потоке. Q – пассивный индикатор, который в области течения, занятой солнечным ветром, будет равен 1, а занятой межзвездным газом – равен 100. Таким образом, астропауза определяется как поверхность, на которой $Q \approx 60$. Стоит отметить, что построение линий тока в течении также является дополнительным возможным способом определения положения астропаузы.

На выходных границах используются мягкие граничные условия для всех параметров потока (равенство нулю производных), а на входных границах значения зафиксированы в соответствии с граничными условиями. Для того чтобы избежать влияния на течение отраженных от выходных границ характеристик, область расчета увеличивается и вблизи границ используются крупные ячейки, чтобы численная диссипация рассеивала возмущения. Результаты протестированы на сетках с различным разрешением.

Расчеты проводились с использованием графического процессора: GeForce GTX 1080 Ti и компилятора Nvidia CUDA (nvcc). Это позволяет ускорить вычисления примерно в пять раз по сравнению с решением на 16 потоках процессора (см. [27]).

2. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Результаты расчетов представлены в декартовой системе координат, центром которой является звезда, ось $X$ направлена против набегающего потока, ось $Z$ совпадает с осью вращения звезды (полярная ось), ось $Y$ дополняет трехгранник до правой тройки. Вычисления производились для трех значений альфвеновского числа Маха звезды (${{M}_{A}} = 4,8,12$) и для большого набора чисел Маха набегающего потока ($0 \leqslant {{M}_{\infty }} \leqslant 3$). Здесь представлены результаты для наиболее близкого к солнечному значению ${{M}_{A}} = 12$, другие числа MA здесь также обсуждаются, но представлены в работе [32]. Параметр $\chi $, не влияющий на стационарное течение, был выбран равным двум, чтобы избежать возможного возникновения неустойчивости Кельвина-Гельмгольца на астропаузе.

Картина течения является трехмерной и сложной для представления, поэтому она подробно описана ниже. На рис. 2 изображены изолинии плотности и линии тока для расчетов с восемью различными значениями числа Маха ${{M}_{\infty }}$. Каждый расчет показан в двух плоскостях: экваториальной – плоскость $XOY$ и полярной – плоскость $XOZ$. В силу сделанных в работе предположений, эти плоскости также являются плоскостями симметрии задачи, поэтому результаты приводятся только в полуплоскостях с положительными значениями $Y$ и $Z$. Расчет для неподвижной межзвездной среды (${{M}_{\infty }} = 0$) представлен в работе [26] и здесь не повторяется.

Первый расчет (1) на рис. 2 представлен для очень слабого набегающего потока ${{M}_{\infty }} = 0.1$. Астропауза выделена красным, на ней сходятся линии тока от источника и набегающего потока. Астропауза слегка наклонена в отрицательном направлении оси $X$ (к хвосту) и представляет собой цилиндрическую поверхность (трубу) с нейтральной осью, близкой к оси Z. В экваториальной плоскости ($XOY$) видно поперечное сечение трубы, форма которого близка к окружности. В полярной плоскости заметны слегка наклоненные крылья трубы. Поверхность астросферной ударной волны (TS) близка к сферической. Качественно форма тангенциальной поверхности близка к случаю, когда набегающий поток отсутствует.

Особый интерес представляет картина течения в хвостовой области. В экваториальной плоскости часть линий тока обтекают астропаузу, образуя точку торможения на оси X при $X \approx - 5.3$. Далее линии тока разворачиваются по направлению к звезде и втыкаются в тангенциальный разрыв, образуя еще одну точку торможения уже на самом разрыве. В полярной плоскости отчетливо видно, что эти линии тока опять поворачивают по направлению к оси $Z$ и уходят вверх и вниз (для симметричных линий тока) по оси $Z$. Этот поток движется далее параллельно трубе. Существует и другая часть линий тока, которые обтекают астропаузу на бóльших расстояниях и не разворачиваются. Здесь полезно посмотреть на распределение модуля скорости на оси $X$ (рис. 3) для ${{M}_{\infty }} = 0.1$ (красная кривая). Модуль скорости представлен в логарифмической шкале. На рисунке отчетливо видны точки торможения. Направление скорости на конкретных участках показано стрелками. В возвратной зоне значение скорости достигает 0.06, что составлет больше половины от скорости набегающего потока (0.1) и также примерно соответствует скорости на оси в хвостовой области. Можно заключить, что возвратное течение является достаточно сильным.

Второй расчет (2), проведенный при значении числа Маха ${{M}_{\infty }} = 0.25$, демонстрирует (рис. 2) большее влияние набегающего потока. Заметно большее искривление тангенциального разрыва. Также интересно отметить форму трубы в перпендикулярном сечении (см. экваториальную плоскость). Она имеет выемку (желобок) у оси $X$, в которую устремляются все линии тока возвратного течения, уходя далее вдоль трубы вверх и вниз по оси $Z$. На рис. 3 (оранжевая кривая) заметны уменьшение скорости течения в возвратной зоне и увеличение в хвостовой (при $X < - 6.2$). При этом астропауза в головной области перемещается ближе к звезде, а в хвостовой удаляется от звезды. Точка торможения также удаляется от звезды ($X \approx - 6$). Качественно можно описать течение следующим образом: набегающий поток стал быстрее, что повлияло на 1) искривление трубы в силу увеличения на нее динамического давления, 2) уменьшение возвратной зоны из-за увеличения инерции набегающего потока, которому теперь “сложнее” развернуться. Скорость после разворота становится меньше, что приводит к меньшему давлению в точке торможения на астропаузе (при $X \approx - 2.5$) и далее к перемещению астропаузы дальше в хвост для уравновешивания давлений на нее с двух сторон.

Третий расчет (3) на рис. 2 вместе с зеленой кривой на рис. 3 выполнен при ${{M}_{\infty }} = 0.3$ и подтверждает предыдущие выводы. Труба изгибается еще больше, астропауза передвигается в хвост, хотя точка торможения в хвостовой части остается примерно в том же месте. Этот расчет был последним, перед бифуркацией режима течения и сменой топологии астропаузы. При дальнейшем увеличении ${{M}_{\infty }}$ происходит “прорыв” звездным ветром точки торможения (на астропаузе в хвостовой части). Расчет (4) при ${{M}_{\infty }} = 0.35$ на рис. 2 качественно отличается от предыдущих. Здесь отсутствует возвратное течение (синяя кривая на рис. 3), полярная плоскость в хвосте полностью занята линиями тока от источника. Однако область “прорыва” очень тонкая, что хорошо видно в экваториальной плоскости – в хвостовой части звездный ветер сливается с набегающим потоком на оси X. Таким образом, можно заключить, что критическое значение числа Маха, при котором происходит бифуркация потока, $M_{\infty }^{*} \approx 0.325$.

Дальнейшее увеличение ${{M}_{\infty }}$ (рис. 2, расчеты (5) и (6)) приводит к расширению астропаузы в экваториальной плоскости (расширение зоны прорыва) и сужению ее в полярной плоскости (еще больший изгиб участков астропаузы, которые были крыльями трубы до бифуркации).

Расчеты (7)–(8) рис. 2 проведены для значений ${{M}_{\infty }} = 1.6$ и, близкому к гелиосферному, 2.2. Произошел переход через точку ${{M}_{\infty }} = 1$, образовались головная ударная волна (TS) и диск Маха в хвостовой зоне. Положения поверхностей разрыва на оси X при переходе из дозвукового обтекания в сверхзвуковое хорошо видны на рис. 4, где изображены графики плотности вдоль оси X для широкого диапазона чисел Маха набегающего потока. При увеличении ${{M}_{\infty }}$ все поверхности в головной области приближаются к звезде, что соответствует классическим представлениям. Магнитное поле звезды уже оказывает слабое влияние, которое проявляется в сплюснутости астропаузы в хвосте в плоскости $XOY$ на 30% по сравнению с плоскостью $XOZ$.

Также были проведены расчеты при ${{M}_{A}} = 8$ и ${{M}_{A}} = 4$ (здесь не показаны). Качественно результаты не изменяются. Однако значения ${{M}_{A}} = 8$ и ${{M}_{A}} = 4$ соответствуют более сильному магнитному полу звезды, поэтому труба сохраняет свою трубчатую форму при больших значениях числа Маха в набегающем потоке. Критические числа Маха, при которых происходит бифуркация, приблизительно равны 0.45 и 0.95 для ${{M}_{A}} = 8$ и ${{M}_{A}} = 4$ соответственно.

ЗАКЛЮЧЕНИЕ

В работе изучается влияние магнитного поля звезды на форму астропаузы. Проведено параметрическое исследование задачи от двух безразмерных параметров: 1) числа Маха набегающего потока (${{M}_{\infty }}$) и 2) альфвеновского числа Маха источника (MA). Результаты можно кратко резюмировать следующим образом:

1. Для малых чисел Маха набегающего потока (${{M}_{\infty }} \to 0$) реализуется трубчатая форма астропаузы (см. рис. 2а) вне зависимости от величины магнитного поля звезды (от MA). Такое заключение справедливо для медленно движущихся в космическом пространстве звезд.

2. При изменении ${{M}_{\infty }}$ в диапазоне $0 \leqslant {{M}_{\infty }} < M_{\infty }^{*}$ наблюдается сгибание трубы (см. рис. 1б) с образованием сложной области течения за трубой, состоящей из вторичной точки торможения и возвратной зоны. $M_{\infty }^{*}$ – критическое число Маха, при котором происходит смена режима течения на режим с классической формой астропаузы. Значения $M_{\infty }^{*}$ определены для трех разных MA. Бифуркация происходит с прорывом звездным ветром астропаузы в узкой области.

3. При увеличении ${{M}_{\infty }}$ от $M_{\infty }^{*}$ до 1 узкая область прорыва расширяется, и астропауза стремится к классической форме (см. рис. 1в). При ${{M}_{\infty }} = 1$ происходит еще одна бифуркация режима течения с образованием головной ударной волны и диска Маха (см. рис. 1г).

4. При дальнейшем увеличении ${{M}_{\infty }}$ картина течения качественно не меняется. На гелиосферных числах Маха (${{M}_{\infty }} = 2.2$) астропауза остается вытянутой по оси вращения звезды на ≈30%.

В целом можно сделать вывод, что влияние магнитного поля звезды важно и должно учитываться в современных моделях астросфер. Результаты расчетов при значениях параметров, характерных для Солнечной системы, подтверждают открытый характер гелиопаузы в хвостовой области. Это согласуется с результатами модели гелиосферы, представленной в работе [21]. В будущем исследование может быть продолжено с учетом влияния внешних магнитных полей и нейтральных атомов на трубчатую форму астропаузы. Так, например, учет внешних магнитных полей может оказать дополнительный удерживающий трубу эффект, увеличив $M_{\infty }^{*}$.

Работа выполнена в рамках гранта РНФ 19-12-00383.

Список литературы

  1. Parker E.N. The Stellar-Wind Regions // Astrophys. J. 531. 1963. https://doi.org/10.1086/147124

  2. Баранов В.Б., Краснобаев К.В., Куликовский А.Г. Модель взаимодействия солнечного ветра с межзвездной средой // Доклады Академии наук СССР. 1970. № 194. С. 41–44.

  3. Баранов В.Б., Лебедев М.Г., Рудерман М.С. Структура области взаимодействия солнечного ветра с межзвездной средой и ее влияние на проникновение атомов Н в солнечный ветер // Astrophys Space Sci. 1979. С. 429–440. https://doi.org/10.1007/BF00650015

  4. Baranov V.M., Malama Iu.G. Model of the solar wind interaction with the local interstellar medium numerical solution of self-consistent problem // JGR. 1993. https://doi.org/10.1029/93JA01171

  5. Bertaux J.L., Blamont J.E. Evidence for a source of an extraterrestrial hydrogen lyman-alpha emission // AAP. 1971. № 11. C. 20.

  6. Thomas G.E., Krassa R.F. OGO 5 Measurements of the Lyman Alpha Sky Background // AAP. 1971. № 11. C. 218.

  7. Wallis M.K. Local interstellar medium // Nature. 1975. №254. C. 202–203.

  8. Баранов В.Б., Рудерман М.С. Взаимодействие солнечного ветра с заряженными и нейтральными компонентами межзвездной среды // Письма в Астрономический журнал. 1979. № 5. С. 615–619.

  9. Баранов В.Б., Ермаков М.К., Лебедев М.Г. Трехкомпонентная газодинамическая модель взаимодействия солнечного ветра с межзвездной средой // Известия Академии наук СССР. Механика жидкости и газа. 1981. № 5. С. 123.

  10. Baranov V.B., Ermakov M.K., Lebedev M.G. Three-component gas-dynamic model of the interaction of the solar wind with the interstellar medium // Fluid Dynamics. 1982. № 17. C. 754–759.

  11. Baranov V.B., Lebedev M.G., Malama Y.G. The influence of the interface between the heliosphere and the local interstellar medium on the penetration of the H atoms to the Solar system // Astrophysical Journal. 1991. T. 375. № 3. C. 347–351. https://doi.org/10.1086/170194

  12. Baranov V.B., Izmodenov V.V. Model Representations of the interaction between the solar wind and the supersonic interstellar medium flow. Prediction and interpretation of experimental data // Fluid Dynamics. 2006. T. 41. № 5. C. 689–707. https://doi.org/10.1007/s10697-006-0089-9

  13. Baranov V.B., Zaitsev N.A. On the problem of the solar wind interaction with magnetized interstellar plasma // Astronomy and Astrophysics. 1995. № 304. C. 631.

  14. Pogorelov N., Matsuda T. Application of numerical methods to modeling the stellar wind and interstellar medium interaction // 1998/ eprint arXiv:physics/9807031.

  15. Linde T.J., Gombosi T.I., Roe P.L., Powell K.G., Dezeeuw D.L. Heliosphere in the magnetized local interstellar medium: Results of a three-dimensional MHD simulation // Journal of Geophysical Research. 1998. № 103. C. 1889–1904. https://doi.org/10.1029/97JA02144

  16. Alexashov D.B., Izmodenov V.V. Kinetic vs. multi-fluid models of H atoms in the heliospheric interface: a comparison // Astronomy and Astrophysics. 2005. № 439. C. 11171–1181. https://doi.org/10.1051/0004-6361:20052821

  17. Yu G. The interstellar wake of the solar wind // Astrophysical Journal. 1974. № 194. C. 187–202. https://doi.org/10.1086/153235

  18. Opher M., Drake J.F., Zieger B., Zieger M., Gombosi T.I. Magnetized Jets Driven by the Sun: The Structure of the Heliosphere Revisited // Astrophysical Journal Letter. 2015. № 800. https://doi.org/10.1088/2041-8205/800/2/L28

  19. Drake J.F., Swisdak M., Opher M. A Model of the Heliosphere with Jets // Astrophysical Journal. 2015. https://doi.org/2015AGUFMSH53C.02D

  20. Izmodenov V.V., Alexashov D.B. Three-dimensional kinetic-MHD model of the global heliosphere with the heliopause-surface fitting // Astrophysical Journal, Supplement Series. 2015. https://doi.org/10.1088/0067-0049/220/2/32

  21. Izmodenov V.V., Alexashov D.B. Magnitude and direction of the local interstellar magnetic field inferred from Voyager 1 and 2 interstellar data and global heliospheric model // Astronomy and Astrophysics. 2020. https://doi.org/10.1051/0004-6361/201937058

  22. Pogorelov N.V., Borovikov S.N., Heerikhuisen J., Zhang M. The Heliotail // Astrophysical Journal. 2015. https://doi.org/10.1088/2041-8205/812/1/L6

  23. Pogorelov N.V., Fichtner H., Czechowski A., Lazarian A., Lembege B., le Roux J.A., Potgieter M.S., Scherer K., Stone E.C., Strauss R.D., Wiengarten T., Wurz P., Zank G.P., Zhang M. Heliosheath Processes and the Structure of the Heliopause: Modeling Energetic Particles, Cosmic Rays, and Magnetic Fields // Space Science Reviews. 2017. https://doi.org/10.1007/s11214-017-0354-8

  24. Parker E.N. Dynamics of the Interplanetary Gas and Magnetic Fields // Astrophysical Journal. 1958. V. 128. P. 664. https://doi.org/10.1086/146579

  25. Golikov E.A., Izmodenov V.V., Alexashov D.B., Belov N.A. Two-jet astrosphere model: effect of azimuthal magnetic field // Monthly Notices of the Royal Astronomical Society. 2017. https://doi.org/10.1093/mnras/stw2402

  26. Golikov E.A., Izmodenov V.V., Alexashov D.B. Two-jet structure of the ow produced by magnetized hypersonic spherical source into the steady unmagnetized medium// Journal of Physics: Conference Series. 2017. https://doi.org/10.1088/1742-6596/815/1/012035

  27. Korolkov S.D., Izmodenov V.V., Alexashov D.B. Numerical modeling of the convective Kelvin-Helmholtz instabilities of astropauses // Journal of Physics: Conference Series. 2020. https://doi.org/10.1088/1742-6596/1640/1/012012

  28. Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. М.: Наука, 1976.

  29. Gurski K.F. An HLLC-type approximate Riemann solver for ideal magnetohydrodynamics // SIAM J. Sci. Comput. 2004. V. 2165. P. 25.

  30. Powell K.G., Roe P.L., Linde T.J., Gombosi T.I., Zeeuw D.L. A Solution-Adaptive Upwind Scheme for Ideal Magnetohydrodynamics // Journal of Computational Physics. 1999. https://doi.org/10.1006/jcph.1999.6299

  31. Osher Level Set Methods and Dynamic Implicit Surfaces. New York: Springer-Verlag, 2003. https://doi.org/10.1007/b98879

  32. Korolkov S.D., Izmodenov V.V. New unexpected flow patterns in the problem of the stellar wind interaction with the interstellar medium: stationary ideal-MHD solutions // Monthly Notices of the Royal Astronomical Society. 2021.https://doi.org/10.1093/mnras/stab1071

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал