Известия РАН. Механика жидкости и газа, 2022, № 6, стр. 41-54

ПЕРЕМЕЩЕНИЕ ПЛАВУЧИХ МАРКЕРОВ ПО ПОВЕРХНОСТИ ВИХРЕВОЙ ВОРОНКИ

Т. О. Чаплина^a, *, А. В. Кистович^a

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

Поступила в редакцию 17.05.2022
После доработки 21.06.2022
Принята к публикации 21.06.2022

EDN: MNRKFD
DOI: 10.31857/S0568528122600278

Аннотация

Экспериментально и теоретически изучены характерные особенности движения маркеров, размещенных на свободной поверхности вихревой воронки, образованной вращением воды в цилиндрическом контейнере. Измерена зависимость угловых и радиальных координат центра масс маркеров от времени, а также зависимость вращения маркера вокруг собственной оси от угла поворота его центра масс вокруг вертикальной оси вихревого потока. Представлена математическая модель движения твердого маркера произвольной формы. Результаты теоретических расчетов хорошо согласуются с экспериментальными данными.

Ключевые слова: вихревая воронка, маркер, твердотельное вращение, угол верчения

Изучение процессов переноса вещества в вихревых течениях – одна из традиционных задач механики жидкости, практическая ценность результатов которой для задач экологии и развития промышленных технологий устойчиво растет.

Особый интерес представляют вихревые течения, допускающие прямое сравнение с расчетами на основе фундаментальных уравнений, среди которых основным служит течение, генерируемое вращающимся диском в свободном пространстве, в узком неподвижном кожухе или в цилиндрической камере ограниченного объема, полностью заполненной жидкостью [1], а также в коническом контейнере [2]. Измеряемыми параметрами здесь являются компоненты скорости и давление.

Большое внимание уделяется изучению процесса распада вихря, который играет принципиальную роль в динамике протяженных вихрей. В частности, возникновение и разрушение вихревых структур присутствуют в различных сценариях развития турбулентности в отрывных и пристенных течениях [3]. Распад вихря и его непредсказуемость являются одними из основных причин, снижающих эффективность вихревых технологий [4]. Разработано довольно много теоретических моделей распада вихря [5, 6], однако в настоящее время отсутствуют адекватные теории, с достаточной точностью предсказывающие момент, положение и разрешения вихря.

Визуализация течения жидкости, определение гидродинамических характеристик, в частности, скорости, путем внесения в течение различных маркирующих предметов были и остаются важными задачами для исследователей. Однако помещаемые в движущуюся жидкость различные маркеры ведут себя по-разному в силу присущих им физических и химических свойств. Перемещение твердотельного объекта, особенно в вихревом течении, осложняется наличием сдвига скоростей на его границах, благодаря чему твердотельный маркер, помимо своего основного движения вокруг центра вихря, начинает вращаться вокруг своей собственной оси. Поскольку плавучий предмет обладает присущими ему физико-химическими характеристиками, отличающимися от характеристик жидкой среды, при описании его движения необходимо вводить поправки, учитывающие взаимодействие среды с маркером. Применительно к геофизике такие поправки могут оказаться полезными, например, при исследованиях, связанных с проблемой накопления пластикового мусора в центрах вихревых образований в открытом океане, а также для корректировки показаний различных зондов-дрифтеров, передающих информацию о морских и океанских течениях.

Настоящая статья посвящена проблеме переноса вихревыми течениями различного рода маркеров, помещенных на свободную поверхность жидкости. Работы выполнялись на экспериментальной установке цилиндрической формы с вращающимся на дне диском-активатором. Разработана методика автоматической обработки результатов поведения маркера на свободной поверхности вихревого течения, основанная на преобразовании растрового изображения в векторное представление, которая позволяет значительно ускорить процесс обработки результатов проводимых экспериментов.

Наряду с экспериментами проведено аналитическое исследование на основе предложенной математической модели движения плоских маркеров произвольной формы на поверхности вихревого потока. Сравнение результатов расчетов с экспериментальными данными показало их хорошее взаимное соответствие.

1. МЕТОДИКА ЭКСПЕРИМЕНТА И ОБРАБОТКИ ДАННЫХ

Систематическое изучение природных вихревых течений осложнено в силу невозможности контроля условий их возникновения и стационарности [7], вследствие чего наиболее предпочтительным является метод лабораторного моделирования, который позволяет получать воспроизводимые результаты, контролировать параметры возникновения и большинство определяющих характеристик на всем протяжении эксперимента.

Установка “ВТК” (Вихревые течения с кручением), на которой проводились описанные ниже эксперименты, создавалась в рамках комплекса установок Лаборатории механики жидкостей ИПМех РАН для изучения закрученного потока, установления набора определяющих параметров и диапазонов их изменения.

Источником вихревого движения является вращение индукторов – гладких дисков, дисков с ребрами различной формы, винтов или прочих тел различной геометрии, которые размещаются у дна или поверхности контейнера. Подробные фото и схема экспериментальной установки приведены в работе [8].

Несмотря на простоту геометрии эксперимента, течение является достаточно сложным и включает как вихревую, так и волновые компоненты и в толще, и на свободной поверхности жидкости. Равномерно вращающийся диск закручивает жидкость вокруг вертикальной оси и отбрасывает к стенке контейнера. В целом жидкость движется от центра вращающегося диска к его кромке, поднимается вдоль стенок контейнера, смещается вдоль свободной поверхности и погружается в окрестности оси вращения. В возникающем течении частицы жидкости двигаются по сложным спиральным и винтовым траекториям. Совместное действие центробежной, вязкой и гравитационной сил создает в контейнере составное вихревое течение со сложным распределением угловой скорости. Сила тяжести и градиенты давления неравномерно деформируют свободную поверхность, создавая поверхностную каверну, на которой могут появляться волновые возмущения различного вида (инерциальные, гравитационные на мелкой или на глубокой воде, капиллярные) и амплитуды.

Для уточнения картины течения и косвенной оценки скорости вращения свободной поверхности жидкости в составном вихре проведена серия экспериментов, где в качестве индикаторов использованы твердые маркеры, рис. 1.

Рис. 1.

Маркер на свободной поверхности: (а) квадрат 1 см × 1 см, $\Omega = 3.3$ с^–1, местоположения маркеров 1–5 соответствуют 1, 4, 18, 19, 33 с после начала эксперимента (наложенные кадры); (б) схема координатных кадров.

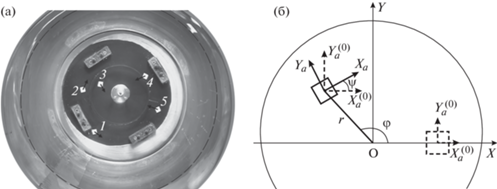
Движение маркера, который перемещается по поверхности жидкости, вовлеченной в составное вихревое течение, сводится к комбинации его обращения вокруг вертикальной оси течения, смещения по направлению к этой оси и одновременного вращения вокруг собственного центра масс. Для удобства описания перемещений маркера по свободной поверхности течения вводятся несколько систем координат. Начало одной из них $XOY$ (прямоугольной декартовой) совпадает с геометрическим центром свободной поверхности, оси направлены вдоль сторон кадра видеозаписи картины течения, плоскость расположения осей координат системы совпадает с уровнем невозмущенной свободной поверхности до включения вращения индуктора (рис. 1). Другая система координат – полярная $(r,\,\,{{\psi }})$ – располагается в той же плоскости и наиболее удобна для регистрации перемещений маркера вокруг вертикальной оси течения. В этой системе ведется отсчет координат центра маркера в зависимости от времени.

С центром маркера связана присоединенная (подвижная) декартова система координат $XOY$, используемая для задания угла “верчения” ${{\psi }}$. На всех маркерах, использованных в экспериментах, были нанесены специальные метки, позволяющие определять их угловое положение. По изображениям, взятым из видеозаписи экспериментов с известным шагом по времени, независимо определялись радиальные и угловые координаты маркеров.

2. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПЕРЕМЕЩЕНИЯ ТВЕРДОТЕЛЬНЫХ МАРКЕРОВ НА ПОВЕРХНОСТИ ВИХРЯ

В проведенных экспериментах использовались полипропиленовые маркеры: квадратной, круглой, эллипсовидной формы, в форме кольца, пятиугольной, треугольной и крестообразной формы; толщина всех маркеров составляет 0.5 мм. Большинство экспериментов проводилось при следующих параметрах: глубина жидкости H = 40 см, частота вращения индуктора $\Omega = 3.3$ с^–1 и менее, что соответствует свободной поверхности с незначительным прогибом в центре для любого размера диска-активатора.

Когда маркер помещается на поверхность, на его нижнюю погруженную поверхность начинают действовать вязкие касательные напряжения со стороны жидкости, которые переносят его в целом по некоторой траектории, лежащей на поверхности, и вращают его вокруг собственного центра масс.

По мере продвижения к центру вихревой воронки маркер попадает в переходную область, пересекает границу между твердотельным и периферийным типами вращения вихря и постепенно меняет собственное вращение относительно центра масс на противоположное, которое сохраняется после полного перехода маркера в область твердотельного вращения.

Круглый маркер после короткого “интервала вовлечения” ($\Delta t = 5$ с) вращается вокруг вертикальной оси с почти постоянной угловой скоростью, значение которой монотонно увеличивается с увеличением частоты вращения диска, оценки которой составляют 2.3, 6.0, 9.9 c^–1 для значений частот вращения индуктора $\Omega = $3.3, 9.2, 16.7 c^–1 соответственно (рис. 2 а).

Рис. 2.

Угол поворота маркера вокруг собственной оси от времени ($H = $ 40 см, $R = $ 7.5 см, Re = 18 750, 51 750, 93 750): (а) круговой цилиндр радиусом 0.5 см и высотой 0.3 см; (б) параллелепипед 1.0 см $ \times $ 1.0 см $ \times $ 0.3 см.

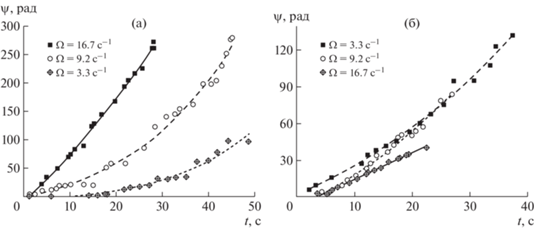
Квадратный маркер вращается с почти постоянной угловой скоростью (рис. 2 ) 2.4, 3.5, 3.4 c^–1 ($\Omega = $ 3.3, 9.2, 16.7 c^–1). В качестве одного из результатов автоматической обработки экспериментальных данных получены зависимости длины радиус-векторов центров масс маркеров различной формы от времени в прямоугольной декартовой системе отсчета $XOY$, рис. 3.

Рис. 3.

Временная зависимость радиусов центров масс маркеров различной формы (H = 40 см, R = 7.5 см, $\Omega = 3.3$ с^–1): 1–3 – пятиугольный, овальный и круглый маркеры с наибольшим размером 1 см.

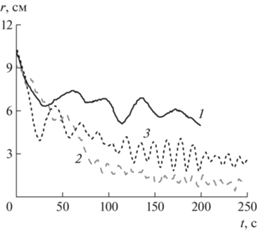
Особенностью всех графиков, представленных на рис. 3, является периодическое изменение координат (биение) центра маркеров при приближении к центру вращающейся свободной поверхности. Эти колебания координат центра маркера связаны с эллиптическими искажениями свободной поверхности, с небольшими колебаниями положения центра вращения свободной поверхности относительно неподвижных боковых стенок контейнера, а также с наличием на свободной поверхности системы бегущих спиральных волн.

Для трехмерных маркеров (цилиндр радиусом 0.5 см и высотой 0.3 см – “круглый”, параллелепипед с одной квадратной гранью 1 см × 1 см и третьим размером 0.3 см – “квадрат”) – зависимость угла “верчения” ${{\psi }}$ от угла поворота ${{\varphi }}$ вокруг оси потока составляет более сложный объект для наблюдения. Скорость “верчения” маркера зависит от его формы и угловой скорости индуктора.

3. АНАЛИТИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ МАРКЕРОВ ПО ПОВЕРХНОСТИ ВИХРЕВОЙ ВПАДИНЫ

Маркер, находящийся на поверхности воды, подвержен действию силы тяжести, архимедовой силы и силы гидродинамического происхождения; последняя представляет собой результат сложения нескольких сил, порожденных различными физическими явлениями.

При оценке силового воздействия водяного потока на маркер используется экспериментальный факт, что его глубина погружения в воду существенно меньше характерных масштабов приповерхностного течения. Это позволяет использовать приближение отсутствия возмущений потока за счет помещения на его поверхность маркера. На основании этого предполагается, что маркер как бы распластывается по поверхности вихря, но при расчетах его характеристик (момент инерции, положение центра масс и т.д.) считается плоским.

Гидродинамическая сила определяется распределением давления по нижней и верхней поверхностям маркера, капиллярными эффектами, возникающими на контактной границе воды на ребре маркера, эффектами увлечения маркера потоком и его торможения за счет его погружения в воду, а также эффектами вязкого взаимодействия с водой на всей контактирующей поверхности.

Получение точных аналитических выражений для всех упомянутых сил в случае маркера произвольной формы представляет собой, по-видимому, неразрешимую задачу и потому в дальнейшем используется ряд приближений, позволяющих получить конструктивные результаты.

Первое приближение состоит в том, что движение маркера всегда описывается перемещением его центра масс и вращением вокруг мгновенной оси, всегда проходящей через него нормально к поверхности жидкости.

Так как в экспериментах использовались маркеры, форма которых проявляет непрерывную или дискретную симметрию поворотов относительно оси, проходящей через центр масс маркера, нормально к его поверхности, то касательная к поверхности жидкости компонента суммарной капиллярной силы, действующей на маркер, равна нулю.

Сила, действующая со стороны потока воды на погруженную часть ребра маркера, определяется выражением

$_{f}\, = \oint\limits_L {{{c}_{f}}(L){\mathbf{\nu }}\left( {{\mathbf{\nu }} \times \left( {{\mathbf{v}} - {{{{\mathbf{\dot {r}}}}}_{c}}} \right)} \right)dL} $

где ${{{\mathbf{r}}}_{c}}$ – радиус-вектор центра масс маркера; ${\mathbf{v}}$ – поле скорости воды, которое по причине малой толщины маркера по сравнению с характерными масштабами течения считается меняющимся только вдоль контура $L$, ограничивающего ребро маркера; ${\mathbf{\nu }}$ – внутренняя нормаль к контуру; ${{c}_{f}}(L)$ – локальный погонный коэффициент сопротивления формы (в случае произвольной формы ограничивающего контура $L$ этот коэффициент – величина трудноопределимая); точки над символами здесь и далее обозначают дифференцирование по времени.

По причине центральной симметричности маркеров, скоростной напор, возникающий на части контура и разгоняющий маркер, практически полностью компенсируется тормозящим эффектом, возникающим на оставшейся части контура. Этот факт позволяет нам игнорировать возмущения начального потока воды из-за размещения маркера на его поверхности и считать оценки $\left| {{\mathbf{v}} - {{{{\mathbf{\dot {r}}}}}_{c}}} \right| \ll \left| {\mathbf{v}} \right|,\left| {{{{{\mathbf{\dot {r}}}}}_{c}}} \right|$ достоверными.

В результате второе приближение состоит в пренебрежении силой ${{{\mathbf{F}}}_{f}}$, порожденной воздействием неравномерности потока на ребро маркера, уже увлеченного потоком вихревой воронки, что позволяет считать маркер бесконечно тонким, а его центр масс расположенным на поверхности жидкости.

Если бы маркер располагался на горизонтальной поверхности, результирующая силы тяжести, архимедовой силы, нормальной к поверхности маркера компоненты капиллярной силы и силы, порожденной разностью давлений на верхней и нижней поверхностях, была бы равна нулю. В случае же наклонной поверхности жидкости эта результирующая сила направлена по касательной к поверхности жидкости, поскольку сам маркер от этой поверхности не отрывается, и задается выражением

${{{\mathbf{F}}}_{t}} = {{\lambda }}mg{{{\mathbf{e}}}_{t}}$

где $m$ – масса маркера; g – ускорение силы тяжести; $\lambda $ – некоторый безразмерный коэффициент, пропорциональный тангенсу угла наклона поверхности жидкости к горизонту; ${{{\mathbf{e}}}_{t}}$ – единичный касательный вектор к поверхности жидкости.

При помещении маркера на поверхность на его нижнюю поверхность начинают действовать вязкие касательные напряжения со стороны жидкости, которые переносят его как целое вдоль некоторой траектории, лежащей на поверхности, и вращают вокруг его собственного центра масс. В рамках сделанных приближений поверхностная плотность этой вязкой силы определяется величиной

${{{\mathbf{f}}}_{{\text{v}}}} = {{\kappa }}\left( {{{{\mathbf{v}}}_{t}} - {{{{\mathbf{\dot {r}}}}}_{c}} - {\mathbf{\omega }} \times {\mathbf{r}}} \right)$

где ${{{\mathbf{v}}}_{t}}$ – касательная к поверхности маркера компонента поля скорости воды в точке с координатой ${{{\mathbf{r}}}_{c}} + {\mathbf{r}}$; ${\mathbf{r}}$ – локальный радиус-вектор точки на поверхности маркера с началом в центре масс, как показано на рис. 1; ${{\kappa }}$ – некоторый коэффициент, характеризующий сцепление поверхности маркера (в зависимости от его материала, шероховатости и т.д.) с жидкостью; член ${{{\mathbf{v}}}_{t}} - {{{\mathbf{\dot {r}}}}_{c}} - {\mathbf{\omega }} \times {\mathbf{r}}$ представляет собой скорость движения точки на дне маркера относительно потока жидкости, ${\mathbf{\omega }}$ – угловая частота вращения маркера вокруг его собственного центра масс (частота “верчения”).

Действующие на маркер полная вязкая сила и полный момент вязких сил относительно оси его вращения, проходящей через центр масс, определяются выражениями

${{{\mathbf{F}}}_{{\text{v}}}} = \int\limits_S {{{{\mathbf{f}}}_{{\text{v}}}}\,dS} ,\,\,\,\,\,{{{\mathbf{M}}}_{{\text{v}}}} = \int\limits_S {{\mathbf{r}} \times {{{\mathbf{f}}}_{{\text{v}}}}\,dS} $

где S – нижняя поверхность маркера.

Момент силы ${{{\mathbf{F}}}_{t}}$, приложенной к центру масс, равен нулю.

Таким образом, в принятой приближенной модели уравнения и начальные условия, описывающие движения маркера по поверхности жидкости, имеют вид

(3.1)

$\begin{gathered} m{{{{\mathbf{\ddot {r}}}}}_{c}} = {{{\mathbf{F}}}_{{\text{v}}}} + {{{\mathbf{F}}}_{t}} = {{\kappa }}\int\limits_S {\left( {{{{\mathbf{v}}}_{w}} - {{{{\mathbf{\dot {r}}}}}_{c}} - {\mathbf{\omega }} \times {\mathbf{r}}} \right)dS} + {{\lambda }}mg{{{\mathbf{e}}}_{t}} \\ J{\mathbf{\dot {\omega }}} = {{\kappa }}\int\limits_S {{\mathbf{r}} \times \left( {{{{\mathbf{v}}}_{w}} - {{{{\mathbf{\dot {r}}}}}_{c}} - {\mathbf{\omega }} \times {\mathbf{r}}} \right)dS} \\ {{\left. {{{{{\mathbf{\dot {r}}}}}_{c}}} \right|}_{{t = 0}}} = 0,\quad {{\left. {{{{\mathbf{r}}}_{c}}} \right|}_{{t = 0}}} = {{{\mathbf{r}}}_{{c0}}},\quad {{\left. {\mathbf{\omega }} \right|}_{{t = 0}}} = 0 \\ \end{gathered} $

Здесь J – момент инерции маркера относительно указанной оси вращения.

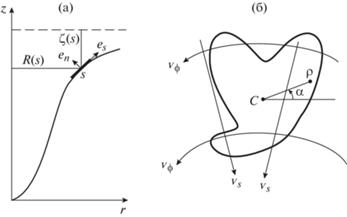
Исследование движения маркера проводится в системе координат, связанной с поверхностью воды [8] и показанной на рис. 4. Положение центра масс маркера описывается координатами s, ${{\varphi }}$ и n = 0 (так как маркер находится на поверхности воды), а его радиус-вектор задается выражением

(3.2)

${{{\mathbf{r}}}_{c}} = \left( {RR{\kern 1pt} ' + {{\zeta \zeta }}{\kern 1pt} '} \right){{{\mathbf{e}}}_{s}} + \left( {{{\zeta }}R{\kern 1pt} ' - R{{\zeta }}{\kern 1pt} '} \right){{{\mathbf{e}}}_{n}}$

где ${{{\mathbf{e}}}_{s}}$, ${{{\mathbf{e}}}_{n}}$ и ${{{\mathbf{e}}}_{{{\varphi }}}}$ – единичные орты, подчиняющиеся правилам дифференцирования

$\begin{gathered} \frac{{\partial {{{\mathbf{e}}}_{s}}}}{{\partial s}} = - \frac{{R_{{}}^{{''}}{{{\mathbf{e}}}_{n}}}}{{{{\zeta }}{\kern 1pt} '}} = \frac{{{{\zeta }}_{{}}^{{''}}{{{\mathbf{e}}}_{n}}}}{{R'}},\quad \frac{{\partial {{{\mathbf{e}}}_{s}}}}{{\partial {{\varphi }}}} = R{\kern 1pt} '{{{\mathbf{e}}}_{{{\varphi }}}},\quad \frac{{\partial {{{\mathbf{e}}}_{s}}}}{{\partial n}} = 0 \\ \frac{{\partial {{{\mathbf{e}}}_{{{\varphi }}}}}}{{\partial s}} = 0,\quad \frac{{\partial {{{\mathbf{e}}}_{{{\varphi }}}}}}{{\partial {{\varphi }}}} = - R{\kern 1pt} '{{{\mathbf{e}}}_{s}} + {{\zeta }}{\kern 1pt} '{{{\mathbf{e}}}_{n}},\quad \frac{{\partial {{{\mathbf{e}}}_{{{\varphi }}}}}}{{\partial n}} = 0 \\ \frac{{\partial {{{\mathbf{e}}}_{n}}}}{{\partial s}} = - \frac{{{{\zeta }}_{{}}^{{''}}{{{\mathbf{e}}}_{s}}}}{{R{\kern 1pt} '}} = \frac{{R''{{{\mathbf{e}}}_{s}}}}{{{{\zeta '}}}},\quad \frac{{\partial {{{\mathbf{e}}}_{n}}}}{{\partial {{\varphi }}}} = - {{\zeta }}{\kern 1pt} '{{{\mathbf{e}}}_{{{\varphi }}}},\quad \frac{{\partial {{{\mathbf{e}}}_{n}}}}{{\partial n}} = 0 \\ \end{gathered} $

на основании которых из (3.2) следует

(3.3)

$\begin{gathered} {{{{\mathbf{\dot {r}}}}}_{c}} = \dot {s}\,{{{\mathbf{e}}}_{s}} + R{{\dot {\varphi }}}\,{{{\mathbf{e}}}_{{{\varphi }}}} \\ {{{{\mathbf{\ddot {r}}}}}_{c}} = (\ddot {s} - RR{\kern 1pt} '{{{{{\dot {\varphi }}}}}^{2}}){{{\mathbf{e}}}_{s}} + (R{{\zeta }}{\kern 1pt} '{{{{{\dot {\varphi }}}}}^{2}} + {{{{\zeta }}_{{}}^{{''}}{{{\dot {s}}}^{2}}} \mathord{\left/ {\vphantom {{{{\zeta }}_{{}}^{{''}}{{{\dot {s}}}^{2}}} {R{\kern 1pt} '}}} \right. \kern-0em} {R{\kern 1pt} '}}){{{\mathbf{e}}}_{n}} + \left( {R{{\ddot {\varphi } + 2}}R{\kern 1pt} '\dot {s}{{\dot {\varphi }}}} \right){{{\mathbf{e}}}_{{{\varphi }}}} \\ \end{gathered} $

а также ${{\partial \,{{{\mathbf{r}}}_{c}}} \mathord{\left/ {\vphantom {{\partial \,{{{\mathbf{r}}}_{c}}} {\partial \,n}}} \right. \kern-0em} {\partial \,n}} = 0$ – это означает, что центр масс маркера во все время движения остается на поверхности жидкости.

Рис. 4.

Схематическое изображение маркера, находящегося на поверхности вихря (а) и поля скорости жидкости, примыкающей к его нижней стороне (б).

Угловая частота верчения маркера в принятых приближениях представляется в виде

(3.4)

${\mathbf{\omega }} = {{\omega }}(s,{{\varphi ,}}t)\,{{{\mathbf{e}}}_{n}}$

где s и ${{\varphi }}$ – координаты центра масс, так что дифференцирование по времени выражения (3.4) приводит к результату

(3.5)

${\mathbf{\dot {\omega }}} = \left( {{{\dot {\omega }}}{{{\mathbf{e}}}_{n}} - {{\omega }}\left( {\frac{{{{\zeta }}_{{}}^{{''}}}}{{R'}}\dot {s}{{{\mathbf{e}}}_{s}} + {{\zeta }}{\kern 1pt} '{{\dot {\varphi }}}{{{\mathbf{e}}}_{{{\varphi }}}}} \right)} \right)$

Так как для маркеров с центральной симметрией справедливы соотношения $\int\limits_S {{\mathbf{r}} \times {{{{\mathbf{\dot {r}}}}}_{c}}\,dS} = 0$ и $\int\limits_S {{\mathbf{\omega }} \times {\mathbf{r}}\,dS} = 0$, то уравнения, описывающие движение, с учетом (3.3) приобретают форму

(3.6)

$\begin{gathered} m[(\ddot {s} - RR{\kern 1pt} '{{{{{\dot {\varphi }}}}}^{2}}){{{\mathbf{e}}}_{s}} + \left( {R{{\ddot {\varphi } + 2}}R{\kern 1pt} '\dot {s}{{\dot {\varphi }}}} \right){{{\mathbf{e}}}_{{{\varphi }}}}] = {{\kappa }}\left[ {\int\limits_S {{{{\mathbf{v}}}_{t}}dS} - S(\dot {s}{{{\mathbf{e}}}_{s}} + R{{\dot {\varphi }}}{{{\mathbf{e}}}_{{{\varphi }}}})} \right] + {{\lambda }}mg{{{\mathbf{e}}}_{t}} \\ J{{\dot {\omega }}} = {{\kappa }}\left[ {\int\limits_S {\left[ {{\mathbf{r}} \times ({{{\mathbf{v}}}_{t}} - {{{{\mathbf{\dot {r}}}}}_{c}})} \right] \times {{{\mathbf{e}}}_{n}}dS} - {{\omega }}\int\limits_S {{{r}^{2}}dS} } \right] \\ \end{gathered} $

В [9] показано, что в пренебрежении поверхностным натяжением скорость жидких частиц на поверхности воды описывается выражением

(3.7)

${{\left. {{{{\mathbf{v}}}_{t}}} \right|}_{{n = 0}}} = \left( { - {{\Omega }_{s}}R{\kern 1pt} '{{{\mathbf{e}}}_{s}} + {{\Omega }_{{{\varphi }}}}{{{\mathbf{e}}}_{{{\varphi }}}}} \right)\left( {R\vartheta (a - R) + \frac{{{{a}^{2}}}}{R}\vartheta (R - a)} \right)$

где ${{\Omega }_{s}}$, ${{\Omega }_{{{\varphi }}}}$ – характерные угловые скорости вдоль направлений ${{{\mathbf{e}}}_{s}}$ и ${{{\mathbf{e}}}_{{{\varphi }}}}$ соответственно, a – радиус твердотельного вращения в вихре; $\vartheta (x)$ – единичная функция Хевисайда.

При этом форма поверхности, по которой движется маркер, задается соотношением

(3.8)

${{\zeta }}(s) = {{{{\zeta }}}_{0}} + \frac{{\Omega _{{{\varphi }}}^{2}}}{{2g}}[{{R}^{2}}(s){{\theta }}\left( {a - R(s)} \right) + {{a}^{2}}(2 - {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {{{R}^{2}}(s)}}} \right. \kern-0em} {{{R}^{2}}(s)}}){{\theta }}\left( {R(s) - a} \right)]$

и описывает формирующуюся вихревую воронку [9], что хорошо согласуется с экспериментами [8, 9].

Для такой формы воронки справедливо выражение

${{\lambda }}mg{{{\mathbf{e}}}_{t}} = - mg{{\zeta }}{\kern 1pt} '{{{\mathbf{e}}}_{s}}$

В экспериментах [10] угловая скорость вращения диска на дне контейнера составляла величину 3.3 с^–1. Так как передача импульса от дна к поверхности контейнера происходит за счет вязких эффектов, то справедливо ограничение сверху ${{\Omega }_{{{\varphi }}}} \leqslant 3.3$ с^–1. В дальнейшем необходимые количественные оценки проводятся именно для этих значений параметров вихревой воронки.

Так как согласно [9] справедливо соотношение $R{\kern 1pt} {{'}^{2}} + {{\zeta }}{\kern 1pt} {{'}^{2}} = 1$, то на основании (3.8) следуют уравнения для функции $R$:

$R{\kern 1pt} '\sqrt {1 + {{{{k}^{2}}{{R}^{2}}} \mathord{\left/ {\vphantom {{{{k}^{2}}{{R}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} = 1,\quad R \leqslant a;\quad R{\kern 1pt} '\sqrt {1 + {{{{k}^{2}}{{a}^{6}}} \mathord{\left/ {\vphantom {{{{k}^{2}}{{a}^{6}}} {{{R}^{6}}}}} \right. \kern-0em} {{{R}^{6}}}}} = 1,\quad R \geqslant a$

где $k = {{\Omega _{{{\varphi }}}^{2}a} \mathord{\left/ {\vphantom {{\Omega _{{{\varphi }}}^{2}a} g}} \right. \kern-0em} g}$.

Оценка сверху в предельном случае при a = 7.5 см (радиус контейнера) дает значение ${{k}_{{\max }}} \leqslant $ ≤ 0.085, так что с хорошим приближением можно положить $R{\kern 1pt} '\; - 1 = 1$, ${{\zeta }}{\kern 1pt} ' = 1$. На основании полученных оценок, с учетом решений вышеприведенных уравнений для функции $R$ и с использованием (3.8), имеет место

${{\zeta }}{\kern 1pt} '(s) \approx \frac{{\Omega _{{{\varphi }}}^{2}}}{g}\left[ {s\,{{\theta }}(a - R(s)) + \frac{{{{a}^{4}}}}{{{{s}^{3}}}}{{\theta }}\left( {R(s) - a} \right)} \right]$

Дальнейшее исследование проблемы существенно зависит от конкретного вида экспериментального маркера и связано с вычислением интегралов, входящих в (3.7).

Маркер в форме диска радиуса ${{\rho }}$. В используемой приближенной модели радиус-вектор ${\mathbf{r}}$, отсчитываемый по поверхности маркера, согласно рис. 4 б представим в виде

(3.9)

${\mathbf{r}} \approx r\,({{{\mathbf{e}}}_{s}}sin{{\alpha + }}{{{\mathbf{e}}}_{{{\varphi }}}}cos{{\alpha }})$

Тогда $\int_S {{{r}^{2}}dS} = {{JS} \mathord{\left/ {\vphantom {{JS} m}} \right. \kern-0em} m}$, где $S = {{\pi }}{{{{\rho }}}^{2}}$ – площадь поверхности диска, $J = {{m{{{{\rho }}}^{2}}} \mathord{\left/ {\vphantom {{m{{{{\rho }}}^{2}}} 2}} \right. \kern-0em} 2}$ – его момент инерции. На основании (3.8) имеют место выражения

(3.10)

$\begin{gathered} \int\limits_S {{{{\mathbf{v}}}_{t}}dS} \approx R{{{{\rho }}}^{2}}\left( {{{f}_{ + }}(x) + \frac{{{{a}^{2}}}}{{{{R}^{2}}}}{{f}_{ - }}(x)} \right)\left( { - {{\Omega }_{s}}{{{\mathbf{e}}}_{s}} + {{\Omega }_{{{\varphi }}}}{{{\mathbf{e}}}_{{{\varphi }}}}} \right) \\ {{f}_{ \pm }}(x) = \frac{{{\pi }}}{2} - \frac{{2{{\rho }}}}{{3R}}{{(1 - {{x}^{2}})}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \pm (arcsin(x) + x\sqrt {1 - {{x}^{2}}} ),\quad x = \frac{{{{s}_{a}} - s}}{{{\rho }}} \\ \end{gathered} $

(3.11)

$\begin{gathered} \int\limits_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} \approx {{\Omega }_{{{\varphi }}}}{{{{\rho }}}^{3}}R\left( {{{h}_{ + }}(x) + \frac{{{{a}^{2}}}}{{{{R}^{2}}}}{{h}_{ - }}(x)} \right) \\ {{h}_{ \pm }}(x) = \frac{{{\rho }}}{{4R}}(\arcsin (x) - x{{(1 - {{x}^{2}})}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}) \pm \left( {\frac{{{{\pi \rho }}}}{{8R}} - \frac{2}{3}{{{(1 - {{x}^{2}})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right),\quad x = \frac{{{{s}_{a}} - s}}{{{\rho }}} \\ \end{gathered} $

где ${{s}_{a}}$ – такое значение координаты s, что $R({{s}_{a}}) = a$ – радиусу твердотельного вращения вихря.

При x = –1 маркер целиком находится на периферии вихря, в этом случае ${{f}_{ + }} = 0$, ${{h}_{ + }} = 0$, так что из (3.10, 3.11) следует

(3.12)

$\int\limits_S {{{{\mathbf{v}}}_{t}}dS} \approx \frac{{{{a}^{2}}}}{R}S\left( { - {{\Omega }_{s}}{{{\mathbf{e}}}_{s}} + {{\Omega }_{{{\varphi }}}}{{{\mathbf{e}}}_{{{\varphi }}}}} \right),\quad \int\limits_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} \approx - {{\Omega }_{{{\varphi }}}}\frac{{{{a}^{2}}{{{{\rho }}}^{2}}}}{{4R}}S$

При x = 1 маркер целиком находится в области твердотельного вращения вихря, в этом случае ${{f}_{ - }} = 0$, ${{h}_{ - }} = 0$ и из (3.10, 3.11) следует

(3.13)

$\int\limits_S {{{{\mathbf{v}}}_{t}}dS} \approx RS\left( { - {{\Omega }_{s}}{{{\mathbf{e}}}_{s}} + {{\Omega }_{{{\varphi }}}}{{{\mathbf{e}}}_{{{\varphi }}}}} \right),\quad \int\limits_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} \approx {{\Omega }_{{{\varphi }}}}\frac{{R{{{{\rho }}}^{2}}}}{4}S$

В переходной зоне $ - 1\,\, < \,\,x\,\, < \,\,1$, когда часть маркера расположена в области твердотельного вращения, а часть – на периферии, необходимые значения определяются по формулам (3.10), (3.11).

Качественное представление о свойствах уравнений движения (3.7) дает запись этих уравнений в виде

(3.14)

$\ddot {s} - s{{{{\dot {\varphi }}}}^{2}} + {{\mu }}\dot {s} \approx \,{{\mu }}{{a}_{s}},\,\,\,\,\,{{\ddot {\varphi }}} + 2{{\dot {s}{{\dot {\varphi }}}} \mathord{\left/ {\vphantom {{\dot {s}{{\dot {\varphi }}}} s}} \right. \kern-0em} s} + {{\mu \dot {\varphi }}} \approx {{\mu }}{{a}_{{{\varphi }}}},\,\,\,\,\,{{\dot {\omega }}} + {{\mu \omega }} \approx \frac{{{{\mu }}{{\Omega }_{{{\varphi }}}}}}{2}{\text{M}}$

и представленные на рис. 5 зависимости величин ${{a}_{s}}$, ${{a}_{{{\varphi }}}}$ и $M$ от $x$, вычисленные согласно соотношениям (3.10, 3.11) при ${{{\rho }} \mathord{\left/ {\vphantom {{{\rho }} a}} \right. \kern-0em} a} = 0.1$, ${{{{\Omega }_{s}}} \mathord{\left/ {\vphantom {{{{\Omega }_{s}}} {{{\Omega }_{{{\varphi }}}}}}} \right. \kern-0em} {{{\Omega }_{{{\varphi }}}}}} = 0.2$.

Рис. 5.

Графики зависимостей величин ${{a}_{{{\varphi }}}}$ (пунктир), ${{a}_{s}}$ (точки) и $M$ (сплошная) в переходной области $ - 1\,\, < \,\,x\,\, < \,\,1$ для маркера в форме диска.

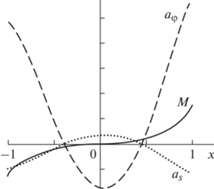
В (3.14) введено обозначение ${{\mu }} = {{{{\kappa }}S} \mathord{\left/ {\vphantom {{{{\kappa }}S} m}} \right. \kern-0em} m}$. При одновременном уменьшении всех линейных размеров маркера ${{\mu }}\, \to \,\infty $, а в случае уменьшения взаимодействия маркера с водой (${{\kappa }}\, \to \,{\text{0}}$) имеет место ${{\mu }}\, \to \,0$.

Вертикальные шкалы на рис. 5 не представлены, поскольку на них изображены величины разных размерностей, но соотношения между ${{a}_{s}}$, ${{a}_{{{\varphi }}}}$ находятся в точном соответствии с выражением (3.10). Вид уравнений (3.14), предельных соотношений (3.12), (3.13) и графиков ${{a}_{s}}$, ${{a}_{{{\varphi }}}}$ рис. 5 показывает, что после помещения на поверхность вихря в области его периферии (x = –1) маркер в виде диска “подхватывается” потоком жидкости и начинает движение к центру вихря (${{a}_{s}}$ принимает отрицательные значения) с одновременным обращением его центра масс в том же направлении, в котором вращается вихрь. Одновременно с этим сам маркер начинает вращаться относительно оси, проходящей через его центр масс, в противоположном направлении ($M$ принимает отрицательные значения), т.е. ${\mathbf{\omega }} \times {{{\mathbf{\Omega }}}_{{{\varphi }}}} < 0$.

По мере продвижения к центру вихревой воронки маркер попадает в переходную область ($ - 1 < x < 1$), пересекает границу между твердотельным и периферийным типами вращения вихря и постепенно меняет собственное вращение относительно центра масс на противоположное, так что начинает выполняться соотношение ${\mathbf{\omega }} \times {{{\mathbf{\Omega }}}_{{{\varphi }}}} > 0$, которое сохраняется после полного перехода маркера в область твердотельного вращения (x = 1).

При помещении маркера в периферийную область вихревой воронки уравнения (3.14) при использовании (3.12) принимают вид

(3.15)

$\ddot {s} - s{{{{\dot {\varphi }}}}^{2}} + {{\mu }}\dot {s} + {{\mu }}\frac{{{{a}^{2}}{{\Omega }_{s}}}}{s} + \frac{{{{a}^{4}}\Omega _{{{\varphi }}}^{2}}}{{{{s}^{3}}}} = 0,\quad {{\ddot {\varphi }}} + 2{{\dot {s}{{\dot {\varphi }}}} \mathord{\left/ {\vphantom {{\dot {s}{{\dot {\varphi }}}} s}} \right. \kern-0em} s} + {{\mu \dot {\varphi }}} - {{\mu }}\frac{{{{a}^{2}}{{\Omega }_{{{\varphi }}}}}}{{{{s}^{2}}}} = 0,\quad {{\dot {\omega }}} + {{\mu \omega + \mu }}\frac{{{{a}^{2}}{{\Omega }_{{{\varphi }}}}}}{{2{{s}^{2}}}} = 0$

Из второго уравнения (3.15) следует

(3.16)

${{\dot {\varphi }}} = \frac{1}{{{{s}^{2}}}}[{{a}^{2}}{{\Omega }_{{{\varphi }}}}(1 - {{{\text{e}}}^{{ - {{\mu }}t}}}) + s_{0}^{2}{{{{\dot {\varphi }}}}_{0}}{{{\text{e}}}^{{ - {{\mu }}t}}}],\quad {{s}_{0}} = {{\left. s \right|}_{{t = 0}}},\quad {{{{\dot {\varphi }}}}_{0}} = {{\left. {{{\dot {\varphi }}}} \right|}_{{t = 0}}}$

Подстановка (3.16) в первое уравнение системы (3.15) приводит к явному виду решений

(3.17)

${{\varphi }} = {{{{\varphi }}}_{0}} + \frac{{{{\Omega }_{s}}}}{{{{\Omega }_{{{\varphi }}}}}}\ln \left( {1 + \frac{{a{{\Omega }_{{{\varphi }}}}}}{{{{s}_{0}}\sqrt {{{\mu }}{{\Omega }_{s}}} }}\left( {{{{\text{e}}}^{{{{\mu }}t}}} - 1} \right)} \right),\quad s = \frac{{a{{\Omega }_{{{\varphi }}}}}}{{\sqrt {{{\mu }}{{\Omega }_{s}}} }}\left( {1 + \left( {\frac{{{{s}_{0}}\sqrt {{{\mu }}{{\Omega }_{s}}} }}{{a{{\Omega }_{{{\varphi }}}}}} - 1} \right){{{\text{e}}}^{{ - {{\mu }}t}}}} \right)$

на основании которых при учете малости величины ${{{{\Omega }_{s}}} \mathord{\left/ {\vphantom {{{{\Omega }_{s}}} {{{\Omega }_{{{\varphi }}}}}}} \right. \kern-0em} {{{\Omega }_{{{\varphi }}}}}}\,\, \ll \,\,1$ методами теории возмущений [11] выявляется связь между координатами центра масс маркера

(3.18)

$s \approx \frac{{a{{\Omega }_{{{\varphi }}}}}}{{\sqrt {{{\mu }}{{\Omega }_{s}}} }}\left( {1 + \left( {1 - \frac{{a{{\Omega }_{{{\varphi }}}}}}{{\sqrt {{{\mu }}{{\Omega }_{s}}} }}} \right){\text{exp}}\left( { - \frac{{{{\Omega }_{{{\varphi }}}}}}{{{{\Omega }_{s}}}}({{\varphi }} - {{{{\varphi }}}_{0}})} \right)} \right)$

которая означает движение по спирали на поверхности вихревой воронки по направлению к ее оси вращения.

Точный вид решения третьего уравнения системы (3.15) имеет слишком громоздкий вид, чтобы быть приведенным здесь, но в начальные моменты времени угловая частота собственного вращения маркера относительно оси, проходящей через его центр масс, определяется выражением

(3.19)

${{\omega }} = - \frac{{{{a}^{2}}{{\mu }}{{\Omega }_{{{\varphi }}}}}}{{s_{0}^{2}}}t + o(t)$

На больших временах выражение для частоты собственного вращения стремится к величине

(3.20)

${{\left. {{\omega }} \right|}_{{t\, \to \,\infty }}} = - \frac{{{{\mu }}{{\Omega }_{s}}}}{{2{{\Omega }_{{{\varphi }}}}}}$

при условии нахождения маркера еще на периферии вихревой воронки. В противном случае его собственное вращение описывается выражениями, приведенными далее.

Вид выражений (3.19, 3.20) указывает на то, что собственное вращение маркера в периферийной области происходит в противоположном направлении вращению вихревой воронки.

В начальные моменты времени поворот маркера относительно собственной оси противоположен повороту относительно оси воронки, а затем частота его собственного вращения постепенно уменьшается до момента времени $t_{*}^{{}} \approx \frac{{s_{0}^{2} - {{{(a + {{\rho }})}}^{2}}}}{{2{{a}^{2}}{{\Omega }_{s}}}}$, когда край маркера начинает входить в переходную зону и его движение уже не описывается системой (3.15). Процесс движения маркера в переходной зоне описывается столь громоздкими соотношениями, что не позволяет привести их явный вид.

В области ядра вихревой воронки движение маркера описывается системой уравнений

(3.21)

$\ddot {s} + {{\mu }}\dot {s} + \left( {{{\mu }}{{\Omega }_{s}} - {{{{{\dot {\varphi }}}}}^{2}} + \Omega _{{{\varphi }}}^{2}} \right)s = 0,\quad {{\ddot {\varphi }}} + 2{{\dot {s}{{\dot {\varphi }}}} \mathord{\left/ {\vphantom {{\dot {s}{{\dot {\varphi }}}} s}} \right. \kern-0em} s} + {{\mu \dot {\varphi }}} - {{\mu }}{{\Omega }_{{{\varphi }}}} = 0,\quad {{\dot {\omega }}} + {{\mu \omega }} - {{\mu }}{{{{\Omega }_{{{\varphi }}}}} \mathord{\left/ {\vphantom {{{{\Omega }_{{{\varphi }}}}} 2}} \right. \kern-0em} 2} = 0$

Решение второго уравнения системы (3.21) имеет вид

(3.22)

${{\dot {\varphi }}} = \frac{{{{\Omega }_{{{\varphi }}}}}}{{{{s}^{2}}}}\sum\limits_{n = 0}^\infty {\frac{{{{{( - 1)}}^{n}}}}{{{{{{\mu }}}^{n}}}}\frac{{{{\partial }^{n}}{{s}^{2}}}}{{\partial {{t}^{n}}}}} $

подстановка которого в первое уравнение системы (3.22) порождает решение вида

(3.23)

$s = {{s}_{*}}{\text{exp}}\left( { - \frac{{{\mu }}}{2}(1 - \sqrt {{\sigma }} )(t - {{t}_{*}})} \right),\quad {{\sigma }} = \frac{1}{2}({{\delta + }}\sqrt {{{{{\delta }}}^{2}} + 16{{\Omega _{{{\varphi }}}^{2}} \mathord{\left/ {\vphantom {{\Omega _{{{\varphi }}}^{2}} {{{{{\mu }}}^{2}}}}} \right. \kern-0em} {{{{{\mu }}}^{2}}}}} ),\quad {{\delta }} = 1 - 4\left( {\frac{{{{\Omega }_{s}}}}{{{\mu }}} + \frac{{\Omega _{{{\varphi }}}^{2}}}{{{{{{\mu }}}^{2}}}}} \right)$

при этом $s_{*}^{{}} = {{\left. s \right|}_{{t = {{t}_{ * }}}}}$, где $t_{*}^{{}}$ – некоторый момент времени, когда маркер целиком входит в область твердотельного вращения вихревой воронки.

Подстановка (3.23) в (3.22) позволяет получить выражение для угла поворота центра масс маркера

(3.24)

${{\varphi }} = \frac{{{{\Omega }_{{{\varphi }}}}}}{{\sqrt {{\sigma }} - 1}}(t - {{t}_{*}}) + {{{{\varphi }}}_{*}},\quad {{{{\varphi }}}_{*}} = {{\left. {{\varphi }} \right|}_{{t\, = \,{{t}_{ * }}}}}$

На основании выражений (24, 25) следует связь координат центра масс маркера вида

(3.25)

$s = {{s}_{*}}\exp \left( { - \frac{{{\mu }}}{{2{{\Omega }_{{{\varphi }}}}}}(\sqrt {{\sigma }} - {{\sigma }})\left( {{{\varphi }} - {{{{\varphi }}}_{*}}} \right)} \right)$

что указывает на то, что и в области твердотельного вращения маркер движется по логарифмической спирали к оси вращения вихревой воронки.

В случае малых частот вращения вихревой воронки, что соответствует условиям экспериментальных наблюдений, когда выполняются соотношения ${{{{\Omega }_{s}}} \mathord{\left/ {\vphantom {{{{\Omega }_{s}}} {{\mu }}}} \right. \kern-0em} {{\mu }}} \ll 1$ и ${{{{\Omega }_{{{\varphi }}}}} \mathord{\left/ {\vphantom {{{{\Omega }_{{{\varphi }}}}} {{\mu }}}} \right. \kern-0em} {{\mu }}} \ll 1$, выражения (3.24, 3.25) приобретают вид

(3.26)

${{\varphi }} = {{{{\varphi }}}_{*}} + {{\Omega }_{{{\varphi }}}}\left( {t - {{t}_{*}}} \right)\left( {1 + 2{{{{\Omega }_{s}}} \mathord{\left/ {\vphantom {{{{\Omega }_{s}}} {{\mu }}}} \right. \kern-0em} {{\mu }}}} \right),\quad s = {{s}_{*}}{\text{exp}}\left( { - \,{{\Omega }_{s}}\left( {t - {{t}_{*}}} \right)\left( {1 + {{{{\Omega }_{s}}} \mathord{\left/ {\vphantom {{{{\Omega }_{s}}} {{\mu }}}} \right. \kern-0em} {{\mu }}}} \right)} \right)$

Подстановка (3.26) в третье уравнение (3.21) приводит к результату

(3.27)

${{\omega }} = \frac{{{{\Omega }_{{{\varphi }}}}}}{2}(1 - {{e}^{{ - {{\mu }}(t - {{t}_{*}})}}}) + {{{{\omega }}}_{*}}{{e}^{{ - {{\mu }}(t - {{t}_{*}})}}},\quad {{\psi }} = {{{{\psi }}}_{*}} + \frac{{{{\Omega }_{{{\varphi }}}}}}{2}\left( {t - {{t}_{*}}} \right) - \frac{1}{{{\mu }}}\left( {\frac{{{{\Omega }_{{{\varphi }}}}}}{2} - {{{{\omega }}}_{*}}} \right)(1 - {{e}^{{ - {{\mu }}(t - {{t}_{*}})}}})$

где ${{\omega }}_{*}^{{}}$ и ${{\psi }}_{*}^{{}}$ – значения координат центра масс, частоты вращения и угла поворота вокруг собственной оси в момент времени $t_{*}^{{}}$ соответственно.

Как видно из (3.27), собственное вращение маркера совпадает по направлению с его вращением вокруг оси вихря, при этом ${{\psi }} - {{{{\psi }}}_{*}} \approx \frac{1}{2}\left( {{{\varphi }} - {{{{\varphi }}}_{*}}} \right)$.

Важная особенность выражений (3.24)–(3.27) состоит в том, что при использовании главных членов в выражениях для координат s и ${{\varphi }}$ центра масс маркера, которые как в области твердотельного вращения, так и на периферии вихревой воронки связаны соотношением общего вида

(3.28)

$s \approx \tilde {s}\exp \left( { - \frac{{{{\Omega }_{s}}}}{{{{\Omega }_{{{\varphi }}}}}}({{\varphi }} - {{\tilde {\varphi }}})} \right)$

где $\tilde {s}$, ${{\tilde {\varphi }}}$ – некоторые постоянные величины.

Уравнение (3.28) описывает логарифмическую спираль на поверхности вихревой воронки, по которой движется центр масс маркера, причем эта спираль совпадает с траекториями жидких частиц вблизи свободной поверхности. Таким образом, маркер увлекается приповерхностным потоком и совершает дополнительное вращение, обусловленное ненулевым моментом вязких сил, действующих на его нижнюю поверхность со стороны жидкости. Как в периферийной области, так и в области твердотельного вращения углы поворота маркера относительно собственной оси и центра масс относительно оси вращения воронки связаны соотношением вида

(3.29)

${{\psi }} - {{{{\psi }}}_{*}} \approx {{c}_{1}}\left( {{{\varphi }} - {{{{\varphi }}}_{*}}} \right) + {{c}_{0}}$

где ${{c}_{0}}$, ${{c}_{1}}$ – некоторые постоянные, в общем случае различные для областей периферии и твердотельного вращения.

Аналитические результаты (3.18), (3.25) для координаты s центра масс маркера не коррелируют с биениями на графиках рис. 3 по причине того, что модель (3.8) формы вихревой воронки идеализирована и не учитывает ее возможную эллиптичность и бегущие спиралевидные поверхностные гравитационно-капиллярные волны.

4. СРАВНЕНИЕ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

В систему (3.6), описывающую движение маркеров в вихревом течении, входит уравнение для изменения кинетического момента маркера. В установившихся режимах, в особенности, когда маркер находится в области твердотельного вращения, его частота ω обращения вокруг собственной оси практически постоянна во времени. Тогда из уравнения для кинетического момента $J{{\dot {\omega }}} = {{\kappa }}\left[ {\int_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} - {{\omega }}\int_S {{{r}^{2}}dS} } \right]$ при ${{\dot {\omega }}}\, \approx \,{\text{0}}$ следует

(4.1)

$\int\limits_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} - {{\omega }}\int\limits_S {{{r}^{2}}dS} \approx 0$

следовательно, имеет место результат

(4.2)

${{\omega }} \approx {{\int\limits_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} } \mathord{\left/ {\vphantom {{\int\limits_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} } {\int\limits_S {{{r}^{2}}dS} }}} \right. \kern-0em} {\int\limits_S {{{r}^{2}}dS} }}$

Рассмотрим ситуацию, когда в качестве маркера выбирается простейшая центральносимметричная относительно центра масс фигура – два маленьких плоских диска, каждый площадью $d\Sigma $ на расстоянии l друг от друга, соединенных бесконечно тонким абсолютно жестким стержнем, как показано на рис. 6.

Рис. 6.

Схема воздействия потока воды в вихревой воронке на маркер.

В этом случае

(4.3)

$\int\limits_S {{{r}^{2}}\,dS} = 2d\Sigma \frac{{{{l}^{2}}}}{4} = \frac{{{{l}^{2}}d\Sigma }}{2}$

Пусть маркер в некоторый момент времени занимает положение, показанное на рис. 1, причем его центр тяжести имеет координату s.

Тогда при использовании приближенного выражения для поля скорости вихревой воронки у поверхности ${{{\mathbf{v}}}_{t}} \approx R{{\Omega }_{{{\varphi }}}}{{{\mathbf{e}}}_{{{\varphi }}}}$ получается оценка

(4.4)

$\int\limits_S {\left[ {{\mathbf{r}} \times {{{\mathbf{v}}}_{t}}} \right] \times {{{\mathbf{e}}}_{n}}dS} = {{\Omega }_{{{\varphi }}}}\sin {{\alpha }}\frac{l}{2}d\Sigma \left( {s + \sin {{\alpha }}\frac{l}{2}} \right) - {{\Omega }_{{{\varphi }}}}\sin {{\alpha }}\frac{l}{2}d\Sigma \left( {s - \sin {{\alpha }}\frac{l}{2}} \right) = {{\Omega }_{{{\varphi }}}}{{\sin }^{2}}{{\alpha }}\frac{{{{l}^{2}}d\Sigma }}{2}$

Подстановка (4.3, 4.4) в (4.2) дает результат

(4.5)

${{\omega }} \approx {{\Omega }_{{{\varphi }}}}{{\sin }^{2}}{{\alpha }}$

Так как угол ${{\alpha }}$ меняется во времени (и, строго говоря, имеет место связь ${{\omega }} = {{\dot {\alpha }}}$), то в среднем за период частота собственного вращения оценивается величиной

(4.6)

${{\bar {\omega }}} \approx {{\Omega }_{{{\varphi }}}}\int\limits_0^{2{{\pi }}} {{{{\sin }}^{2}}{{\alpha }}\,d{{\alpha }}} = \frac{{{{\Omega }_{{{\varphi }}}}}}{2}$

Только в отдельные моменты времени, когда ${{\alpha }} = {{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2} + {{\pi }}n,$ $n = 1,2,...$, мгновенная частота собственного вращения сравнивается с частотой вращения поверхности вихря в твердотельной области.

Так как любой маркер, обладающий центральной симметрией относительно центра масс, можно разбить на пары таких вот маленьких маркеров в виде гантели, то следует ожидать результата, что независимо от формы собственное вращение маркера в области твердотельного вращения вихря будет подчиняться соотношению (4.6). Конечно, сам маркер при этом должен удовлетворять условию малости своего максимального размера по сравнению с наименьшим (по абсолютному значению) радиусом кривизны поверхности вихревой воронки, чтобы удовлетворять условию справедливости системы (7).

Так как углы ${{\varphi }}$ и ${{\psi }}$ в области твердотельного вращения подчиняются зависимостям φ = = ${{{{\varphi }}}_{0}} + {{\Omega }_{{{\varphi }}}}t$, ${{\psi }} = {{{{\psi }}}_{0}} + {{\omega }}t$, то при больших временах имеет место

(4.7)

$\frac{{d\,{{\psi }}}}{{d\,{{\varphi }}}}\, = \,\frac{{{\omega }}}{{{{\Omega }_{{{\varphi }}}}}} = \frac{1}{2}$

Проведенные опыты показали, что, кроме вращения маркера вокруг центра свободной поверхности вихревого течения, он также вращается вокруг собственной оси. Полученные экспериментальные данные позволяют построить график зависимости $\psi (\varphi )$ угла верчения маркера от угла поворота маркера относительно оси вихревой воронки, рис. 7.

Рис. 7.

Взаимосвязь углов вращения ${{\varphi }}$ и верчения ${{\psi }}$ для ($\Omega = $ 3.3 с^–1); (а) прямоугольные маркеры: 1, 2 – 0.5 см × $ \times $ 1.0 см $ \times $ 0.3 см, H = 40 и 20 см, 3, 4 – 1.0 см $ \times $ 2.0 см $ \times $ 0.3 см, H = 20 и 40 см; (б) крестообразные маркеры 1.5 см × $ \times $ 1.5 см $ \times $ 0.3 см: 1, 2 – H = 20, 40 см.

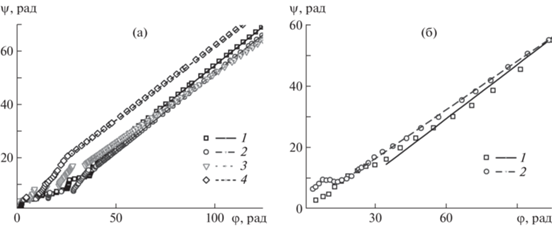
Начальные части графиков, представленных на рис. 7, представляют собой начальные моменты движения – “интервалы вовлечения” маркеров в движение вихревой воронки. Параметры линейных приближений после “интервалов вовлечения” представлены в табл. 1.

Таблица 1.

Линейная интерполяция ${{\psi }}({{\varphi }})$ коэффициентами наклона

Рис.	Прямая	Маркер	Размеры, см	Глубина жидкости, см	Наклон $\Delta {{\psi /}}\Delta {{\varphi }}$
7а	1	прямоугольник	0.5 × 1.0	40	0.595
	2		0.5 × 1.0	20	0.587
	3		1.0 × 2.0	20	0.518
	4		1.0 × 2.0	40	0.558
7б	1	крест	1.5 × 1.5	20	0.590
7б	2	крест	1.5 × 1.5	40	0.532

Экспериментальные результаты, приведенные в табл. 1, показывают хорошее совпадение с теоретическими расчетами (4.7) для маркеров, обладающих центральной симметрией.

То, что зависимость (4.7) свойственна только маркерам, обладающим центральносимметричными формами, наглядно демонстрируется на рис. 8, где показаны ${{\psi }}({{\varphi }})$ для маркеров в виде пятиугольной звезды, прямоугольника и правильного треугольника.

Рис. 8.

Сравнение зависимостей ${{\psi }}({{\varphi }})$ для маркера, обладающего центральной симметрией (2 – прямоугольник), и маркеров, у которых такой симметрии нет (1 –пятиконечная звезда, 3 – правильный треугольник).

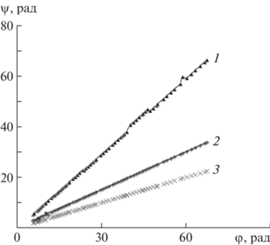
Лишь один из этих трех маркеров – маркер прямоугольной формы, – обладающий центральной симметрией, подчиняется зависимости (4.7), в то время как поведение двух остальных маркеров описывается общим соотношением (3.29) теоретической модели.

Необходимо также отметить экспериментально наблюдаемую важную особенность в поведении маркеров: после помещения на поверхность вихря в области его периферии маркер (например, в виде диска) “подхватывается” потоком жидкости и начинает движение к центру вихря с одновременным обращением его центра масс в том же направлении, в котором вращается вихрь. Одновременно с этим сам маркер начинает вращаться относительно оси, проходящей через его центр масс, в противоположном направлении. По мере продвижения к центру вихревой воронки маркер попадает в переходную область, пересекает границу между периферийным и твердотельным типами вращения вихря и постепенно меняет собственное вращение относительно центра масс на направление, совпадающее с направлением вращения жидкости в вихревой воронке, и которое сохраняется после полного перехода маркера в область твердотельного вращения, что также соответствует представленной выше теоретической модели.

ЗАКЛЮЧЕНИЕ

Проведенные экспериментальные и теоретические исследования показали, что движение маркера, размещенного на поверхности жидкой вихревой воронки, является сложным и включает тангенциальное смещение (вращение относительно центра потока вихревого желоба), радиальное смещение и вращение относительно собственной оси. Характер движения зависит от условий эксперимента (глубина жидкости и частота вращения диска индуктора) и формы маркера. Экспериментальные зависимости угла верчения от угла поворота в области вращения твердого тела хорошо согласуются с теоретическими зависимостями, полученными на основе предложенной математической модели.

Также экспериментально и теоретически доказано, что на периферии вихревой воронки, вне области ее твердотельного вращения, направление вращения маркера вокруг собственной оси, проходящей перпендикулярно его плоскости через центр масс, направлено в противоположную сторону по отношению к направлению вращения жидкостной полости. В области твердотельного вращения вихревой воронки указанные направления совпадают.

Предложенная модель переноса плавающих маркеров по поверхности вихревой воронки также может быть использована для изучения динамики переноса “островов” мусора крупномасштабными океаническими вихрями.

Работа выполнена при финансовой поддержке проекта Российской Федерации в лице Министерства образования и науки России № 075-15-2020-802.

Список литературы

Escudier M.P. Observations of the flow produced in a cylindrical container by a rotating endwall // Exp. Fluids. 1984. 2. P. 189–196.
Escudier M.P., O’Leary, R.J. Poole Flow produced in a conical container by a rotating endwall // Int. J. Heat Fluid Flow. 2007. V. 28. Iss. 6. P. 1418–1428.
Grigors’ev Y.N., Ershov I.V. Energy Estimate of the Critical Reynolds Numbers in a Compressible Couette Flow. Effect of Bulk Viscosity// J. Appl. Mech. Tech. Phys. 2010. V. 51. P. 669–675. https://doi.org/10.1007/s10808-010-0086-y
Алексеенко С.В., Шторк С.И. Бегущий распад вихря // Письма в ЖТФ. 1997. Т. 23. Вып. 22. С. 24–28.
Esculier M.P. // Prog. Aerospace Sci. 1988. V. 25. P. 189–229.
Randall J.D., Leibovich S. The critical state: a trapped wave model of vortex breakdown // J. Fluid. Mech. 1973. № 58. P. 495–515.
Roland Becker. Mesh Adaptation for Stationary Flow Control // J. Math. Fluid. Mech. 2001. V. 3 (4). P. 317–341. 2001. https://doi.org/10.1007/PL00000974
Степанова Е.В., Чаплина Т.О., Чашечкин Ю.Д. Формы частичного распада масляного тела в составном вихре // Изв. РАН. МЖГ. 2014. № 5. С. 52–64.
Кистович А.В., Чаплина Т.О., Степанова Е.В. Спиральная структура траекторий жидких частиц вблизи поверхности вихря // Вычислительные технологии. 2019. Т. 24. № 2. С. 67–77.
Чаплина Т.О., Степанова Е.В. Характер углового перемещения маркеров различного вида на поверхности сложного вихревого потока // Процессы в геосредах. 2018. 1 (14). С. 793–803.
Найфэ А. Введение в методы возмущений. М.: Мир, 1984, 536 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал