1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2022

Известия РАН. Механика жидкости и газа, 2022, № 6, стр. 55-62

НЕИЗОТЕРМИЧЕСКОЕ ТЕЧЕНИЕ НЕНЬЮТОНОВСКОЙ ЖИДКОСТИ СО СВОБОДНОЙ ПОВЕРХНОСТЬЮ В КОАКСИАЛЬНОМ КАНАЛЕ

Е. И. Борзенко a, *, О. А. Дьякова a, Г. Р. Шрагер a

a Томский государственный университет
Томск, Россия

* E-mail: borzenko@ftf.tsu.ru

Поступила в редакцию 20.05.2022
После доработки 21.06.2022
Принята к публикации 21.06.2022

Полный текст (PDF)

Аннотация

Исследовано неизотермическое течение неньютоновской жидкости в поле силы тяжести с учетом диссипативного разогрева, зависимости эффективной вязкости от температуры и наличия свободной поверхности, реализуемое при заполнении коаксиального канала. Реологическое поведение среды описывается моделью Сross-WLF. Задача решается численно с использованием оригинальной вычислительной технологии на основе метода контрольного объема и метода инвариантов для удовлетворения граничных условий на свободной границе. Продемонстрированы характеристики потока в процессе заполнения при различных значениях определяющих параметров.

Ключевые слова: неизотермическое течение, свободная поверхность, неньютоновская жидкость, коаксиальный канал, численное моделирование

Течения жидкости со свободной поверхностью широко распространены в природе и технических приложениях. В частности, в металлургии при переработке полимерных материалов методом литья реализуется процесс заполнения емкостей жидкой средой, характерной особенностью которого является наличие свободной поверхности. Течения подобного типа во многих случаях осуществляются в неизотермических условиях, а реологическое поведение жидких сред зависит от интенсивности тензора скоростей деформаций и температуры [1]. Плоские и осесимметричные течения вязких сред при заполнении каналов достаточно хорошо изучены. Подробное описание кинематики изотермического течения вязкой жидкости и эволюции свободной поверхности изложено в [2–5]. Влияние вязкой диссипации и зависимости вязкости от температуры на характеристики гидродинамического процесса изложено в [6–9]. Учет неньютоновского поведения жидкости при заполнении плоских каналов и круглых труб реализуется в [10–16]. Следует отметить не достаточно полное представление результатов исследования течений жидкости при заполнении коаксиального канала [1, 17–19]. Особенности технологии литьевого формования изделий описаны в [1]. В [17] представлены исследования эволюции формы свободной границы для неизотермического течения аномально вязкой жидкости. В [18] представлены результаты численного моделирования ползущего изотермического течения нелинейно-вязкопластичной жидкости, описана динамика выделенных макрообъемов. Процесс заполнения круглой трубы с центральным телом ньютоновской жидкостью исследован в [19].

Целью данной работы является исследование процесса заполнения коаксиального канала неньютоновской жидкостью с учетом вязкой диссипации и зависимости реологических свойств от температуры. В настоящей статье впервые представлены результаты исследования эволюции свободной поверхности, кинематических и динамических характеристик потока жидкости, описываемой реологической моделью Cross-WLF, при заполнении коаксиального канала в неизотермических условиях.

1. ПОСТАНОВКА ЗАДАЧИ

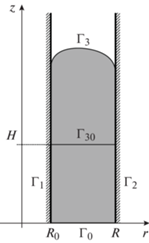
Исследуется неизотермическое осесимметричное течение неньютоновской жидкости в поле силы тяжести с учетом диссипативного разогрева, зависимости эффективной вязкости от температуры и наличия свободной поверхности, реализуемое при заполнении коаксиального канала с внешним радиусом R и внутренним R0. Математическая постановка задачи включает уравнения движения, неразрывности и энергии. Предполагается, что изменения теплоемкости, плотности и коэффициента теплопроводности в рассматриваемых температурных диапазонах незначительны, и поэтому считаются постоянными. Область течения схематично представлена на рис. 1.

Рис. 1.

Область течения.

Жидкость подается через входное сечение Г0 с заданным постоянным расходом и температурой. На внутренней Г1 и внешней Г2 стенках заданы значения температуры Т1 и T2 соответственно и выполняется условие прилипания. На свободной поверхности Г3 реализуются условия отсутствия касательных напряжений и равенства нормального – внешнему давлению, которое без ограничения общности принимается равным нулю. Движение свободной границы осуществляется в соответствии с кинематическим условием. В начальный момент времени канал заполнен жидкостью до высоты $H = 2R - {{R}_{0}}$, свободная поверхность имеет плоскую горизонтальную форму Г30, а температура жидкости равна Т1.

Реологическое поведение среды описывается моделью Сross-WLF (Williams–Landel–Ferry) [20–22], согласно которой формула для определения эффективной вязкости имеет вид

(1.1)
$\eta \left( {\dot {\gamma },T} \right) = {{\eta }_{0}}\left( T \right){\text{/}}[1 + {{\left( {{{\eta }_{0}}\left( T \right)\dot {\gamma }{\text{/}}\tau {\kern 1pt} *} \right)}^{{1 - m}}}]$
где ${{\eta }_{0}}\left( T \right) = {{\eta }_{1}}{\text{exp}}\left( {\frac{A}{{T - T{\kern 1pt} *}}} \right)$ – предельное значение вязкости при малых величинах интенсивности тензора скоростей деформации $\dot {\gamma }$, Т – температура жидкости в потоке, ${{\eta }_{1}}$, τ*, А, m и T* – параметры модели. Данная модель адекватно описывает реологические свойства аморфных полимеров и часто используется в математических постановках задач о течениях подобных сред [23, 24].

Поставленная задача решается в безразмерных переменных. В качестве масштабов обезразмеривания выбраны следующие величины: длины – внешний радиус канала R, скорости – среднерасходная скорость во входном сечении U0, времени – R/U0, вязкости – величина ${{\eta }_{1}}$, давления – ${{\eta }_{1}}{{U}_{0}}{\text{/}}R$. Безразмерная температура определяется формулой $\theta = \left( {T - T{\kern 1pt} *} \right){\text{/}}{{T}_{1}}$. Таким образом, уравнения движения, неразрывности в векторной форме и уравнение энергии с сохранением обозначения для безразмерных переменных запишутся в виде

$\begin{gathered} \operatorname{Re} \frac{{d{\mathbf{U}}}}{{dt}} = - \nabla p + \nabla \left( {2\eta E} \right) + {\mathbf{W}} \\ \nabla \times {\mathbf{U}} = 0 \\ {\text{Pe}}\frac{{d{{\theta }}}}{{dt}} = {{\nabla }^{2}}\theta + {\text{Br}}\,{\text{Ф}} \\ \end{gathered} $

Здесь U – вектор скорости с компонентами Ur, Uz в цилиндрической системе координат (r, z), t – время, p – давление, E – тензор скоростей деформации, η – безразмерная эффективная вязкость, W = (0, –W), Ф – диссипативная функция. В постановку задачи вошли следующие безразмерные критерии: $\operatorname{Re} = \rho {{U}_{0}}R{\text{/}}{{\eta }_{1}}$ – число Рейнольдса; ${\text{Pe}} = c\rho {{U}_{0}}R{\text{/}}\lambda $ – число Пекле; Br = ${{\eta }_{1}}U_{0}^{2}{\text{/}}\left( {{{T}_{1}}\lambda } \right)$ – число Бринкмана; ${\text{W}} = \rho g{{R}^{2}}{\text{/}}\left( {{{\eta }_{1}}{{U}_{0}}} \right)$ – число, характеризующее соотношение гравитационных и вязких сил, где ρ – плотность, g – ускорение силы тяжести, λ – коэффициент теплопроводности, c –теплоемкость.

Эффективная вязкость среды в безразмерном виде определяется формулой

$\eta = \frac{{{{\eta }_{0}}\left( \theta \right)}}{{1 + {{{\left( {{{C}_{1}}{{\eta }_{0}}\left( \theta \right) \times \dot {\gamma }} \right)}}^{{1 - m}}}}},\quad {{\eta }_{0}}\left( \theta \right) = {\text{exp}}\left( {\frac{{{{C}_{2}}}}{\theta }} \right)$
где ${{C}_{1}} = {{\eta }_{1}}{{U}_{0}}{\text{/}}\tau {\kern 1pt} *R$, ${{C}_{2}} = A{\text{/}}{{T}_{1}}$ – безразмерные числа.

Граничные условия записываются следующим образом

$\begin{gathered} {{{\text{Г}}}_{0}}:{{U}_{r}} = 0,\quad {{U}_{z}} = {{f}_{1}}\left( r \right),\quad \theta = {{f}_{2}}\left( r \right) \\ {{{\text{Г}}}_{1}}:{{U}_{r}} = 0,\quad {{U}_{z}} = 0,\quad \theta = {{\theta }_{1}} \\ \end{gathered} $
$\begin{gathered} {{{\text{Г}}}_{2}}:{{U}_{r}} = 0,\quad {{U}_{z}} = 0,\quad \theta = {{\theta }_{2}} \\ {{{\text{Г}}}_{3}}:\frac{{\partial {{U}_{n}}}}{{\partial s}} + \frac{{\partial {{U}_{s}}}}{{\partial n}} = 0,\quad - p + 2\eta \frac{{\partial {{U}_{n}}}}{{\partial n}} = 0,\quad \frac{{\partial \theta }}{{\partial n}} = 0 \\ \end{gathered} $

Здесь ${{\theta }_{1}} = \left( {{{T}_{1}} - T{\kern 1pt} *} \right){\text{/}}{{T}_{1}}$ и ${{\theta }_{2}} = \left( {{{T}_{2}} - T*} \right){\text{/}}{{T}_{1}}$ – значения безразмерных температур на внутренней и внешней стенках канала; ${{U}_{n}}$ и ${{U}_{s}}$ – нормальная и касательная компоненты вектора скорости на свободной поверхности соответственно;  f1(r), f2(r) – функции скорости и температуры, соответствующие установившемуся течению данной жидкости в коаксиальном зазоре с заданным постоянным расходом, которые определяются численно в результате решения одномерной задачи. Математическая постановка одномерной задачи включает стационарные уравнения движения и энергии относительно координаты r с учетом диссипативного разогрева и формулы для эффективной вязкости (1.1) с условиями прилипания и заданной температурой на твердой стенке. Конечно-разностные аналоги уравнений системы записываются в форме, используемой для реализации метода прогонки. Совместное решение уравнений для получения стационарных полей скорости и температуры обуславливает организацию итерационного процесса.

2. МЕТОД РЕШЕНИЯ

Сформулированная задача решается численно методом контрольного объема для расчета характеристик потока. Алгоритм SIMPLE [25] применяется для удовлетворения уравнения неразрывности. Для численной реализации граничных условий на свободной поверхности используется метод инвариантов [26]. На линии трехфазного контакта используется условие проскальзывания при динамическом краевом угле, равном π [27].

Тестирование методики расчета проводилось для значений теплофизических характеристик полиэтилена марки PE2042E из экспериментальной работы [23] для случая заполнения коаксиального зазора с внешним радиусом 0.01 м со среднерасходной скоростью 0.02 м/с, что соответствует следующим значениям безразмерных критериев Re = 0.0001, W = 0.0244, Pe = 1252, C1 = = 0.066, m = 0.3, ${{R}_{0}}{\text{/}}R = 0.2$. Температура стенок соответствует значениям, которые обеспечивают переработку полиэтилена данной марки методом литья под давлением.

Для проверки аппроксимационной сходимости проведена серия расчетов на последовательности сеток при температуре внутренней и внешней стенок ${{T}_{1}} = {{T}_{2}} = 200^\circ {\text{C}}$. Сходимость проверяется по координатам и компоненте скорости Uz точки свободной поверхности с максимальным значением z в момент времени t = 1. Данные, представленные в табл. 1, демонстрируют сходимость.

Таблица 1.

Значения характеристик свободной поверхности (${{\theta }_{1}} = {{\theta }_{2}} = 0.55$, C2 = 1, Br = 0.0045)

hr hz rmax zmax Uz
1/12 2/12 0.5028 2.9098 1.0743
1/25 2/25 0.5518 2.8903 1.0203
1/50 2/50 0.5749 2.8972 1.0108

Дальнейшие расчеты проводились на прямоугольной сетке с шагами по пространству hr = = 1/25 и hz = 2/25 и шагом по времени Δt = 10–4.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

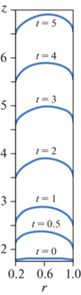
Все представленные ниже результаты параметрических исследований получены для следующих значений безразмерных чисел: Re = 0.0001, W = 0.0244, Pe = 1252, m = 0.3, C1 = 0.066, ${{R}_{0}}{\text{/}}R = 0.2$. Значения параметров, относительно которых определяются зависимости характеристик течения, помещены в подписях к рисункам и таблице. В процессе заполнения первоначально плоская свободная поверхность выгибается, принимая выпуклую форму, и перемещается вдоль канала со среднерасходной скоростью, что демонстрирует рис. 2. Как и в случае заполнения круглой трубы или плоского канала [9, 28], для коаксиального зазора наблюдается фонтанирующий характер течения. Отметим, что фонтанирующим течением принято называть движение среды в окрестности поверхности раздела двух несмешивающихся потоков, когда одна жидкость вытесняет другую [29].

Рис. 2.

Эволюция формы свободной поверхности (θ1 = 0.55, θ2 = 0.66, C2 = 1, Br = 0.0045).

На рис. 3а представлены линии тока в неподвижной системе координат, а на рис. 3б – в системе, движущейся со среднерасходной скоростью, в момент времени t = 5.

Рис. 3.

Линии тока в неподвижной (а) и подвижной (б) системах координат в момент времени t = 5 (θ1 = 0.55, θ2 = 0.66, C2 = 1, Br = 0.0045).

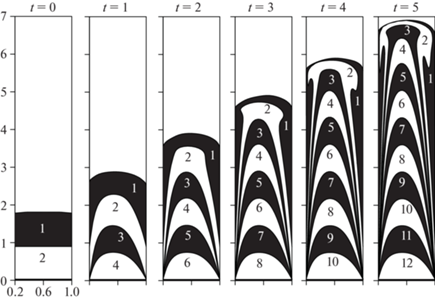
Дополнительную информацию о характере течения дают топограммы массораспределения порций жидкости, которые представляют собой объемы жидкости, последовательно поступающие в канал через входное сечение в течение заданного промежутка времени. На рис. 4 приведены топограммы, в которых порции отличаются цветами, а цифрами обозначены их порядковые номера. В области одномерного течения порции деформируются в соответствии с профилем аксиальной скорости. В окрестности свободной поверхности порции приобретают характерную грибовидную форму и перераспределяются вдоль стенок канала.

Рис. 4.

Топограммы массораспределения в различные моменты времени при θ1 = 0.55, θ2 = 0.66, C2 = 1, Br = 0.0045.

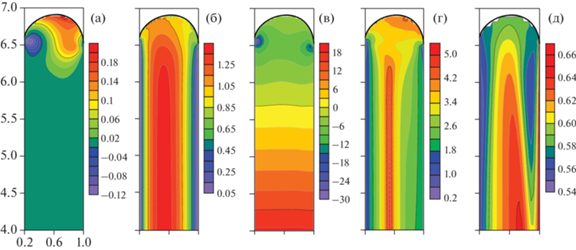
Распределения характеристик потока в момент времени t = 5 представлены на рис. 5. Анализ распределений компонент вектора скорости и давления показывает, что в потоке условно можно выделить две области: зона двумерного течения в окрестности свободной поверхности и область одномерного течения в остальной части потока. Распределение вязкости (рис. 5г) также подтверждает описанную кинематику течения. Поле температуры имеет двумерный характер по всей области течения (рис. 5д).

Рис. 5.

Распределения характеристик потока в момент времени t = 5 при θ1 = 0.55, θ2 = 0.66, C2 = 1, Br = 0.0045: а – поле скорости Ur, б – поле скорости Uz, в – поле давления, г – поле эффективной вязкости, д – поле температуры.

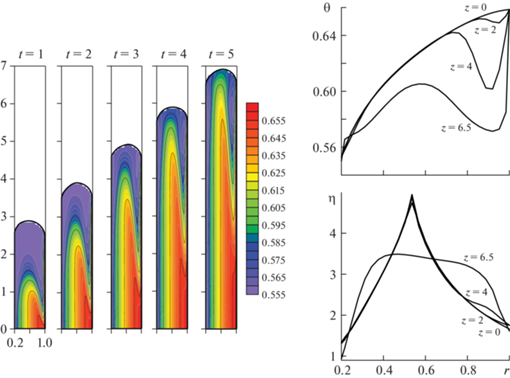
Эволюция поля температуры с течением времени представлена на рис. 6а. Поскольку при Pe = 1252 доминирует конвективный механизм переноса тепла в потоке, то и распределения температуры также подтверждают описанную выше кинематику течения. Диссипативный разогрев жидкости и зависимость эффективной вязкости от температуры формируют наблюдаемый профиль температуры в потоке (рис. 6б). В области одномерного течения профиль аксиальной скорости предполагает наличие экстремума, в окрестности которого интенсивность тензора скоростей деформаций стремится к нулю, что приводит к резкому увеличению эффективной вязкости согласно формуле (1.1). В зоне фонтанирующего течения профиль вязкости сглаживается за счет двумерного характера течения.

Рис. 6.

Эволюция поля температур с течением времени (а) и распределения температуры и эффективной вязкости в поперечных сечениях z = const в момент времени t = 5 (б) при θ1 = 0.55, θ2 = 0.66, C2 = 1, Br = 0.0045.

Влияние граничных условий на твердых стенках на распределение температуры демонстрирует рис. 7. В случае совпадения значений температуры на внешней и внутренней стенках канала в потоке наблюдается небольшая неоднородность ее распределения, связанная с диссипативным эффектом. Для варианта задания граничных условий с различными температурами на стенках распределения температуры соответствуют кинематике фонтанирующего течения в окрестности свободной поверхности. Изменение величины радиуса внутреннего цилиндра при прочих равных не приводит к качественным изменениям в распределении теплофизических характеристик потока.

Рис. 7.

Поля температур (а) и профили скорости $U_{r}^{{\max }}$ (б) при различных значениях граничных условий на твердых стенках: 1 – θ1 = θ2 = 0.55, C2 = 1, Br = 0.0045; 2 – θ1 = 0.6, θ2 = 0.5, C2 = 0.91, Br = 0.0041; 3 – θ1 = 0.55, θ2 = 0.66, C2 = 1, Br = 0.0045; 4 – θ1 = θ2 = 0.6, C2 = 0.91, Br = 0.0041.

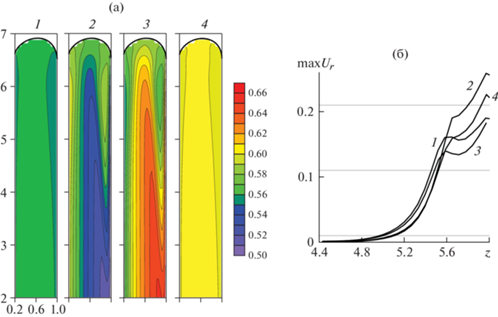
Распределения максимальных значений радиальной компоненты вектора скорости в поперечных сечениях вдоль оси z представлено на рис. 7б в момент времени, когда координата вершины свободной поверхности z = 6. Характер распределений подтверждает формирование двух зон: одномерное и фонтанирующее течения. Область, в которой скорость отлична от нуля, соответствует двухмерному течению вблизи свободной поверхности.

ЗАКЛЮЧЕНИЕ

Выполнено исследование процесса неизотермического заполнения коаксиального канала жидкостью Cross-WLF с учетом диссипативного разогрева и зависимости реологических характеристик от температуры. Теплофизические характеристики среды соответствуют полиэтилену марки PE2042E. Задача решена численно с использованием оригинальной вычислительной технологии на основе метода контрольного объема и метода инвариантов для удовлетворения граничных условий на свободной границе. Продемонстрированы характеристики потока в процессе заполнения при различных значениях определяющих параметров. Выявлены зона двумерного течения в окрестности свободной поверхности и зона одномерного течения вдали от нее. Установлено, что температура стенок в диапазоне 200–250°С оказывает слабое влияние на кинематику потока. В области одномерного течения изотермы параллельны стенкам канала, а в окрестности свободной поверхности они деформируются в соответствии с кинематикой фонтанирующего течения.

Исследование выполнено при поддержке гранта РНФ (проект № 18-19-00021-П).

Список литературы

  1. Глушков И.А., Милехин Ю.М., Меркулов В.М., Банзула Ю.Б. Моделирование формования изделий из свободно-литьевых композиций. М.: Архитектура-С, 2007. 362 с.

  2. Борзенко Е.И., Якутенок В.А. Эволюция свободной поверхности при заполнении плоских каналов вязкой жидкостью // Изв. РАН. МЖГ. 2008. № 1. С. 24–30.

  3. Mitsoulis E. Fountain flow revisited: The effect of various fluid mechanics parameters // AIChE J. 2010. V. 56. № 5. P. 1147–1162.

  4. Mavridis H., Hrymak A.N., Vlachopoulos J. Mathematical modeling of injection mold filling: A review // Adv. Polym. Technol. 1986. V. 6. № 4. P. 457–466.

  5. Coyle D.J., Blake J.W., Macosko C.W. The kinematics of fountain flow in mold-filling // AIChE J. 1987. V. 33. № 7. P. 1168–1177.

  6. Nguyen-Chung T., Mennig G. Non-isothermal transient flow and molecular orientation during injection mold filling // Rheol. Acta. 2001. V. 40. № 1. P. 67–73.

  7. Otmani R.E., Zinet M., Boutaous M., Benhadid H. Numerical simulation and thermal analysis of the filling stage in the injection molding process: Role of the mold-polymer interface // J. Appl. Polym. Sci. 2011. V. 121. № 3. P. 1579–1592.

  8. Wang W., Li X., Han X. Numerical simulation and experimental verification of the filling stage in injection molding // Polym. Eng. Sci. 2012. V. 52. № 1. P. 42–51.

  9. Борзенко Е.И., Фролов О.Ю., Шрагер Г.Р. Фонтанирующее течение вязкой жидкости при заполнении канала с учетом диссипативного разогрева // Изв. РАН. МЖГ. 2014. № 1. С. 45–55.

  10. Otmani E.R., Zinet M., Boutaous M., Chantrenne P., Benhadid H. Numerical simulation of the filling phase in the polymer injection moulding process with a conservative level set method // Int. J. Mater. Form. 2008. V. 1. № S1. P. 731–734.

  11. Липанов А.М., Альес М.Ю., Константинов Ю.Н. Численное моделирование ползущих течений неньютоновских жидкостей со свободной поверхностью // Математическое моделирование. 1993. В. 5. № 7. С. 3–9.

  12. Mavridis H., Hrymak A.N., Vlachopoulos J. Finite element simulation of fountain flow in injection molding // Polym. Eng. Sci. 1986. V. 26. № 7. P. 449–454.

  13. Gogos C.G., Huang C.F., Schmidt L.R. The process of cavity filling including the fountain flow in injection molding // Polym. Eng. Sci. 1986. V. 26. № 20. P. 1457–1466.

  14. Mitsoulis E. Fountain flow of pseudoplastic and viscoplastic fluids // J. Nonnewton. Fluid Mech. 2010. V. 165. № 1–2. P. 45–55.

  15. Borzenko E.I., Ryltseva K.E., Shrager G.R. Free-surface flow of a viscoplastic fluid during the filling of a planar channel // J. Nonnewton. Fluid Mech. 2018. V. 254. P. 12–22.

  16. Borzenko E.I., Frolov O.Y., Shrager G.R. Kinematics of the fountain flow during pipe filling with a power-law fluid // AIChE J. 2019. V. 65. № 2. P. 850–858.

  17. Чехонин К.А., Липанов А.М., Булгаков В.К. Заполнение области между вертикальными коаксиальными цилиндрами аномально-вязкой жидкостью в неизотермических условиях // ИФЖ. 1989. В. 57. № 4. С. 577–583.

  18. Чехонин К.А., Сухинин П.А. Движение нелинейно вязкопластичной жидкости со свободной поверхностью при заполнении осесимметричного объема // Математическое моделирование. 2001. В. 13. № 3. С. 89–102.

  19. Борзенко Е.И., Шрагер Г.Р. Кинематика течения вязкой жидкости при заполнении трубы с коаксиальным центральным телом // Изв. РАН. МЖГ. 2020. № 3. С. 51–58.

  20. Cross M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems // J. Colloid Sci. 1965. V. 20. № 5. P. 417–437.

  21. Williams M.L., Landel R.F., Ferry J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids // J. Am. Chem. Soc. 1955. V. 77. № 14. P. 3701–3707.

  22. Виноградов Г.В., Малкин А.Я. Реология полимеров. М: Химия, 1977. 440 с.

  23. Sleiman G.E.H., Petit I., Allanic N., Belhabib S., Madec Y., Launay J., Deterre R. Study of the rheological behavior of polypropylene/polyethylene extruded mixture using an instrumented die // AIP Conf. Proc. 1914. 2017. P. 040005-1–040005-5.

  24. Sorrentino A., Pantani R. Determination of the effect of pressure on viscosity of an isotactic polypropylene // Polym. Bull. 2013. V. 70. № 7. P. 2005–2014.

  25. Patankar S.V. Numerical heat transfer and fluid flow. N.Y.: Hemisphere Pub. Corp., 1980. 197 p.

  26. Васенин И.М., Сидонский О.Б., Шрагер Г.Р. Численное решение задачи о движении вязкой жидкости со свободной поверхностью // Доклады АН СССР. 1974. В. 217. № 2. С. 295–298.

  27. Борзенко Е.И., Шрагер Г.Р. Влияние вида граничных условий на линии трехфазного контакта на характеристики течения при заполнении канала // Прикладная механика и техническая физика. 2015. В. 56. № 2. С. 3–14.

  28. Борзенко Е.И., Фролов О.Ю., Шрагер Г.Р. Фонтанирующее неизотермическое течение вязкой жидкости при заполнении круглой трубы // Теоретические основы химической технологии. 2014. В. 48. № 6. С. 677–684.

  29. Rose W. Fluid–Fluid Interfaces in Steady Motion // Nature. 1961. V. 191. P. 242–243.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал