Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 66-76

НАЧАЛЬНО-КРАЕВАЯ ЗАДАЧА О ПОВЕДЕНИИ ЛЕДЯНОГО ПОКРОВА ПОД ДЕЙСТВИЕМ НАГРУЗКИ ПРИ НАЛИЧИИ СДВИГОВОГО ПОТОКА

Л. А. Ткачева^*

Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 11.10.2021
После доработки 10.11.2021
Принята к публикации 20.11.2021

EDN: MNHJWF
DOI: 10.31857/S0568528122020104

Аннотация

Построено решение задачи о поведении ледяного покрова на поверхности идеальной несжимаемой жидкости конечной глубины под действием локальной области давления при наличии потока со сдвигом скорости. Рассмотрены случаи импульсного воздействия и периодической по времени осесимметричной нагрузки. Использован метод преобразования Фурье в рамках линейной теории волн. Исследован прогиб ледяного покрова в зависимости от градиента скорости течения, коэффициента сжатия и толщины ледяного покрова.

Ключевые слова: тонкая упругая плавающая пластина, изгибно-гравитационные волны, сдвиг скорости, начально-краевая задача

Изучение волновых процессов в море с плавающим ледяным покровом является одним из важнейших условий эффективного освоения и использования морских ресурсов в условиях северных морей. Имеется значительное число работ о влиянии различных физических факторов на характер распространения изгибно-гравитационных волн в плавающем ледяном покрове. Однако влияние течения со сдвигом скорости изучено недостаточно. Имеется всего несколько работ на эту тему [1–5]. Во всех этих работах рассмотрена двумерная задача. В этом случае возмущения в жидкости носят потенциальный характер.

Достаточно хорошо изучено влияние сдвига скорости течения на поверхностные волны (см. [6–13] и имеющуюся в них библиографию). В трехмерном случае возмущения не потенциальны, носят вихревой характер [13]. Волны, вызванные начальными осесимметричными возмущениями, в жидкости под ледяным покровом в отсутствие течения исследовались в работе [14] и с учетом неравномерного сжатия ледяного покрова в [15].

В настоящей работе приведено решение задачи о поведении плавающего ледяного покрова под действием осесимметричной нагрузки, импульсной и периодической по времени, при наличии течения с постоянным сдвигом скорости.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается бесконечный ледяной покров, плывущий на поверхности потока идеальной несжимаемой жидкости конечной глубины $H$ с вертикальным сдвигом скорости. Ледяной покров моделируется упругой бесконечной пластиной постоянной толщины. В подвижной декартовой системе координат, связанной с пластиной, с центром на верхней границе жидкости, осью $Ox$, направленной противоположно основному течению и осью $Oz$, направленной вертикально вверх, вектор скорости жидкости можно представить в виде

${\mathbf{v}}(x,y,z,t) = (U(z) + u,v,w),\quad U(z) = \gamma z$

где основное течение жидкости $U(z)$ не потенциально, имеет постоянную завихренность, $u$, $v$, $w$ – возмущенные компоненты скорости, малые по сравнению с основным течением. В момент времени $t = 0$ на ледяной покров начинает действовать заданное внешнее давление ${{p}_{0}}({\mathbf{r}},t),{\mathbf{r}} = (x,y)$, сосредоточенное в конечной области ${\text{|}}{\mathbf{r}}{\text{|}} < L$. Необходимо определить движение жидкости и пластины при $t > 0$.

Скорость течения жидкости удовлетворяет уравнениям Эйлера и неразрывности

(1.1)

$\begin{gathered} \frac{{d{\mathbf{v}}}}{{dt}} = - \nabla P{\text{/}}\rho - g{{{\mathbf{i}}}_{z}},\quad \nabla \cdot {\mathbf{v}} = 0 \\ P = - \rho gz + p \\ \end{gathered} $

Здесь $d{\text{/}}dt$ – полная производная по времени, $g$ – ускорение свободного падения, $P$ – гидродинамическое давление, которое складывается из гидростатической части и возмущенного гидродинамического давления $p$, $\rho $ – плотность жидкости, ${{{\mathbf{i}}}_{z}}$ – единичный орт оси $Oz$. Прогиб ледяного покрова $\eta (x,y,t)$ описывается уравнением изгиба тонких упругих пластин Кирхгофа–Лява

(1.2)

$\begin{gathered} D{{\Delta }^{2}}\eta + Q\Delta \eta + {{\rho }_{0}}h{{d}^{2}}\eta {\text{/}}d{{t}^{2}} = - \rho g\eta + p(x,y,0,t) + {{p}_{0}}(x,y,t), \\ \Delta = {{\partial }^{2}}{\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{y}^{2}},\quad D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}} \\ \end{gathered} $

где $D$ – цилиндрическая жесткость пластины, $E$ – модуль Юнга, ${{\rho }_{0}}$, $h$ – плотность и толщина льда, $\nu $ – коэффициент Пуассона, $Q$ – продольные напряжения в пластине (сжатие при $Q > 0$ и растяжение при $Q < 0$). Для устойчивости пластины должно быть выполнено условие $Q < 2\sqrt {\rho gD} $ [16].

Задача решается в линейном приближении. В предположении малости возмущенных скоростей по сравнению с основным течением уравнения (1.1) линеаризуются

(1.3)

$\begin{gathered} {{u}_{t}} + U(z){{u}_{x}} + \gamma {{w}_{z}} = - {{p}_{x}}{\text{/}}\rho \\ {{v}_{t}} + U(z){{v}_{x}} = - {{p}_{y}}{\text{/}}\rho \\ {{w}_{t}} + U(z){{w}_{x}} = - {{p}_{z}}{\text{/}}\rho \\ {{u}_{x}} + {{v}_{y}} + {{w}_{z}} = 0 \\ \end{gathered} $

Ставятся граничные условия: условие непротекания на дне

(1.4)

$w(x,y, - H,t) = 0$

а на верхней границе жидкости кинематическое условие

(1.5)

$w(x,y,0,t) = d\eta {\text{/}}dt$

и динамическое условие (1.2). При $t < 0$ условия покоя

(1.6)

$\eta (x,y,t) = {{\eta }_{t}}(x,y,t) = 0\quad (t < 0),\quad (u,v,w){{{\text{|}}}_{{t < 0}}} = (0,0,0)$

2. РЕШЕНИЕ ЗАДАЧИ

Введем безразмерные переменные и параметры по формулам

(2.1)

$\begin{gathered} (x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} ',H{\kern 1pt} ') = (x,y,z,H){\text{/}}L,\quad t{\kern 1pt} ' = t\sqrt {g{\text{/}}L} \\ S = \gamma \sqrt {L{\text{/}}g} ,\quad \beta = \frac{D}{{\rho g{{L}^{4}}}},\quad q = \frac{Q}{{\rho g{{L}^{2}}}},\quad \chi = \frac{{{{\rho }_{0}}h}}{{\rho L}} \\ \end{gathered} $

Штрихи далее опускаем. Коэффициенты в уравнениях (1.3) не зависят от $x$, $y$, $t$, но зависят от $z$. Применяем преобразование Фурье по переменным $x$, $y$. Неизвестные функции $u$, $v$, $w$, $\eta $, $p$ ищем в виде

$(u,v,w)(x,y,z,t) = \frac{{\sqrt {gL} }}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty (\bar {u},\bar {v},\bar {w})({{k}_{1}},{{k}_{2}},z,t){\kern 1pt} e{{{\kern 1pt} }^{{i({{k}_{1}}x + {{k}_{2}}y)}}}d{{k}_{1}}d{{k}_{2}}$

$\eta (x,y,t) = \frac{L}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty \bar {\eta }({{k}_{1}},{{k}_{2}},t){\kern 1pt} e{{{\kern 1pt} }^{{i({{k}_{1}}x + {{k}_{2}}y)}}}d{{k}_{1}}d{{k}_{2}}$

$p(x,y,z,t) = \frac{{\rho gL}}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty \bar {p}({{k}_{1}},{{k}_{2}},z,t){\kern 1pt} e{{{\kern 1pt} }^{{i({{k}_{1}}x + {{k}_{2}}y)}}}d{{k}_{1}}d{{k}_{2}}$

Функцию ${{p}_{0}}(x,y,t)$ также представим в виде

${{p}_{0}}(x,y,t) = \frac{{\rho gL}}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty {{\bar {p}}_{0}}({{k}_{1}},{{k}_{2}},t){\kern 1pt} e{{{\kern 1pt} }^{{i({{k}_{1}}x + {{k}_{2}}y)}}}d{{k}_{1}}d{{k}_{2}}$

Тогда система уравнений (1.3) записывается в виде

${{\bar {u}}_{t}} + i{{k}_{1}}Sz\bar {u} + S\bar {w} = - i{{k}_{1}}\bar {p}$

${{\bar {v}}_{t}} + i{{k}_{1}}Sz\bar {v} = - i{{k}_{2}}\bar {p}$

${{\bar {w}}_{t}} + i{{k}_{1}}Sz\bar {w} = - {{\bar {p}}_{z}}$

$i{{k}_{1}}\bar {u} + i{{k}_{2}}\bar {v} + {{\bar {w}}_{z}} = 0$

Умножим первое уравнение на $i{{k}_{1}}$, второе уравнение на $i{{k}_{2}}$ и сложим. С помощью остальных уравнений исключаем $u$, $v$, $p$

(2.2)

$\left( {\frac{\partial }{{\partial t}} + i{{k}_{1}}Sz} \right)\left( { - \frac{{\partial{ \bar {w}}}}{{\partial z}}} \right) + i{{k}_{1}}S\bar {w} = {{k}^{2}}\bar {p},\quad k = \sqrt {k_{1}^{2} + k_{2}^{2}} $

Дифференцируем по $z$

$\left( {\frac{\partial }{{\partial t}} + i{{k}_{1}}Sz} \right)\left( {\frac{{{{\partial }^{2}}\bar {w}}}{{\partial {{z}^{2}}}} - {{k}^{2}}\bar {w}} \right) = 0$

Решение этого уравнения имеет вид

$\frac{{{{\partial }^{2}}\bar {w}}}{{\partial {{z}^{2}}}} - {{k}^{2}}\bar {w} = C({{k}_{1}},{{k}_{2}},z){\kern 1pt} e{{{\kern 1pt} }^{{ - i{{k}_{1}}Szt}}}$

где $C({{k}_{1}},{{k}_{2}},z)$ – произвольная функция. Из начальных условий (1.6) следует

(2.3)

$C({{k}_{1}},{{k}_{2}},z) = 0,\quad \frac{{{{\partial }^{2}}\bar {w}}}{{\partial {{z}^{2}}}} - {{k}^{2}}\bar {w} = 0$

Решение уравнения (2.3) с условием (1.4) на дне записывается в виде

$\bar {w}(k,z,t) = A(k,t){\kern 1pt} {\text{sh}}{\kern 1pt} k(z + H)$

Подставляем это выражение в уравнение (2.2) и находим давление при z =0

${{k}^{2}}\bar {p}{{{\text{|}}}_{{z = 0}}} = - \partial A{\text{/}}\partial tk{\kern 1pt} {\text{ch}}{\kern 1pt} kH + i{{k}_{1}}SA(k,t){\kern 1pt} {\text{sh}}{\kern 1pt} kH$

Из условия (1.5) следует

(2.4)

$\partial{ \bar {\eta }}{\text{/}}\partial t = A(k,t){\kern 1pt} {\text{sh}}{\kern 1pt} kH$

Тогда уравнение движения пластины (1.2) записывается в виде

(2.5)

$(\beta {{k}^{4}} - q{{k}^{2}} + 1)\bar {\eta } + \chi {{\partial }^{2}}\bar {\eta }{\text{/}}\partial {{t}^{2}} = - \frac{1}{{{{k}^{2}}}}[\partial A{\text{/}}\partial tk{\kern 1pt} {\text{ch}}{\kern 1pt} kH - i{{k}_{1}}SA{\kern 1pt} {\text{sh}}{\kern 1pt} kH] + {{\bar {p}}_{0}}$

Из уравнений (2.4), (2.5) получаем

(2.6)

$(\chi k + {\text{cth}}{\kern 1pt} kH)\frac{{{{\partial }^{2}}\bar {\eta }}}{{\partial {{t}^{2}}}} - \frac{{i{{k}_{1}}S}}{k}\frac{{\partial{ \bar {\eta }}}}{{\partial t}} + k(\beta {{k}^{4}} - q{{k}^{2}} + 1)\bar {\eta } = k{{\bar {p}}_{0}}$

1. Рассмотрим случай импульсной осесимметричной нагрузки, которая действует очень короткое время. Все написанные уравнения справедливы во время ее действия, но мы пренебрегаем длительностью этого промежутка времени. Тогда

${{p}_{0}}(x,y,t) = - {{P}_{0}}(r)\delta (t),\quad r = \sqrt {{{x}^{2}} + {{y}^{2}}} $

где $\delta (t)$ – дельта-функция Дирака.

Интегрируя уравнения (2.4), (2.6) по $t$, получаем

$\bar {\eta }{{{\text{|}}}_{{t = 0 + }}} = 0,\quad {{\bar {\eta }}_{t}}{{{\text{|}}}_{{t = 0 + }}} = - \frac{{k{{{\bar {P}}}_{0}}(k)}}{{\chi k + {\text{cth}}{\kern 1pt} kH}},\quad {{\bar {P}}_{0}}(k) = \int\limits_0^L {{P}_{0}}(r){{J}_{0}}(kr)rdr$

При $t > 0$ правая часть в уравнении (2.6) равна нулю. Поэтому решение уравнения (2.6) при $t > 0$ имеет вид

$\bar {\eta }({{k}_{1}},{{k}_{2}},t) = {{a}_{ + }}({{k}_{1}},{{k}_{2}}){\kern 1pt} e{{{\kern 1pt} }^{{ - i{{\omega }_{ + }}t}}} + {{a}_{ - }}({{k}_{1}},{{k}_{2}}){\kern 1pt} e{{{\kern 1pt} }^{{ - i{{\omega }_{ - }}t}}},\quad {{\omega }_{ \pm }} = - {{\omega }_{1}} \pm {{\omega }_{2}}$

${{\omega }_{1}} = \frac{{S\cos \alpha }}{{2(\chi k + {\text{cth}}{\kern 1pt} kH)}},\quad {{\omega }_{2}} = \frac{{\sqrt {{{S}^{2}}\mathop {\cos }\nolimits^2 \alpha + 4k(\chi k + {\text{cth}}{\kern 1pt} kH)(\beta {{k}^{4}} - q{{k}^{2}} + 1)} }}{{2(\chi k + {\text{cth}}{\kern 1pt} kH)}}$

где $\cos \alpha = {{k}_{1}}{\text{/}}k$. Неизвестные функции ${{a}_{ \pm }}({{k}_{1}},{{k}_{2}})$ находим из начальных условий при $t = 0 + $

${{a}_{ + }} + {{a}_{ - }} = \bar {\eta }{{{\text{|}}}_{{t = 0 + }}}$

$ - i{{\omega }_{ + }}{{a}_{ + }} - i{{\omega }_{ - }}{{a}_{ - }} = {{\bar {\eta }}_{t}}{{{\text{|}}}_{{t = 0 + }}}$

Получаем

${{a}_{ + }} = - {{a}_{ - }} = \frac{1}{{i({{\omega }_{ - }} - {{\omega }_{ + }})}}{{\bar {\eta }}_{t}}{{{\text{|}}}_{{t = 0 + }}}$

В результате находим

$\eta (x,y,t) = - \frac{L}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty \frac{{k{{{\bar {P}}}_{0}}(k){\kern 1pt} e{{{\kern 1pt} }^{{i({\mathbf{k}} \cdot {\mathbf{r}} + {{\omega }_{1}}t)}}}\sin ({{\omega }_{2}}t)}}{{{{\omega }_{2}}(\chi k + {\text{cth}}{\kern 1pt} kH)}}d{{k}_{1}}d{{k}_{2}},\quad {\mathbf{k}} = ({{k}_{1}},{{k}_{2}}),\quad t > 0$

В качестве примера выберем Гауссово распределение давления, где $\epsilon $ – малый безразмерный параметр, достаточный, чтобы была справедлива линеаризация,

(2.7)

${{P}_{0}}(r) = \epsilon {\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - {{{(\pi r)}}^{2}}}}},\quad {{\bar {P}}_{0}}(k) = \frac{\epsilon }{\pi }{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - {{{(k/2\pi )}}^{2}}}}}$

Тогда

$\eta (x,y,t) = - \frac{{\epsilon L}}{{{{\pi }^{3}}}}\int\limits_0^\infty \int\limits_0^{\pi /2} \frac{{{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - {{{(k/2\pi )}}^{2}}}}}\cos (kx\cos \alpha + {{\omega }_{1}}t)\cos (ky\sin \alpha )\sin ({{\omega }_{2}}t){{k}^{2}}dkd\alpha }}{{{{\omega }_{2}}(\chi k + {\text{cth}}{\kern 1pt} kH)}}$

2. Рассмотрим случай осциллирующей нагрузки с частотой ω. В безразмерных переменных (2.1)

${{p}_{0}}(r,t) = {{P}_{0}}(r){\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i\lambda t}}},\quad \lambda = \omega \sqrt {L{\text{/}}g} $

Тогда уравнение (2.6) запишется в виде

$(\chi k + {\text{cth}}{\kern 1pt} kH){{\partial }^{2}}\bar {\eta }{\text{/}}\partial {{t}^{2}} - iS\cos \alpha \partial{ \bar {\eta }}{\text{/}}\partial t + k(\beta {{k}^{4}} - q{{k}^{2}} + 1)\bar {\eta } = k{{\bar {P}}_{0}}(k){\kern 1pt} e{{{\kern 1pt} }^{{ - i\lambda t}}}$

Решение имеет вид

$\bar {\eta } = {{a}_{1}}{\kern 1pt} e{{{\kern 1pt} }^{{ - i{{\lambda }_{1}}t}}} + {{a}_{2}}{\kern 1pt} e{{{\kern 1pt} }^{{ - i{{\lambda }_{2}}t}}} + {{a}_{0}}{\kern 1pt} e{{{\kern 1pt} }^{{ - i\lambda t}}},\quad {{\lambda }_{{1,2}}} = - {{\omega }_{1}} \pm {{\omega }_{2}}$

${{a}_{0}} = \frac{{k{{{\bar {P}}}_{0}}(k)}}{{k(\beta {{k}^{4}} - q{{k}^{2}} + 1) - S\lambda \cos \alpha - {{\lambda }^{2}}(\chi k + {\text{cth}}{\kern 1pt} kH)}}$

Коэффициенты ${{a}_{1}}$, ${{a}_{2}}$ находим из начальных условий

${{a}_{1}} + {{a}_{2}} + {{a}_{0}} = 0,\quad - i{{\lambda }_{1}}{{a}_{1}} - i{{\lambda }_{2}}{{a}_{2}} - i\lambda {{a}_{0}} = 0$

$\bar {\eta }({{k}_{1}},{{k}_{2}},t) = {{a}_{0}}\left( {{\text{e}}{{{\kern 1pt} }^{{ - i\lambda t}}} + \frac{{\lambda - {{\lambda }_{2}}}}{{{{\lambda }_{2}} - {{\lambda }_{1}}}}{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{1}}t}}} + \frac{{\lambda - {{\lambda }_{1}}}}{{{{\lambda }_{1}} - {{\lambda }_{2}}}}{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{2}}t}}}} \right)$

Если задано Гауссово распределение давления (2.7), то формула для прогиба ледяного покрова приобретает вид

(2.8)

$\begin{gathered} \eta (x,y,t) = \frac{{\epsilon L}}{{2{{\pi }^{3}}}}\int\limits_0^\infty \int\limits_0^\pi \frac{{({{\lambda }_{2}} - {{\lambda }_{1}}){\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i\lambda t}}} + (\lambda - {{\lambda }_{2}}){\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{1}}t}}} - (\lambda - {{\lambda }_{1}}){\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{2}}t}}}}}{{({{\lambda }_{2}} - {{\lambda }_{1}})[k(\beta {{k}^{4}} - q{{k}^{2}} + 1) - S\lambda \cos \alpha - {{\lambda }^{2}}(\chi k + {\text{cth}}{\kern 1pt} kH)]}} \times \\ \, \times {{k}^{2}}{\kern 1pt} e{{{\kern 1pt} }^{{ - {{{(k/2\pi )}}^{2}}}}}{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ikx\cos \alpha }}}\cos (ky\sin \alpha )dkd\alpha \\ \end{gathered} $

Знаменатель подынтегрального выражения может обращаться в нуль при некоторых значениях чисел ${{k}_{0}}$, $\alpha $. Тогда при этих числах ${{k}_{0}}$, $\alpha $ выполнено равенство $\lambda = {{\lambda }_{1}}$, поскольку ${{\lambda }_{2}} < 0$. Можно показать, что числитель подынтегрального выражения тоже обращается в нуль, т.е. особенность является устранимой. Дробь в формуле (2.8) преобразуется к виду

$\frac{{it{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{1}}t}}}}}{{(\chi {{k}_{0}} + {\text{cth}}{\kern 1pt} {{k}_{0}}H)({{\lambda }_{1}} - {{\lambda }_{2}})}} + \frac{{{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{1}}t}}} - {\kern 1pt} \,{\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{2}}t}}}}}{{(\chi {{k}_{0}} + {\text{cth}}{\kern 1pt} {{k}_{0}}H)({{\lambda }_{1}} - {{\lambda }_{2}}{{)}^{2}}}}$

В случае отсутствия сдвига скорости известно [17], что если безразмерный коэффициент сжатия ледяной пластины q больше некоторого критического значения ${{q}_{*}}$, то дисперсионное соотношение для изгибно-гравитационных волн в пластине для некоторых частот колебаний действующей нагрузки имеет не один корень, а три различных корня. При $q < {{q}_{*}}$ безразмерная частота изгибно-гравитационных волн

$\lambda (k) = \sqrt {\frac{{k(\beta {{k}^{4}} - q{{k}^{2}} + 1)}}{{\chi k + {\text{cth}}{\kern 1pt} kH}}} $

является монотонной функцией от волнового числа k, при $q = {{q}_{*}}$ имеется точка перегиба, в которой первая и вторая производные равны нулю. При $q > {{q}_{*}}$ функция $\lambda (k)$ имеет локальный максимум, после которого убывает до некоторого локального минимума, затем монотонно возрастает. Второй по величине корень имеет отрицательную групповую скорость.

Наличие сдвига скорости приводит к тому, что диапазон частот внешней нагрузки, при которых имеются три различных корня дисперсионного соотношения, расширяется за счет члена $S\lambda \cos \alpha $, так как $\cos \alpha $ может иметь различный знак, т.е. находятся такие значения углов $\alpha $, при которых существуют три различных корня.

При вычислении интеграла (2.8) можно деформировать контур интегрирования вокруг корней так, чтобы ${\kern 1pt} {\text{Re}}{\kern 1pt} ( - i{{\lambda }_{1}}) < 0$, ${\kern 1pt} {\text{Re}}{\kern 1pt} ( - i{{\lambda }_{2}}) < 0$, т.е. ${\kern 1pt} {\text{Im}}{\kern 1pt} ({{\lambda }_{1}}) < 0$, ${\kern 1pt} {\text{Im}}{\kern 1pt} ({{\lambda }_{2}}) < 0$. Тогда при $t \to \infty $ интегралы от членов с экспонентами ${\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{1}}t}}}$, ${\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i{{\lambda }_{2}}t}}}$ стремятся к нулю по лемме Римана–Лебега, наличие этих членов связано с начальными условиями. Если $q < {{q}_{*}}$, то с течением времени достаточно быстро колебания ледяного покрова и жидкости становятся установившимися гармоническими. Установившиеся колебания ледяного покрова при $t \to \infty $ выражаются формулой

(2.9)

$\eta (x,y,t) = \frac{{\epsilon L{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - i\lambda t}}}}}{{4{{\pi }^{3}}}}\int\limits_0^\infty \int\limits_0^{2\pi } \frac{{{{k}^{2}}{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ - {{{(k/2\pi )}}^{2}}}}}{\kern 1pt} {\text{e}}{{{\kern 1pt} }^{{ik \cdot r}}}dkd\alpha }}{{k(\beta {{k}^{4}} - q{{k}^{2}} + 1) - S\lambda \cos \alpha - {{\lambda }^{2}}(\chi k + {\text{cth}}{\kern 1pt} kH)}}$

Обход корней знаменателя подынтегрального выражения в формуле (2.9) производится снизу, и таким образом выполняется условие излучения, волны должны уходить на бесконечность. При $q > {{q}_{*}}$ колебания ледяного покрова представляют собой наложение волн различной длины.

3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Проводились численные расчеты для ледяного покрова при следующих входных параметрах задачи: $E = 5$ ГПа, $\rho = 1025$ кг/м³, ${{\rho }_{0}} = 922.5$ кг/м³, $\nu = 0.3$, $L = 20$ м. Толщина льда $h = 0.5$, 1 и 2 м. Основные расчеты проводились для глубины жидкости $H = 400$ м. Сжимающие усилия в пластине заданы в виде $Q = \bar {Q}\sqrt {\rho gD} $, $\bar {Q} = 0$, 1 и 1.5. Все графики ниже приведены для безразмерного времени.

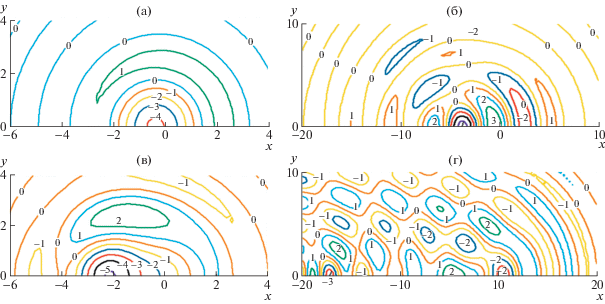
На рис. 1 приведены изолинии прогиба ледяного покрова толщиной h = 1 м при импульсном воздействии при отсутствии сжатия $\bar {Q} = 0$, $S = 1$, 5 в моменты безразмерного времени $t = 1$, 9. Величину прогиба на линии можно получить, если умножить величину шага на номер линии. Видно, что наличие завихренности приводит к неравномерному распространению волн в разных направлениях. Эта неравномерность возрастает с увеличением градиента сдвига скорости – параметра $S$. С ростом времени вихри дробятся, их количество растет. Особенно это проявляется при больших значениях параметра $S$. На рис. 2 изображены аналогичные графики при $\bar {Q} = 1.5$. Видно, что сжатие ледяного покрова приводит к увеличению его прогиба.

Рис. 1.

Изолинии безразмерного прогиба ледяного покрова $\eta /(\varepsilon L)$ при импульсном воздействии при $\bar {Q} = 0$, h = 1 м, S = 1 (а, б) и S = 5 (в, г), t = 1 (а, в) и t = 9 (б, г): (а) – с шагом 0.01 от –0.03 до 0.01; (б) – с шагом 0.002 от –0.008 до 0.004; (в) – с шагом 0.005 от –0.03 до 0.015; (г) – с шагом 0.002 от –0.002 до 0.004.

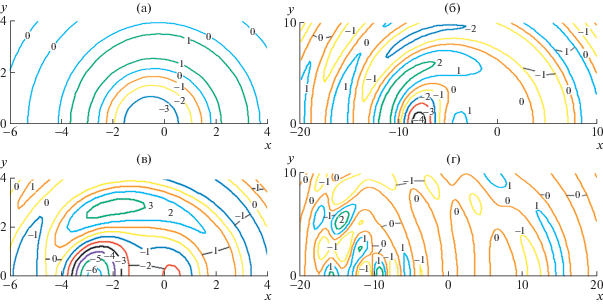
Рис. 2.

Изолинии безразмерного прогиба ледяного покрова $\eta /(\varepsilon L)$ при импульсном воздействии при $\bar {Q} = 1.5$, h = 1 м, S = 1 (а, б) и S = 5 (в, г), t = 1 (а, в) и t = 9 (б, г): (а) – с шагом 0.02 от –0.06 до 0.02; (б) – с шагом 0.005 от –0.02 до 0.015; (в) – с шагом 0.01 от –0.05 до 0.02; (г) – с шагом 0.002 от –0.006 до 0.004.

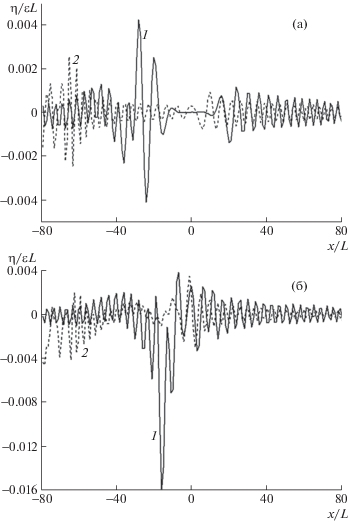
На рис. 3 представлены зависимости от координаты $x$ прогиба ледяного покрова толщиной $h = 1$ м при импульсном воздействии в момент безразмерного времени $t = 30$, при $S = 1$ (сплошные кривые) и $S = 5$ (штриховые): (а) – $\bar {Q} = 0$, (б) – $\bar {Q} = 1.5$. Видно, что увеличение градиента скорости сглаживает большие пики амплитуд прогиба льда и увеличивает амплитуды прогиба ниже по течению. При $\bar {Q} = 0$ с течением времени прогиб в начале координат достаточно быстро становится близким к нулю, возмущения уносятся на бесконечность. При увеличении коэффициента сжатия, например при $\bar {Q} = 1$, прогиб ледяного покрова значительно больше, и близость к нулю достигается при значительно больших временах. При сверхкритическом сжатии $\bar {Q} = 1.5$ этого явления не наблюдается, так как существуют волны с отрицательной групповой скоростью.

Рис. 3.

Зависимости от координаты x безразмерного прогиба ледяного покрова $\eta /(\varepsilon L)$ при импульсном воздействии в момент времени t = 30, h = 1 м, S = 1 (сплошные кривые) и S = 5 (штриховые): (а) – $\bar {Q} = 0$, (б) – $\bar {Q} = 1.5$.

Далее приводятся численные результаты для периодической по времени нагрузки. Выше было отмечено, что наличие сдвига скорости приводит к тому, что диапазон частот, при которых существуют три различных корня дисперсионного соотношения, расширяется в случае $q > {{q}_{*}}$. Так, например, для пластины толщиной $h = 1$ м и глубины жидкости H = 400 м критическое значение коэффициента сжатия ${{\bar {Q}}_{*}} = 1.475$ [15], что соответствует ${{q}_{*}} = 1.475\sqrt \beta $. При $\bar {Q} = 1.5$ и $S = 0$ диапазон частот, при которых существуют три различных корня дисперсионного соотношения, очень узкий – от 0.4768 до 0.4786 1/с. При $S = 1$ этот диапазон частот от 0.247 до 0.922 1/с, при $S = 5$ диапазон частот еще больше расширяется – от 0.066 до 3.437 1/с.

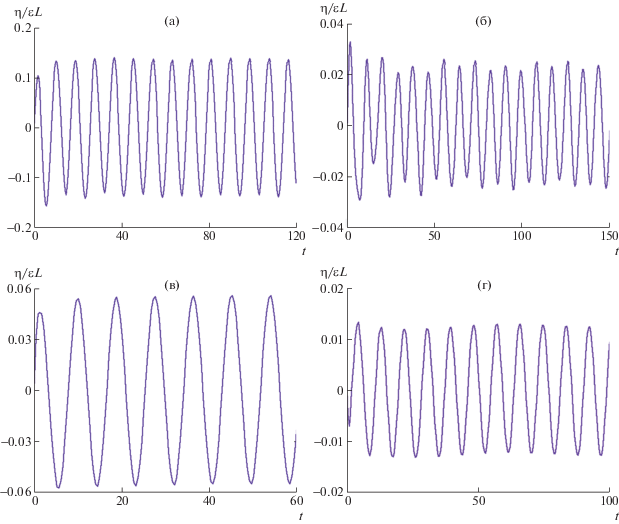
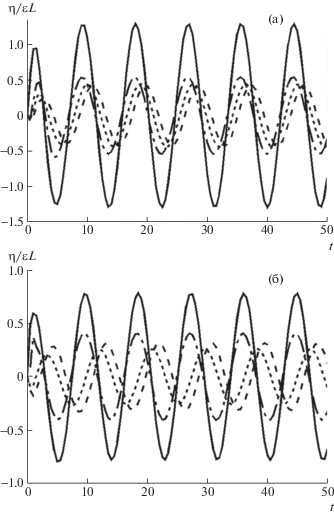
На рис. 4 представлены зависимости прогиба ледяного покрова от времени при периодическом воздействии с частотой $\omega = 0.5$ c^–1 и параметрах $h = 0.5$ м, $\bar {Q} = 0$, $S = 1$ и $S = 5$ в центре области давления (0, 0), а также в точках на границе области: (1, 0), (0, 1), (–1, 0). Видно, что колебания быстро становятся установившимися. Максимальная амплитуда колебаний в центре. Увеличение сдвига скорости приводит к уменьшению амплитуд колебаний.

Рис. 4.

Зависимости безразмерного прогиба ледяного покрова $\eta {\text{/}}(\varepsilon L)$ от времени при периодическом воздействии с частотой ω = 0.5 с^–1 и параметрах h = 0.5 м, $\bar {Q} = 0$, S = 1 (a) и S = 5 (б) в точках: (0, 0) – сплошная кривая, (1, 0) – штриховая, (0, 1) – штрихпунктирная, (–1, 0) – пунктирная.

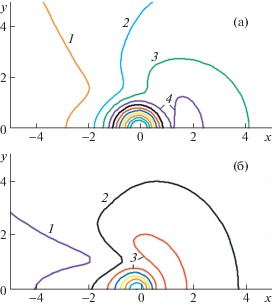
На рис. 5 изображены изолинии установившихся колебаний ледяного покрова при периодическом воздействии с частотой $\omega = 0.5$ c^–1 при тех же параметрах, что на рис. 4. Форма изолиний при $S = 1$ и $S = 5$ подобна. Проведено сравнение амплитуд установившихся колебаний, вычисленных по формуле (2.9) c амплитудами неустановившегося решения при $t = 20$. Графически два решения, полученные разным способом, совпали, что свидетельствует от корректности результатов.

Рис. 5.

Изолинии амплитуд установившихся колебаний ледяного покрова $\eta {\text{/}}(\varepsilon L)$ при периодическом воздействии с частотой ω = 0.5 с^–1 и параметрах h = 0.5 м, $\bar {Q} = 0$, S = 1 (а) и S = 5 (б) с шагом 0.1: (а) – от 0.1 до 1.1, (б) – от 0.1 до 0.7.

Аналогичные расчеты были проведены для пластины толщиной $h = 2$ м. Получены зависимости прогиба льда от времени, подобные тем, что на рис. 4, но амплитуды прогиба значительно меньше. Форма изолиний амплитуд установившихся колебаний ледяного покрова также подобна изображенным на рис. 5.

На рис. 6 приведены зависимости безразмерного прогиба ледяного покрова от времени при периодическом воздействии с частотой $\omega = 0.5$ с^–1 и параметрах $h = 1$ м, $\bar {Q} = 1.5$, $S = 1$ и $S = 5$ в центре области нагрузки (0,0) и на ее крае в точке (1,0). Видно, что колебания ледяного покрова не являются гармоническими. Это вызвано тем, что при данных параметрах дисперсионное соотношение имеет три различных корня, происходит наложение волн различной длины. Максимальные амплитуды колебания ледяного покрова наблюдаются в центре области нагрузки.

Рис. 6.

Зависимости безразмерного прогиба ледяного покрова $\eta {\text{/}}(\varepsilon L)$ от времени при периодическом воздействии с частотой ω = 0.5 с^–1 и параметрах h = 1 м, $\bar {Q} = 1.5$, S = 1 (a, б) и S = 5 (в, г) в точках: (0, 0) (а, в) и (1, 0) (б, г).

ЗАКЛЮЧЕНИЕ

Исследовано влияние сдвига скорости жидкости на нестационарные изгибно-гравитационные волны в ледяном покрове при импульсном и периодическом по времени воздействии локальной осесимметричной нагрузки в рамках линейной теории. Поле скоростей жидкости не потенциально.

Показано, что наличие завихренности приводит к неравномерному распространению волн в разных направлениях. Эта неравномерность возрастает с увеличением градиента сдвига. Изолинии прогиба ледяного покрова показывают, что с течением времени при импульсном воздействии ниже по течению образуются вихри, которые дробятся, число их растет. При увеличении коэффициента сжатия амплитуды прогиба ледяного покрова растут.

Если коэффициент сжатия пластины больше критического значения, то дисперсионное соотношение имеет не один, а три различных корня при некоторых частотах, и один корень имеет отрицательную групповую скорость. Диапазон частот, при которых имеются три различных корня, резко возрастает с увеличением градиента скорости течения. Наличие волн с отрицательной групповой скоростью приводит к тому, что в случае сверхкритического сжатия при импульсном воздействии прогиб пластины в начале координат с течением времени не становится близким к нулю, как в случае докритического сжатия.

В случае периодической нагрузки, если коэффициент сжатия пластины меньше критического значения, то с течением времени достаточно быстро колебания ледяного покрова устанавливаются. При сверхкритическом сжатии прогиб пластины в точке представляет собой наложение колебаний с различной длиной волны.

Список литературы

Букатов А.Е., Мордашев В.И. Влияние продольно сжатой упругой пластинки на развитие волнового возмущения потока однородной жидкости с вертикальным сдвигом скорости // ПМТФ. 1981. № 1. С. 122–129.
Суворов А.М. Развитие колебаний ледяного покрова в море при наличии горизонтального течения со сдвигом скорости // Поверхностные и внутренние волны. Севастополь: МГИ АН УССР. 1979. С. 63–69.
Суворов А.М., Черкесов Л.В. Нестационарные вынужденные колебания упругой пластинки, плавающей на поверхности потока жидкости со сдвигом скорости // Прикладная механика. 1980. № 5. С. 102–106.
Букатов А.Е. Волны в море с плавающим ледяным покровом. Морской гидрофизический институт РАН. Севастополь. 2017. 357 с.
Das S., Kar P., Sahoo T., Meylan M.H. Flexural-gravity wave motion in the presence of shear current: Wave blocking and negative energy waves // Phys. Fluids. 2018. V. 30. 106606; https://doi.org/10.1063/1.5052228
Суворов А.М., Тананаев А.Н., Черкесов Л.В. Нестационарные пространственные волны в потоке однородной жидкости со сдвигом скорости // Поверхностные и внутренние волны. Севастополь: МГИ АН УССР. 1979. С. 14–21.
Санников В.Ф. Корабельные волны в однородном море с линейным профилем скорости по глубине // Поверхностные и внутренние волны // Поверхностные и внутренние волны. Севастополь: МГИ АН УССР. 1979. С. 22–31.
Суворов А.М., Черкесов Л.В. Волны от поверхностных возмущений в потоке стратифицированной жидкости со сдвигом скорости // Поверхностные и внутренние волны. Севастополь: МГИ АН УССР. 1979. С. 128–138.
Ellingsen S.A. Initial surface disturbance on shear current: The Cauchy-Poisson problem with a twist // Phys. Fluids. 2014. V. 26. 082104.
Li Y., Ellingsen S.A. Initial Value Problems for Water Waves in the Presence of a Shear Current // Proc. 25-th Intern. Ocean and Polar Engng Conf. 2015. Kona. Big Island. Hawaii. USA. June 21-26 2015. P. 543–549.
Ellingsen S.A. Ship waves in the presence of uniform vorticity // J. Fluid Mech. 2014. V. 742. R2. https://doi.org/10.1017/jfm.2014.28
Li Y., Ellingsen S.A. Ship waves on uniform shear current at finite depth: wave resistance and critical velocity // J. Fluid Mech. 2016. V. 791. P. 539–567.
Ellingsen S.A. Oblique waves on a vertical sheared current are rotational // Eur. J. Mech. B. Fluids. 2016. V. 56. P. 156–160.
Maiti P., Mandal B.N. Water waves generated due to axisymmetric disturbances in water with an ice-cover // Arch. Appl. Mech. 2005. V. 74. P. 629–636.
Стурова И.В. Влияние неравномерного сжатия упругой пластины, плавающей на поверхности жидкости, на развитие нестационарных изгибно-гравитационных волн // Известия РАН. МЖГ. 2021. № 2. С. 63–71.
Хейсин Д.Е. Динамика ледяного покрова. Л.: Гидрометеоиздат. 1967. 215 с.
Schulkes R.M.S.M., Hosking R.J., Sneyd A.D. Waves due to a steadily moving source on a floating ice plate. Pt. 2 // J. Fluid Mech. 1987. V. 180. P. 297–318.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал