1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 2, 2022

Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 77-86

ВЕРТИКАЛЬНЫЙ ПЕРЕНОС ИМПУЛЬСА ИНЕРЦИОННО-ГРАВИТАЦИОННЫМИ ВНУТРЕННИМИ ВОЛНАМИ НА ТЕЧЕНИИ ПРИ УЧЕТЕ ТУРБУЛЕНТНОЙ ВЯЗКОСТИ И ДИФФУЗИИ

А. А. Слепышев *

ФИЦ “Морской гидрофизический институт” РАН
Севастополь, Россия

* E-mail: slep55@mail.ru

Поступила в редакцию 06.09.2021
После доработки 27.09.2021
Принята к публикации 09.10.2021

Полный текст (PDF)

Аннотация

В приближении Буссинеска рассматриваются свободные внутренние волны при учете вращения Земли на двумерном вертикально-неоднородном стратифицированном течении при учете турбулентной вязкости и диффузии. Применяется неявный метод Адамса третьего порядка точности для численного решения краевой задачи для амплитуды вертикальной скорости внутренних волн. Получено, что собственная функция и частота волны – комплексные. Учет турбулентной вязкости и диффузии приводит к тому, что мнимая часть частоты волны отрицательная, т.е. волна затухает. Вертикальные волновые потоки импульса отличны от нуля и могут быть сравнимы или превышать соответствующие турбулентные потоки.

Ключевые слова: внутренние волны, мнимая поправка к частоте, волновой поток импульса, турбулентная вязкость и диффузия

Вертикальный перенос в морской среде обычно связывают с процессами обмена, в которых ключевую роль играет мелкомасштабная турбулентность. Механизмы генерации турбулентности самые разнообразные – ветровое перемешивание в приповерхностном слое, гидродинамическая неустойчивость течений и внутренних волн, обрушение внутренних волн, донное трение, продуцирующее генерацию турбулентности в придонном пограничном слое. Захват и фокусировка внутренних волн горизонтальными неоднородностями стратификации и течений также приводят к обрушению внутренних волн и генерации турбулентности [1]. Аналогичный эффект имеет место при захвате внутренних волн наклонным дном [2]. Возможна стохастизация волнового поля в геометрическом аттракторе внутренних волн, обусловленным геометрией дна и границ бассейна [2, 3]. Однако в стратифицированной морской среде мелкомасштабная турбулентность имеет перемежаемый характер и можно для описания обменных процессов использовать эффективный коэффициент турбулентного обмена.

Внутренние волны повсеместно присутствуют в океане, благодаря действию источников, их порождающих. Это воздействие атмосферных возмущений, взаимодействие течений и приливов с неоднородностями рельефа дна, генерация внутренних волн вихрями. Дисперсионные свойства внутренних волн на сдвиговых течениях исследовались в ряде работ при отсутствии турбулентной вязкости и диффузии и учета вращения Земли [4, 5]. В этом случае уравнение для амплитуды вертикальной скорости имеет действительные коэффициенты и в гидродинамически устойчивом течении при соблюдении критерия Майлса [6, 7] частота волны действительная для фиксированного волнового числа для каждой моды внутренних волн. Течение приводит к анизотропии волнового поля, особенно для коротких внутренних волн [5].

Внутренние волны при учете турбулентной вязкости и диффузии затухают [8–10]. Вертикальные волновые потоки импульса при этом отличны от нуля [11]. Указанные потоки определялись, когда уравнение для амплитуды вертикальной скорости решалось асимптотическим методом Люстерника–Вишика [12]. Решение и частота волны раскладывались в ряд по малому параметру, пропорциональному горизонтальной турбулентной вязкости. Получено, что мнимая поправка к частоте отрицательная [11], т.е. волна затухает. В настоящей работе это уравнение решается прямым численным методом по неявной схеме Адамса третьего порядка точности и находится комплексное значение частоты. В [13] показано, что в двумерном течении с вертикальным сдвигом скорости при учете вращения Земли вертикальный волновой поток импульса отличен от нуля и без учета турбулентной вязкости и диффузии. В этом случае уравнение для амплитуды вертикальной скорости имеет комплексные коэффициенты, собственная функция краевой задачи для внутренних волн – комплексная, и частота волны также комплексная. Сдвиг фаз между колебаниями вертикальной и горизонтальной скорости отличен от π/2, и вертикальный волновой поток импульса отличен от нуля. В настоящей работе исследуется влияние горизонтальной турбулентной вязкости и диффузии на этот эффект. Ввиду того, что коэффициенты горизонтального турбулентного обмена на 3–4 порядка превышают соответствующие коэффициенты вертикального турбулентного обмена, то последними пренебрегается.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматриваются свободные инерционно-гравитационные внутренние волны на двумерном стратифицированном течении с вертикальным сдвигом скорости в безграничном бассейне постоянной глубины. Коэффициенты горизонтальной турбулентной вязкости K и диффузии M предполагаются постоянными. Две компоненты скорости течения ${{U}_{0}}(z),\,\,{{V}_{0}}(z)$ зависят от вертикальной координаты. В линейном приближении решается краевая задача для амплитуды вертикальной скорости и находится дисперсионное соотношение. Вертикальные потоки импульса определяются во втором порядке по амплитуде волны. Горизонтальным изменением поля средней плотности и скорости течения на рассматриваемых масштабах пренебрегается.

Уравнения гидродинамики в приближении Буссинеска для волновых возмущений имеют вид

(1.1)
$\frac{{Du}}{{Dt}} - fv + w\frac{{d{{U}_{0}}}}{{dz}} = - \frac{1}{{{{\rho }_{0}}(0)}}\frac{{\partial P}}{{\partial x}} + K{{\Delta }_{h}}u$
(1.2)
$\frac{{Dv}}{{Dt}} + fu + w\frac{{d{{V}_{0}}}}{{dz}} = - \frac{1}{{{{\rho }_{0}}(0)}}\frac{{\partial P}}{{\partial y}} + K{{\Delta }_{h}}v$
(1.3)
$\frac{{Dw}}{{Dt}} = - \frac{1}{{{{\rho }_{0}}(0)}}\frac{{\partial P}}{{\partial z}} - \frac{{g\rho }}{{{{\rho }_{0}}(0)}} + K{{\Delta }_{h}}w$
(1.4)
$\frac{{D\rho }}{{Dt}} = - w\frac{{d{{\rho }_{0}}}}{{dz}} + M{{\Delta }_{h}}\rho $
(1.5)
$\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0$
где $u,\,\,v,\,\,w$ – соответственно две горизонтальные и вертикальная компоненты волновой скорости течения; $\rho $, $P$ – волновые возмущения плотности и давления; ${{\rho }_{0}}(z)$ – профиль средней плотности; $x,y,z$ – горизонтальные и вертикальная координаты; ось z направлена вертикально вверх; f – параметр Кориолиса; ${{U}_{0}}(z),{{V}_{0}}(z)$ – две компоненты скорости среднего течения; ${{\Delta }_{h}}\, = \,\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}\, + \,\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}$ – двумерный оператор Лапласа.

Действие оператора $D{\text{/}}Dt$ раскрывается по формуле

$\frac{D}{{Dt}} = \frac{\partial }{{\partial t}} + (u + {{U}_{0}})\frac{\partial }{{\partial x}} + (v + {{V}_{0}})\frac{\partial }{{\partial y}} + w\frac{\partial }{{\partial z}}$.

Граничные условия на поверхности моря (z = 0) – условие “твердой крышки”, которое отфильтровывает внутренние волны от поверхностных волн [14] и отсутствие тангенциальных напряжений [9, 15]

(1.6)
$w(0) = 0,\quad K\frac{{\partial w}}{{\partial x}} = 0,\quad K\frac{{\partial w}}{{\partial y}} = 0,\quad z = 0$

Граничные условия на дне – условие непротекания и отсутствие тангенциальных напряжений (условие “гладкого скольжения” [9])

(1.7)
$\begin{gathered} {{w}_{{10}}}( - H) = 0 \\ K\frac{{\partial w}}{{\partial x}} = 0,\quad K\frac{{\partial w}}{{\partial y}} = 0,\quad z = - H \\ \end{gathered} $

2. ЛИНЕЙНОЕ ПРИБЛИЖЕНИЕ

Решения линейного приближения ищутся в виде

(2.1)
$\begin{gathered} u_{1}^{{}} = {{u}_{{10}}}(z)A{{e}^{{i\theta }}} + {\text{c}}{\text{.c}}.,\quad v_{1}^{{}} = {{v}_{{10}}}(z)A{{e}^{{i\theta }}} + {\text{c}}{\text{.c}}.,\quad {{w}_{1}} = {{w}_{{10}}}(z)A{{e}^{{i\theta }}} + {\text{c}}{\text{.c}}. \\ {{P}_{1}} = {{P}_{{10}}}(z)A{{e}^{{i\theta }}} + {\text{c}}{\text{.c}}.,\quad {{\rho }_{1}} = {{\rho }_{{10}}}(z)A{{e}^{{i\theta }}} + {\text{c}}{\text{.c}}. \\ \end{gathered} $
где c.c. – комплексно сопряженные слагаемые, A – амплитудный множитель, θ – фаза волны; $\partial \theta {\text{/}}\partial x = k,\partial {{\theta /}}\partial t = - \omega $, k – горизонтальное волновое число, $\omega $ – частота волны. Предполагается, что волна распространяется вдоль оси x.

После подстановки (2.1) в систему (1.1)–(1.5) следует связь амплитудных функций ${{u}_{{10}}},\,\,{{v}_{{10}}},\,\,{{\rho }_{{10}}},\,\,{{P}_{{10}}}\,$ с ${{w}_{{10}}}$

(2.2)
${{u}_{{10}}} = \frac{i}{k}\frac{{d{{w}_{{10}}}}}{{dz}},\quad \Omega = \omega - k \cdot {{U}_{0}}$
(2.3)
$\begin{gathered} \frac{{{{P}_{{10}}}}}{{{{\rho }_{0}}(0)}} = \frac{i}{k}\left[ {\frac{{(\Omega + i{{k}^{2}}K)}}{k}\frac{{d{{w}_{{10}}}}}{{dz}} + \frac{{d{{U}_{0}}}}{{dz}}{{w}_{{10}}} + \frac{f}{{\Omega + i{{k}^{2}}K}}\left( {i\frac{{d{{V}_{0}}}}{{dz}}{{w}_{{10}}} - \frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}}} \right)} \right] \\ {{\rho }_{{10}}} = - \frac{i}{{(\Omega + i{{k}^{2}}M)}}{{w}_{{10}}}\frac{{d{{\rho }_{0}}}}{{dz}},\quad {{v}_{{10}}} = \frac{1}{{(\Omega + i{{k}^{2}}K)}}\left( {\frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}} - i{{w}_{{10}}}\frac{{d{{V}_{0}}}}{{dz}}} \right) \\ \end{gathered} $

Функция w10 удовлетворяет уравнению

(2.4)
$\frac{{{{d}^{2}}{{w}_{{10}}}}}{{d{{z}^{2}}}} + a(z)\frac{{d{{w}_{{10}}}}}{{dz}} + b(z) \cdot {{w}_{{10}}} = 0$

где

$a(z) = k\left[ {\frac{{if}}{{\Omega + i{{k}^{2}}K}} \cdot \frac{{d{{V}_{0}}}}{{dz}} - \frac{{{{f}^{2}}}}{{{{{(\Omega + i{{k}^{2}}K)}}^{2}}}} \cdot \frac{{d{{U}_{0}}}}{{dz}}} \right] \cdot {{\left[ {\Omega + i{{k}^{2}}K - \frac{{{{f}^{2}}}}{{(\Omega + i{{k}^{2}}K)}}} \right]}^{{ - 1}}}$
$\begin{gathered} b(z) = k\left[ {\frac{{if \cdot k}}{{{{{\left( {\Omega + i{{k}^{2}}K} \right)}}^{2}}}} \cdot \frac{{d{{V}_{0}}}}{{dz}} \cdot \frac{{d{{U}_{0}}}}{{dz}} + \frac{{if}}{{(\Omega + i{{k}^{2}}K)}} \cdot \frac{{{{d}^{2}}{{V}_{0}}}}{{d{{z}^{2}}}} - k(\Omega + i{{k}^{2}}K) + \frac{{{{N}^{2}}k}}{{(\Omega + i{{k}^{2}}M)}} + \frac{{{{d}^{2}}{{U}_{0}}}}{{d{{z}^{2}}}}} \right] \times \\ \, \times {{\left[ {\Omega + i{{k}^{2}}K - \frac{{{{f}^{2}}}}{{(\Omega + i{{k}^{2}}K)}}} \right]}^{{ - 1}}} \\ \end{gathered} $

где ${{N}^{2}} = - \frac{g}{{{{\rho }_{0}}(0)}}\frac{{d{{\rho }_{0}}}}{{dz}}$ – квадрат частоты Брента–Вяйсяля.

Граничные условия для w10

(2.5)
$z = 0{\text{:}}\;{{w}_{{10}}} = 0$
(2.6)
$z = - H{\text{:}}\;{{w}_{{10}}} = 0$

Граничные условия (1.6), (1.7) выполняются автоматически.

Краевая задача (2.4)–(2.6) решалась численно по неявной схеме Адамса третьего порядка точности без учета турбулентной вязкости и диффузии в работе [13]. Было получено, что собственная функция – решение этой краевой задачи – комплексная, частота волны – тоже комплексная величина. Мнимая часть частоты волны мала и может быть как положительна, так и отрицательна, т.е. в зависимости от частоты волны и номера моды возможно как слабое усиление, так и слабое затухание. Ниже в ходе численных расчетов показано, что при учете турбулентной вязкости и диффузии волна всегда затухает, т.е. мнимая часть частоты волны отрицательна.

3. ВОЛНОВЫЕ ПОТОКИ ИМПУЛЬСА

Вертикальные волновые потоки импульса $\overline {uw} $, $\overline {vw} $ находим, учитывая (2.1), (2.2), (2.3)

(3.1)
$\overline {uw} = \frac{i}{k}\left| {A_{1}^{2}} \right|\left( {w_{{10}}^{*}\frac{{dw_{{10}}^{{}}}}{{dz}} - w_{{10}}^{{}}\frac{{dw_{{10}}^{*}}}{{dz}}} \right)$
(3.2)
$\overline {vw} = \frac{{w_{{10}}^{*}{\text{|}}A_{1}^{2}{\text{|}}}}{{(\Omega + i{{k}^{2}}K)}}\left( {\frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}} - i{{w}_{{10}}}\frac{{d{{V}_{0}}}}{{dz}}} \right) + {\text{c}}{\text{.c}}{\text{.}}$
где ${{A}_{1}} = A\exp (\delta \omega \cdot t)$, $\delta \omega = \operatorname{Im} (\omega )$ – мнимая часть частоты. Черта сверху означает осреднение по периоду волны.

Вертикальный волновой поток импульса $\overline {vw} $ у инерционно-гравитационных внутренних волн отличен от нуля как при отсутствии течения, так и при отсутствии турбулентной вязкости и диффузии. Поток импульса $\overline {uw} $ не равен 0 при учете турбулентной вязкости и диффузии, если турбулентная вязкость и диффузия не учитываются, то только при наличии среднего течения, у которого поперечная к направлению распространения волны компонента скорости ${{V}_{0}}$ зависит от вертикальной координаты. При отсутствии вращения Земли при  f = 0 волновые потоки импульса ненулевые только при учете турбулентной вязкости и диффузии.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

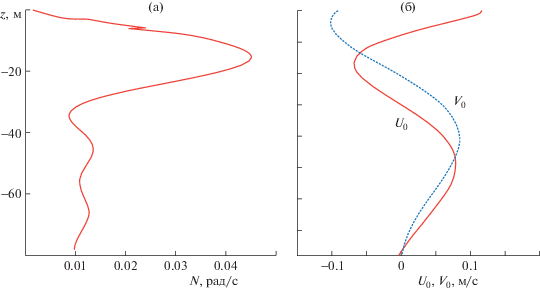
Вертикальные волновые потоки импульса рассчитаем для 15-минутных внутренних волн второй моды, наблюдавшихся в натурном эксперименте на северо-западном шельфе Черного моря в третьем этапе 45 рейса НИС “Михаил Ломоносов” [16, 13 ]. Максимальная амплитуда этих волн составила 0.5 м. Характерное значение коэффициента горизонтального обмена на рассматриваемых масштабах оценено как K = 1 м2/с [17]. Вертикальные профили частоты Брента–Вяйсяля и компонент скорости течения показаны на рис. 1.

Рис. 1.

Вертикальные профили частоты Брента–Вяйсяля (а) и компонент скорости течения (б) (данные [13, 16]).

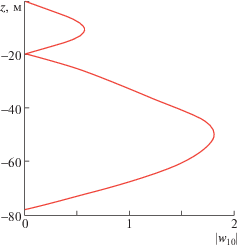
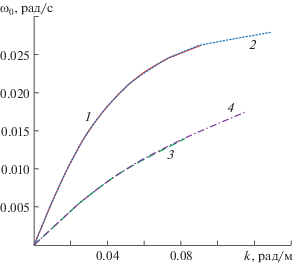
Краевая задача (2.4)–(2.6) по определению w10 решается численно по неявной схеме Адамса третьего порядка точности при $M = 0.5 \cdot K$. Волновое число и мнимая часть частоты при фиксированной действительной части частоты находились методом пристрелки, из необходимости выполнения граничных условий (2.5, 2.6). Длина волны у 15-минутных внутренних волн второй моды равна 195 м. Профиль модуля собственной функции показан на рис. 2. Зависимость действительной части частоты ${{\omega }_{0}} = \operatorname{Re} (\omega )$ от волнового числа для первых двух мод представлена на рис. 3 как при учете турбулентной вязкости и диффузии, так и без их учета. Сплошная кривая (1) соответствует первой моде при учете турбулентной вязкости и диффузии, пунктирная кривая (2) – соответствует случаю неучета турбулентной вязкости и диффузии для первой моды. Штриховая кривая (3) на рис. 3 соответствует зависимости действительной части частоты волны от волнового числа для второй моды при учете турбулентной вязкости и диффузии, штрихпунктирная кривая (4) соответствует случаю неучета турбулентной вязкости и диффузии. Из рис. 3 следует, что турбулентная вязкость и диффузия очень слабо влияют на зависимость действительной части частоты волны от волнового числа. Незначительные отклонения заметны лишь для больших волновых чисел при $k > 0.05\,$ рад/м для первой моды и для $k > 0.06\,$ рад/м у второй моды.

Рис. 2.

Модуль собственной функции 15-минутных внутренних волн второй моды.

Рис. 3.

Зависимость действительной части частоты от волнового числа.

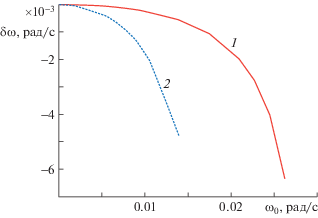
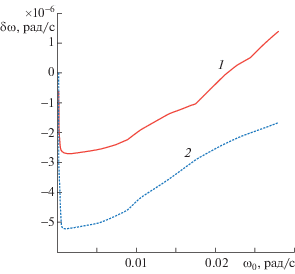
Зависимость мнимой части частоты $\delta \omega = \operatorname{Im} (\omega )$ от действительной части частоты для первых двух мод представлена на рис. 4. Далее действительную часть частоты ω0 будем называть просто частотой.

Рис. 4.

Зависимость мнимой части частоты от частоты волны для первой –1 и второй –2 мод.

Из рис. 4 следует, что мнимая часть частоты всегда отрицательная и волна затухает, декремент $\delta \omega $ у второй моды по модулю больше, чем у первой моды. На рис. 5 показаны аналогичные зависимости при отсутствии турбулентной вязкости и диффузии. Мнимая часть частоты у первой моды при ${{\omega }_{0}} < 0.022$ рад/с отрицательная, а при ${{\omega }_{0}} > 0.022$ рад/с – положительная. У второй моды мнимая часть отрицательная. Таким образом, учет турбулентной вязкости и диффузии приводит к тому, что мнимая часть всегда отрицательная (рис. 4). Характер зависимости мнимой части частоты от частоты волны существенно разный при учете и неучете турбулентной вязкости и диффузии (рис. 4, 5). При учете турбулентной вязкости и диффузии декремент затухания монотонно по модулю растет с ростом частоты и достигает величин порядка 10–3 рад/с, в то время как без учета турбулентной вязкости и диффузии (рис. 5) декремент на два–три порядка меньше. Без учета турбулентной вязкости и диффузии модуль мнимой части частоты убывает при ${{\omega }_{0}} > 0.001$ рад/с для второй моды. У первой моды при ${{\omega }_{0}} > 0.001$ рад/с декремент с ростом частоты по модулю также убывает, пока он остается отрицательным (рис. 5).

Рис. 5.

Зависимость мнимой части частоты волны для первой 1 и второй 2 мод при отсутствии турбулентной вязкости и диффузии.

Нормирующий множитель ${{A}_{1}}$ находится по известной максимальной амплитуде вертикальных смещений [13, 16].

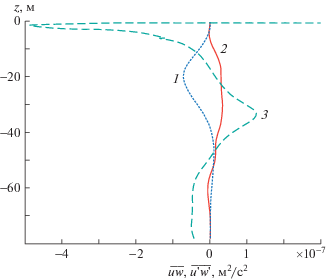
Вертикальные профили волнового $\overline {uw} $ (3.1) и турбулентного $\overline {u_{{}}^{/}w_{{}}^{/}} $ потоков импульса показаны на рис. 6. Турбулентный поток импульса определяется по формуле $\overline {u_{{}}^{/}w_{{}}^{/}} = - {{K}_{z}} \cdot d{{U}_{0}}{\text{/}}dz$, коэффициент вертикального турбулентного обмена для рассматриваемого случая сильной стратификации оценивается по формуле ${{K}_{z}} \cong 0.93 \times {{10}^{{ - 4}}}N_{c}^{{ - 1}}$ м2/c, ${{N}_{c}}$ соответствует частоте Брента–Вяйсяля в цикл/ч [18, 19]. Волновой поток импульса $\overline {uw} $ определяется для 15-минутных внутренних волн первой (1) и второй (2) мод с максимальной амплитудой 0.5 м. Волновой поток импульса второй моды заметно уступает потоку первой моды и турбулентному потоку. У первой моды нет подавляющего преимущества волнового потока над турбулентным, только в интервале глубин 15–25 м волновой поток по модулю превосходит турбулентный.

Рис. 6.

Профили волнового $\overline {uw} $ и турбулентного $\overline {u_{{}}^{/}w_{{}}^{/}} $ вертикальных потоков импульса; 1 – первая мода, 2 – вторая мода внутренних волн, 3 – турбулентный поток.

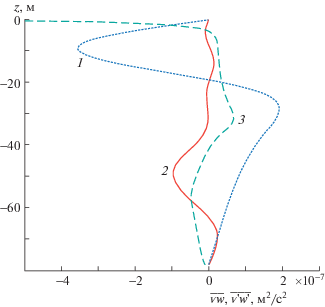
Вертикальные профили волнового $\overline {vw} $ (3.2) и турбулентного $\overline {v_{{}}^{/}w_{{}}^{/}} $ потоков импульса показаны на рис. 7. Турбулентный поток импульса определяется по формуле $\overline {v_{{}}^{/}w_{{}}^{/}} = - {{K}_{z}} \cdot d{{V}_{0}}{\text{/}}dz$. Волновой поток импульса $\overline {vw} $ определяется для 15-минутных внутренних волн первой (1) и второй (2) моды с максимальной амплитудой 0.5 м. Нельзя сказать, что волновой поток импульса второй моды на рис. 7 всюду уступает турбулентному, скорее всего глубже 30 м они сопоставимы по модулю. Глубже приповерхностного 2-метрового слоя вертикальный волновой поток импульса у первой моды по абсолютной величине доминирует над турбулентным и над потоком второй моды.

Рис. 7.

Профили волнового $\overline {vw} $ и турбулентного $\overline {v_{{}}^{/}w_{{}}^{/}} $ вертикальных потоков импульса; 1 – первая мода, 2 – вторая мода внутренних волн, 3 – турбулентный поток.

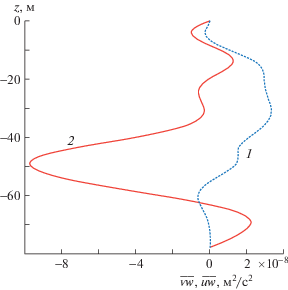
Сопоставим волновые потоки импульса $\overline {uw} $, $\overline {vw} $ для второй моды. На рис. 8 представлены вертикальные профили потоков импульса $\overline {uw} $, $\overline {vw} $ для второй моды 15-минутных внутренних волн. Глубже 40 м поток импульса $\overline {vw} $ доминирует по модулю над $\overline {uw} $.

Рис. 8.

Вертикальное распределение потоков импульса $\overline {uw} $ 1 и $\overline {vw} $ 2 для второй моды внутренних волн.

Сравним вертикальные волновые потоки диффузии и без их учета. На рис. 9 представлены профили вертикального потока импульса $\overline {uw} $ при учете турбулентной вязкости и диффузии (1) и без их учета (2). При учете турбулентной вязкости и диффузии поток заметно больше в верхнем 40-метровом слое.

Рис. 9.

Вертикальное распределение потоков импульса $\overline {uw} $ при учете турбулентной вязкости и диффузии 1 и без их учета 2.

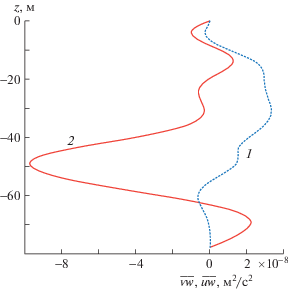
На рис. 10 представлены профили вертикального потока импульса $\overline {vw} $ при учете турбулентной вязкости и диффузии (1) и без их учета (2). При учете турбулентной вязкости и диффузии поток заметно больше в интервале глубин 40–60 м.

Рис. 10.

Вертикальное распределение потоков импульса $\overline {vw} $ при учете турбулентной вязкости и диффузии 1 и без их учета 2.

ЗАКЛЮЧЕНИЕ

Инерционно-гравитационные внутренние волны в двумерном стратифицированном течении при учете турбулентной вязкости и диффузии имеют комплексную собственную функцию и частоту. Мнимая поправка к частоте отрицательная, т.е. волна затухает. Декремент затухания у второй моды по абсолютной величине больше, чем у первой для волны фиксированного периода.

На зависимость действительной части частоты от волнового числа турбулентная вязкость и диффузия практически влияния не оказывают. На зависимость мнимой части частоты волны от частоты волны турбулентная вязкость и диффузия оказывают существенное влияние. Мнимая поправка к частоте по модулю на два-три порядка больше при учете турбулентной вязкости и диффузии и всегда отрицательная.

Волновой поток импульса $\overline {vw} $ доминирует по модулю над потоком $\overline {uw} $ глубже 40 м для второй моды 15-минутных внутренних волн при учете турбулентной вязкости и диффузии.

Сравнение волнового $\overline {vw} $ и турбулентного $\overline {v_{{}}^{/}w_{{}}^{/}} $ потоков импульса показывает, что для первой моды 15-минутных внутренних волн волновой поток по модулю доминирует над турбулентным глубже приповерхностного 2-метрового слоя. У второй моды эти потоки сравнимы по абсолютной величине.

Сравнение волнового $\overline {uw} $ и турбулентного $\overline {u_{{}}^{/}w_{{}}^{/}} $ потоков импульса показывает, что для первой моды 15-минутных внутренних волн волновой поток по модулю, вообще говоря, меньше турбулентного и сопоставим с ним на глубинах 10–30 м. У второй моды турбулентный поток импульса больше по абсолютной величине волнового.

Волновой поток импульса $\overline {uw} $ для второй моды при учете турбулентной вязкости и диффузии выше, чем при их неучете в верхнем 40-метровом слое.

Волновой поток импульса $\overline {vw} $ для второй моды при учете турбулентной вязкости и диффузии выше, чем при их неучете в слое 40–60 м.

Автор благодарен М.В. Рыбалкиной за проведение численных расчетов при решении краевой задачи. Работа выполнена в рамках государственного задания 0555-2021-0004.

Список литературы

  1. Бадулин С.И., Цимринг Л.Ш., Шрира В.И. Захват и вертикальная фокусировка внутренних волн в пикноклине горизонтальными неоднородностями стратификации и течений // Доклады АН СССР. 1983. Т. 273. № 2. С. 459–463.

  2. Sibgatullin I.N., Ermanyuk E.V. Internal and Inertial Wave Attractors: a Review // J. Appl. Mech. Tech. 2019. V. 60. № 2. P. 284–302. https://doi.org/10.1134/S002189441902010X

  3. Brouzet C., Ermanyuk E.V., Joubaud S., Sibgatullin I., Dauxois T. Energy cascade in internal-wave attractors // EPL (Europhysics Letters), V. 113. № 4. https://doi.org/10.1209/0295-5075/113/44001

  4. Сабинин К.Д., Успенская Т.М. К влиянию сдвиговых течений на кинематические характеристики внутренних волн // Океанология. 1990. № 6. С. 932–935.

  5. Bulatov V.V., Vladimirov Yu.V. and Vladimirov I.Yu. Phase Structure of Internal Gravity Waves in the Ocean with Shear Flows. Physical Oceanography, [e-journal]. 2021. V. 28. Iss. 4. P. 438–453. https://doi.org/10.22449/1573-160X-2021-4-438-453

  6. Miles J.W. On the stability of heterogeneous shear flows // J. Fluid Mech. 1961. V. 10. Iss. 4. P. 496–508. https://doi.org/10.1017/S0022112061000305

  7. Howard L.N. Note on a paper of John W. Miles // J. Fluid Mech. 1961. V. 10. Iss. 4. P. 509–512. https://doi.org/10.1017/S0022112061000317

  8. Ле Блон П., Майсек Л. Волны в океане. М.: Мир, 1981. Ч. 2. 363 с.

  9. LeBlond P.H. On damping of internal gravity waves in a continuously stratified ocean // J. Fluid Mech. 1966. V. 25. Iss. 1. P. 121–142. https://doi.org/10.1017/S0022112066000089

  10. Островский Л.А., Соустова И.А. Верхний перемешанный слой как сток энергии внутренних волн // Океанология. 1979. Т. 19. Вып. 6. С. 973–981.

  11. Слепышев А.А. Вертикальный перенос импульса внутренними волнами при учете турбулентной вязкости и диффузии // Изв. РАН. ФАО. 2016. Т. 52. № 3. С. 342–350. https://doi.org/10.7868/S0002351516030111

  12. Вишик М.И., Люстерник Л.А. Регулярное вырождение и пограничный слой для линейных дифференциальных уравнений с малым параметром // УМН. 1957. Т. XII. Вып. 5 (77). С. 3–122.

  13. Анкудинов Н.О., Слепышев А.А. Вертикальный перенос импульса внутренними волнами в двумерном потоке // Изв. РАН. МЖГ. 2021. № 3. С. 39–47.

  14. Миропольский Ю.З. Динамика внутренних гравитационных волн в океане. Л.: Гидрометеоиздат, 1981. 302 с.

  15. Черкесов Л.В. Гидродинамика волн. К.: Наукова думка, 1980. 259 с.

  16. Пантелеев Н.А. Отчет о работах в 44-м рейсе (3-й этап) НИС “Михаил Ломоносов” 7 августа–15 сентября 1985 г. Севастополь: МГИ АН УССР, 1985. Т. 1. 135 с.

  17. Боуден К. Физическая океанография прибрежных вод. Москва: Мир, 1988. С. 285.

  18. Иванов В.А., Самодуров А.С., Чухарев А.М., Носова А.В. Интенсификация вертикального турбулентного обмена в районах сопряжения шельфа и континентального склона в Черном море // Доп. НАН України. 2008. № 6. С. 108–112.

  19. Samodurov A.S. Complimentarity of Different Approaches for Assessing Vertical Turbulent Exchange Intensity in Natural Stratified Basins // J. Phys. Oceanogr. 2016. Iss. 6. P. 32–42. https://doi.org/10.22449/1573-160X-2016-6-32-42

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал