1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2021

Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 25-37

СТЕКАНИЕ ПЛЕНКИ НЕНЬЮТОНОВСКОЙ ЖИДКОСТИ ПО НАКЛОННОЙ ПЛОСКОСТИ С ПЕРИОДИЧЕСКИМ РЕЛЬЕФОМ

Е. И. Могилевский a, *

a Московский государственниый университет им. М.В. Ломоносова, Механико-математический факультет
Москва, Россия

* E-mail: Evgeny.Mogilevskiy@math.msu.ru

Поступила в редакцию 28.05.2021
После доработки 22.06.2021
Принята к публикации 22.06.2021

Полный текст (PDF)

Аннотация

Рассматривается течение тонкого слоя нелинейно-вязкой жидкости по наклонной плоскости под действием силы тяжести. Предполагается, что капиллярные силы существенны, реология описывается степенным законом. Изучается влияние малого периодического рельефа, нанесенного на плоскость, на характеристики стационарного течения и его устойчивость в линейном приближении; расчеты проводятся для синусоидального рельефа. Показано, что независимо от реологии пленка на плоскости имеет большую среднюю толщину, чем на гладкой при том же расходе, изменение средней толщины пропорционально второй степени амплитуды рельефа. Изменения коэффициентов усиления нормальных мод и критического числа Рейнольдса также пропорциональны второй степени амплитуды рельефа. Длинноволновой рельеф увеличивает критическое число Рейнольдса, причем для дилатантных жидкостей этот эффект достигается при меньших значениях периода, чем для псевдопластических.

Ключевые слова: гидродинамическая неустойчивость, тонкие пленки, теория Флоке, микрорельеф, неньютоновские жидкости

При нанесении покрытий на твердые поверхности, а также для организации процессов тепло- и массообмена часто используются тонкие слои жидкости, которые движутся под действием силы тяжести [1]. Такие течения сопровождаются волнообразованием на свободной поверхности: наблюдаются различные по своей структуре течения [2], которые, в частности, приводят к существенным изменениям параметров обменных процессов [3]. Математической моделью таких течений является движение слоя по наклонной плоскости. Одним из эффективных инструментов для описания волновых режимов течения пленки является модель Шкадова [4], основной идеей которой является переход от уравнений Навье–Стокса к уравнениям тонкого слоя с последующим осреденением поперек слоя в предположении, что в каждом сечении в каждый момент времени профиль скорости подобен стационарному, а гравитационные, взякие и капиллярные силы имеют один порядок. В рамках этой модели возможно описание регулярных периодических и уединенных волн [5]; параметры нелинейных волновых режимов хорошо соответствуют экспериментам [3, 6].

Некоторые жидкости, которые используются в технологических процессах, например, нефтепродукты [7], растворы и расплавы полимеров [8] не описываются ньютоновской моделью вязкого трения, что приводит к существенным изменениям характеристик пленочных течений [9], при этом многие эффекты могут моделироваться с использованием модели обобщенно-ньютоновской среды, которая предполагает наличие эффективного коэффициента вязкости, зависящего от локальной мгновенной скорости сдвига. Часто для описания пленочных течений используется модель Оствальда–де Виля [10–12], постулирующая эту зависимость в виде степенной функции и содержащая один размерный и один безразмерный параметр. Модель Шкадова обобщается для этого и любого другого реологического соотношения: вводятся интегральные параметры, которые характеризуют свойства среды [13, 14]. Неньютоновские свойства жидкости изменяют параметры неустойчивости стекающей пленки количественно; новые качественные эффекты, такие как доминирование сдвиговых мод неустойчивости (Толмина–Шлихтинга) [15], трехмерных возмущений [16, 17] имеют место только при крайне малых углах наклона плоскости к горизонту.

Для управления волнообразованием и, соответственно, параметрами обменных процессов в течение можно вносить периодические по времени или пространству возмущения, например, осцилляции твердой поверхности [18, 19], по которой течет пленка, или микрорельеф на этой поверхности [20]. При продольных осцилляциях плоскости основное течение имеет плоскую свободную поверхность, однако скорость жидкости является периодической функцией времени. Анализ устойчивости такого течения для ньютоновской жидкости показывает, что диапазоны частот, стабилизирующих и дестабилизирующих течения, чередуются, влияние осцилляций быстро убывает с ростом частоты. Для неньютоновских жидкостей осцилляции изменяют средние характеристики основного течения (например, расход при фиксированной толщине) [21, 22], характер этого изменения противоположный для псевдопластических и дилатантных жидкостей (наблюдается увеличение и уменьшение среднего расхода соответственно). При несимметричных осцилляциях с нулевым средним значением смещения плоскости возможно наблюдение отрицательного среднего расхода [23], что соответствует восходящему движению. Влияние осцилляций на параметры неустойчивости для неньютоновских жидкостей существенно сильнее,чем для ньютоновских [24], высокочастотные колебания стабилизируют течение псевдо-пластических жидкостей, низкочастотные – дилатантных.

В настоящей работе рассматриваются периодические по пространству возмущения, вносимые в систему через микрорельеф на поверхности. В экспериментальных работах [25, 26] показано, что нейтральные кривые при наличии рельефа значительно усложняются по сравнению с течением по гладкой плоскости: возможно появление изолированных областей устойчивости и неустойчивости – так называемых островов. Первичная неустойчивость остается двумерной, более того, течение в канале конечной ширины с рельефом на боковых стенках имеет нейтральную кривую, аналогичную плоскому течению с рельефом на нижней поверхности [27]. Обзорная работа [28] содержит описание основных эффектов, которые наблюдаются при течении пленки по плоскости с микрорельефом.

Устойчивость течений ньютоновских жидкостей по плоскости с микрорельефом рассмотрена в рамках полных уравнений Навье–Стокса [29], в длинноволновом приближении для малых чисел Рейнольдса [30], в рамках уравнений Шкадова [31, 32]. Некоторые общие свойства стационарных течений, в том числе с учетом неньютоновской реологии показаны в [11]. В [33, 34] исследована линейная устойчивость течения ньютоновской жидкости, получено аналитическое выражение для поправки к коэффициенту усиления при малой амплитуде неровностей, проведена классификация топологических типов нейтральных кривых, которая совпадает с полученной экспериментально в [25], при этом анализ оказывается существенно проще, чем при использовании метода взвешенных невязок [35], который применялся в [36].

Целью работы является анализ влияния неньютоновских свойств среды на характеристики стационарного течения пленки по наклонной плоскости с микрорельефом и его устойчивость. В частности, ставится задача о качественном сравнении эффекта внешних возмущений, периодических по пространству, с периодическими по времени, рассмотренными в [22].

1. ПОСТАНОВКА ЗАДАЧИ

Введем основные обозначения и кратко приведем вывод уравнений, описывающих течение тонкого слоя степенной жидкости по наклонной плоскости с микрорельефом [11, 31].

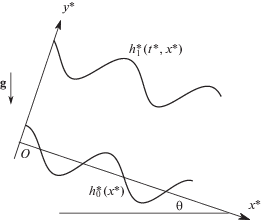
Рассматривается двумерное течение слоя неньютоновской жидкости плотностью $\rho $, стекающего под действием силы тяжести (ускорение свободного падения $g$) по наклонной плоскости с периодическим рельефом, причем его величина не зависит от горизонтальной координаты. В декартовой системе координат $Ox{\text{*}}y{\text{*}}z{\text{*}}$ ось $Oz{\text{*}}$ горизонтальна и направлена вдоль плоскости, ось $Ox{\text{*}}$ – вниз вдоль среднего положения твердой поверхности, $Oy{\text{*}}$ – в сторону жидкости; скорость жидкости лежит в плоскости $Ox{\text{*}}y{\text{*}}$. Ось $Ox{\text{*}}$ образует с горизонтом угол $\theta $. Рельеф описывается уравнением $y* = h_{0}^{ * }(x*)$, функция $h_{0}^{ * }(x)$ имеет период $\lambda * = 2\pi {\text{/}}\alpha {\text{*}}$. На свободной поверхности жидкости $y* = h_{1}^{ * }(t*,x*)$, где t* – время, действует поверхностное натяжение с коэффициентом $\sigma $ (рис. 1). Здесь и далее звездочкой обозначены размерные величины.

Рис. 1.

Схема течения.

Реология описывается обобщенно-ньютоновской моделью: тензор вязких напряжений пропорционален тензору скоростей деформаций с коэффициентом, зависящим от скорости сдвига $\dot {\gamma }{\text{*}}$ или, что эквивалентно, второго инварианта тензора скоростей деформаций $I_{2}^{ * } = {{\dot {\gamma }}^{{*2}}}{\text{/}}2$, – эффективным коэффициентом вязкости. В настоящей работе рассматривается степенная зависимость (степенная модель, модель Оствальда–де Виля [8]), которая содержит один размерный параметр $K$ и один безразмерный параметр $n$

(1.1)
$\begin{gathered} \tau _{{ij}}^{ * } = 2\mu {\text{*}}(\dot {\gamma }*)e_{{ij}}^{ * },\quad \mu * = K{{(\dot {\gamma }*)}^{{n - 1}}}\quad i,j = 1,\;2 \\ \dot {\gamma }* = {{(2e_{{ij}}^{ * }e_{{ji}}^{ * })}^{{1/2}}} \\ e_{{ij}}^{*} = \frac{1}{2}\left( {\frac{{\partial V_{i}^{*}}}{{\partial X_{j}^{*}}} + \frac{{\partial V_{j}^{*}}}{{\partial X_{i}^{*}}}} \right) \\ X_{1}^{*} = x*,\quad X_{2}^{*} = y{\text{*}} \\ \end{gathered} $
где $V_{1}^{ * } = u{\text{*}}$, $V_{2}^{ * } = {v}{\text{*}}$ проекции вектора скорости ${\mathbf{V}}{\text{*}}$ на оси $Ox{\text{*}}$, $Oy{\text{*}}$, по повторяющимся индексам идет суммирование. При n = 1 реология соответствует ньютоновскому поведению, при n > 1 и n < 1 степенная модель описывает дилатантное и псевдопластическое поведение среды.

Уравнения движения и неразрывности имеют вид (через $p{\text{*}}$ обозначено давление)

(1.2)
$\begin{gathered} \rho \frac{{d{\mathbf{V}}_{i}^{ * }}}{{dt{\text{*}}}} = - \frac{{\partial p{\text{*}}}}{{\partial X_{i}^{ * }}} + \frac{{\partial \tau _{{ij}}^{ * }}}{{\partial X_{j}^{ * }}} + {{g}_{i}} \\ \frac{{\partial V_{i}^{ * }}}{{\partial X_{i}^{ * }}} = 0 \\ {{g}_{1}} = gsin,\quad {{g}_{2}} = - gcos \\ \end{gathered} $

На твердой поверхности условие прилипания; на свободной поверхности выполнено кинематическое условие, касательные напряжения непрерывны, а нормальные отличаются от внешнего постоянного атмосферного давления $p_{a}^{ * }$ за счет давления Лапласа

(1.3)
$\begin{gathered} y* = h_{0}^{ * }(x*){\text{:}}\quad u* = {v}* = 0 \\ y* = h_{1}^{ * }(t*,x*){\text{:}}\quad \frac{{\partial h_{1}^{ * }}}{{\partial t{\text{*}}}} + u{\text{*}}\frac{{\partial h_{1}^{ * }}}{{\partial x*}} = {v}{\text{*}} \\ \tau _{{12}}^{*}(1 - {{b}^{2}}) - b(\tau _{{11}}^{*} - \tau _{{22}}^{*}) = 0 \\ p{\text{*}} - \tau _{{ij}}^{*}{{n}_{i}}{{n}_{j}} = p_{a}^{ * } + \sigma \frac{{\partial {{n}_{1}}}}{{\partial x{\text{*}}}} \\ {{n}_{1}} = - \frac{b}{{\sqrt {1 + {{b}^{2}}} }},\quad {{n}_{2}} = \frac{1}{{\sqrt {1 + {{b}^{2}}} }},\quad b = \frac{{\partial h_{1}^{ * }}}{{\partial x{\text{*}}}} \\ \end{gathered} $

В качестве масштабов для перехода к безразмерным переменным используются следующие величины. Для координаты $y{\text{*}}$, рельефа и свободной поверхности – толщина пленки H, стекающей по плоскости без рельефа (гладкой) в стационарном режиме; для проекции скорости на $Ox{\text{*}}$ – средняя по толщине скорость жидкости при таком течении U. Для координаты $x{\text{*}}$, периода рельефа λ* вводится масштаб $L = {{\varepsilon }^{{ - 1}}}H$, при этом предполагается, что $\varepsilon \ll 1$, точное определение $\varepsilon $ будет дано ниже. Таким образом, безразмерные переменные имеют вид (используются те же символы, что и для размерных, без индекса *)

(1.4)
$\begin{array}{*{20}{c}} {t = \frac{{\varepsilon Ut{\text{*}}}}{H},\quad x = \frac{{\varepsilon x{\text{*}}}}{H},\quad y = \frac{{y{\text{*}}}}{H}} \\ {u = \frac{{u{\text{*}}}}{U},\quad {v} = \frac{{{v}{\text{*}}}}{{\varepsilon U}},\quad p = \frac{{p{\text{*}} - p_{a}^{ * }}}{{\rho {{U}^{2}}}}} \end{array}$

Величины $H$ и $U$ связаны соотношением, следующим из решения задачи о стационарном cтекании слоя жидкости по наклонной плоскости. Безразмерная скорость сдвига $\dot {\gamma }$ имеет вид

$\dot {\gamma } = \left| {\frac{{\partial u}}{{\partial y}} + O({{\varepsilon }^{2}})} \right|$

Вводится характерное размерное значение эффективного коэффициента вязкости

${{\mu }_{c}} = \mu {\text{*}}\left( {\frac{U}{H}} \right) = K\mathop {\left( {\frac{U}{H}} \right)}\nolimits^{n - 1} $
и согласно (1.1) безразмерный эффективный коэффициент вязкости c точностью до членов O(ε2) выражается формулой

$\mu = \frac{{\mu {\text{*}}}}{{{{\mu }_{c}}}} = \mathop {\left| {\frac{{\partial u}}{{\partial y}}} \right|}\nolimits^{n - 1} $

Задача определяется следующими безразмерными параметрами

(1.5)
$\operatorname{Re} = \frac{{\rho UH}}{{{{\mu }_{c}}}},\quad {\text{We}} = \frac{{\rho {{U}^{2}}H}}{\sigma },\quad n,\quad \theta $
а также безразмерной функцией ${{h}_{0}}(x)$.

Распределение скоростей ${{u}_{s}}(y)$ при стационарном течении слоя жидкости по гладкой наклонной плоскости ${{h}_{0}}(x) \equiv 0$ с плоской свободной границей ${{h}_{1}} = 1$ описывается решением краевой задачи, которая получается из (1.2), (2.3) с учетом (1.4)

(1.6)
$\begin{array}{*{20}{c}} {\frac{d}{{dy}}\left[ {\mu \left( {\frac{{d{{u}_{s}}}}{{dy}}} \right)\frac{{d{{u}_{s}}}}{{dy}}} \right] + m = 0} \\ {{{u}_{s}}(0) = 0,\quad \mathop {\left. {\frac{{d{{u}_{s}}}}{{dy}}} \right|}\nolimits_{y = 1} = 0} \\ {\int\limits_0^1 {{{u}_{s}}} dy = 1,\quad m = \frac{{\rho g{{H}^{2}}{\text{sin}}\theta }}{{{{\mu }_{c}}U}}} \end{array}$

Значение константы $m$ определяется реологией и находится в процессе решения задачи относительно ${{u}_{s}}$ из интегрального условия нормировки. Для степенной жидкости имеем

$\begin{array}{*{20}{c}} {m = \frac{{\rho g{{H}^{{n + 1}}}sin}}{{K{{U}^{n}}}} = \mathop {\left( {\frac{{2n + 1}}{n}} \right)}\nolimits^n ,\quad U = \frac{n}{{2n + 1}}\mathop {\left( {\frac{{\rho g{{H}^{{n + 1}}}sin\theta }}{K}} \right)}\nolimits^{1/n} } \\ {{{u}_{s}}(y) = \frac{{2n + 1}}{{n + 1}}(1 - {{{(1 - y)}}^{{1 + 1/n}}})} \end{array}$

Предполагается, что ${{\varepsilon }^{2}},\varepsilon {{\operatorname{Re} }^{{ - 1}}} \ll 1$. Тогда проекция уравнения движения на ось y и граничное условие для нормальных напряжений отделяются от остальной задачи, определяя задачу для давления. После подстановки решения задачи для давления в проекцию уравнения движения на Ox и интегрирования поперек слоя получаем

(1.7)
$\begin{gathered} \varepsilon \operatorname{Re} \left[ {\frac{{\partial q}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\int\limits_{{{h}_{0}}}^{{{h}_{1}}} {{{u}^{2}}} dy} \right)} \right] = \frac{{{{\varepsilon }^{3}}\operatorname{Re} }}{{{\text{We}}}}h\frac{{{{\partial }^{3}}h}}{{\partial {{x}^{3}}}} - m\varepsilon {\text{ctg}}\theta h\frac{{\partial h}}{{\partial x}} + mh - \tau \\ q = \int\limits_{{{h}_{0}}}^{{{h}_{1}}} u dy,\quad \tau = \mu \mathop {\left. {\left( {\left| {\frac{{\partial u}}{{\partial y}}} \right|} \right)\frac{{\partial u}}{{\partial y}}} \right|}\nolimits_{y = {{h}_{0}}} ,\quad h = {{h}_{1}} - {{h}_{0}} \\ \end{gathered} $

Интегрирование уравнения неразрывности поперек слоя с учетом граничных условий дает

(1.8)
$\frac{{\partial h}}{{\partial t}} + \frac{{\partial q}}{{\partial x}} = 0$

Отношение масштабов длин ε определяется так, чтобы коэффициент при капиллярном члене был равен m, при этом определяется новый параметр подобия $\delta $ [37]

(1.9)
$\frac{{{{\varepsilon }^{3}}\operatorname{Re} }}{{{\text{We}}}} = m,\quad \varepsilon \operatorname{Re} = 5m\delta $

Для замыкания системы уравнений (1.7)–(1.8) требуется задать связь толщины пленки $h$ и локального расхода q с трением на твердой поверхности $\tau $ и потоком импульса $\int_{{{h}_{0}}}^{{{h}_{1}}} {{{u}^{2}}} dy$. Метод Шкадова [4], который является частным случаем метода Галеркина, предполагает сохранение профиля скорости во всех сечениях в каждый момент времени: для течения по гладкой плоскости это означает $u(t,x,y) = q(t,x){{u}_{s}}(\eta ){\text{/}}h(t,x)$, $\eta = y{\text{/}}h(t,x)$, ${{u}_{s}}(\eta )$ – решение задачи (1.6). Такой метод замыкания системы уравнений для неньютоновской жидкости использовался в работе [14]. Другой способ задания профиля скорости [22] состоит в том, что выбирается функция, которая является решением задачи (1.6), в которой фиксируется значение толщины пленки, ставится условие равенства интеграла заданному расходу, а свободный член в уравнении подбирается для выполнения этого условия. Этот способ физически означает предположение о том, что в каждый момент времени в каждом сечении профиль скорости соответствует стационарному течению с заданной толщиной и массовой силой, равной сумме силы тяжести и не зависящей от поперечной координаты силы инерции. Для ньютоновской и степенной жидкостей оба подхода дают одинаковый результат. Для течения по плоскости с микрорельефом уравнения для интегральных характеристик имеют вид [11]

(1.10)
$\begin{array}{*{20}{c}} {\frac{{\partial h}}{{\partial t}} + \frac{{\partial q}}{{\partial x}} = 0} \\ {5\delta \left[ {\frac{{\partial q}}{{\partial t}} + B\frac{\partial }{{\partial x}}\left( {\frac{{{{q}^{2}}}}{h}} \right)} \right] = h\frac{{{{\partial }^{3}}h}}{{\partial {{x}^{3}}}} - \beta h\frac{{\partial h}}{{\partial x}} + h - \mathop {\left( {\frac{q}{{{{h}^{2}}}}} \right)}\nolimits^n + h\left[ {\frac{{{{\partial }^{3}}{{h}_{0}}}}{{\partial {{x}^{3}}}} - \beta \frac{{\partial {{h}_{0}}}}{{\partial x}}} \right]} \\ {B = \frac{{2(2n + 1)}}{{3n + 2}},\quad \beta = \varepsilon {\text{ctg}}\theta } \end{array}$

Реологические свойства жидкости проявляются в значениях коэффициента B и показателя степени в слагаемом, соответствующем трению на твердой поверхности. При $n = 1$ получаются уравнения, описывающие течение ньютоновской жидкости [32–34].

В данной работе исследуется течение по плоскости с синусоидальным рельефом

(1.11)
${{h}_{0}} = acos\alpha x$

при этом основное внимание уделяется случаю $a \ll 1$, так как такое предположение позволяет получить приближенные аналитические результаты [11, 33, 34] и провести качественный анализ свойств стационарного течения и его устойчивости.

2. СТАЦИОНАРНОЕ ТЕЧЕНИЕ

Для не зависящих от времени функций q, $h$ из уравнения неразрывности следует $q = {{q}_{0}}$ = const. В [11] значение ${{q}_{0}}$ полагалось неизвестным, а нормировка проводилась с помощью условия на среднее значение толщины пленки $\left\langle h \right\rangle = 1$. При такой постановке задачи, по крайней мере для ньютоновских жидкостей, имеется несколько семейств стационарных периодических решений [30]. Одно из семейств имеет тот же период, что и рельеф, и при стремлении амплитуды рельефа к нулю стремится к тривиальному решению (1.10) $h = {\text{const}}$. Только решения этого семейства существуют в постановке ${{q}_{0}} = 1$ и наблюдаются в экспериментах [20]. В настоящей работе также используется условие нормировки ${{q}_{0}} = 1$.

Толщина пленки при стационарном течении ${{h}_{s}}(x)$ является решением уравнения, следующего из (1.10) при условии (1.11)

(2.1)
$\begin{array}{*{20}{c}} {h_{s}^{{'''}} - \beta h_{s}^{'} + 1 - \frac{1}{{h_{s}^{{2n + 1}}}} + \frac{{5\delta B}}{{h_{s}^{3}}}h_{s}^{'} + a\alpha ({{\alpha }^{2}} + \beta )sin\alpha x = 0} \\ {{{h}_{s}}(x) = {{h}_{s}}\left( {x + \frac{{2\pi }}{\alpha }} \right),\quad h_{s}^{'}(x) = h_{s}^{'}\left( {x + \frac{{2\pi }}{\alpha }} \right),\quad h_{s}^{{''}}(x) = h_{s}^{{''}}\left( {x + \frac{{2\pi }}{\alpha }} \right)} \end{array}$

Решение этой задачи находится численно методом стрельбы [11, 31] или путем сведения к системе нелинейных алгебраических уравнений относительно коэффициентов разложения искомой функции ${{h}_{s}}$ в ряд Фурье [32]

(2.2)
${{h}_{s}}(x) = \sum\limits_{l = - \infty }^\infty {{{h}^{{(l)}}}} {{e}^{{il\alpha x}}},\quad {{h}^{{(l)}}} = \overline {{{h}^{{( - l)}}}} $

Разложение решения в ряд по $a$ в предположении малости амплитуды рельефа [11] показывает, что ${{h}^{{(l)}}} = O({{a}^{{|l|}}})$, ${{h}^{{(0)}}} = 1 + O({{a}^{2}})$. Последовательные применения разложений по степеням a и по гармоникам (2.2) приводят к следующим результатам

(2.3)
$\begin{array}{*{20}{c}} {{{h}^{{(1)}}} = \overline {{{h}^{{( - 1)}}}} = \frac{{\alpha ({{\alpha }^{2}} + \beta )}}{{(2n + 1) - i\alpha ({{\alpha }^{2}} + \beta - 5\delta B)}}\frac{{ia}}{2} + O({{a}^{3}})} \\ {{{h}^{{(0)}}} = 1 + 2(n + 1){{h}^{{(1)}}}\overline {{{h}^{{(1)}}}} } \end{array}$

При любых значениях $n$ и $a \ne 0$ величина средней толщины пленки ${{h}^{{(0)}}}$ превосходит единицу – толщину пленки при течении по гладкой плоскости. Этот результат качественно отличает пространственно-периодическое воздействие на течение пленки от периодического по времени воздействия – продольные осцилляции плоскости. Эксперименты [21] и теоретические исследования [22, 23] показывают, что осцилляции плоскости приводят к увеличению средней толщины слоя при сохранении среднего расхода только для дилатантных жидкостей ($n > 1$) и к уменьшению для псевдопластических ($n < 1$).

Форма свободной поверхности определяется соотношением

${{h}_{1}} = {{h}_{0}} + {{h}_{s}}$

Разложение этой функции в ряд Фурье отличается от ${{h}_{s}}$ только значением коэффициента при первой гармонике. С точностью до членов $O({{a}^{2}})$ свободная поверхность представляет собой синусоиду с амплитудой A, такой что

(2.4)
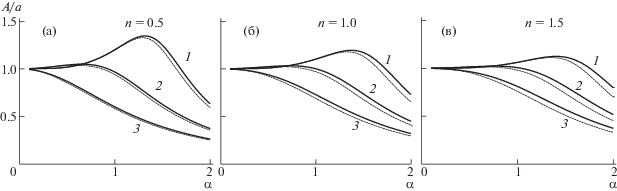
${{A}^{2}} = \frac{{{{{(2n + 1)}}^{2}} + {{{(5\delta \alpha B)}}^{2}}}}{{{{{(2n + 1)}}^{2}} + {{\alpha }^{2}}{{{({{\alpha }^{2}} + \beta - 5\delta \alpha B)}}^{2}}}}{{a}^{2}}$

Амплитуда свободной поверхности совпадает с амплитудой рельефа при длинноволновом рельефе ($\alpha \to 0$). Неровности свободной поверхности, вызванные коротковолновым рельефом, сглаживаются поверхностным натяжением, и амплитуда свободной поверхности стремится к нулю при $\alpha \to \infty $. При некоторых значениях параметров зависимость нормированной амплитуды свободной поверхности A/a от волнового числа рельефа α немонотонна, она имеет ровно один максимум, так называемый линейный резонанс [31]. Величина этого максимума уменьшается с ростом $n$ при фиксированных параметрах течения $\delta $, $\beta $, а также уменьшается с ростом относительного вклада градиента гидростатического давления (параметр $\beta $) при фиксированных $n$, $\delta $.

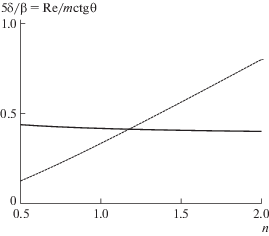
Результат вычислений по приближенной формуле (2.4) хорошо совпадает с численными расчетами (рис. 2). Для решения нелинейного уравнения (2.1) под амплитудой свободной поверхности понимается полуразность между максимальным и минимальным значениями ${{h}_{1}}(x)$. Для значения малого параметра $a = 0.2$ отличие приближенного решения от численного при $\alpha < 2$ не превосходит 10%. При увеличении $\alpha $ относительная ошибка возрастает, однако абсолютные значения амплитуд, полученных аналитически и численно, стремятся к нулю.

Рис. 2.

Нормированная амплитуда свободной поверхности при $\delta = 0.25$ для течений (а) псевдопластической n = 0.5, (б) ньютоновской n = 1 и (в) дилатантной жидкостей n = 1.5. Сплошные линии – аналитическое решение, штриховые – численное при $a = 0.2$: 1–3 – $\beta = 0,\;2,\;4$.

Анализ формулы (2.4) показывает, что резонанс имеет место при выполнении условия

(2.5)
$\beta < 10\delta B$
или, что эквивалентно

${\text{ctg}}\theta < \frac{{2B}}{m}\operatorname{Re} $

Подобным же образом записывается критерий неустойчивости течения пленки по гладкой плоскости [22] – эти критерии выражают ограничение на соотношение между инерционными членами и градиентом гидростатического давления

(2.6)
$\beta < 5\delta \frac{{2n + 1}}{{{{n}^{2}}}} \Leftrightarrow {\text{ctg}}\theta < \frac{{2n + 1}}{{{{n}^{2}}m}}\operatorname{Re} $

В зависимости от реологического показателя $n$ возможны различные соотношения между критериями существования резонанса и устойчивости течения. На рис. 3 показаны критерии (2.5), (2.6). Неравенства выполнены в области, расположенной выше соответствующих кривых. Течение по вертикальной плоскости ($\beta = 0$) всегда неустойчиво при отсутствии рельефа и допускает амплитуду свободной поверхности, большую чем амплитуда рельефа. Для определенных $n$ ($n > 1.18$) возможно наличие резонанса при параметрах, соответствующих устойчивому течению на гладкой плоскости.

Рис. 3.

Границы областей существования резонанса (сплошная линия) и устойчивости течения по гладкой плоскости (штриховая линия).

3. УСТОЙЧИВОСТЬ К МАЛЫМ ВОЗМУЩЕНИЯМ

Для исследования влияния рельефа на устойчивость течения используется метод нормальных мод. Пусть имеются малые возмущения стационарного решения

$q(t,x) = 1 + {{q}_{d}}(t,x),\quad h(t,x) = {{h}_{s}}(x) + {{h}_{d}}(t,x)$

Рассматриваются периодические по времени возмущения

${{q}_{d}}(t,x) = Q(x){{e}^{{ - i\omega t}}},\quad {{h}_{d}}(t,x) = {{H}_{d}}(x){{e}^{{ - i\omega t}}},\quad \omega \in \mathbb{R}$

Подстановка возмущений в таком виде в уравнения (1.10) и линеаризация приводят к обыкновенному дифференциальному уравнению четвертого порядка с периодическими коэффициентами относительно $Q$

(3.1)
$\begin{array}{*{20}{c}} {{{Q}^{{i{v}}}} = Q{\text{''}}\left[ { - \frac{{5\delta B}}{{h_{s}^{3}}} + \beta } \right] + Q'\left[ {5\delta B\left( {\frac{{3h_{s}^{'}}}{{h_{s}^{4}}} + \frac{{2i\omega }}{{h_{s}^{2}}}} \right) - \frac{{2n + 1}}{{h_{s}^{{2n + 2}}}}} \right] + } \\ { + \;Q\left[ {\frac{{5{{\delta }^{2}}\omega }}{{{{h}_{s}}}} - i\omega \left( {\frac{{10\delta Bh_{s}^{'}}}{{h_{s}^{3}}} - \frac{n}{{h_{s}^{{2n + 1}}}}} \right)} \right]} \end{array}$

Для течения по гладкой плоскости коэффициенты уравнения постоянны, поэтому общее решение имеет вид

$Q = \sum\limits_{j = 1}^4 {{{c}_{j}}} {{e}^{{i{{k}_{j}}x}}}$
где $k = {{k}_{j}}$ удовлетворяют характеристическому уравнению

(3.2)
${{k}^{4}} + {{k}^{2}}\left[ { - 5\delta B + \beta } \right] + k(10\delta B\omega + i(2n + 1)) - 5\delta {{\omega }^{2}} - i\omega n = 0$

Характеристики неустойчивости течения по плоскости с синусоидальным рельефом определяются с помощью теории Флоке. Общее решение уравнения (3.1) представляется в виде произведения периодической функции и экспоненциальной. Неустойчивость соответствует наличию среди показателей экспонент числа с положительной действительной частью. Алгоритм определения коэффициентов усиления [31–34, 36] состоит из следующих шагов: вычисление компонент матрицы монодромии с помощью четырехкратного решения задачи Коши на отрезке $[0;2\pi {\text{/}}\alpha ]$ с линейно независимыми начальными условиями, решение задачи на собственные значения $\nu $ для матрицы монодромии, вычисление коэффициента усиления I по формуле

$I = \frac{\alpha }{2}ln\left| \nu \right|$
для каждого собственного числа $\nu $. В [33] показано, что только один из четырех показателей только один имеет физический смысл, по аналогии с корнями характеристического уравнения (3.2). Этот корень близок к значению собственного числа спектральной задачи для уравнения Орра–Зоммерфельда, соответствующему собственной функции, близкой к рассматриваемому типу возмущений. Фазовая скорость и коэффициент усиления, которые определяются этим корнем, близки к таковым для периодических по пространству возмущений. Для других корней не имеется такого соответствия.

Численный метод, основанный на вычислении компонент матрицы монодромии, имеет сложности в реализации при малых $\alpha $, так как среди решений уравнения (3.1) есть быстрорастущие: система жесткая, а интегрирование ведется на большом пространственном интервале. В [33] предложен метод приближенного определения коэффициента усиления возмущения заданной частоты при $a \ll 1$, а в [34] проведено подробное исследование устойчивости течения ньютоновской жидкости по наклонной плоскости с малым синусоидальным рельефом и показана эффективность этого метода. В [33] доказана следующая теорема. Пусть $k$ – имеющий физический смысл корень характеристического многочлена (3.2). Уравнение (3.1) представляется в виде

$\mathcal{L}Q = 0,\quad \mathcal{L} = {{\mathcal{L}}_{0}} + a{{\mathcal{L}}_{1}} + {{a}^{2}}{{\mathcal{L}}_{2}} + O({{a}^{3}})$

При этом

$\begin{gathered} {{\mathcal{L}}_{1}} = \mathcal{L}_{1}^{ + } + \mathcal{L}_{1}^{ - } \\ {{\mathcal{L}}_{2}} = \mathcal{L}_{2}^{0} + \mathcal{L}_{2}^{ + } + \mathcal{L}_{2}^{ - } \\ {{\mathcal{L}}_{0}} = \frac{{{{d}^{4}}}}{{d{{x}^{4}}}} + {{C}_{2}}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + {{C}_{1}}\frac{d}{{dx}} + {{C}_{0}} \\ \end{gathered} $
$\begin{gathered} \mathcal{L}_{1}^{ + } = exp(i\alpha x)\left( {A_{2}^{1}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + A_{1}^{1}\frac{d}{{dx}} + A_{0}^{1}} \right) \\ \mathcal{L}_{1}^{ - } = exp( - i\alpha x)\left( {B_{2}^{1}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + B_{1}^{1}\frac{d}{{dx}} + B_{0}^{1}} \right) \\ \end{gathered} $
$\begin{gathered} \mathcal{L}_{2}^{0} = \left( {{{D}_{2}}\frac{d}{{dx}} + {{D}_{1}}\frac{d}{{dx}} + {{D}_{0}}} \right) \\ \mathcal{L}_{2}^{ + } = exp(i2\alpha x)\left( {A_{2}^{2}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + A_{1}^{2}\frac{d}{{dx}} + A_{0}^{2}} \right) \\ \mathcal{L}_{2}^{ - } = exp( - i2\alpha x)\left( {B_{2}^{2}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + B_{1}^{2}\frac{d}{{dx}} + B_{0}^{2}} \right) \\ \end{gathered} $
где $A_{j}^{l}$, $B_{j}^{l}$, Cj, Dj – постоянные, зависящие от ω, α, δ, β. Тогда коэффициент усиления вычисляется по формуле
(3.3)
$\begin{array}{*{20}{c}} {I = - {\text{Imag}}(k) + {{a}^{2}} + O({{a}^{3}})} \\ {\delta = \delta (\omega ,\alpha ,\delta ,\beta ) = - {\text{Real}}\left\{ {\frac{1}{{{{\mathcal{L}}_{0}}\left( {xexp(ikx)} \right)}}\left[ {\mathcal{L}_{2}^{0}exp(ikx){{ - }_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}} \right.} \right.} \\ { - \;\frac{{\mathcal{L}_{1}^{ - }exp(ikx)\mathcal{L}_{1}^{ + }exp\left[ {i(k - \alpha )x} \right]}}{{{{\mathcal{L}}_{0}}exp\left[ {i(k - \alpha )x} \right]}}\left. {\left. { - \frac{{\mathcal{L}_{1}^{ + }exp(ikx)\mathcal{L}_{1}^{ - }exp\left[ {i(k + \alpha )x} \right]}}{{{{\mathcal{L}}_{0}}exp\left[ {i(k + \alpha )x} \right]}}} \right]} \right\}} \end{array}$
Real, Imag означают действительную и мнимую часть числа.

Для течений неньютоновской жидкости коэффициенты $A_{j}^{l}$, $B_{j}^{l}$, Cj, Dj имеют вид

$\begin{gathered} A_{2}^{1} = - 15\delta B{{h}^{{(1)}}},\quad B_{2}^{1} = - 15\delta B\overline {{{h}^{{(1)}}}} \\ A_{1}^{1} = ( - (2n + 1)(2n + 2) + i20\omega \delta B - i15\delta \alpha B){{h}^{{(1)}}} \\ B_{1}^{1} = ( - (2n + 1)(2n + 2) + i20\omega \delta B + i15\delta \alpha B)\overline {{{h}^{{(1)}}}} \\ A_{0}^{1} = (5\delta {{\omega }^{2}} - 10\omega \delta \alpha B + in(2n + 1)\omega ){{h}^{{(1)}}} \\ B_{0}^{1} = (5\delta {{\omega }^{2}} + 10\omega \delta \alpha B + in(2n + 1)\omega )\overline {{{h}^{{(1)}}}} \\ {{D}_{2}} = 30\delta (n - 1)B{{h}^{{(1)}}}\overline {{{h}^{{(1)}}}} \\ {{D}_{1}} = ((2n + 1)(2n + 2) + i20(2n - 1)\delta \omega B){{h}^{{(1)}}}\overline {{{h}^{{(1)}}}} ,\quad {{D}_{0}} = 10n\delta {{\omega }^{2}}{{h}^{{(1)}}}\overline {{{h}^{{(1)}}}} \\ {{C}_{2}} = 5\delta B - \beta ,\quad {{C}_{1}} = (2n + 1) - i10\delta \omega B,\quad {{C}_{0}} = - 5\delta {{\omega }^{2}} - in\omega \\ \end{gathered} $

Использование для вычисления ${{h}^{{(1)}}}$ формулы (2.3) сохраняет порядок точности.

На рис. 4 показана зависимость коэффициента усиления от частоты возмущений при различных значениях параметров. При рассмотренных параметрах ($0.5 \leqslant n \leqslant 1.5$, $\delta = 0.25$, $\beta \leqslant 4$, $\omega < 15$, $a \leqslant 0.2$) численный анализ уравнения (3.1) и аналитическая формула (3.3) дают результаты, отличающиеся друг от друга в пределах 1%, так что на рисунке показаны только графики зависимостей, полученных по аналитической формуле. Для сравнения приведены зависимости коэффициента усиления от частоты при течении жидкости с теми же параметрами по гладкой плоскости – мнимой части одного из корней уравнения (3.2), взятой с обратным знаком.

Рис. 4.

Зависимость коэффициента усиления от частоты возмущения при $\delta = 0.25$, $\delta = 1$, $a = 0.2$ для течений (а) псевдопластической $n = 0.5$, (б) ньютоновской n = 1 и (в) дилатантной жидкостей $n = 1.5$. Cплошные линии – аналитическое решение, пунктирные – результат для гладкой плоскости: 1–3 – $\beta = 0,\;2,\;4$.

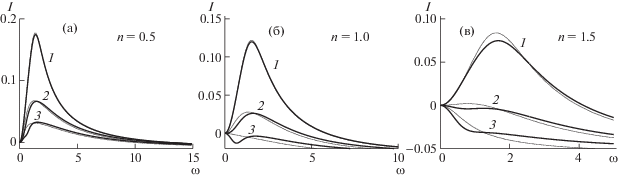
Один и тот же рельеф в разных диапазонах частот приводит либо к увеличению, либо к уменьшению коэффициента усиления. В результате существенно усложняется форма нейтральной кривой, разделяющей на плоскости $(\omega ,\operatorname{Re} )$ или $(\omega ,\delta )$ области нарастающих и затухающих возмущений. С ростом a изменяется топология нейтральной кривой, на плоскости параметров появляются изолированные области устойчивости и неустойчивости – острова в терминологии работы [25]. Острова устойчивости или неустойчивости возникают в окрестности оси $\omega = 0$ и растут в сторону больших значений ω с ростом a. При малых $\omega $ коэффициент усиления возмущений на гладкой плоскости, как и поправки к нему за счет рельефа, пропорциональны ω2, т.е. выражение для коэффициента усиления имеет вид

(3.4)
$I = ({{f}_{0}}(n,\delta ,\beta ) + {{a}^{2}}{{f}_{1}}(n,\delta ,\beta ,\alpha )){{\omega }^{2}} + O({{a}^{3}},{{\omega }^{3}}),\quad {{f}_{0}} = \frac{{5\delta (2n + 1) - {{n}^{2}}\beta }}{{{{{(2n + 1)}}^{3}}}}$

В [34] подробно рассмотрен случай n = 1, и найдены все возможные случаи взаимного расположения корней функций f0 и f1, локальных экстремумов функции $ - {{f}_{0}}{\text{/}}{{f}_{1}}$. Таким образом, определены значения амплитуды неровностей, при которой поправки за счет рельефа изменяют характер устойчивости течения относительно возмущений бесконечно малой частоты. Расчеты показали, что учет неньютоновских свойств среды в рамках данного подхода не изменяет качественной картины. В рамках настоящей работы основное внимание уделяется влиянию рельефа на величину критического числа Рейнольдса – минимального числа Рейнольдса, при котором имеются нарастающие возмущения.

Уравнения (3.1) содержат параметры подобия $\delta $, $\beta $, $\alpha $, $a$, а также реологический параметр $n$. В определение всех этих параметров, за исключением реологического, входит толщина пленки, следовательно, они будут изменяться при изменении числа Рейнольдса при фиксированных свойствах жидкости и размерных параметрах рельефа. Вводится новый набор параметров подобия, которые позволяют разделить свойства жидкости, течения и рельефа: число Капицы $\Gamma $ зависит только от свойств среды, число Бонда ${\text{Bo}}$ и произведение амплитуды рельефа на его волновое число характеризуют рельеф не зависимым от течения образом, собственно течение пленки характеризуется числом Рейнольдса Re

$\begin{array}{*{20}{c}} {\Gamma = \frac{{\sigma {{\rho }^{{(2 - n)/(2 + n)}}}}}{{{{g}^{{(3n - 2)/(n + 2)}}}{{K}^{{4/(n + 2)}}}}},\quad {\text{Bo}} = \mathop {(\alpha {\text{*}})}\nolimits^{ - 2} \frac{{\rho g}}{\sigma },\quad \zeta = \alpha {\text{*}}a{\text{*}}} \end{array}$

Согласно этим определениям и (1.5), (1.9), связь между наборами параметров подобия задается соотношениями

${{(5\delta )}^{{3(n + 2)}}} = {{c}^{{ - (5n + 2)}}}{{\Gamma }^{{ - (n + 2)}}}{{(\sin \theta )}^{{3n - 2}}}{{\operatorname{Re} }^{{5n + 6}}}$
${{\beta }^{{3(n + 2)}}} = {{c}^{{2n(2 - n)}}}{{\Gamma }^{{ - (n + 2)}}}{{(\sin \theta )}^{{3n - 2}}}{{\operatorname{Re} }^{{2n}}}{{({\text{ctg}}{\kern 1pt} {\kern 1pt} \theta )}^{{3(n + 2)}}}$
${{\alpha }^{{3(n + 2)}}} = {{c}^{{n(2 - n)}}}{{\Gamma }^{{ - 3(n + 2)/2}}}{{(\sin \theta )}^{{ - 4}}}{\text{B}}{{{\text{o}}}^{{ - 1/2}}}{{\operatorname{Re} }^{n}}$
$a = {{3}^{{ - 1/3}}}{{\Gamma }^{{1/2}}}{{(\sin \theta )}^{{1/3}}}{\text{B}}{{{\text{o}}}^{{1/2}}}{{\operatorname{Re} }^{{1/3}}}\zeta $
${{\varepsilon }^{{3(n + 2)}}} = {{c}^{{2n(2 - n)}}}{{\Gamma }^{{ - (n + 2)}}}{{(\sin \theta )}^{{3n - 2}}}{{\operatorname{Re} }^{{2n}}}$
$c = (2n + 1){\text{/}}n$

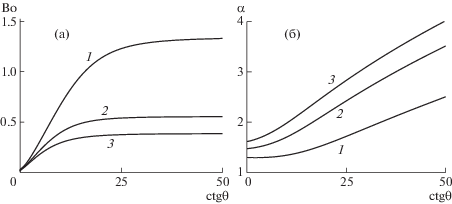
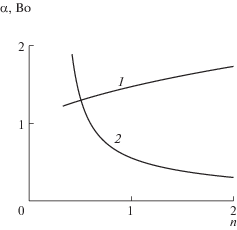
Направление изменения критического числа Рейнольдса за счет рельефа определяется знаком значения функции f1 в формуле (3.4) при аргументах, соответствующих критическому Re на гладкой плоскости: если ${{f}_{1}} > 0$, то коэффициент усиления положителен и течение неустойчиво. В этом случае критическое число Рейнольдса уменьшается, и рассматриваемый рельеф является дестабилизирующим. Нейтральным называется рельеф, для которого ${{f}_{1}} = 0$. На рис. 5 показана зависимость числа Бонда, соответствующего нейтральному рельефу, и волнового числа такого рельефа от котангенса угла наклона плоскости. Рельеф с большим числом Бонда (большим периодом, малым волновым числом) является стабилизирующим. Число Бонда нейтрального рельефа стремится к конечной величине порядка единицы при уменьшении угла наклона и составляет малую величину на вертикальной плоскости. Волновое число рельефа конечно при стремлении угла наклона к прямому. На рис. 6 показаны зависимости предельных значений ${\text{Bo}}$ и $\alpha $ при ${\text{ctg}}\theta $, стремящемся к бесконечности и к нулю, соответственно, от реологического параметра n. Для стабилизации течения дилатантных жидкостей требуется рельеф меньшего периода, чем для псевдопластических.

Рис. 5.

Период нейтрального рельефа в зависимости от котангенса угла наклона плоскости (а) число Бонда и (б) волновое число при $\Gamma = 3000$: 1–3 – $n = 0.5,\;1,\;1.5$.

Рис. 6.

Предельные значения характеристик нейтрального рельефа в зависимости от реологического показателя n при $\Gamma = 3000$: волновое число на вертикальной плоскости (1) и число Бонда на плоскости с малым углом наклона (2).

ЗАКЛЮЧЕНИЕ

Рассмотрено стационарное течение пленки неньютоновской жидкости по плоскости с синусоидальным рельефом. Показано, что амплитуда свободной поверхности совпадает с амплитудой твердой при длинноволновом рельефе; при течении по коротковолновому рельефу поверхностное натяжение сглаживает свободную поверхность и ее амплитуда стремится к нулю. В отличие от течения по осциллирующей плоскости, при фиксированном значении расхода жидкости наличие рельефа приводит к увеличению средней толщины пленки вне зависимости от параметров рельефа и реологии.

Показано, что при больших углах наклона плоскости имеет место максимум амплитуды свободной поверхности в зависимости от периода рельефа (резонанс), на плоскости с малым углом наклона такая зависимость монотонна. Критерий существования резонанса свободной поверхности, как и критерий усточивости течения по гладкой плоскости, отражает соотношение между дестабилизирующими инерционными силами и стабилизирующим градиентом самоиндуцированного гидростатического давления. Резонанс свободной поверхности при условии устойчивости течения по гладкой стенке имеет место только для дилатантных жидкостей ($n > 1.18$).

Получено приближенное аналитическое выражение для поправки к коэффициенту усиления малых периодических по времени возмущений при условии малости амплтуды рельефа. Показано, что поправки пропорциональны второй степени амплитуды. В качестве глобальной меры стабилизации или дестабилизации течения выбрано изменение критического числа Рейнольдса. Вне зависимости от реологии рельеф с коротким периодом дестабилизирует, а с длинным – стабилизирует течение в указанном смысле. При этом период нейтрального рельефа зависит от реологии: течение дилатантной жидкости стабилизируется рельефом меньшего периода, чем псевдопластической при фиксированном значении капиллярной длины.

Работа выполнена в рамках госбюджетного плана МГУ им. М.В. Ломоносова.

Список литературы

  1. Weinstein S.J., Ruschak K.J. Coating flows // Annual Review of Fluid Mechanics. 2004. V. 36. № 1. P. 29–53.

  2. Капица П.Л., Капица С.П. Волновые течения тонких слоев жидкости // ЖЭТФ. 1949. Т. 19. № 2. С. 105–120.

  3. Алексеенко С.В., Накоряков В.Е., Покусаев Б.Г. Волновое течение пленок жидкости. Новосибирск: Наука, 1992. 255 с.

  4. Шкадов В.Я. Волновые режимы течения тонкого слоя вязкой жидкости под действием силы тяжести // Изв. АН СССР. МЖГ. 1967. № 1. С. 43–51.

  5. Шкадов В.Я. Уединенные волны в слое вязкой жидкости // Изв. АН СССР. МЖГ. 1977. № 1. С. 63–66.

  6. Шкадов В.Я., Белоглазкин А.Н. Интегральные соотношения пограничного слоя в теории волновых течений капиллярных пленок // Вест. МГУ. Сер. Математика. Механика. 2017. № 6. С. 38–50.

  7. Wilkinson W.L. Non-Newtonian Fluids: Fluid Mechanics, Mixing and Heat Transfer. Pergamon Press. 1960. 138 p. = Уилкинсон У.Л. Неньютоновские жидкости: гидромеханика, перемешивание и теплообмен. М.: Мир, 1964. 215 с.

  8. Bird R.B., Armstrong R.C., Hassager O. Dynamics of polymeric liquids. V. 1. Fluid mechanics. N.Y.: Willey, 1987. 672 p.

  9. Шульман З.П., Байков В.И. Реодинамика и тепломассообмен в пленочных течениях. Минск: Наука и техника, 1979. 296 с.

  10. Miladinova S., Lebon S., Toshev E. Thin-film flow of a power-law liquid falling down an inclined plate // J. Non-Newt. Fluid Mech. 2004. V. 122. № 1. P. 69–78.

  11. Могилевский Е.И., Шкадов В.Я. Влияние рельефа подложки на течение пленки неньютоновской жидкости по наклонной плоскости // Вест. МГУ. Сер. Математика. Механика. 2007. № 3. С. 49–56.

  12. Sisoev G.M., Dandapat B.S., Matveyev K.S., Mukhopadhyay A. Bifurcation analysis of the travelling waves on a falling power-law fluid film // J. Non-Newton. Fluid Mech. 2007. V. 141. № 2. P. 128–137.

  13. Цвелодуб О.Ю. Волновые режимы на пленке обобщенной ньютоновской жидкости, стекающей по вертикальной плоскости // Изв. РАН. МЖГ. 2007. № 4. С. 3–15.

  14. Могилевский Е.И., Шкадов В.Я. Неустойчивость и волны при течении пленки обобщенно-ньютоновской жидкости по вертикальной стенке // Изв. РАН. МЖГ. 2010. № 3. С. 43–56.

  15. Floryan J.M., Davis S.H., Kelly R.E. Instabilities of a liquid film flowing down a slightly inclined plane // Phys. Fluids. 1987. V. 30. P. 983–989.

  16. Zayko J., Eglit M. Stability of downslope flows to two-dimensional perturbations // Phys. Fluids. 2019. V. 31, № 8. P. 086601.

  17. Mogilevskiy E. Stability of a non-Newtonian falling film due to three-dimensional disturbances // Phys. Fluids. 2020. V. 32. № 7. P. 073101.

  18. Woods D.R., Lin S.P. Instabilities of a liquid film flow over a vibrating inclined plane // J. Fluid Mech. 1995. V. 294. P. 391–407.

  19. Буря А.Г., Шкадов В.Я. Устойчивость пленки жидкости, стекающей по колеблющейся наклонной поверхности // Изв. РАН. МЖГ. 2001. № 5. С. 3–13.

  20. Argyriadi K., Vlachogiannis M., Bontozoglou V. Experimental study of inclined film flow along periodic corrugations: The effect of wall steepness // Phys. Fluids. V. 18. P. 012102.

  21. Sobolik V. Film flow of pseudoplastic liquids along an oscillating wall // Rheol. Acta. 1994. V. 33. № 2. P. 136–144.

  22. Mogilevskiy E., Vakhitova R. Falling film of power-law fluid on a high-frequency oscillating inclined plane // J. Non-Newton. Fluid Mech. 2019. V. 269. P. 28–36.

  23. Любимов Д.В., Перминов А.В. Воздействие несимметричных вибраций на движение тонкого слоя вязкопластичной жидкости // Изв. РАН. МЖГ. 2011. № 1. С. 30–41.

  24. Mogilevskiy E. Stability of a generalized Newtonian liquid falling film on an oscillating inclined plane // J. Non-Newt. Fluid Mech. 2020. V. 282. P. 104334-1–104334-11.

  25. Schoerner M., Reck D., Aksel N. Stability phenomena far beyond the Nusselt flow – Revealed by experimental asymptotics // Phys. Fluids. 2016. V. 28. P. 022102.

  26. Pollak T., Aksel N. Crucial flow stabilization and multiple instability branches of gravity-driven films over topography // Phys. Fluids. 2013. V. 25. P. 024103.

  27. Koegel A., Aksel N. Stability of the channel flow – new phenomena in an old problem // Acta Mech. 2020. V. 231. P. 1063–1082.

  28. Aksel N., Schoerner M. Films over topography: from creeping flow to linear stability, theory, and experiments, a review // Acta Mech. 2018. V. 229. № 4. P. 1453–1482.

  29. Trifonov Y. Stability of a film flowing down an inclined corrugated plate: The direct Navier–Stokes computations and Floquet theory // Phys. Fluids. 2014. V. 26. P. 114101.

  30. Tseluiko D., Blyth M.G., Papageorgiou D.T. Stability of film flow over inclined topography based on a long-wave nonlinear model // J. Fluid Mech. 2013. V. 729. P. 638–671.

  31. Heining C., Bontozoglou V., Aksel N., Wierschem A. Nonlinear resonance in viscous films on inclined wavy planes // Int. J. of Multiphase Flow. 2009. V. 35. P. 78–90.

  32. Трифонов Ю.Я. Устойчивость и нелинейные волновые режимы при стекании пленок по гофрированной поверхности // ПМТФ. 2007. № 1. С. 110–120.

  33. Могилевский Е.И., Шкадов В.Я. Анализ устойчивости стекающей пленки на плоскости с синусоидальными неровностями // Изв. РАН. МЖГ. 2018. № 3. С. 40–53.

  34. Mogilevskiy E., Shkadov V. Stability of a thin film flow on a weakly wavy wall // Int. J. Multiphase Flow. 2019. V. 114. P. 168–179.

  35. Ruyer-Quil C., Manneville P. Improved modeling of flows down inclined planes // Eur. Phys. J. B. 2000. V. 15. № 2. P. 357–369.

  36. Veremieiev S., Wacks D.H. Modelling gravity-driven film flow on inclined corrugated substrate using a high fidelity weighted residual integral boundary-layer method // Phys. Fluids. 2019. V. 31. № 2. P. 022101.

  37. Шкадов В.Я. К теории волновых течений тонкого слоя вязкой жидкости // Изв. АН СССР. МЖГ. 1968. № 2. С. 20–25.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал