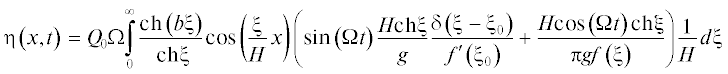1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2021

Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 19-24

ЭВОЛЮЦИЯ ВОЗМУЩЕНИЙ СВОБОДНОЙ ПОВЕРХНОСТИ ОТ ПУЛЬСИРУЮЩЕГО ЗАГЛУБЛЕННОГО ИСТОЧНИКА В ЖИДКОСТИ КОНЕЧНОЙ ГЛУБИНЫ

А. Т. Ильичев a, b, *, А. С. Савин b, **

a Математический институт им. В.А. Стеклова РАН
Москва, Россия

b Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

* E-mail: ilichev@mi-ras.ru
** E-mail: assavin@list.ru

Поступила в редакцию 31.03.2021
После доработки 02.06.2021
Принята к публикации 22.06.2021

Полный текст (PDF)

Аннотация

Рассматривается плоская задача об эволюции возмущений поверхности идеальной несжимаемой жидкости конечной глубины, вызванных заглубленным пульсирующим точечным источником, начинающим свою работу в изначально невозмущенной среде. Описан процесс установления поверхностных волн, распространяющихся симметрично в обе стороны от источника. Жидкость предполагается идеальной и несжимаемой, а ее движение – потенциальным.

Ключевые слова: установление поверхностной волны, пульсирующий источник, сингулярный интеграл

Описанию волн на поверхности жидкости, генерируемых объектами в толще жидкости, посвящено значительное число работ. Установившиеся бегущие волны, возникающие на свободной поверхности бесконечно глубокой жидкости в результате равномерного горизонтального движения изначально покоящейся гидродинамической особенности n-го порядка в толще жидкости, найдены в [1]. Процесс установления волн на свободной поверхности в рамках формулировки [1] описан в [2]. В работе [3] исследуется задача о предельном режиме, описывающем установившиеся волны при работе периодического по времени заглубленного источника с применением аппарата теории обобщенных функций. Эта классическая задача рассматривалась еще Л.Н. Сретенским [4] без строгого обоснования предельного перехода при $t \to \infty $. В дальнейшем эволюции волн на свободной поверхности жидкости стало уделяться меньше внимания, а вопросы об установлении того или иного режима поверхностных волн долгое время оставались без математически корректного ответа.

Возможно, это связано с тем, что больший интерес стали вызывать более общие задачи генерации изгибно-гравитационных волн подводными объектами на поверхности жидкости под ледяным покровом. В работах [5, 6] рассматривается генерация волн на ледяном покрове неподвижным источником переменной интенсивности, расположенным в жидкости под ледяным покровом. Получены общие выражения для потенциала скорости, а также рассмотрены частные случаи импульсного, постоянного и гармонически осциллирующего источника. Представлены асимптотические выражения для потенциала скорости течения при длительной работе осциллирующего источника, а также для потенциала вдали от источника. В работе [7] изучены изгибные волны, возникающие в ледяном покрове при мгновенном выбросе некоторой массы точечным источником, расположенным в жидкости. Обобщение на случай источника с переменной интенсивностью рассматривается в [8].

В [9] обсуждается нестационарное движение источника подо льдом и полученные интегральные формулы проанализированы численно. Установившиеся плоские стационарные волны на ледяном покрове в результате горизонтального движения изначально покоящейся гидродинамической особенности n-го порядка в толще жидкости найдены в [10]. В работе [11] выведен потенциал скорости для источника произвольной силы, совершающего произвольное трехмерное движение. Первоначально неподвижная жидкость бесконечной глубины считается невязкой, несжимаемой и однородной. Свободная поверхность жидкости покрыта тонким слоем упругого материала однородной плотности с боковыми напряжениями. Подробно обсуждается влияние ледяного покрова и битого льда на гидродинамические нагрузки. В [12] рассмотрена асимптотика решения для движения диполя для случая докритических скоростей движения диполя. В [13] в линейном приближении изучаются волновые движения сжатого упругого ледяного покрова, вызванные движением двумерного диполя в воде под ледяным покровом. Поток жидкости описывается теорией потенциала, а ледяной покров моделируется при помощи тонкой упругой пластины, плавающей на поверхности воды. Получено решение для вертикального смещения ледяного покрова для диполя, совершающего произвольное двумерное движение. В работе [14] проведено рассмотрение временной эволюции волн возмущений на ледяном покрове, возникающих в результате движения диполя в плоском слое идеальной жидкости бесконечной глубины. В [15] построено решение линейной стационарной задачи об обтекании сферы равномерным потоком идеальной несжимаемой жидкости бесконечной глубины под ледяным покровом, который моделируется тонкой упругой пластиной Кирхгофа–Лява. Задачи излучения изгибно-гравитационных волн погруженным цилиндром рассмотрены в [16].

Целью настоящей статьи является анализ решения плоской задачи о временной эволюции возмущений свободной поверхности изначально неподвижного слоя идеальной жидкости конечной глубины, возникающих под воздействием заглубленного пульсирующего источника, начинающего свою работу в некоторый момент времени. и описание процесса установления поверхностных волн.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим плоский горизонтальный слой жидкости конечной глубины H, находящуюся в состоянии покоя. Направим ось x декартовой системы координат направо, вдоль невозмущенной поверхности жидкости, а ось y – вверх. Предположим, что в жидкости в момент времени t = 0 в точке $\left( {{{x}_{0}},{{y}_{0}}} \right) = \left( {0, - l} \right)$, 0 < l < H, начинает работать источник, пульсирующий по гармоническому закону Q(t) = ${{Q}_{0}}$sin(Ω t).

Далее будем предполагать, что волны, возникающие на поверхности, являются линейными, т.е. для них выполняется соотношение a/H $ \ll 1$, где a – характерная величина амплитуды. Изложенное означает, что будет использоваться линеаризованная формулировка. Жидкость будет предполагаться идеальной и несжимаемой, а ее течение потенциальным всюду, кроме точки локализации источника.

При этих предположениях скорость имеет потенциал Ф = Ф(x, y, t), который можно представить в виде Ф(x, y, t) = ${{{\text{Ф}}}_{0}}$(x, y, t) + ${{\varphi }}$(x, y, t), где ${{{\text{Ф}}}_{0}} = {{{\text{Ф}}}_{0}}$(x, y, t) – потенциал скорости, создаваемой источником, а $\varphi = \varphi $(x, y, t) – волновой потенциал скорости жидкости. В [3] показано, что

${{\left( {{{{\text{Ф}}}_{0}}} \right)}_{x}} = \frac{{Q(t)}}{{2\pi }}\frac{x}{{{{x}^{2}}~ + {{y}^{2}}~}},\quad {{\left( {{{{\text{Ф}}}_{0}}} \right)}_{y}} = \frac{{Q\left( t \right)}}{{2\pi }}\frac{{y + l}}{{{{x}^{2}}~ + {{{\left( {y + l} \right)}}^{2}}~}}$
и $~{{\varphi }_{{xx}}}$ + ${{\varphi }_{{yy}}}$ = 0, –∞ < x <+∞, –H < y < 0
$~{{\varphi }_{t}} + g\eta (x,t) = - {{{\text{(}}{{{\text{Ф}}}_{0}}(x,0,t){\text{)}}}_{t}},\quad y = 0,$
${{\eta }_{t}} = \frac{{Q\left( t \right)}}{{2\pi }}\frac{l}{{{{x}^{2}} + {{l}^{2}}}} + {{\varphi }_{y}},\quad y = 0$
${{\varphi }_{y}} = \frac{{Q(t)}}{{2\pi }}\frac{{H - l}}{{{{x}^{2}} + {{{(H - l)}}^{2}}}},$
где y = $~\eta \left( {x,t} \right)$ – уравнение свободной поверхности жидкости, а буквенный индекс внизу означает дифференцирование по соответствующей переменной.

Для Фурье образа S($\lambda ,t)$ = $\int_{ - \infty }^{ + \infty } {\eta (x,t){{e}^{{ - i\lambda x}}}dx} $ отклонения поверхности, имеем уравнение [3]

(1.1)
${{S}_{{tt}}} + {{\omega }^{2}}S = Q'(t)G({\text{|}}\lambda {\text{|}})$
где ${{\omega }^{2}} = {{\omega }^{2}}\left( {\left| \lambda \right|} \right)$ = $\left| {~\lambda } \right|g$ th$\left( {\left| \lambda \right|H} \right)$, G$\left( {\left| \lambda \right|} \right)$ = ch$\left( {\left| \lambda \right|\left( {H - l} \right)} \right)$/ch$\left( {\left| \lambda \right|H} \right)$, а g – ускорение свободного падения.

Поскольку источник начал свою работу при t = 0, имеем

(1.2)
$S(\lambda , - \infty ) = 0,\quad {{S}_{t}}(\lambda , - \infty ) = 0,\quad Q( - \infty ) = 0$

Решение уравнения (1.1) при условиях (1.2) записывается в виде [3]

(1.3)
$S(\lambda ,t) = G\left( {\left| \lambda \right|} \right)\mathop \smallint \limits_{ - \infty }^t Q\left( \tau \right)\cos (\omega (t - \tau ))d\tau $

2. УСТАНОВИВШАЯСЯ ВОЛНОВАЯ КОНФИГУРАЦИЯ ПРИ $t \to \infty $

Отклонение свободной границы жидкости можно определить, взяв обратное преобразование Фурье

$\eta \left( {x,t} \right) = \frac{1}{{2\pi }}\mathop \smallint \limits_{ - \infty }^\infty S\left( {\lambda ,t} \right){{e}^{{i\lambda x}}}d\lambda = \frac{1}{{2\pi }}\mathop \smallint \limits_{ - \infty }^\infty S\left( {\lambda ,t} \right)(\cos (\lambda x) + i\sin (\lambda x))d\lambda $

Подставив (1.3) в последнее равенство и пользуясь тем, что подынтегральная функция является четной по λ, а источник начинает работать в момент времени t = 0, получим

(2.1)
$\eta \left( {x,t} \right) = \frac{{{{Q}_{0}}}}{\pi }\mathop \smallint \limits_0^\infty G\left( \lambda \right)\cos (\lambda x)\int\limits_0^t {\sin (\Omega t)\cos (\omega (t - \tau ))d\tau d\lambda } $

В [3] показано, что интеграл (2.1) может быть переписан в виде

$\eta (x,t) = \frac{{{{Q}_{0}}}}{\pi }{\text{Im}}\left\{ {{{e}^{{i{{\Omega }}t}}}\mathop \smallint \limits_0^\infty G\left( \lambda \right){\text{cos}}\left( {\lambda x} \right)J\left( t \right)d\lambda } \right\}$
(2.2)
$J\left( t \right) = \frac{1}{2}\left( {\frac{{{{e}^{{it\left( {\omega - {{\Omega }}} \right)}}}}}{{i((\omega - {{\Omega }}}}--\frac{{{{e}^{{it\left( {\omega + {{\Omega }}} \right)}}}}}{{i\left( {\omega + {{\Omega }}} \right)}} + \frac{{2i{{\Omega }}}}{{{{\omega }^{2}} - {{{{\Omega }}}^{2}}}}} \right)~~~~~$
где

${{\omega }^{2}} - {{\Omega }^{2}} = \frac{g}{H}\frac{{f(\xi )}}{{{\text{ch}}\xi }},\quad f(\xi ) = \xi {\text{ch}}\xi - \nu {\text{ch}}\xi ,\quad \nu = \frac{{{{\Omega }^{2}}H}}{g},\quad \xi = \lambda H$

Известно [3], что множество корней функции f($\xi )$ исчерпывается двумя действительными корнями $ \pm {{\xi }_{0}}$ = $ \pm {{\lambda }_{0}}$H, ${{\lambda }_{0}} > 0$ и счетным множеством мнимых корней $ \pm i{{\mu }_{k}}$, k = 1, 2, …, ${{\mu }_{k}} > 0$.

Пользуясь теорией обобщенных функций, в [3] установлено, что интеграл в (2.2) равен интегралу

(2.3)
где b = $\frac{{H - l}}{H}$, а $\delta $ – дельта функция. Из (2.3) следует, что

(2.4)
$~\eta \left( {x,t} \right) = \frac{{{{Q}_{0}}{{\Omega }}}}{g}\left( {\frac{{\cos \left( {{{\lambda }_{0}}x} \right){\text{ch}}\left( {b{{\xi }_{0}}} \right)}}{{f{\kern 1pt} '\left( {{{\xi }_{0}}} \right)}} + P} \right),\quad P = \frac{1}{\pi }{\text{cos}}\left( {{{\Omega }}t} \right)\mathop \smallint \limits_0^\infty \frac{{{\text{cos}}\left( {{{\xi }_{0}}{\text{/}}H} \right){\text{ch}}\left( {b{{\xi }_{0}}} \right)}}{{f\left( \xi \right)}}d\xi $

Интеграл P в (2.4) вычисляется при помощи смещения контура интегрирования с положительной полуоси в контур С, который составлен из отрезков действительной оси ${{I}_{1}} = $ [0, ${{{{\xi }}}_{0}} - \rho $], ${{I}_{2}} = $ [${{{{\xi }}}_{0}} + \rho ,~R]$, отрезков 2${{I}_{3}} = $ [R, R + iR], ${{I}_{4}} = $ [R + iR, 0] и замыкающeй полуокружности ${{C}_{\rho }}$ с центром в точке ${{\xi }_{0}}$ и имеющей радиус ρ. Искомый интеграл P равен сумме интегралов от продолжения подынтегральной функции на отрезки ${{I}_{k}}$, k = 2, 3, 4 и ${{C}_{\rho }}$ по этим отрезкам и полуокружности, взятым со знаком минус [3] при R $ \to \infty $ и $\rho $ $ \to 0$. В [3] показано, что интеграл по дуге, параметризованной γ $ \in {{I}_{3}}$ стремится к нулю при R $ \to \infty $, интеграл полуокружности ${{C}_{\rho }}$ равен половине вычета от соответствующей подынтегральной функции, а интеграл по ${{I}_{4}}$ явно вычислен и дается выражением в виде ряда, описывающим неподвижную волну, которая экспоненциально убывает по x и гармонически осциллирует по времени t. Отклонение свободной поверхности при $ - \infty < x < \infty $, при $t \to \infty $ дается выражением

$\eta \left( {x,t} \right) = {{W}_{1}} + {{W}_{2}},\quad {{W}_{1}} = \frac{{{{Q}_{0}}{{\Omega }}}}{g}{{\omega }_{0}}\sin \left( {{{\Omega }}t - \frac{{{{\xi }_{0}}\left| x \right|}}{H}} \right),$
(2.5)
${{W}_{2}} = \frac{{{{Q}_{0}}{{\Omega }}}}{g}\cos ({{\Omega }}t)\mathop \sum \limits_{k = 1}^\infty {{\omega }_{k}}{{e}^{{ - \frac{{\left| x \right|{{\mu }_{k}}}}{H}}}}$
где

${{\omega }_{0}} = \frac{{{\text{ch}}(b{{\xi }_{0}})}}{{f{\kern 1pt} '({{\xi }_{0}})}},\quad {{\omega }_{k}} = \cos (b{{\mu }_{k}}){{\sin }^{{ - 1}}}{{\mu }_{k}}{{(1 - \nu - \mu _{k}^{2}{\text{/}}\nu )}^{{ - 1}}}$

Это симметричная волна, описанная еще Л.Н. Сретенским в [4].

3. ЭВОЛЮЦИЯ ВОЛНЫ, ВЫЗВАННОЙ ПУЛЬСИРУЮЩИМ ИСТОЧНИКОМ

Из формулы (2.5) следует, что при больших временах t отклонение свободной поверхности имеет вид

(3.1)
$\eta \left( {x,t} \right) = {{W}_{1}} + {{W}_{2}} + r\left( {x,t} \right)$
где $\mathop {\lim }\limits_{t \to \infty } r\left( {x,t} \right) = 0$.

Следует отметить, что из результатов предыдущего параграфа следует, во-первых, что $r\left( {x,t} \right) \to 0$ при $t \to \infty $, при всех $ - \infty < x < \infty $, а во-вторых, что волна W2 устанавливается сразу при начале работы источника и асимптотическое поведение $r\left( {x,t} \right)$ в (3.1) связано только с первой волной W1. Иными словами, процессу установления подвергается только первая бегущая волна, которая стремится к W1.

Волна W2 является неподвижной пульсирующей, локализованной (быстро убывающей по пространству) волной, сразу возникающей над источником. В [3] показано, что ряд в (2.4), описывающий форму волны W2, абсолютно сходится при всех $x \ne 0.~$ Тот факт, что волна отклонения свободной поверхности $\eta \left( {x,t} \right)$ в (3.1) имеет конечную амплитуду при всех x, следует из того обстоятельства, что после вычисления внутреннего интеграла в формуле (2.1) получим, что отклонение свободной поверхности представляется в виде сходящегося при всех x интеграла

(3.2)
$\eta \left( {x,t} \right) = \frac{{{{Q}_{0}}{{\Omega }}}}{\pi }\mathop \smallint \limits_0^\infty G\left( \lambda \right){\text{cos}}\left( {\lambda x} \right)\frac{{\cos \left( {{{\Omega }}t} \right) - {\text{cos}}\left( {{{\omega }}t} \right)}}{{{{\omega }^{2}} - {{{{\Omega }}}^{2}}}}d\lambda $

Формула (3.2) представляется наиболее удобной для численного расчета волны, генерируемой пульсирующим источником; пример такой волны при конкретном значении физических параметров приведен в [3].

Как уже отмечалось, сразу после начала работы источника устанавливается локализованная волна W2. Другая бегущая волна распространяется при больших временах внутри сектора D = = $\left\{ {\left( {x,t} \right): - Vt < x < Vt} \right\},~V > 0$, со скоростью, асимптотически стремящейся при $t \to \infty $ к скорости V, которая определяется следующим образом

$V = \frac{{d\omega \left( {{{\lambda }_{0}}} \right)}}{{d\lambda }}$

Например, для значений физических параметров Ω =$~\pi $ c–1, H = 5 м, l = 2 м, ${{Q}_{0}}$ = 1 м2 с–1, g = = 10 мс–2 имеем ${{\lambda }_{0}} = 0.987$ м–1, V = 1.593 м c–1. Асимптотически по времени вне сектора D имеем только неподвижную волну W2, которая экспоненциально стремится к нулю – (см. рис. 1). Первая волна, распространяющаяся внутри сектора с групповой скоростью V, асимптотически при $t \to \infty $ стремится к профилю бегущей волны W1 в (2.5).

Рис. 1.

Схема процесса установления профиля свободной поверхности для достаточно больших t (${{t}_{2}}$ > ${{t}_{1}}$) и эволюция асимптотического профиля в заданной точке x0.

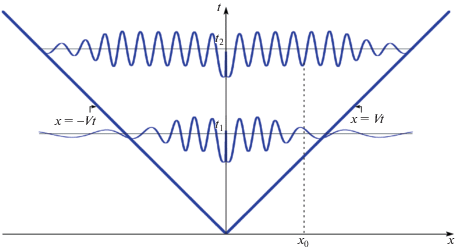
Таким образом, процесс установления профиля свободной поверхности жидкости при возрастании времени t представляет собой эволюцию волны, которая со временем занимает область пространства внутри конуса D и распространяется вправо и влево со скоростью, асимптотически близкой к скорости V.

При $x \in D$ форма поверхности в каждой точке стремится к профилю Сретенского (2.5). Иными словами, для сколь угодно малого $\epsilon > 0$ и любой точки x0 найдется такое T$\left( {{{x}_{0}}} \right)$, что при t > T$\left( {{{x}_{0}}} \right)$, $\left| {\eta \left( {x,t} \right) - \eta \left( {{{x}_{0}},t} \right)} \right| < $ $\epsilon .$ Вне сектора D при $t \to \infty $ находятся “хвосты” неподвижной волны W2, которые экспоненциально малы, вследствие (2.5) (см. рис. 1).

4. ОБСУЖДЕНИЕ

Ранее было показано [3], что в результате эволюции асимптотически при стремлении времени к бесконечности образуются две волны, симметрично распространяющиеся по обе стороны источника и локализованная стоячая волна, пульсирующая по времени. В данной работе рассмотрен режим установления волн на свободной поверхности, генерируемых пульсирующим источником, которые в пределе стремятся к волновой конфигурации, рассмотренной в [3].

Процесс установления волн от источника возмущений рассматривался также в [2] для свободной поверхности жидкости бесконечной глубины и в [14] для волн на поверхности раздела вода–лед для жидкости под ледяным покровом. В обоих случаях источником возмущений являлся диполь, равномерно движущийся в толще жидкости конечной глубины. Задача о процессе установления волны, рассмотренная в [2] и, тем более, задача, рассмотренная в [14] в некотором смысле сложнее, чем задача о процессе установления волны, рассмотренная здесь. В самом деле, установление профиля свободной поверхности жидкости связано с возникновением двух волн, одна из которых подвергается дисперсионному расплыванию и затухает, а другая (имеющая меньшую скорость) с течением времени трансформируется в свободную волну Келдыша [17].

В жидкости под ледяным покровом таких волны четыре, две из них с течением времени затухают, а две другие трансформируются в стационарную (в системе отсчета связанной с движущимся диполем) волновую конфигурацию, найденную в [10]. В настоящей работе разобран случай, когда формируется одна симметричная бегущая волна, которая с течением времени трансформируется в бегущую волну W1. Заметим, что, несмотря на отмеченную относительную простоту рассмотренной задачи, без проведенных рассуждений в общей картине представлений о процессах установления волн на границах раздела различных сред, основанной на корректном математическом подходе, недоставало бы весьма существенного фрагмента.

ЗАКЛЮЧЕНИЕ

Установлен характер эволюции возмущений свободной поверхности плоского слоя идеальной несжимаемой жидкости конечной глубины, возникающих в случае работы пульсирующего источника в толще жидкости. Полученное решение может быть полезным при оценке характерного времени установления волнового режима в заданной области пространства при работе источников периодических возмущений, например, волнопродукторов при проведении лабораторных и натурных экспериментов.

Список литературы

  1. Савин А.С. Установление поверхностных волн, вызываемых гидродинамическими особенностями в плоском потоке // Изв. РАН. МЖГ. 2002. № 3. С. 78–81 = Savin A.S. Establishment of Surface Waves Generated by Hydrodynamic Singularities in Plane Flow // Fluid Dynamics. 2002. V. 37. P. 421–424.

  2. Ильичев А.Т., Савин А.С. О характере процесса установления поверхностных волн в плоском потоке // Изв. РАН. МЖГ. 2004. № 4. С. 75–83 = Il’ichev A.T., Savin A.S. On the process of establishment of surface waves in plane flow // Fluid Dynamics. 2004. V. 39. P. 574–581.

  3. Павельева Е.Б., Савин А.С. Установление волн от пульсирующего источника в жидкости конечной глубины // Изв. РАН. МЖГ. 2018. № 4. С. 12–23 = Pavelyeva E.B., Savin A.S. Establishment of Waves Generated by a Pulsating Source in a Finite-Depth Fluid // Fluid Dynamics. 2018. V. 53. P. 461–470.

  4. Сретенский Л.Н. Теория волновых движений жидкости. М.: Наука, 1977. 815 с.

  5. Chowdhury R.G., Mandal B.N. Motion due to fundamental singularities in finite depth water with an elastic solid cover // Fluid Dynam. Res. 2006. V. 38. P. 224–240.

  6. Савин А.А., Савин А.С. Генерация волн на ледяном покрове пульсирующим в жидкости источником // Изв. РАН. МЖГ. 2013. № 3. С. 24–30 = Savin A.A., Savin A.S. Waves generated on an ice cover by a source pulsating in fluid // Fluid Dynamics. 2013. V. 48. P. 303–309).

  7. Lu D.Q., Dai S.Q. Generation of transient waves by impulsive disturbances in an inviscid fluid with an ice-cover // Arch. Appl. Mech. 2006. V. 76. P. 49–63.

  8. Lu D.Q., Dai S.Q. Flexural- and capillary-gravity waves due to fundamental singularities in an inviscid fluid of finite depth // Internat. J. Eng. Sci. 2008. V. 46. P. 1183–1193.

  9. Погорелова А.В. Нестационарное движение источника в жидкости под плавающей пластиной // ПМТФ. 2011. Т. 52. С. 49–59 = Pogorelova A.V. Unsteady motion of a source in a fluid under a floating plate // J. Appl. Tech. Phys. 2011. V. 2011. P. 717–727.

  10. Савин А.А., Савин А.С. Возмущение ледяного покрова движущимся в жидкости диполем // Изв. РАН. МЖГ. 2012. № 2. С. 3–10. = Savin A.A., Savin A.S. Ice cover perturbation by a dipole in motion within a liquid // Fluid Dynamics. 2012. V. 47. P. 139–146.

  11. Sturova I.V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications // J. Fluid Mech. 2013. V. 730. P. 392–418.

  12. Савин А.А., Савин А.С. Пространственная задача о возмущении ледяного покрова движущимся в жидкости диполем //Изв. РАН. МЖГ. 2015. № 5. С. 16–23 = Savin A.A., Savin A.S. Three-dimensional problem of disturbing an ice cover by a dipole moving in fluid // Fluid Dynamics. 2015. V. 50. P. 613–620.

  13. Stepanyants Yu.A., Sturova I.V. Waves on a compressed floating ice plate caused by motion of a dipole in water // J. Fluid Mech. 2021. V. 907. A7.

  14. Ильичев А.Т., Савин А.С. Процесс установления системы плоских волн на ледовом покрове над диполем, равномерно движущимся в толще идеальной жидкости // Теор. мат. физ. 2017. Т. 193. № 3. С. 455–465 = Il’ichev A.T., Savin A.S. Process of establishing a plane-wave system on ice cover over a dipole moving uniformly in an ideal fluid column // Theor. Math. Phys. 2017. V.193. P. 1801–1810.

  15. Стурова И.В. Движение погруженной сферы в жидкости под ледяным покровом // ПММ. 2012. Т. 3. С. 406–417 = Sturova I.V. The motion of a submerged sphere in a liquid under an ice sheet // J. Appl. Math. Mech. 2012. V. 76. P. 293–301.

  16. Sturova I.V. Radiation of waves by a cylinder submerged in water with ice floe or polynya // J. Fluid Mech. 2015. V. 784. P. 373–395.

  17. Келдыш М.В. Замечания о некоторых движениях тяжелой жидкости / Избр. тр. Механика. М.: Наука, 1985. С. 100–103.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал