Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 3-13
СТАЦИОНАРНЫЕ РЕЖИМЫ ЭЛЕКТРОКОНВЕКЦИИ СЛАБОПРОВОДЯЩЕЙ ЖИДКОСТИ ПРИ УНИПОЛЯРНОЙ ИНЖЕКЦИИ ЗАРЯДА В ПОСТОЯННОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ
В. А. Ильин a, *, Т. И. Чигорина a
a Пермский государственный национальный исследовательский университет
Пермь, Россия
* E-mail: ilin1@psu.ru
Поступила в редакцию 04.12.2020
После доработки 28.04.2021
Принята к публикации 11.05.2021
Аннотация
Исследованы стационарные нелинейные режимы электроконвекции слабопроводящей жидкости в горизонтальном конденсаторе в поле тяжести и постоянном электрическом поле при униполярной инжекции заряда. Рассмотрена модель, в которой плотность инжектируемых с катода зарядов пропорциональна напряженности электрического поля в конденсаторе. Нелинейные режимы электроконвекции исследованы при нагреве снизу. Найдены зависимости порогов возникновения режимов электроконвекции в зависимости от степени нагрева и степени инжекции заряда.
Изучение конвекции слабопроводящих жидкостей в электрическом поле представляет интерес, потому что является способом прямого преобразования энергии электрического поля в энергию движения [1–4]. Электрическое поле может изменить пороги тепловой конвекции и обеспечить эффективный способ управления движением жидкостей.
Несмотря на большое количество экспериментальных и теоретических работ, остаются открытыми вопросы, связанные с возникновением и эволюцией электроконвективных движений [3]. Существуют различные механизмы зарядообразования в жидкостях [3, 5]. Нелинейные режимы электроконвекции идеального диэлектрика в переменном электрическом поле с диэлектрофоретическим механизмом зарядообразования изучены в [6]. Электротермоконвективная неустойчивость слоя слабопроводящей жидкости с электрокондуктивным механизмом зарядообразования в модулированном электрическом поле изучена в [7], а нелинейные режимы с таким же механизмом исследованы на основе маломодовой модели в [8]. Инжекционный механизм зарядообразования связан с инжекцией зарядов с поверхности электрода. В силу сложности проблемы существует много моделей, описывающих инжекцию заряда в слабопроводящей жидкости, например, в работах [9–13] проведено исследование особенностей электроконвекции на их основе.
Ряд экспериментальных данных описываются моделью, в которой инжектируемый с катода заряд зависит от напряженности электрического поля в конденсаторе [13, 14]. В настоящей работе в рамках этой модели рассматривается электроконвекция неоднородно нагретой слабопроводящей жидкости в горизонтальном конденсаторе в поле тяжести и в постоянном электрическом поле при униполярной инжекции заряда. Используется электрогидродинамическое приближение (магнитными эффектами по сравнению c электрическими пренебрегают). Инжектируемые с поверхности катода заряды движутся через слой жидкости, изменяя в ней распределение электрического поля. Диффузия заряда не учитывается. Считается, что время диффузии заряда пренебрежимо мало по сравнению с характерным гидродинамическим временем и временем релаксации заряда.
В статье [13] в аналогичной постановке проведено исследование линейной устойчивости изотермической слабопроводящей жидкости, нагрев жидкости в ней не рассматривался. В работе [14] исследовано влияние подвижности носителей заряда на критические параметры задачи, изучены нелинейные режимы электроконвекции при нагреве сверху. Линейный анализ устойчивости равновесия при нагреве снизу проведен в работе [15], в ней определены пороги возникновения монотонной конвекции. В [16] в одномерном случае проведено исследование динамики переноса заряда в изотермической жидкости в модулированном электрическом поле и в двумерном случае приведены результаты исследования двух стационарных нелинейных режимов при больших нагревах снизу (при числах Рэлея больше Ra = 500) в постоянном электрическом поле. Нестационарные и стационарные нелинейные режимы при нагреве сверху рассмотрены в [17]. В настоящей работе в нелинейной постановке изучено поведение стационарных режимов электроконвекции при меньших нагревах снизу, чем в статье [16] (при числах Рэлея меньше Ra = 500); определены зависимости критических параметров от степени нагрева и инжекции заряда.
1. ПОСТАНОВКА ЗАДАЧИ
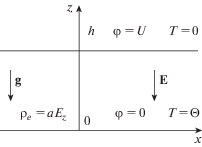
Рассмотрим бесконечный плоский горизонтальный слой вязкой несжимаемой слабопроводящей жидкости в вертикальном постоянном электрическом поле и поле тяжести с ускорением свободного падения g. Ось x направлена вдоль нижней границы слоя, ось z – перпендикулярна границам слоя. Два плоских электрода лежат в плоскостях z = 0 и z = h (рис. 1), h – толщина слоя.
Идеально тепло- и электропроводные пластины конденсатора нагреты до разной температуры – T(0) = Θ, T(h) = 0. Здесь T – температура, отсчитываемая от температуры верхнего электрода, Θ – характерная разность температур. Случай Θ > 0 соответствует нагреву снизу. На катоде (нижнем электроде) потенциал равен нулю $\varphi \left( 0 \right) = 0$, на аноде (верхнем электроде) – $\varphi \left( h \right) = U$. Здесь U – напряжение электрического поля.
Под действием электрического поля в узком слое вблизи катода в результате электрохимических реакций образуется заряд. Плотность свободных зарядов у катода пропорциональна нормальной составляющей вектора напряженности поля ${{\rho }_{e}} = a{{E}_{z}}$, где a – коэффициент, характеризующий степень инжекции. Инжектированный заряд под действием поля движется в глубь жидкости. Двигаясь к аноду, заряд может увлекать за собой жидкость, вызывая электроконвективное течение. Движение жидкости и свободных зарядов в слое описывается системой уравнений электрогидродинамики
(1.1)
$\frac{{\partial {{\rho }_{e}}}}{{\partial t}} + {\text{div(}}{{\rho }_{e}}v - b{{\rho }_{e}}{\mathbf{E}}{\text{)}} = {\text{0}}$Границы слоя считаются твердыми, непроницаемыми, на них выполняются условия прилипания – скорость равна нулю
Используем безразмерные переменные на основе масштабов: времени – время вязкой диссипации $\left[ t \right] = {{h}^{2}}{\text{/}}{{\nu }_{0}}$, расстояния – расстояние между электродами ${\text{[}}{\mathbf{r}}{\text{]}} = h$, скорости – [v] = ${{\nu }_{0}}$/h, потенциала – $[\varphi ] = U$, давления – $\left[ p \right] = \rho \nu _{0}^{2}{\text{/}}{{h}^{2}}$, температуры – $[T] = \Theta $, плотности заряда – [ρe] = $\varepsilon {{\varepsilon }_{0}}U{\text{/}}{{h}^{2}}$.
После обезразмеривания система уравнений (1.1) с граничными условиями (1.2) приводится к виду:
Здесь введены безразмерные параметры – тепловое число Рэлея Ra, электрические параметры ${{T}_{e}}$ и M, число Прандтля Pr и параметр инжекции A
(1.5)
${\text{Ra}} = \frac{{g\beta \Theta {{h}^{3}}}}{{\nu _{0}^{{}}\chi }},\quad {{T}_{{\text{e}}}} = \frac{{\varepsilon {{\varepsilon }_{0}}U}}{{b\rho \nu _{0}^{{}}}},\quad {\text{M}} = \frac{1}{b}{{\left( {\frac{{\varepsilon {{\varepsilon }_{0}}}}{\rho }} \right)}^{{1/2}}},\quad \Pr = \frac{{{{\nu }_{0}}}}{\chi },\quad {\text{A}} = \frac{{ah}}{{\varepsilon {{\varepsilon }_{0}}}}$В работе [13] были использованы другие безразмерные параметры – электрическое число Грасгофа ${\text{G}}{{{\text{r}}}_{{\text{e}}}} = {{\varepsilon {{\varepsilon }_{0}}{{U}^{2}}} \mathord{\left/ {\vphantom {{\varepsilon {{\varepsilon }_{0}}{{U}^{2}}} {\rho \nu _{0}^{2}}}} \right. \kern-0em} {\rho \nu _{0}^{2}}}$, параметр подвижности зарядов ${\text{B}} = {{bU} \mathord{\left/ {\vphantom {{bU} {{{\nu }_{0}}}}} \right. \kern-0em} {{{\nu }_{0}}}}$. Они связаны с нашими параметрами следующим образом: ${\text{G}}{{{\text{r}}}_{e}} = {{T_{e}^{2}} \mathord{\left/ {\vphantom {{T_{e}^{2}} {{{{\text{M}}}^{2}}}}} \right. \kern-0em} {{{{\text{M}}}^{2}}}}$, ${\text{B}} = {{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} {{{{\text{M}}}^{2}}}}} \right. \kern-0em} {{{{\text{M}}}^{2}}}}$. В работе [13] безразмерные параметры варьировались с учетом их зависимости от безразмерного напряжения F так: ${\text{G}}{{{\text{r}}}_{e}}$ = = 5000F 2, B = 5F (F пропорционален размерной величине напряжения U). В соответствии с этими соотношениями электрические параметры ${{T}_{e}}$ и M будут равны: ${{T}_{e}} = {{10}^{3}}F$, ${\text{M}} = 14.14$ (M2 = 200).
Связь безразмерного напряжения F с размерной величиной напряжения U можно описать следующим образом: $U = F \times {{10}^{4}}В = F \times 10$ кВ ($F = {U \mathord{\left/ {\vphantom {U {10}}} \right. \kern-0em} {10}}$ кВ). То есть F является долей от 10 кВ. Для оценки параметров возьмем трансформаторное масло с диэлектрической проницаемостью $\varepsilon = 2.2$, плотностью $\rho = 883$ кг/м3, вязкостью ${{\nu }_{0}} = 22.5 \times {{10}^{{ - 6}}}$ м2/с2, ${{\varepsilon }_{0}} = 8.85 \times {{10}^{{ - 12}}}$ Кл2/Нм2, подвижность зарядов возьмем равной $b = {{10}^{{ - 8}}}$ м2/Вс [3]. Тогда получим, что Gre = 4.4 × 10–5U 2 = = $4.4 \times {{10}^{3}}{{F}^{2}}$, $B = 4.4 \times {{10}^{{ - 4}}}U = 4.4F$, или в новых параметрах ${{T}_{e}} = 0.98 \times {{10}^{3}}F$, ${\text{M}} = \sqrt {2.2} \times 10$ = = 14.85. Эти величины близки к величинам, которые были использованы в работе [13]. Если поварьировать значениями диэлектрической проницаемости, плотности, вязкости жидкости и подвижности зарядов или рассмотреть другую связь F с U, то можно получить полное соответствие полученных соотношений для ${\text{G}}{{{\text{r}}}_{e}}$ и B со значениями, использованными в статье [13].
Далее рассмотрим плоские возмущения ${\mathbf{v}} = (u,0,w)$ и ${\partial \mathord{\left/ {\vphantom {\partial {\partial y = 0}}} \right. \kern-0em} {\partial y = 0}}$. Для исследования нелинейных режимов электроконвекции вводятся функция тока ψ и вихрь скорости Φ
(1.6)
${{{v}}_{x}} = - \frac{{\partial \psi }}{{\partial z}},\quad {{{v}}_{z}} = \frac{{\partial \psi }}{{\partial x}},\quad \Phi = {{{\text{(rot}}{\mathbf{v}}{\text{)}}}_{y}} = - \Delta \psi $Вследствие слабой инжекции нелинейную задачу можно решать в безындукционном приближении, в котором предполагается, что изменение распределения заряда, возникающее в результате появления электроконвективных структур, по сравнению с равновесным его значением, не вызывает заметного изменения потенциала электрического поля [13, 14]. Система (1.3) в безындукционном приближении примет вид
(1.7)
$\frac{{\partial {{\rho }_{e}}}}{{\partial t}} + \frac{{\partial \psi }}{{\partial x}}\frac{{\partial {{\rho }_{e}}}}{{\partial z}} - \frac{{\partial \psi }}{{\partial z}}\frac{{\partial {{\rho }_{e}}}}{{\partial x}} = \frac{{{{T}_{e}}}}{{{\text{M}}_{{}}^{{\text{2}}}}}\left( {\rho _{e}^{2} + E\frac{{\partial {{\rho }_{e}}}}{{\partial z}}} \right)$(1.8)
$z = 0{\text{:}}\,\psi = 0,{{\quad \partial \psi } \mathord{\left/ {\vphantom {{\quad \partial \psi } {\partial z}}} \right. \kern-0em} {\partial z}} = 0,\quad {{\rho }_{e}} = AE,\quad T = 1$На боковых границах для всех искомых функций выполняются условия периодичности.
2. НЕЛИНЕЙНЫЕ РЕЖИМЫ КОНВЕКЦИИ ПРИ НАГРЕВЕ СНИЗУ
Система (1.7)–(1.8) аппроксимировалась конечно-разностными отношениями. Эволюционные уравнения решались по явной схеме, конвективные слагаемые в уравнении для заряда и температуры аппроксимировались разностями “против потока” [14]. Для уравнения переноса тепла использовались центральные разности. Для удобства работы с условиями периодичности к сетке добавлялись два вертикальных ряда. Вихрь скорости на горизонтальных границах вычислялся по формуле Тома. Для решения уравнения Пуассона использовался метод последовательной верхней релаксации.
Для вычислений выбиралась прямоугольная ячейка с пространственными размерами Lz = 1, Lx = 2. Горизонтальная ячейка соответствует волновому числу k = 3.14. Размер сетки брался 21 × × 41 узел. Число Прандтля Pr = 10, электрический параметр M = 14.14, параметр инжекции заряда А = 0.25. Вычислялись зависимости максимальной функции тока от параметра Te для разных нагревов снизу – теплового числа Рэлея Ra. При рассмотренных параметрах наблюдались два режима стационарной конвекции разной интенсивности – режим с малой интенсивностью вихрей (режим 1) и режим с большой интенсивностью вихрей (режим 2), между которыми происходили гистерезисные переходы.
Для более детальной характеристики установившихся конвективных режимов были проведены вычисления безразмерного теплопотока – числа Нуссельта, и исследованы пространственные распределения полей функций.
Для анализа интенсивности теплопереноса через конденсатор вычислялся усредненный по длине ячейки безразмерный тепловой поток на границе слоя (число Нуссельта) следующим образом:
(2.1)
${\text{Nu}} = - \frac{1}{L}\int\limits_0^L {{{{\left( {\frac{{\partial T}}{{\partial z}}} \right)}}_{{z = 0}}}dx} $Случай Nu = 1 соответствует процессу молекулярного теплопереноса, превышение числа Нуссельта над единицей Nu > 1 свидетельствует о возникновении конвекции. Полный заряд определялся как сумма зарядов по всем узлам сетки: $Q = \sum\nolimits_{i,j} {{{\rho }_{{{{e}_{{i,j}}}}}}} $.
Разложение полей в ряд Фурье по пространственным гармоникам несет информацию о характере течения жидкости в слое. В нашем случае, как и в предыдущих исследованиях электроконвекции [11, 12, 14], мы ограничимся разложением искомых функций лишь в горизонтальном направлении, в сечении, соответствующем середине слоя (z = 0.5)
(2.2)
$F\left( {x,1{\text{/}}2,t} \right) = {{F}_{0}}\left( t \right) + \sum\limits_{n = 1}^\infty {{{F}_{n}}\left( t \right)} \exp \left( {inkx} \right)$В исследованной области параметров наблюдаются двухвихревые движения, поэтому ограничимся при рассмотрении пространственных характеристик структур первой ${{F}_{1}}\left( t \right)$, второй ${{F}_{2}}\left( t \right)$ и третьей ${{F}_{3}}\left( t \right)$ модами разложения.
На основе данных статьи [16] была выявлена следующая закономерность: с уменьшением значения числа Рэлея уменьшается интервал существования режима 1 с малой интенсивностью вихрей. В настоящей работе эта закономерность была продолжена. Для этого были проведены расчеты при значениях числа Рэлея меньше Ra = 400.
На рис. 2 представлена зависимость максимальной функции тока от электрического параметра Te для Ra = 400. Крестом на рисунке отмечена точка возникновения режима 1 с малой интенсивностью, стрелками обозначено направление гистерезиса. Интенсивность режима с большой интенсивностью вихрей – режима 2 – растет с увеличением Те. При расчете с постоянными начальными условиями было обнаружено, что электроконвекция возникает мягким образом при значении Te = 4.8 × 103, наблюдается режим с малой интенсивностью вихрей (режим 1). При Te = 5.8 × 103 происходит переход к режиму с большой интенсивностью вихрей (режим 2). Методом продолжения по параметру найдена точка возникновения режима 2: Te = 1.5 × 103.
Рис. 2.
Зависимость максимальной функции тока от параметра Те: А = 0.25, Ra = 400, 1 – режим с малой интенсивностью вихрей, 2 – режим с большой интенсивностью вихрей.
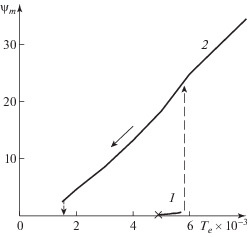
В интервале электрического параметра 1.5 × 103 ≤ Te ≤ 4.7 × 103 в зависимости от начальных условий реализуется либо равновесное распределение, либо стационарный режим 2 с большой интенсивностью, при большем поле 4.8 × 103 ≤ Te ≤ 5.7 × 103 может реализоваться как режим 1, так и режим 2. При Te ≥ 5.8 × 103 сколь угодно малые возмущения приводят систему после переходных процессов к стационарному режиму 2 с большой интенсивностью.
На рис. 3 представлены изолинии полей функции тока (а, б), температуры (в, г) и плотности заряда (д, е) электроконвективного течения для Ra = 400. Опишем различия найденных режимов: режима 1 при Te = 5.7 × 103 (изолинии а, в, д на рис. 3) и режима 2 при Te = 5.8 × 103 (изолинии б, г, е на рис. 3).
Рис. 3.
Изолинии функции тока (а, б), температуры (в, г) и плотности заряда (д, е): Ra = 400, А = 0.25; а, в, д – режим 1 с малой интенсивностью вихрей (Те = 5.7 × 103); б, г, е – режим 2 с большой интенсивностью вихрей (Те = 5.8 × 103).
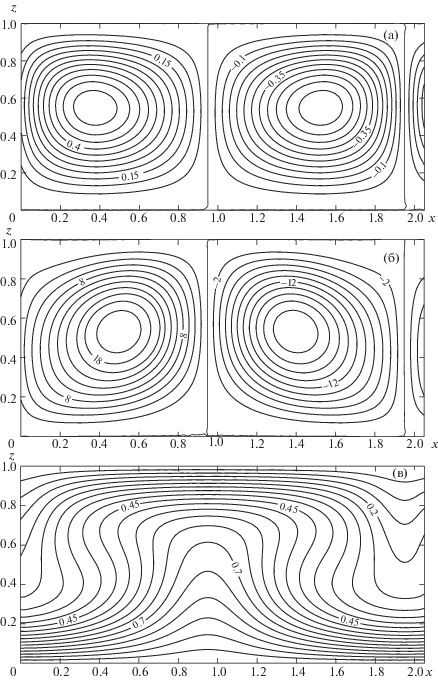
Рис. 3.
Окончание.
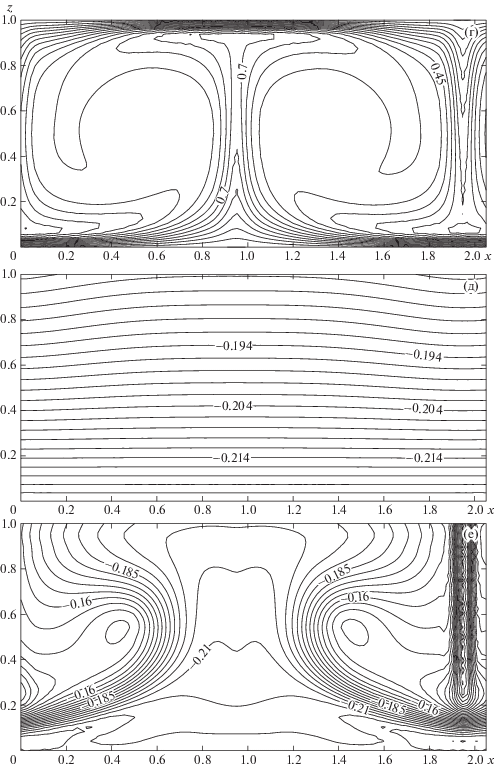
Поток тепла в режиме 2 превосходит по интенсивности поток тепла в режиме 1 более чем 5 раз: в слабоинтенсивном режиме число Нуссельта Nu = 2.14, в режиме большой интенсивности Nu = 11.7. Максимальное значение функции тока в режиме 1 ${{\psi }_{{\max }}}$ = 0.59, в режиме 2 ${{\psi }_{{\max }}}$ = 21.8, что представляет собой скачок почти в 37 раз.
Заряды в обоих режимах мало различаются: в режиме 1 средний заряд ${{\bar {\rho }}_{e}}$ = –0.21, в режиме 2 ${{\bar {\rho }}_{e}}$ = –0.19; полные заряды в слое соответственно равны: ${{Q}_{1}} = - 178$ и ${{Q}_{2}} = - 162$. Но в режиме 2 заряд имеет более сложное поведение – разброс между его максимальным и минимальным значениями (${{\rho }_{e}}_{{\max }} = - 0.09$, ${{\rho }_{e}}_{{\min }} = - 0.23$) больше, чем в слабоинтенсивном режиме (${{\rho }_{e}}_{{\max }} = - 0.18$, ${{\rho }_{e}}_{{\min }} = - 0.22$).
Далее были рассмотрены пространственные характеристики режимов. Был проведен пространственный фурье-анализ (2.2) – вычислены абсолютные значения первых трех мод разложения в ряд фурье-функции тока ($\left| {{{\psi }_{1}}} \right|$, $\left| {{{\psi }_{2}}} \right|$, $\left| {{{\psi }_{3}}} \right|$), температуры ($\left| {{{T}_{1}}} \right|$, $\left| {{{T}_{2}}} \right|$, $\left| {{{T}_{3}}} \right|$) и плотности заряда ($\left| {{{\rho }_{e}}_{1}} \right|$, $\left| {{{\rho }_{e}}_{2}} \right|$, $\left| {{{\rho }_{e}}_{3}} \right|$). Для каждого режима эти моды были нормированы на соответствующую режиму величину первой моды.
В слабоинтенсивном режиме для функции тока отношение модулей второй моды к первой получилось равным ${{\left| {{{\psi }_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{2}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}} = 0.12$, третьей моды к первой: ${{\left| {{{\psi }_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{3}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}} = 0.009$. В режиме большой интенсивности соответственно: ${{\left| {{{\psi }_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{2}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}} = 0.095$, ${{\left| {{{\psi }_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{3}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}} = 0.035$. Относительные значения вторых мод у режимов мало отличаются, но нормированная третья мода в режиме 2 почти в 4 раза больше, чем в режиме 1.
В слабоинтенсивном режиме для температуры отношение модулей второй моды к первой получилось равным ${{\left| {{{T}_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{2}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 0.017$, третьей моды к первой: ${{\left| {{{T}_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{3}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 0.095$. В режиме большой интенсивности соответственно: ${{\left| {{{T}_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{2}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 0.29$, ${{\left| {{{T}_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{3}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 1.13$. Относительное значение второй моды для температуры у режима большой интенсивности по сравнению с режимом слабой интенсивности больше в 17 раз, третьей моды – почти в 12 раз.
В режиме 1 для плотности заряда отношение модулей плотности заряда второй моды к первой получилось равным ${{\left| {{{\rho }_{e}}_{2}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{2}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.23$, третьей моды к первой: ${{\left| {{{\rho }_{e}}_{3}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{3}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.022$. В режиме 2 соответственно: ${{\left| {{{\rho }_{e}}_{2}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{2}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.516$, ${{\left| {{{\rho }_{e}}_{3}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{3}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.177$. Относительное значение второй моды заряда увеличилось более чем в 2 раза, третьей моды – почти в 8 раз. Пространственное распределение заряда в режиме 2 имеет более сложную структуру.
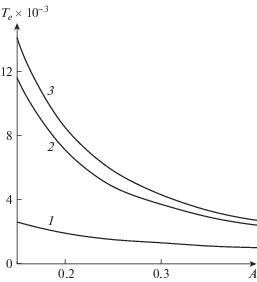
Пороги переходов между режимами электроконвекции для разных чисел Ra представлены на рис. 4. Как видно из него, с уменьшением числа Рэлея интервал существования режима 1 сужается, и режим исчезает.
Рис. 4.
Зависимость пороговых значений Те от теплового числа Рэлея Ra для М = 14.14. Кривая 1 отображает пороги возникновения режима 2 с большой интенсивностью вихрей, 2 – пороги возникновения режима 1 с малой интенсивностью вихрей, 3 – пороги перехода от режима 1 к режиму 2.
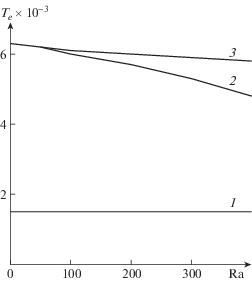
При Ra = 51 режим 1 с малой интенсивностью еще существует. Вычисления показали, что при таком нагреве при Те = 6.1 × 103 мягко возникающий режим с малой интенсивностью вихрей наблюдается. При Те = 6.2 × 103 происходит скачкообразный переход к режиму 2 с большой интенсивностью вихрей. При движении в пространстве параметров справа налево режим 2 существует до Те = 1.5 × 103. При меньшей напряженности поля Те < 1.5 × 103 в системе независимо от начальных условий затухают все возмущения, и устанавливается равновесие.
При Ra = 50 режим 1 с малой интенсивностью не наблюдается. При Те = 6.1 × 103 после длительного переходного процесса устанавливается равновесие. При Те = 6.2 × 103 происходит скачкообразный переход к режиму 2 с большой интенсивностью. При меньшем числе Ra присутствует только режим 2 с большой интенсивностью. Точка перехода к режиму 2 продолжает расти, в невесомости (Ra = 0) этот переход происходит при Те = 6.3 × 103.
Проведем оценки, соответствующие реальной ситуации. Определим число Рэлея. Для трансформаторного масла $\chi = 7.56 \times {{10}^{{ - 8}}}$ м2/с, $\beta = 6.9 \times {{10}^{{ - 4}}}$ 1/°C, толщину конденсатора возьмем h = = 1 см, тогда число Рэлея будет равно ${\text{Ra}} = 4 \times {{10}^{3}}\Theta $. Для Ra = 400 нагрев между пластинами конденсатора получится небольшим: $\Theta = 0.1$°C. Для меньших чисел Рэлея нагрев будет еще меньше.
Определим напряжение в конденсаторе. В нашей задаче для рассматриваемых режимов $F = {{T}_{e}} \times {{10}^{{ - 3}}}$ меняется примерно до 6.3. Если $U = {\text{F}} \times 10$ кВ, то напряжение в реальной ситуации будет в пределах 63 кВ.
3. РЕЖИМЫ ЭЛЕКТРОКОНВЕКЦИИ ПРИ РАЗНЫХ СТЕПЕНЯХ ИНЖЕКЦИИ
При фиксированном нагреве (Ra = 400) производились расчеты по вычислению зависимости максимальной функции тока от параметра Те при различных степенях инжекции заряда с катода – параметра А. Приведем данные вычислений для А = 0.15. Зависимость максимальной функции тока от электрического параметра Te в этом случае аналогична зависимости, представленной на рис. 2.
Было обнаружено, что электроконвекция возникает мягким образом при Те = 11.6 × 103, наблюдается режим с малой интенсивностью вихрей (режим 1). При Те = 14.1 × 103 происходит скачкообразный переход к режиму с большой интенсивностью вихрей (режим 2). Интенсивность этого режима растет с ростом Те. В интервале $2.6 \times {{10}^{3}} \leqslant {{Т}_{е}} \leqslant 11.2 \times {{10}^{3}}$ в зависимости от начальных условий реализуется либо равновесное распределение, либо стационарный режим 2, при $11.3 \times {{10}^{3}} \leqslant {{Т}_{е}} \leqslant 14.0 \times {{10}^{3}}$ может реализоваться как режим 1, так и режим 2. При ${{Т}_{е}} \geqslant 14.1$ × 103 сколь угодно малые возмущения приводят систему после переходных процессов к стационарному режиму 2 с большой интенсивностью вихрей.
Опишем различия найденных режимов: режима 1 при Te = 14 × 103 и режима 2 при Te = 14.1 × 103. Поток тепла в режиме 2 превосходит по интенсивности поток тепла в режиме 1 почти в 5 раз: в слабоинтенсивном режиме число Нуссельта Nu = 2.4, в режиме большой интенсивности Nu = = 11.6. Максимальное значение функции тока в режиме 1 ${{\psi }_{{\max }}}$ = 0.9, в режиме 2 ${{\psi }_{{\max }}}$ = 53.
Заряды в обоих режимах мало различаются: в режиме 1 средний заряд ${{\bar {\rho }}_{e}}$ = –0.13, в режиме 2 ${{\bar {\rho }}_{e}}$ = –0.15; полные заряды в слое соответственно равны: ${{Q}_{1}} = - 115$ и ${{Q}_{2}} = - 99$. Но в режиме 2 заряд имеет более сложное поведение – разброс между максимальным и минимальным значениями заряда в нем больше (${{\rho }_{e}}_{{\max }} = - 0.002$, ${{\rho }_{e}}_{{\min }} = - 0.15$), чем в слабоинтенсивном режиме (${{\rho }_{e}}_{{\max }}$ = = –0.12, ${{\rho }_{e}}_{{\min }} = - 0.14$).
В слабоинтенсивном режиме для функции тока отношение модулей функции тока второй моды разложения в ряд Фурье к первой моде получилось равным ${{\left| {{{\psi }_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{2}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}} = 0.2$, третьей моды к первой: ${{\left| {{{\psi }_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{3}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}} = 0.01$. В режиме большой интенсивности соответственно: ${{\left| {{{\psi }_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{2}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}} = 0.1$, ${{\left| {{{\psi }_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\psi }_{3}}} \right|} {\left| {{{\psi }_{1}}} \right|}}} \right. \kern-0em} {\left| {{{\psi }_{1}}} \right|}}$ = = 0.04. Относительное значение второй моды функции тока уменьшилось, а третьей моды – увеличилось.
В слабоинтенсивном режиме для температуры отношение модулей температуры второй и третьей мод к первой получилось равным соответственно ${{\left| {{{T}_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{2}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 0.09$, ${{\left| {{{T}_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{3}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 0.17$. В режиме большой интенсивности соответственно: ${{\left| {{{T}_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{2}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 0.35$, ${{\left| {{{T}_{3}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{T}_{3}}} \right|} {\left| {{{T}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{T}_{1}}} \right|}} = 1.03$. Относительные значения второй и третьих мод температуры увеличились.
В режиме 1 для плотности заряда отношение модулей плотности заряда второй моды к первой получилось равным ${{\left| {{{\rho }_{e}}_{2}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{2}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.36$, третьей моды к первой: ${{\left| {{{\rho }_{e}}_{3}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{3}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.03$. В режиме 2 соответственно: ${{\left| {{{\rho }_{e}}_{2}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{2}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.43$, ${{\left| {{{\rho }_{e}}_{3}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\rho }_{e}}_{3}} \right|} {\left| {{{\rho }_{e}}_{1}} \right|}}} \right. \kern-0em} {\left| {{{\rho }_{e}}_{1}} \right|}} = 0.36$. Относительные значения мод заряда увеличились.
В целом можно сделать вывод, что пространственные распределения функции тока, температуры и заряда в более интенсивном режиме имеют более сложную структуру, чем в слабоинтенсивном режиме.
Вычисления для разных значений параметра А были систематизированы и по ним построен график изменения значений порогов возникновения режимов и переходов между режимами в зависимости от параметра инжекции (рис. 5). Параметр инжекции А существенно изменяет плотность распределения заряда в слое. Как видно из рис. 5, с увеличением инжекции заряда интервал существования режима 1 с малой интенсивностью вихрей (расстояние между кривыми 2 и 3) уменьшается и пороги режимов понижаются.
ЗАКЛЮЧЕНИЕ
Проведено исследование нелинейных режимов электроконвекции неизотермической слабопроводящей жидкости, находящейся в горизонтальном конденсаторе в гравитационном и постоянном электрическом поле при униполярной инжекции заряда. Рассмотрен нагрев снизу и различные значения инжекции. Использована модель, в которой плотность инжектируемых с катода зарядов пропорциональна напряженности электрического поля в конденсаторе. Изучены нелинейные режимы электроконвекции. Обнаружены и исследованы два нелинейных стационарных режима со значительно отличающейся интенсивностью течения и гистерезисные переходы между ними. Изучено их различие по теплопотоку, заряду и пространственным фурье-спектрам. Найдены пороги возникновения режимов электроконвекции в зависимости от степени нагрева и степени инжекции заряда. Пространственные распределения полей в более интенсивном режиме имеют более сложную структуру, чем в слабоинтенсивном режиме.
Выявлено, что при уменьшении нагрева жидкости режим с малой интенсивностью течения исчезает, остается только режим с большой интенсивностью течения. С увеличением степени инжекции заряда пороги режимов уменьшаются, поскольку заряда в жидкости становится больше, электрическое поле эффективнее действует на движение жидкости, и оно возникает при меньших напряжениях.
Слабоинтенсивный режим возникает мягко. Более интенсивный режим, возникающий жестко, не определяется при линейном анализе, но был обнаружен при нелинейном анализе. В зависимости от параметров задачи возможно разное ветвление режимов, например, в работе [11] электроконвекция возникает мягко, в [12] описано жесткое возбуждение электроконвекции. Переход от мягкого ветвления к жесткому определяется коэффициентами в уравнении Ландау [18]. В дальнейшем планируется продолжить работу и произвести исследование по определению коэффициентов Ландау, из которого будут определены условия жесткого или мягкого ветвлений.
Список литературы
Остроумов Г.А. Взаимодействие электрических и гидродинамических полей: Физические основы электрогидродинамики. М.: Наука, 1979. 319 с.
Саранин В.А. Устойчивость равновесия, зарядка, конвекция и взаимодействие жидких масс в электрических полях. М.–Ижевск: НИЦ РХД, 2009. 332 с.
Жакин А.И. Электрогидродинамика // УФН. 2012. Т. 182. № 5. С. 495–520.
Стишков Ю.К. Электрофизические процессы в жидкостях при воздействии сильных электрических полей. М.: Юстицинформ, 2019. 262 с.
Панкратьева И.Л., Полянский В.А. Основные механизмы электризации слабопроводящих многокомпонентных сред // Изв. РАН. МЖГ. 2017. № 5. С. 15–22.
Ильин В.А. Модель электротермической конвекции идеального диэлектрика в горизонтальном конденсаторе // Изв. РАН. МЖГ. 2016. № 5. С. 10–16.
Веларде М.Г., Смородин Б.Л. Конвективная неустойчивость плоского горизонтального слоя слабопроводящей жидкости в переменных и модулированных электрических полях // Изв. РАН. МЖГ. 2000. № 3. С. 31–38.
Ильин В.А., Пономарева Л.А. Модель электроконвекции слабопроводящей жидкости в высокочастотном электрическом поле // Прикладная механика и техническая физика. 2018. Т. 59. № 2. С. 12–22.
Ермолаев И.А., Жбанов А.И. Численное исследование униполярной инжекции при электроконвективном движении в плоском слое трансформаторного масла // Изв. РАН. МЖГ. 2003. № 6. С. 1–7. 6.
Смородин Б.Л., Тараут А.В. Параметрическая конвекция слабопроводящей жидкости в переменном электрическом поле // Изв. РАН. МЖГ. 2010. № 1. С. 3–11.
Смородин Б.Л., Тараут А.В. Электроконвекция при наличии автономной униполярной инжекции и остаточной проводимости // Журнал экспериментальной и теоретической физики. 2012. Т. 142. Вып. 2 (8). С. 403–412.
Смородин Б.Л., Тараут А.В. Динамика волновых электроконвективных течений в модулированном электрическом поле // Журнал экспериментальной и теоретической физики. 2014. Т. 145. Вып. 1. С. 180–188.
Верещага А.Н. Унарная электроконвекция в плоском слое // Гидродинамика и процессы тепломассопереноса. 1989. С. 42–47.
Мордвинов А.Н., Смородин Б.Л. Электроконвекция при инжекции с катода и нагреве сверху // Журнал экспериментальной и теоретической физики. 2012. Т. 141. Вып. 5. С. 997–1005.
Ильин В.А., Мордвинов А.Н., Петров Д.А. Электроконвекция слабопроводящей жидкости при униполярной инжекции заряда в постоянном электрическом поле // Журнал экспериментальной и теоретической физики. 2015. Т. 147. Вып. 1. С. 181–188.
Ильин В.А. Электроконвекция слабопроводящей жидкости в горизонтальном конденсаторе при униполярной инжекции заряда // Журнал технической физики. 2017. Т. 87. Вып. 1. С. 5–9.
Ильин В.А., Александрова В.Н. Электроконвекция слабопроводящей жидкости при униполярной инжекции заряда в постоянном электрическом поле при нагреве сверху // Журнал экспериментальной и теоретической физики. 2020. Т. 157. Вып. 2. С. 349–356.
Ландау Л.Д., Лившиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1986. 736 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа