Известия РАН. Механика жидкости и газа, 2021, № 3, стр. 16-29

ОБОБЩЕНИЕ РЕШЕНИЯ ЖУКОВСКОГО ДЛЯ ПУЗЫРЯ В КАНАЛЕ

М. М. Алимов^*

Казанский (Приволжский) федеральный университет
Казань, Россия

Поступила в редакцию 11.06.2020
После доработки 11.09.2020
Принята к публикации 01.10.2020

DOI: 10.31857/S0568528121030014

Аннотация

Для задачи обтекания двумерного пузыря потенциальным потоком капиллярной жидкости в прямолинейном канале построено новое точное решение, которое является обобщением известного частного решения Н.Е. Жуковского. Показано, что в одном из предельных случаев бесконечно малого пузыря это решение совпадает с точным решением Мак-Леода для пузыря в безграничном потоке.

Ключевые слова: капиллярная жидкость, двумерный пузырь, комплексная переменная

Рассматривается плоскопараллельное бесциркуляционное обтекание цилиндрической газовой полости (двумерного газового пузыря) стационарным потенциальным потоком идеальной невесомой и несжимаемой жидкости в прямолинейном канале при учете действия капиллярных сил. Как отмечается в [1], эта задача является лишь качественным аналогом реальной трехмерной задачи обтекания пузыря. Тем не менее вопрос о том, какую форму примет такая полость в результате суммарного действия капиллярных и гидродинамических сил, представляет самостоятельный интерес, о чем свидетельствует множество публикаций [2–5]. Кроме того, математическая постановка этой задачи родственна постановкам задачи определения конфигурации установившихся капиллярных волн [6], а также постановкам задачи о стационарной конфигурации поверхности проводящей жидкости в электрическом поле [7]. Касаясь последней работы, заметим, что в ней, с одной стороны, выявлено, что задача обтекания двумерного пузыря имеет прямую аналогию в упомянутой области электростатики; с другой стороны, ее авторы конструируют “новое” решение задачи, не замечая, что оно идентично решению Жуковского [2].

Постановка задачи, возникающая в таких различных областях, существенно нелинейна. Тем не менее имеется большое количество примеров ее точного решения – помимо упомянутых выше здесь можно отметить работы [8–11]. Это позволяет надеяться на отыскание и других ее точных решений, хотя бы и частного характера. Цель данной работы – получить новое точное решение задачи обтекания двумерного пузыря в канале путем обобщения найденного Н.Е. Жуковским частного решения.

1. ПОСТАНОВКА ЗАДАЧИ ОБТЕКАНИЯ ПУЗЫРЯ В КАНАЛЕ

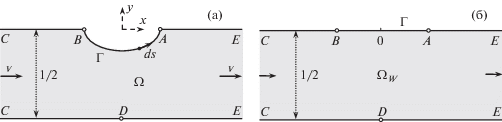
Ввиду широкой области применимости задачи целесообразно привести ее безразмерную постановку. На рис. 1а представлена картина течения с учетом имеющейся симметрии относительно центральной оси канала: нижняя стенка канала $CDE$ и центральная его ось $BC \cup EA$ прямолинейны, а граница пузыря $\Gamma = AB$ свободна. Область течения обозначена через $\Omega $.

Рис. 1.

Картина течения в физической плоскости (а) и вид плоскости комплексного потенциала $W$ (б).

За характерный размер задачи примем ширину канала ${{L}_{*}}$, а за характерную скорость – скорость течения на бесконечности ${{V}_{*}}$. Тогда безразмерная ширина канала будет равна 1, течение будет характеризоваться безразмерной скоростью v, а модуль ее скорости $v$ на бесконечности ${\text{|}}x{\text{|}} \to \infty $ будет удовлетворять условию нормировки $v = 1$.

Всюду в области течения Ω предполагается выполнение уравнений ${\mathbf{v}} = \nabla \varphi $, $\nabla \cdot {\mathbf{v}} = 0$, где $\varphi (x,y)$ – потенциал течения. Для потенциала имеет место краевая задача

(1.1)

$\Omega {\kern 1pt} {\kern 1pt} :\quad \Delta \varphi = 0;\quad \partial \Omega :\quad \frac{{\partial \varphi }}{{\partial n}} = 0;\quad C,E:\quad \frac{{\partial \varphi }}{{\partial x}} = 1$

где n – нормаль к границе $\partial \Omega $. Задача (1.1) пока незамкнута, поскольку участок $\Gamma $ границы $\partial \Omega $ является свободным и на нем необходимо задать дополнительное условие. Его можно получить, выписав на границе пузыря два соотношения [12]

(1.2)

$\Gamma :\quad {{p}_{{air}}} = p + \frac{\sigma }{{{{L}_{*}}}}\frac{{d\theta }}{{ds}},\quad p + \frac{{\rho V_{*}^{2}}}{2}{{v}^{2}} = {{p}_{0}}$

Первое представляет собой закон Лапласа, а второе – интеграл Бернулли. Здесь ${{p}_{{air}}}$ – давление воздуха в пузыре, ${{p}_{0}}$ – давление торможения потока, $p$ – давление жидкости, ρ – ее плотность, σ – коэффициент поверхностного натяжения, θ – угол наклона к горизонту касательной к границе $\Gamma $, s – безразмерная дуговая абсцисса границы Γ. Величина ${{d\theta } \mathord{\left/ {\vphantom {{d\theta } {ds}}} \right. \kern-0em} {ds}}$ представляет собой кривизну границы $\Gamma $, причем ${{d\theta } \mathord{\left/ {\vphantom {{d\theta } {ds}}} \right. \kern-0em} {ds}} > 0$ для границы, выпуклой в сторону жидкости (см. рис. 1а).

Исключая давление p из двух соотношений (1.2) и используя соотношение $ds = {{v}^{{ - 1}}}d\varphi $ на $\Gamma $, получим искомое дополнительное условие на этой границе [12]

(1.3)

$\Gamma {\text{:}}\quad \frac{{d\theta }}{{d\varphi }} = (\alpha {{v}^{{ - 1}}} + \beta v)$

Входящие в него безразмерные комплексы $\alpha $ (число Эйлера) и $\beta $ (число Вебера)

$\alpha = \frac{{{{L}_{*}}\left( {{{p}_{{air}}} - {{p}_{0}}} \right)}}{\sigma },\quad \beta = \frac{{\rho V_{*}^{2}{{L}_{*}}}}{{2\sigma }} > 0$

являются определяющими параметрами задачи, при этом параметр β необходимо положителен, а параметр α может быть и положительным, и отрицательным.

Для краевой задачи (1.1), (1.3) можно ввести комплексную плоскость $z = x + iy$ и комплексный потенциал $W = \varphi + i\psi $, где $\psi $ – функция тока [13]. Сама задача сводится к нахождению вида функции комплексного переменного $W(z)$.

Можно использовать прием параметризации: ввести вспомогательную плоскость комплексного переменного, скажем, ζ канонического вида, и вспомогательные функции $\chi (\zeta )$ либо $\omega (\zeta )$, связанные с производной ${{dz} \mathord{\left/ {\vphantom {{dz} {dW}}} \right. \kern-0em} {dW}}$ выражениями

(1.4)

$\chi (\zeta ) = \frac{{dz}}{{dW}} = {{v}^{{ - 1}}}{{e}^{{i\theta }}};\quad \omega (\zeta ) = \ln \left( {\frac{{dz}}{{dW}}} \right) = \ln {{v}^{{ - 1}}}{\kern 1pt} + i\theta $

где $\theta $ – угол наклона к горизонту вектора скорости. Тогда задача (1.1), (1.3) сводится к определению вида двух функций: функции $W(\zeta )$ и какой-либо из функций $\chi (\zeta )$, $\omega (\zeta )$ [12]. При этом функция $W(\zeta )$ легко определяется в замкнутом виде, и основная проблема состоит в определении функции $\chi (\zeta )$, либо $\omega (\zeta )$.

2. РЕШЕНИЕ ЖУКОВСКОГО

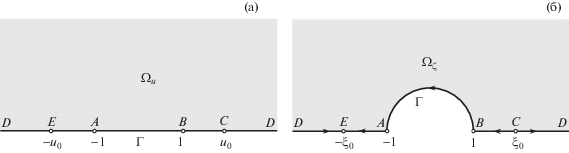
В качестве вспомогательной плоскости Н.Е. Жуковский выбрал верхнюю полуплоскость [2, 12], обозначим ее через $u$ (рис. 2а). Тогда функция $W(u)$ имеет вид

(2.1)

$W(u) = \frac{1}{{2\pi }}\ln \left( {\frac{{u - {{u}_{0}}}}{{u + {{u}_{0}}}}} \right)$

Рис. 2.

Вид вспомогательных плоскостей $u$ (а) и $\zeta $ (б).

В плоскости u ей отвечает течение от источника мощности 1 в точке C: $u = {{u}_{0}}$ к стоку той же мощности в точке $E$: $u = - {{u}_{0}}$, где ${{u}_{0}} > 1$ – неопределенный параметр.

Н.Е. Жуковский строил функцию $\omega (u)$ в виде суммы двух функций, $\omega (u) = {{\omega }_{{re}}}(u) + i{{\omega }_{{im}}}(u)$, обладающими на границе $\Gamma $ наперед заданными свойствами

(2.2)

$\Gamma :\quad {{\omega }_{{re}}}(u) = \ln {{v}^{{ - 1}}},\quad {{\omega }_{{im}}}(u) = \theta $

Подставим выражения (2.2) в граничное условие (1.3), умножим на ${{dW} \mathord{\left/ {\vphantom {{dW} {du}}} \right. \kern-0em} {du}}$ и проинтегрируем его вдоль границы $\Gamma $. В результате получим выражение [2, 12]

(2.3)

$\Gamma {\text{:}}\quad {{\omega }_{{im}}}(u) = \int {\left( {\alpha {{e}^{{{{\omega }_{{re}}}(u)}}} + \beta {{e}^{{ - {\kern 1pt} {{\omega }_{{re}}}(u)}}}} \right)\frac{{dW}}{{du}}du} $

Задаваясь подходящим видом функции ${{\omega }_{{re}}}(u)$, из формулы (2.3) при учете (2.1) можно найти соответствующий вид функции ${{\omega }_{{im}}}(u)$, а значит и всей функции $\omega (u)$. При этом необходимо добиться того, чтобы сохранялось условие непроницаемости на прямолинейных границах области $\partial \Omega {{\backslash }}\Gamma $, а единственными сингулярностями отображения $W \to z$ в замыкании области $\bar {\Omega }$ оставались бы точки A и B в соответствии с качественными оценками

(2.4)

$z \sim {{z}_{A}}{\text{:}}\quad \frac{{dW}}{{dz}} = O(z - {{z}_{A}});\quad z \sim {{z}_{B}}{\text{:}}\quad \frac{{dW}}{{dz}} = O(z - {{z}_{B}})$

Н.Е. Жуковский приводит один подходящий вид функции ${{\omega }_{{re}}}(u)$ [2, 12]

(2.5)

${{\omega }_{{re}}}(u) = \ln \left( {\frac{{{{\gamma }_{0}}}}{{\sqrt {1 - {{u}^{2}}} }}} \right)$

где параметр ${{\gamma }_{0}}$ – вещественный и положительный. Здесь у многозначной функции $\sqrt {} $ выбирается ветвь, которая на участке $\Gamma = AB$ совпадает корнем квадратным, а у многозначной функции $\ln $ – ветвь, которая на этом участке чисто вещественна.

Параметризованное решение содержит четыре вещественных параметра: $\alpha $, $\beta $, ${{u}_{0}}$ и ${{\gamma }_{0}}$. Подставив формулы (2.1), (2.5) в выражение (2.3) и наложив два дополнительных условия на параметры решения [2, 12]

(2.6)

$1 + \frac{{\alpha \gamma _{0}^{2}}}{\beta } = u_{0}^{2},\quad \frac{{{{u}_{0}}\beta }}{{{{\gamma }_{0}}}} = \pi $

можно определить оставшуюся часть функции $\omega (u)$ – функцию ${{\omega }_{{im}}}(u)$

${{\omega }_{{im}}}(u) = - i\frac{{{{u}_{0}}\beta }}{{\pi {{\gamma }_{0}}}}\ln \left( {\sqrt {1 - {{u}^{2}}} - iu} \right)$

Соответственно можно найти функцию $\omega (u)$ и производную ${{dz} \mathord{\left/ {\vphantom {{dz} {dW}}} \right. \kern-0em} {dW}}$

(2.7)

$\frac{{dz}}{{dW}} = {{\gamma }_{0}}\left( {1 - i\frac{u}{{\sqrt {1 - {{u}^{2}}} }}} \right)$

Подставляя это выражение в условие нормировки, можно найти параметр ${{\gamma }_{0}}$

(2.8)

${{\gamma }_{0}} = \sqrt {u_{0}^{2} - 1} {{\left( {{{u}_{0}} + \sqrt {u_{0}^{2} - 1} } \right)}^{{ - 1}}}$

Далее, используя формулы (2.1), (2.7), можно найти производную ${{dz} \mathord{\left/ {\vphantom {{dz} {du}}} \right. \kern-0em} {du}}$, а после ее интегрирования и саму функцию $z(u)$ [2, 12]

(2.9)

$z(u) = \frac{{\sqrt {u_{0}^{2} - 1} }}{{\left( {{{u}_{0}} + \sqrt {u_{0}^{2} - 1} } \right)}}\left[ {\frac{1}{{2\pi }}\ln \left( {\frac{{u - {{u}_{0}}}}{{u + {{u}_{0}}}}} \right) - i\frac{{{{u}_{0}}}}{{\pi \sqrt {u_{0}^{2} - 1} }}\arctan \sqrt {\frac{{1 - {{u}^{2}}}}{{u_{0}^{2} - 1}}} } \right]$

Кроме того, из уравнений (2.6) при учете формулы (2.8) можно найти выражения параметров $\alpha $ и $\beta $ через основной параметр u₀ решения

(2.10)

$\alpha = \frac{{\pi \sqrt {u_{0}^{2} - 1} }}{{{{u}_{0}}\left( {{{u}_{0}} - \sqrt {u_{0}^{2} - 1} } \right)}},\quad \beta = \frac{{\pi \sqrt {u_{0}^{2} - 1} }}{{{{u}_{0}}\left( {{{u}_{0}} + \sqrt {u_{0}^{2} - 1} } \right)}}$

Выражения (2.9), (2.10) представляют собой полученное Н.Е. Жуковским частное однопараметрическое решение задачи о пузыре в канале. Фактически он предложил метод конструирования точных решений задач со свободной границей для потенциальных течений капиллярной жидкости, который был, в частности, использован в работе [9] для построения новых точных решений некоторых задач. Однако для задачи обтекания пузыря в канале новых решений получено не было, что можно объяснить наличием у метода Жуковского двух существенных недостатков. Первый состоит в том, что довольно сложно, глядя на вид (2.5) функции ${{\omega }_{{re}}}(u)$, представить себе структуру ее возможного обобщения. Второй недостаток заключается в необходимости выполнения трудоемкой процедуры интегрирования функции сложного вида в соотношении (2.3).

Соответственно прежде всего целесообразно модифицировать метод Жуковского, устранив эти недостатки, но сохранив основную идею: ограничиться параметризованными решениями, в которых граничное условие (1.3) порождает явную связь между функциями ${{\omega }_{{re}}}(u)$, ${{\omega }_{{im}}}(u)$.

3. МОДИФИКАЦИЯ МЕТОДА ЖУКОВСКОГО

В качестве вспомогательной плоскости $\zeta = \xi + i{\kern 1pt} \eta $ вместо полуплоскости $u$ выберем верхнюю половину внешности единичного круга ${{\Omega }_{\zeta }}$ (см. рис. 2б). Тогда функция $W(\zeta )$ будет иметь вид

(3.1)

$W(\zeta ) = \frac{1}{{2\pi }}\ln \frac{{\left( {\zeta - {{\xi }_{0}}} \right)(\zeta - \xi _{0}^{{{\kern 1pt} - 1}})}}{{\left( {\zeta + {{\xi }_{0}}} \right)(\zeta + \xi _{0}^{{{\kern 1pt} - 1}})}}$

где ${{\xi }_{0}} > 1$ – неопределенный вещественный параметр.

Конформные отображения ${{\Omega }_{u}} \to {{\Omega }_{\zeta }}$, ${{\Omega }_{\zeta }} \to {{\Omega }_{u}}$ реализуют функции [14]

(3.2)

$u = \frac{1}{2}(\zeta + {{\zeta }^{{ - 1}}}),\quad \zeta = u + i\sqrt {1 - {{u}^{2}}} $

где у многозначной функции $\sqrt {} $ выделяется ветвь, которая совпадает с корнем арифметическим на участке границы $\Gamma = AB$.

Используя первую формулу (3.2) и выражение (2.7), можно сразу выписать решение Жуковского в терминах функции $\chi (\zeta ) = {{dz} \mathord{\left/ {\vphantom {{dz} {dW}}} \right. \kern-0em} {dW}}$

(3.3)

$\chi (\zeta ) = \frac{{2{{\gamma }_{0}}{{\zeta }^{2}}}}{{({{\zeta }^{2}} - 1)}}$

Анализ полученного решения показывает, что функция $\chi (\zeta )$ рациональна, имеет два простых полюса в точках $A$ и $B$ ($\zeta = \pm 1$) и нуль второго порядка в точке ζ = 0, что согласуется с оценками (2.4). Далее, на обеих осях $\xi $ и $\eta $ функция $\chi (\zeta )$ вещественна, что согласуется с картиной течения (см. рис. 1а). Действительно, комплексно сопряженная скорость течения ${{dW} \mathord{\left/ {\vphantom {{dW} {dz}}} \right. \kern-0em} {dz}}$ должна быть вещественна на стенках канала, на его линии симметрии, а также на вертикальной оси, проходящей через геометрический центр пузыря, поскольку для идеальной жидкости пузырь необходимо должен обладать двойной симметрией относительно и горизонтальной, и вертикальной оси, проходящей через его геометрический центр.

Отмеченные свойства функции (3.3) решения Жуковского позволяют сразу указать структуру его возможного обобщения – это функция $\chi (\zeta )$ из класса рациональных функций следующего вида

(3.4)

$\chi (\zeta ) = \gamma \frac{{{{\zeta }^{{2 + 2J - 2K}}}}}{{({{\zeta }^{2}} - 1)}}\left[ {\prod\limits_{k = 1}^K {({{\zeta }^{2}} - {{a}_{k}})} } \right]{{\left[ {\prod\limits_{j = 1}^J {({{\zeta }^{2}} - {{b}_{j}})} } \right]}^{{ - 1}}},\quad K \geqslant 0,\quad J \geqslant 0$

где параметры $\gamma $, ${{a}_{k}}$ ($k = 1,...,K$) и ${{b}_{j}}$ ($j = 1,...,J$) вещественны, причем $\gamma > 0$, $\zeta = \pm \sqrt {{{a}_{k}}} $ – это нули, а $\zeta = \pm \sqrt {{{b}_{j}}} $ – полюса рациональной функции $\chi (\zeta )$ (нули и полюса могут быть кратными, тогда они просто повторяются). Требование конформности отображения $z \to W$ означает, что эти дополнительные в сравнении с видом (3.3) нули и полюса функции $\chi (\zeta )$ должны лежать внутри единичного круга

(3.5)

$\left| {{{a}_{k}}} \right| < 1,\quad k = 1,...,K;\quad \left| {{{b}_{j}}} \right| < 1,\quad j = 1,...,J$

Следует отметить, что именно с классом рациональных функций связаны основные успехи в построении точных решений нестационарной задачи о стягивании контура нефтеносности [15], а также родственной ей задачи об эволюции межфазной границы в течениях Хеле-Шоу [16–18]. Соответственно некоторые эффективные приемы, использованные в этих работах, можно применить и здесь. Одним из таких приемов является замена в граничных соотношениях на $\Gamma $ операции комплексного сопряжения на оператор $\mathcal{P}$ [15], определенный следующим образом

(3.6)

$\Gamma {\text{:}}\quad \overline {f(\zeta )} = \mathcal{P}\left[ {f(\zeta )} \right],\quad \mathcal{P}\left[ {f(\zeta )} \right] = {{\left. {f{\kern 1pt} *(\zeta )} \right|}_{{\zeta \to {{\zeta }^{{ - 1}}}}}}$

где знак черты означает операцию комплексного сопряжения, а верхний индекс звездочка – операцию сопряжения только по параметрам (но не переменным) функции.

Выразим основную идею метода Жуковского в терминах функции $\chi (\zeta )$, а именно: представим эту функцию в виде произведения двух функций ${{\chi }_{{\bmod }}}(\zeta )$, ${{\chi }_{{\arg }}}(\zeta )$

$\chi (\zeta ) = {{\chi }_{{\bmod }}}(\zeta ){{\chi }_{{\arg }}}(\zeta )$

которые на границе $\Gamma $ обладают такими свойствами

(3.7)

$\Gamma {\text{:}}\quad {{\chi }_{{\bmod }}}(\zeta ) = \left| {\chi (\zeta )} \right| \equiv {{v}^{{ - 1}}},\quad {{\chi }_{{\arg }}}(\zeta ) = {{e}^{{{\kern 1pt} i{\kern 1pt} \arg \chi (\zeta )}}} \equiv {{e}^{{{\kern 1pt} i{\kern 1pt} \theta }}}$

Вид этих функций можно найти с помощью оператора $\mathcal{P}$

${{\chi }_{{\bmod }}}(\zeta ) = {{\left\{ {\chi (\zeta )\mathcal{P}{{{\left[ {\chi (\zeta )} \right]}}^{}}} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\quad {{\chi }_{{\arg }}}(\zeta ) = {{\left\{ {\frac{{\chi (\zeta )}}{{\mathcal{P}\left[ {\chi (\zeta )} \right]}}} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$

Подставляя сюда общий вид (3.4) функции $\chi (\zeta )$ и раскрывая действие оператора $\mathcal{P}$ согласно формуле (3.6), получим явные выражения

(3.8)

${{\chi }_{{\bmod }}}(\zeta ) = i\gamma \frac{{{{\zeta }^{{1 + J - K}}}}}{{({{\zeta }^{2}} - 1)}}{{\left[ {\prod\limits_{k = 1}^K {({{\zeta }^{2}} - {{a}_{k}})(1 - {{a}_{k}}{{\zeta }^{2}})} } \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\left[ {\prod\limits_{j = 1}^J {({{\zeta }^{2}} - {{b}_{j}})(1 - {{b}_{j}}{{\zeta }^{2}})} } \right]}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$

(3.9)

${{\chi }_{{\arg }}}(\zeta ) = - i{{\zeta }^{{1 + J - K}}}{{\left[ {\prod\limits_{k = 1}^K {({{\zeta }^{2}} - {{a}_{k}})} \prod\limits_{j = 1}^J {(1 - {{b}_{j}}{{\zeta }^{2}})} } \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\left[ {\prod\limits_{j = 1}^J {({{\zeta }^{2}} - {{b}_{j}})} \prod\limits_{k = 1}^K {(1 - {{a}_{k}}{{\zeta }^{2}})} } \right]}^{{{{{\kern 1pt} - 1} \mathord{\left/ {\vphantom {{{\kern 1pt} - 1} 2}} \right. \kern-0em} 2}}}}$

Как видим, мультипликативные части ${{\chi }_{{\bmod }}}(\zeta )$, ${{\chi }_{{\arg }}}(\zeta )$ функции $\chi (\zeta )$, принадлежащей классу рациональных функций (3.4), в общем случае уже не будут рациональными функциями. Это приводит к существенным проблемам при конструировании точных решений [15, 16]. Поэтому из общего класса рациональных функций (3.4) целесообразно выделить более узкий класс функций $\chi (\zeta )$

(3.10)

$\chi (\zeta ) = \gamma \frac{{{{\zeta }^{{2 + 4J - 4K}}}}}{{({{\zeta }^{2}} - 1)}}\left[ {\prod\limits_{k = 1}^K {{{{({{\zeta }^{2}} - {{a}_{k}})}}^{2}}} } \right]{{\left[ {\prod\limits_{j = 1}^J {{{{({{\zeta }^{2}} - {{b}_{j}})}}^{2}}} } \right]}^{{{\kern 1pt} - 1}}}$

мультипликативные части которых ${{\chi }_{{\bmod }}}(\zeta )$, ${{\chi }_{{\arg }}}(\zeta )$ также будут рациональными функциями. Действительно, из формул (3.8), (3.9) при учете (3.4), (3.10) следует

(3.11)

${{\chi }_{{\bmod }}}(\zeta ) = i\gamma \frac{{{{\zeta }^{{1 + 2J - 2K}}}}}{{({{\zeta }^{2}} - 1)}}\left[ {\prod\limits_{k = 1}^K {({{\zeta }^{2}} - {{a}_{k}})(1 - {{a}_{k}}{{\zeta }^{2}})} } \right]{{\left[ {\prod\limits_{j = 1}^J {({{\zeta }^{2}} - {{b}_{j}})(1 - {{b}_{j}}{{\zeta }^{2}})} } \right]}^{{{\kern 1pt} - 1}}}$

(3.12)

${{\chi }_{{\arg }}}(\zeta ) = - i{{\zeta }^{{1 + 2J - 2K}}}\left[ {\prod\limits_{k = 1}^K {({{\zeta }^{2}} - {{a}_{k}})} \prod\limits_{j = 1}^J {(1 - {{b}_{j}}{{\zeta }^{2}})} } \right]{{\left[ {\prod\limits_{j = 1}^J {({{\zeta }^{2}} - {{b}_{j}})} \prod\limits_{k = 1}^K {(1 - {{a}_{k}}{{\zeta }^{2}})} } \right]}^{{{\kern 1pt} - 1}}}$

Далее, аналогично оригинальному методу Жуковского из граничного условия (1.3) можно вывести соотношение, связывающее мультипликативные части ${{\chi }_{{\bmod }}}(\zeta )$, ${{\chi }_{{\arg }}}(\zeta )$ функции $\chi (\zeta )$. Действительно, перепишем условие (1.3) в виде

$\Gamma {\text{:}}\quad d\theta = (\alpha {{v}^{{ - 1}}} + \beta v)\frac{{dW}}{{d\zeta }}d\zeta $

и умножим левую и правую его части на $i{{e}^{{{\kern 1pt} i{\kern 1pt} \theta }}}$. Имеем

(3.13)

$\Gamma {\text{:}}\quad i{{e}^{{i{\kern 1pt} \theta }}}d\theta = i(\alpha {{v}^{{ - 1}}}{{e}^{{i{\kern 1pt} \theta }}} + \beta v{{e}^{{{\kern 1pt} i{\kern 1pt} \theta }}})\frac{{dW}}{{d\zeta }}d\zeta $

Используя определение (3.7) функции ${{\chi }_{{\arg }}}(\zeta )$, левую часть соотношения (3.13) можно преобразовать к такому виду

(3.14)

$\Gamma {\text{:}}\quad i{{e}^{{i{\kern 1pt} \theta }}}d\theta = \left( {\frac{{d{{e}^{{i{\kern 1pt} \theta }}}}}{{d\zeta }}} \right)d\zeta = \frac{{d{{\chi }_{{\arg }}}}}{{d\zeta }}d\zeta $

Правую часть соотношения (3.13) также можно преобразовать, используя вытекающие из формул (1.4), (3.6) выражения

${{\Gamma :}}\quad {{v}^{{ - 1}}}{{e}^{{i{\kern 1pt} \theta }}} = \chi (\zeta ),\quad v{{e}^{{i{\kern 1pt} \theta }}} = \frac{1}{{\mathcal{P}\left[ {\chi (\zeta )} \right]}}$

Тогда правая часть соотношения (3.13) примет вид

(3.15)

$\Gamma {\text{:}}\quad i(\alpha {{v}^{{ - 1}}}{{e}^{{{\kern 1pt} i{\kern 1pt} \theta }}} + \beta v{{e}^{{{\kern 1pt} i{\kern 1pt} \theta }}})\frac{{dW}}{{d\zeta }}d\zeta = i\left\{ {\alpha \chi (\zeta ) + \frac{\beta }{{\mathcal{P}\left[ {\chi (\zeta )} \right]}}} \right\}\frac{{dW}}{{d\zeta }}d\zeta $

Подставляя выражения (3.14), (3.15) в соотношение (3.13), получим

(3.16)

$\Gamma {\text{:}}\quad \frac{{d{{\chi }_{{\arg }}}}}{{d\zeta }} = i\left\{ {\alpha \chi (\zeta ) + \frac{\beta }{{\mathcal{P}\left[ {\chi (\zeta )} \right]}}} \right\}\frac{{dW}}{{d\zeta }}$

Это основное соотношение, которое надо выполнить, чтобы функция $\chi (\zeta )$ удовлетворяла граничному условию (1.3). Анализ соотношения (3.16) показывает, что его левая и правая части представляют собой рациональные функции и его выполнение принципиально возможно. Параметры решения $\alpha $, $\beta $, $\gamma $, ${{a}_{k}}$ и ${{b}_{j}}$ выступают некоторыми степенями свободы. Однако общий вид (3.10) функции $\chi (\zeta )$ для анализа слишком сложен, и следует ограничиться более простым видом функции.

4. ОБОБЩЕНИЕ РЕШЕНИЯ ЖУКОВСКОГО

Выберем функцию $\chi (\zeta )$ из класса функций (3.10), положив J = 0, K = 1

(4.1)

$\chi (\zeta ) = \gamma \frac{{{{{({{\zeta }^{2}} - {{a}_{1}})}}^{2}}}}{{({{\zeta }^{2}} - 1){{\zeta }^{2}}}}$

где вещественный параметр ${{a}_{1}}$, согласно (3.5), должен удовлетворять требованию

(4.2)

$ - 1 < {{a}_{1}}\; < 1$

Из формул (3.11), (3.12) найдем вид функций ${{\chi }_{{\bmod }}}(\zeta )$, ${{\chi }_{{\arg }}}(\zeta )$ для функции (4.1)

(4.3)

${{\chi }_{{\bmod }}}(\zeta ) = - i\gamma \frac{{({{\zeta }^{2}} - {{a}_{1}})({{a}_{1}}{{\zeta }^{2}} - 1)}}{{\zeta ({{\zeta }^{2}} - 1)}};\quad {{\chi }_{{\arg }}}(\zeta ) = \frac{i}{\zeta }\frac{{({{\zeta }^{2}} - {{a}_{1}})}}{{({{a}_{1}}{{\zeta }^{2}} - 1)}}$

Применяя оператор $\mathcal{P}$ к функции $\chi (\zeta )$, получим

(4.4)

$\mathcal{P}\left[ {\chi (\zeta )} \right] = - \gamma {{({{a}_{1}}{{\zeta }^{2}} - 1)}^{2}}{{({{\zeta }^{2}} - 1)}^{{ - 1}}}$

Продифференцировав второе выражение (4.3), найдем производную ${{d{{\chi }_{{\arg }}}} \mathord{\left/ {\vphantom {{d{{\chi }_{{\arg }}}} {d\zeta }}} \right. \kern-0em} {d\zeta }}$

(4.5)

$\frac{{d{{\chi }_{{\arg }}}}}{{d\zeta }} = i\frac{{(3a_{1}^{2} - 1){{\zeta }^{2}} - {{a}_{1}}({{\zeta }^{4}} + 1)}}{{{{\zeta }^{2}}{{{({{a}_{1}}{{\zeta }^{2}} - 1)}}^{2}}}}$

Продифференцировав выражение (3.1), найдем производную ${{dW} \mathord{\left/ {\vphantom {{dW} {d\zeta }}} \right. \kern-0em} {d\zeta }}$

(4.6)

$\frac{{dW}}{{d\zeta }} = \frac{{({{\xi }_{0}} + \xi _{0}^{{ - 1}})({{\zeta }^{2}} - 1)}}{{\pi ({{\zeta }^{2}} - \xi _{0}^{2})({{\zeta }^{2}} - \xi _{0}^{{{\kern 1pt} - 2}})}}$

Подставив формулы (4.4)–(4.6) в основное соотношение (3.16), получим

(4.7)

$\Gamma :\quad \frac{{(3a_{1}^{2} - 1){{\zeta }^{2}} - {{a}_{1}}({{\zeta }^{4}} + 1)}}{{{{\zeta }^{2}}{{{({{a}_{1}}{{\zeta }^{2}} - 1)}}^{2}}}} = \left[ {\frac{{\alpha \gamma {{{({{\zeta }^{2}} - {{a}_{1}})}}^{2}}}}{{({{\zeta }^{2}} - 1){{\zeta }^{2}}}} - \frac{{\beta ({{\zeta }^{2}} - 1)}}{{\gamma {{{({{a}_{1}}{{\zeta }^{2}} - 1)}}^{2}}}}} \right]\frac{{({{\xi }_{0}} + \xi _{0}^{{{\kern 1pt} - 1}})({{\zeta }^{2}} - 1)}}{{\pi ({{\zeta }^{2}} - \xi _{0}^{2})({{\zeta }^{2}} - \xi _{0}^{{ - 2}})}}$

Если ввести обозначения $A$ и $B$ для следующих комбинаций параметров

(4.8)

$A = \frac{{\alpha {\kern 1pt} \gamma }}{\pi }({{\xi }_{0}} + \xi _{0}^{{ - 1}}),\quad B = \frac{\beta }{{\pi \gamma }}({{\xi }_{0}} + \xi _{0}^{{ - 1}}) > 0$

то соотношение (4.7) можно привести к виду

$\Gamma {\text{:}}\quad \frac{{[(3a_{1}^{2} - 1){{\zeta }^{2}} - {{a}_{1}}({{\zeta }^{4}} + 1)]({{\zeta }^{2}} - \xi _{0}^{2})({{\zeta }^{2}} - \xi _{0}^{{ - 2}})}}{{{{\zeta }^{2}}{{{({{a}_{1}}{{\zeta }^{2}} - 1)}}^{2}}}} = \frac{{A{{{({{\zeta }^{2}} - {{a}_{1}})}}^{2}}}}{{{{\zeta }^{2}}}} - \frac{{B{{{({{\zeta }^{2}} - 1)}}^{2}}}}{{{{{({{a}_{1}}{{\zeta }^{2}} - 1)}}^{2}}}}$

В этом соотношении левую и правую части можно привести к одному и тому же знаменателю и сократить его. В результате получим соотношение

(4.9)

$\begin{gathered} \Gamma {\text{:}}\quad - {{a}_{1}}{{({{\zeta }^{4}} + 1)}^{2}} + {{\zeta }^{2}}({{\zeta }^{4}} + 1)[(3a_{1}^{2} - 1) + {{a}_{1}}(\xi _{0}^{2} + \xi _{0}^{{{\kern 1pt} - 2}})] - {{\zeta }^{4}}(3a_{1}^{2} - 1)(\xi _{0}^{2} + \xi _{0}^{{{\kern 1pt} - 2}}) = \\ \, = Aa_{1}^{2}{{({{\zeta }^{4}} + 1)}^{2}} - {{\zeta }^{2}}({{\zeta }^{4}} + 1)[2A{{a}_{1}}(a_{1}^{2} + 1) + B] + {{\zeta }^{4}}[A{{(a_{1}^{2} + 1)}^{2}} + 2B] \\ \end{gathered} $

Проанализируем его. Очевидно, что оно будет выполнено, если параметры решения будут удовлетворять всего лишь трем условиям:

(4.10)

$Aa_{1}^{2} = - {{a}_{1}}$

(4.11)

$(3a_{1}^{2} - 1) + {{a}_{1}}(\xi _{0}^{2} + \xi _{0}^{{{\kern 1pt} - 2}}) = - 2A{{a}_{1}}(a_{1}^{2} + 1) - B$

(4.12)

$(3a_{1}^{2} - 1)(\xi _{0}^{2} + \xi _{0}^{{{\kern 1pt} - 2}}) = - A{{(a_{1}^{2} + 1)}^{2}} - 2B$

(где в условии (4.10) не следует сокращать ${{a}_{1}}$, поскольку тем самым будет отброшено возможное его решение ${{a}_{1}} = 0$). В то же время само соотношение (4.9) зависит от четырех параметров: A, B, ${{a}_{1}}$, ${{\xi }_{0}}$. Таким образом, это соотношение может быть выполнено для целого интервала значений основного параметра, скажем, ${{a}_{1}}$, при том, что остальные параметры A, B, ${{\xi }_{0}}$ будут выражены через ${{a}_{1}}$. Последний меняется в интервале (4.2), но здесь приходится отдельно рассмотреть два случая: ${{a}_{1}} \ne 0$ и ${{a}_{1}} = 0$.

Случай ${{a}_{1}}{\kern 1pt} \ne 0$. После введения обозначения

(4.13)

$F({{a}_{1}}) = \frac{{6 - a_{1}^{{ - 1}}{{{(1 + a_{1}^{2})}}^{2}} - 2a_{1}^{2}}}{{1 - 3a_{1}^{2} + 2{{a}_{1}}}}$

из системы уравнений (4.10)–(4.12) можно найти явные выражения параметров $A$, $B$ и ${{\xi }_{0}}$ через ${{a}_{1}}$ (см. Приложение А)

(4.14)

$A = - a_{1}^{{ - 1}},\quad B = 3 - a_{1}^{2} - {{a}_{1}}F({{a}_{1}}),\quad {{\xi }_{0}} = \sqrt {0.5\left[ {F({{a}_{1}}) + \sqrt {{{F}^{2}}({{a}_{1}}) - 4} } \right]} $

Однако только в части интервала $ - 1 < {{a}_{1}}\; < 1$, а именно – в интервале

(4.15)

$ - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3} < {{a}_{1}} < 0$

решение (4.14) физически содержательно: параметр ${{\xi }_{0}}$ – вещественен и $B > 0$.

Величину $\gamma $ найдем подстановкой выражения (4.1) в условие нормировки

(4.16)

$\gamma = (\xi _{0}^{2} - 1){{(\xi _{0}^{2} - {{a}_{1}})}^{{ - 2}}}\xi _{0}^{2}$

Наконец из формул (4.8) найдем выражения для параметров $\alpha $ и $\beta $

(4.17)

$\alpha = \frac{{\pi A}}{{\gamma ({{\xi }_{0}} + \xi _{0}^{{ - 1}})}},\quad \beta = \frac{{\pi B\gamma }}{{({{\xi }_{0}} + \xi _{0}^{{ - 1}})}}$

Случай ${{a}_{1}} = 0$. Система уравнений (4.10)–(4.12) вырождается, поскольку уравнение (4.10) выполняется тождественно. Оставшиеся уравнения и условие нормировки дают

(4.18)

$A = {{({{\xi }_{0}} - \xi _{0}^{{{\kern 1pt} - 1}})}^{2}},\quad B = 1,\quad \gamma = 1 - \xi _{0}^{{{\kern 1pt} - 2}}$

Далее из формул (4.8) получаются те же самые выражения (4.17) для параметров $\alpha $ и $\beta $. Подставляя в них формулы (4.18), получим

(4.19)

$\alpha = \pi {{\xi }_{0}}\left( {\frac{{\xi _{0}^{2} - 1}}{{\xi _{0}^{2} + 1}}} \right),\quad \beta = \frac{\pi }{{{{\xi }_{0}}}}\left( {\frac{{\xi _{0}^{2} - 1}}{{\xi _{0}^{2} + 1}}} \right)$

Очевидно, что это однопараметрическое решение с основным параметром ${{\xi }_{0}} > 1$ – другая форма представления решения Жуковского, см. раздел 2. Параметры ${{\xi }_{0}}$ и ${{u}_{0}}$ связаны выражением ${{\xi }_{0}} = {{u}_{0}} + {{(u_{0}^{2} - 1)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, вытекающим из связи (3.2) переменных $\zeta $ и $u$, формулы (4.19) перейдут в формулы (2.10), а параметры γ и ${{\gamma }_{0}}$ будут связаны выражением $\gamma = 2{{\gamma }_{0}}$.

5. ОПРЕДЕЛЕНИЕ КОНФИГУРАЦИИ ПУЗЫРЯ И ЕГО ПЛОЩАДИ

Производную ${{dz} \mathord{\left/ {\vphantom {{dz} {d\zeta }}} \right. \kern-0em} {d\zeta }}$ можно получить как произведение функций $\chi (\zeta )$ и ${{dW} \mathord{\left/ {\vphantom {{dW} {d\zeta }}} \right. \kern-0em} {d\zeta }}$ известного вида (4.1) и (4.6)

(5.1)

$\frac{{dz}}{{d\zeta }} = \frac{{\gamma ({{\xi }_{0}} + \xi _{0}^{{ - 1}}){{{({{\zeta }^{2}} - {{a}_{1}})}}^{2}}}}{{\pi ({{\zeta }^{2}} - \xi _{0}^{2})({{\zeta }^{2}} - \xi _{0}^{{{\kern 1pt} - 2}}){{\zeta }^{2}}}}$

Интегрируя выражение (5.1), найдем и функцию $z(\zeta )$

(5.2)

$z(\zeta ) = - \frac{{\gamma a_{1}^{2}({{\xi }_{0}} + \xi _{0}^{{{\kern 1pt} - 1}})}}{{\pi \zeta }} + {{C}_{1}}\ln \left( {\frac{{{{\xi }_{0}} - \zeta }}{{{{\xi }_{0}} + \zeta }}} \right) - {{D}_{1}}\ln \left( {\frac{{{{\xi }_{0}} - {{\zeta }^{{ - 1}}}}}{{{{\xi }_{0}} + {{\zeta }^{{ - 1}}}}}} \right)$

с точностью до несущественной аддитивной константы. Здесь для многозначных функций логарифмов в выражении (5.2) выбираются те их однозначные ветви, которые вещественны на границе $BC$, а через ${{C}_{1}}$ и ${{D}_{1}}$ обозначены константы следующего вида

(5.3)

${{C}_{1}} = \frac{{\gamma (a_{1}^{2} - 2{{a}_{1}}\xi _{0}^{2} + \xi _{0}^{4})}}{{2\pi \xi _{0}^{2}(\xi _{0}^{2} - 1)}},\quad {{D}_{1}} = \frac{{\gamma (a_{1}^{2}\xi _{0}^{4} - 2{{a}_{1}}\xi _{0}^{2} + 1)}}{{2\pi (\xi _{0}^{2} - 1)}}$

Производная ${{dz} \mathord{\left/ {\vphantom {{dz} {d\zeta }}} \right. \kern-0em} {d\zeta }}$ вида (5.1), очевидно, вещественна при $\zeta $ – вещественном. Это позволяет продолжить область определения функций ${{dz} \mathord{\left/ {\vphantom {{dz} {d\zeta }}} \right. \kern-0em} {d\zeta }}$ и $z(\zeta )$ до внешности единичного круга: ${\text{|}}\zeta {\text{|}} > 1$ [14]. Полагая $\zeta = {{e}^{{{\kern 1pt} i\sigma }}}$, $\sigma = [0,\;2\pi ]$ в выражении (5.2), получим параметрическое уравнение контура пузыря.

Площадь пузыря $S$ можно вычислить как комбинацию контурных интегралов вдоль единичной окружности ${{C}_{\zeta }}$: ${\text{|}}\zeta {\text{|}} = 1$ (см. Приложение В)

(5.4)

$S = \frac{{\gamma ({{\xi }_{0}} + \xi _{0}^{{ - 1}})}}{{2\pi i}}\left[ {\mathop{\int\mkern-20.8mu \circlearrowleft}\limits_{{{C}_{\zeta }}} {\frac{{{{\Phi }^{ - }}(\zeta )d\zeta }}{{({{\zeta }^{2}} - \xi _{0}^{{ - 2}})}}} - \mathop{\int\mkern-20.8mu \circlearrowleft}\limits_{{{C}_{\zeta }}} {\frac{{{{\Phi }^{ + }}(\zeta )d\zeta }}{{({{\zeta }^{2}} - \xi _{0}^{2})}}} } \right]$

где введены вспомогательные функции ${{\Phi }^{ - }}(\zeta )$ и ${{\Phi }^{ + }}(\zeta )$

(5.5)

${{\Phi }^{ - }}(\zeta ) = \frac{{{{C}_{1}}{{{(1 - {{a}_{1}}{{\zeta }^{2}})}}^{2}}}}{{({{\zeta }^{2}} - \xi _{0}^{2})}}\ln \left( {\frac{{{{\xi }_{0}} - \zeta }}{{{{\xi }_{0}} + \zeta }}} \right),\quad {{\Phi }^{ + }}(\zeta ) = \frac{{{{{(1 - {{a}_{1}}{{\zeta }^{2}})}}^{2}}}}{{({{\zeta }^{2}} - \xi _{0}^{{ - 2}})}}\left[ {\frac{{\gamma a_{1}^{2}({{\xi }_{0}} + \xi _{0}^{{{\kern 1pt} - 1}})}}{{\pi \zeta }} + {{D}_{1}}\ln \left( {\frac{{{{\xi }_{0}} - {{\zeta }^{{ - 1}}}}}{{{{\xi }_{0}} + {{\zeta }^{{ - 1}}}}}} \right)} \right]$

Оба контурных интеграла в формуле (5.4) вычисляются с помощью теории вычетов [14]. В результате для площади пузыря $S$ получим точное выражение

(5.6)

$S = \frac{{\gamma ({{\xi }_{0}} + \xi _{0}^{{ - 1}})}}{2}\left[ {{{\xi }_{0}}{{\Phi }^{ - }}(\xi _{0}^{{{\kern 1pt} - 1}}) - {{\xi }_{0}}{{\Phi }^{ - }}( - \xi _{0}^{{ - 1}}) + \frac{{{{\Phi }^{ + }}({{\xi }_{0}})}}{{{{\xi }_{0}}}} - \frac{{{{\Phi }^{ + }}( - {{\xi }_{0}})}}{{{{\xi }_{0}}}} - \frac{{2\gamma a_{1}^{4}({{\xi }_{0}} + \xi _{0}^{{ - 1}})}}{\pi } + \frac{{4a_{1}^{2}{{D}_{1}}}}{{{{\xi }_{0}}}}} \right]$

Отметим, что формулами (5.1)–(5.3) и (5.5), (5.6) можно пользоваться как в случае $ - (1{\text{/}}3) < {{a}_{1}}$ < < 0, так и в случае ${{a}_{1}} = 0$.

6. АНАЛИЗ ПОЛУЧЕННОГО РЕШЕНИЯ

Выражение (5.2) при учете формул (5.3), (5.6) представляет собой частное решение краевой задачи (1.1), (1.3). По сути, оно охватывает два отдельных частных решения: первое – невырожденное решение с основным параметром ${{a}_{1}}$ надо дополнить формулами (4.13)–(4.17); второе – вырожденное решение (решение Жуковского) с основным параметром ${{\xi }_{0}} > 1$ надо дополнить формулами (4.18), (4.19).

На рис. 3а, б представлены зависимости определяющих параметров $\alpha $, $\beta $ и площади пузыря S от основного параметра a₁ для невырожденного решения и соответственно от основного параметра ${{\xi }_{0}}$ для вырожденного решения. Отметим, что параметр $\beta $ для невырожденного решения меняется в интервале от 0 до бесконечности, в то время, как для вырожденного решения – только в интервале $0 < \beta \leqslant 0.{\text{9434}}$, где максимум $\beta $ достигается при ${{\xi }_{0}}{\kern 1pt} = 2.0568$.

Рис. 3.

Зависимости параметров α (пунктирная линия), $\beta $ (штриховая линия) и площади пузыря S (сплошная линия) от основного параметра ${{a}_{1}}$ для невырожденного (а) и соответственно от основного параметра ${{\xi }_{0}}$ для вырожденного решения (б).

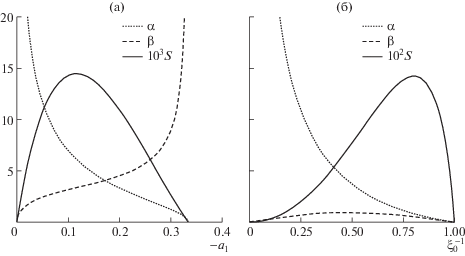
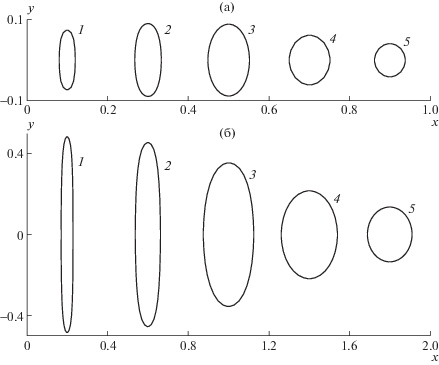
Для обоих решений площадь пузыря $S$ ведет себя качественно одинаково на всем интервале изменения основного параметра: на концах интервала $S = 0$, а в средней его части имеет выраженный максимум $S = {{S}_{{\max }}}$, для невырожденного решения ${{S}_{{\max }}} = 0.0145$, для вырожденного решения ${{S}_{{\max }}} = 0.1425$. Более подробный анализ конфигураций пузыря предлагается провести для пяти значений основного параметра в обоих решениях: одного значения, отвечающего $S = {{S}_{{\max }}}$, двум, отвечающим $S = {{2{{S}_{{\max }}}} \mathord{\left/ {\vphantom {{2{{S}_{{\max }}}} 3}} \right. \kern-0em} 3}$, и еще двум, отвечающим $S = {{{{S}_{{\max }}}} \mathord{\left/ {\vphantom {{{{S}_{{\max }}}} 3}} \right. \kern-0em} 3}$, см. табл. 1. На рис. 4 представлены конфигурации пузыря, отвечающие невырожденному и вырожденному решению для приведенных в таблице пяти значений соответствующего основного параметра.

Таблица 1

n	Невырожденное решение				Вырожденное решение
n	Основной параметр ${{a}_{1}}$	$\alpha $	$\beta $	S	Основной параметр ${{\xi }_{0}}$	$\alpha $	$\beta $	S
1	–0.2746	1.7326	6.7503	0.0048	1.02	0.0634	0.0609	0.0475
2	–0.2172	2.8996	4.8212	0.0096	1.0611	0.1976	0.1755	0.095
3	–0.1158	6.0987	3.3381	0.0145	1.2423	0.8339	0.5403	0.1425
4	–0.0423	13.041	2.2603	0.0096	1.7649	2.8498	0.9149	0.095
5	–0.0174	22.285	1.5553	0.0048	2.5685	5.9449	0.9011	0.0475

Рис. 4.

Конфигурации пузыря 1–5, отвечающие невырожденному (а) и вырожденному решению (б) для конкретных значений основного параметра, приведенных в табл. 1.

Отметим, что решение задачи (1.1), (1.3) для конкретной пары определяющих параметров $(\alpha ,\;\beta )$ отображается точкой в плоскости α, β. Общее решение задачи должно заполнять эту плоскость целиком, а найденное здесь частное решение прочертит в ней две непересекающиеся кривые, представленные на рис. 5а сплошной (невырожденное решение) и пунктирной (вырожденное решение) линией.

Рис. 5.

(а) Изолинии невырожденного (сплошная линия) и вырожденного (пунктирная линия) решений в плоскости определяющих параметров $\alpha ,\beta $; (б) зависимости от $\alpha $ поперечного диаметра пузыря $\Delta y$ (кривые 1) и отношения продольного диаметра к поперечному ${{\Delta x} \mathord{\left/ {\vphantom {{\Delta x} {\Delta y}}} \right. \kern-0em} {\Delta y}}$ (кривые 2) для невырожденного (сплошные линии) и вырожденного (пунктирные линии) решения.

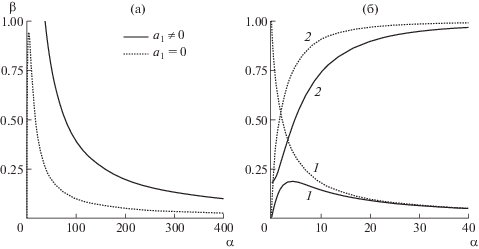
Интересно сравнить, как меняются продольный $\Delta {\kern 1pt} x$ и поперечный $\Delta {\kern 1pt} y$ диаметры пузыря в этих двух решениях. Заметим, что основной параметр в решениях разный, а параметр $\alpha $ изменяется монотонно в интервале от 0 до бесконечности. Поэтому для сравнения характеристик решений целесообразно в качестве оси абсциссы выбрать именно $\alpha $. На рис. 5б представлены зависимости от α поперечного диаметра пузыря $\Delta {\kern 1pt} y$ (кривые 1) и отношения диаметров ${{\Delta {\kern 1pt} x} \mathord{\left/ {\vphantom {{\Delta {\kern 1pt} x} {\Delta {\kern 1pt} y}}} \right. \kern-0em} {\Delta {\kern 1pt} y}}$ (кривые 2) для невырожденного (сплошные линии) и вырожденного (пунктирные линии) решения.

Предел $\alpha \to \infty $ в обоих решениях одинаков – это практически круглый пузырь бесконечно малой площади. В то же время в пределе $\alpha \to 0$ решения существенно различаются. У вырожденного решения это – практически плоский пузырь бесконечно малой площади, который почти перекрывает канал, при этом в верхней и нижней точке контура пузыря достигаются бесконечные величины скорости течения и кривизны границы пузыря. У невырожденного решения в этом пределе оба диаметра $\Delta {\kern 1pt} x$ и $\Delta {\kern 1pt} y$ стремятся к нулю, а их отношение ${{\Delta {\kern 1pt} x} \mathord{\left/ {\vphantom {{\Delta {\kern 1pt} x} {\Delta {\kern 1pt} y}}} \right. \kern-0em} {\Delta {\kern 1pt} y}}$ стремится к величине 2/11. Эта величина совпадает с отношением диаметров ${{\Delta {\kern 1pt} x} \mathord{\left/ {\vphantom {{\Delta {\kern 1pt} x} {\Delta y}}} \right. \kern-0em} {\Delta y}}$ в точном решении Мак-Леода для двумерного пузыря в безграничном потоке [3, 5]. Таким образом, невырожденное решение в пределе $\alpha \to 0$ совпадает с решением Мак-Леода.

Заметим, что решение Мак-Леода можно получить и непосредственно с помощью предложенного метода, сохранив тот же самый вид (4.1) функции $\chi (\zeta )$ и выписав вместо (3.1) соответствующий вид функции $W(\zeta )$ для безграничного потока.

ЗАКЛЮЧЕНИЕ

Предложена модификация метода Жуковского конструирования точных решений задач для потенциальных течений со свободной границей, на которой действует условие капиллярного типа. С использованием модифицированного метода построено новое точное решение задачи обтекания двумерного газового пузыря потоком капиллярной жидкости в прямолинейном канале, которое является обобщением известного решения Жуковского. Также установлено, что в одном из предельных случаев бесконечно малого пузыря это решение совпадает с точным решением Мак-Леода для пузыря в безграничном потоке.

Работа выполнена за счет средств субсидии, выделенной в рамках государственной поддержки Казанского (Приволжского) федерального университета в целях повышения его конкурентоспособности среди ведущих мировых научно-образовательных центров.

Список литературы

Петров А.Г. Об устойчивости жидкого цилиндра в плоскопараллельном потоке идеальной жидкости // ПММ. 2016. Т. 80. Вып. 3. С. 366–374.
Жуковский Н.Е. Определение движения жидкости при каком-нибудь условии, данном на линии тока // Собрание соч. Т. 2. М.; Л.: Гостехиздат, 1949. С. 640–653.
McLeod E.B. The explicit solution of a free boundary problem involving surface tension // J. Ration. Mech. Anal. 1955. V. 4. № 4. P. 557–567.
Киселев О.М. К задаче о газовом пузыре в плоском потоке идеальной жидкости // Изв. АН СССР. МЖГ. 1969. № 4. С. 13–23.
Shankar P.N. On the shape of a two-dimensional bubble in uniform motion // J. Fluid Mech. 1992. V. 244. P. 187–200.
Сретенский Л.Н. Теория волновых движений жидкости. М.: Наука, 1977. 815 с.
Волков Н.Б., Зубарев Н.М., Зубарева О.В. Точные решения задачи о форме незаряженной струи проводящей жидкости в поперечном электрическом поле // ЖЭТФ. 2016. Т. 149. Вып. 5. С. 1096–1101.
Crapper G.D. An exact solution for progressive capillary waves of arbitrary amplitude // J. Fluid Mech. 1957. V. 2. P. 532–540.
Киселев О.М. О точных решениях струйных задач с учетом сил поверхностного натяжения // Тр. сем. по краевым задачам. Казань, Изд-во Казанского ун-та. 1967. Вып. 4. С. 53–60.
Kinnersley W. Exact large amplitude capillary waves on sheets of fluid // J. Fluid Mech. 1976. V. 77. № 2. P. 229–241.
Зубарев Н.М., Зубарева О.В. Равновесная конфигурация поверхности проводящей жидкости во внешнем пространственно-периодическом электрическом поле // Письма в ЖТФ. 2010. Т. 36. Вып. 9. С. 54–59.
Гуревич М.И. Теория струй идеальной жидкости. М.: ГИФМЛ, 1961. 496 с.
Lamb H. Hydrodynamics. Cambridge: Univ. Press, 1932 = Ламб Г. Гидродинамика. М.; Л.: Гостехиздат, 1947. 928 с.
Лаврентьев М.А., Шабат Б.В. Методы теории функции комплексного переменного. М.: Наука, 1973. 736 с.
Куфарев П.П. Решение задачи о контуре нефтеносности для круга // Докл. АН СССР. 1948. Т. 60. № 8. С. 1333–1334.
Howison S.D. Complex variable methods in Hele-Shaw moving boundary problems // Europ. J. Appl. Math. 1992. V. 3. № 3. P. 209–224.
Алимов М.М. Нестационарное движение пузыря в лотке Хеле-Шоу // Изв. РАН. МЖГ. 2016. № 2. С. 129–141.
Алимов М.М. Точное решение задачи Маскета–Лейбензона для растущего эллиптического пузыря // Изв. РАН. МЖГ. 2016. № 5. С. 86–98.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал