Известия РАН. Механика жидкости и газа, 2021, № 3, стр. 121-138
ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАГРЕТОГО КОЛЕБЛЮЩЕГОСЯ СЛОЯ НЕНЬЮТОНОВСКОЙ ЖИДКОСТИ
М. А. Сирвах a, *, С. А. Алхараши b, c, **, ***
a Университет Танта, Научный факультет, Кафедра математики
Танта, Египет
b Кесна технический колледж, Министерство высшего образования
Каир, Египет
c Колледж технологических исследований, Кафедра прикладных наук, ПААЕТ
Кувейт, Contry
* E-mail: magdy.sirwah@science.tanta.edu.eg
** E-mail: sameh7977@yahoo.com
*** E-mail: sa.alkharashi@paaet.edu.kw
Поступила в редакцию 02.02.2020
После доработки 10.08.2020
Принята к публикации 01.10.2020
Аннотация
Численное обращение преобразования Лапласа эффективно использовано для исследования нестационарного течения тонкой нагретой пленки вязкоупругой жидкости, текущей по бесконечно длинной плоской подложке. В некоторых предельных случаях получены точные аналитические решения. Модель, описывающая рассматриваемую задачу, представляет собой систему уравнений, связывающую линеаризованное уравнение Навье–Стокса для вязкоупругой жидкости с учетом силы тяжести как внешней силы с температурным соотношением для распределения энергии. В предположении, что жидкости несжимаемые, впервые получена новая система уравнений, включающих в себя дополнительные члены, связанные с нерастворимыми поверхностно-активными веществами, и учитывающие вязкоупругий характер течения. Получены распределения скорости и температуры и детально обсуждается влияние константы взаимодействия, параметров вязкоупругости и межфазных поверхностно-активных веществ на жидкую пленку. Достоверность полученных решений проверяется численными расчетами, которые демонстрируют влияние различных параметров, характеризующих задачу, и изображают процесс эволюции течения жидкости в зависимости от времени.
Изучение динамических свойств течения тонкого слоя жидкости на нагретой бесконечно длинной пластине все еще является важным для большого количества технологических методов и имеет широчайшие приложения в промышленности. Движущиеся жидкие пленки всесторонне используются в различных технологических исследованиях по причине возможности их применения в современных технологиях и индустрии. Такие течения реализуются в производстве микрочипов, конденсаторов, теплообменников, в биоинженерии, в обработке материалов, при нанесении покрытий на бумагу или пластик, производстве испарителей, в пищевой и химической промышленности и многих других отраслях. Преобразование Лапласа представляет собой чрезвычайно полезный инструмент для работы с дифференциальными уравнениями. Однако для аналитического расчета обратного преобразования Лапласа решений, полученных при использовании прямого преобразования Лапласа, имеется очень важная, но весьма сложная процедура. Чтобы сделать обзор предыдущих исследований по этой теме, упомянем множество алгоритмов численного обращения преобразования Лапласа, изложенных в литературе [1–7]. В [4] преобразование Лапласа было использовано, чтобы иллюстрировать задачу нестационарного безвихревого течения диполярной жидкости, приводимой в движение ускорением плоской первоначально покоящейся пластины. Были представлены некоторые значимые новые результаты, касающиеся стационарных течений. Полученные результаты сравнивались с аналогичным случаем для вязкой ньютоновской жидкости, для которой получено точное общее решение.
В [5] метод преобразования Лапласа был использован для нахождения точных решений для двух течений Куэтта некоторой второсортной жидкости в пористом жидком слое, когда нижняя подложка неожиданно приходит в движение и колеблется. В [6] были исследованы нестационарные вязкие течения и первая задача Стокса. В этой работе была исследована взаимосвязь между течением Куэтта, течением Пуазейля и течением в пограничном слое в случае нестационарного движения в свете первой задачи Стокса. В [7] методика численного обращения преобразования Лапласа, предложенная Дурбиным, была использована для иллюстрации движения в слое вязкоупругой жидкости в присутствии теплообмена в прямоугольном сосуде, который подвергается периодическим колебаниям.
Неньютоновские жидкости были очень важной тематикой научных исследований ввиду возможности их разнообразного использования в важных промышленных процессах. В категорию неньютоновских жидкостей включают несколько сложных жидкостей, таких как расплавы полимеров, разные виды нефти, различные типы буровых растворов и глиняных покрытий, многие виды эмульсии. Многие авторы исследовали течения неньютоновских жидкостей [8–11]. В [8] поведение тепловой неустойчивости Бенара–Марангони было исследовано с помощью линейного анализа устойчивости слоя жидкости Джеффриса с вязкоупругим характером, ограниченного сверху реалистичной свободной деформируемой поверхностью, а снизу некоторой плоской поверхностью. Было продемонстрировано, что и время релаксации, и деформация поверхности имеют дестабилизирующее воздействие, в отличие от времени запаздывания.
В [9] двумерное течение жидкости, представленной B" моделью Уолтера, было исследовано в вязкоупругой области, нисходящей вдоль наклонной нагретой подложки в режиме конечной амплитуды, при котором предполагается наличие линейного изменения температуры. В [10] упоминаются аналитические решения, относящиеся к двум модам однонаправленных течений обобщенной жидкости Олдройда Б с производной дробного порядка, заключенных между двумя параллельными плоскостями, в которых течение нестационарное. В [11] ускоренные течения жидкости рассматриваются на основе парциальной модели Бюргерса, в которой жидкость имеет вязкоупругие свойства. Получены точные решения задач для течения, индуцированного постоянно ускоряющейся пластиной, и течения, вызванного изменяющейся ускоряющейся подложкой.
С другой стороны, присутствие поверхностно-активных веществ оказывает важное воздействие на форму и движение поверхностей раздела. Поверхностно-активные вещества также имеют громадную область применения в нефтяной индустрии, например, при очистке разливов нефти и при добыче нефти с искусственным поддержанием энергии пласта. Некоторое количество исследований было посвящено пределу нерастворимых поверхностно-активных веществ. В пределе бесконечно малых чисел Рейнольдса [12] влияние поверхностно-активных веществ было проиллюстрировано на течении, обусловленном силой тяжести, для тонкого слоя жидкости, стекающего по наклонной стенке с зубцами или периодической волнистостью.
Предметом исследования в [13] является течение в тонких пленках. Обсуждаются эволюционные соотношения для концентрации поверхностно-активных веществ и толщины пленки в рамках линейной устойчивости и приведены результаты численных расчетов.
В [14] в линейном приближении была исследована длинноволновая конвекция Марангони в жидкой тонкой пленке с поверхностно-активным веществом на ее поверхности. В этом случае рассматриваемый слой подвергался воздействию поперечного градиента температуры, а движение поверхностно-активного вещества ограничено диапазоном межфазных скоростей и поверхностно-активное вещество диффундирует только по свободной поверхности.
Целью настоящего исследования является численное и аналитическое изучение воздействия неньютоновских свойств жидкости вместе с влиянием теплообмена и нерастворимых поверхностно-активных веществ на процесс возникновения поверхностных волн, образующихся на свободной поверхности жидкого слоя в рамках вязкоупругости. Движение жидкости происходило на горизонтально колеблющейся бесконечной подложке. С этой точки зрения, настоящее исследование представляет собой некоторое расширение предмета ранее опубликованных исследований, использующих преобразование Лапласа. Действительно, метод преобразования Лапласа очень важен для решения некоторых задач и все еще используется в недавно проведенных исследованиях, например в [15], где рассматриваются течения в нестационарном ламинарном пограничном слое максвелловской жидкости над экспоненциально ускоряющейся вертикальной плоской стенкой, которая находится под воздействием ньютоновского нагрева и фрикционного нагрева при скольжении на границе. Полуаналитические решения для безразмерной задачи были получены за счет использования обратного преобразования Лапласа для полей температуры и скоростей. В [16] преобразование Лапласа было использовано для исследования задачи свободного конвекционного течения в модели вязкой жидкости с дробными производными около бесконечной вертикальной пластинки с экспоненциальным нагревом. Движение жидкости было вызвано пластинкой, что приводило к необходимости учета произвольного, зависящего от времени сдвигового напряжения, определяющего это движение.
Подводя итоги, можно сказать, что фундаментальная разница между проведенным исследованием и выполненными ранее состоит в выяснении роли и степени влияния поверхностно-активных веществ, а также времен запаздывания и релаксации, на устойчивость рассматриваемой системы за счет использования преобразования Лапласа для получения численного и полуаналитического решений в исходной области и нахождения воздействия некоторых параметров жидкости. В предельных случаях получены точные и аналитические результаты. Кроме того, в будущих исследованиях предмет настоящей работы может быть расширен, чтобы включить в себя движение в пористой среде, пористой подложке, по волнистой поверхности или наложенное сдвиговое напряжение на поверхности, а также влияние магнитного поля или электрического поля, индуцированного поверхностным зарядом. Далее, результаты, представленные в настоящем исследовании, могут найти применение в развитии современных технологий и в промышленности, в таких областях, как дизельные и газотурбинные двигатели, производство пластиков, нефтяных горелок, металлических порошков, жидкостных ракетных двигателей и смазочных веществ.
1. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Рассматриваемая задача состоит в исследовании двумерного течения нагретой вязкоупругой жидкой пленке по бесконечно длинной подложке. Предполагается, что вдали от основной массы жидкости, на свободной поверхности имеются нерастворимые поверхностно-активные вещества. Возникающее течение и вид граничных условий изображены на рис. 1. Первоначально подложка и жидкости находятся в состоянии покоя. Внезапно пластинка приводится в движение в горизонтальном направлении с осциллирующей скоростью.
1.1. Уравнения движения
Основные определяющие уравнения состоят из уравнения сохранения массы (уравнение неразрывности), уравнения количества движения для жидкой пленки и уравнения теплопроводности для температуры [17–19]
где ${\mathbf{u}}$ $ = (u,v)$ обозначает вектор скорости, $\rho $ есть плотность жидкой пленки, символ $d{\text{/}}dt \equiv \partial {\text{/}}\partial t + ({\mathbf{u}}.\nabla )$ обозначает конвективную производную, g есть сила тяжести, $\nabla \equiv (d{\text{/}}dx,d{\text{/}}dy)$ обозначает оператор градиента, и p есть давление. Кроме того, в уравнении T отождествляется с полем температуры и $\kappa $ представляет собой теплопроводность, тогда как as ${{c}_{p}}$ обозначает удельную теплоемкость при постоянном давлении.В настоящей работе используется модель Олдройда Б, которая представляет собой определяющий метод, приложимый к течению вязкоупругих жидкостей. Определяющее уравнение для вязкоупругой жидкости имеет вид [8, 9]
(1.4)
$\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\Pi = \mu \left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right)[\nabla {\mathbf{u}} + \nabla {{{\mathbf{u}}}^{{{{T}_{r}}}}}],$1.2. Начальные и граничные условия
Для завершения постановки задачи (1.2)–(1.4) укажем соответствующие граничные условия на ограничивающей поверхности и межфазные ограничения. При положительном значении времени подложка при нулевой вертикальной оси начинает внезапно скользить, оставаясь на том же уровне, с некоторой осциллирующей скоростью. Эти обстоятельства могут быть сформулированы следующим образом:
(1.5)
$u(y,t) = \left\{ {\begin{array}{*{20}{l}} {0\quad {\text{при}}\quad t = 0,\quad y > 0,} \\ {} \\ {{{U}_{0}}sin\omega t\quad {\text{при}}\quad t > 0,\quad y = 0.} \end{array}} \right.$Условие, наложенное на поле температуры, выглядит следующим образом:
Пусть деформируемая свободная поверхность имеет вид $y = h(x,t)$$ = \ell + \eta (x,t)$. Когда поверхность раздела всегда содержит одни и те же жидкие частицы, в этом случае накладывается кинематическое условие и поэтому функция $y = h(x,t)$, график которой определяет поверхность раздела, должна удовлетворять уравнению
Скачок нормальной компоненты поверхностного напряжения через свободную поверхность уравновешивается поверхностным натяжением, умноженным на кривизну, что можно выразить следующим образом:
(1.8)
${{p}_{{_{{{\text{air}}}}}}} - p + {\mathbf{n}} \cdot \Pi \cdot {\mathbf{n}} = 2H\sigma (\Gamma ,T),$Величина $\sigma (\Gamma ,T)$ обозначает поверхностное натяжение, которое изменяется согласно линейному закону в зависимости от температуры и концентрации поверхностно-активного вещества, в обеих из них учитывается эффект Марангони, так что [9]
(1.9)
$\sigma (\Gamma ,T) = {{\sigma }_{0}}({{\Gamma }_{0}},{{T}_{s}}) - {{\sigma }_{T}}(T - {{T}_{s}}) - {{\sigma }_{\Gamma }}(\Gamma - {{\Gamma }_{0}}),$(1.10)
${\mathbf{n}} \cdot \Pi \cdot {\mathbf{t}} = \nabla \sigma (\Gamma ,T) \cdot \cdot {\mathbf{t}},$Здесь t обозначает единичный вектор, направленный по касательной в той точке, где ${\mathbf{n}} \times $ ${\mathbf{t}}$ = 0. В качестве ограничений, связанных с температурой, задается ньютоновский закон охлаждения, который происходит из условия непрерывности потока тепла через свободную поверхность
где ${{h}_{{\text{g}}}}$ представляет собой параметр, характеризующий теплообмен между жидкостью и воздухом. На свободной поверхности слой жидкости содержит нерастворимое поверхностно-активное вещество с концентрацией $\Gamma (x,t)$. Распределение концентрации изменяется согласно уравнению переноса [12–14]:(1.12)
$\frac{{\partial (N\Gamma )}}{{\partial t}} + \frac{{\partial (N\Gamma u)}}{{\partial x}} = {{D}_{s}}\frac{\partial }{{\partial x}}\left( {\frac{1}{N}\frac{{\partial \Gamma }}{{\partial x}}} \right).$В этом уравнении $N = \sqrt {1 + {{{\left( {\frac{{\partial h}}{{\partial x}}} \right)}}^{2}}} $ и ${{D}_{s}}$ характеризует коэффициент поверхностной диффузии, в котором эффектом плавучести можно пренебречь, т.е. предполагается, что пленка достаточно тонкая.
1.3. Масштабирование и обезразмеривание. Прежде чем решать задачу, принято удалить единицы, относящиеся к вышеупомянутой размерной системе, использующей физические величины, и определить шкалу отсчета. Используя толщину невозмущенной пленки $\ell $ в качестве характерной длины, можно задать следующие параметры, чтобы сформировать следующие безразмерные основные уравнения и граничные условия
(1.13)
$\Pi = \frac{{\mu \sqrt {\ell g} }}{\ell }\Pi *,\quad T = ({{T}_{w}} - {{T}_{s}})T{\text{*}} + {{T}_{s}},\quad \Gamma = {{\Gamma }_{0}}\Gamma {\text{*}}.$Для простоты, звездочка $ * $, обозначающая безразмерные величины, в дальнейшем будет опущена. Таким образом, используя введенные выше безразмерные величины в вышеупомянутых основных уравнениях и связанных с ними граничных условиях, приходим к следующей системе уравнений:
(1.14)
${{R}_{e}}\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{du}}{{dt}} = - \left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{\partial p}}{{\partial x}} + \left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right){{\nabla }^{2}}u,$(1.15)
${{R}_{e}}\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{d{v}}}{{dt}} = - \left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{\partial p}}{{\partial y}} + \left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right){{\nabla }^{2}}{v} - 1,$Межфазное напряжение, создаваемое градиентом поверхностного натяжения, включая эффект Марангони и связанные с ним моды неустойчивости, известно как термокапиллярная неустойчивость. Таким образом, граничные условия на свободной поверхности $y = h(x,t)$ можно записать в виде
(1.18)
$ = \;\frac{{\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)}}{{{{N}^{3}}}}\left\{ {\frac{1}{{{{C}_{a}}}} - {{M}_{a}}T - {{N}_{e}}(\Gamma - 1)} \right\}\frac{{{{\partial }^{2}}h}}{{\partial {{x}^{2}}}},$(1.19)
$ = \; - N\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\left\{ {{{M}_{a}}\left( {\frac{{\partial T}}{{\partial x}} + \frac{{\partial T}}{{\partial y}}\frac{{\partial h}}{{\partial x}}} \right) + {{N}_{e}}\frac{{\partial \Gamma }}{{\partial x}}} \right\},$(1.21)
$\frac{{\partial (N\Gamma )}}{{\partial t}} + \frac{{\partial (N\Gamma u)}}{{\partial x}} = \frac{1}{{{{P}_{{es}}}}}\frac{\partial }{{\partial x}}\left( {\frac{1}{N}\frac{{\partial \Gamma }}{{\partial x}}} \right),$(1.22)
$\frac{{\partial T}}{{\partial y}} - \frac{{\partial h}}{{\partial x}}\frac{{\partial T}}{{\partial x}} + N{{B}_{i}}T = 0,$2. МЕТОД РЕШЕНИЯ
2.1. Решение для основного состояния
Когда система невозмущенная, в базовом ламинарном состоянии профиль скорости и температурная область отделены друг от друга. В зависимости от этого базовое распределение скорости и соотношения для энергии могут быть получены при использовании основных уравнений нулевого порядка и связанных ограничений на плоских и поверхностных границах. Рассматривая неподвижное начальное состояние, можно получить решения для базового состояния и, следовательно, базовая скорость в жидкой пленке равна нулю, так что течение не зависит от времени и полностью развито.
В невозмущенном случае уравнение энергии для безразмерного поля температуры имеет вид
и связано с основными граничными для температуры(2.3)
$\frac{{\partial {{T}_{b}}(y)}}{{\partial y}} + {{B}_{i}}{{T}_{b}}(y) = 0\quad {\text{при}}\quad y = 1.$Уравнение (2.1) вместе с уравнениями (2.2) и (2.3) дают основное поле температуры
где соотношение описывает гидростатическое давление, в котором $\mathop {\hat {p}}\nolimits_0 $ обозначает постоянное давление, обусловленное окружающим воздухом.2.2. Возмущенное течение
Чтобы задать возмущение скоростей, давления, температуры, положения межфазной границы и концентрации поверхностно-активного вещества, введем для этих величин небольшое возмущение их основного состояния
(2.6)
${\mathbf{u}} = 0 + (\tilde {u},{\tilde {v}}),\quad p = {{p}_{0}} + \tilde {p},\quad T = {{T}_{b}} + \tilde {T},\quad h = 1 + \eta ,\quad \Gamma = 1 + \tilde {\Gamma }.$Для облегчения нахождения решения вышеупомянутой системы основных уравнений и соответствующих граничных условий, введем функцию тока $\psi (x,y,t)$
(2.7)
$\tilde {u} = \frac{{\partial \psi }}{{\partial y}},\quad {\tilde {v}} = - \frac{{\partial \psi }}{{\partial x}}.$Решение настоящей задачи определяется преобразованием Лапласа. Преобразование Лапласа по времени имеет общий стандартный вид
где $s \geqslant 0$ представляет собой параметр преобразования. Применяя преобразование Лапласа к уравнениям (1.15) и (1.16), с помощью уравнения (2.8) получаем(2.9)
${{\nabla }^{4}}\bar {\psi }(x,y,s) - \frac{{s{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}{{\nabla }^{2}}\bar {\psi }(x,y,s) = 0,$(2.10)
${{\nabla }^{2}}\bar {\tilde {T}}(x,y,s) - {{P}_{e}}\left( {s\bar {\tilde {T}}(x,y,s) - \frac{{d{{T}_{b}}}}{{dy}}\frac{{\partial{ \bar {\psi }}}}{{\partial x}}} \right) = 0.$Кроме того, соответствующие граничные условия преобразуются к следующему виду:
(2.11)
$\bar {\psi } = 0,\quad \frac{{\partial{ \bar {\psi }}}}{{\partial y}} = \bar {U}(s)\quad {\text{при}}\quad y = 0,$(2.13)
$\frac{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}{{{{R}_{e}}}}\left( {\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{y}^{3}}}} + 3\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{x}^{2}}\partial y}}} \right) - s\frac{{\partial{ \bar {\psi }}}}{{\partial y}} - \frac{{\partial{ \bar {\eta }}}}{{\partial x}} + \left( {\frac{1}{{{{C}_{a}}}} - {{M}_{a}}\frac{{d{{T}_{b}}}}{{dy}}} \right)\frac{{{{\partial }^{3}}\bar {\eta }}}{{\partial {{x}^{3}}}} = 0\quad {\text{при}}\quad y = 1,$(2.14)
$F({{\lambda }_{1}},{{\lambda }_{2}},s)\left( {\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{y}^{2}}}} - \frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{x}^{2}}}}} \right) + {{M}_{a}}\left( {\frac{{d{{T}_{b}}}}{{dy}}\frac{{\partial{ \bar {\eta }}}}{{\partial x}} + \frac{{\partial{ \bar {\tilde {T}}}}}{{\partial x}}} \right) + {{N}_{e}}\frac{{\partial{ \bar {\tilde {\Gamma }}}}}{{\partial x}} = 0\quad {\text{при}}\quad y = 1,$(2.15)
$s\bar {\eta } + \frac{{\partial{ \bar {\psi }}}}{{\partial x}} = 0\quad {\text{при}}\quad y = 1,$(2.16)
$\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial x\partial y}} + s\bar {\tilde {\Gamma }} - \frac{1}{{{{P}_{{es}}}}}\frac{{{{\partial }^{2}}\bar {\tilde {\Gamma }}}}{{\partial {{x}^{2}}}} = 0\quad {\text{при}}\quad y = 1,$(2.17)
$\frac{{\partial{ \bar {\tilde {T}}}}}{{\partial y}} + {{B}_{i}}\left( {\bar {\tilde {T}} + \frac{{d{{T}_{b}}}}{{dy}}\bar {\eta }} \right) = 0\quad {\text{при}}\quad y = 1.$Решение вышеприведенной задачи может быть записано в виде
Следовательно, величины $\bar {f}$ и ${{\bar {g}}}$ определяются следующими уравнениями:
(2.20)
$\frac{{{{d}^{4}}\bar {f}}}{{d{{y}^{4}}}} - \left( {2{{k}^{2}} + \frac{{s{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}} \right)\frac{{{{d}^{2}}\bar {f}}}{{d{{y}^{2}}}} + {{k}^{2}}\left( {{{k}^{2}} + \frac{{s{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}} \right)\bar {f} = 0,$(2.21)
$\frac{{{{d}^{2}}{{\bar {g}}}}}{{d{{y}^{2}}}} - ({{k}^{2}} + s{{P}_{e}}){{\bar {g}}} + \frac{{k{{P}_{e}}{{B}_{i}}}}{{1 + {{B}_{i}}}}\bar {f} = 0.$С помощью граничных условий (2.11)–(2.17) можно получить следующие выражения для функций $\bar {f}$ и ${{\bar {g}}}$
(2.22)
$\bar {f} = {{c}_{1}}ch(\gamma y) + {{c}_{2}}sh(\gamma y) + {{c}_{3}}ch(ky) + {{c}_{4}}sh(ky),$(2.23)
$\begin{gathered} {{\bar {g}}} = \frac{{k{{P}_{e}}{{B}_{i}}{{{(1 + {{B}_{i}})}}^{{ - 1}}}}}{{({{k}^{2}} - {{\delta }^{2}})({{\delta }^{2}} - {{\gamma }^{2}})}}\{ ({{k}^{2}} - {{\delta }^{2}})[{{c}_{1}}ch(\gamma y) + {{c}_{2}}sh(\gamma y)] - \\ - \;({{\delta }^{2}} - {{\gamma }^{2}}) \times \left[ {{{c}_{3}}ch(ky) + {{c}_{4}}sh(ky)} \right]\} + {{c}_{5}}ch(\delta y) + {{c}_{6}}sh(\delta y), \\ \end{gathered} $Таким образом, уравнения (2.9) и (2.10) дадут следующие результаты:
(2.24)
$\bar {\psi }(x,y,s) = \left\{ {{{c}_{1}}ch(\gamma y) + {{c}_{2}}sh(\gamma y) + {{c}_{3}}ch(ky) + {{c}_{4}}sh(ky)} \right\}cos(kx) + \bar {U}(s)y,$(2.25)
$ - \left. {\left. {({{\delta }^{2}} - {{\gamma }^{2}})[{{c}_{3}}ch(ky) + {{c}_{4}}sh(ky)]} \right\} + {{c}_{5}}ch(\delta y) + {{c}_{6}}sh(\delta y} \right\}sin(kx),$(2.26)
$\bar {\eta }(x,s) = \frac{k}{s}\left\{ {{{c}_{1}}ch\gamma + {{c}_{2}}sh\gamma + {{c}_{3}}chk + {{c}_{4}}shk} \right\}sin(kx).$В Приложении приведены математические формулы для коэффициентов ${{c}_{1}},{{c}_{2}}, \ldots {{c}_{6}}$.
Теперь стоит определить расход жидкости (иначе называемый объемным расходом жидкости или объемной скоростью). Будучи зависимым от положения сечения канала и скорости жидкости, расход жидкости в своем физическом значении может быть определен как количество жидкости, которое проходит через данное сечение за единицу времени. Расход потока $Q(x,s)$ обычно задается соотношением
(2.27)
$ = \;\left\{ {{{c}_{1}}[ch(h\gamma ) - 1] + {{c}_{2}}sh(h\gamma ) + {{c}_{3}}[ch(hk) - 1] + {{c}_{4}}sh(hk)} \right\}cos(kx) + h\bar {U}(s).$Кроме того, можно вычислить напряжение сдвига, чтобы получить поверхностное трение $S$ на нижней границе
(2.28)
$S = {{\left. {\frac{{\partial{ \bar {u}}}}{{\partial y}}} \right|}_{{y = 0}}} = {{\left. {\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{y}^{2}}}}} \right|}_{{y = 0}}} = \{ {{c}_{1}}{{\gamma }^{2}} + {{c}_{3}}{{k}^{2}}\} cos(kx).$Выражения (2.27) и (2.28) согласуются с ранее полученными результатами (см. [22–24]).
2.3. Обращение преобразования Лапласа
В комплексном виде обозначение инверсии для преобразования Лапласа $\bar {f}(x,y,s)$ области $f(x,y,t)$ (sic!) задается следующим контурным интегралом [1, 2]
(2.29)
$f(x,y,t) = \frac{1}{{2\pi i}}\mathop {lim}\limits_{{\text{c}} \to \infty } \int\limits_{\upsilon - i{\text{c}}}^{\upsilon + i{\text{c}}} {\bar {f}} (x,y,s){{e}^{{st}}}ds.$Здесь $\upsilon + i{\text{c}}$ и $\upsilon $ больше, чем действительная часть любой сингулярности в преобразованной функции $\bar {f}(x,y,s)$. Для получения искомых физических функций было выбрано численное обращение в форме, предложенной Дурбиным [25, 26]
(2.30)
$ - \;{\text{Im}}\left. {\left. {\left\{ {\bar {f}\left( {x,y,\upsilon + i\frac{{j\pi }}{\tau }} \right)} \right\}sin\frac{{j\pi }}{\tau }t} \right\}} \right],\quad 0 < t < 2\tau ,$(2.31)
${{e}^{{\upsilon t}}}\left\{ {{\text{Re}}\left\{ {\bar {f}\left( {x,y,\upsilon + i\frac{{j\pi }}{\tau }} \right)} \right\}cos\frac{{j\pi }}{\tau }t - {\text{Im}}\left\{ {\bar {f}\left( {x,y,\upsilon + i\frac{{j\pi }}{\tau }} \right)} \right\}sin\frac{{j\pi }}{\tau }t} \right\} \leqslant \varepsilon ,$2.4. Предельные случаи
В дальнейшем полезно исследовать некоторые важные предельные ситуации.
2.4.1. Случай изотермического жидкого слоя. В этом случае предполагается, что рассматриваемый жидкий слой является изотермическим и, таким образом, перенос тепла в жидкой пленке отсутствует. Тогда уравнения движения такие же, как и уравнение (2.9), а соответствующие условия имеют вид
(2.32)
$\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{y}^{3}}}} + 3\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{x}^{2}}\partial y}} + \frac{{{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}\left( {\frac{1}{s}\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{x}^{2}}}} - s\frac{{\partial{ \bar {\psi }}}}{{\partial y}} - \frac{1}{{s{{C}_{a}}}}\frac{{{{\partial }^{4}}\bar {\psi }}}{{\partial {{x}^{4}}}}} \right) = 0\quad {\text{при}}\quad y = 1,$(2.33)
$\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{y}^{2}}}} - \frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{x}^{2}}}} + \frac{{{{N}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}\frac{{\partial{ \bar {\tilde {\Gamma }}}}}{{\partial x}} = 0\quad {\text{при}}\quad y = 1,$(2.34)
$\bar {\psi }(x,y,s) = \left\{ {A[ch(\gamma y) + ch(ky)] + B[\gamma sh(ky) - ksh(\gamma y)]} \right\}cos(kx) + \bar {U}(s)y,$(2.35)
$\bar {\eta }(x,s) = \frac{k}{s}\left\{ {A[ch\gamma + chk] + B\,[\gamma shk - ksh\gamma ]} \right\}sin(kx),$2.4.2. Случай малого числа Рейнольдса. В этом случае берется течение ньютоновской жидкости, а число Рейнольдса задается много меньше единицы, т.е. оно стремится к нулю, и тогда γ = k + + $\tfrac{s}{{2k}}{{R}_{e}} + O(R_{e}^{2})$ и ${{e}^{{\gamma y}}} = {{e}^{{ky}}}\left( {1 + \tfrac{{sy}}{{2k}}{{R}_{e}}} \right) + O(R_{e}^{2})$. В этом пределе функция тока имеет вид
(2.36)
$\bar {\psi }(x,y,s) = \frac{{{{U}_{0}}\omega y}}{{{{s}^{2}} + {{\omega }^{2}}}} + \frac{{({{\varsigma }_{{11}}}{{s}^{2}} + k{{\varsigma }_{{12}}}s)cos(kx)}}{{k({{\varsigma }_{{01}}}{{s}^{3}} + {{\varsigma }_{{02}}}{{s}^{2}} + {{\varsigma }_{{03}}}s + {{\varsigma }_{0}})}}.$Учитывая обратное преобразование Лапласа, изменение функции тока и отклонение поверхности могут быть представлены как следующие функции времени:
(2.37)
$\psi (x,y,t) = [{{U}_{0}}y + {{L}_{1}}cos(kx)]sin(\omega t) + cos(kx)\{ {{L}_{2}}cos(\omega t) + {{L}_{3}}{{e}^{{(\alpha + \sqrt \beta )t}}} + {{L}_{4}}{{e}^{{(\alpha - \sqrt \beta )t}}}\} ,$(2.38)
$\bar {\eta }(x,s) = \frac{k}{s}\{ {{L}_{1}}sin(\omega t) + {{L}_{2}}cos(\omega t) + {{L}_{3}}{{e}^{{(\alpha + \sqrt \beta )t}}} + {{L}_{4}}{{e}^{{(\alpha - \sqrt \beta )t}}}\} sin(kx).$Величины $\varsigma $ и L, так же как $\alpha $ и $\beta $, которые присутствуют в этих соотношениях, представляют собой коэффициенты основных определяющих параметров рассматриваемой задачи. Выражения для этих коэффициентов очень громоздки и опущены в настоящем исследовании. Во всяком случае, их можно получить, запросив у авторов. Полученные результаты находятся в хорошем согласии с тем, что упоминается в исследованиях [20, 21].
3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ
В этом разделе задаются значения параметров $\upsilon t = 9$, $J = 700$, $\tau = 2{{t}_{{{\text{max}}}}}$ = 200, причем для их выбора был проведен целый ряд численных оценок. Формула Дурбина (2.30) для обратного преобразования Фурье дает устойчивые и сходящиеся результаты во всех исследованных случаях. Расчеты были проведены с помощью подходящего персонального компьютера, а сходимость численных оценок была установлена простым методом проб и ошибок за счет увеличения параметра J, характеризующего количество сохраненных членов ряда, при исследовании устойчивости численных значений вычисленных результатов.
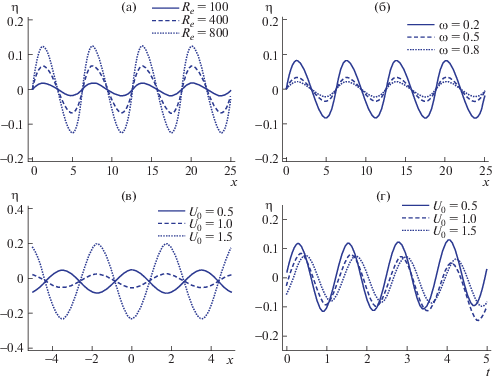
На всех графиках численное исследование происходит при задании фиксированных значений всех физических параметров, за исключением одного, который изменяется с целью сравнения. В нижеприведенных расчетах все физические переменные ищутся в безразмерном виде, как было указано ранее. Рисунки 2а и 2б были построены с целью демонстрации влияния изменений скорости U0 и угловой частоты ω на зависимость от времени свободной поверхности, описываемой уравнением (2.26). Графики построены в плоскости (t, η), а значения всех других величин поддерживаются постоянными, как указано в подписи к рис. 2. Графики на рис. 2а построены для трех значений U0 = 0.1, 0.4 и 0.7, которым соответствуют непрерывная и пунктирная линии и линии из точек. Результаты, изображенные пунктирными и точечными кривыми, позволяют понять, что качественного изменения поведения поверхностных волн со временем не происходит при различных значениях скорости U0, тогда как наблюдается значительный рост значений $\eta $. При сравнении между собой кривых, изображенных на рис. 2б, можно заметить, что частота имеет регулярное воздействие на высоту поверхностной волны, особенно при значении времени $t > 3$.
Рис. 2.
Высота свободной поверхности как функция времени в соответствии с (2.26) для системы с параметрами ${{B}_{i}} = 0.7$, ${{M}_{a}} = 1$, ${{P}_{e}} = 2$, ${{C}_{a}} = 0.05,$ ${{P}_{{{\text{es}}}}} = 0.5,$ ${{\lambda }_{1}} = 0.3,$ ${{\lambda }_{2}} = 0.1,$ ${{N}_{e}} = 0.5$, ${{R}_{e}} = 5$ и $x = 3$; (а) $\omega $ = 2, (б) ${{U}_{0}}$ = 0.5, тогда как рисунок (в) изображает изменение ${{\lambda }_{1}}$ = $0.01,0.4,0.9$, а рис. 2,г изображает изменение ${{\lambda }_{2}}$ = $0.01,0.5,0.8$.
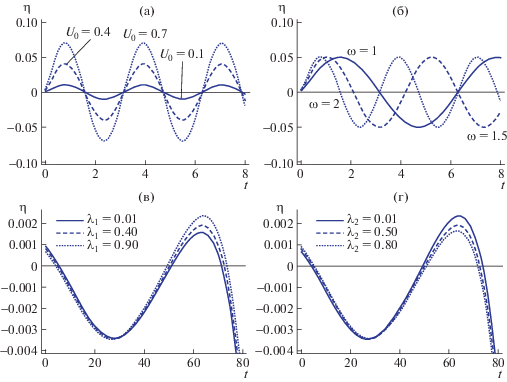
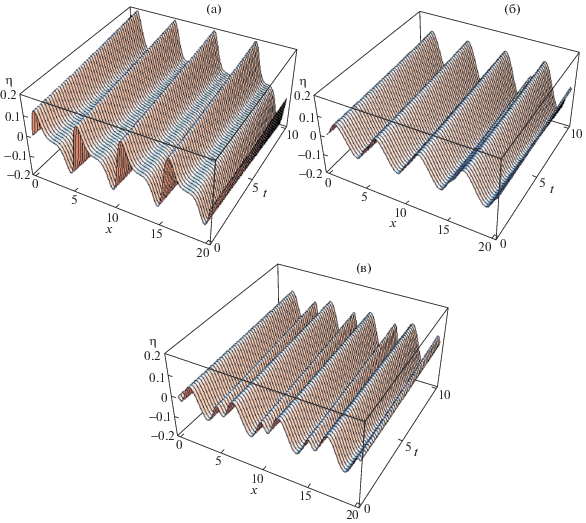
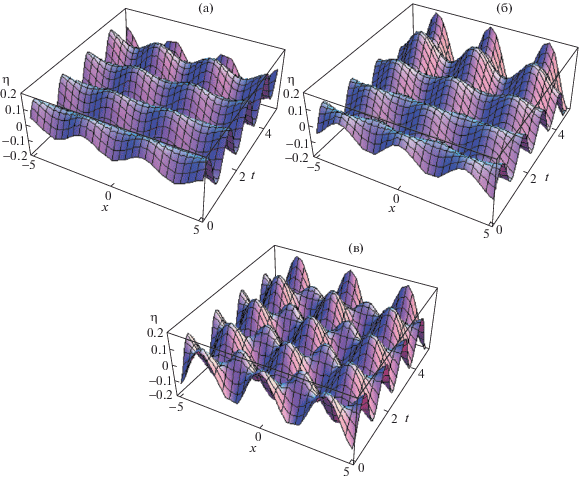
Графики на рис. 2в и 2г, на которых высота поверхности изображена как функция времени, иллюстрируют влияние как времени релаксации ${{\lambda }_{1}}$, так и времени запаздывания ${{\lambda }_{2}}$ на профили поверхностных волн. Сравнивая влияния времени релаксации и времени запаздывания, можно увидеть некоторые отличия. На рис. 2в были взяты значения ${{\lambda }_{1}}$ = 0.01, 0.4 и 0.9, которым соответствуют непрерывная, пунктирная и точечная линии. Анализируя изображение, приведенное на рис. 2в, можно увидеть эффект двоякой (внутренне противоречивой) роли роста времени релаксации: одна из этих двух ролей состоит в слабом влиянии в диапазоне $0 < t < 50$ (очень слабое увеличение высоты поверхностных волн) и второй эффект состоит в значительном увеличении высоты поверхностных волн при $50 < t < 80$. Графики на рис. 2г построены при ${{\lambda }_{2}}$ = 0.01, 0.5 и 0.8. Из их рассмотрения видно, что общая тенденция состоит в том, что влияние времени запаздывания на высоту поверхностных волн противоположно влиянию времени релаксации. Очевидно, что времена релаксации и запаздывания имеют едва заметный эффект на высоту поверхности при $t < 50$, но при времени, большем, чем 50, можно наблюдать, что как время релаксации, так и время запаздывания оказывают существенное влияние на движение слоя. Эти выводы находятся в полном согласии с выводами, сделанными в [10]. С другой стороны, моды, представленные на рис. 3 посредством ее членения на отдельные рисунки, дают графическое объяснение воздействия растущего значения числа Марангони на свободную поверхность жидкости на трехмерной границе раздела. Из этих отдельных рисунков видно, что движение свободной поверхности постепенно уменьшается при больших значениях числа Марангони. Более того, можно отметить некоторое осциллирующее движение в случае растущего числа Марангони при изменении горизонтального положения жидкой моды.
Рис. 3.
Трехмерная пространственная эволюция деформации свободной поверхности для системы с параметрами ${{R}_{e}} = 1000$, ${{B}_{i}} = 0.7$, ${{P}_{e}} = 2$, ${{C}_{a}} = 30$, ${{P}_{{{\text{es}}}}} = 0.5$, ${{U}_{0}} = 0.3$, ${{\lambda }_{1}} = 0.3$, ${{\lambda }_{2}} = 0.1$, ${{N}_{e}} = 0.5$ и $\omega = 0.2$; (а), (б) и (в) построены для ${{M}_{a}} = 1$, 4 и 10 соответственно.
Целью численных расчетов, представленных на рис. 4а и 4б, является изучение влияние числа Био ${{B}_{i}}$ на поведение распределения температуры, когда число Био имеет значения меньше или больше единицы. На этих отдельных рисунках безразмерная температура изображена в зависимости от горизонтального положения. На рис. 4а непрерывная, пунктирная и точечная кривые соответствуют значениям числа Био, равным 0.1, 0.2 и 0.3, тогда как для этих кривых на рис. 4б выбраны значения 1, 2 и 3. При рассмотрении рис. 4а и 4б видно, что, вообще говоря, распределение температуры жидкости в общем и целом растет как функция горизонтального положения до тех пор, пока оно не достигнет максимального значения, после чего начинается постепенное убывание с ростом горизонтальной координаты. С другой стороны, сравнивая результаты, изображенные на рис. 4а и 4б, можно отметить поразительный факт, что влияние роста числа Био, когда его значение меньше единицы, состоит в увеличении распределения температуры жидкости. При этом верно противоположное утверждение касательно увеличения числа Био, когда оно имеет значения большие или равные единице на интервале $0 < x < 2$, так что можно сделать вывод, что распределение температуры жидкости сильно зависит от числа Био.
Рис. 4.
Изменение распределения температуры со временем в зависимости от горизонтального положения для той же системы, которая исследована на рис. 3, при ${{R}_{e}} = 800$, ${{M}_{a}} = 1$, соответствующей ${{B}_{i}}$ = 0.1, 0.2, 0.3 (а) и ${{B}_{i}}$ = 1, 2, 3 (б). Распределение температуры внутри пленки со временем при ${{B}_{i}} = 0.7$: при ${{C}_{a}} = 5$ (в), где ${{P}_{e}}$ = 1, 2, 3, при ${{P}_{e}} = 3$ (г), где ${{C}_{a}}$ = 1, 5 и 9.
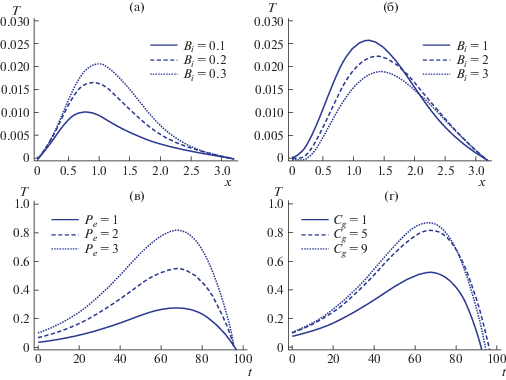
Рисунки 4в и 4г дают графическую иллюстрацию поля температуры в жидкости в пределах жидкого слоя в зависимости от времени при изменении как числа Пекле, так и капиллярного числа соответственно. В контрасте с результатам, представленными на этих графиках, стоит отметить, что все три кривые пересекаются в одной и той же точке t = 95 при росте числа Пекле ${{P}_{e}}$ (оно увеличивается скачкообразно с 1 до 3) на рис. 4в, тогда как при росте капиллярного числа Ca (оно увеличивается скачкообразно с 1 до 9) эти кривые пересекают ось t в трех близких точках на рис. 4г. С другой стороны, при изучении численных результатов, продемонстрированных на этих отдельных рисунках, можно видеть, что рост как капиллярного числа, так и числа Пекле приводит к росту максимальных значений температуры жидкости.
Для лучшего понимания поведения течения на рис. 5 изображены обезразмеренные линии тока и соответствующие изотермы в той же области. Линии тока представляют собой эффективный аппарат для визуализации качественного характера поведения потока во время течения. Линия тока есть кривая, образованная векторами скорости каждой жидкой частицы в некоторый момент времени, так что касательная в каждой точке этой кривой показывает направление движения жидкости в этой точке. На рис. 5а–5в изображены моментальные снимки мгновенных линий тока, картина линий тока получена при задании фиксированных значений всех физических параметров за исключением числа Рейнольдса ${{R}_{e}}$, которое равнялось 1, 400 и 800 при $t$ = 5. Когда число Рейнольдса возрастает, количество обезразмеренных линий тока также возрастает (растет плотность ячеек линий тока); это происходит из-за того, что эффекты вязкости убывают при росте числа Рейнольдса.
Рис. 5.
Линии тока для системы с параметрами, рассмотренными на рис. 4: (а) ${{R}_{e}}$ = 1, (б) ${{R}_{e}}$ = 400, (в) ${{R}_{e}}$ = 800; соответствующие изотермы показаны на рисунках (г)–(е).
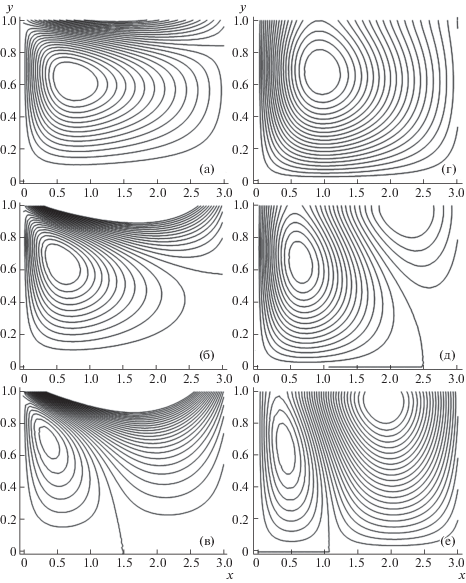
Изменение числа Рейнольдса, проведенное при построении рис. 5г–5е, оказывает влияние на обезразмеренные изотермы, причем изотермы постепенно трансформируются в два множества ячеек (рис. 5д и 5е). Это происходит из-за эффекта конвективной теплопередачи, который растет при увеличении числа Рейнольдса. Из сравнения изотерм, изображенных на рис. 5г и 5е, можно сделать вывод, что бóльшие значения числа Рейнольдса увеличивают концентрацию изотерм при движении жидкости. Аналогичные результаты были так же найдены в [29–31].
На рис. 6а и 6б продемонстрированы эффекты как числа Рейнольдса, так и угловой частоты периодической горизонтальной скорости на отклонения свободной границы в поверхностных волнах в предельном случае отсутствия теплопередачи в жидком слое. На рис. 6а и 6б графики построены в плоскости (x, η) и для рис. 6а выбраны значения числа Рейнольдса, равные 100, 400 и 800, тогда как для рис. 6б заданы три разных значения угловой частоты (равные 0.2, 0.5 и 0.8) с целью установления различия. Остальные заданные величины указаны в подписи к рисунку. Из рис. 6а видно, что при росте числа Рейнольдса возвышение межфазной границы становится больше; в то же время при росте угловой частоты (рис. 6б) верно обратное. Сравнивая результаты, изображенные рис. 6а и 6б, стоит отметить, что воздействие растущего числа Рейнольдса на течение в жидкой пленке противоположно влиянию угловой частоты.
Рис. 6.
Изотермический случай в плоскости (x, η), где ${{U}_{0}} = 0.7$, ${{C}_{a}} = 0.1$, ${{N}_{e}} = 0.1$, ${{P}_{{{\text{es}}}}} = 1$, ${{\lambda }_{1}} = 0.3$ и ${{\lambda }_{2}} = 0.1$: (а) $\omega = 0.2$, где ${{R}_{e}}$ = 100, 400 и 800, (б) ${{R}_{e}} = 500$, где $\omega $ = 0.2, 0.5 и 0.8. Влияние значения скорости ${{U}_{0}} = 0.7$, 1.0 и 1.5 при t = 2 иллюстрирует рисунок (в), а рисунок (г) при x = 1.
Когда число Рейнольдса исчезающе мало, численные иллюстрации, представленные на рис. 6в и 6г имеют цель исследовать влияние роста параметра скорости на область поверхностных волн при изменении как горизонтального уровня, так и времени. Для этой цели использованы две плоскости (x, η) и (t, η), которые соответствуют рис. 6в и 6г. Исследование численных результатов, изображенных на рис. 6в и 6г, позволяет сделать вывод, что рост скорости приводит к существенному увеличению возвышения $\eta $ (рис. 6в). В то же время влияние скорости на движение свободной поверхности будет постепенно, но незначительно уменьшаться при эволюции во времени, как это изображено на рис. 6г. С другой стороны, следует отметить, что эволюция поверхности подвержена небольшому росту со временем из-за роста скорости. Это означает, что движение жидкого слоя незначительно неустойчиво по отношению к увеличению скорости. Однако такое поведение можно объяснить физически, если исследовать специальный случай малых значений числа Рейнольдса, достаточных для большой вязкости, откуда система получается более устойчивой. Аналогичное поведение описано в [32]. Чтобы дать более наглядное представление волнового движении, на рис. 7 графически проиллюстрировано воздействие растущего значения скорости на свободную поверхность жидкости в трехмерной области, в ситуации, соответствующей случаям, изображенным на рис. 6в и 6г, причем рис. 7а, 7б, и 7в, соответствуют ситуациям, показанным непрерывными, штриховыми и точечными кривыми на рис. 6.
Рис. 7.
Трехмерная пространственная эволюция деформации свободной поверхности для такой же системы, что рассмотрена на рис. 6.
ВЫВОДЫ
В настоящем исследовании изучено двумерное течение вязкоупругой жидкой пленки по бесконечно длинной нагретой пластине в присутствии нерастворимых поверхностно-активных веществ, распределенных на свободной поверхности. В начальный момент времени подложка и жидкость находятся в состоянии покоя. Внезапно пластина, оставаясь на том же уровне, приводится в движение с осциллирующей скоростью. Решение основных определяющих уравнений производится с помощью обычного преобразования Лапласа. Однако численное обращение преобразования Лапласа используется для трансформации результирующих решений из области параметров Лапласа обратно в исходную область. В этом случае решения во временной области получаются за счет использования метода численного обращения преобразования Лапласа в форме, предложенной Дурбиным. Это показывает, что при решении задач для течения в пограничном слое численное обращение преобразования Лапласа является очень полезной и эффективной схемой.
Численные результаты изображены в графическом виде для прояснения воздействия нескольких физических величин на поведение модели поверхностных волн, перестройку распределения температуры внутри жидкой пленки, линий тока и изотерм. Результаты проведенного исследования показали, что времена релаксации и запаздывания воздействуют незначительно на возвышение поверхности, когда значение безразмерного времени менее 50, и их влияние имеет обратный эффект при большем значении времени. При рассмотрении межфазной границы в трехмерном пространстве отмечено ее колебательное поведение при растущем числе Марангони, так что свободная поверхность прогрессивно уменьшается. Увеличение параметра Рейнольдса показывает, что имеет место непрерывное увеличение значений температуры слоя жидкости по мере приближения к середине слоя, после чего значение температуры будет убывать до достижения конца слоя. Аналогичное поведение отмечается для эффекта числа Марангони. Влияние роста числа Био, когда его значение меньше единицы, состоит в повышении уровня распределения температуры жидкости. В то же время при значениях числа Марангони больше или равных единице имеет место обратный эффект при увеличении числа Био. Найдено, что рост капиллярного числа и числа Пекле приводит к увеличению максимальных значений температуры жидкости. Когда число Рейнольдса возрастает, безразмерная плотность линий тока увеличивается (плотность ячеек линий тока растет); это происходит из-за того, что эффект вязкости убывает при росте числа Рейнольдса.
В предельном случае отсутствия теплопереноса в жидком слое найдено, что число Рейнольдса увеличивает движение поверхностных волн, при этом обратное поведение верно при росте угловой частоты. Стоит отметить, что воздействие возрастающего числа Рейнольдса на изотермический слой жидкости противоположен воздействию угловой частоты. В особом случае малых значений параметра Рейнольдса (${{R}_{e}} \ll 1$) найдено, что влияние увеличения капиллярного числа противоположно влиянию увеличения числа упругости.
Список литературы
Weeks W.T. Numerical inversion of Laplace transforms using Laguerre functions // Journal of the ACM. 1966. V. 13. № 3. P. 419–429.
Hoog F.R., Knight J.H., Stokes A.N. An improved method for numerical inversion of Laplace transforms // SIAM Journal on Scientific and Statistical Computing. 1982. V. 3. № 3. P. 357–366.
Valsa J., Brancik L. Approximate formulae for numerical inversion of Laplace transforms // International Journal of Numerical Modelling. 1998. V. 1. P. 153–166.
Jordan P.M., Puri P. Exact solutions for the flow of a dipolar fluid on a suddenly accelerated flat plate // Acta Mechanica. 1999. V. 137. P. 183–194.
Hayat T., Khan M., Ayub M., Siddiqui A.M. The unsteady Couette flow of a second grade fluid in a layer of porous medium // Arch. Mech. 2005. V. 57. № 5. P. 405–416.
Muzychka Y.S., Yovanovich M.M. Unsteady viscous flows and Stokes’s first problem // International Journal of Thermal Sciences. 2010. V. 49. P. 820–828.
Sirwah M.A. Sloshing waves in a heated viscoelastic fluid layer in an excited rectangular tank // Physics Letters A. 2014. V. 378. P. 3289–3300.
Ramkissoon H., Ramdath G., Comissiong D., Rahaman K. On thermal instabilities in a viscoelastic fluid // International Journal of Non–Linear Mechanics. 2006. V. 41. P. 18–25.
Mukhopadhyay A., Haldar S. Long–wave instabilities of viscoelastic fluid film flowing down an inclined plane with linear temperature variation // Z. Naturforsch. 2010. V. 65a. P. 618–632.
Haitao Q., Mingyu X. Some unsteady unidirectional flows of a generalized Oldroyd–B fluid with fractional derivative // Applied Mathematical Modelling. 2009. V. 33. P. 4184–4191.
Khan S.M., Ali H., Qi H. On accelerated flows of a viscoelastic fluid with the fractional Burgers’ model // Nonlinear Analysis: Real World Applications. 2009. V. 10. P. 2286–2296.
Pozrikidis C. Effect of surfactants on film flow down a periodic wall // J. Fluid Mech. 2003. V. 496. P. 105–127.
Yiantsios S.G., Higgins B.G. A mechanism of Marangoni instability in evaporating thin liquid films due to soluble surfactant // Physics of Fluids. 2010, V. 22. 022102. P. 1–12.
Mikishev A.B., Nepomnyashchy A.A. Long–wavelength Marangoni convection in a liquid layer with insoluble surfactant: Linear theory // Microgravity Sci. Technol. 2020. V. 22. P. 415–423.
Imran M.A., Riaz M.B., Shah N.A, Zafar A.A. Boundary layer flow of MHD generalized Maxwell fluid over an exponentially accelerated infinite vertical surface with slip and Newtonian heating at the boundary // Results in Physics. 2018. V. 8. P. 1061–1067.
Shah N.A., Zafar A.A., Fetecau C. Free convection flows over a vertical plate that applies shear stress to a fractional viscous fluid // Alexandria Engineering Journal. 2018. V. 57. P. 2529–2540.
Qi H., Jin H. Unsteady helical flows of a generalized Oldroyd–B fluid with fractional derivative // Nonlinear Analysis: Real World Applications. 2009. V. 10. P. 2700–2708.
Hayat T., Imtiaz M., Alsaedi A. Boundary layer flow of Oldroyd–B fluid by exponentially stretching sheet // Applied Mathematics and Mechanics (Engl. Ed.). 2016. V. 37. № 5. P. 573–582.
Zakaria K., Sirwah M., Alkharashi S. A two–layer model for superposed electrified Maxwell fluids in presence of heat transfer // Commun. Theor. Phys. 2012. V. 55. № 6. P. 1077–1094.
Jordan P.M., Puri P. Stokes’ first problem for a Rivlin–Ericksen fluid of second grade in a porous half–space // International Journal of Non–Linear Mechanics. 2003. V. 38. P. 1019–1025.
Xue C., Nie J., Tan W. An exact solution of start–up flow for the fractional generalized Burgers’ fluid in a porous half–space // Nonlinear Analysis. 2008. V. 69. P. 2086–2094.
Ruyer-Quil C., Manneville P. Modeling film flows down inclined planes // Eur. Phys. J. B. 1998. V. 6. P. 277–292.
Ajadi S.O. A note of the unsteady flow of dusty viscous fluid between two parallel plates // J. Appl. Math. & Computing. 2005. V. 18. P. 393–403.
Amatousse N., Abderrahmane H.A., Mehidi N. Traveling waves on a falling weakly viscoelastic fluid film // International Journal of Engineering Science. 2012. V. 54. P. 27–41.
Durbin F. Numerical inversion of Laplace transforms: an effective improvement of Dubner and Abate’s method // Comput. J. 1973. V. 17. P. 371–376.
Fan S.C., Li S.M., Yu G.Y. Dynamic fluid–structure interaction analysis using boundary finite element method – finite element method // J. Appl. Mech. 2005. V. 72. P. 591–598.
Honig G., Hirdes U. A method for the numerical inversion of Laplace transforms // J. Comput. Appl. Math. 1984. V. 10. P. 113–132.
Su Y.C., Ma C.C. Transient wave analysis of a cantilever Timoshenko beam subjected to impact loading by Laplace transform and normal mode methods // Int. J. Solids Struct. 2012. V. 49. P. 1158–1176.
Agarwal S., Bhadauria B.S. Flow patterns in linear state of Rayleigh–Bénard convection in a rotating nanofluid layer // Applied Nanoscience. 2014. V. 4. № 8. P. 935–941.
Allias R., Nasir M.A.S., Kechil S.A. Steady thermosolutocapillary instability in fluid layer with nondeformable free surface in the presence of insoluble surfactant and gravity // Appl. Math. Inf. Sci. 2017. V. 11. № 1. P. 87–94.
Alkharashi S.A., Alrashidi A. Dynamical behavior of a porous liquid layer of an Oldroyd–B model flowing over an oscillatory heated substrate // Sadhana, 2020. V. 45. № 7. P. 1–16.
Alkharashi S.A. A model of two viscoelastic liquid films traveling down in an inclined electrified channel // Applied Mathematics and Computation. 2019. V. 355. P. 553–575.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа