1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2021

Известия РАН. Механика жидкости и газа, 2021, № 3, стр. 139-150

ИССЛЕДОВАНИЕ КОНВЕКЦИИ В ВЕРХНЕЙ МАНТИИ, ТЕРМОМЕХАНИЧЕСКИ СВЯЗАННОЙ С ЗОНОЙ СУБДУКЦИИ, И ЕЕ ГЕОДИНАМИЧЕСКИЕ ПРИЛОЖЕНИЯ ДЛЯ АРКТИКИ И СЕВЕРО-ВОСТОЧНОЙ АЗИИ

Л. И. Лобковский a, b, *, М. М. Рамазанов c, **

a Институт океанологии им. П.П. Ширшова РАН
Москва, Россия

b Московский физико-технический институт (Национальный исследовательский университет)
Московская обл., Долгопрудный, Россия

c Институт проблем геотермии и возобновляемой энергетики – филиал Объединенного института высоких температур РАН
Махачкала, Республика Дагестан, Россия

* E-mail: llobkovsky@ocean.ru
** E-mail: mukamay-ipg@mail.ru

Поступила в редакцию 22.07.2020
После доработки 02.10.2020
Принята к публикации 25.12.2020

Полный текст (PDF)

Аннотация

Построено аналитическое решение задачи термической конвекции в верхней мантии, сопряженной с зоной субдукции. При постановке задачи используются результаты по сейсмотомографическому просвечиванию мантии. Путем аналитических методов удается проинтегрировать соответствующую нелинейную задачу математической физики и свести ее к системе нелинейных алгебраических уравнений, которая существенно проще. Основная цель работы заключалась в том, чтобы математически обосновать новую региональную геодинамическую модель эволюции литосферы Арктики и Северо-Восточной Азии [1–5]. В частности, требовалось проверить возможность существования сильно вытянутой по горизонтали одноячеистой структуры течений в верхней мантии.

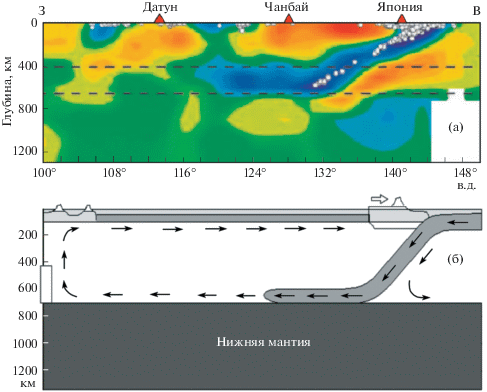
Ключевые слова: верхнемантийная конвекция, субдукция, сейсмотомография, термическая конвекция, ряд Фурье, метод Галеркина

В работах [1–5] изложена новая региональная геодинамическая модель, описывающая меловую и кайнозойскую эволюцию литосферы Арктики и Северо-Восточной Азии. Модель основывается на представлении о существовании горизонтально протяженной конвективной ячейки в верхней мантии, сопряженной с конвейерным механизмом субдукции (движение одной из литосферных плит под другую и погружение в мантию Земли) Тихоокеанской литосферы. Обоснованием модели являются результаты по сейсмотомографическому просвечиванию мантии, опубликованные в [6–8] для Северо-Восточной и Восточной Азии с прилегающими окраинными морями северо-западной части Тихого океана. В качестве примера на рис. 1а показан один из сейсмотомографических разрезов верхней мантии, проведенный перпендикулярно простиранию Японской зоны субдукции. Из этого разреза видно, как погружающийся в зоне субдукции холодный слой литосферы, показанный темным (синим) цветом, достигая переходной зоны между верхней и нижней мантией, трансформируется в протяженный горизонтальный слой мантийного вещества, который распространяется далеко (на первые тысячи километров) под Евразийский континент.

Рис. 1.

Один из вертикальных разрезов мантии в виде сейсмотомограммы [5–7] (а); модель мантийной конвекции, сопряженной с зоной субдукции [1–5] (б).

Отметим, что некоторые аспекты конвекции в верхней мантии, связанной с субдукцией, ранее были исследованы как теоретически [9], так и с помощью физических экспериментов [10] и численного моделирования [4, 5, 11]. В частности, результаты численного моделирования [11] показали характер взаимодействия субдуцированной литосферы, движущейся по подошве верхней мантии, с конвективными течениями в вышележащих слоях мантии.

В настоящей работе, развивающей данное направление исследований, с помощью аналитических и численных методов рассматривается задача о развитии различных режимов верхнемантийной конвекции в области под континентом, примыкающей к зоне субдукции, с учетом движущегося горизонтально вдоль подошвы верхней мантии относительно холодного слоя литосферного вещества. Для выяснения условий возникновения различных режимов конвекции в нашей постановке мы ограничимся простыми исходными предположениями о квазиоднородном слое с постоянной вязкостью, ограниченном снизу фазовой границей, движущейся горизонтально, а сверху – свободной от напряжений горизонтальной поверхностью.

1. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Будем рассматривать квазистационарную двухмерную модель конвекции в верхней мантии, которая считается однородной жидкостью с постоянной вязкостью. Для простоты в математической постановке область, показанную на рис. 1б, будем считать прямоугольной, т.е. примем, что океаническая плита (холодный поток жидкости) в зоне субдукции погружается вертикально вниз и затем движется влево. Горизонтальные границы рассматриваемой области считаются непроницаемыми и, кроме того, верхняя граница свободна (касательное напряжение равно нулю). На нижней фазовой границе 670 км задаем условие прилипания к движущейся со скоростью ${{v}_{1}}$ влево литосфере, хотя, как следует из рис. 1, такое условие следовало бы задавать лишь на части основания, занимаемой в данный момент времени литосферным слоем. Однако для оценки максимального эффекта движения плиты будем это условие задавать на всем основании. Рассмотрим условия для температуры. В результате вертикального погружения холодной плиты можно считать температуру на правой границе равной условному нулю. На нижней границе температура растет от нуля до невозмущенного значения, равного единице в безразмерном исчислении. Для простоты будем считать указанный рост линейным. На левой вертикальной границе полагаем, что температура равна невозмущенному распределению, т.е. линейно убывает от единицы до нуля. Наконец, на верхней границе температура должна быть равна условному нулю. Все эти граничные условия показаны на рис. 2.

Рис. 2.

Постановочный рисунок к задаче с указанием граничных условий. Основание прямоугольника L = 5.5.

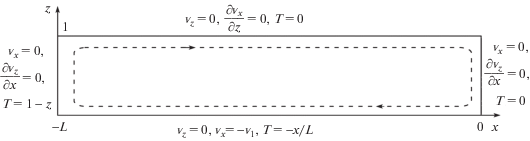
Граничное условие для скорости на правой границе (рис. 2) отражает условие скольжения, хотя более адекватным было бы использовать условие прилипания к погружающейся плите. Ниже будет показано, что картина конвекции от такой подмены слегка меняется лишь в окрестности плиты, а в основной области ее характеристики от этого не зависят. С целью обоснования этого утверждения ниже рассматривается вспомогательная линейная задача.

Рассматриваемая квазистационарная задача в безынерционном приближении Стокса и в приближении Буссинеска [12] подчиняется следующей системе уравнений

$ - \nabla p + \mu \Delta {\mathbf{v}} + {{\rho }_{0}}\left[ {1 - \beta \left( {T - {{T}_{0}}} \right)} \right]{\mathbf{g}} = 0$
(1.1)
$\nabla {\mathbf{v}} = 0,\quad {{\rho }_{0}} = {\text{const}}$
${\mathbf{v}}\nabla T = \chi \Delta T,\quad \chi = \frac{\lambda }{{{{\rho }_{0}}{{C}_{p}}}}$

Здесь: ${\mathbf{v}}$ – поле скоростей; $T$ – температура; $\mu $ – динамическая вязкость; $\beta $ – коэффициент теплового расширения; g – ускорение свободного падения; $\lambda $ – коэффициент теплопроводности; ${{С}_{p}}$ – удельная изобарическая теплоемкость; $\chi $ – температуропроводность.

Введем функцию тока – Ψ и систему координат, как показано на рис. 2. Используя следующие характерные масштабы величин: h – толщина верхней мантии; ${{\rho }_{0}}$ – значение плотности среды; $\lambda {\text{/}}{{\rho }_{0}}{{С}_{p}}h$ – скорости; ${{\rho }_{0}}{{С}_{p}}{{h}^{2}}{\text{/}}\lambda $ – времени; $\Delta T$ – перепад температур на левой границе слоя, запишем систему (1.1) в безразмерном виде

(1.2)
$\begin{gathered} {{\Delta }^{2}}\Psi = Ra\frac{{\partial T}}{{\partial x}},\quad {{v}_{x}}\frac{{\partial T}}{{\partial x}} + {{v}_{z}}\frac{{\partial T}}{{\partial z}} = \frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}} \\ {{v}_{x}} = \frac{{\partial \Psi }}{{\partial z}},\quad {{v}_{z}} = - \frac{{\partial \Psi }}{{\partial x}} \\ Ra = \frac{{\rho _{0}^{2}{{C}_{p}}g\beta \Delta T{{h}^{3}}}}{{\lambda \mu }} \\ \end{gathered} $
Ra – число Рэлея.

Граничные условия

(1.3)
$\begin{gathered} x = 0{\kern 1pt} :\quad \Psi = 0,\quad \frac{{{{\partial }^{2}}\Psi }}{{\partial {{x}^{2}}}} = 0,\quad T = 0 \\ x = - L{\kern 1pt} :\quad \Psi = 0,\quad \frac{{{{\partial }^{2}}\Psi }}{{\partial {{x}^{2}}}} = 0,\quad T = 1 - z \\ z = 0{\kern 1pt} :\quad \Psi = 0,\quad \frac{{\partial \Psi }}{{\partial z}} = - {{v}_{1}},\quad T = - \frac{x}{L} \\ z = 1{\kern 1pt} :\quad \Psi = 0,\quad \frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}} = 0,\quad T = 0 \\ \end{gathered} $

Это полная нелинейная задача. Прежде чем приступить к ее решению, рассмотрим вспомогательную линейную задачу.

2. ЛИНЕЙНАЯ ЗАДАЧА ДЛЯ ПОЛЯ СКОРОСТЕЙ

Эта задача отличается от основной двумя фактами. С одной стороны ее граничные условия ближе к обозначенной геофизической задаче, а с другой – в ней температура не вычисляется, а задается в виде функции двух переменных, которая удовлетворяет всем граничным условиям. Уравнение и граничные условия для функции тока имеют вид

(2.1)
$\begin{gathered} {{\Delta }^{2}}\Psi = Ra\frac{{\partial T}}{{\partial x}} \\ {{v}_{x}} = \frac{{\partial \Psi }}{{\partial z}},\quad {{v}_{z}} = - \frac{{\partial \Psi }}{{\partial x}} \\ \end{gathered} $
(2.2)
$\begin{gathered} x = 0{\kern 1pt} :\quad \Psi = 0,\quad \frac{{\partial \Psi }}{{\partial x}} = {{v}_{0}} \\ x = - L{\kern 1pt} :\quad \Psi = 0,\quad \frac{{{{\partial }^{2}}\Psi }}{{\partial {{x}^{2}}}} = 0 \\ z = 0{\kern 1pt} :\quad \Psi = 0,\quad \frac{{\partial \Psi }}{{\partial z}} = - {{v}_{1}} \\ z = 1{\kern 1pt} :\quad \Psi = 0,\quad \frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}} = 0 \\ \end{gathered} $
где ${{v}_{0}}$ – скорость погружения плиты; ${{v}_{1}}$ – скорость движения плиты вдоль основания.

В отличие от основной задачи (1.3), здесь на правой границе задана скорость погружения плиты, а не условие скольжения.

Ищем решение в виде суммы двух функций

(2.3)
$\Psi = {{\Psi }_{1}} + {{\Psi }_{2}}$

Первая из этих функций удовлетворяет неоднородному уравнению (2.1) и граничным условиям (1.3), а вторая функция однородному уравнению (2.1) и граничным условиям, выбранным так, чтобы суммарная функция (2.3) удовлетворяла условиям (2.2). В силу линейности задачи сумма (2.3) будет удовлетворять задаче (2.1), (2.2) полностью.

В качестве температуры, удовлетворяющей всем условиям (1.3), возьмем следующую функцию:

$T = \frac{{\left( {z - 1} \right)x}}{L}$

Для получения решения используем метод Галеркина и разложения Фурье. Можно показать, что первая функция (2.3), т.е. точное решение неоднородного уравнения (2.1) с условиями (1.3) имеет вид

(2.4)
${{\Psi }_{1}} = Ra\sum\limits_{k = 1}^{{{N}_{x}}} {{{\varphi }_{{1k}}}(z)\sin {{\alpha }_{k}}x} + {{v}_{1}}\sum\limits_{k = 1}^{{{N}_{x}}} {{{\psi }_{{1k}}}(z)\sin {{\alpha }_{k}}x} $
(2.5)
$\left\{ \begin{gathered} {{\varphi }_{{1k}}} = {{A}_{k}}\left( {z - 1} \right)\left( {1 - \frac{{{\text{ch}}{{\alpha }_{k}}z + {\text{ch}}{{\alpha }_{k}}(z - 1)}}{{1 + {\text{ch}}{{\alpha }_{k}}}}} \right) + {{C}_{{1k}}}\left( {z - 1} \right){\text{sh}}{{\alpha }_{k}}z + {{C}_{{2k}}}z{\text{sh}}{{\alpha }_{k}}\left( {z - 1} \right) \hfill \\ {{C}_{{1k}}} = {{A}_{k}}\frac{{{\text{sh}}{{\alpha }_{k}}\left( {{\text{sh}}{{\alpha }_{k}} + {{\alpha }_{k}}} \right)}}{{\left( {1 + {\text{ch}}{{\alpha }_{k}}} \right)\left( {{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}} \right)}},\quad {{C}_{{2k}}} = - {{A}_{k}}\frac{{{{\alpha }_{k}}{\text{sh}}{{\alpha }_{k}}}}{{\left( {{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}} \right)}} \hfill \\ {{\alpha }_{k}} = \frac{{\pi k}}{L},\quad {{A}_{k}} = - \frac{{2\left( {1 - cos{{\alpha }_{k}}L} \right)}}{{{{\alpha }_{k}}^{5}{{L}^{2}}}},\quad k = 1,2,... \hfill \\ \end{gathered} \right.$
$\left\{ \begin{gathered} {{\psi }_{{1k}}} = 2\frac{{1 - \cos \pi k}}{{\pi k}}\left[ {{{C}_{{3k}}}z{\text{sh}}{{\alpha }_{k}}(z - 1) + {{C}_{{4k}}}\left( {z - 1} \right){\text{sh}}{{\alpha }_{k}}z} \right] \hfill \\ {{C}_{{3k}}} = - \frac{{{\text{ch}}{{\alpha }_{k}}}}{{{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}}},\quad {{C}_{{4k}}} = \frac{1}{{{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}}} \hfill \\ \end{gathered} \right.$

Решение однородного уравнения запишем в виде

(2.6)
${{\Psi }_{2}} = \sum\limits_{k = 1}^{{{N}_{x}}} {{{a}_{k}}{{\varphi }_{{2k}}}(z)\sin {{\alpha }_{k}}x + } \sum\limits_{m = 1}^{{{N}_{z}}} {{{b}_{m}}{{\psi }_{{2m}}}(x)\sin \pi mz} \,$
$\begin{gathered} x = 0{\kern 1pt} :\quad {{\Psi }_{2}} = 0,\quad \frac{{\partial {{\Psi }_{2}}}}{{\partial x}} = {{v}_{0}} - \frac{{\partial {{\Psi }_{1}}}}{{\partial x}} \\ x = - L{\kern 1pt} :\quad {{\Psi }_{2}} = 0,\quad \frac{{{{\partial }^{2}}{{\Psi }_{2}}}}{{\partial {{x}^{2}}}} = 0 \\ z = 0{\kern 1pt} :\quad {{\Psi }_{2}} = 0,\quad \frac{{\partial {{\Psi }_{2}}}}{{\partial z}} = 0 \\ z = 1{\kern 1pt} :\quad \Psi = 0,\quad \frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}} = 0 \\ \end{gathered} $
где ${{a}_{k}},{{b}_{m}}$ $k,m = 1,2,...$ – искомые постоянные числа.

Функции ${{\varphi }_{{2k}}}(z),$ ${{\psi }_{{2m}}}(x)$ – являются решениями следующих задач:

$\varphi _{{2k}}^{{IV}} - 2\alpha _{k}^{2}\varphi _{{2k}}^{{''}} + \alpha _{k}^{4}{{\varphi }_{{2k}}} = 0$
$\begin{gathered} z = 0{\kern 1pt} :\quad {{\varphi }_{{2k}}} = 0,\quad \varphi _{{2k}}^{'} = 1 \\ z = 1{\kern 1pt} :\quad {{\varphi }_{{2k}}} = 0,\quad \varphi _{{2k}}^{{''}} = 0 \\ \end{gathered} $
$\psi _{{2m}}^{{IV}} - 2{{\pi }^{2}}{{m}^{2}}\psi _{{2m}}^{{''}} + {{\pi }^{4}}{{m}^{4}}{{\psi }_{{2m}}} = 0$
$\begin{gathered} x = 0{\kern 1pt} :\quad {{\psi }_{{2m}}} = 0,\quad \psi _{{2m}}^{'} = 1 \\ x = - L{\kern 1pt} :\quad \,{{\psi }_{{2m}}} = 0,\quad \psi _{{2m}}^{{''}} = 0 \\ \end{gathered} $

Решение первой задачи есть

$\begin{gathered} {{\varphi }_{{2k}}}(z) = {{d}_{{1k}}}z{\text{sh}}{{\alpha }_{k}}(z - 1) + {{d}_{{2k}}}(z - 1){\text{sh}}{{\alpha }_{k}}z,\quad {{\alpha }_{k}} = \frac{{\pi k}}{L} \\ {{d}_{{1k}}} = - \frac{{2{\text{ch}}{{\alpha }_{k}}}}{{{\text{sh}}2{{\alpha }_{k}} - 2{{\alpha }_{k}}}},\quad {{d}_{{2k}}} = \frac{2}{{{\text{sh}}2{{\alpha }_{k}} - 2{{\alpha }_{k}}}} \\ \end{gathered} $

Решение второй задачи получим в виде

$\begin{gathered} {{\psi }_{{2m}}}(x) = {{c}_{{1m}}}x{\text{sh}}\pi m(x + L) + {{c}_{{2m}}}(x + L){\text{sh}}\pi mx \\ {{c}_{{1m}}} = \frac{{2{\text{ch}}\pi mL}}{{{\text{sh}}2\pi mL - 2\pi mL}},\quad {{c}_{{2m}}} = - \frac{2}{{{\text{sh}}2\pi mL - 2\pi mL}} \\ \end{gathered} $

Невыполненными остались следующие два условия:

$\begin{gathered} z = 0{\kern 1pt} :\quad \frac{{\partial {{\Psi }_{2}}}}{{\partial z}} = 0 \\ x = 0{\kern 1pt} :\quad \frac{{\partial {{\Psi }_{2}}}}{{\partial x}} = {{\operatorname{v} }_{0}} - \frac{{\partial {{\Psi }_{1}}}}{{\partial x}} \\ \end{gathered} $

Эти условия запишутся в виде

(2.7)
$\begin{gathered} \sum\limits_{k = 1}^{{{N}_{x}}} {{{a}_{k}}\sin {{\alpha }_{k}}x + } \sum\limits_{m = 1}^{{{N}_{z}}} {{{b}_{m}}\pi m} {{\psi }_{{2m}}}(x) = 0 \\ \sum\limits_{k = 1}^{{{N}_{x}}} {{{a}_{k}}{{\alpha }_{k}}{{\varphi }_{{2k}}}(z) + } \sum\limits_{m = 1}^{{{N}_{z}}} {{{b}_{m}}\sin \pi mz} = {{v}_{0}} - Ra\sum\limits_{k = 1}^{{{N}_{x}}} {{{\alpha }_{k}}{{\varphi }_{{1k}}}(z)} - {{v}_{1}}\sum\limits_{k = 1}^{{{N}_{x}}} {{{\alpha }_{k}}{{\psi }_{{1k}}}(z)} \\ \end{gathered} $

Из (2.7) найдем все коэффициенты ${{a}_{k}},{{b}_{m}}$ $k{\text{,}}m = 1,2,...$. Умножая первое и второе уравнения (2.7) соответственно на функции $\sin {{\alpha }_{i}}x$ и $\sin \pi jz$ и, интегрируя их на соответствующем отрезке, получим

$\begin{gathered} {{a}_{i}} + \sum\limits_{m = 1}^{{{N}_{z}}} {{{A}_{{mi}}}{{b}_{m}}} = 0,\quad i = 1,2... \\ \sum\limits_{k = 1}^{{{N}_{x}}} {{{B}_{{kj}}}{{a}_{k}} + } \,{{b}_{j}} = \int\limits_0^1 {\left( {{{v}_{0}} - Ra\sum\limits_{k = 1}^{{{N}_{x}}} {{{\alpha }_{k}}{{\varphi }_{{1k}}}(z)} - {{v}_{1}}\sum\limits_{k = 1}^{{{N}_{x}}} {{{\alpha }_{k}}{{\psi }_{{1k}}}(z)} } \right)} \sin \pi jzdz,\quad j = 1,2,... \\ \end{gathered} $
${{A}_{{mi}}} = \pi m\int\limits_{ - L}^0 {{{\psi }_{{2m}}}(x) \cdot \sin {{\alpha }_{i}}xdx} = 0,\quad {{B}_{{kj}}} = {{\alpha }_{k}}\int\limits_0^1 {{{\varphi }_{{2k}}}(z) \cdot \sin \pi jzdz} $

Определяя из этой системы ${{a}_{k}},{{b}_{m}}$ $k{\text{,}}m = 1,2,...$, найдем второе решение (2.6), а вместе с ним и полное аналитическое решение

$\Psi = {{\Psi }_{1}} + {{\Psi }_{2}}$

Обсуждение этих решений приводится ниже.

3. НЕЛИНЕЙНАЯ ЗАДАЧА

Перейдем к нелинейной задаче, в которой температура нелинейно взаимосвязана с функцией тока, т.е. к задаче (1.2)–(1.3). Представим решение в виде конечных сумм Фурье по координате x следующим образом

(3.1)
$T = \frac{{\left( {z - 1} \right)x}}{L} + \sum\limits_{i = 1}^{{{N}_{z}}} {\sum\limits_{k = 1}^{{{N}_{x}}} {{{\xi }_{{ik}}}\sin \pi iz\sin {{\alpha }_{k}}x} } ,\quad \Psi = \sum\limits_{k = 1}^{{{N}_{x}}} {{{\psi }_{k}}(z)} \sin {{\alpha }_{k}}x,\quad {{\alpha }_{k}} = \frac{{\pi k}}{L}$

В (3.1) неизвестными являются функции ${{\psi }_{k}}(z),$ $k = 1,2,...$ и постоянные числа ${{\xi }_{{ik}}},i = 1,2,...;$ $k = 1,2,...$. При этом температура удовлетворяет всем граничным условиям, а функция тока пока только условиям на вертикальных границах. Остальным условиям необходимо удовлетворить с помощью функций ${{\psi }_{k}}(z),$ $k = 1,2,...$. Найдем эти функции. Подставляя (3.1) в первое уравнение в системе (1.2), (1.3), имеем

(3.2)
$\begin{gathered} \psi _{k}^{{IV}} - 2\alpha _{k}^{2}\psi _{k}^{{''}} + \alpha _{k}^{4}{{\psi }_{k}} = - Ra\frac{{2\left( {1 - cos{{\alpha }_{k}}L} \right)\left( {z - 1} \right)}}{{{{\alpha }_{k}}{{L}^{2}}}} + Ra\sum\limits_{i = 1}^{{{N}_{x}}} {\sum\limits_{m = 1}^{{{N}_{z}}} {{{\alpha }_{m}}{{\xi }_{{im}}}c_{{km}}^{0}\sin \pi iz} } \\ c_{{km}}^{0} = \frac{{2{{\alpha }_{m}}}}{L}\int\limits_{ - L}^0 {\cos {{\alpha }_{m}}x\sin {{\alpha }_{k}}xdx} ,\quad {{\alpha }_{m}} = \frac{{\pi m}}{L},\quad m = 1,2,... \\ \end{gathered} $

Граничные условия

(3.3)
$\begin{gathered} z = 0{\kern 1pt} :\quad {{\psi }_{k}} = 0,\quad \psi _{k}^{'} = {{v}_{1}}\frac{{2\left( {1 - \cos \pi k} \right)}}{{\pi k}},\quad k = 1,2,... \\ z = 1{\kern 1pt} :\quad {{\psi }_{k}} = 0,\quad \psi _{k}^{{''}} = 0 \\ \end{gathered} $

Можно показать, что решение этой задачи имеет вид

(3.4)
${{\psi }_{k}} = Ra\left[ {{{\psi }_{{1k}}} + \sum\limits_{i = 1}^{{{N}_{z}}} {\sum\limits_{m = 1}^{{{N}_{x}}} {{{\psi }_{{ki}}}{{\alpha }_{m}}c_{{km}}^{0}{{\xi }_{{im}}}} } } \right] + {{v}_{1}}{{\psi }_{{2k}}},\quad k = 1,2,...{{N}_{x}}$
$\left\{ \begin{gathered} {{\psi }_{{1k}}} = {{A}_{k}}\left( {z - 1} \right)\left( {1 - \frac{{{\text{ch}}{{\alpha }_{k}}z + {\text{ch}}{{\alpha }_{k}}(z - 1)}}{{1 + {\text{ch}}{{\alpha }_{k}}}}} \right) + {{C}_{{1k}}}\left( {z - 1} \right){\text{sh}}{{\alpha }_{k}}z + {{C}_{{2k}}}z{\text{sh}}{{\alpha }_{k}}\left( {z - 1} \right) \hfill \\ {{C}_{{1k}}} = {{A}_{k}}\frac{{{\text{sh}}{{\alpha }_{k}}\left( {{\text{sh}}{{\alpha }_{k}} + {{\alpha }_{k}}} \right)}}{{\left( {1 + {\text{ch}}{{\alpha }_{k}}} \right)\left( {{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}} \right)}},\quad {{C}_{{2k}}} = - {{A}_{k}}\frac{{{{\alpha }_{k}}{\text{sh}}{{\alpha }_{k}}}}{{\left( {{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}} \right)}} \hfill \\ {{\alpha }_{k}} = \frac{{\pi k}}{L},\quad {{A}_{k}} = - \frac{{2\left( {1 - cos{{\alpha }_{k}}L} \right)}}{{{{\alpha }_{k}}^{5}{{L}^{2}}}},\quad k = 1,2,... \hfill \\ \end{gathered} \right.$
$\left\{ \begin{gathered} {{\psi }_{{ki}}} = \frac{{\sin \pi iz}}{{{{{({{\pi }^{2}}{{i}^{2}} + \alpha _{k}^{2})}}^{2}}}} + {{B}_{{ki}}}z{\text{sh}}{{\alpha }_{k}}(z - 1) + {{C}_{{ki}}}(z - 1){\text{sh}}{{\alpha }_{k}}z \hfill \\ {{B}_{{ki}}} = \frac{{\pi i{\text{ch}}{{\alpha }_{k}}}}{{{{{({{\pi }^{2}}{{i}^{2}} + \alpha _{k}^{2})}}^{2}}\left( {{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}} \right)}},\quad {{C}_{{ki}}} = - \frac{1}{{{\text{ch}}{{\alpha }_{k}}}}{{B}_{{ki}}},\quad {{\alpha }_{k}} = \frac{{\pi k}}{L},\quad k = 1,2,... \hfill \\ \end{gathered} \right.$
$\left\{ \begin{gathered} {{\psi }_{{2k}}} = 2\frac{{1 - \cos \pi k}}{{\pi k}}\left[ {{{C}_{{3k}}}z{\text{sh}}{{\alpha }_{k}}(z - 1) + {{C}_{{4k}}}\left( {z - 1} \right)sh{{\alpha }_{k}}z} \right] \hfill \\ {{C}_{{3k}}} = - \frac{{{\text{ch}}{{\alpha }_{k}}}}{{{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}}},\quad {{C}_{{4k}}} = \frac{1}{{{\text{sh}}{{\alpha }_{k}}{\text{ch}}{{\alpha }_{k}} - {{\alpha }_{k}}}},\quad {{\alpha }_{k}} = \frac{{\pi k}}{L},\quad k = 1,2,... \hfill \\ \end{gathered} \right.$

В решении (3.2)–(3.4) неизвестными остались лишь постоянные числа ${{\xi }_{{ik}}},$ $i = 1,2,...{{N}_{z}};$ $k = 1,2,...{{N}_{x}}$. Для их нахождения необходимо использовать уравнение переноса тепла.

Рассмотрим это уравнение

(3.5)
$\frac{{\partial \Psi }}{{\partial z}}\frac{{\partial T}}{{\partial x}} - \frac{{\partial \Psi }}{{\partial x}}\frac{{\partial T}}{{\partial z}} = \Delta T$

Для нахождения искомых величин, умножая уравнение (3.5) на $\sin \pi mz \cdot \sin {{\alpha }_{n}}x,$ $m = 1,2,...{{N}_{z}};$ $n = 1,2,...{{N}_{x}}$ и, интегрируя по всей области, имеем следующую нелинейную алгебраическую систему уравнений

(3.6)
$\int\limits_0^1 {\int\limits_{ - L}^0 {\left( {\frac{{\partial \Psi }}{{\partial z}}\frac{{\partial T}}{{\partial x}} - \frac{{\partial \Psi }}{{\partial x}}\frac{{\partial T}}{{\partial z}} - \Delta T} \right)} } \sin \pi mz \cdot \sin {{\alpha }_{n}}xdxdz = 0,\quad m = 1,2,...{{N}_{z}};\quad n = 1,2,...{{N}_{x}}$

Система (3.6) дает ${{N}_{z}}{{N}_{x}}$ уравнений для определения ${{N}_{z}}{{N}_{x}}$ чисел ${{\xi }_{{ik}}}$. Отметим, что все двойные интегралы в (3.6) удается вычислить и в результате в явном виде получаем нелинейную алгебраическую систему уравнений относительно чисел ${{\xi }_{{ik}}}$

${{I}_{1}}(m,n) + {{I}_{2}}(m,n) + {{I}_{3}}(m,n) = 0,\quad m = 1,2,...{{N}_{z}};\quad n = 1,2,...{{N}_{x}}$
$\begin{gathered} {{I}_{1}}(m,n) = \frac{1}{L}\sum\limits_{k = 1}^{{{N}_{x}}} {{{F}_{{13}}}(k,m){{a}_{{13}}}(k,n)} + \sum\limits_{k = 1}^{Nx} {\sum\limits_{l = 1}^{Nx} {{{F}_{{14}}}(k,l,m){{a}_{{14}}}(k,l,n)} } \\ {{I}_{2}}(m,n) = \sum\limits_{k = 1}^{{{N}_{x}}} {{{F}_{{21}}}(k,m)} {{a}_{{21}}}(k,n) + \sum\limits_{k = 1}^{Nx} {\sum\limits_{l = 1}^{Nx} {{{F}_{{22}}}(k,l,m){{a}_{{22}}}(k,l,n)} } \\ {{I}_{3}}(m,n) = \sum\limits_{k = 1}^{{{N}_{x}}} {{{F}_{{13}}}(k,m){{a}_{{13}}}(k,n)} \\ \end{gathered} $
$\begin{gathered} {{a}_{{11}}}(n) = \int\limits_{ - L}^0 {sin{{\alpha }_{n}}xdx} ,\quad {{a}_{{12}}}(m,n) = \int\limits_{ - L}^0 {cos{{\alpha }_{m}}xsin{{\alpha }_{n}}xdx} ,\quad {{a}_{{13}}}(k,n) = \int\limits_{ - L}^0 {\sin {{\alpha }_{k}}xsin{{\alpha }_{n}}xdx} \\ {{a}_{{14}}}(k,m,n) = \int\limits_{ - L}^0 {\sin {{\alpha }_{k}}xcos{{\alpha }_{m}}xsin{{\alpha }_{n}}xdx,\quad } {{a}_{{21}}}(k,n) = \int\limits_{ - L}^0 {\frac{x}{L}cos{{\alpha }_{k}}xsin{{\alpha }_{n}}xdx} \\ {{a}_{{22}}}(k,m,n) = \int\limits_{ - L}^0 {cos{{\alpha }_{k}}xsin{{\alpha }_{m}}xsin{{\alpha }_{n}}xdx} ,\quad {{a}_{{31}}}(k,n) = \int\limits_{ - L}^0 {\sin {{\alpha }_{k}}xsin{{\alpha }_{n}}xdx} \\ \end{gathered} $
$\begin{gathered} {{F}_{{11}}}(m) = \int\limits_0^1 {\left( {z - 1} \right)} \sin \pi mzdz,\quad {{F}_{{12}}}(k,m) = \int\limits_0^1 {{{f}_{3}}(k,z)} \sin \pi mzdz \\ {{F}_{{13}}}(k,m) = \int\limits_0^1 {\left( {z - 1} \right)\psi _{k}^{'}(k,z)} \sin \pi mzdz,\quad {{F}_{{14}}}(k,l,m) = \int\limits_0^1 {{{f}_{1}}(k,z)} {{f}_{3}}(l,z)\sin \pi mzdz \\ {{F}_{{21}}}(k,m) = \int\limits_0^1 {{{f}_{2}}(k,z)\sin \pi mzdz} ,\quad {{F}_{{22}}}(k,l,m) = \int\limits_0^1 {{{f}_{2}}(k,z){{f}_{4}}(l,z)\sin \pi mzdz} \\ \end{gathered} $
$\begin{gathered} {{F}_{{31}}}(k,m) = \int\limits_0^1 {{{f}_{5}}(k,z)\sin \pi mzdz} \\ {{f}_{1}}(k,z) = \psi _{k}^{'},\quad {{f}_{2}}(k,z) = - {{\alpha }_{k}}{{\psi }_{k}},\quad {{f}_{3}}(k,z) = {{\alpha }_{k}}{{\theta }_{k}},\quad {{f}_{4}}(k,z) = \theta _{k}^{'},\quad {{f}_{5}}(k,z) = - [\theta _{k}^{{''}} - \alpha _{k}^{2}{{\theta }_{k}}] \\ {{\theta }_{k}} = \sum\limits_{i = 1}^{{{N}_{z}}} {{{\xi }_{{ik}}}} \sin \pi iz \\ \end{gathered} $

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Выбранное распределение температуры на правой и нижней границах основано, в частности, на рис. 1a. Из этого разреза мантии видно, как погружающееся в зону субдукции холодное вещество, достигая переходной зоны между верхней и нижней мантией, поворачивает и далее трансформируется в протяженный горизонтальный слой. Приведем оценку, позволяющую показать, что при погружении холодной плиты она, достигнув границы между верхней и нижней мантией, не успевает существенно нагреться. Для этого приведем сравнение характерных времен погружения холодной плиты и ее разогрева до температуры окружающей среды:

(4.1)
${{t}_{{{\text{погр}}{\text{.}}}}} = \frac{{{{H}_{{{\text{в}}{\text{.м}}{\text{.}}}}}}}{{{{v}_{{{\text{погр}}{\text{.}}}}}}},\quad {{t}_{{{\text{нагр}}{\text{.}}}}} = \frac{{{{{\left( {{{H}_{{{\text{т}}{\text{.п}}{\text{.}}}}}} \right)}}^{2}}}}{\chi }$

Здесь ${{t}_{{{\text{погр}}{\text{.}}}}},\,\,{{t}_{{{\text{нагр}}{\text{.}}}}}$ – характерные времена погружения вещества холодной плиты на глубину верхней мантии и прогрева толщины плиты соответственно; ${{H}_{{{\text{в}}{\text{.м}}{\text{.}}}}},\,\,{{H}_{{{\text{т}}{\text{.п}}{\text{.}}}}}$ – толщина верхней мантии и толщина погружающейся плиты соответственно; ${{v}_{{{\text{погр}}}}}$ – скорость погружения плиты; $\chi $ – температуропроводность горных пород.

Примем следующие характерные значения указанных величин: Hв.м. = 700 км = 7 × 105 м, Hт.п. = 50–100 км ≈ 75 км = 0,75 × 105 м

(4.2)
${{v}_{{{\text{погр}}{\text{.}}}}} = 5\,\,{\text{см/год}} \approx 1.6 \times {{10}^{{ - 9}}}\,\,{\text{м/c}},\quad \chi = {{10}^{{ - 6}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 7}}}\,\,{{{\text{м}}}^{{\text{2}}}}{\text{/c}} \approx 0.5 \times {{10}^{{ - 6}}}\,\,{{{\text{м}}}^{{\text{2}}}}{\text{/c}}$

Подставляя величины (4.2) в формулы (4.1), получим

$\frac{{{{t}_{{{\text{погр}}{\text{.}}}}}}}{{{{t}_{{{\text{нагр}}{\text{.}}}}}}} = 0.039\sim 4 \times {{10}^{{ - 2}}}$

Видно, что для прогрева плиты до температуры окружающей среды необходимо более чем на порядок больше времени и, следовательно, плита не успевает существенно нагреться. Поэтому, благодаря быстрому погружению плиты, температуру на правой границе можно считать равной условному нулю.

Результаты решения задачи, полученные в рамках линейной задачи для числа Рэлея ${\text{Ra}} = 2.4 \times {{10}^{4}}$ и скоростей плиты ${{v}_{0}} = {{v}_{1}} = 4.6$ см/год, показаны на рис. 3. Решение состоит из двух слагаемых (2.4)–(2.6). Первая составляющая связана с конвективным течением, обусловленным неоднородностью температуры и движением плиты вдоль основания области со скоростью ${{v}_{1}}$ (кривые 1 на рис. 3). Второе слагаемое дает поле течений, вызванное погружением литосферной плиты со скоростью ${{v}_{0}}$, т.е. непосредственно субдукцией. Эта составляющая на рис. 3 обозначена кривой 2. Кривые 3 на рис. 3 – это сумма первых двух составляющих. Из кривой 2 видно, что погружающаяся плита вызывает заметное поле течений только в небольшой области, примыкающей к плите. В то же время конвективная составляющая вызывает конечное течение во всей области. Сказанное подтверждает сравнение первой и третьей кривых.

Рис. 3.

Зависимости функции тока (а), вертикальной (б) и горизонтальной (в) компонент скорости от горизонтальной координаты x при ${\text{Ra}} = 2.4 \times {{10}^{4}}$; ${{v}_{0}} = {{v}_{1}} = 4.6$ см/год; $z = 0.5$ для (а), (б); $z = 0.99$ для (в); линии: 1 – составляющая, связанная с неоднородностью температуры и движением плиты по основанию области (подошвы); 2 – составляющая, связанная только с погружением литосферной плиты на правой границе; 3 – суммарная составляющая.

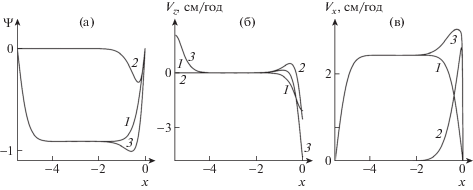
На рис. 3б,в показаны характерные распределения вертикальных и горизонтальных компонент скорости. Эти рисунки подтверждают, что для характерных значений параметров задачи первая составляющая, т.е. течение, вызванное неоднородностью температуры и движением плиты по основанию области, существенно доминирует над гидродинамическим воздействием, вызванным погружением плиты везде за исключением примыкающей к плите области толщиной, сопоставимой с толщиной самой плиты.

Рассмотрим результаты по нелинейной задаче. Задача, помимо отмеченного выше метода Галеркина, была решена и другим методом, причем в нестационарном варианте. А именно, на текущем временном шаге при заданной матрице ${{\xi }_{{k,i}}}$ поле скоростей определяется аналитическими выражениями (3.1)–(3.4). Затем при заданном поле скоростей нестационарное уравнение переноса тепла на данном временном шаге решается методом прогонки. Далее из поля температуры ${{T}_{{k,i}}}$, используя (3.1) и обратное преобразование Фурье, находим новые значения ${{\xi }_{{k,i}}}$. После определенного числа итерационных шагов переходим на новый временной шаг. Процесс продолжается до выхода на стационарное решение. При тестовых расчетах результаты, полученные обоими методами, совпали. Для рис. 4a уже значения ${{N}_{x}} = 10,$ ${{N}_{z}} = 3$ в методе Галеркина дают хорошую точность. Однако с ростом числа Рэлея число мод требуется все больше и время счета становится больше, чем у второго метода.

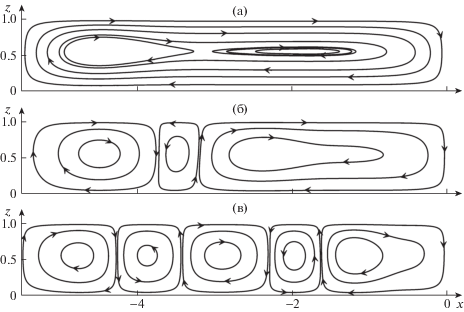
Рис. 4.

Структура конвекции в области верхней мантии без учета движения плиты (${{v}_{1}}$ = 0) при числах Рэлея: Ra = 103 (а); Ra = 5 × 103 (б); Ra = 5 × 104 (в).

Рассмотрим следующие характерные для верхней мантии значения параметров

${{H}_{{в.м.}}} = 6.7 \times {{10}^{5}}\,\,{\text{м}},\quad \Delta T = 2 \times {{10}^{3}}{{\,}^{{^{ \circ }}}}{\text{C}},\quad \chi = 5 \times {{10}^{{ - 7}}}\;{{{\text{м}}}^{{\text{2}}}}{\text{/c}},\quad \beta = {{10}^{{ - 5}}}\,\,1{\text{/}}{}^{{^{ \circ }}}{\text{C}},\quad \nu = 5 \times {{10}^{{18}}}\;{{{\text{м}}}^{{\text{2}}}}{\text{/c}}$

Для этих величин получим следующую оценку при числе Рэлея ${\text{Ra}} = 2.4 \times {{10}^{4}}$.

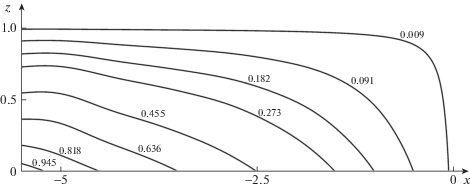
Ниже за основную принята близкая величина ${\text{Ra}} = 5 \times {{10}^{4}}$. Сначала рассмотрим случай, когда подошва покоится (${{v}_{1}} = 0$). На рис. 4a показаны результаты расчета линий тока при числе Рэлея ${\text{Ra}} = {{10}^{3}}$. Видно, что внешние линии тока охватывают всю рассматриваемую область и соответствуют одноячеистой структуре. Однако в центральной части образуются две индуцированные ячейки, вращающиеся в ту же сторону, что и внешняя ячейка.

На рис. 4б показаны линии тока для бо̀льшего числа Рэлея ${\text{Ra}} = 5 \times {{10}^{3}}$. Как видно из рисунка, в этом случае течение распадается на три неравномерных ячейки. При дальнейшем увеличении числа Рэлея образуется бо̀льшее число ячеек, как это показано на рис. 4в. Из рисунка видно, что в случае ${\text{Ra}} = 5 \times {{10}^{4}}$ образуется пять неравных конвективных ячеек.

На рис. 5 показаны изотермы для числа Рэлея Ra = 1000. Обратим внимание на то, что на рисунках 4а, 6б и 6в внутренние ячейки образуют встречное близкое к вертикальному течение в примыкающей области и может возникнуть впечатление, что течение может быть неустойчивым. В этой связи отметим, что критическое число Грасгофа, превышение которого вызывает неустойчивость встречных параллельных вертикальных течений для больших чисел Прандтля Pr, равно ${\text{G}}{{{\text{r}}}_{*}} = {{470} \mathord{\left/ {\vphantom {{470} {\sqrt {Pr} }}} \right. \kern-0em} {\sqrt {Pr} }}$ [12]. Отсюда, так как ${\text{Ra}} = Gr \cdot Pr$ для критического числа Рэлея, получим ${\text{R}}{{{\text{a}}}_{*}} = {\text{G}}{{{\text{r}}}_{*}} \cdot {\text{Pr}} = 470 \cdot \sqrt {{\text{Pr}}} $. Поскольку для мантии $\nu \sim {{10}^{{18}}}{\kern 1pt} - {\kern 1pt} {{10}^{{19}}}$ м/с2, $\chi \sim {{10}^{{ - 7}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 6}}}$ м/с2, ${\text{Pr}} = \nu {\text{/}}\chi \sim {{10}^{{25}}}$, в нашем случае получим следующую оценку ${\text{R}}{{{\text{a}}}_{*}}\sim {{10}^{{15}}}$. В то же время максимальные числа Рэлея, о которых идет речь в данной статье, равны ${\text{Ra}} = {{10}^{5}} \ll {\text{R}}{{{\text{a}}}_{*}}$, т.е. на много порядков меньше критического. Поэтому даже если точное значение критического Рэлея в настоящей задаче отличается от [12], это отличие будет не больше чем на порядок, поэтому устойчивость полученного решения очевидна.

Рис. 5.

Изотермы при конвекции в области верхней мантии при числе Рэлея Ra, равном 1000.

Рассмотрим случаи, когда учитывается движение нижней границы, что соответствует горизонтальному движению литосферной плиты со скоростью ${{v}_{1}}$. В этом случае движение плиты нелинейным образом влияет на конвекцию, вызванную неоднородностью температуры. На рис. 6 показано течение для того же числа Рэлея, что и на рис. 4в, но с движущейся нижней границей: на рис. 6a при ${{v}_{1}} = 200$ (0.46 см/год), на рис. 6б при ${{v}_{1}} = 500$ (1.15 см/год), на рис. 6в при ${{v}_{1}} = 2000$ (4.6 см/год). Видно, что движение плиты переводит внутрь области течения большие ячейки, вращающиеся по часовой стрелке, т.е. сонаправленно с циркуляцией жидкости, вызванной плитой, и вытесняет меньшие ячейки, которые при отсутствии плиты вращались в противоположную сторону. На рис. 6б одна из таких малых ячеек еще сохраняется, а при бо̀льших скоростях плиты и она разрушается и исчезает, как это видно из рис. 6в.

Рис. 6.

Структура течений при ${\text{Ra}} = 5 \times {{10}^{4}}$ с учетом движения плиты со скоростями: (a) ${{v}_{1}} = 200$ (0.46 см/год); (б) ${{{v}}_{1}} = 500$ (1.15 см/год); (в) ${{{v}}_{1}} = 2000$ (4.6 см/год).

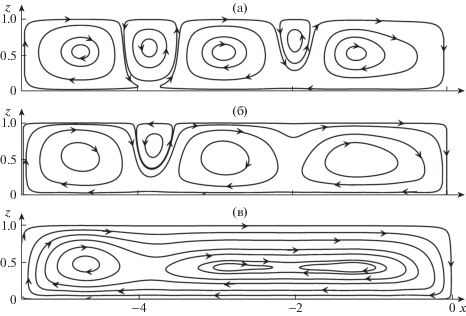
Как показывает рис. 6в при больших скоростях движения плиты, внешние линии тока охватывают всю рассматриваемую область, однако внутри нее образуются три ячейки, вращающиеся в ту же сторону, что и внешнее течение.

Отметим, что очень важна степень влияния эффекта движения плиты при характерных для верхней мантии числах Рэлея и конкретных, характерных для зон субдукции, скоростях движения плиты, т.е. 5–10 см/год, от которых указанное влияние зависит. Как показывает рис. 6в, при таких скоростях и характерном для верхней мантии числе Рэлея во внешней области имеет место как раз одноячеистая структура течений в согласии с экспериментальными данными (рис. 1a).

Существенные отличия полученных нами результатов о конвекции в области верхней мантии, примыкающей к зоне субдукции, от результатов исследований аналогичной задачи, выполненных в предыдущих работах [9, 10], можно сформулировать следующим образом. Во-первых, в данной работе, наряду с влиянием горизонтального градиента температуры на развитие длинной горизонтальной ячейки, показана важная роль движущегося горизонтально литосферного слоя, подстилающего конвективную область выше фазовой границы 670 км, существование которого установлено по данным сейсмотомографии мантии в переходной зоне от Тихого океана к Восточной и Северо-Восточной Азии и Арктике. Во-вторых, в нашей более общей постановке задачи двухмерной конвекции получены режимы не только одноячеистой структуры течений в длинном горизонтальном слое, но и более сложные формы конвекции, сочетающие области длинных горизонтальных ячеек с изометричными зонами конвекции, что определяется небольшими изменениями значений числа Релея. В действительности, геолого-геофизические данные о распределении рифтовых зон и магматических провинций во времени и пространстве, а также рассеянных деформациях и смещениях поверхности литосферы свидетельствуют о реализации обоих режимов конвекции в процессе эволюции Восточной и Северо-Восточной Азии и Арктики за последние 100 млн лет.

ЗАКЛЮЧЕНИЕ

Получено решение задачи термической конвекции в верхней мантии в области, сопряженной с зоной субдукции. Из решения соответствующих уравнений следует, что при относительно малых числах Рэлея (Ra = 103) внешнее течение охватывает всю ячейку, даже без учета движения плиты вдоль основания. При бо̀льших числах Рэлея, характерных для верхней мантии (${\text{Ra}} = 5 \times {{10}^{4}}$), возникает ряд неравномерных ячеек. Однако движение погружающейся плиты вдоль основания с характерными для зон субдукции скоростями 7–10 см/год приводит к возникновению во внешней области линий тока, охватывающих всю область, т.е. к одноячеистой структуре. При этом внутри области сохраняются ячейки, вращающиеся в том же направлении, что и внешняя ячейка, а ячейки, которые при отсутствии плиты вращались в противоположном направлении, вытесняются вверх и разрушаются.

Полученное решение позволяет найти и другие характеристики конвекции, распределение теплового потока на верхней границе, а также поле вязких напряжений в тектонических активных районах.

Таким образом, в рамках классической модели термической конвекции получено дополнительное математическое обоснование предложенной в [1–5] геодинамической модели эволюции Арктики и Северо-Восточной Азии, естественным образом объясняющей основные известные тектономагматические процессы, характерные для литосферы рассматриваемых областей.

Работа выполнена в рамках государственного задания Института океанологии им. П.П. Ширшова РАН (тема № 0149-2019-0005), государственной программы “5-100” МФТИ и проекта РФФИ “Ресурсы Арктики” № 18-05-7002.

Список литературы

  1. Лобковский Л.И., Вержбицкий В.Е., Кононов М.В., Шрейдер А.А., Гарагаш И.А., Соколов С.Д., Тучкова М.И., Котелкин В.Д., Верниковский В.А. Геодинамическая модель эволюции Арктического региона в позднем мезозое – кайнозое и проблема внешней границы континентального шельфа России// Арктика: экология и экономика. 2011. № 1 (1). С. 104–115. https://doi.org/10.25283/2223-4594

  2. Лобковский Л.И., Шипилов Э.В., Кононов М.В. Геодинамическая модель верхнемантийной конвекции и преобразования литосферы Арктики в мезозое и кайнозое// Физика Земли. 2013. № 6. С. 20–38. https://doi.org/10.7868/S0002333713060100

  3. Лобковский Л.И. Тектоника деформируемых литосферных плит и модель региональной геодинамики применительно к Арктике и Северо-восточной Азии// Геология и геофизика. 2016. Т. 57. № 3. С. 476–495. https://doi.org/10.15372/GiG20160302

  4. Котелкин В.Д., Лобковский Л.И. Обоснование геодинамической модели эволюции Арктического региона // Сб. тр. XII Всероссийского съезда по фундаментальным проблемам теоретической и прикладной механики. г. Уфа, 2019. Т. 4. С. 63–65. https://doi.org/10.22226./2410-3535-2019congress-v4

  5. Котелкин В.Д., Лобковский Л.И. Геодинамика континентальных окраин и модель эволюции Арктического региона //Сб. “Современные проблемы математики и механики”. Материалы междунар. конф., посв. 80-летию акад. В.А. Садовничего. М: МАКС Пресс, 2019. Т. 2. С. 720–723. https://doi.org/10.29003/m978-5-317-06111-1

  6. Zhao D. Global tomographic images of mantle plumes and subducting slabs: insight into deep Earth dynamics// Phys. Earth Planet. Int. 2004. V. 146. № 1. P. 3–34. https://doi.org/10.1016/j.pepi.2003.07.032

  7. Zhao D. Multiscale seismic tomography and mantle dynamics // Gondwana Res. 2009. V. 15. P. 297–323. https://doi.org/10.1016/j.gr.2008.07.003

  8. Zhao D., Tian Y., Ley J., Liu L., Zheng S. Seismic image and origin of the Changbai intraplate volcano in East Asia: Role of big mantle wedge above the stagnant Pacific slab // Phys. Earth Planet. Int. 2009. V. 173. P. 197–206. https://doi.org/10.1016/j.pepi.2008.11.009

  9. Кирдяшкин А.А., Кирдяшкин А.Г., Добрецов Н.Л. Влияние субдукции на структуру тепловых гравитационных течений в астеносфере под континентом // Геология и геофизика. 2000. Т. 41. № 2. С. 207–219.

  10. Кирдяшкин А.А., Добрецов Н.Л., Кирдяшкин А.Г. Экспериментальное моделирование влияния субдукции на пространственную структуру конвективных течений в астеносфере под континентом // Докл. Академии наук. 2002. Т. 384. № 5. С. 682–686.

  11. Лобковский Л.И., Инюхин А.В., Котелкин В.Д. Субдукция и цикличность процессов верхней мантии // Докл. Академии наук. 2014. Т. 459. № 3. С. 332–336. https://doi.org/10.1134/S1028334X14110233

  12. Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. Главная редакция физ.-мат. лит. изд. М.: Наука, 1972. 392 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал