1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2019

Известия РАН. Механика жидкости и газа, 2019, № 6, стр. 129-140

Анализ экспериментальных данных по конвективному нагреву модели марсианского спускаемого аппарата с использованием алгебраических моделей турбулентности

С. Т. Суржиков a, b, *

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

b Всероссийский научно-исследовательский институт автоматики им. Н.Л. Духова
Москва, Россия

* E-mail: surg@ipmnet.ru

Поступила в редакцию 05.06.2019
После доработки 25.06.2019
Принята к публикации 25.06.2019

Полный текст (PDF)

Аннотация

Выполнено расчетное исследование экспериментальных данных по конвективному нагреву лобовой поверхности модели спускаемого аппарата Mars Science Laboratory (MSL) при ее пространственном обтекании в широком диапазоне изменения чисел Рейнольдса. Показано, что использование алгебраических моделей турбулентности Болдуина–Ломакса и модели смешения Прандтля совместно с усредненными по Рейнольдсу уравнениями Навье–Стокса позволяет получить удовлетворительное согласие с экспериментальными и расчетными данными других авторов.

Ключевые слова: турбулентное течение, конвективный нагрев, модель марсианского спускаемого аппарата, экспериментальные данные, усредненные по Рейнольдсу уравнения Навье-Стокса, алгебраические модели турбулентности, численные решения

Экспериментальное исследование конвективного нагрева поверхности модели марсианского спускаемого аппарата Mars Science Laboratory (MSL) в условиях ламинарного, переходного и турбулентного режимов течения молекулярного азота было проведено с использованием двух аэродинамических труб при числах Маха 6, 8 и 10 [1]. Основная серия экспериментов выполнялась на гиперзвуковой аэродинамической трубе AEDC Tunnel 9 [2]. Семь экспериментов отвечало скорости потока с М = 10 и пятнадцать – М = 8.

Условия испытаний модели спускаемого аппарата MSL с диаметром в миделевом сечении Dmid =15.24 см при указанных числах Маха были таковы, что обеспечивались режимы ламинарного, переходного и турбулентного обтекания. Числа Рейнольдса набегающего потока при М = 8 изменялись в диапазоне ${{\operatorname{Re} }_{\infty }}$ = (1.3 × 107–16 × 107) 1/м и при М = 10: ${{\operatorname{Re} }_{\infty }}$ = (0.39 × 107–62 × 107) 1/м.

Дополнительные тестовые эксперименты были проведены в 20-ти дюймовой аэродинамической трубе М6 LRC (Langley Research Center) при числах Рейнольдса ${{\operatorname{Re} }_{\infty }}$ = (0.36 × 107–2.2 × 107) 1/м [3].

Время испытаний в аэродинамической трубе AEDC Tunnel 9 $\Delta t = $ 0.25–15 с позволило изменять угол атаки испытуемой модели в одном эксперименте в диапазоне α = –10 – +50° со скоростью $\Delta {\alpha }$ = 80° 1/с. В аэродинамической трубе М6 LRC время испытаний достигало 15 мин, хотя было установлено, что для получения требуемых данных достаточно нескольких секунд.

Помимо экспериментальных данных по конвективному нагреву наветренной поверхности модели MSL под разными углами атаки α = 0–24° при ламинарном, переходном и турбулентном характере обтекания в статье [1] приведены результаты расчетов с использованием компьютерного кода LAURA (Langley Aerothermodynamic Upwind Relaxation Algorithm) [4]. Это один из широко используемых в НАСА компьютерных кодов по аэротермодинамике спускаемых аппаратов, заслуженно завоевавший высокую репутацию вследствие большого числа успешных верификационных и валидационных исследований. Указанный компьютерный код использует модели совершенного газа, химически равновесных и неравновесных газовых смесей. В зависимости от физической постановки расчеты выполняются по разным моделям течения на основе уравнений Эйлера, Навье–Стокса и усредненных по Рейнольдсу уравнений Навье–Стокса.

В статье [1] приведены результаты расчетной интерпретации экспериментальных данных с использованием модели параболизованных уравнений Навье–Стокса и алгебраических моделей турбулентности Себечи–Смита и Болдуина–Ломакса [5]. Важным результатом [1] является демонстрация удовлетворительного расчетного описания экспериментальных данных по конвективному нагреву модели СА MSL в исследованных условиях. Учитывая концептуальную простоту алгебраических моделей, основанных, тем не менее, на разумных физических представлениях о структуре турбулентного пограничного слоя вблизи плоской поверхности, а также их относительную универсальность к интерпретации особенностей турбулентного конвективного нагрева во множестве других расчетных случаев, следует признать практическую обоснованность их использования.

В настоящей работе алгебраические модели турбулентного смешения используются для замыкания усредненных по Рейнольдсу уравнений Навье–Стокса с целью интерпретации экспериментальных данных [1] по конвективному нагреву поверхности спускаемого аппарата MSL. В качестве базового выбран авторский компьютерный код NERAT-3D, который также прошел многочисленное тестирование на различных задачах радиационной аэротермодинамики спускаемых космических аппаратов [6]. В данном случае, как и в [1], выбрана модель совершенного газа, но решается полная система усредненных по Рейнольдсу уравнений Навье–Стокса в трехмерной постановке. Помимо сравнительного анализа расчетных и экспериментальных данных, обсуждается способ использования алгебраических моделей турбулентного смешения применительно к полным уравнениям Навье–Стокса.

1. РАСЧЕТНАЯ МОДЕЛЬ УСРЕДНЕННЫХ ПО РЕЙНОЛЬДСУ УРАВНЕНИЙ НАВЬЕ–СТОКСА С ИСПОЛЬЗОВАНИЕМ АЛГЕБРАИЧЕСКИХ МОДЕЛЕЙ ТУРБУЛЕНТНОСТИ

Вычислительная модель NERAT-3D реализует интегрирование системы уравнений вязкого сжимаемого газа методом установления. На каждом итерационном шаге (аналог шага по времени) последовательно интегрируется система уравнений неразрывности и усредненных по Рейнольдсу уравнений Навье–Стокса, а также уравнение сохранения энергии в форме уравнения теплопроводность Фурье–Кирхгоффа

(1.1)
$\frac{{\partial {\rho }}}{{\partial t}} + \frac{{\partial {\rho }u}}{{\partial x}} + \frac{{\partial {\rho }{v}}}{{\partial y}} + \frac{{\partial {\rho }w}}{{\partial z}} = 0$
(1.2)
$\begin{gathered} \frac{{\partial {\rho }u}}{{\partial t}} + {\text{div}}\left( {{\rho }u{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial x}} - \frac{2}{3}\frac{\partial }{{\partial x}}\left( {{{{\mu }}_{{eff}}}{\text{div}}{\mathbf{V}}} \right) + 2\frac{\partial }{{\partial x}}\left( {{{{\mu }}_{{eff}}}\frac{{\partial u}}{{\partial x}}} \right) + \\ + \;\frac{\partial }{{\partial y}}\left[ {{{{\mu }}_{{eff}}}\left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + \frac{\partial }{{\partial z}}\left[ {{{{\mu }}_{{eff}}}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \right] \\ \end{gathered} $
(1.3)
$\begin{gathered} \frac{{\partial {\rho }{v}}}{{\partial t}} + {\text{div}}\left( {{\rho }{v}{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial r}} - \frac{2}{3}\frac{\partial }{{\partial y}}\left( {{{{\mu }}_{{eff}}}{\text{div}}{\mathbf{V}}} \right) + 2\frac{\partial }{{\partial y}}\left( {{{{\mu }}_{{eff}}}\frac{{\partial {v}}}{{\partial y}}} \right) + \\ + \;\frac{\partial }{{\partial x}}\left[ {{{{\mu }}_{{eff}}}\left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + \frac{\partial }{{\partial z}}\left[ {{{{\mu }}_{{eff}}}\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial {v}}}{{\partial z}}} \right)} \right] \\ \end{gathered} $
(1.4)
$\begin{gathered} \frac{{\partial {\rho }w}}{{\partial t}} + {\text{div}}\left( {{\rho }w{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial z}} - \frac{2}{3}\frac{\partial }{{\partial z}}\left( {{{{\mu }}_{{eff}}}{\text{div}}{\mathbf{V}}} \right) + 2\frac{\partial }{{\partial z}}\left( {{{{\mu }}_{{eff}}}\frac{{\partial w}}{{\partial z}}} \right) + \\ + \;\frac{\partial }{{\partial x}}\left[ {{{{\mu }}_{{eff}}}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \right] + \frac{\partial }{{\partial y}}\left[ {{{{\mu }}_{{eff}}}\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}} \right)} \right] \\ \end{gathered} $
(1.5)
${\rho }{{c}_{p}}\frac{{\partial T}}{{\partial t}} + {\rho }{{c}_{p}}{\mathbf{V}}\operatorname{grad} T = \operatorname{div} \left( {{{{\lambda }}_{{eff}}}\operatorname{grad} T} \right) + \frac{{\partial p}}{{\partial t}} + {\mathbf{V}}\operatorname{grad} p + {{\Phi }_{{\mu }}}$
где $u$, $v$, $w$ – проекции вектора скорости потока V на оси прямоугольной декартовой системы координат x, y, z; $p$, ${\rho }$, $T$ – давление, плотность и температура газа; ${\mu }$, ${\lambda }$, ${{{\mu }}_{t}}$, ${{{\lambda }}_{t}}$, ${{{\mu }}_{{{\text{eff}}}}} = {\mu + }{{{\mu }}_{t}}$, ${{{\lambda }}_{{eff}}} = {\lambda + }{{{\lambda }}_{t}}$ – молекулярная, турбулентная и эффективная вязкости и теплопроводность, ${{c}_{p}}$ – удельная теплоемкость при постоянном давлении
$\begin{gathered} {{{\Phi }}_{\mu }} = {{{\mu }}_{{eff}}}\left[ {2{{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial w}}{{\partial z}}} \right)}}^{2}} + } \right. \\ + \;\left. {{{{\left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)}}^{2}} + {{{\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial {v}}}{{\partial z}}} \right)}}^{2}} + {{{\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}}^{2}} - \frac{2}{3}{{{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right)}}^{2}}} \right] \\ \end{gathered} $
диссипативная функция.

Использовалось термическое уравнение состояния идеального газа

(1.6)
$p = {\rho }\frac{{{{R}_{0}}}}{M}T$
где ${{R}_{0}}$ – универсальная газовая постоянная, М = 28 г/моль молекулярный вес N2.

Замыкающие термодинамические и теплофизические характеристики задавались следующим образом:

${\gamma } = \frac{{{{c}_{p}}}}{{{{c}_{{v}}}}} = 1.4,\quad {{c}_{{v}}} = \frac{{{{R}_{0}}}}{{({\gamma } - 1)M}},\quad {\mu } = \frac{{1.45 \times {{{10}}^{{ - 5}}}{{T}^{{1.5}}}}}{{110.4 + T}}\,\,\,{\text{г/}}({\text{см}} \cdot {\text{с}})$
${\lambda } = \frac{{{\mu }{{c}_{p}}}}{{\Pr }},\quad {{{\lambda }}_{t}} = \frac{{{{{\mu }}_{t}}{{c}_{p}}}}{{{{{\Pr }}_{t}}}},\quad \Pr = 0.7,\quad {{\Pr }_{t}} = 1.0$

В качестве граничных условий для системы уравнений (1.1)–(1.5) применялись условия в невозмущенном набегающем потоке (см. табл. 1), условия прилипания на поверхности и условия Дирихле в выходном сечении расчетной области, где течение всегда было сверхзвуковым. Температура лобовой поверхности полагалась равной Tw = 360 K.

Таблица 1.
Название эксперимента Re, м–1 M p, Па ${{T}_{\infty }},$ K ${{{\rho }}_{\infty }},$ кг/м3 ${{V}_{\infty }},$ м/с
Run 3020 5.85E+06 9.56 285.1 58.1 0.0165 1486.3
Run 3021 3.74E+06 9.47 167.9 54.8 0.0103 1428.0
Run 3025 6.06E+07 10.32 2068.1 48.3 0.1444 1461.8
Run 3029 5.40E+07 7.64 4988.8 80.7 0.2082 1398.3
Run 3030 6.85E+07 7.77 6158.7 76.6 0.2709 1386.0
Run 3047 9.64E+07 7.75 8231.8 73.8 0.3760 1356.4
Run 3048 1.57E+08 7.98 11918.6 69.3 0.5792 1350.9

Использовались две алгебраические модели турбулентного смешения в пограничном слое. Первая из них, модель смешения Прандтля, является одной из первых и наиболее исследованных моделей. В разных вариациях данная модель излагается, например, в [5, 7, 8]. Турбулентная вязкость определяется по хорошо известному феноменологическому соотношению

(1.7)
${{{\mu }}_{t}} = {\rho }L_{m}^{2}\left| \Omega \right|$
где ${{L}_{m}}$ – длина смещения Прандтля; $\left| \Omega \right|$ – функция завихренности скорости.

В случае простейшего течения вблизи пластины без градиента давления во внешнем потоке приближенно полагают

(1.8)
$\left| \Omega \right| = \left| {\frac{{\partial u}}{{\partial y}}} \right|$

Рассматривается двухслойная модель, в соответствии с которой длина пути смешения Прандтля определяется по формуле

(1.9)
$\begin{gathered} L_{m}^{{in}} = {\chi }y\left[ {1 - \exp \left( { - \frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)} \right],\quad \frac{y}{{\delta }} < 0.2 \\ L_{m}^{{out}} = 0.085{\delta },\quad \frac{y}{{\delta }} > 0.2 \\ \end{gathered} $
${{y}^{ + }} = \frac{y}{{{{{\nu }}_{w}}}}{{u}_{{\tau }}},\quad {{u}_{{\tau }}} = \sqrt {\frac{{{{{\tau }}_{w}}}}{{{{{\rho }}_{w}}}}} ,\quad {{{\tau }}_{w}} = {{{\mu }}_{w}}{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}_{w}}$
где δ – толщина динамического пограничного слоя; χ = 0.43 – эмпирическая константа; А+ = 26; ${{{\nu }}_{w}}$ − кинематическая вязкость вблизи поверхности.

Поскольку ${\mu } = {\rho \nu }$, то

(1.10)
${{y}^{ + }} = \frac{y}{{{{{\mu }}_{w}}}}{{{\rho }}_{w}}{{u}_{{\tau }}} = \frac{y}{{{{{\mu }}_{w}}}}\sqrt {{{{\rho }}_{w}}{{{\tau }}_{w}}} = y{{\sqrt {\frac{{{{{\rho }}_{w}}}}{{{{{\mu }}_{w}}}}\left( {\frac{{\partial u}}{{\partial y}}} \right)} }_{w}}$

В модели Болдуина–Ломакса [9] также рассматривается двухслойная структура пограничного слоя. В каждом слое определяется своя турбулентная вязкость.

Во внутреннем, прилегающем к поверхности слое

(1.11)
${{{\mu }}_{{t,in}}} = {\rho }\left( {{\chi }yD} \right)\left| \Omega \right|$
где χ = 0.4; D – демпфирующая функция Ван-Дриста

$D = 1 - \exp \left( { - \frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)$

В двумерном случае

$\Omega = \frac{{\partial {v}}}{{\partial x}} - \frac{{\partial u}}{{\partial y}}$
и в трехмерном случае
${{\Omega }^{2}} = {{\left( {\frac{{\partial u}}{{\partial y}} - \frac{{\partial {v}}}{{\partial x}}} \right)}^{2}} + {{\left( {\frac{{\partial w}}{{\partial y}} - \frac{{\partial {v}}}{{\partial z}}} \right)}^{2}} + {{\left( {\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right)}^{2}}$
где, в общем случае пограничного слоя у криволинейной поверхности, под $u$, ${v}$, w следует понимать локальные составляющие скорости вдоль и по нормали к поверхности.
${\text{Во внешнем слое }}{{{\mu }}_{{t,out}}} = K{{C}_{{av}}}{\rho }{{F}_{{wake}}}{{F}_{{kleb}}}\left( y \right)$
$\begin{gathered} {{F}_{{kleb}}}\left( y \right) = {{\left[ {1 + 5.5{{{\left( {y\frac{{{{C}_{{kleb}}}}}{{{{y}_{{\max }}}}}} \right)}}^{6}}} \right]}^{{ - 1}}},\quad {{C}_{{kleb}}} = 0.3 \\ {{F}_{{wake}}} = {{y}_{{\max }}}{{F}_{{\max }}},\quad F\left( y \right) = y\left| \Omega \right|D \\ \end{gathered} $
где K = 0.018, Сav = 1.6; ymax – определяется локальной координатой, нормальной к поверхности y, где $\left| \Omega \right|$ достигает своего максимума, а Fmax = F(ymax).

Турбулентная вязкость, подставляемая в уравнения (1.2)–(1.4), находится следующим образом:

$\begin{gathered} {{\mu }_{{t,in}}},\quad y \leqslant {{y}_{{cross}}} \\ {{\mu }_{{t,out}}},\quad y > {{y}_{{cross}}} \\ \end{gathered} $
где ycross – координата y, при которой μt, in = μt, out (первый раз по мере увеличения y).

Заметим, что использование алгебраических моделей турбулентности совместно с полной моделью Навье–Стокса сталкивается с рядом проблем, которые отсутствуют при решении задачи в классической погранслойной постановке. В рассматриваемом случае пространственного обтекания модели спускаемого аппарата MSL не во всех точках вблизи поверхности удается формально выделить область пограничного слоя (например, в окрестности критической линии тока), а также ограничить толщину пограничного слоя при наличии ударных волн. Поэтому при практической реализации алгебраических моделей турбулентности анализировались распределения турбулентной вязкости по локальной нормали к поверхности и не допускалось наличия осцилляций этой функции после достижения локального максимума. Подробно этот алгоритм рассмотрен в статье [10]. Вопрос о выборе толщины пограничного слоя в сверхзвуковом течении с ударными волнами с целью использования алгебраических моделей турбулентности обсуждался также в [11, 12].

2. АЛГОРИТМ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ

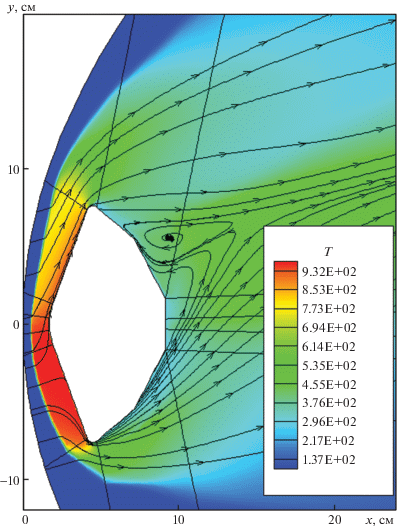
На рис. 1 показано расчетное поле температур, отвечающее одному из расчетных случаев (эксперимент [1] с названием Run3020, см. табл. 1). На этой фигуре показаны границы 8 расчетных блоков, 2 из которых охватывают ось симметрии спускаемого аппарата в зоне сферического затупления лобовой поверхности и задней поверхности, а другие 6 блоков расчетной сетки опираются на лобовую и боковую поверхность. Отдельный блок опирается на боковую кромку лобового аэродинамического щита.

Рис. 1.

Поле течения для эксперимента Run3020 при угле атаки 16°

В пределах каждого блока вводилось взаимно-однозначное преобразование координат вида ${\xi } = {\xi }(x,y,z)$, ${\eta } = {\eta }(x,y,z)$ и ${\zeta } = {\zeta }(x,y,z)$, что позволило проводить численное интегрирование системы уравнений (1.1)–(1.5) с использованием неоднородных структурированных расчетных сеток со сгущением расчетных узлов вблизи обтекаемой поверхности и фронта головной ударной волны. Общее число узлов первичной расчетной сетки составляло около 120 000, с числом узлов по нормали к лобовой поверхности 61. Компоненты якобиана преобразования координат находились численно. Расчетная сетка в физическом пространстве создавалась с использованием аналитических функций.

На каждом итерационном шаге система уравнений (1.1)–(1.5) интегрировалась в два этапа. Уравнения (1.1)–(1.4) интегрировались явным методом с использованием AUSM алгоритма [13] приближенного решения задачи о распаде произвольного разрыва. Вторые производные этих уравнений, связанные с вязкой диссипацией, аппроксимировались центральными разностями.

На втором этапе решалось уравнение теплопроводности в форме Фурье–Кирхгофа (1.5) с использованием неявной пятиточечной расчетной схемы. Система конечно-разностных уравнений интегрировалась методом последовательной нижней релаксации с прогонкой по линиям в нормальном к поверхности направлении. Итерационный шаг по фиктивному времени выбирался из условия не превосходства максимальной невязки наперед заданной величины $\varepsilon \sim 0.01$ определения искомых функций по всему полю течения. При уменьшении ${\varepsilon } < 0.001$ шаг по фиктивному времени увеличивался в 1.7 раза. Так, построенный алгоритм численного решения обеспечивал весьма быструю сходимость итерационного процесса (за несколько сот итераций). Очевидно, что существенного ускорения скорости расчетов удавалось достичь при использовании результатов вычислений, близких по исходным данным.

При переходе с одного итерационного слоя на другой рассчитывались термодинамические и теплофизические данные, включая расчет по формулам алгебраических моделей турбулентности.

3. СРАВНЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ И ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ

Расчеты аэродинамических характеристик и конвективного нагрева модели СА MSL проводились для экспериментальных условий, представленных в табл. 1.

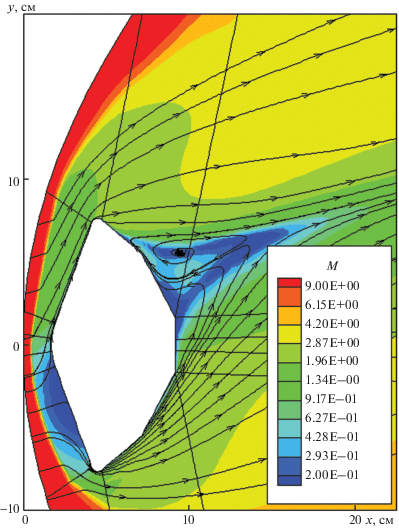
На рис. 1–3 показаны поля температуры, чисел Маха и давления, а также линии тока для экспериментальных условий Run3020, в которых реализовывался ламинарный режим течения.

Рис. 2.

Числа Маха при обтекании модели СА MSL в эксперименте Run3020 при угле атаки 16°

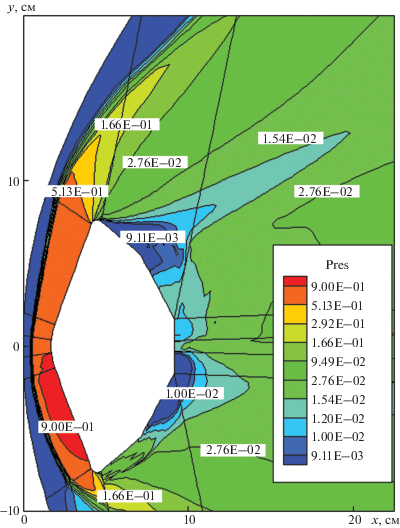
Рис. 3.

Давление $\Pr {\text{es}} = {p \mathord{\left/ {\vphantom {p {({{{\rho }}_{\infty }}}}} \right. \kern-0em} {({{{\rho }}_{\infty }}}}V_{\infty }^{2})$ для эксперимента Run3020 при угле атаки 16°

Прежде чем рассмотреть результаты расчетов плотностей конвективных тепловых потоков на лобовой поверхности спускаемого аппарата MSL, отметим основные особенности обтекания модели в данных экспериментах.

В рассматриваемом случае число Маха набегающего потока равно М = 9.56, поэтому вблизи лобовой наветренной стороны модели образуется достаточно толстый ударный слой, в большей части которого реализуется дозвуковой режим течения (см. рис. 2). Видно, что вблизи наветренной части лобовой поверхности от критической линии тока до нижней кромки и вверх практически до верхней кромки модели реализуется дозвуковое течение. Причем, если вниз от критической линии тока дозвуковое движение реализуется практически по всей толщине сжатого слоя, то вверх на подветренной стороне лобовой поверхности наблюдается относительно тонкий пограничный слой с М < 0.99 на внешней поверхности. Вблизи нижней и верхней кромок поток разгоняется до М = 1.66.

Более точно картину течения у лобовой поверхности, а также вблизи задней поверхности модели аппарата MSL, можно получить из анализа температурного поля (рис. 1) и давления (рис. 3). На рис. 1 также приведены линии тока. От критической линии тока, на которой достигается температура, близкая температуре торможения, в растекающемся вдоль поверхности потоке газа температура в сжатом слое падает более, чем на 200 K. При этом давление падает примерно в 2 раза, от ${{p}_{0}}$ = 0.364 × 105 Па до $p$ = 0.513, ${{p}_{0}}$ = 0.187 × 105 Па.

Течение в отрывной зоне за кромкой лобовой поверхности не имеет непосредственного влияния на изучаемый в данной работе конвективный нагрев лобовой поверхности, тем не менее, оно представляет значительный интерес, в том числе для анализа конвективного нагрева задней поверхности. Сравнение рис. 1 и 2 показывает на весьма сложный характер течения в отрывной зоне. За боковой кромкой обтекаемой модели наблюдается ускорение газового потока с одновременным, резким падением давления и заметным падением температуры.

На рис. 3 видна торообразная зона пониженного давления, смещенная к верхней границе задней поверхности. Здесь давление примерно в 100 раз меньше давления у лобовой поверхности. На рис. 1 линии тока демонстрируют возвратно-вихревое движение, а на рис. 2 видно, что в окрестности пограничных слоев, отделяющих указанную вихревую структуру от основного потока, имеются зоны с дозвуковой скоростью движения.

Возвращаясь к проблеме расчета плотностей конвективных тепловых потоков к лобовой поверхности, отметим исключительно сложный характер течения, включающего область сильно до- и сверхзвукового движения вблизи конической поверхности, сопряженной со сферическим сегментом. Обратим внимание, что при угле атаки α > 5° критическая линия тока приходится на коническую поверхность.

Для количественной характеристики плотностей конвективных тепловых потоков будем использовать безразмерный параметр теплового потока, рассчитываемый с использованием критериев Стантона и Рейнольдса ${{Q}_{w}} = {\text{St}} \times \sqrt {\operatorname{Re} } $, которые определяются по параметрам набегающего потока (нижний индекс ∞)

${\text{St}} = \frac{{{{q}_{w}}}}{{{{{\rho }}_{\infty }}{{V}_{\infty }}\Delta H}},\quad \operatorname{Re} = \frac{{{{{\rho }}_{\infty }}{{V}_{\infty }}{{D}_{{mid}}}}}{{{{{\mu }}_{\infty }}}}$
где qw – плотность конвективного теплового потока к поверхности с температурой Tw; Dmid – диаметр Миделя модели; $\Delta H = {{c}_{p}}{{T}_{\infty }} + V_{\infty }^{2}{\text{/}}2 + {{c}_{p}}{{T}_{w}}$. Отметим, что параметр Qw слабо зависит от тестового времени эксперимента, в течение которого изменяется температура поверхности испытуемой модели, поскольку сомножители qw и $\Delta H$ взаимно компенсируют друг друга при изменении температуры поверхности. К тому же, в [1] показана слабая зависимость Qw от Re.

Распределения плотностей конвективных тепловых потоков вдоль поверхности модели MSL в плоскости симметрии от нижней кромки лобового щита (${x \mathord{\left/ {\vphantom {x {{{R}_{{mid}}} = - 1}}} \right. \kern-0em} {{{R}_{{mid}}} = - 1}}$) до верхней кромки (${x \mathord{\left/ {\vphantom {x {{{R}_{{mid}}} = + 1}}} \right. \kern-0em} {{{R}_{{mid}}} = + 1}}$) показаны на рис. 4 для условий эксперимента Run3021 при трех углах атаки. Здесь ${{R}_{{mid}}}$ – радиус миделевого сечения. В [1] указанные условия отнесены к ламинарному режиму обтекания, поэтому расчеты с использованием компьютерного кода NERAT-3D выполнены без учета турбулентной вязкости. Отметим удовлетворительное совпадение с экспериментальными данными, погрешность которых оценивается в [1] на уровне 26%. Причем погрешность порядка $ \pm $20%, по мнению авторов [1], относится к неопределенности знания теплофизических свойств материалов модели и датчиков теплового потока. Меньшая часть погрешности обусловлена согласно [1] недостаточностью данных о параметрах набегающего потока, угле атаки модели и точности измерительной аппаратуры.

Рис. 4.

Распределение параметра теплообмена вдоль лобовой поверхности модели спускаемого аппарата MSL в условиях эксперимента Run3021 при ламинарном режиме обтекания для трех углов атаки: 1–3 – эксперимент [1]; 4–6 – расчет NERAT-3D; 1, 4 – α = 0; 2, 5 – α = 16°; 3, 6 – α = 24°

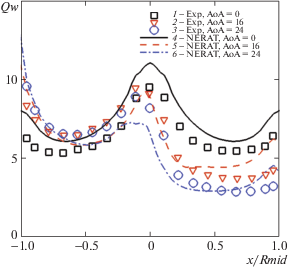
Помимо удовлетворительной точности описания экспериментальных данных, отметим такую важную особенность в распределении плотности конвективного теплового потока, как примерно двукратное их падение на подветренной стороне лобовой поверхности после локального увеличения тепловых потоков в области сферического сегмента.

В распределениях плотностей конвективных тепловых потоков при турбулентном характере течения наблюдается качественно иная картина. На подветренной части лобовой поверхности наблюдается более чем двукратное увеличение плотности конвективного теплового потока. На рис. 5 показаны экспериментальные и расчетные распределения параметра теплообмена Qw вдоль поверхности модели спускаемого аппарата MSL в плоскости симметрии для двух углов атаки ${\alpha }$ = 16 и 24° и условий эксперимента Run3025. Здесь использовалась алгебраическая модель Болдуина–Ломакса.

Рис. 5.

Распределение параметра теплообмена вдоль лобовой поверхности модели спускаемого аппарата MSL в условиях эксперимента Run3025 при переходном ламинарно-турбулентном режиме обтекания для двух углов атаки: 1, 2 – эксперимент [1]; 3, 4 – расчет NERAT-3D; 5 – расчет LAURA; 1, 3, 5 – α = 16°; 2, 4 – α = 24°

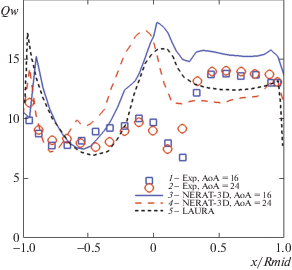
В [1] условия обтекания в этом эксперименте относятся к переходному режиму. В самом деле, это хорошо видно из экспериментальных данных. При отходе от критической точки (${x \mathord{\left/ {\vphantom {x {{{R}_{{mid}}}}}} \right. \kern-0em} {{{R}_{{mid}}}}}$ ~ –0.45) вверх по поверхности наблюдается увеличение Qw, отвечающее сферическому сегменту с относительно малым радиусом кривизны, с последующим снижением Qw при переходе к подветренной стороне лобовой поверхности. Но при ${x \mathord{\left/ {\vphantom {x {{{R}_{{mid}}} > 0.2}}} \right. \kern-0em} {{{R}_{{mid}}} > 0.2}}$ наблюдается резкое увеличение плотности теплового потока более, чем в 2 раза, что очевидно связано с ламинарно-турбулентным переходом. Отметим хорошее совпадение расчетных данных для ${\alpha }$ = 16°, получаемых по компьютерным кодам NERAT-3D и LAURA. Подчеркнем, что в данных расчетах не использовался какой-либо критерий ламинарно-турбулентного перехода.

На рис. 6 приведены аналогичные данные для турбулентного режима течения в эксперименте Run3030. В данном случае наибольшая величина параметра теплообмена достигается в области сферического сегмента. Но выше по потоку его заметного падения не наблюдается, что с очевидностью соответствует конвективному нагреву с турбулентным режимом течения. При нулевом угле атаки распределение интенсивности нагрева несколько ниже вблизи критической точки. Здесь наблюдается наименьшая плотность тепловых потоков, но по мере отхода к боковой кромке величина qw заметно возрастает.

Рис. 6.

Распределение параметра теплообмена вдоль лобовой поверхности модели спускаемого аппарата MSL в условиях эксперимента Run3030 при турбулентном режиме обтекания для трех углов атаки: 1–3 – эксперимент [1]; 4–6 – расчет NERAT-3D; 7 – расчет LAURA; 1, 4 – α = 0; 2, 5, 7 – α = 16°, 3, 6 – α = 20°

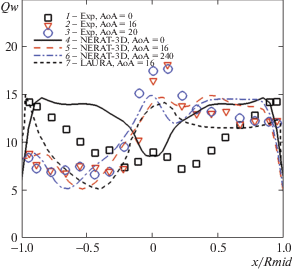
На рис. 7–9 дано сравнение расчетных данных с использованием алгебраических моделей Болдуина–Ломакса (BLm) и смешения Прандтля (PMm), а также результатов расчетов по коду LAURA с экспериментальными данными для условий экспериментов Run3029, 3047 и 3048 по мере увеличения числа Рейнольдса (см. значения в табл. 1). Для сравнения на этих же рисунках показаны расчетные распределения параметра теплообмена, полученные по компьютерным кодам NERAT-3D и LAURA для ламинарного режима течения. Отметим, что с увеличением числа Re параметр Qw на подветренной стороне лобовой поверхности сначала возрастает, а затем перестает изменяться.

Рис. 7.

Распределение параметра теплообмена вдоль лобовой поверхности модели спускаемого аппарата MSL в условиях эксперимента Run3029 при турбулентном режиме обтекания для α = 16°: 1 – эксперимент [1]; 2, 3 – расчет LAURA; 4–6 – расчет NERAT-3D; 2, 4 – расчетная модель ламинарного течения; 3, 5, 6 – расчетная модель турбулентного течения; 5 – модель Болдуина–Ломакса; 6 – модель смешения Прандтля

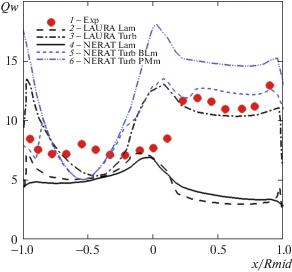
Рис. 8.

Распределение параметра теплообмена вдоль лобовой поверхности модели спускаемого аппарата MSL в условиях эксперимента Run3047 при турбулентном режиме обтекания для угла атаки α = 16°; обозначения как на рис. 7

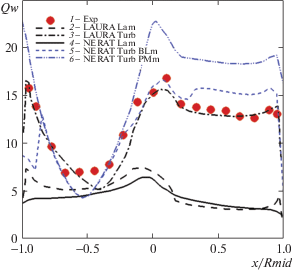
Рис. 9.

Распределение параметра теплообмена вдоль лобовой поверхности модели спускаемого аппарата MSL в условиях эксперимента Run3048 при турбулентном режиме обтекания для угла атаки α = 16°; обозначения как на рис. 7

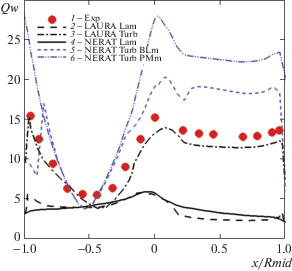
Расчетные данные показывают, что вблизи критической точки экспериментальные значения параметра Qw близки к тому, что дает ламинарный расчет, а в зоне турбулентного течения интенсивность конвективного нагрева превышает значения ламинарного нагрева более, чем в 3 раза. При этом две использованные алгебраические модели дают достаточно близкие результаты, хотя модель смешения Прандтля показывает небольшое систематическое завышение.

Таким образом, представленные данные демонстрируют удовлетворительное согласие расчетных данных LAURA и NERAT-3D и, в свою очередь, их удовлетворительное описание экспериментальных данных при турбулентном режиме течения в широком диапазоне чисел Рейнольдса. Полученные данные являются полезным дополнением к обширным данным по результатам расчетов конвективного нагрева летательных аппаратов, в том числе с использованием алгебраических моделей турбулентности [14].

ЗАКЛЮЧЕНИЕ

Выполненное в данной работе расчетное исследование показало, что использование алгебраических моделей турбулентности Болдуина–Ломакса и смешения Прандтля совместно с усредненными по Рейнольдсу уравнениями Навье–Стокса позволяет получить удовлетворительное согласие с экспериментальными данными по конвективному нагреву лобовой поверхности модели спускаемого аппарата MSL при ее пространственном обтекании в широком диапазоне изменения чисел Рейнольдса.

Продемонстрировано удовлетворительное согласие с расчетными данными, полученными с использованием компьютерного кода LAURA, в котором алгебраические модели турбулентности использовались в рамках параболизованных уравнений Навье–Стокса для анализа этих же экспериментальных данных.

Полученные расчетные данные подтверждают сложившееся в прикладных аэродинамических исследованиях мнение о том, что, несмотря на развитие и применение широкого спектра моделей турбулентного смешения, каждая из которых имеет свою область применения, алгебраические модели турбулентности в настоящее время оказываются предпочтительнее для расчетов теплообмена при решении сложных задач внешней аэротермодинамики в силу своей простоты и, в то же самое время, за счет разумных феноменологических представлений о структуре усредненного движения в пристеночных областях турбулентных пограничных слоев, положенных в основу этих моделей.

Список литературы

  1. Hollis B.R., Collier A.S. Turbulent Aeroheating Testing of Mars Science Laboratory Entry Vehicle in Perfect-Gas Nitrogen // AIAA 2007-1208. 2007. 20 p.

  2. Marren D., Lafferty J. The AEDC Hypervelocity Wind Tunnel 9. Advanced Hypersonic Test Facilities, Progress in Aeronautics and Astronautics. 2002. Vol.198. AIAA, Reston, VA. pp. 467–477.

  3. Micol J.R. Langley Aerothermodynamic Facilities Complex: Enhancements and Testing Capabilities // AIAA 98-0147. 1998.

  4. Gnoffo P.A. An Upwind-Based, Point-Implicit Algorithm for Viscous, Compressible Perfect-Gas Flows. 1990. NASA TP-2953.

  5. Tannehill J.C., Anderson D.A., Pletcher R.H. Computational Fluid Mechanics and Heat transfer. Taylor & Francis, 1997. 792 p.

  6. Суржиков С.Т. Пространственная задача радиационной газовой динамики командного модуля Аполлон-4 при сверхорбитальном входе в атмосферу// Изв. РАН. МЖГ. 2018. № 2. С. 149–160.

  7. Date A.W. Introduction to Computational Fluid Dynamics. Cambridge Univ. Press., 2005. 377 p.

  8. Cebeci T., Bradshaw P. Physical and Computational Aspects of Connective Heat Transfer. Springer–Verlag, 2012. 486 p.

  9. Baldwin B.S., Lomax H. Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows // AIAA Paper 78–0257. 1978 8 p.

  10. Surzhikov S.T. Analysis of the turbulent boundary layer on a plane plate at M = 6÷8.8 with the use of NERAT-2D code and algebraic turbulence models // IOP J. Phys.: Conf. Ser. 2018. V. 1009.

  11. Shirazi S.A., Truman C.R. Comparison of Algebraic Turbulence Model for PNS Predictions of Supersonic Flow Past a Sphere-Cone // AIAA 87-0544. 1987. 12 p.

  12. Shang J.S., Scherr S.J. Navier-Stockes Solution for a Complete Re–Entry Configuration // J. Aircraft. 1986. V. 23. № 2. P. 881–888.

  13. Edwards J.R., Liou M.-S. Low-Diffusion Flux-Splitting Methods for Flow at all Speeds // AIAA J. 1998. V. 36. № 9. P. 1610–1617.

  14. Землянский Б.А., Лунев В.В., Власов В.И. и др. Конвективный теплообмен летательных аппаратов. М.: Физматлит, 2014. 330 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал