Известия РАН. Механика жидкости и газа, 2019, № 5, стр. 52-58

ВОЛНООБРАЗОВАНИЕ ПЕРЕД ГЛИССИРУЮЩЕЙ ПЛАСТИНКОЙ

Е. В. Филатов^a, *, А. Ю. Якимов^a, **

^a МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия

^* E-mail: eugenifilatow@yandexl.ru
^** E-mail: ajkimov@mail.ru

Поступила в редакцию 20.11.2018
После доработки 11.02.2019
Принята к публикации 09.03.2019

DOI: 10.1134/S0568528119050037

Аннотация

Представлены результаты проведенных в гидроканале МГУ экспериментов по движению пластинки, жестко закрепленной на динамометрической тележке. Исследовались волновой след за телом и течение перед ним в жидкости конечной глубины при околокритических скоростях движения и малых углах глиссирования. Наблюдения показали, что стационарный периодический волновой след возникает вместе с носовой волной неизменной формы, а при отставании кормовых волн возбуждаются волны перед глиссирующей пластинкой. Получено экспериментальное подтверждение известной формулы Рассела для амплитуды уединенной волны. С точностью до малых параметров показано ее совпадение с результатом М.А. Лаврентьева. Приводятся результаты численного моделирования условий эксперимента с использованием программного комплекса XFlow™. Результаты экспериментов в гидроканале совпадают с численными.

Ключевые слова: уединенная волна, формула Лаврентьева, глиссирование, потенциальное течение, свободная поверхность, гидроканал, ондулярный бор

Настоящее исследование является продолжением работы [1], где получено выражение для силы, действующей на глиссирующую пластинку, и предложен приближенный критерий образования уходящих вперед по отношению к пластинке волн. Подобное явление описано Расселом [2]. В [3] освещено современное состояние темы и экспериментально исследованы волны перед вертикальной пластиной. Это нестационарное течение в литературе называется ондулярным бором. В настоящей работе получены режимы с тремя или четырьмя волнами неизменной формы (около 30 глубин канала), что позволило выдвинуть стационарную постановку и сравнить результаты экспериментов со свободными нелинейными волнами.

1. ОПИСАНИЕ ЭКСПЕРИМЕНТА

Для экспериментальных исследований использовался гидроканал Института механики МГУ. Длина канала 60 м, ширина канала 1.5 м, глубина воды изменялась от 0.25 до 0.53 м. Канал оснащен динамометрической тележкой для буксировки моделей. В качестве пластины использовался лист толщиной 15 мм, шириной 1.5 м и длиной 3 м. В экспериментах угол наклона изменялся в пределах от 10 до 20°. Заглубление задней кромки пластинки изменялось от 10 до 70 мм. Скорость тележки составляла от 1 до 2.5 м в секунду. Тележка с закрепленной пластинкой проходила дистанцию около 25 м и останавливалась (рис. 1).

Рис. 1.

Схема гидроканала

Для регистрации волнения перед пластинкой использовалась видеокамера, закрепленная на легкой тележке. Тележка вручную передвигалась по рельсам со скоростью волнового фронта. На стенку гидроканала была нанесена вертикальная разметка с шагом 1 м для определения скорости вершины волны по числу кадров видеозаписи (рис. 2). Стационарность высоты волны оценивалась по горизонтальной разметке с шагом 50 мм. Видеосъемка волнового фронта велась на дистанции от 10 до 19 м, поскольку волны уходили от пластинки во время ее движения.

Рис. 2.

Кадр видеосъемки уходящей волны движущейся камерой

Более точно амплитуда измерялась по видеосъемке через смотровое окно с горизонтальной разметкой шагом 20 мм (рис. 3).

Рис. 3.

Кадр видеосъемки уходящей волны через смотровое окно

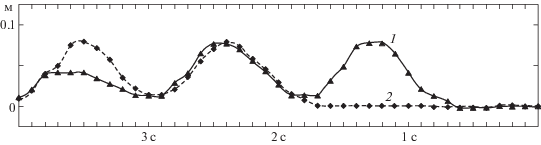
Для построения профиля волны и определения ее длины использовались показания двух акустических датчиков с частотой 10 Гц, установленных в двух метрах друг от друга. Показания акустических датчиков приведены на рис. 4.

Рис. 4.

Зависимость подъема поверхности от времени по показаниям акустических датчиков 1 и 2

Проводилось численное моделирование условий эксперимента. В расчетах использовался численный метод решеточных уравнений Больцмана [4, 5], при использовании которого уравнения Навье–Стокса не решаются, а моделируется течение ньютоновской жидкости с помощью дискретного кинетического уравнения Больцмана. Для численного моделирования процесса образования волн использовался вычислительный пакет XFlow™ [6].

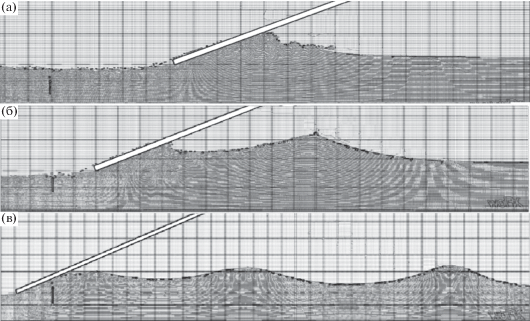
Механизм ухода волн от пластинки просматривается на последовательности волновых течений в численном эксперименте (рис. 5).

Рис. 5.

Численный эксперимент. Движение пластинки с носовой волной (а), отделение первой волны и образование следующей (б), волновой цуг (в)

2. ВОЛНЫ ПЕРЕД ТЕЛОМ

Сравним наблюдаемые волны со свободными нелинейными волнами [7], полученные с помощью формулы Лаврентьева (рис. 4 и 5 в)

(2.1)

$\left| {\frac{{{{V}_{Т}}}}{V}} \right| = \left| {f'} \right| \approx \frac{h}{Y}\left( {1 + \frac{1}{3}YY''\, + \frac{1}{3}Y{{'}^{2}}} \right)$

где Y и V_T – текущие глубина и скорость жидкости в системе координат, связанной с волной, f – конформное отображение плоскости течения на прямую полосу шириной h, V – скорость волны.

Форма свободной поверхности должна удовлетворять условиям, указанным в [7, 8], суть которых сводится к малому отклонению волновой поверхности от горизонтали и малом изменении ее кривизны. В указанном безразмерном виде формула (2.1) представлена в [8]. Применение (2.1) без учета последнего члена приведет к известному уравнению

(2.2)

$z{\kern 1pt} ''\, + 3\alpha z + \frac{9}{2}{{z}^{2}} = 0$

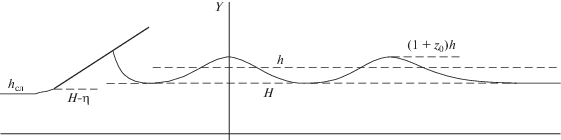
где $z = \frac{{Y - 1}}{h}$ и малый параметр $\alpha = \frac{{gh}}{{{{V}^{2}}}} - 1 = \frac{1}{{F{{r}^{2}}}} - 1$. V и h совпадают со скоростью жидкости и ее уровнем в точке поверхности с нулевой кривизной (рис. 6). Необходимо установить связь между числом Фруда Fr и числом Фруда $FR = \frac{C}{{\sqrt {gH} }}$ на невозмущенном уровне канала.

Рис. 6.

Картина течения в рамках теоретической модели

В [7] в точке волновой поверхности высотой h формула Лаврентьева сводится к гидравлическому приближению $\frac{V}{C} = \frac{H}{h}$. Добавим интеграл Бернулли $\frac{{{{C}^{2}}}}{2} + gH = \frac{{{{V}^{2}}}}{2} + gh$ и из двух последних уравнений получим $\frac{1}{{Fr}} = \frac{1}{{FR}}{{\left( {\frac{{F{{R}^{2}}}}{4} + \frac{{FR}}{2}\sqrt {\frac{{F{{R}^{2}}}}{4} + 2} } \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$(краткий вывод содержится в [1]). С точностью до $\frac{1}{{16}}{{\alpha }^{2}}$ получим $FR = \sqrt {1 + \alpha } = \frac{1}{{Fr}}$, то есть введенные числа Фруда в указанном приближении обратны. Из равенства расходов следует $h = HF{{r}^{{ - {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}$. Заметим, что амплитуда уединенной волны в [7] равна $\alpha = \frac{1}{{F{{r}^{2}}}} - 1$, а по известным результатам Рассела [2] и Релея, приведенными в [9], $A = F{{R}^{2}} - 1$. Таким образом, в предложенном приближении результаты совпадают.

По экспериментальным наблюдениям подошвы волн расположены незначительно выше глубины H. Воспользуемся этим и, в отличие от [7], выдвинем граничное условие для уравнения (2.2) не на вершине, а на подошве волны. Запишем первый интеграл уравнения (2.2) в виде z'² = = $3(\alpha z_{1}^{2} - z_{1}^{3} - \alpha {{z}^{2}} - {{z}^{3}})$, где ${{z}_{1}} = \frac{{H - h}}{h} = F{{R}^{{{{ - 4} \mathord{\left/ {\vphantom {{ - 4} 3}} \right. \kern-0em} 3}}}} - 1$. Тогда вершина волны

${{z}_{0}} = \frac{1}{2}\sqrt {F{{R}^{2}} + F{{R}^{{ - \frac{4}{3}}}} - 2} \left( {\sqrt {F{{R}^{2}} - 3F{{R}^{{ - \frac{4}{3}}}} + 2} - \sqrt {F{{R}^{2}} + 3F{{R}^{{ - \frac{4}{3}}}} - 2} } \right)$

обезразмеренная на H амплитуда волны $A = \sqrt[3]{{F{{R}^{4}}}}\left( {{{z}_{0}} - {{z}_{1}}} \right)$. Безразмерная длина волны

$\lambda = \sqrt[3]{{F{{R}^{4}}}}\int\limits_{{{z}_{1}}}^{{{z}_{0}}} {\frac{2}{{\sqrt {3{{{\left( {F{{R}^{{ - \frac{4}{3}}}} - 1} \right)}}^{2}}\left( {F{{R}^{2}} + F{{R}^{{ - \frac{4}{3}}}} - 2} \right) - (F{{R}^{2}} - 1){{z}^{2}} - } {{z}^{3}}}}} dz$

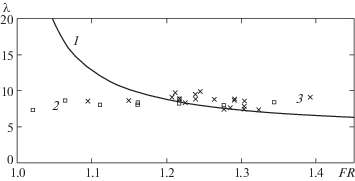
Сравнение с экспериментами проводится на рис. 7 и 8 . Согласно [9] высота волны не может превышать глубину канала, а по графику видно, что максимальная амплитуда уходящих волн составляет около 0.75 глубины канала, что более соответствует 0.827H [10]. Волны при этой амплитуде приобретали заостренную форму, сохраняли ее в течение малого времени (порядка секунды) и опрокидывались. При FR ~ 1.1 наблюдались затухающие волны малой амплитуды. В диапазоне наблюдения устойчивых волн (FR ~ 1.2–1.3) теория дает хорошее соответствие эксперименту.

Рис. 7.

Сравнение теоретической (1) амплитуды уходящей волны с результатами экспериментов в гидроканале (2) и численными расчетами (3)

Рис. 8.

Сравнение теоретической (1) длины уходящих волн с результатами экспериментов в гидроканале (2) и численными расчетами (3)

3. ПРИБЛИЖЕННАЯ ОЦЕНКА ЗАВИСИМОСТИ АМПЛИТУДЫ УХОДЯЩИХ ВОЛН ОТ ПАРАМЕТРОВ ДВИЖЕНИЯ ПЛАСТИНКИ

Поскольку стационарной картины в виде уходящего подъема поверхности перед пластинкой не наблюдается, введем h как ординату точки с нулевой кривизной. Для приближенного определения h аналогично [1] воспользуемся формулой Лаврентьева локально на задней кромке пластинки. В [1] получен критерий появления уходящих от пластинки волн по наличию возвратной струи

$\delta = H - \frac{{H - \eta }}{{{{C}_{{пл}}}(1 + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}{{\beta }^{2}})}}\sqrt {C_{{пл}}^{2} + 2g\eta } $

где $\beta $ – малый угол схода струи на задней кромке тела, $\eta > 0.04H$ – глубина погружения задней кромки пластинки; отметим, что при $\eta \approx 0$ данный подход не применим и существенного волнения не наблюдается.

При δ > 0 волновой след отстает от пластинки. В этом случае ограничимся уходящими волнами. Из приведенных в [1] уравнений для скорости жидкости V на бесконечности за пластинкой следует кубическое уравнение

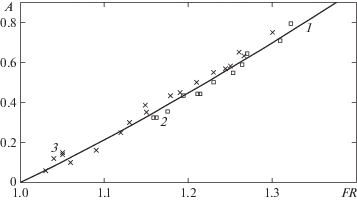
$V_{{сл}}^{3} - (C_{{пл}}^{2} + 2gH){{V}_{{сл}}} + 2{{C}_{{пл}}}g\left( {H - \delta } \right) = 0$

один из корней которого отрицательный, а другой меньше скорости тела, что противоречит постановке задачи. Воспользовавшись большим C положительным корнем, получим

$\begin{gathered} {{V}_{{сл}}} = \frac{C}{{FR}}\left( {{{{\left( {\sqrt {F{{R}^{2}}{{{\left( {1 - \frac{\delta }{H}} \right)}}^{2}} - \frac{{{{{(F{{R}^{2}} + 2)}}^{3}}}}{{27}}} - FR\left( {1 - \frac{\delta }{H}} \right)} \right)}}^{{\frac{1}{3}}}} + } \right. \\ \left. { + \;{{{\left( { - \sqrt {F{{R}^{2}}{{{\left( {1 - \frac{\delta }{H}} \right)}}^{2}} - \frac{{{{{(F{{R}^{2}} + 2)}}^{3}}}}{{27}}} - FR\left( {1 - \frac{\delta }{H}} \right)} \right)}}^{{\frac{1}{3}}}}} \right) \\ \end{gathered} $

Расположение экспериментальных точек на рис. 9 указывает на существование зависимости амплитуды уходящей волны от числа $J = {{FR_{{пл}}^{2}} \mathord{\left/ {\vphantom {{FR_{{пл}}^{2}} 2}} \right. \kern-0em} 2} + {\eta \mathord{\left/ {\vphantom {\eta H}} \right. \kern-0em} H}$, где$F{{R}_{{пл}}} = \frac{{{{C}_{{пл}}}}}{{\sqrt {gH} }}$ – число Фруда пластинки при фиксированном угле глиссирования.

Рис. 9.

Сравнение теоретической зависимости (1) амплитуды уходящей волны от параметров движения пластинки с результатами экспериментов в гидроканале (2) и численными расчетами (3)

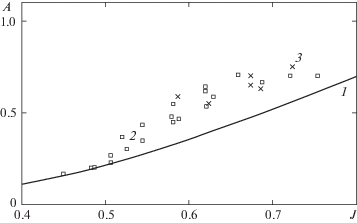
Считая ${\eta \mathord{\left/ {\vphantom {\eta H}} \right. \kern-0em} H}$ малым относительно параметра J, получим приближенные формулы

$\begin{gathered} {{V}_{{сл}}} = \sqrt {gH} \left( {{{{\left( {\sqrt {{{{\left( {\frac{{\sqrt {2J} }}{{1 + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 3}} \right. \kern-0em} 3}}}} \right)}}^{2}} - {{{\left( {\frac{2}{3}\left( {J + 1} \right)} \right)}}^{3}}} - \frac{{\sqrt {2J} }}{{1 + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 3}} \right. \kern-0em} 3}}}} \right)}}^{{\frac{1}{3}}}} + } \right. \\ \left. { + \;{{{\left( { - \sqrt {{{{\left( {\frac{{\sqrt {2J} }}{{1 + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 3}} \right. \kern-0em} 3}}}} \right)}}^{2}} - {{{\left( {\frac{2}{3}\left( {J + 1} \right)} \right)}}^{3}}} - \frac{{\sqrt {2J} }}{{1 + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 3}} \right. \kern-0em} 3}}}} \right)}}^{{\frac{1}{3}}}}} \right), \\ \end{gathered} $

${{h}_{{сл}}} = \frac{{H\sqrt {gH} }}{V}\frac{{\sqrt {2J} }}{{1 + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 3}} \right. \kern-0em} 3}}}$

Таким образом нами найдены скорость и глубина жидкости на бесконечности за телом. В системе координат, связанной с пластинкой, движение не стационарно и по интегралу Бернулли $\frac{V}{2} + gh + \frac{{\partial \Phi }}{{\partial t}} = \frac{{V_{{сл}}^{2}}}{2} + g{{h}_{{сл}}}$.

Наблюдения показывают, что скорость уходящих волн не более чем на 20% превосходит скорость пластинки. Предполагая независимость потенциала скоростей Φ от времени t из равенства расходов и интеграла Бернулли на поверхности жидкости, получим систему уравнений

$\left\{ \begin{gathered} Vh = {{V}_{{сл}}}{{h}_{{сл}}} \hfill \\ \frac{{V_{{сл}}^{2}}}{2} + g{{h}_{{сл}}} = \frac{{{{V}^{2}}}}{2} + gh \hfill \\ \end{gathered} \right.$

Как показано выше, ${{{{V}_{{сл}}}} \mathord{\left/ {\vphantom {{{{V}_{{сл}}}} {\sqrt {g{{h}_{{сл}}}} }}} \right. \kern-0em} {\sqrt {g{{h}_{{сл}}}} }} \approx {{\sqrt {gh} } \mathord{\left/ {\vphantom {{\sqrt {gh} } V}} \right. \kern-0em} V}$ и $h = {{\sqrt[3]{{{{{{V}_{{сл}}}} \mathord{\left/ {\vphantom {{{{V}_{{сл}}}} {g{{h}_{{сл}}}}}} \right. \kern-0em} {g{{h}_{{сл}}}}}}}}^{4}}$. Теперь известны глубины, по которым находим скорости и числа Фруда перед пластинкой. Приведем зависимость амплитуды $\left( {{{z}_{0}} - {{z}_{1}}} \right){h \mathord{\left/ {\vphantom {h H}} \right. \kern-0em} H}$ от числа J и результаты экспериментов (рис. 9).

ЗАКЛЮЧЕНИЕ

Амплитуда полученной в гидроканале МГУ уединенной волны совпадает с наблюдениями Рассела и с известной формулой ${{{{C}^{2}}} \mathord{\left/ {\vphantom {{{{C}^{2}}} g}} \right. \kern-0em} g} - H$. С точностью до малых параметров показано совпадение с результатом М.А. Лаврентьева.

Безразмерная длина волны в экспериментах оказывается постоянной, что не совпадает с теорией.

Предложенная приближенная зависимость амплитуды уходящей волны от параметров движения глиссера качественно соответствует эксперименту.

Результаты численных расчетов и экспериментов в гидроканале совпадают.

Найдено простое приближение интеграла Бернулли при равенстве расходов в виде обратной зависимости чисел Фруда.

Работа выполнена при поддержке гранта РФФИ №16-08-00807.

Список литературы

Филатов Е.В., Якимов А.Ю. Сопротивление пластинки, глиссирующей на мелкой воде с образованием волн // Изв. РАН. МЖГ. 2018. № 5. С. 29–37.
Russell S. Report on Waves, Brit. Ass. Rep., 1844.
Букреев В.И., Гусев А.В. Волны в канале впереди вертикальной пластины // Изв. РАН. МЖГ. 1999. № 1. С. 82–90.
Chen S., Doolen G. Lattice Boltzmann method for fluid flows // Annu. Rev. Fluid Mech. 1998. V. 30. P. 329–364.
Succi S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford University Press 2001. P. 82–84.
Xflow – новый программный комплекс для моделирования физических процессов, связанных с гидрогазодинамикой и тепломассообменом URL: http://www.cadmaster.ru/magazin/articles/cm_60_13.html
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1973. 736 с.
Якимов Ю.Л. О приближенной формуле для растяжения при конформном отображении области, имеющей узкий участок // Сиб. мат. журн. 1962. Т. 3. № 6. С. 956–960.
Сретенский Л.Н. Теория волновых движений жидкости. М.: Наука, 1977. 816 с.
Longuet-Higgins M.S., Fenton J.D. On the mass, momentum, energy and circulation of a solitary wave. II. Proc. Roy. Soc. London, A340, 1974, 471–493.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал