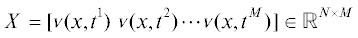Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 95-110
Экспериментальное исследование нелинейной аэроупругости одиночного профиля NACA в следе при наличии вибраций
А. Вань a, Х. Оуян a, Х. Се a, Я. У a, *
a School of Mechanical Engineering, Shanghai Jiao Tong University
200240 Shanghai, China
* E-mail: yadongwu@sjtu.edu.cn
Поступила в редакцию 30.05.2018
После доработки 31.07.2018
Принята к публикации 31.07.2018
Аннотация
Современные экономические и экологические стандарты требуют, чтобы лопасти турбин и крылья самолетов были возможно более легкими и гибкими при увеличении на них механической и аэродинамической нагрузки. Однако наличие аэродинамического возбуждения может привести к росту числа факторов, влияющих на вибрацию конструкции, в результате чего возникает задача аэроупругости. В отличие от случая механических резонансных вибраций, конструкция может взаимодействовать с аэродинамическим возбуждением и это возбуждение способно привести к захвату частоты в области, превышающей 10% от собственной частоты конструкции. Это явление расширяет диапазон высокоамплитудной реакции и должно учитываться при проектировании с учетом требований безопасности. В настоящей работе экспериментально исследуется реакция конструкции на аэродинамическое возбуждение. Экспериментальная установка включает цилиндр, находящийся выше по потоку, и одиночный профиль NACA ниже по потоку, размещенные в аэродинамической трубе. Передний цилиндр генерирует вихри, которые воздействуют на профиль NACA, возбуждая периодические колебания гибкой конструкции. Скорость потока измерялась термоанемометром, синхронно в положениях вверх и вниз по потоку от тела. Для условий, соответствующих эксперименту, выполнено численное моделирование, результаты которого сопоставлены с данными измерений. Для одного типичного случая основные особенности структуры течения выявлены методом собственно ортогонального разложения. Структурные свойства профиля, включая собственную частоту и скорость затухания, определены посредством конечно-элементного анализа и испытания обстукиванием. Основываясь на свойствах жидкости и конструкции, становится возможно провести взаимосвязанный тест и анализ. Характеристики вибраций профиля NACA в модах первого и второго порядка исследовались при изменении скорости набегающего потока и диаметра цилиндра. Для вынужденных вибраций первой моды характерно явление захвата частоты, а максимальная амплитуда не приходится на точку резонанса. В то же время вибрации второй моды обнаруживают типичное резонансное поведение.
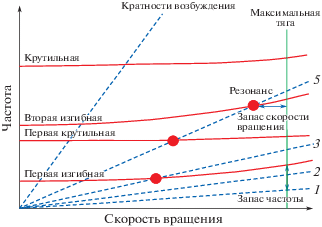
По мере того как требования экономики, сбережения энергии и защиты окружающей среды приобретают все большую важность, все больше внимания обращается на облегчение лопастей турбомашин и крыльев самолетов при увеличении на них механической и аэродинамической нагрузки. С ростом этих нагрузок конструкция становится более эффективной, но более чувствительной. Когда механическое и аэродинамическое возбуждения воздействуют на конструкцию, ее реакция при определенных условиях может создать серьезные проблемы. Поэтому, во избежание проблем с безопасностью, запас надежности конструкции должен быть аккуратно просчитан. Классический способ оценки проблем вынужденной реакции конструкции дает метод диаграммы Кэмпбелла. Как показано на рис. 1, кратности возбуждения представляют собой внешние возбуждения, связанные со скоростью вращения и ее гармониками. Собственные частоты определяют структурные свойства тела. Точки резонанса указывают на пересечение внешнего возбуждения и собственной частоты, что может привести к большим вибрациям, повреждениям и выходу из строя. Требуется избежать резонанса при обычных условиях работы, например, при крейсерской и максимальной тяге. Для этого должен быть достаточный запас по частоте для конкретных рабочих условий. Такой типичный запас для изгибной моды первого порядка составляет более 10% [1]. Частота возбуждения механических вибраций отчетлива и сильно зависит от демпфирования конструкции. Однако аэродинамически привнесенные вибрации более сложны вследствие взаимодействия жидкости и конструкции, что приводит к возникновению проблемы аэроупругости. Последняя определяется как междисциплинарная область, в которой конструкция и жидкость взаимодействуют друг с другом через аэродинамические и механические силы, а также силы инерции.
В теории аэроупругости широко известны проблемы вибраций, вызванных вихрями (VIV) и следами (WIV), которые исследовались во многих работах с привлечением различных методов. Так, в работе [2] проведены эксперименты в аэродинамической трубе малых скоростей с целью установить влияние импульсного нагружения на результирующую вибрацию и деформацию лопасти на простой опоре. Результаты показали, что свойства вибраций были характерны для механической системы, в которой можно было различить лишь собственную частоту.
В [3] изучена двумерная система взаимодействия осцилляторов в следе с конструкцией и количественно описаны основные явления, свойственные двумерным вибрациям, вызванным вихрями. В [4] сообщается, что в случае поперечно обтекаемого цилиндра граница области захвата частоты несимметрична относительно частоты схода вихрей. В [5] экспериментально установлены широкие диапазоны частот и амплитуд наложенных пульсаций в следе за цилиндром. В работе [6] обсуждаются вибрации, наведенные вихрями, и явление захвата частоты для профиля под большим углом атаки и указаны соответствующие диапазоны. В [7] исследованы вызванные вихрями вибрации системы двух разнесенных цилиндров с двумя степенями свободы; эксперименты проведены в гидроканале. Результаты показывают, что возбуждение, вызванное следом, ослабевает, когда находящийся ниже по течению цилиндр смещается от центральной линии следа вбок. В работе [8] проведен аналогичный эксперимент, но основное внимание уделено другому явлению. Изучались вибрации цилиндра, наведенные потоком жидкости в следе за другим цилиндром, применительно к взаимодействию между вертикальными райзерами высокого натяжения в глубокой воде. Относительная важность VIV- и WIV-вибраций зависит от отношения масс структуры и перемещенной среды. В [9] указан механизм захвата частоты при VIV-вибрациях при малых числах Рейнольдса Re; результаты показывают, что явление захвата частоты в этом случае может быть подразделено на два класса в соответствии с доминирующим механизмом, а именно, резонансом и флаттером. В работе [10] исследовано влияние изменения формы крыла в полете на нестационарную аэродинамику; численно исследовано обтекание деформируемой машущей пластины при малых числах Рейнольдса. При малом удлинении деформируемой пластины (AR = 2) результаты обнаруживают те же тенденции, что и в двумерном случае, несмотря на наличие трехмерных эффектов. В работе [11] численно исследован вопрос об управлении следом тела, расположенного выше по течению, в тандеме двух цилиндров с целью уменьшения аэродинамического шума. Поле течения моделировалось на основе двумерных нестационарных, осредненных по Рейнольдсу уравнений Навье–Стокса (RANS) с k – ${\omega } - $моделью турбулентности; показано, что управление передним телом играет важную роль в стабилизации следа.
Вибрации, вызванные следом, представляют собой проблему вынужденной вибрации. В данной работе эти вибрации исследуются экспериментально с системой, состоящей из переднего цилиндра и расположенного ниже по течению гибкого профиля. Основная вихревая дорожка порождается передним цилиндром, а не вибрирующим профилем. Аэродинамические пульсации вихря, сходящего с переднего тела, периодически воздействуют на гибкий профиль. Характеристики аэродинамического возбуждения и свойства конструкции исследуются экспериментально. Частота схода вихрей измеряется термоанемометром, а собственная частота гибкого тела определяется методом простукивания. Для верификации экспериментальных результатов используется численное моделирование. По известным параметрам течения и конструкции можно провести исследование их совместного эффекта. Аэроупругое поведение профиля можно оценить по данным о частоте вибраций и амплитуде реакции. В работе показано, что явление захвата частоты присуще изгибной моде профиля первого порядка, тогда как изгибная мода второго порядка обнаруживает типичное резонансное поведение.
1. ОБЪЕКТ ИССЛЕДОВАНИЯ И ИЗМЕРЕНИЯ
Экспериментальная установка изображена на рис. 2. Единичный профиль, закрепленный одним концом, размещен в прямоугольной рабочей части аэродинамической трубы, а находящийся выше по потоку цилиндр создает кармановскую вихревую дорожку, оказывающую периодическое силовое воздействие на профиль. В этом случае пульсации аэродинамической силы об-условлены срывом вихрей, а уравнение, описывающее движение профиля как системы с N степенями свободы, можно представить в следующем общем виде
Рис. 2.
Аэродинамическая труба и экспериментальная установка для исследования поля течения посредством термоанемометра и вибраций тела при помощи лазерного доплеровского измерителя скорости (ЛДИС).
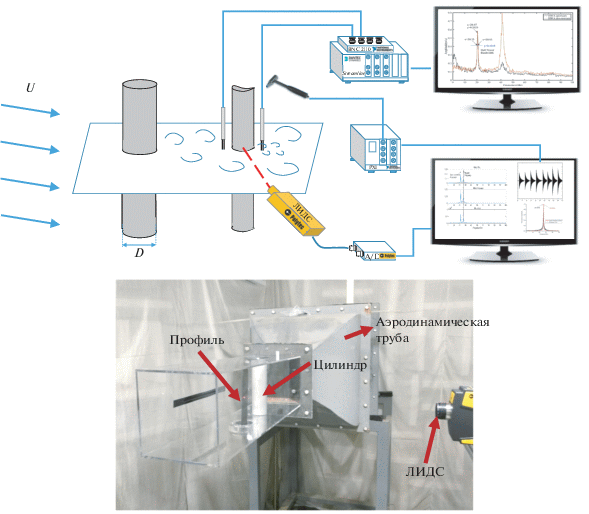
Здесь M – матрица масс, C – коэффициент демпфирования и K – коэффициент жесткости. При изучении реакции на механическое возбуждение внешняя сила задана, и основная проблема состоит в определении демпфирования. В рассматриваемом нами случае передний цилиндр индуцирует аэродинамическую силу. Вихри, сходящие с цилиндра в след, воздействуют на расположенное ниже по потоку тело и создают непрерывное возбуждение с существенно постоянной частотой. Эта вынуждающая частота определяется числом Струхаля St
где f – частота схода вихрей в след (в герцах), D – диаметр цилиндра и ${{U}_{\infty }}$ – скорость набегающего потока. Число Струхаля остается примерно постоянным в диапазоне чисел Рейнольдса, соответствующем условиям экспериментов ($1.0 \times {{10}^{4}}\sim 5.1 \times {{10}^{4}}$) [12]. Иными словами, частотой схода вихрей можно управлять, меняя диаметр цилиндра D и скорость набегающего потока ${{U}_{\infty }}$.1.1 . Объект исследования
Рассматривался профиль прямого крыла NACA 6510. Материал, из которого изготовлено тело, был пластик акрилонитрил-будадиен-стирол (ABS) с модулем Юнга $2.0 \times {{10}^{3}}\quad$ МПа и плотностью 950 кг/м3. Рабочая часть трубы имела 600 мм в длину и квадратное поперечное сечение 180 × 180 мм. Длина профиля была 178 мм, а длина хорды 36 мм. Для возбуждения первой и второй моды колебаний использовались два различных цилиндра, создающие вихревую дорожку, а именно, цилиндр диаметром 50 мм для возбуждения первой моды и диаметром 20 мм для второй моды.
Аэродинамическая труба находилась внутри акустически заглушенной камеры, так что на фигуре видны лишь сужающийся участок и рабочая часть. Качество потока данной трубы было установлено в предыдущих экспериментах [13]. Интенсивность турбулентности в центральной части потока менее 0.4%, а равномерность средней скорости находится в пределах 0.1%. Таким образом, данная установка может обеспечить приемлемую равномерность поля течения на входе.
1.2 . Измерения
Как показано на рис. 2, скорость вибраций профиля измерялась лазерным доплеровским виброметром фирмы Polytec® со сканирующей головкой PSV-500 и прецизионным оптическим измерителем с разрешением 458 мкм/с в диапазоне 12 м/с. Виброметр расположен в середине размаха профиля; это место чувствительно к вибрациям профиля как первого, так и второго порядка. Скорость потока измерялась двумя одномерными термоанемометрами, расположенными выше и ниже по потоку от исследуемого тела. Измерения переднего датчика показывают уровень аэродинамического возбуждения, а заднего датчика – результат на выходе, обусловленный также вибрациями тела. В целом были получены точные данные о скорости течения и далее анализировался частотный диапазон вибраций профиля и возбуждения в потоке.
2. АНАЛИЗ ПОЛЯ ТЕЧЕНИЯ
Проведены измерения поля течения и его численное моделирование. Основные определяющие факторы поля течения измерены с хорошей по времени точностью термоанемометром и результаты подтверждены данными численного моделирования и модального анализа. Эти данные дают возможность определить силу и тип аэродинамического возбуждения.
2.1. Измерение поля течения
Два термоанемометрических датчика размещались выше и ниже по течению от тестируемого профиля для определения входного (перед профилем) и выходного (за телом) аэродинамического возбуждения; они обозначены как P1 и P2 соответственно. При увеличении скорости набегающего потока число Рейнольдса Re возрастает, но число Струхаля остается в данном диапазоне Re неизменным. Таким образом, частота схода вихрей растет с ростом скорости набегающего потока. Рассмотрены несколько случаев, в которых менялась скорость набегающего потока. Диаграммы зависимости частоты от Re представлены на рис. 3; для них характерны два главных пика, представляющие частоту схода вихрей и его вторую гармонику. Частота схода линейно растет с Re, а амплитуда частоты схода больше, чем для второй гармоники.
Рис. 3.
Частотный спектр, измеренный термоанемометром, в зависимости от Reа. Ширина полосы частот на уровне половинной мощности для первого пика возбуждения выше по потоку от профиля в зависимости от Re.
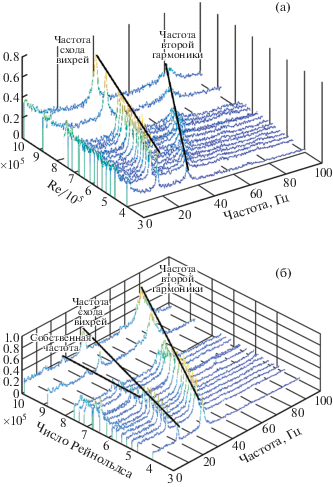
Ширина пика частоты схода вихрей может быть определена как ширина полосы частот на уровне половинной мощности; она растет с увеличением Re. Ширина полосы указывает на то, что аэродинамическое возбуждение представляет собой сигнал не на дискретной частоте, а узкочастотный случайный сигнал. Полоса частоты второй гармоники указывает на подобие пар сходящих вихрей; ее индуцирует также нестационарность течения.
Другой датчик помещался ниже по потоку от тестируемого профиля. Полоса частоты второй гармоники сигнала скорости, снимаемого датчиком, существенно расширяется за профилем вследствие того, что картина сходящих вихрей меняется после соударения с телом: теперь вихрь, сходящий с каждой стороны цилиндра, одинаковым образом влияет на скорость. Другой уникальный феномен состоит в том, что когда частота в потоке приближается к собственной частоте механического возбуждения, ветвь частоты сходящих вихрей смещается к этой механической частоте и не растет с Re.
Различие между результатами, выдаваемыми передним и задним датчиками, показывает, что наличие профиля изменяет характер аэродинамического возбуждения, а вибрации тела взаимодействуют с полем течения, порождая дополнительную частоту. В диаграмме Кэмпбелла точки пересечения кратностей возбуждения и собственной частоты всегда ярко выражены, но аэродинамическое возбуждение влияет на более широкую область частотного диапазона, чем механическое возбуждение, что связано именно с указанным взаимодействием.
На рис. 4 представлены два типичных частотных спектра скорости при различных Re. При частоте аэродинамического возбуждения 20.67 Гц, что меньше собственной частоты конструкции, первый пик при 20.67 Гц соответствует частоте схода вихрей, а второй пик представляет вторую гармонику. Перед профилем амплитуда первого пика больше, чем второго, а после профиля второй пик очевидно возрастает. Для определения входного возбуждения была измерена ширина полосы первого пика по уровню половинной мощности: она составила 0.6 Гц. Первые пики спектров, измеренных выше и ниже по течению, имеют очень близкие частоты и амплитуды; что касается второго пика, здесь имеет место большое расхождение по амплитуде, но частоты снова близки. Когда аэродинамическое возбуждение происходит на частоте 29.02 Гц, большей, чем собственная частота, частотные характеристики меняются. Во-первых, в спектре, измеренном термоанемометром в области выше по потоку, ширина полосы частот первого пика расширяется до 1.17 Гц, что свидетельствует о росте полосы частот аэродинамического возбуждения с ростом Re. Во-вторых, первый пик спектра, измеренного в области ниже по потоку, не совпадает с частотой аэродинамического возбуждения, а частота 26.04 Гц близка к собственной частоте конструкции. Второй пик спектра, измеренного в области ниже по потоку, сохраняет прежнюю форму, однако, он становится шире и имеет много острых выступов. Форма этого пика требует дальнейших исследований, чтобы объяснить различие между случаями, соответствующими частотам 29.02 и 26.04 Гц. Ширина полосы частот первого пика в спектре, измеренном в области выше по потоку, также существенно растет с ростом Re.
Рис. 4.
Типичный спектр скорости, снятый термоанемометром вверх и вниз по потоку от профиля (а) Аэродинамическое возбуждение при 20.67 Гц; (б) Аэродинамическое возбуждение при 29.02 Гц.
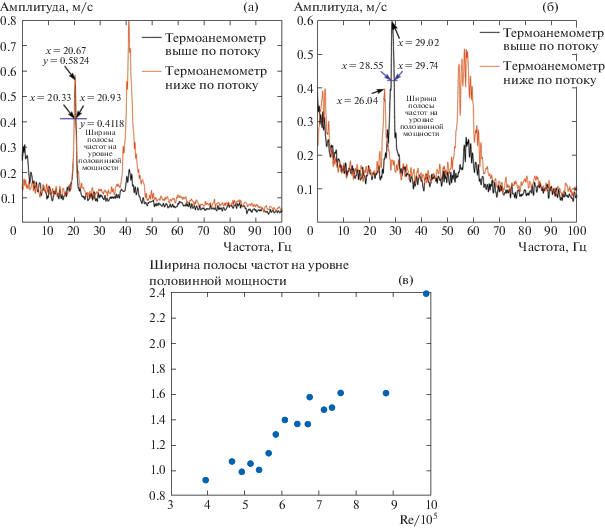
Исследование полей течений помогает лучше понять природу аэродинамического возбуждения сходящих вихрей. Во-первых, входной сигнал возбуждения узкополосный. Когда узкополосный сигнал включает в себя собственную частоту, амплитуда вибраций конструкции возрастает. Во-вторых, ширина полосы частот на уровне половинной мощности для возбуждения в области выше по потоку также возрастает с Re. В случае обычной реакции на механическое воздействие входное возбуждение представляет собой сигнал дискретной частоты и ситуация весьма проста. Результаты измерений в области ниже по потоку показывают, что вибрации профиля оказывают воздействие на аэродинамическое возбуждение, так что в ходе вибраций тела имеет место совместный эффект. Частота аэродинамического возбуждения, действующего на профиль, может измениться, что может привести к расширению опасной области.
2.2. Численное моделирование и модальный анализ поля течения
Численное моделирование все чаще применяется в исследованиях по мере роста вычислительных мощностей. Сопряженная система уравнений упругости конструкции и Эйлера или Навье–Стокса приводится к виду, удобному для решения, при помощи того или иного алгоритма и используется для решения реальных проблем или сопоставления с экспериментальными результатами. Моделирование пониженного порядка широко распространено при исследовании таких проблем аэроупругости, как флаттер, отклик на воздействие, рассогласование и т.д. В работе [14] приведены результаты численного исследования вынужденной реакции облопаченного диска на такие воздействия, как рассогласование и аэродинамическое демпфирование. Полученные данные были введены в динамическую систему и результаты решения сравнивались с экспериментальными данными. В работе [6] метод собственно ортогонального разложения также использовался для анализа нестационарного поля давления при больших углах атаки. В [15] описаны нелинейные аэродинамические модели пониженного порядка, позволяющие предсказать аэросервоупругое поведение решетки параллельных профилей в режиме открытой или замкнутой петли. В работе [16] предложены многослойные модели пониженного порядка для решения задач аэроупругости. Были рассчитаны аэродинамические силы, колебания предельного цикла и флаттер трансзвукового профиля NACA 64A010, которые оказались в хорошем согласии с результатами высокоточного численного моделирования. Таким образом, численное моделирование представляет собой удобный и надежный инструмент, позволяющий дополнить экспериментально полученную информацию, а модальный анализ позволяет проиллюстрировать структуру течения.
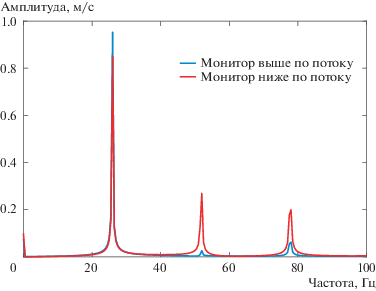
Численное моделирование течения свидетельствует о пульсациях в следе за цилиндром и их влиянии на профиль. Выполнено двумерное RANS моделирование для условий, соответствующих эксперименту. Выбранная модель турбулентности $k - \varepsilon $ [17] хорошо подходит для моделирования двумерного следа за цилиндром. Величина $\quad{{Y}^{ + }}$ сетки была выбрана равной Y+ = = $0.172*R{{e}^{{0.9}}}{*\Delta }y{\text{/}}L$, ${{Y}^{ + }} \approx 1$, откуда вычислялась высота первого слоя ${\Delta }y$. Были опробованы сетки с 40 390, 64 318 и 87 442 узлами, причем различие по скорости между сетками с 64 318 и 87 442 узлами составляло менее 1%. Для дальнейших расчетов была выбрана сетка с 64 318 узлами. Шаг по времени при решении нестационарной задачи составлял 2–4 с, а результаты выдавались каждые 5 шагов, что соответствует частоте опроса в ходе моделирования 1000 Гц. Длительность рассчитанного интервала времени была 2 с с разрешением по частоте в 0.5 Гц. Hz. Результаты одного моделирования с типичными граничными условиями, когда частота схода вихрей была 26 Гц, представлены на рис. 6. Построены спектры по результатам измерений мониторами скоростей в областях выше и ниже по течению. Монитор, расположенный выше по течению, обнаруживает более заметный пик на частоте схода 26 Гц, тогда как монитор, расположенный ниже по течению, показывает более выраженные гармоники. Общая картина согласуется с экспериментальными результатами.
Рис. 6.
Спектры поля течения по показаниям мониторов, расположенных выше и ниже по потоку от профиля.
Для лучшего понимания структуры течения и картины возбуждения к результатам нестационарного расчета было применено собственно ортогональное разложение (СОР). СОР представляет собой метод разложения по модам, позволяющий извлечь когерентные структуры из турбулентного поля течения на основе оптимизации по среднеквадратичному значению рассматриваемой переменной. Этот метод был впервые применен в гидродинамике в работе [18] и с тех пор широко используется во многих приложениях. Получение СОР-кадров представляется оптимальным методом при работе с сеткой больших размеров при малом шаге по времени [19, 20]. Векторное поле $u(x,t)$ в поле течения $x \in {{\mathbb{R}}^{N}}$ (N – размер сетки) может быть извлечено в виде M кадров течения с постоянной частотой опроса. На шаге по времени m векторное поле имеет вид
где m = 1, 2, 3, …, M, а u включает в себя среднюю по времени и пульсационную компоненты. Последняя может быть представлена в видеЭта пульсационная компонента может быть выражена как линейная комбинация ортогональных мод и их соответствующих коэффициентов, зависящих от времени
(2.3)
$v\left( {x,t} \right) = \mathop \sum \limits_j {{a}_{j}}\left( t \right){{\phi }_{j}}\left( x \right)$Далее m кадров группируются в матричной форме
Целью СОР анализа является найти оптимальные базисные векторы, наилучшим образом представляющие заданные величины. Векторы ${{\phi }_{j}}\left( x \right)$ должны представить u(x) оптимальным образом при наименьшем числе мод. Эта проблема может быть решена путем определения собственных векторов ${{\phi }_{j}}$ и собственных значений ${{\lambda }_{j}}$ из системы
(2.5)
${{X}^{T}}X{{\phi }_{j}} = {{\lambda }_{j}}{{\phi }_{j}},\quad {{\phi }_{j}} \in {{\mathbb{R}}^{M}},\quad\quad M < N$Размерность векторов ${{\phi }_{j}} \in {{\mathbb{R}}^{M}}$ меньше, чем размерность изначальных векторов ${{\psi }_{j}} \in {{\mathbb{R}}^{N}}$ в СОР. При решении задачи на меньшие собственные значения СОР моды могут быть восстановлены
СОР моды ${{\psi }_{j}}$ могут улавливать основную кинетическую энергию из поля течения через собственные значения. Пусть r мод представляют поле течения(2.7)
${{\mathop \sum \limits_{j = 1}^r {{\lambda }_{j}}} \mathord{\left/ {\vphantom {{\mathop \sum \limits_{j = 1}^r {{\lambda }_{j}}} {\mathop \sum \limits_{j = 1}^N {{\lambda }_{j}}}}} \right. \kern-0em} {\mathop \sum \limits_{j = 1}^N {{\lambda }_{j}}}} \approx 1$При количестве СОР мод, равномr, поле течения может быть представлено в виде
(2.8)
$u\left( {x,t} \right) = \bar {u}\left( x \right) + \mathop \sum \limits_{j = 1}^r {{a}_{j}}\left( t \right){{\psi }_{j}}\left( x \right)$(2.9)
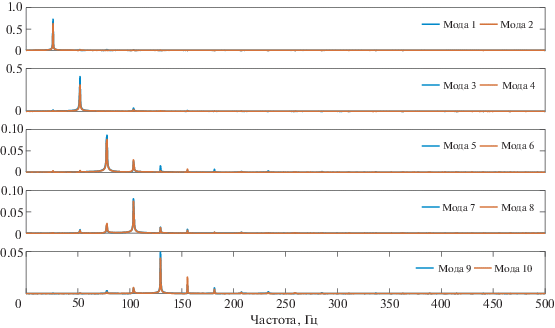
${{a}_{j}}\left( t \right) = \left\langle {v\left( {x,t} \right),{{\psi }_{j}}\left( x \right)} \right\rangle $В этом случае при рассмотрении цилиндра без расположенного ниже по потоку тела СОР моды нестационарного периодического следа за цилиндром воспроизводят разложение Фурье. Они возникают парами, представляя две фазы первой и более высоких гармоник. [21]. Однако наличие тела ниже по течению вносит дополнительные переменные в поле течения. Первые 10 СОР мод для продольной компоненты скорости и процентные соотношения соответствующих коэффициентов λ представлены на рис. 7. Если мода 0 соответствует среднему по времени полю течения, то зона, соответствующая обтеканию цилиндра, симметрична, а симметрия зоны обтекания профиля искажена углом профиля. Как показано на рис. 8, спектры нестационарных коэффициентов каждой моды показывают, что каждая пара СОР мод имеет один и тот же главный пик частоты. Моды 1 и 2 представляют собой частоты схода вихрей Кармана в частотной области, но имеют различные фазы и амплитуды. В случае следа одиночного цилиндра первая пара СОР мод имеют одинаковые частоту и амплитуду, но противоположные фазы. Различие амплитуд может быть вызвано расположенным ниже по течению профилем, соударяющимся с вихрем. СОР моды высших порядков также парны и представляют собой гармоники частот схода вихрей. Энергетический уровень каждой пары быстро убывает с порядком гармоники.
Рис. 7.
Среднее по времени поле течения и первые 10 СОР мод. Визуализация продольной компоненты скорости.
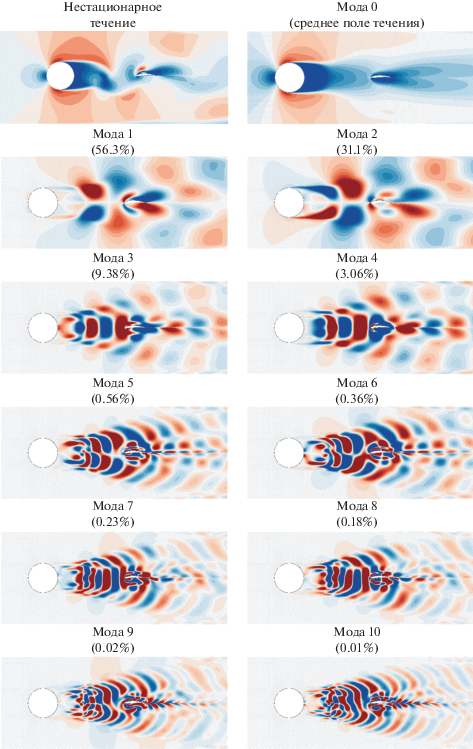
Остаток от первой пары СОР мод составляет 12.6%, которые в основном представляют пульсации поля течения. Остаток от первых 11 СОР мод убывает до 0.000777%. Они хорошо представляют сложное поле течения и аэродинамического возбуждения при наличии профиля ниже по течению.
3. РЕЗУЛЬТАТЫ АНАЛИЗА ВИБРАЦИЙ
Исследование вынужденной реакции на возбуждение основано на главных характеристиках испытуемого тела. Для обеспечения точности измерений и проведения адекватного анализа требуется знать его собственную частоту и формы мод. С этой целью проводятся конечно-элементный анализ и экспериментальное исследование. В этом случае результаты по вибрациям, индуцированным следом, могут дать представление о совместном эффекте аэродинамического возбуждения и конструкции.
3.1 . Характеристики конструкции
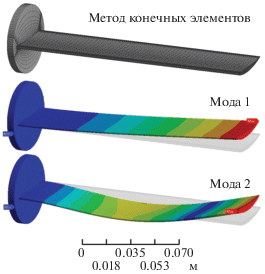
1) Конечно-элементный анализ
Свойства материала ABS задаются производителем. Сетка конечно-элементной модели и результаты модального анализа изгибных мод первого и второго порядка представлены на рис. 9. Окончательное число элементов сетки было выбрано равным 66 040 по критерию независимости результатов от этого числа. Пластина прикреплена к круговой плите, которая представляет собой неподвижную опору. Первая мода всегда содержит в себе бóльшую часть энергии и деформируется в наибольшей степени среди всех мод, поэтому она и является основным объектом исследования. Конечно-элементный анализ показывает, что собственная частота первой моды равна 26.39 Гц и это типичная изгибная мода с максимальной деформацией на конце пластины.
2) Испытание обстукиванием
Испытание обстукиванием определяет собственную частоту тела и область частот, представляющую интерес в будущих исследованиях. Данные испытаний во временнóй области представлены на рис. 10. Общая продолжительность вибрационного сигнала была 192 с; простукивание совершалось непрерывным образом вручную. Быстрое преобразование Фурье проводится по линейному среднему 20 интервалов сигнала продолжительностью 9.6 с каждый. Частота первой изгибной моды, полученная быстрым преобразованием Фурье, оказалась равной 26.33 Гц.
Рис. 10.
Реакция на обстукивание во временной и частотной области и спектр гармонической реакции, полученный методом конечных элементов.
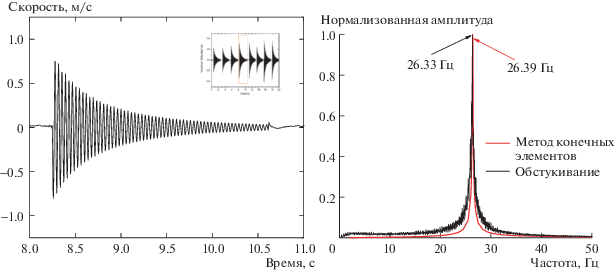
По результатам конечно-элементного анализа и обстукивания собственная частота первой моды составляет 26.39 и 26.33 Гц соответственно. Относительная ошибка равна 0.22%, что приемлемо для последующих испытаний и анализа. Результаты обстукивания также позволяют рассчитать величину механического демпфирования испытуемого тела и ввести полученные данные в метод конечных элементов. Нормализованный спектр гармонической реакции, полученный с использованием данных измерения модального демпфирования, также построен на рис. 10. По сравнению с результатами обстукивания, соответствующие ему амплитуды ниже в частотной области вдали от точки резонанса. Однако в основном формы спектра хорошо совпадают, так что метод конечных элементов в сочетании с поправкой на механическое демпфирование может обеспечить в дальнейшем анализе быстрое вычисление частотной реакции на механическое возбуждение.
3.2 . Вибрации, индуцированные следом
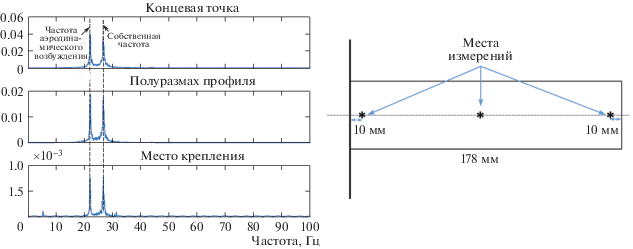
Эксперимент с вибрацией профиля демонстрирует непосредственную реакцию механической системы на аэродинамическое возбуждение при наличии демпфирования. Места измерений и результаты вибрационного теста при заданных условиях представлены на рис. 11.
В трех местах измерений получены сходные результаты с двумя главными пиками. Как показано выше, собственная частота первой моды равна 26.33 Гц. Один из пиков близок к собственной частоте, но не совпадает с ней. Частота другого пика равна примерно 20.6 Гц, что соответствует аэродинамическому возбуждению. При механической вынужденной реакции в измерениях обнаруживается лишь сама частота возбуждения и ее гармоники, а амплитуда вибраций на собственной частоте не достигает даже соответствующего порядка величины. При аэродинамическом возбуждении с частотой, меньшей собственной частоты, амплитуда возбуждения больше, чем амплитуда на собственной частоте, при измерениях в концевой точке и в середине размаха, но в месте крепления картина противоположная. Во всех трех местах измерений результаты по частоте получены с приемлемыми отклонениями (максимальное отклонение в 0.6% имеет место для собственной частоты). Поэтому в дальнейшем анализе используются результаты, полученные в середине размаха.
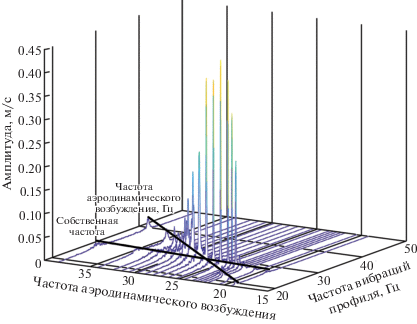
Результаты по вибрациям в середине размаха профиля представлены на рис. 12. Когда число Re мало, частота аэродинамического возбуждения значительно ниже собственной частоты профиля и в спектре имеются два пика. С увеличением Re частота аэродинамического возбуждения растет до 23.17 Гц, приближаясь к собственной частоте. Тогда два пика внезапно сливаются в один пик с существенно возросшей амплитудой. В этом случае вибрации профиля представляют собой устойчивый ограниченный колебательный цикл, амплитуда которого ни возрастает, ни убывает. Затем амплитуда начинает медленно убывать. Пока частота аэродинамического возбуждения остается ниже 30.60 Гц, сигнал вибрации является высокоамплитудным и содержит лишь один главный пик. Затем вновь появляются два пика.
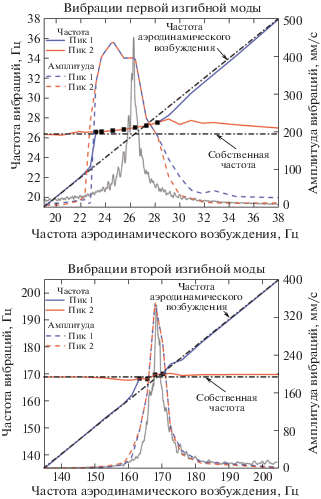
На рис. 13 представлены результаты по первой и второй изгибным модам, включая амплитуды и частоты двух основных пиков. Один из пиков (пик 1) отслеживает частоту аэродинамического возбуждения, а другой (пик 2) собственную частоту профиля. Синие и красные линии соответствуют пикам 1 и 2, сплошные линии представляют результаты по частоте, а штриховые по амплитуде. Горизонтальная штрихпунктирная линия показывает собственную частоту профиля, а наклонная штрихпунктирная линия – ожидаемую частоту аэродинамического возбуждения. Серая линия дает частоту реакции, представленную на рис. 10 с нормализованной амплитудой.
В первой изгибной моде максимальная амплитуда вибраций равна 439 мм/с. Область частот, где амплитуды выше, чем 20% от максимальной амплитуды, рассматривается как область высокоамплитудной реакции; здесь частота аэродинамического возбуждения меняется от 22.52 до 29.87 Гц. По сравнению со спектром реакции в первой моде, различие в диапазонах и рассогласование по амплитуде очевидны. Когда частота аэродинамического возбуждения меньше 22.52 Гц, амплитуда вынужденной реакции весьма мала в обоих пиках. В этой области, когда частота аэродинамического возбуждения возрастает от 22.80 Гц, амплитуда быстро растет до примерно 400 мм/с и остается на этом уровне, пока не будет достигнута точка резонанса. Затем амплитуда сравнительно медленно убывает, пока частота аэродинамического возбуждения не покидает этот диапазон частот. Следует заметить, что максимальная амплитуда вибраций имеет место не в точке резонанса. Внутри области высокоамплитудной реакции есть только один ясно выраженный доминирующий пик, частота которого медленно возрастает от 26.59 до 27.53 Гц. Это, по-видимому, область перехода от собственной частоты к частоте аэродинамической силы.
Широкая частотная область высокоамплитудной реакции представляет собой неожиданное явление при изучении вынужденных реакций. Это поведение определяется двумя важными факторами, во-первых, тем, что аэродинамическое возбуждение представляет собой узкополосный сигнал, и, во-вторых, тем, что это возбуждение взаимодействует с механическими вибрациями. Очевидное влияние этих факторов демонстрируют результаты термоанемометрических измерений, подтвержденных результатами измерения вибраций. Они показывают, что точка резонанса конструкции не является наиболее критической точкой при некоторых вынужденных реакциях на аэродинамическое возбуждение благодаря совместному эффекту аэроупругости, который может рассматриваться как явление захвата частот. Диапазон захвата составляет 87.8% ~ 116.3% от собственной частоты.
Однако поведение второй изгибной моды вибраций отлично. В точке резонанса второй моды амплитуда вибраций максимальна: 350 мм/с. 20% от максимальной амплитуды составляет 70 мм/с, а соответствующий диапазон частот простирается от 163.20 до 173.80 Гц или от 96.7% до 103.0% от собственной частоты. В частотном спектре реакции второй изгибной моды диапазоны частот и амплитуд хорошо согласованы. Столь широкая высокоамплитудная область, как для первой моды, не имеет места и явление захвата частоты, присущее первой моде, не реализуется.
Различное поведение вибраций в первой и второй модах определяется различиями в эффекте взаимодействия. Амплитуды скоростей в обеих модах находятся на близком уровне, но амплитуда смещений для первой моды значительно больше, чем для второй моды. Таким образом, вибрации первой моды сильнее воздействуют на поле течения, чем вибрации во второй моде. Амплитуда смещения при вибрациях и масштаб вихря являются главными параметрами, определяющими наличие феномена захвата частоты.
ЗАКЛЮЧЕНИЕ
Экспериментально и численно исследовано явление вынужденной реакции на аэродинамическое возбуждение. Исследование основано на независимом анализе характеристик этого возбуждения и свойств конструкции. Вихрь, сходящий с расположенного выше по течению цилиндра, порождает силу аэродинамического возбуждения, действующую на расположенный ниже по течению профиль. Пульсации в потоке измерялись термоанемометром, а результаты проверялись численным моделированием и модальным собственно ортогональным разложением.
Вибрации конструкции измерялись лазерным доплеровским виброметром. Они обнаруживают эффекты взаимодействия двух факторов. Аэродинамическое возбуждение ставит, таким образом, новые проблемы при исследовании вынужденных реакций. Основные отличия аэродинамических сил от механических перечислены ниже.
1. Аэродинамическое возбуждение сходящими вихрями имеет узкополосную частотную характеристику. Вибрации определяются не только центральной частотой возбуждения, но и целой полосой частот, ширина которой зависит от числа Рейнольдса.
2. Частота аэродинамического возбуждения определяется не только параметрами переднего цилиндра и скоростью потока, но и взаимодействием с вибрирующим телом, что приводит к сдвигу частоты в направлении собственной частоты тела.
Численное моделирование иллюстрирует структуры течения, а собственно ортогональное разложение демонстрирует виды аэродинамического возбуждения:
1. Частота поля течения определяется частотой схода вихрей с переднего цилиндра. Моды, соответствующие первой паре вихрей, охватывают 87.4% полной кинетической энергии поля течения.
2. Тело, расположенное ниже по течению, разрезает вихрь и создает гармонические колебания. Моды высшего порядка охватывают меньше кинетической энергии, чем первая пара мод, а первые 10 мод могут эффективно представить поле течения в целом.
Весьма интересны вибрации тела при аэродинамическом возбуждении. Основные особенности первой изгибной моды следующие:
1. Область высокоамплитудной реакции простирается от 22.52 до 29.87 Гц, то есть более чем на $ \pm $10% собственной частоты. Частота аэродинамического возбуждения захватывается собственной частотой тела, так что имеется лишь один доминирующий пик. Частота этого пика медленно растет от 26.59 до 27.53 Гц.
2. Максимальная амплитуда вибраций достигается не в точке резонанса. Когда частота аэродинамического возбуждения меньше собственной частоты, достигается максимальная амплитуда возбужденных вибраций тела.
В случае второй моды явление захвата частоты при вибрациях, присущее первой моде, не реализуется. В этом случае имеет место типичное резонансное поведение. Различное поведение в этих двух случаях может быть вызвано различными величинами смещения, соответствующими амплитуде вибраций, в зону схода вихрей, что приводит к различным уровням взаимодействия.
В будущем исследовании аэродинамическое возбуждение предполагается осуществить более управляемым образом, а объект испытаний будет более специфичен для индустрии авиационных двигателей.
Список литературы
Sever I.A. Experimental validation of turbomachinery blade vibration predictions // Appl. Biochemistry & Biotechnology. 2004. V. 161. P. 1–21.
Krausse T.S. Study of impulse forcing on a simply supported blade // AIAA J. 2005. V. 43.
Facchinetti M.L., de Langre E., Biolley F. Coupling of structure and wake oscillators in vortex-induced vibrations // J. Fluids Structures. 2004. V. 19. P. 123–140.
Spiker M.A. Development of an efficient design method for non-synchronous vibrations // Dissertations & Theses – Gradworks. 2008. P. 735–747.
Mikheev A.N., Mikheev N.I., Molochnikov V.M. Vortex formation behind a cylinder in a fluctuating flow // Fluid Dynamics. 2014. V. 49. P. 596–601.
Besem F.M., Kamrass J.D., Thomas J.P., Tang D., Kielb R.E. Vortex-induced vibration and frequency lock-in of an airfoil at high angles of attack // J. Fluids Eng. 2014. V07BT35A008.
Assi G.R.S. Wake-induced vibration of tandem and staggered cylinders with two degrees of freedom // J. Fluids Structures. 2014. V. 50. P. 340–357.
Chaplin J.R., Batten W.M.J. Simultaneous wake- and vortex-induced vibrations of a cylinder with two degrees of freedom in each direction // J. Offshore Mechanics & Arctic Engineering. 2014. V. 136. P. 031101.
Zhang W., Li X., Ye Z., Jiang Y. Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers // J. Fluid Mech. 2015. V. 783. P. 72–102.
Li C., Dong H., Liu G. Effects of a dynamic trailing-edge flap on the aerodynamic performance and flow structures in hovering flight // J. Fluids Structures. 2015. V. 58. P. 49–65.
Liu H., Wang Y., Wei J., Qu Z. The importance of controlling the upstream body wake in tandem cylinders system for noise reduction //J. Aerospace Engineering. 2018. V. 232. P. 517.
Fey U., König M., Eckelmann H. A new Strouhal–Reynolds-number relationship for the circular cylinder in the range 47 < Re < 2 × 105 // Phys. Fluids. 1998. V. 10. P. 1547–1549.
Zhu Y., Ouyang H., Du Z. Prediction of flowfield and acoustic signature of a split-type air conditioner // Intern. J. Ventilation. 2009. V. 8. P. 45–56.
Mayorca M.A., Vogt D.M., Andersson C., Mårtensson H., Fransson T. Uncertainty of forced response numerical predictions of an industrial blisk: Comparison with experiments // Proc. ASME. Structures and Dynamics. Parts 1 and 2. 2012. V. 7. P. 1537–1548.
Huang R., Li H., Hu H., Zhao Y. Open/closed-loop aeroservoelastic predictions via nonlinear, reduced-order aerodynamic models // AIAA J. 2015. V. 53. P. 1812–1824.
Kou J., Zhang W. Layered reduced-order models for nonlinear aerodynamics and aeroelasticity // J. Fluids Structures. 2017. V. 68. P. 174–193.
Chen J. 2D numerical simulation and wake analysis on flow around circular cylinder // Computer Aided Engineering. 2013.
Lumley J. The structure of inhomogeneous turbulence / Yaglom A.M., Tatarski V.I. (eds.). Atmospheric turbulence and wave propagation (Nauka, Moscow, 1967), P. 166.
Taira K., Brunton S.L., Dawson S.T.M., Rowley C.W., Colonius T., McKeon B.J., Schmidt O.T., Gordeyev S., Theofilis V., Ukeiley L.S. Modal analysis of fluid fFlows: An overview // AIAA J. 2017. V. 55. P. 4013–4041.
Sirovich L. Turbulence and the dynamics of coherent structures. I – Coherent structures. II – Symmetries and transformations. III – Dynamics and scaling // Quarterly Appl. Math. 1987. V. 45. P. 561–571.
Noack B.R., Afanasiev K., Morzynski M., Tadmor G., Thiele F. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake // J. Fluid Mech. 2003. V. 497. P. 335–363.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа