Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 82-94

Моделирование движения смеси твердых частиц и жидкости в пористых средах с учетом внутренней суффозии

А. А. Папин^a, *, А. Н. Сибин^a, **

^a Алтайский государственный университет, Факультет математики и информационных технологий
Барнаул, Россия

^* E-mail: papin@math.asu.ru
^** E-mail: sibin_anton@mail.ru

Поступила в редакцию 27.04.2018
После доработки 15.10.2018
Принята к публикации 19.10.2018

DOI: 10.1134/S0568528119030101

Аннотация

Рассматривается математическая модель изотермической внутренней эрозии грунта без учета деформации пористой среды. При достижении определенной величины скорости фильтрации происходит вынос частиц грунта из области течения. В качестве математической модели используются уравнения сохранения массы для воды, подвижных твердых частиц и неподвижного пористого скелета, а также аналог закона Дарси для воды и подвижных твердых частиц и соотношение для интенсивности суффозионного потока. Подвижные частицы грунта рассматривались как отдельная фаза, имеющая свою скорость фильтрации, которая определяется в ходе решения задачи. Данное предположение позволило построить замкнутую модель. Предложен алгоритм численного решения начально-краевой задачи фильтрации грунтовых вод с учетом внутренней эрозии грунта и проведены тестовые численные расчеты. Результаты расчетов хорошо коррелируют с экспериментальными данными.

Ключевые слова: многофазная фильтрация, пористая среда, суффозия, фазовый переход, насыщенность, численное решение

Проблемы, связанные с эрозией почвогрунтов, широко исследуются на протяжении последнего столетия. Данный процесс имеет большое значение при решении прикладных задач в сельском хозяйстве: ирригация и дренаж сельскохозяйственных полей [1] и процесс внутренней эрозии, сопутствующий канальному орошению почвогрунтов [2, 3]. Процесс эрозии необходимо учитывать в исследованиях, связанных с прогнозом распространения загрязнений, фильтрацией вблизи водохранилищ и других гидротехнических сооружений [4, 5]. Более того, аналогичные проблемы, связанные с процессом эрозии грунта, возникают и в других областях, включая добычу нефти и газа [6].

Существуют различные подходы при моделировании процесса внутренней эрозии. В работах В.Н. Николаевского процесс эрозии моделируется на основе моделей однофазной фильтрации и упругопластических критериев разрушения [7]. Для насыщенных водой почвогрунтов при рассмотрении процесса эрозии может быть использована модель Био [8].

Принципиально иные подходы к моделированию эрозии используются в работах Бонелли [9, 10]. В этих работах вводится неизвестная граница раздела между твердым скелетом и водой с подвижными твердыми частицами со стандартной реологией. Для определения неизвестной границы используются аналоги кинематического и динамических условий в задачах со свободными границами.

Наиболее полные модели теории движения воды и подвижных твердых частиц в пористой среде предложены в работах I. Vardoulakis и его последователей (см., например, [11–14]). Почвогрунты в данных работах, с одной стороны, рассматривались как многофазные среды, но в то же время предполагалась пропорциональность скоростей воды и подвижных частиц грунта. Это являлось следствием предположения о равенстве давлений подвижных фаз. Несовпадение давлений в фазах может иметь место, в частности, из-за капиллярных эффектов [15]. Основной проблемой при таком подходе является описание силового взаимодействия и совместного деформирования фаз. Подробно описание силового взаимодействия жидкости (газа) и твердых частиц, движущихся в потоке, изложено в работах [16–18]. Но в них процесс суффозии не описывался.

Цель данной работы – восполнить пробел в описании процесса взаимопроникающего движения двух сред (вода, твердые подвижные частицы) в пористой среде с учетом суффозионных процессов.

В серии работ (см., например, [19, 20]) для моделирования движения смеси воды и подвижных твердых частиц в пористой среде используется следующий подход: рассматривается движение подвижных твердых частиц в потоке жидкости и два “вида” неподвижных твердых частиц, для нахождения концентраций которых используются уравнения кинетики. В этом подходе истинная скорость подвижных твердых частиц не определяется, скорость жидкости находится из закона Дарси. Отрыв частиц от матрицы породы описывается на основе уравнения кинетики.

В работе [20], как и в работах I. Vardoulakis [12, 13] предполагается, что скорость подвижных твердых частиц меньше скорости фильтрующейся жидкости и является заданным параметром, определяемым экспериментально [20]. Кроме того, скорость воды считается заданной функцией времени [20], изменяющаяся при отрыве частиц пористость не определяется в ходе решения задачи. Возникает ряд других параметров, связанных с уравнением кинетики и определяющихся экспериментально.

Следует также отметить, что не существует единого подхода к описанию процесса обмена массой между пористым скелетом и твердыми подвижными частицами грунта. На наш взгляд, корректное описание фазового перехода должно гарантировать выполнение физических принципов максимума для пористости и концентрации фаз. В настоящей работе предложена математическая модель фильтрации жидкости в пористой среде, подверженной внутренней эрозии с учетом капиллярных сил. Рассматриваемый подход позволяет определять скорости воды и псевдоожиженных частиц грунта в ходе решения начально-краевой задачи.

Следуя общепринятым положениям, грунт можно характеризовать двумя параметрами [21]: средним диаметром частиц $d$ и степенью неоднородности $\eta $. Вынос мелкой фракции зависит от диаметра минимальных поровых каналов ${{d}_{{п о р }}}$ между крупными зернами, который определяется экспериментально (см., например, [21]). Приведенные в монографии [22] данные измерений устойчивости разнородных грунтов показывают, что при $\eta < 10$ суффозия практически отсутствует и слой в своей массе переходит в псевдоожиженное состояние без выделения мелких частиц. При $\eta > 20$, напротив, происходит интенсивная суффозия мелкозернистого “наполнителя” задолго до того, как основной “скелет” из крупнозернистых частиц потеряет устойчивость. В настоящей работе рассматриваются процессы фильтрации подземных вод и внутренней механической суффозии в грунтах со степенью неоднородности $\eta > 20$.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматриваются процессы фильтрации подземных вод и внутренней суффозии. Грунт моделируется как трехфазная сплошная пористая среда. Поры полностью заполнены смесью воды (i = 1) и подвижных частиц грунта (псевдоожиженный слой i = 2). Доля пор в грунте (i = 3) определяется пористостью $\phi = ({{V}_{1}} + {{V}_{2}}){\text{/}}V$, где $V = {{V}_{1}} + {{V}_{2}} + {{V}_{3}}$ – общий объем грунта, ${{V}_{1}},\;{{V}_{2}},\;{{V}_{3}}$ – соответственно объемы воды, подвижных твердых частиц и скелета грунта. Уравнения сохранения массы и импульса для каждой из фаз имеют вид [15]

(1.1)

$\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + \nabla \cdot ({{\rho }_{i}}{{{\mathbf{u}}}_{i}}) = \sum\limits_{j = 1}^3 {{I}_{{ji}}},\quad (i = 1,\;...,\;3)$

(1.2)

$\frac{{\partial {{\rho }_{i}}{{{\mathbf{u}}}_{i}}}}{{\partial t}} + {{\nabla }^{k}}({{\rho }_{i}}{{{\mathbf{u}}}_{i}}{\text{u}}_{i}^{k}) = {{\nabla }^{k}}\sigma _{i}^{k} + {{\rho }_{i}}{{{\mathbf{g}}}_{i}} + \sum\limits_{j = 1}^3 {{{\mathbf{P}}}_{{ji}}}$

Здесь ${{\nabla }^{k}} \equiv \partial {\text{/}}\partial {{x}_{k}}$, $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$ – декартова система координат в ${{R}^{3}}$, $\nabla = (\partial {\text{/}}\partial {{x}_{1}},\partial {\text{/}}\partial {{x}_{2}},\partial {\text{/}}\partial {{x}_{3}})$ – оператор градиента; ${{{\mathbf{u}}}_{i}} \cdot \nabla = u_{i}^{k}{{\nabla }^{k}}$ = $\sum\nolimits_{k = 1}^3 {u_{i}^{k}\partial {\text{/}}\partial {{x}_{k}}} $, $\nabla \cdot {{{\mathbf{u}}}_{i}}$ = $\sum\nolimits_{k = 1}^3 {\partial u_{i}^{k}{\text{/}}\partial {{x}_{k}}} $ и по повторяющемуся индексу используется “немое” суммирование; ${{{\mathbf{u}}}_{1}},{{{\mathbf{u}}}_{2}},{{{\mathbf{u}}}_{3}}$ – соответственно истинные скорости воды, подвижных твердых частиц грунта и скелета грунта; ${{\rho }_{1}} = \phi {{s}_{1}}\rho _{1}^{0}$, ${{\rho }_{2}} = \phi {{s}_{2}}\rho _{2}^{0}$, ${{\rho }_{3}} = (1 - \phi )\rho _{3}^{0}$ – приведенные плотности воды, подвижных твердых частиц грунта и скелета; ${{s}_{1}} = {{V}_{1}}{\text{/}}({{V}_{1}} + {{V}_{2}})$, ${{s}_{2}} = {{V}_{2}}{\text{/}}({{V}_{1}} + {{V}_{2}})$ – концентрации воды (насыщенность) и подвижных твердых частиц в порах; $\rho _{1}^{0},\rho _{2}^{0},\rho _{3}^{0}$ – истинные плотности воды, подвижных твердых частиц грунта и скелета грунта. В рассматриваемом случае $\rho _{3}^{0} = \rho _{2}^{0}$, так как подвижные частицы захватываются суффозионным потоком из грунта; ${{I}_{{ji}}}$ – интенсивность перехода массы из j-й в i-ю составляющую (или наоборот, из i-й в j-ю, тогда ${{I}_{{ji}}} < 0$) в единице объема смеси и в единицу времени. Из закона сохранения массы при различных физико-химических превращениях (формально полагая ${{I}_{{ii}}} = 0$) имеем ${{I}_{{ji}}} = - {{I}_{{ij}}}$. Аналогично ${{{\mathbf{P}}}_{{ji}}}$ – интенсивность обмена импульсом между i-й и j-й составляющими. Из закона сохранения импульса следует ${{{\mathbf{P}}}_{{ji}}} = - {{{\mathbf{P}}}_{{ij}}}$ (${{{\mathbf{P}}}_{{ii}}} = 0$). В уравнениях сохранения импульса ${{\sigma }_{i}}$ – тензор напряжений i-й фазы, ${{{\mathbf{g}}}_{i}}$ – вектор ускорения (обусловленный внешними силами).

Используя уравнения неразрывности (1.1) и обозначение ${{d}_{i}}{\text{/}}dt \equiv \partial {\text{/}}\partial t + {{{\mathbf{u}}}_{i}}\nabla $, уравнения (1.2) можно представить в виде [15]

(1.3)

${{\rho }_{i}}\frac{{{{d}_{i}}{{{\mathbf{u}}}_{i}}}}{{dt}} = {{\nabla }^{k}}\sigma _{i}^{k} + {{\rho }_{i}}{{{\mathbf{g}}}_{i}} + \sum\limits_{j = 1}^N ({{{\mathbf{P}}}_{{ji}}} - {{I}_{{ji}}}{{{\mathbf{u}}}_{i}})$

Система уравнений (1.1), (1.3) является недоопределенной. Для ее замыкания необходимо конкретизировать величины, описывающие внутрифазные (силовое ${{\sigma }_{i}}$) и межфазные (массовое ${{I}_{{ji}}}$, силовое ${{{\mathbf{P}}}_{{ji}}}$) взаимодействия.

Следуя [15, с. 28], положим

${{{\mathbf{P}}}_{{ji}}} = - {{{\mathbf{P}}}_{{ij}}} = {{{\mathbf{R}}}_{{ji}}} + {{I}_{{ji}}}{{{\mathbf{u}}}_{{ji}}}$

где ${{{\mathbf{R}}}_{{ji}}}$ – межфазная сила, ${{I}_{{ji}}}{{{\mathbf{u}}}_{{ji}}}$ – обмен импульсом из-за фазовых превращений, ${{{\mathbf{u}}}_{{ji}}}$ – скорость вещества i-й фазы на границе с j-й (для гетерогенных смесей вязкиx жидкостей ${{{\mathbf{u}}}_{{ji}}} = {{{\mathbf{u}}}_{{ij}}}$ [15] и, следовательно, ${{{\mathbf{R}}}_{{ji}}} = - {{{\mathbf{R}}}_{{ij}}}$).

Для тензора напряжений σ_i и вектора ${{{\mathbf{R}}}_{{ji}}}$ используется схема Х.А. Рахматулина силового взаимодействия и совместного деформирования фаз [23, 24]. В этой схеме тензор σ_i представляется в симметричном виде [7, c. 313; 15, c. 31]

(1.4)

$\sigma _{i}^{{kl}} = - \phi {{s}_{i}}{{p}_{i}}{{\delta }^{{kl}}} + \tau _{i}^{{kl}},\quad \phi {{s}_{i}}{{p}_{i}} \equiv - \frac{1}{3}\sigma _{i}^{{kk}},\quad \tau _{i}^{{kl}} = \tau _{i}^{{lk}},\quad \tau _{i}^{{kk}} = 0$

Для вязких компонент $\tau _{i}^{{kl}}$ тензора напряжений и суммарной силы межфазного взаимодействия принимаются зависимости [15, c. 31]

(1.5)

$\tau _{i}^{{kl}} = \phi {{s}_{i}}\left( { - \frac{2}{3}{{\mu }_{i}}e_{i}^{{mm}}{{\delta }^{{kl}}} + 2{{\mu }_{i}}e_{i}^{{kl}}} \right),\quad e_{i}^{{kl}} \equiv \frac{1}{2}\left( {\frac{{\partial v_{i}^{k}}}{{\partial {{x}_{l}}}} + \frac{{\partial v_{i}^{l}}}{{\partial {{x}_{k}}}}} \right)$

$\sum\limits_{j = 1}^3 {{{\mathbf{R}}}_{{ji}}} = {{p}_{i}}\nabla (\phi {{s}_{i}}) + \sum\limits_{j = 1}^3 {{{\mathbf{F}}}_{{ji}}},\quad {{{\mathbf{F}}}_{{ji}}} = - {{{\mathbf{F}}}_{{ij}}}$

где ${{\delta }^{{kl}}}$ – символ Кронекера, ${{p}_{i}}\nabla ({{s}_{i}})$ – сила, возникающая из-за “расширения трубки тока фазы” [15, c. 57], ${{{\mathbf{F}}}_{{ji}}}$ – сила сопротивления. Для ${{{\mathbf{F}}}_{{ji}}}$ обычно используется соотношение ${{{\mathbf{F}}}_{{ji}}} = {{K}_{{ji}}}({{{\mathbf{u}}}_{j}} - {{{\mathbf{u}}}_{i}})$ [15, 25, 26].

При обтекании однородным потоком частицы без учета силы тяжести выделяют три основных силы: сила сопротивления Стокса, сила присоединенных масс и сила Бассе [16–18]. В случае обтекания частицы неоднородным потоком, строго говоря, необходимо было бы учесть также силу, вызванную неравномерностью распределения давления. Нужно отметить, что, помимо рассмотренных выше сил, на твердую частицу могут действовать силы, обусловленные вращением твердой частицы (сила Магнуса), наличием градиента скорости потока (сила Сэфмана) и выталкивающая сила Архимеда.

Из всех перечисленных сил основное внимание в настоящей работе уделяется силе Стокса (следуя выводу уравнений движения псевдоожиженного слоя [17]), т.е. сила межфазного взаимодействия пропорциональна разности скоростей фаз. Поскольку ускорения малы, то силой Бассе и силой присоединенных масс можно пренебречь.

Если учитывать вращение частицы, т.е. угловую скорость и размеры частицы, то модель существенно усложняется. С другой стороны, вектор угловой скорости твердых частиц может быть ориентирован случайным образом и вкладом силы Магнуса можно пренебречь. Силой Архимеда также пренебрегаем, поскольку объемы частиц малы. Силой Сэфмана пренебрегаем, так как градиент скорости потока мал.

Согласно работам [16, 17] совместное взаимопроникающее движение жидкости и твердых частиц рассматривается в рамках континуальной модели механики многофазных сплошных сред и, в частности, жидкость и подвижные твердые частицы рассматриваются как вязкие среды со своими характеристиками. Основной проблемой при таком подходе является описание силового взаимодействия и совместного деформирования фаз. Подробно описание силового взаимодействия жидкости (газа) и твердых частиц движущихся в потоке изложено в работах [16–18]. В работе [16] вводится понятие эффективного давления жидкости p^e и эффективного давления псевдоожиженной фазы ${{p}^{{se}}}$, так что давление жидкости есть ${{p}_{1}} = {{s}_{1}}{{p}^{e}}$, а давление твердых подвижных частиц ${{p}_{2}} = {{s}_{2}}{{p}^{{se}}}$, причем ${{p}^{e}} = {{p}^{{se}}} + {{p}_{c}}({{s}_{1}})$ и функция ${{p}_{c}}({{s}_{1}})$ обладает свойствами ${{p}_{c}}({{s}_{1}}) \to \infty $ при ${{s}_{1}} \to 0$, ${{p}_{c}}(1) = 0$. Следуя изложенному выше подходу, положим

(1.6)

${{p}_{2}} - {{p}_{1}} = {{p}_{c}}(s)$

Здесь ${{p}_{c}}$ – заданная функция, обладающая свойствами

${{p}_{c}}(s) > 0,\quad {{p}_{c}}(1) = 0,\quad \frac{{\partial {{p}_{c}}}}{{\partial s}} < 0,\quad {{p}_{c}}(s) \to \infty ,\quad (s \to 0)$

где $s = {{s}_{1}}$ – концентрация жидкости (насыщенность) ($1 - s = {{s}_{2}}$). Такой же подход принят в работах [16, 27].

Следует отметить, что несовпадение давлений в фазах может иметь место, в частности, из-за капиллярных эффектов. Так, в классических моделях двухфазной фильтрации предполагается, что давления в фазах отличаются на величину капиллярного скачка [28–33].

Используя сделанные предположения (1.4) и (1.5), считая малыми вязкие компоненты тензора напряжений ($\tau _{i}^{{kl}} = 0$) и силы взаимодействия воды и псевдоожиженных частиц грунта (${{K}_{{12}}} = {{K}_{{21}}} = 0$), запишем уравнения (1.4) в виде [34]:

(1.7)

$\rho _{1}^{0}s\phi \frac{{{{d}_{1}}{{{\mathbf{u}}}_{1}}}}{{dt}} = - s\phi \nabla {{p}_{1}} + {{K}_{{31}}}({{{\mathbf{u}}}_{3}} - {{{\mathbf{u}}}_{1}}) + \rho _{1}^{0}s\phi {\mathbf{g}}$

(1.8)

$\rho _{2}^{0}(1 - s)\phi \frac{{{{d}_{2}}{{{\mathbf{u}}}_{2}}}}{{dt}} = - (1 - s)\phi \nabla {{p}_{2}} + {{K}_{{32}}}({{{\mathbf{u}}}_{3}} - {{{\mathbf{u}}}_{2}}) + \rho _{2}^{0}(1 - s)\phi {\mathbf{g}}$

При моделировании фильтрационных течений можно пренебречь инерциальными силами [34]. Отбрасывая левые части уравнений (1.7), (1.8), получим обобщенный закон Дарси

(1.9)

$\phi s({{{\mathbf{u}}}_{1}} - {{{\mathbf{u}}}_{3}}) = - K_{{_{{31}}}}^{{ - 1}}{{\phi }^{2}}{{s}^{2}}(\nabla {{p}_{1}} - \rho _{1}^{0}{\mathbf{g}})$

(1.10)

$\phi (1 - s)({{{\mathbf{u}}}_{2}} - {{{\mathbf{u}}}_{3}}) = - K_{{_{{32}}}}^{{ - 1}}{{\phi }^{2}}{{(1 - s)}^{2}}(\nabla {{p}_{2}} - \rho _{2}^{0}{\mathbf{g}})$

Удобно использовать следующие обозначения (по аналогии с обобщенным законом Дарси для двухфазной фильтрации) $K_{{3i}}^{{ - 1}}{{\phi }^{2}}{{s}^{2}} = {{K}_{0}}{{\bar {k}}_{{0i}}}{\text{/}}{{\mu }_{i}},$ где ${{K}_{0}}(\phi )$ – симметрический тензор проницаемости пористой среды; ${{\overline k }_{{0i}}}$ – коэффициенты, обладающие свойствами ${{\bar {k}}_{{0i}}} = {{\bar {k}}_{{0i}}}({{s}_{i}}) \geqslant 0,{{\bar {k}}_{{0i}}}{{{\text{|}}}_{{_{{{{s}_{i}} = 0}}}}} = 0,$ $0 \leqslant {{s}_{i}} \leqslant 1$; ${{\mu }_{i}}$ – коэффициенты динамической вязкости; g – ускорение силы тяжести. Эффективная динамическая вязкость псевдоожиженного слоя и коэффициенты ${{\bar {k}}_{{0i}}}$, ${{K}_{0}}$ могут быть измерены экспериментально [16, 17, 32].

В дальнейшем рассматривается изотермический суффозионный процесс в недеформируемой пористой среде (скорость скелета грунта ${{{\mathbf{u}}}_{3}} = 0$). Положим ${{I}_{{32}}} = I$ и будем считать истинные плотности $\rho _{i}^{0}$ постоянными. В этом случае система приводится к эллиптико-параболической системе [33] и уравнению кинетики. Действительно, используя сделанные предположения вместо (1.1), (1.9), (1.10) получим

(1.11)

$\frac{{\partial (s\phi )}}{{\partial t}} + \nabla \cdot (s\phi {{{\mathbf{u}}}_{1}}) = 0$

(1.12)

$\frac{{\partial (1 - s)\phi }}{{\partial t}} + \nabla \cdot ((1 - s)\phi {{{\mathbf{u}}}_{2}}) = \frac{I}{{\rho _{2}^{0}}}$

(1.13)

$\frac{{\partial (1 - \phi )}}{{\partial t}} = - \frac{I}{{\rho _{3}^{0}}}$

(1.14)

${{s}_{i}}\phi {{{\mathbf{u}}}_{i}} = - {{K}_{0}}(\phi ){{k}_{{0i}}}(\nabla {{p}_{i}} - \rho _{i}^{0}{\mathbf{g}}),\quad {{k}_{{0i}}} = \frac{{{{{\bar {k}}}_{{0i}}}}}{{{{\mu }_{i}}}}$

Сложив уравнения (1.11), (1.12) и (1.13), получим

(1.15)

$\nabla \cdot (s\phi {{{\mathbf{u}}}_{1}} + (1 - s)\phi {{{\mathbf{u}}}_{2}}) = 0$

Положим

${\mathbf{v}} = s\phi {{{\mathbf{u}}}_{1}} + (1 - s)\phi {{{\mathbf{u}}}_{2}}$

Используя (1.14) и (1.6) для ${\mathbf{v}}$ получим следующее представление:

(1.16)

$\begin{gathered} - {\mathbf{v}} = {{K}_{0}}(\phi )({{k}_{{01}}}(\nabla ({{p}_{2}} - {{p}_{c}}) - \rho _{1}^{0}{\mathbf{g}}) + {{k}_{{02}}}(\nabla {{p}_{2}} - \rho _{2}^{0}{\mathbf{g}})) = \\ = {{K}_{0}}\left( {k\left( {\nabla {{p}_{2}} - \frac{{{{k}_{{01}}}}}{k}\frac{{\partial {{p}_{c}}}}{{\partial s}}\nabla s} \right) - {\mathbf{g}}(\rho _{2}^{0}{{k}_{{02}}} + \rho _{1}^{0}{{k}_{{01}}})} \right) = \\ = {{K}_{0}}\left( {k\nabla \left( {{{p}_{2}} + \int\limits_s^1 \frac{{{{k}_{{01}}}(\xi )}}{{k(\xi )}}\frac{{\partial {{p}_{c}}}}{{\partial \xi }}d\xi } \right) - {\mathbf{g}}(\rho _{2}^{0}{{k}_{{02}}} + \rho _{1}^{0}{{k}_{{01}}})} \right) = K\nabla p + {\mathbf{f}} \\ \end{gathered} $

где p – так называемое “приведенное” давление [33]

(1.17)

$p = {{p}_{2}} + \int\limits_s^1 \frac{{{{k}_{{01}}}(\xi )}}{{k(\xi )}}\frac{{\partial {{p}_{c}}}}{{\partial \xi }}d\xi $

Здесь введены обозначения:

$k(s) = {{k}_{{01}}} + {{k}_{{02}}}$

$K(s,\phi ) = {{K}_{0}}(\phi )k(s)$

${\mathbf{f}}(s,\phi ) = - {{K}_{0}}{\mathbf{g}}({{k}_{{01}}}\rho _{1}^{0} + {{k}_{{02}}}\rho _{2}^{0})$

С учетом (1.17) для ${{{\mathbf{v}}}_{2}} = (1 - s)\phi {{{\mathbf{u}}}_{2}}$ имеем

(1.18)

$ - {{{\mathbf{v}}}_{2}} = - a\nabla s + {{K}_{0}}{{k}_{{02}}}\nabla p + {{{\mathbf{f}}}_{0}}$

$a(s,\phi ) = - {{K}_{0}}\frac{{{{k}_{{01}}}{{k}_{{02}}}}}{k}\frac{{\partial {{p}_{c}}}}{{\partial s}}$

${{{\mathbf{f}}}_{0}}(s,\phi ) = - {{K}_{0}}{{k}_{{02}}}\rho _{2}^{0}{\mathbf{g}}$

Используя (1.16), находим

${{K}_{0}}{{k}_{{02}}}\nabla p = - \frac{{{{k}_{{02}}}({\mathbf{v}} + {\mathbf{f}})}}{k}$

Тогда вместо (1.18) получим

(1.19)

$ - {{{\mathbf{v}}}_{2}} = - a\nabla s - b{\mathbf{v}} - {\mathbf{F}}$

${\mathbf{F}}(s,\phi ) = b{\mathbf{f}} - {{{\mathbf{f}}}_{0}} = \frac{{{{k}_{{01}}}{{k}_{{02}}}{{K}_{0}}{\mathbf{g}}}}{k}(\rho _{2}^{0} - \rho _{1}^{0}),\quad b(s) = \frac{{{{k}_{{02}}}}}{k}$

Складывая уравнения (1.12), (1.13) и привлекая соотношение (1.18), приходим к уравнению

(1.20)

$\frac{{\partial (s\phi )}}{{\partial t}} = \nabla \cdot (a\nabla s - {{K}_{0}}{{k}_{{02}}}\nabla p - {{{\mathbf{f}}}_{0}})$

Уравнения (1.13) и (1.15) можно переписать в виде

(1.21)

$\nabla \cdot (K\nabla p + {\mathbf{f}}) = 0$

(1.22)

$\rho _{3}^{0}\frac{{\partial (1 - \phi )}}{{\partial t}} = - I$

Система уравнений (1.20), (1.21) и (1.22) рассматривается относительно $s$, $p$ и $\phi $. Последнюю систему с учетом (1.19) можно привести к следующей эквивалентной форме

(1.23)

$\frac{{\partial s\phi }}{{\partial t}} = \nabla \cdot (a\nabla s + b{\mathbf{v}} + {\mathbf{F}})$

(1.24)

$\nabla \cdot {\mathbf{v}} = 0$

(1.25)

$\rho _{3}^{0}\frac{{\partial (1 - \phi )}}{{\partial t}} = - I$

(1.26)

$ - {\mathbf{v}} = K\nabla p + {\mathbf{f}}$

Особенностью рассматриваемой задачи является возможное вырождение на решение уравнения (1.20), поскольку $a(0,\varphi ) = a(1,\varphi ) = 0$, а коэффициент фильтрации, как правило, задается следующим образом ${{K}_{0}} = B{{\phi }^{3}}{\text{/}}{{(1 - \phi )}^{2}}$ или ${{K}_{0}} = B{{\varphi }^{\alpha }},3 \leqslant \alpha \leqslant 5$ [31]. Кроме того, пористость и насыщенность должны удовлетворять условиям $0 \leqslant s \leqslant 1$, $0 \leqslant \phi < 1$.

2. СУФФОЗИОННЫЙ ПОТОК

Главной причиной фильтрационных деформаций и фильтрационных разрушений грунтов является вынос частиц грунта из области фильтрации. К. Терцаги [35] получил условие равновесия грунта

(2.1)

${{I}_{*}} = (\gamma - 1)(1 - \phi )$

Здесь ${{I}_{*}}$ – критический градиент напора, при котором грунт находится во взвешенном состоянии; $\gamma $ – удельный вес грунта.

В книге [35, с. 316] на основе экспериментальных данных сделан вывод, что формула (2.1) дает заниженные результаты, так как не учитывает вес воды в порах грунта, и вместо (2.1) предложена зависимость

${{I}_{*}} = (\gamma - 1)(1 - \phi ) + 0.5\phi $

Эта формула подтверждалась лабораторными опытами. Однако в данных опытах не было учтено влияние стенок прибора, что привело к завышению критических градиентов напора.

В работе [35, с. 319] критическую скорость суффозии ${{\text{v}}_{k}}$ рекомендуется находить по формуле, полученной на основе достаточно обширных натурных данных

${{v}_{k}} = 60\sqrt[3]{{{{K}_{0}}}}$

где ${{K}_{0}}$ – коэффициент фильтрации грунта. В [35] показано, что все несвязанные грунты, механические составы которых выражаются в полулогарифмических координатах прямой линией или кривой, близкой к ней, практически могут оцениваться как несуффозионные.

На основе обработки экспериментальных данных были предложены различные формулы для интенсивности фазового перехода. В работе [36] суффозионный поток определяется следующим образом

(2.2)

${{I}_{{er}}} = \rho _{2}^{0}\lambda (1 - \phi ){{s}_{2}}\left\| {\mathbf{v}} \right\|$

где $\lambda $ – определяемая экспериментально функция (отвечает за устойчивость грунта суффозионному воздействию), ${\mathbf{v}}$ – скорость смеси воды и подвижных частиц грунта.

В работе [36] интенсивность суффозионного процесса предложено определять как разность

(2.3)

$I = {{I}_{{er}}} - {{I}_{{dep}}}$

где ${{I}_{{er}}}$ – поток твердых частиц (процесс суффозии), ${{I}_{{dep}}}$ – поток осевших твердых частиц (процесс кольматации).

Для определения ${{I}_{{dep}}}$ в работе [36] предлагается использовать соотношение

(2.4)

${{I}_{{dep}}} = \rho _{2}^{0}\lambda (1 - \phi )\frac{{s_{2}^{2}}}{{{{s}_{{cr}}}}}\left\| {\mathbf{v}} \right\|$

Здесь ${{s}_{{cr}}}$ – критическое значение концентрации подвижных твердых частиц грунта при достижении которой (${{s}_{2}} = {{s}_{{cr}}}$) процессы суффозии и кольматации уравновешивают друг друга. Подставив (2.2) и (2.4) в (2.3), получим соотношение [36]

$I = \rho _{2}^{0}\lambda (1 - \phi )\left( {{{s}_{2}} - \frac{{s_{2}^{2}}}{{{{s}_{{cr}}}}}} \right)\left\| {\mathbf{v}} \right\|$

В работе [13] скорость подвижных частиц грунта определялась из гипотезы ${{\text{v}}_{2}} = \chi {{\text{v}}_{1}}$ ($0 < \chi < 1$), а поток твердых частиц определялся следующим образом:

${{I}_{{er}}} = \rho _{2}^{0}\lambda (1 - \phi ){{s}_{2}}{\text{||}}{{v}_{2}}{\text{||}}\rho $

В работе [37] проведен анализ экспериментальных данных, из которого следует, что суффозионный процесс начинается после достижения скоростью фильтрации критического значения ${{v}_{k}}$. Так же из обработки результатов экспериментов получено соотношение для определения критической скорости фильтрации воды

${{v}_{k}} = 4.2\phi \sqrt[9]{{g{{\nu }^{7}}}}{{\left[ {37.21\frac{{\nu {{K}_{0}}}}{{\phi g}}} \right]}^{{ - 1/3}}}$

где $\nu $ – кинематический коэффициент вязкости воды, $g$ – модуль ускорения силы тяжести.

В работе [6] для $I$ используется зависимость

$I = \left\{ \begin{gathered} \lambda \rho _{3}^{0}(1 - \phi )(1 - s)\left( {1 - \frac{{1 - s}}{{1 - {{s}_{{cr}}}}}} \right){\text{|}}{\mathbf{v}}{\text{|}},\quad ({\text{|}}{\mathbf{v}}{\text{|}} \geqslant {\text{|}}{{{\mathbf{v}}}_{k}}{\text{|}}) \hfill \\ 0,\,\,\,\,\,\rho \left( {{\text{|}}v{\text{|}} < {\text{|}}{{v}_{k}}{\text{|}}} \right)\rho \hfill \\ \end{gathered} \right.$

В работах S. Bonelli (см., например, [38, с. 187]) движение воды, подвижных частиц и отрыв частиц от скелета моделируется на основе подходов, развитых в задачах с неизвестной границей. Вода и подвижные частицы грунта рассматриваются как однородная смесь (несжимаемая вязкая жидкость со стандартной реологией), которая движется со скоростью ${\mathbf{u}}$ и имеет плотность $\rho = \phi \rho _{1}^{0} + (1 - \phi )\rho _{3}^{0}$. Неизвестная граница $\Gamma $ между областями, занятыми смесью и твердым скелетом, определяется из уравнения переноса вида

$\frac{{\partial \psi }}{{\partial t}} + {\mathbf{c}} \cdot \nabla \psi = 0$

где функция $\psi $ имеет следующие свойства: $\psi = 0$ на $\Gamma $, $\psi > 0$ в твердом скелете, а в области фильтрации $\psi < 0$; ${\mathbf{c}} = {{c}_{\Gamma }}{\mathbf{n}}$, ${\mathbf{n}}$ – вектор нормали к границе $\Gamma $. Скорость движения последней равна

${{c}_{\Gamma }} = \left\{ \begin{gathered} {{k}_{d}}(\tau - {{\tau }_{c}}),\quad (\tau \geqslant {{\tau }_{c}}) \hfill \\ 0,\quad (\tau < {{\tau }_{c}}) \hfill \\ \end{gathered} \right.$

где ${{k}_{d}}$ – коэффициент пропорциональности, $\tau $– модуль касательного напряжения

$\tau = \sqrt {{{{(T{\mathbf{n}})}}^{2}} - {{{({\mathbf{n}}T{\mathbf{n}})}}^{2}}} $

${{\tau }_{c}}$ – критическое значение касательного напряжения при достижении которого начинается суффозионный процесс.

Тензор напряжений и тензор скоростей деформации имеют вид

$T = - PI + 2{{\mu }_{w}}D({\mathbf{u}}),\quad D({\mathbf{u}}) = \frac{1}{2}(\nabla {\mathbf{u}} + {{(\nabla {\mathbf{u}})}^{T}})$

В данном подходе интенсивность фазового перехода определяется формулой

$I = \rho ({{c}_{\Gamma }} - {\mathbf{u}} \cdot {\mathbf{n}})$

В работе [39] рассматривалось двухфазное течение (вода ($i = 1$), подвижные частицы ($i = 2$), ${{s}_{1}} + {{s}_{2}} = 1$) и использовалось следующее модельное соотношение для определения суффозионного потока:

$I = \rho _{3}^{0}\delta (s)R(\phi ){\text{max}}\{ {\text{|}}{{{\mathbf{v}}}_{1}}{\text{|}} - {{v}_{k}},0\} $

$\delta (s) = \left\{ {\begin{array}{*{20}{l}} {0,\quad (s \geqslant 1)} \\ {1 - s,\quad (0 < s < 1)} \\ {1,\quad (s \leqslant 0)} \end{array}} \right.\quad R(\phi ) = \left\{ {\begin{array}{*{20}{l}} {1,\quad (\phi \geqslant 1)} \\ {\phi (1 - \phi ),\quad (0 < s < 1)} \\ {0,\quad (\phi \leqslant 0)} \end{array}} \right.$

Такой выбор интенсивности фазового перехода позволяет гарантировать выполнение физического принципа максимума для пористости и насыщенности.

3. АЛГОРИТМ ЧИСЛЕННОГО РЕШЕНИЯ ОДНОМЕРНОЙ ЗАДАЧИ

В одномерном случае система уравнений (1.23)–(1.26) примет вид

(3.1)

$\phi \frac{{\partial s}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {a\frac{{\partial s}}{{\partial x}} + bv + F} \right) - s\frac{{\partial \phi }}{{\partial t}}$

(3.2)

$\frac{\partial }{{\partial x}}\left( {K\frac{{\partial p}}{{\partial x}} + f} \right) = 0$

(3.3)

$\frac{{\partial \phi }}{{\partial t}} = \frac{I}{{\rho _{3}^{0}}}$

Для системы (3.1)–(3.3) рассматривается следующая начально-краевая задача:

(3.4)

$s(x,0) = {{s}_{1}},\quad s(0,t) = {{s}_{0}},\quad s(l,t) = {{s}_{l}}$

$\phi (x,0) = {{\phi }_{0}},\quad \frac{{\partial p}}{{\partial x}}(0,t) = {{p}_{0}}(t),\quad p(l,t) = {{p}_{l}}(t),$$x \in [0,l]$

Пусть ${{t}_{{sc}}}$, ${{x}_{{sc}}}$ – время и длина есть заданные постоянные. Положим

$\tilde {t} = \frac{t}{{{{t}_{{sc}}}}},\quad \tilde {x} = \frac{x}{{{{x}_{{sc}}}}},\quad \tilde {p} = \frac{p}{{{{p}_{{sc}}}}},\quad \tilde {v} = \frac{v}{{{{v}_{{sc}}}}}$

${{v}_{{sc}}} = \frac{{{{x}_{{sc}}}}}{{{{t}_{{sc}}}}},\quad \mu = \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}},\quad g = \tilde {g}\frac{{{{x}_{{sc}}}}}{{t_{{sc}}^{2}}},\quad {{p}_{{sc}}} = \frac{{\rho _{1}^{0}x_{{sc}}^{2}}}{{t_{{sc}}^{2}}}$

В безразмерных переменных система (3.1)–(3.3) принимает следующую форму:

$\phi \frac{{\partial s}}{{\partial{ \tilde {t}}}} = \frac{\partial }{{\partial{ \tilde {x}}}}\left( {\tilde {a}\frac{{\partial s}}{{\partial{ \tilde {x}}}} + b\tilde {v} + \tilde {F}} \right) - s\frac{{\partial \phi }}{{\partial{ \tilde {t}}}}$

$\frac{\partial }{{\partial{ \tilde {x}}}}\left( {\tilde {K}\frac{{\partial{ \tilde {p}}}}{{\partial{ \tilde {x}}}} + \tilde {f}} \right) = 0$

$\frac{{\partial \phi }}{{\partial{ \tilde {t}}}} = \tilde {I}$

Здесь

$\tilde {a}(s,\varphi ) = - {{\tilde {K}}_{0}}\frac{{{{{\bar {k}}}_{{01}}}{{{\bar {k}}}_{{02}}}}}{{\mu {{{\bar {k}}}_{{01}}} + {{{\bar {k}}}_{{02}}}}}\frac{{\partial {{{\tilde {p}}}_{c}}}}{{\partial s}},\quad v = \tilde {v}\frac{{{{x}_{{sc}}}}}{{{{t}_{{sc}}}}} = {{\tilde {v}}_{1}} + {{\tilde {v}}_{2}},\quad {{\tilde {v}}_{1}} = - {{\tilde {K}}_{0}}{{\bar {k}}_{{01}}}\left( {\frac{{\partial {{{\tilde {p}}}_{1}}}}{{\partial{ \tilde {x}}}} - \tilde {g}} \right)$

${{\tilde {v}}_{2}} = - {{\tilde {K}}_{0}}\frac{{{{{\bar {k}}}_{{02}}}}}{\mu }\left( {\frac{{\partial {{{\tilde {p}}}_{2}}}}{{\partial{ \tilde {x}}}} - \frac{{\rho _{2}^{0}}}{{\rho _{1}^{0}}}\tilde {g}} \right),\quad b(s) = \frac{{{{{\bar {k}}}_{{02}}}}}{{\mu {{{\bar {k}}}_{{01}}} + {{{\bar {k}}}_{{02}}}}}$

$\tilde {F} = {{\tilde {K}}_{0}}\tilde {g}{{\bar {k}}_{{01}}}{{\bar {k}}_{{02}}}\left( {\frac{{\rho _{2}^{0}}}{{\rho _{1}^{0}}} - 1} \right){{(\mu {{\bar {k}}_{{01}}} + {{\bar {k}}_{{02}}})}^{{ - 1}}},\quad {{\tilde {K}}_{0}} = \frac{{B{{p}_{{sc}}}{{t}_{{sc}}}}}{{x_{{sc}}^{2}{{\mu }_{1}}}}{{\hat {K}}_{0}}$

${{\hat {K}}_{0}} = \frac{{{{\varphi }^{3}}}}{{{{{(1 - \varphi )}}^{2}}}}$

$\tilde {f} = - {{\tilde {K}}_{0}}\left( {{{{\bar {k}}}_{{01}}} + \frac{{\rho _{2}^{0}{{\mu }_{1}}}}{{\rho _{1}^{0}{{\mu }_{2}}}}{{{\bar {k}}}_{{02}}}} \right)\tilde {g},\quad \tilde {k} = {{\bar {k}}_{{01}}} + \frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}{{\bar {k}}_{{02}}}$

$\tilde {K} = {{\tilde {K}}_{0}}\tilde {k}$

$\tilde {I} = \left\{ \begin{gathered} \tilde {\lambda }(1 - \phi )(1 - s)\phi ({\text{|}}{{{\tilde {v}}}_{1}}{\text{|}} - \;{\text{|}}{{{\tilde {v}}}_{k}}{\text{|}}),{\text{|}}{{{\tilde {v}}}_{1}}{\text{|}} \geqslant {\text{|}}{{{\tilde {v}}}_{k}}{\text{|}} \hfill \\ 0,\quad {\text{|}}{{{\tilde {v}}}_{1}}{\text{|}} < {\text{|}}{{{\tilde {v}}}_{k}}{\text{|}} \hfill \\ \end{gathered} \right.$

$\tilde {\lambda } = \lambda {{x}_{{sc}}},\quad {{v}_{k}} = {{\tilde {v}}_{k}}\frac{{{{x}_{{sc}}}}}{{{{t}_{{sc}}}}}$

Опуская крышки и волны, получим

(3.5)

$\phi \frac{{\partial s}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {a(s,\phi )\frac{{\partial s}}{{\partial x}} + b(s)v(t) + F(s,\phi )} \right) - s\frac{{\partial \phi }}{{\partial t}}$

(3.6)

$\frac{{\partial \text{v}}}{{\partial x}} = \frac{\partial }{{\partial x}}\left( {K(s,\phi )\frac{{\partial p}}{{\partial x}} + f(s,\phi )} \right) = 0$

(3.7)

$\frac{{\partial \phi }}{{\partial t}} = I(s,\phi ,p)$

Следует отметить, что $v(t)$ является искомой функцией и определяется из равенства (1.16) в ходе решения задачи.

Введем сетку с распределенными узлами x_i = ih, ${{t}_{n}} = n\tau ;i = 0,...,N,n = 0,...,T$, $h$ – шаг по пространственной координате, $\tau $ – шаг по времени.

При аппроксимации уравнения (3.5) используется направленная разность для конвективного слагаемого. Уравнение (3.6) аппроксимируется неявной схемой второго порядка точности. В результате получаем систему разностных уравнений

$\begin{gathered} \phi _{i}^{n}\frac{{s_{i}^{{n + 1}} - s_{i}^{n}}}{\tau } = a_{{i + 1/2}}^{n}\frac{{s_{{i + 1}}^{{n + 1}} - s_{i}^{{n + 1}}}}{{{{h}^{2}}}} - a_{{i - 1/2}}^{n}\frac{{s_{i}^{{n + 1}} - s_{{i - 1}}^{{n + 1}}}}{{{{h}^{2}}}} + \\ + \;\frac{{({\text{|}}G_{i}^{n}{\text{|}} + G_{i}^{n})s_{{i + 1}}^{{n + 1}} - 2{\text{|}}G_{i}^{n}{\text{|}}s_{i}^{{n + 1}} + ({\text{|}}G_{i}^{n}{\text{|}} - G_{i}^{n})s_{{i - 1}}^{{n + 1}}}}{{2h}} + F_{{\varphi i}}^{n}\frac{{\phi _{{i + 1}}^{n} - \phi _{{i - 1}}^{n}}}{{2h}} - s_{i}^{n}\frac{{\phi _{i}^{{n + 1}} - \varphi _{i}^{n}}}{\tau } \\ K_{{i + 1/2}}^{n}\frac{{p_{{i + 1}}^{n} - p_{i}^{n}}}{{{{h}^{2}}}} - K_{{i - 1/2}}^{n}\frac{{p_{i}^{n} - p_{{i - 1}}^{n}}}{{{{h}^{2}}}} + f_{{si}}^{n}\frac{{s_{{i + 1}}^{n} - s_{{i - 1}}^{n}}}{{2h}} + f_{{\varphi i}}^{n}\frac{{\phi _{{i + 1}}^{n} - \phi _{{i - 1}}^{n}}}{{2h}} = 0 \\ \end{gathered} $

Здесь $i = 1,\;...,\;N - 1$, $\tau = 0,\;...,\;T - 1$. Уравнение (3.7) аппроксимируется неявной схемой Рунге-Кутты второго порядка точности. Причем, найденное на первом этапе значение

(3.8)

$\tilde {\phi }_{i}^{{n + 1}} = \phi _{i}^{n} + \tau I_{i}^{n}$

затем уточняется следующим образом:

(3.9)

$\phi _{i}^{{n + 1}} = \phi _{i}^{n} + \tau \frac{{I(\phi _{i}^{n},s_{i}^{n}) + I(\tilde {\phi }_{i}^{n},s_{i}^{n})}}{2}$

Здесь $i = 0,\;...,\;N$, $\tau = 0,\;...,\;T - 1$

$a_{{i - 1/2}}^{n} = \frac{{2a(s_{{i - 1}}^{n},\phi _{{i - 1}}^{n})a(s_{i}^{n},\phi _{i}^{n})}}{{a(s_{{i - 1}}^{n},\phi _{{i - 1}}^{n}) + a(s_{i}^{n},\phi _{i}^{n})}}\quad a_{{i + 1/2}}^{n} = \frac{{2a(s_{{i + 1}}^{n},\phi _{{i + 1}}^{n})a(s_{i}^{n},\phi _{i}^{n})}}{{a(s_{{i + 1}}^{n},\phi _{{i + 1}}^{n}) + a(s_{i}^{n},\phi _{i}^{n})}}$

$F_{{\varphi i}}^{n} = \frac{{\partial F}}{{\partial \phi }}(s_{i}^{n},\phi _{i}^{n}),\quad f_{{si}}^{n} = \frac{{\partial f}}{{\partial s}}(s_{i}^{n},\phi _{i}^{n}),\quad f_{{\varphi i}}^{n} = \frac{{\partial f}}{{\partial \varphi }}(s_{i}^{n},\phi _{i}^{n})$

$G_{i}^{n} = \frac{{\partial F}}{{\partial s}}(s_{i}^{n},\phi _{i}^{n}) + v({{t}_{n}})\frac{{\partial b}}{{\partial s}}(s_{i}^{n}),\quad K_{{i - 1/2}}^{n} = \frac{{2K(\phi _{{i - 1}}^{n},s_{{i - 1}}^{n})K(\phi _{i}^{n},s_{i}^{n})}}{{K(\phi _{{i - 1}}^{n},s_{{i - 1}}^{n}) + K(\phi _{i}^{n},s_{i}^{n})}}$

$K_{{i + 1/2}}^{n} = \frac{{2K(\phi _{{i + 1}}^{n},s_{{i + 1}}^{n})K(\phi _{i}^{n},s_{i}^{n})}}{{K(\phi _{{i + 1}}^{n},s_{{i + 1}}^{n}) + K(\phi _{i}^{n},s_{i}^{n})}}$

$I_{i}^{n} = \left\{ \begin{gathered} \lambda (1 - \phi _{i}^{n})(1 - s_{i}^{n})\phi _{i}^{n}({\text{|}}v_{{1i}}^{n}{\text{|}} - \;{\text{|}}{{v}_{k}}{\text{|}}),\quad ({\text{|}}v_{{1i}}^{n}{\text{|}} \geqslant {\text{|}}{{v}_{k}}{\text{|}}) \hfill \\ 0,\quad ({\text{|}}v_{{1i}}^{n}{\text{|}} < {\text{|}}{{v}_{k}}{\text{|}}) \hfill \\ \end{gathered} \right.$

Алгоритм численного решения начально-краевой задачи следующий: используя начальное значение пористости $\phi _{i}^{0}$ и концентрации $s_{i}^{0}$, находим начальное распределение приведенного давления $p_{i}^{0}$ ($i = 0,\;...,\;N$) из уравнения (3.6). Используя найденное давление, определяем скорости фильтрации воды и подвижных частиц грунта $v_{{1i}}^{0}$ и $v_{{2i}}^{0}$. Из равенства (3.8) находим пористость грунта $\phi _{i}^{1}$ на следующем шаге по времени. Из уравнения (3.5) находим концентрацию воды $s_{i}^{1}$. Рассчитываем давление на следующем шаге по времени (n = 1). Используя найденные значения искомых функций $\tilde {\phi }_{i}^{1}$, $s_{i}^{1}$, $p_{i}^{0}$, $p_{i}^{1}$, делаем коррекцию значения пористости на первом шаге по времени, используя формулу (3.9). Повторяя данный алгоритм для следующих шагов по времени, найдем значения искомых функций на всем временном интервале.

4. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ОДНОМЕРНОЙ ЗАДАЧИ

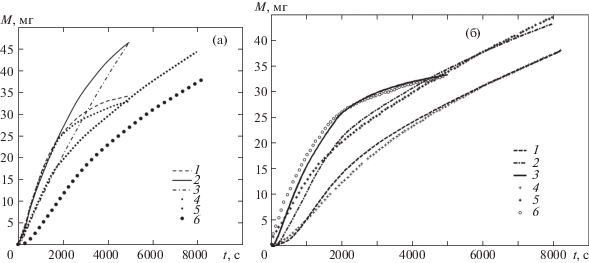
В работе [11] A. Chetti и соавт. предложили математическую модель внутренней суффозии на основе уравнения диффузии. Для замыкания модели использовалась гипотеза равенства скоростей подвижных частиц грунта и воды. Сравнение результатов вычислений с экспериментальными данными показало, что модель дает хорошее совпадение с результатами эксперимента [11] в случае, когда эффектом физико-химических процессов на эрозию можно пренебречь (мала ионная сила раствора, составляющего несущую фазу) и грунт подвержен внутренней суффозии ($\lambda = 8.5$), но завышает значения эродированной и вынесенной массы грунта из области фильтрации для грунтов, слабо подверженных суффозии ($\lambda = 4$ и $\lambda = 1$, см. рис. 1a). В работе [13] предложено определять скорости подвижных частиц грунта из соотношения ${{v}_{1}} = \beta {{v}_{2}}$ ($0 < \beta < 1$), т.е. постулировалось, что скорость частиц грунта меньше скорости фильтрации воды, но из каких соображений выбирается коэффициент $\beta = {\text{const}}$, не разъясняется.

Рис. 1.

Результаты моделирования (1–3), представленные в работе [11] (а): 4–6 –экспериментальные данные; $\lambda = $ 8.5, 4, 1 (1–3) и (4–6). Результаты (1–3) численного моделирования (б): 4–6 – экспериментальные данные; λ = 1, 4, 8.5 (1–3) и (4–6);$M$ – эродированная масса грунта, t – время.

В данной работе для тестирования предложенной математической модели используются результаты эксперимента, представленного в работе [11]. Экспериментальная установка состоит из резервуара, наполненного жидкостью и создающего гидравлическую нагрузку, приложенную к горизонтальной трубе, заполненной образцом почвы. В ходе эксперимента были исследованы несколько образцов почвы с разной суффозионной устойчивостью (за суффозионную устойчивость отвечает параметр $\lambda $ [11]). Суффозионные тесты были проведены для смеси крупного песка, размеры частичек которого изменялись между 0.315 и 1.60 мм, и мелких частиц, размеры которых изменялись от 1 до 80 микрон. Концентрация мелких частиц в смеси песка изменялась от 2 до 8 процентов от веса. Смеси были подготовлены смешиванием песка и мелких частиц с 3-х процентным содержанием воды, затем смесь хранилась в течение 24 ч перед тем, как она загружалась в экспериментальную установку методом двукратного прессования.

При численном исследовании начально краевой задачи (3.1)–(3.4) использовалась следующая эмпирическая зависимость [40] ${{p}_{c}}(s) = \gamma (1{\text{/}}s - 1)$, здесь $\gamma $ – размерный параметр [Па] (в численных расчетах $\gamma = 0.001$ определялся подбором в ходе решения задачи и сопоставления результатов моделирования и экспериментальных данных). Полученные результаты вычислений тестировались на экспериментальных данных, представленных в работе [11]. Скорость движения подвижных частиц грунта определяется в ходе решения задачи, используя уравнение (1.14) (см. также [41]).

В численных расчетах использовался следующий набор модельных параметров: g = 0 м/с², ${{v}_{k}} = 0$ м/с, ${{K}_{0}}(\phi ) = {{\phi }^{3}}{\text{/}}(1 - {{\phi }^{2}}),$ ${{k}_{{0i}}} = s_{i}^{3}$ если $0 \leqslant s \leqslant 1$, ${{k}_{{0i}}} = 0$ если ${{s}_{i}} \leqslant 0$, ${{k}_{{0i}}} = 1$ если ${{s}_{i}} \geqslant 1$. Начальные и граничные условия задавались в виде

$\frac{{\partial {{p}_{1}}}}{{\partial x}}(0,t) = H$

$\frac{{\partial p}}{{\partial x}}(0,t) = H + \frac{{{{k}_{{02}}}(s)}}{{k(s)}}\frac{{\partial {{p}_{c}}}}{{\partial s}}\frac{{\partial s}}{{\partial x}}$

где $H$ – напор воды (в численных расчетах H = 2.4). Предполагалось что $s(0,t) = {{s}_{0}} = 1$, т.е. на границе x = 0 нет подвижных частиц грунта. На другом конце рассматриваемой области x = l граничное условие имело вид $p(l,t) = 101325$ Па (атмосферное давление). Для концентрации подвижных частиц грунта на границе рассматривались два варианта $\partial s(x,t){\text{/}}\partial x{{{\text{|}}}_{{x = l}}} = 0$ и $s(l,t) = {{s}_{h}}(t)$, где ${{s}_{h}}$ – дискретная функция, значения которой определялись экспериментально в работе [11]. В начальный момент времени пористость предполагалась постоянной $\phi (x,0) = 0.35$, а водонасыщенность $s$ задавалась равной единице $s(x,0) = 1$ для первого граничного условия и линейной функцией от $x$, $s(x,0) = x({{s}_{h}}(0) - {{s}_{0}}){\text{/}}l + {{s}_{0}}$ – для второго.

В численных расчетах использовались следующие параметры [11]:

$h = 0.00123,\quad N = 1000,\quad \tau = 0.0001,\quad T = 1000$

$\rho _{1}^{0} = 1000$ кг/м³, $\rho _{2}^{0} = 2600$ кг/м³, $l = 123$ мм

${{\mu }_{1}} = 0.001787$ кг/мс², ${{\mu }_{2}} = 0.003574{\kern 1pt} $ кг/мс²

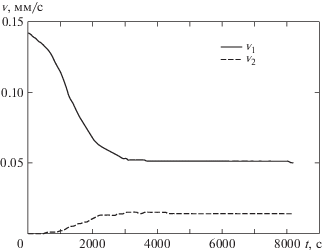
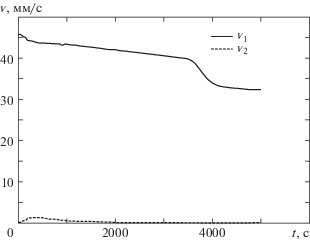
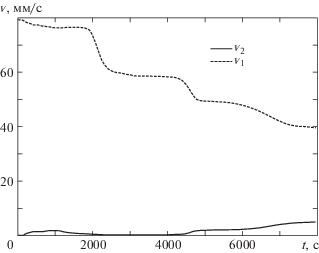
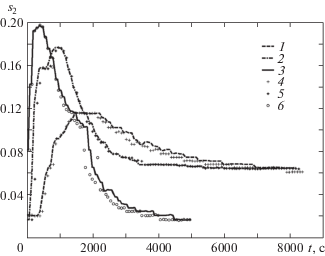
На рис. 2–4 представлены результаты численных расчетов модуля скорости фильтрации воды ${{v}_{1}}$ и модуля скорости подвижных частиц грунта, на рис. 5 концентрации подвижных частиц грунта. Расчеты показали, что скорость подвижных частиц грунта много меньше скорости воды для грунтов слабо подверженных суффозии (λ = 4 и λ = 1). На рис. 1б представлено сравнение рассчитанных значений вынесенной массы из области фильтрации с экспериментальными данными, взятыми из работы [11]. Сравнение рассчитанных значений скоростей фильтрации воды и подвижных частиц грунта показало, что модуль скорости воды заметно превосходит модуль скорости подвижных частиц грунта. При моделировании фильтрации жидкости в грунтах, слабо подверженных суффозионному воздействию (например, см. рис. 3 и 4 ), необходимо учитывать изменения скоростей фильтрации воды и подвижных частиц грунта. Условие $g = 0$ не является принципиальным, а взято для сравнения численного решения с имеющимися экспериментальными данными.

Рис. 2.

Скорости воды и подвижных частиц грунта: $\lambda = 1$, $x = 123$ мм.

Рис. 3.

То же, что на рис. 2: $\lambda = 8.5$.

Рис. 4.

То же, что на рис. 2: $\lambda = 4$.

Рис. 5.

Результаты численного моделирования изменения концентрации псевдоожиженных частиц (1–3) и экспериментальные данные (4–6): $\lambda = 1$, 4, 8.5 (1–3) и (4–6); $x = 123$ мм.

Устойчивость и порядок сходимости вычислительного алгоритма проверяются путем вычислительных экспериментов, применяя известное правило Рунге [42]: достаточно провести три расчета на сетках c шагами ${{h}_{1}} = h$, ${{h}_{2}} = h{\text{/}}2$, ${{h}_{3}} = h{\text{/}}4$, ${{\tau }_{i}} = \lambda {{h}_{i}}$, $\lambda = {\text{const}}$, $i = 1,2,3$. Если основной величиной наблюдения является концентрация воды s, то экспериментальный порядок сходимости $R \approx 1.1$ и приближенно определяемая относительная погрешность $\varepsilon \approx 1$%.

Экспериментальные данные позволили провести верификацию свободного параметра $\gamma $ и провести сравнения результатов моделирования с экспериментом. В работе [11] интенсивность фазового перехода задавалась другой формулой. Поэтому прямое сравнение результатов моделирования настоящей работы и результатов из работы [11] не проводилось.

ЗАКЛЮЧЕНИЕ

В работе предложена новая математическая модель фильтрации жидкости с учетом суффозионных процессов. Подвижные частицы грунта рассматриваются как отдельная фаза, скорость которой определяется в ходе решения задачи. Данное предположение позволило построить замкнутую математическую модель и провести на ее основе численные расчеты, которые хорошо согласуются с экспериментальными данными из литературных источников. Модель применима для широкого класса суффозионных течений.

Предложен алгоритм численного решения начально-краевой задачи фильтрации грунтовых вод с учетом внутренней эрозии грунта и проведены тестовые численные расчеты. Найдены скорости движения и давление грунтовых вод, пористость и концентрация подвижных твердых частиц для грунтов, имеющих различную суффозионную устойчивость.

Список литературы

Dalmo A.N.V., Seth D.M. Modeling edge effects of tillage erosion // Soil and Tillage Research. 2011. V. 111. № 2. P. 197–207. https://doi.org/10.1016/j.still.2010.10.007
Wilson G. Understanding soil-pipe flow and its role in ephemeral gully erosion // Hydrol. Process. 2011. V. 25. № 15. P. 2354–2364. https://doi.org/10.1002/hyp.7998
Zhou J., Tang Y., Zhang X., She T., Yang P., Wang J. The influence of water content on soil erosion in the desertification area of Guizhou, China // Carbonates Evaporites. 2012. V. 27. № 2. P. 185–192. https://doi.org/10.3390/w10070915
Einstein H.A. Der Geschiebetrieb als wahrscheinlichkeits Problem. Mitt. d. Versuchsanstaltf Wasserbau. Zurich: Eidg. T. H., 1937. P. 112.
Parron Vera M.A., Yakhlef F., Rubio Cintas M.D., Castillo Lopez O., Dubujet P., Khamlichi A., Bezzazic M. Analytical solution of coupled soil erosion and consolidation equations by asymptotic expansion approach // Applied Mathematical Modelling. 2014. V. 38. № 15. P. 4086–4098. https://doi.org/10.1016/j.apm.2014.02.006
Wang J., Walters D.A., Settari A., Wan R.G. Simulation of Cold Heavy Oil Production Using an Integrated Modular Approach with Emphasis on Foamy Oil Flow and Sand Production Effects // 1st Heavy Oil Conf. Beijing. 2006. P. 424–433.
Николаевский В.Н. Собр. тр. Геомеханика. Т. 1. Разрушение и дилатансия. Нефть и газ. М.: Ижевск: НИЦ “Регулярная и хаотическая динамика”, Ин-т компьютерных исслед., 2010. 640 с.
Biot M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid // J. Acoustical Society of America. 1956. V. 28. № 2. P. 168–178.
Bonelli S., Marot D. Micromechanical modeling of internal erosion // Europ. J. Environmental and Civil Engineering. 2011. V. 15. № 8. P. 1207–1224.
Mercier F., Bonelli S., Golay F., Anselmet F., Philippe P., Borghi R. Numerical modelling of concentrated leak erosion during Hole Erosion Tests // Acta Geotechnica. 2015. V. 10. № 3. P. 319–332. https://doi.org/10.1007/s1144
Chetti A., Benamar A., Hazzab A. Modeling of Particle Migration in Porous Media: Application to Soil Suffusion // Transport in Porous Media. 2016. V. 113. № 3. P. 591–606. https://doi.org/10.1007/s11242-016-0714-y
Vardoulakis I. Sand production // Geomechanics in energy production. 2006. V. 10. № 6. P. 817–828.
Vardoulakis I., Papanastasiou P., Stavropoulou M. Sand Erosion in Axial Flow Conditions // Transport in Porous Media. 2001. V. 45. № 2. P. 267–280. https://doi.org/10.1023/A:1012035031463
Muhlhaus H., Gross L., Scheuermann A. Sand erosion as an internal boundary value problem // Acta Geotechnica. 2015. V. 10. № 3. P. 333–342. https://doi.org/10.1007/s11440-014-0322-3
Нигматулин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987. 464 с.
Garg S.K., Pritchett J.W. Dynamics of gasfluidized beds // J. Appl. Phys. 1975. V. 46. P. 4493–4450.
Протодьяконов И.О., Чесноков Ю.Г. Гидромеханика псевдоожиженного слоя. Л.: Химия, 1982. 264 с.
Шагапов В.Ш., Хусаинов И.Г., Дмитриев В.Л. Распространение линейных волн в насыщенных газом пористых средах с учетом межфазного теплообмена // ПМТФ. 2004. Т. 45. № 4. С. 114–120.
Rege S.D., Fogler H.S. A Network Model for Deep Bed Filtration of Solid Particles and Emulsion Drops // AIChE J. 1988. V. 34. № 11. P. 1761–1772.
Yang Y., Siqueira F.D., Vaz A.S.L., You Z., Bedrikovetsky P. Slow migration of detached fine particles over rock surface in porous media // J. Natural Gas Science and Engineering. 2016. V. 34. P. 1159–1173. https://doi.org/10.1016/j.jngse.2016.07.056
Тодес О.М., Цитович О.Б. Аппараты с кипящим зернистым слоем: Гидравлические и тепловые основы работы. Л.: Химия, 1981. 296 с.
Истомина В.С. Фильтрационная устойчивость грунтов. М.: Госстройиздат, 1957. 295 с.
Рахматулин Х.А. Основы газодинамики взаимопроникающих движений сжимаемых сред // Прикладная математика и механика. 1956. Т. 20. № 2. С. 184–195.
Рахматулин Х.А. Газовая и волновая динамика. М.: МГУ, 1983. 196 с.
Файзуллаев Д.Ф., Умаров А.И., Шакиров А.А. Гидродинамика одно- и двухфазных сред и ее практическое приложение. Ташкент: Фан, 1980. 165 с.
Steward H.B., Wendroff B. Two-phase flows: models and methods // J. Comp. Phys. 1984. V. 56. № 3. P. 363–409.
Полубаринова-Кочина П.Я. Теория движения грунтовых вод: Учеб. пособ. для студентов ун-тов, обучающихся по специальности “Механика”. 2-е изд., перераб. и доп. М.: Наука, 1977. 664 с.
Коллинз Р. Течения жидкостей через пористые материалы. М.: Мир, 1964. 350 с.
Полубаринова-Кочина П.Я. Гидродинамика и теория фильтрации: избранные труды. М.: Наука, 1991. 351 с.
Muskat M. The flow of homogeneous fluids through porous media. Edwards Ann Arbor, 1937. 763 p.
Бэр Я. Физико-математические основы фильтрации воды. М.: Мир, 1971. 452 с.
Гельперин Н.И., Айнштейн В.Г., Кваша В.Б. Основы техники псевдоожижения. М.: Химия, 1967. 177 с.
Антонцев С.Н., Кажихов А.В., Монахов В.Н. Краевые задачи механики неоднородных жидкостей. Новосибирск: Наука, 1983. 320 с.
Ведерников В.В., Николаевский В.Н. Уравнение механики пористых сред, насыщенных двухфазной жидкостью // Изв. АН СССР. МЖГ. 1978. Т. 5. С. 165–169.
Полубаринова-Кочина П.Я. Развитие исследований по теории фильтрации в СССР. Изд. 2-е. M.: Наука, 1969. 548 с.
Vardoulakis I., Stavropoulou M., Papanastasiou P. Hydro-Mechanical Aspects of the Sand Production Problem // Transport in Porous Media. 1996. V. 22. № 2. P. 225–244.
Рекомендации по методике лабораторных испытаний грунтов на водопроницаемость и суффозионную устойчивость. М.: ВНИИГ им. Б.Е. Веденеева, 1983. 55 с.
Bonelli S. Erosion of Geomaterials. London: Wiley, 2012. 384 p.
Папин А.А., Вайгант В.А., Сибин А.Н. Математическая модель неизотермической внутренней эрозии // Изв. АлтГУ. 2015. Т. 1. № 1. С. 89–93.
Bocharov O.B., Rudyak V.Ya., Seryakov A.V. Simplest deformation models of a fluid-saturated poroelastic medium // J. Mining Science. 2014. V. 50. № 2. P. 235–248. https://doi.org/10.1134/S1062739114020057
Garde R.J., Ranga Raju K.G. Mechanics of Sediment Transportation and Alluvial Stream Problems. John Wiley and Sons Inc, 1977. 484 p.
Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал