1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 2, 2019

Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 126-133

АКУСТИЧЕСКИЕ ВОЛНЫ В ЖИДКОСТИ С ПУЗЫРЬКАМИ ГАЗА, ПОКРЫТЫМИ ВЯЗКОУПРУГОЙ ОБОЛОЧКОЙ

Д. А. Губайдуллин a, *, Ю. В. Федоров a, **

a ФИЦ Казанский научный центр РАН, Институт механики и машиностроения
Казань, Россия

* E-mail: gubaidullin@imm.knc.ru
** E-mail: kopperfildd@ya.ru

Поступила в редакцию 17.04.2018
После доработки 27.06.2018
Принята к публикации 27.06.2018

Полный текст (PDF)

Аннотация

Исследовано распространение акустических волн в смеси жидкости с пузырьками газа, покрытыми вязкоупругой оболочкой. Приведена система дифференциальных уравнений возмущенного движения смеси, найдено дисперсионное соотношение. Получены низкочастотные асимптотики фазовой скорости и коэффициента затухания. Установлена и проиллюстрирована зависимость равновесной скорости звука от частоты возмущений и размера покрытых пузырьков. Дано сравнение теории с известными экспериментальными данными.

Ключевые слова: акустическая волна, пузырьковая жидкость, вязкоупругая оболочка, модуль сдвига, коэффициент затухания, равновесная скорость звука

Исследование акустических свойств сложных пузырьковых сред актуально. Различные проблемы акустики смеси жидкости с пузырьками газа или пара рассмотрены в монографиях [1–4]. В работах [5–7] представлены результаты экспериментов по изучению частотных зависимостей фазовой скорости и коэффициента затухания в жидкости с пузырьками газа. Теоретические результаты опубликованы, к примеру, в работах [8–10]. С большим количеством публикаций можно ознакомиться в обзорах [11, 12].

Покрытые оболочкой пузырьки встречаются во многих областях. Большое применение они нашли в биомедицине, где используются в качестве контрастных веществ для ультразвуковой диагностики [13, 14]. В [15] приведено описание наноробота, способного перемещаться в жидкой среде новым способом. На поверхности устройства прикрепляются пузырьки газа, заключенные в специальные капсулы. Под воздействием ультразвуковых колебаний пузырьки начинают поочередно расширяться и сжиматься, оказывая давление на стенку, к которой они прикреплены. Частота колебаний зависит от размеров пузырьков, и чем ближе она к их резонансной частоте, тем эффективнее происходит движение наноробота.

Существующие теоретические модели основаны на различных формах записи уравнений колебаний сферических пузырьков с учетом упругости и вязкости поверхностного слоя. В [16] получено модифицированное уравнение Релея–Плессета, учитывающее радиальные колебания газового пузырька с вязкоупругой оболочкой конечной толщины в жидкости на основе реологического уравнения Кельвина–Фойгта. Проанализировано влияние параметров оболочки. Впоследствии модель [16] была упрощена на случай, когда толщина вязкоупругой оболочки пузырьков близка к нулю [17]. Найдено теоретически и экспериментально влияние полимерной оболочки микропузырьков на затухание импульсного возмущения. В [18] изучено поведение газовых пузырьков, имеющих упругую оболочку, под действием ультразвука в упругой среде. В линейном приближении получены выражения для амплитуды рассеяния и резонансной частоты колебаний включений. Радиальные колебания газового пузырька в сжимаемой вязкоупругой жидкости исследованы в [19]. Показано, что при радиальных пульсациях упругие и вязкие свойства оболочки пузырьков преобладают над вязкоупругими свойствами жидкости.

В настоящей работе представлена математическая модель, определяющая распространение акустической волны в жидкости с покрытыми оболочкой пузырьками газа.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим газовую полость, покрытую тонкой сферической вязкоупругой оболочкой внутри массива неподвижной, несжимаемой жидкости (рис. 1). Ввиду непроницаемости оболочки скорость изменения ее радиуса $\dot {R}_{1}^{{}} = d{{R}_{1}}{\text{/}}dt$ совпадает с радиальной скоростью движения на поверхности $u({{R}_{1}},t)$.

Рис. 1.

Схема пузырька с оболочкой: g – газ, s – оболочка, l – жидкость

Уравнение неразрывности в сферической системе координат при наличии центральной симметрии имеет вид

$\frac{1}{{{{r}^{2}}}}\frac{d}{{dr}}({{r}^{2}}u) = 0$
решение которого записывается следующим образом

(1.1)
$u(r,t) = \frac{{R_{1}^{2}(t)}}{{{{r}^{2}}}}{{\dot {R}}_{1}}(t)$

Уравнение сохранения импульса в сферических координатах берется в виде

(1.2)
$\rho \left( {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial r}}} \right) = - \frac{{\partial p}}{{\partial r}} + \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}({{r}^{2}}{{\tau }_{{rr}}}) - \frac{{{{\tau }_{{\theta \theta }}} + {{\tau }_{{\varphi \varphi }}}}}{r}$
где ρ – плотность, p – давление, τ – компоненты тензора напряжений.

Проинтегрируем уравнение (1.2) от r до ∞ с учетом (1.1) и соотношения для компонентов тензора сферы ${{\tau }_{{rr}}} = - ({{\tau }_{{\theta \theta }}} + {{\tau }_{{\varphi \varphi }}})$ [20]. Интервал от r до ∞ разбивается на два подинтервала: от ${{R}_{1}}$ до ${{R}_{2}}$ и от ${{R}_{2}}$ до ∞. Первый от ${{R}_{1}}$ до ${{R}_{2}}$ будет соответствовать параметрам вязкоупругого слоя, второй от ${{R}_{2}}$ до ∞ – параметрам жидкости. После интегрирования и необходимых математических действий получим

(1.3)
$\begin{gathered} {{\rho }_{s}}{{R}_{1}}\ddot {R}_{1}^{{}}\left( {1 + \frac{{{{\rho }_{l}} - {{\rho }_{s}}}}{{{{\rho }_{s}}}}\frac{{{{R}_{1}}}}{{{{R}_{2}}}}} \right) + {{\rho }_{s}}\dot {R}_{1}^{2}\left( {\frac{3}{2} + \frac{{{{\rho }_{l}} - {{\rho }_{s}}}}{{{{\rho }_{s}}}}\frac{{4R_{2}^{3} - R_{1}^{3}}}{{2R_{2}^{3}}}\frac{{{{R}_{1}}}}{{{{R}_{2}}}}} \right) = - {{p}_{s}}({{R}_{2}},t) + {{p}_{s}}({{R}_{1}},t) + \\ + \;{{p}_{l}}({{R}_{2}},t) - {{p}_{\infty }} + {{\tau }_{{s,rr}}}({{R}_{2}},t) - {{\tau }_{{s,rr}}}({{R}_{1}},t) - {{\tau }_{{l,rr}}}({{R}_{2}},t) + 3\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\frac{{{{\tau }_{{s,rr}}}}}{r}} dr + 3\int\limits_{{{R}_{2}}}^\infty {\frac{{{{\tau }_{{l,rr}}}}}{r}} dr \\ \end{gathered} $

Запишем граничные условия между движущимися средами при учете сил поверхностного натяжения [20]

(1.4)
${{p}_{s}}({{R}_{1}},t) - {{p}_{g}}({{R}_{1}},t) + \frac{{2{{\sigma }_{1}}}}{{{{R}_{1}}}} = {{\tau }_{{s,rr}}}({{R}_{1}},t) - {{\tau }_{{g,rr}}}({{R}_{1}},t)$
(1.5)
${{p}_{l}}({{R}_{2}},t) - {{p}_{s}}({{R}_{2}},t) + \frac{{2{{\sigma }_{2}}}}{{{{R}_{2}}}} = {{\tau }_{{l,rr}}}({{R}_{2}},t) - {{\tau }_{{s,rr}}}({{R}_{2}},t)$
где σ – коэффициент поверхностного натяжения. Если касательные напряжения отсутствуют $\tau = 0$, то имеет место простое уравнение Лапласа [20, 21]. Компоненты тензора напряжений для жидкости и газа задаются следующим образом

(1.6)
${{\tau }_{{l,rr}}} = 2{{\mu }_{l}}\frac{{\partial u}}{{\partial r}}$, ${{\tau }_{{g,rr}}} = 2{{\mu }_{g}}\frac{{\partial u}}{{\partial r}}$

Здесь µ – динамическая вязкость. Отметим, что величина ${{\tau }_{{g,rr}}}$ по порядку меньше чем ${{\tau }_{{l,rr}}}$, поскольку вязкость газа меньше вязкости жидкости, поэтому в дальнейшем данной величиной можно пренебречь.

Тензор напряжений для вязкоупругой оболочки зададим следующим соотношением [16]:

(1.7)
${{\tau }_{{s,rr}}} = - 4(R_{1}^{2}{\text{/}}{{r}^{3}})[{{G}_{s}}({{R}_{1}} - {{R}_{{e1}}}) + {{\mu }_{s}}{{\dot {R}}_{1}}]$
${{R}_{{e1}}} = {{R}_{{10}}}(1 + Z)$, $Z = \frac{1}{{4{{G}_{s}}}}\frac{{R_{{20}}^{3}}}{{{{V}_{s}}}}\left( {\frac{{2{{\sigma }_{1}}}}{{{{R}_{{10}}}}} + \frac{{2{{\sigma }_{2}}}}{{{{R}_{{20}}}}}} \right)$, ${{V}_{s}} = R_{{20}}^{3} - R_{{10}}^{3}$

С учетом (1.4)–(1.7) после алгебраических преобразований уравнение (1.3) окончательно примет вид

(1.8)
$\begin{gathered} {{\rho }_{s}}{{R}_{1}}\ddot {R}_{1}^{{}}\left( {1 + \frac{{{{\rho }_{l}} - {{\rho }_{s}}}}{{{{\rho }_{s}}}}\frac{{{{R}_{1}}}}{{{{R}_{2}}}}} \right) + {{\rho }_{s}}\dot {R}_{1}^{2}\left( {\frac{3}{2} + \frac{{{{\rho }_{l}} - {{\rho }_{s}}}}{{{{\rho }_{s}}}}\frac{{4R_{2}^{3} - R_{1}^{3}}}{{2R_{2}^{3}}}\frac{{{{R}_{1}}}}{{{{R}_{2}}}}} \right) = \\ = \;{{P}_{g}} - {{P}_{l}} - \frac{{2{{\sigma }_{1}}}}{{{{R}_{1}}}} - \frac{{2{{\sigma }_{2}}}}{{{{R}_{2}}}} - 4\frac{{\dot {R}_{1}^{{}}}}{{{{R}_{1}}}}\left( {\frac{{{{V}_{s}}{{\mu }_{s}} + R_{1}^{3}{{\mu }_{l}}}}{{R_{2}^{3}}}} \right) - \frac{{4{{V}_{s}}{{G}_{s}}}}{{R_{2}^{3}}}\left( {1 - \frac{{{{R}_{{e1}}}}}{{{{R}_{1}}}}} \right) \\ \end{gathered} $

Отметим, что данное модифицированное уравнение Релея–Плессета с учетом вязкоупругой оболочки пузырьков впервые было получено в работе [16].

Линеаризуем данное уравнение (1.8): $\psi = {{\psi }_{0}} + \psi '$, $\psi ' \ll {{\psi }_{0}}$ $\psi = {{R}_{1}}$, ${{R}_{2}}$, P. Учитывая условие несжимаемости оболочки $R_{1}^{2}{{\dot {R}}_{1}} = R_{2}^{2}\dot {R}_{2}^{{}}$ [22], находим связь между возмущениями $R_{{20}}^{2}R_{2}^{'} = R_{{10}}^{2}R_{1}^{'}$. После необходимых математических действий линеаризованное уравнение (1.8) запишется в виде

(1.9)
${{R}_{*}}\frac{{\partial w_{R}^{'}}}{{\partial t}} + \frac{4}{{{{R}_{{{\text{**}}}}}}}w_{R}^{'} = \frac{{P_{g}^{'} - P_{l}^{'}}}{{{{\rho }_{s}}}} - XR_{1}^{'},\quad w_{R}^{'} = \frac{{\partial R_{1}^{'}}}{{\partial t}}$,
${{R}_{*}} = {{R}_{{10}}}\left( {1 + \frac{{{{\rho }_{l}} - {{\rho }_{s}}}}{{{{\rho }_{s}}}}\frac{{{{R}_{{10}}}}}{{{{R}_{{20}}}}}} \right)$, ${{R}_{{{\text{**}}}}} = \frac{{{{\rho }_{s}}{{R}_{{10}}}R_{{20}}^{3}}}{{{{V}_{s}}{{\mu }_{s}} + R_{{10}}^{3}{{\mu }_{l}}}}$
$X = \frac{1}{{{{\rho }_{s}}}}\left( {\frac{{4{{G}_{s}}{{V}_{s}}{{R}_{{e1}}}}}{{R_{{10}}^{2}R_{{20}}^{3}}} - \frac{{12{{G}_{s}}{{V}_{s}}R_{{10}}^{2}}}{{R_{{20}}^{6}}}\left( {1 - \frac{{{{R}_{{e1}}}}}{{{{R}_{{10}}}}}} \right) - \frac{{2{{\sigma }_{1}}}}{{R_{{10}}^{2}}} - \frac{{2{{\sigma }_{2}}R_{{10}}^{2}}}{{R_{{20}}^{4}}}} \right)$

Если упругая оболочка пузырьков отсутствует и не учитывается поверхностное натяжение, т.е. ${{R}_{{20}}} = {{R}_{{10}}}$, ${{\rho }_{l}} = {{\rho }_{s}}$, ${{\sigma }_{1}} = {{\sigma }_{2}} = 0$, то уравнение Релея принимает стандартный вид.

Для исследования распространения акустических волн в пузырьковой смеси запишем линеаризованные уравнения сохранения массы, количества пузырьков, энергии, а также уравнение состояния согласно [10] в простейшем монодисперсном случае

(1.10)
$\begin{gathered} {{\alpha }_{l}}\frac{{\partial \rho _{l}^{'}}}{{\partial t}} + {{\rho }_{l}}\frac{{\partial \alpha _{l}^{'}}}{{\partial t}} + {{\rho }_{l}}\frac{{\partial v_{l}^{'}}}{{\partial x}} = 0,\quad {{\alpha }_{g}}\frac{{\partial \rho _{g}^{'}}}{{\partial t}} + {{\rho }_{g}}\frac{{\partial \alpha _{g}^{'}}}{{\partial t}} + {{\rho }_{g}}\frac{{\partial v_{L}^{'}}}{{\partial x}} = 0 \\ \frac{{\partial n'}}{{\partial t}} + {{n}_{0}}\frac{{\partial v_{l}^{'}}}{{\partial x}} = 0,\quad \alpha _{g}^{'} = \frac{{{{\alpha }_{g}}}}{{{{n}_{0}}}}n' + \frac{{3{{\alpha }_{g}}}}{{{{R}_{{10}}}}}R_{1}^{'},\quad \alpha _{l}^{'} + \alpha _{g}^{'} = 0 \\ \frac{{\partial P_{g}^{'}}}{{\partial t}} = - 3{{\gamma }_{g}}{{P}_{g}}\frac{{\dot {R}_{1}^{'}}}{{{{R}_{{10}}}}} + 3({{\gamma }_{g}} - 1)\frac{q}{{{{R}_{{10}}}}} \\ \end{gathered} $
$q = i\omega {{R}_{{10}}}P_{g}^{'}\frac{{y{\text{cth}}y - 1}}{{{{y}^{2}}}}$, $y = \sqrt { - \frac{{i\omega R_{{10}}^{2}}}{{{{\kappa }_{g}}}}} $
$\frac{{\partial R_{1}^{'}}}{{\partial t}} = w_{R}^{'} + w_{A}^{'}$, $w_{A}^{'} = \frac{{P_{g}^{'} - P_{l}^{'}}}{{{{\rho }_{l}}{{C}_{l}}\alpha _{g}^{{1/6}}}}$
$P_{l}^{'} = C_{l}^{2}\rho _{l}^{'}$, $\frac{{P_{g}^{'}}}{{{{P}_{0}}}} = \frac{{\rho _{g}^{'}}}{{{{\rho }_{g}}}} + \frac{{T_{g}^{'}}}{{{{T}_{0}}}}$

Система уравнений (1.9), (1.10) замкнута. Подчеркнем, что упругая сферическая оболочка учитывается при радиальных пульсациях пузырьков лишь в уравнении Релея–Плессета (1.9).

Исследуем решения полученной системы уравнений, имеющие вид гармонических волн для возмущений $\varphi '$, где $\varphi ' = \rho _{l}^{'}$, $\rho _{g}^{'}$, $v_{l}^{'}$, $R_{1}^{'}$ …

(1.11)
$\varphi ' = {{A}_{\varphi }}\exp [i({{K}_{*}}x - \omega t)],\quad {{K}_{*}} = K + i{{K}_{{{\text{**}}}}},\quad {{C}_{p}} = \omega {\text{/}}K,\quad {{i}^{2}} = - 1$

В результате подстановки (1.11) в систему (1.9), (1.10) имеем систему линейных алгебраических уравнений относительно неизвестных амплитуд ${{A}_{\varphi }}$. Исключая неизвестные амплитуды и из условия существования у линейной системы уравнений нетривиального решения, получено следующее дисперсионное соотношение

(1.12)
${{\left( {\frac{{{{K}_{*}}}}{\omega }} \right)}^{2}} = \frac{1}{{C_{f}^{2}}} + \frac{{3{{\alpha }_{g}}{{\alpha }_{l}}{{\rho }_{l}}Q}}{{3{{\gamma }_{g}}{{P}_{0}} - QS}},\quad {{C}_{f}} = \frac{{{{C}_{l}}}}{{{{\alpha }_{l}}}}$
$Q = 1 + 3({{\gamma }_{g}} - 1)\frac{{y{\text{cth}}y - 1}}{{{{y}^{2}}}}$, $y = \sqrt { - \frac{{i\omega R_{{10}}^{2}}}{{{{\kappa }_{g}}}}} $, $S = \frac{{{{\rho }_{s}}{{\rho }_{l}}R_{{10}}^{2}(i\omega {{R}_{*}}h - X)}}{{{{\rho }_{l}}{{R}_{{10}}} + {{\rho }_{s}}{{R}_{*}}hz}}$
$h = - i\omega + \frac{1}{\tau }$, $\tau = \frac{{{{R}_{*}}{{R}_{{*{\text{*}}}}}}}{4}$, $z = \frac{{{{R}_{{10}}}}}{{{{C}_{l}}\alpha _{g}^{{1/6}}}}$

При предельном переходе $\omega \to 0$ из дисперсионного соотношения (1.12) получено выражение равновесной скорости звука

(1.13)
$\frac{1}{{C_{e}^{2}}} = \frac{1}{{C_{f}^{2}}} + \frac{{3{{\alpha }_{g}}{{\alpha }_{l}}{{\rho }_{l}}({{\rho }_{l}}{{R}_{{10}}}{{R}_{{{\text{**}}}}} + 4z{{\rho }_{s}})}}{{3{{P}_{0}}{{\gamma }_{g}}({{\rho }_{l}}{{R}_{{10}}}{{R}_{{{\text{**}}}}} + 4z{{\rho }_{s}}) + R_{{10}}^{2}X{{\rho }_{l}}{{\rho }_{s}}{{R}_{{{\text{**}}}}}}}$

В случае отсутствия упругой оболочки пузырьков равновесная скорость звука принимает известное выражение [1]

(1.14)
$\frac{1}{{C_{e}^{2}}} = \frac{1}{{C_{f}^{2}}} + \frac{{{{\alpha }_{g}}{{\alpha }_{l}}{{\rho }_{l}}}}{{{{P}_{0}}{{\gamma }_{g}}}}$

Сравнив выражения (1.13) и (1.14), делаем вывод о том, что для пузырьков без оболочки равновесная скорость звука не зависит от частоты возмущений и размера пузырьков, в то время как для покрытых пузырьков может наблюдаться обратная ситуация. Дело в том, что вязкость материала ${{\mu }_{s}}$ и модуль упругости ${{G}_{s}}$, вообще говоря, могут зависеть от частоты возмущений.

При предельном переходе $\omega \to \infty $ в соотношении (1.12) фазовая скорость стремится к скорости звука в несущей фазе.

Асимптотика коэффициента затухания, справедливая на низких частотах $\omega \tau \ll 1$, имеет вид

(1.15)
$K_{{**}}^{{(0)}}(\omega ) = \frac{{{{C}_{e}}}}{2}\frac{{3R_{{10}}^{2}{{R}_{*}}{{\alpha }_{g}}{{\alpha }_{l}}\rho _{l}^{2}{{\rho }_{s}}\xi }}{{{{{(3{{P}_{0}}z{{\gamma }_{g}}{{\rho }_{s}}{{R}_{*}} + \phi )}}^{2}}}}{{\omega }^{2}}$
$\xi = {{R}_{{10}}}\tau {{\rho }_{l}} + {{\rho }_{s}}z({{R}_{*}} - X{{\tau }^{2}})$, $\phi = {{R}_{{10}}}\tau {{\rho }_{l}}(3{{P}_{0}}{{\gamma }_{g}} + {{R}_{{10}}}X{{\rho }_{s}})$

2. РЕЗУЛЬТАТЫ РАСЧЕТОВ

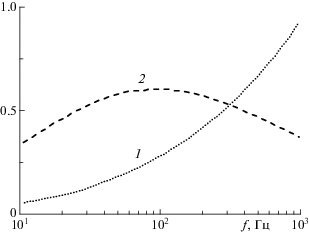
В работе [23] приведены экспериментальные данные для зависимости коэффициента затухания от частоты возмущений в смеси воды с воздушными шариками, покрытые резиновой оболочкой. Температура воды ${{T}_{0}} = 303$ К, давление ${{P}_{0}} = 1.21 \times {{10}^{5}}$ Па. Радиусы шаров составляли примерно 6 и 8 см, толщина резиновой оболочки – 1.6 мм, плотность ${{\rho }_{s}} = 1476$ кг/м3, а объемное содержание газа менялось от 0.005 до 0.02. Частотные зависимости модуля сдвига и вязкости резины приведены в [23] и представлены на рис. 2.

Рис. 2.

Частотные зависимости модуля сдвига (1) и вязкости резины (2): 1 – ${{G}_{s}}{\text{/}}20$ МПа, 2 – ${{\mu }_{s}}{\text{/}}6$ кПа ⋅ с

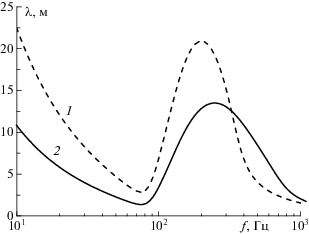
Для применения континуальной модели необходимо выполнение следующих условий: 1) длина волны должна быть намного больше размеров включений; 2) объемное содержание включений мало, ${{\alpha }_{g}} \ll 1$. Второе условие в эксперименте очевидно выполняется. Чтобы проверить выполнение первого условия, на рис. 3 представлены зависимости длины волны $\lambda = {{C}_{p}}{\text{/}}f$ от частоты возмущений при минимальном и максимальном объемном газосодержании в эксперименте. Видно, что при наименьшем значении объемного содержания включений длина волны изменяется от 2.8 до 22 м, а при наибольшем значении – от 1.3 до 13.5 м.

Рис. 3.

Зависимости длины волны от частоты возмущений при ${{R}_{{10}}} = 0.0796$ м, ${{R}_{s}} = {{R}_{{20}}} - {{R}_{{10}}} = 0.0016$ м: 1, 2 – ${{\alpha }_{g}} = 0.0047$, 0.021

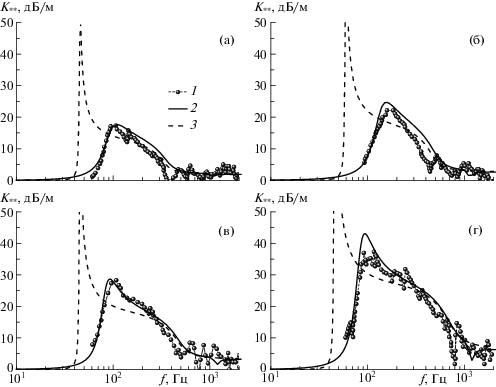
В целом условие $\lambda \gg {{R}_{{10}}}$ выполняется, поэтому можно применить полученную теорию к результатам эксперимента [23], рис. 4. Здесь 1 – экспериментальные данные, теоретическая кривая 2 рассчитана по формуле (1.12) с учетом упругой оболочки пузырьков, теоретическая кривая 3 без учета упругой оболочки пузырьков. Напомним, что в окрестности резонансной частоты пузырьков, которая может быть определена по формуле Миннаэрта

${{f}_{0}} = \frac{1}{{2\pi {{R}_{{10}}}}}\sqrt {\frac{{3{{\gamma }_{g}}{{P}_{0}}}}{{{{\rho }_{L}}}}} $
наблюдается максимум коэффициента затухания (кривая 3). Наличие упругой оболочки пузырьков приводит к смещению данного максимума в сторону увеличения частоты возмущений (кривая 2), что хорошо подтверждается экспериментальными данными. Взяв производную от правой части выражения (1.12) и решив задачу на экстремум, находим критическое значение частоты

$f_{0}^{2} = \frac{1}{{{{R}_{*}}}}\left( {\frac{{3{{\gamma }_{g}}{{P}_{0}}}}{{{{\rho }_{s}}{{R}_{{10}}}}} + X} \right)$
Рис. 4.

Сравнение зависимостей коэффициента затухания от частоты возмущений с экспериментальными данными [23]: (а) ${{\alpha }_{g}} = 0.0047$, ${{R}_{{10}}} = 0.0796$ м; (б) ${{\alpha }_{g}} = 0.0053$, ${{R}_{{10}}} = 0.0608$ м; (в) ${{\alpha }_{g}} = 0.0094$, ${{R}_{{10}}} = 0.0796$ м; (г) ${{\alpha }_{g}} = 0.021$, ${{R}_{{10}}} = 0.0796$ м; 1 – данные эксперимента [23]; 2, 3 – расчет по (1.12) с учетом и без учета упругой оболочки пузырьков

Далее подставив выражения для ${{R}_{*}}$ и X, получим

$f_{0}^{2} = \frac{1}{{{{\rho }_{s}}R_{{10}}^{2}\eta }}\left( {3{{\gamma }_{g}}{{P}_{0}} - \frac{{2{{\sigma }_{1}}}}{{{{R}_{{10}}}}} - \frac{{2{{\sigma }_{2}}R_{{10}}^{3}}}{{R_{{20}}^{4}}} + \frac{{4{{V}_{s}}{{G}_{s}}}}{{R_{{20}}^{3}}}\left( {1 + Z\left( {1 + \frac{{3R_{{10}}^{3}}}{{R_{{20}}^{3}}}} \right)} \right)} \right)$
$\eta = 1 + \frac{{{{\rho }_{l}} - {{\rho }_{s}}}}{{{{\rho }_{s}}}}\frac{{{{R}_{{10}}}}}{{{{R}_{{20}}}}}$

При отсутствии упругой оболочки пузырьков формула (2.2) переходит в (2.1). Еще один важный вывод, который можно сделать из рис. 4, состоит в том, что наличие упругой оболочки приводит к уменьшению максимума коэффициента затухания. Очевидно, резиновая оболочка замедляет радиальные колебания пузырьков и происходит меньшее рассеяние акустической волны. Несмотря на некоторый разброс экспериментальных данных, теоретические результаты удовлетворительно описывают эксперимент.

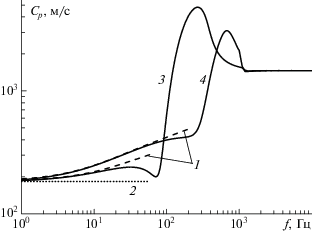
На рис. 5 даны зависимости фазовой скорости от частоты возмущений при разных значениях радиуса пузырьков и представлены низкочастотные асимптотики по формулам (1.13) и (1.14). Как следует из фигуры и сравнения (1.13) и (1.14), делаем вывод о том, что для пузырьков без оболочки равновесная скорость звука не зависит от частоты возмущений и размера пузырьков (линия 2), а для покрытых пузырьков может наблюдаться обратная ситуация (монотонно возрастающая кривая 1). Здесь равновесная скорость заметно зависит от размера пузырьков, а также вязкости оболочки и модуля сдвига, которые в свою очередь зависят от частоты возмущений (рис. 2). Таким образом, акустика жидкости с покрытыми пузырьками существенно различна при низких и умеренных частотах.

Рис. 5.

Частотные зависимости фазовой скорости и ее низкочастотные асимптотики с учетом (1) и без учета (2) упругой оболочки; 3 – ${{R}_{{10}}} = 0.0796$ м; 4 – ${{R}_{{10}}} = 0.0396$ м, ${{\alpha }_{g}} = 0.005$

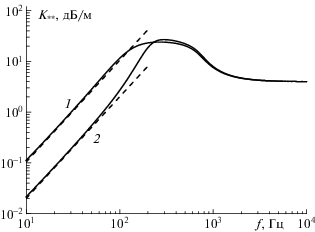
На рис. 6 представлены зависимости коэффициента затухания от частоты возмущений при разных значениях модуля сдвига материала и проиллюстрированы низкочастотные асимптотики по формуле (1.15). Приняв во внимание формулу (2.2), из рис. 6 следует, что увеличение модуля сдвига приводит к смещению резонансной частоты в сторону увеличения частоты возмущений. Исходя из асимптотики (1.15) коэффициент затухания при низких частотах пропорционален квадрату частоты возмущений, а также равновесной скорости звука, и существенно зависит от параметров материала оболочки пузырьков.

Рис. 6.

Зависимости коэффициента затухания от частоты возмущений и ее низкочастотные асимптотики при ${{\mu }_{s}} = 3.5 \times {{10}^{3}}$ Па ⋅ с, ${{R}_{{10}}} = 0.0396$ м: 1, 2 – ${{G}_{s}} = {{10}^{6}}$, $5 \times {{10}^{6}}$

ЗАКЛЮЧЕНИЕ

Получено, что для пузырьков без оболочки равновесная скорость звука не зависит от частоты возмущений и размера пузырьков, в то время для покрытых пузырьков установлена зависимость равновесной скорости звука от частоты возмущений, размера пузырьков и параметров оболочки.

Установлено, что учет вязкоупругой оболочки пузырьков приводит к увеличению резонансной частоты возмущений, что хорошо подтверждается экспериментальными данными.

Показано, что коэффициент затухания на низких частотах для рассматриваемой смеси пропорционален квадрату частоты возмущений, равновесной скорости звука, и во многом зависит от размера и параметров оболочки пузырьков.

Исследование выполнено за счет гранта Российского научного фонда (проект № 15-11-10016).

Список литературы

  1. Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987.

  2. Накоряков В.Е., Покусаев Б.Г., Шрейбер И.Р. Волновая динамика газо- и парожидкостных сред. М.: Энергоатомиздат, 1990.

  3. Leighton T.G. The Acoustic Bubble. London: Acad. London, 1994.

  4. Temkin S. Suspension Acoustics: An Introduction to the Physics of Suspensions. Cambridge: Univ. Press, 2005.

  5. Wilson P.S., Roy R.A., Carey W.M. Phase speed and attenuation in bubbly liquids inferred from impedance measurements near the individual bubble resonance frequency // J. Acoust. Soc. Amer. 2005. V. 117. № 4. P. 1895–1910.

  6. Duro V., Rajaona D.R., Decultot D., Maze G. Experimental study of sound propagation through bubbly water: comparison with optical measurements // IEEE J. Oceanic Engineering. 2011. V. 36. № 1. P. 114–125.

  7. Leroy V., Strybulevych A., Page J.H., Scanlon M.G. Sound velocity and attenuation in bubbly gels measured by transmission experiments // J. Acoust. Soc. Amer. 2008. V. 123. № 4. P. 1931–1940.

  8. Commander K.W., Prosperetti A. Linear pressure waves in bubbly liquids: Comparison between theory and experiments // J. Acoust. Soc. Amer. 1989. V. 85. № 2. P. 732–746.

  9. Chung N.M., Lin W.K. Sound velocity and its relationship with interfacial area density in a steam/water, two-phase bubbly flow // Flow Measurements and Instrumentation. 1992. V. 3. № 2. P. 65–71.

  10. Губайдуллин Д.А., Федоров Ю.В. Звуковые волны в двухфракционных полидисперсных пузырьковых средах // ПММ. 2013. Т. 77. № 5. С. 743–753.

  11. Вараксин А.Ю. Гидрогазодинамика и теплофизика двухфазных потоков: проблемы и достижения // ТВТ. 2013. Т. 51. № 3. С. 421–455.

  12. Prosperetti A. Vapor bubbles // Annu. Rev. Fluid Mech. 2017. V. 49. P. 221–248.

  13. Goldberg B.B., Raichlen J.S., Editors F.F. Ultrasound contrast agents. Basic principles and clinical applications. Martin Dunitz, 2001.

  14. Sboros V. Response of contrast agents to ultrasound // Advanced Drug Delivery Reviews. 2008. V. 60. P. 1117–1136.

  15. Ma X., Wang X., Hahn K., Sanchez S. Motion control of urea-powered biocompatible hollow microcapsules // ACS Nano. 2016. V. 10. P. 3597–3605.

  16. Church C.C. The effects of an elastic solid surface layer on the radial pulsations of gas bubbles // J. Acoust. Soc. Amer. 1995. V. 97. № 3. P. 1510–1521.

  17. Hoff L., Sontum P.C., Hovem J.M. Oscillations of polymeric microbubbles: Effects of the encapsulating shell // J. Acoust. Soc. Amer. 2000. V. 107. № 4. P. 2272–2280.

  18. Алексеев В.Н., Рыбак С.А. Колебания газовых пузырьков в упругих средах // Акуст. журн. 1999. Т. 45. № 5. С. 603–609.

  19. Khismatullin D.B., Nadim A. Radial oscillations of encapsulated microbubbles in viscoelastic liquids // Phys. Fluids. 2002. V. 14. № 10. P. 3534–3557.

  20. Ландау Л.Д., Лившиц Е.М. Теоретическая физика. Т. VI. Гидродинамика, М.: Наука, 1988.

  21. Петров А.Г. Аналитическая гидродинамика. М.: Физматлит, 2010. 520 с.

  22. Coulouvrat F., Thomas J.L., Astafyeva K., Taulier N., Conoir J.M., Urbach W. A model for ultrasound absorption and dispersion in dilute suspensions of nanometric contrast agents // J. Acoust. Soc. Amer. 2012. V. 136. № 6. P. 3748–3759.

  23. Lee K.M., Wilson P.S., Wochner M.S. Attenuation of low-frequency underwater sound using an array of air-filled balloons and comparison to effective medium theory // J. Acoust. Soc. Amer. 2017. V. 142. № 6. P. 3443–3449.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал