Известия РАН. Механика твердого тела, 2022, № 3, стр. 142-152
МЕХАНИКА ДЕФОРМИРОВАНИЯ ПОЛОГОЙ ОБОЛОЧКИ
a МГТУ им Н.Э. Баумана
Москва, Россия
* E-mail: yuvino@rambler.ru
Поступила в редакцию 05.10.2020
После доработки 20.11.2020
Принята к публикации 28.01.2021
- EDN: AQSHHY
- DOI: 10.31857/S0572329922030126
Аннотация
Уравнения с частными производными механики деформирования пологой оболочки декомпозицией, разделением переменных, приводятся к обыкновенным и уравнениям связи их в точке пересечения независимых переменных. Решения однородных обыкновенных дифференциальных уравнений определяются матричными сходящимися рядами. Они удовлетворяют произвольным начальным условиям. Это позволяет исключить из решений постоянные интегрирования. Решения устанавливают связь между величинами, характеризующими состояния сечений оболочки, в том числе и на краях, необходимые для задания краевых условий. Для декомпозиции и моделирования поверхностной нагрузки наносится сетка на элементе оболочки. Параметрические исследования при сгущении сетки показали быструю сходимость решения.
Введение. Актуальной проблемой является решение задач механики деформирования элементов пластин и оболочек [1–4] в тех случаях, когда не удается методом Фурье разделить переменные в уравнениях с частными производными и упростить задачу решением обыкновенных дифференциальных уравнений [5, 6]. Проблема преодолевается решением уравнений с частными производными с контролируемой погрешностью. Закладываются основы построения конечных элементов оболочек, на которых математические модели их деформирования решаются с контролируемой погрешностью. Таким образом, становится возможным построения алгоритмов решения задач механики деформирования тонкостенных конструкций с определением мест концентрации напряжений и их максимальных значений, что необходимо при решении задач прочности, например, летательных аппаратов. В работе представлена методика решения краевых задач механики деформирования пологой оболочки двоякой кривизны. Методика основана на решении линейных обыкновенных дифференциальных уравнений удовлетворяющих произвольным начальным условиям. Вероятно, впервые такое решение было получено А.Н. Крыловым методом Коши [7]. Декомпозицией [8] уравнения с частными производными механики деформирования пологой оболочки приводятся к обыкновенным и алгебраическим уравнениям их связи. Решения однородных обыкновенных дифференциальных уравнений и частные решения для их правых частей получены на основе известных работ [9–12] в виде формул. Они опубликованы в работах [13–15]. Построен и реализован алгоритм решения на ЭВМ краевой задачи механики деформирования элемента пологой защемленной по краям оболочки при поверхностном давлении.
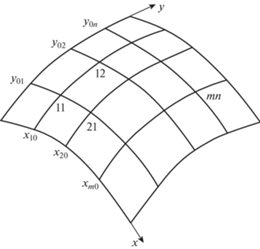
1. Реализация. Рассматривается пологая оболочка двоякой кривизны, прямоугольная в плане, контур которой образован меридианами и параллелями, параллельными линиям главных кривизн (рис. 1). В качестве математической модели механики деформирования оболочки используются общие разрешающие уравнения оболочки двоякой кривизны в перемещениях:
(1.1)
$\begin{gathered} \frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \frac{{1 - \mu }}{2}\frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} + \frac{{1 + \mu }}{2}\frac{{{{\partial }^{2}}{v}}}{{\partial x\partial y}} + \left( {\frac{1}{{{{r}_{1}}}} + \frac{\mu }{{{{r}_{2}}}}} \right)\frac{{\partial w}}{{\partial x}} = \frac{{{{q}_{1}}}}{{\bar {B}}} \\ \frac{{1 + \mu }}{2}\frac{{{{\partial }^{2}}u}}{{\partial x\partial y}} + \frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}} + \frac{{1 - \mu }}{2}\frac{{{{\partial }^{2}}{v}}}{{\partial {{x}^{2}}}} + \left( {\frac{1}{{{{r}_{1}}}} + \frac{\mu }{{{{r}_{2}}}}} \right)\frac{{\partial w}}{{\partial y}} = \frac{{{{q}_{2}}}}{{\bar {B}}} \\ \frac{{12}}{{{{h}^{2}}}}\left( {\frac{1}{{{{r}_{1}}}} + \frac{\mu }{{{{r}_{2}}}}} \right)\frac{{\partial u}}{{\partial x}} + \frac{{12}}{{{{h}^{2}}}}\left( {\frac{1}{{{{r}_{2}}}} + \frac{\mu }{{{{r}_{1}}}}} \right)\frac{{\partial {v}}}{{\partial y}} \\ + \frac{{12}}{{{{h}^{2}}}}\left( {\frac{1}{{r_{1}^{2}}} + \frac{1}{{r_{2}^{2}}} + \frac{{2\mu }}{{{{r}_{1}}{{r}_{2}}}}} \right)w + \frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + 2\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{2}}\partial {{y}^{2}}}} + \frac{{{{\partial }^{4}}w}}{{\partial {{y}^{4}}}} = \frac{{{{q}_{3}}}}{D} \\ \end{gathered} $Методом декомпозиции [8] система уравнений в частных производных (1.1) приводится к следующей системе дифференциальных уравнений:
(1.2)
$\begin{gathered} \frac{{1 - \mu }}{2}\frac{{{{\partial }^{2}}{v}_{2}^{{(1)}}}}{{\partial {{x}^{2}}}} = f_{2}^{{(1)}}(x,y) \\ \frac{{{{\partial }^{2}}{v}_{2}^{{(2)}}}}{{\partial {{y}^{2}}}} + \left( {\frac{1}{{{{r}_{1}}}} + \frac{\mu }{{{{r}_{2}}}}} \right)\frac{{\partial w_{2}^{{(2)}}}}{{\partial y}} = f_{2}^{{(2)}}(x,y) \\ \frac{{1 + \mu }}{2}\frac{{\partial \left[ {\frac{{\partial u_{2}^{{(3)}}}}{{\partial y}}} \right]}}{{\partial y}} = f_{2}^{{(3)}}(x,y) \\ \end{gathered} $(1.3)
$\begin{gathered} \frac{{{{q}_{1}}}}{{\bar {B}}} = f_{1}^{{(1)}}(x,y) + f_{1}^{{(2)}}(x,y) + f_{1}^{{(3)}}(x,y) \\ \frac{{{{q}_{2}}}}{{\bar {B}}} = f_{2}^{{(1)}}(x,y) + f_{2}^{{(2)}}(x,y) + f_{2}^{{(3)}}(x,y) \\ \frac{{{{q}_{3}}}}{{\bar {B}}} = f_{3}^{{(1)}}(x,y) + f_{3}^{{(2)}}(x,y) + f_{3}^{{(3)}}(x,y) \\ u_{1}^{{(1)}} = u_{3}^{{(1)}},\quad \frac{{\partial u_{3}^{{(1)}}}}{{\partial x}} = \frac{{\partial u_{2}^{{(3)}}}}{{\partial x}} \\ {v}_{2}^{{(1)}} = {v}_{2}^{{(1)}},\quad \frac{{\partial {v}_{3}^{{(1)}}}}{{\partial y}} = \frac{{\partial {v}_{2}^{{(2)}}}}{{\partial y}} \\ w_{1}^{{(1)}} = w_{3}^{{(1)}},\quad \frac{{{{\partial }^{2}}w_{3}^{{(3)}}}}{{\partial {{y}^{2}}}} = \frac{{{{\partial }^{2}}u_{2}^{{(3)}}}}{{\partial {{y}^{2}}}} \\ \end{gathered} $В системе уравнений (1.2) $f_{1}^{{\left( 1 \right)}}(x,y) \ldots f_{3}^{{\left( 3 \right)}}(x,y)$ – неизвестные функции, введенные при декомпозиции. Эти функции подлежат определению путем удовлетворения уравнений связи (1.3). Проанализируем уравнения системы (1.2).
Первое, четвертое и седьмое и уравнение системы (1.2) – уравнения в частных производных, содержащие производные только по x. Эти уравнения будем рассматривать как обыкновенные дифференциальные уравнения (ОДУ) с параметром y.
Второе, пятое и восьмое уравнение системы (1.2) – уравнения в частных производных, содержащее производные только по y. Аналогично, рассматриваем эти уравнения как ОДУ с параметром х.
Третье, шестое и девятое уравнение – уравнения со смешанными производными. Эти уравнения будем рассматривать как ОДУ с параметром, но не относительно искомой функции, а относительно одной из производных. Так на примере третьего уравнения $\frac{{1 + {{\mu }}}}{2}\frac{{{{\partial }^{2}}{v}_{1}^{{\left( 3 \right)}}}}{{\partial x\partial y}} = f_{1}^{{\left( 3 \right)}}(x,y)$ записано как $\frac{{\partial \left[ {\frac{{\partial {v}_{1}^{{\left( 3 \right)}}}}{{\partial y}}} \right]}}{{\partial x}} = \frac{2}{{1 + {{\mu }}}}f_{1}^{{\left( 3 \right)}}(x,y)$. Оно будет решено относительно $\frac{{\partial {v}_{1}^{{\left( 3 \right)}}}}{{\partial y}}$. В свою очередь ${v}_{1}^{{\left( 3 \right)}}$ определять из этого уравнения не будем, знания лишь величины $\frac{{\partial {v}_{1}^{{\left( 3 \right)}}}}{{\partial y}}$ достаточно для предлагаемого удовлетворения уравнениям связи.
Разобъем сторону оболочки вдоль оси Ox на m + 1 интервалов точками x10, x20, …, xm0, а сторону оболочки вдоль оси Oy на n + 1 интервалов точками y01, y02, … , y0n (рис. 1). Эти точки для значений параметров указанных выше ОДУ.
Далее нанесем сетку меридианов и параллелей через выбранные точки. Вдоль каждого меридиана и параллели теперь можно записать ОДУ с дифференцированием по $x$ или по $y$ соответственно. Меридианы и параллели пересекаются в точках. В точках пересечения меридианов и параллелей будем выполнять уравнения связи (1.3), в точках контура оболочки – краевые условия.
Для каждой точки (на контуре и на пересечении меридианов и параллелей) запишем по столбцу, содержащему перемещения и производные от них:
(1.4)
${{{\mathbf{w}}}_{{xij}}} = {{\left\| {\begin{array}{*{20}{c}} {u_{{3ij}}^{{\left( 1 \right)}}}&{{{{\frac{{\partial u_{3}^{{\left( 1 \right)}}}}{{\partial x}}}}_{{ij}}}}&{{v}_{{2ij}}^{{\left( 1 \right)}}}&{{{{\frac{{\partial {v}_{2}^{{\left( 1 \right)}}}}{{\partial x}}}}_{{ij}}}}&{{{{\frac{{\partial {v}_{1}^{{\left( 3 \right)}}}}{{\partial y}}}}_{{ij}}}}&{w_{{3ij}}^{{\left( 1 \right)}}}&{{{{\frac{{\partial w_{3}^{{\left( 1 \right)}}}}{{\partial x}}}}_{{ij}}}}&{{{{\frac{{{{\partial }^{2}}w_{3}^{{\left( 1 \right)}}}}{{\partial {{x}^{2}}}}}}_{{ij}}}}&{{{{\frac{{{{\partial }^{3}}w_{3}^{{\left( 1 \right)}}}}{{\partial {{x}^{3}}}}}}_{{ij}}}}&{{{{\frac{{{{\partial }^{2}}w_{3}^{{\left( 3 \right)}}}}{{\partial {{y}^{2}}}}}}_{{ij}}}}&{{{{\frac{{{{\partial }^{3}}w_{3}^{{\left( 3 \right)}}}}{{\partial {{y}^{2}}\partial x}}}}_{{ij}}}} \end{array}} \right\|}^{T}}$(1.5)
${{{\mathbf{w}}}_{{yij}}} = {{\left\| {\begin{array}{*{20}{c}} {u_{{1ij}}^{{\left( 1 \right)}}}&{{{{\frac{{\partial u_{1}^{{\left( 2 \right)}}}}{{\partial y}}}}_{{ij}}}}&{{{{\frac{{\partial u_{2}^{{\left( 3 \right)}}}}{{\partial x}}}}_{{ij}}}}&{{v}_{{2ij}}^{{\left( 2 \right)}}}&{{{{\frac{{\partial {v}_{2}^{{\left( 2 \right)}}}}{{\partial y}}}}_{{ij}}}}&{w_{{3ij}}^{{\left( 2 \right)}}}&{{{{\frac{{\partial w_{3}^{{\left( 2 \right)}}}}{{\partial y}}}}_{{ij}}}}&{{{{\frac{{{{\partial }^{2}}w_{3}^{{\left( 2 \right)}}}}{{\partial {{y}^{2}}}}}}_{{ij}}}}&{{{{\frac{{{{\partial }^{3}}w_{3}^{{\left( 2 \right)}}}}{{\partial {{y}^{3}}}}}}_{{ij}}}} \end{array}} \right\|}^{T}}$Комбинированием производных, входящих в столбцы (1.4) и (1.5), по известным формулам могут быть вычислены силовые факторы, характеризующие состояние сечения оболочки: нормальные, обобщенные сдвиговые силы, изгибающие моменты, обобщенные перерезывающие силы.
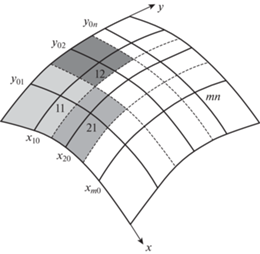
Неизвестные функции $f_{1}^{{\left( 1 \right)}}(x,y) \ldots f_{3}^{{\left( 3 \right)}}(x,y)$ аппроксимируем кусочно-постоянными. Для этого другими меридианами и параллелями разбиваем оболочку на области (рис. 2) таким образом, чтобы каждая из точек (например, 11, 12, 21, …, mn) попадала внутрь одной из областей. Принимаем значения неизвестных функций $f_{1}^{{\left( 1 \right)}}(x,y) \ldots f_{3}^{{\left( 3 \right)}}(x,y)$ постоянными и равными их значениям в точках 11, 12, 21, …, mn. Для каждой из точек 11, 12, 21, …, mn запишем столбец значений неизвестных функций:
(1.6)
${{{\mathbf{f}}}_{{ij}}} = {{\left\| {\begin{array}{*{20}{c}} {f_{{1ij}}^{{\left( 1 \right)}}}&{f_{{1ij}}^{{\left( 2 \right)}}}&{f_{{1ij}}^{{\left( 3 \right)}}}&{f_{{2ij}}^{{\left( 1 \right)}}}&{f_{{2ij}}^{{\left( 2 \right)}}}&{f_{{2ij}}^{{\left( 3 \right)}}}&{f_{{3ij}}^{{\left( 1 \right)}}}&{f_{{3ij}}^{{\left( 2 \right)}}}&{f_{{3ij}}^{{\left( 3 \right)}}} \end{array}} \right\|}^{T}}$Вдоль каждого меридиана и параллели запишем соответствующие дифференциальные уравнения системы (1.2) в матричной форме:
(1.7)
$\frac{\partial }{{\partial x}}\left\| \begin{gathered} u_{3}^{{(1)}} \\ \frac{{\partial u_{3}^{{(2)}}}}{{\partial {{x}_{1}}}} \\ {v}_{2}^{{(1)}} \\ \frac{{\partial {v}_{2}^{{(1)}}}}{{\partial x}} \\ \frac{{\partial {v}_{1}^{{(3)}}}}{{\partial y}} \\ W_{3}^{{(1)}} \\ \frac{{\partial w_{3}^{{(1)}}}}{{\partial x}} \\ \frac{{{{\partial }^{2}}w_{3}^{{(1)}}}}{{\partial {{x}^{2}}}} \\ \frac{{{{\partial }^{3}}w_{3}^{{(1)}}}}{{\partial {{x}^{3}}}} \\ \frac{{{{\partial }^{2}}w_{3}^{{(3)}}}}{{\partial {{y}^{2}}}} \\ \frac{{{{\partial }^{3}}w_{3}^{{(3)}}}}{{\partial {{y}^{2}}\partial x}} \\ \end{gathered} \right\|\, = \,\left\| {\begin{array}{*{20}{c}} 0&1&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&{{{a}_{{x27}}}}&0&0&0&0 \\ 0&0&0&1&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&1&0&0&0&0 \\ 0&0&0&0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&0&0&0&1&0&0 \\ 0&{{{a}_{{x92}}}}&0&0&0&{{{a}_{{x96}}}}&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&1 \\ 0&0&0&0&0&0&0&0&0&0&0 \end{array}} \right\|\left\| \begin{gathered} u_{3}^{{(1)}} \\ \frac{{\partial u_{3}^{{(1)}}}}{{\partial x}} \\ {v}_{2}^{{(1)}} \\ \frac{{\partial {v}_{2}^{{(1)}}}}{{\partial x}} \\ \frac{{\partial {v}_{1}^{{(3)}}}}{{\partial y}} \\ W_{3}^{{(1)}} \\ \frac{{\partial w_{3}^{{(1)}}}}{{\partial x}} \\ \frac{{{{\partial }^{2}}w_{3}^{{(1)}}}}{{\partial {{x}^{2}}}} \\ \frac{{{{\partial }^{3}}w_{3}^{{(1)}}}}{{\partial {{x}^{3}}}} \\ \frac{{{{\partial }^{2}}w_{3}^{{(3)}}}}{{\partial {{y}^{2}}}} \\ \frac{{{{\partial }^{3}}w_{3}^{{(3)}}}}{{\partial {{y}^{2}}\partial x}} \\ \end{gathered} \right\|\, + \,\left\| {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&{{{c}_{{x44}}}}&0&0&0&0&0 \\ 0&0&{{{c}_{{x53}}}}&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&{\frac{1}{2}} \end{array}} \right\|\left\| \begin{gathered} f_{1}^{{(1)}} \\ f_{1}^{{(2)}} \\ f_{1}^{{(3)}} \\ f_{2}^{{(1)}} \\ f_{2}^{{(2)}} \\ f_{2}^{{(3)}} \\ f_{3}^{{(1)}} \\ f_{3}^{{(2)}} \\ f_{3}^{{(3)}} \\ \end{gathered} \right\|$В краткой форме:
(1.8)
$\frac{\partial }{{\partial x}}{{{\mathbf{w}}}_{x}} = {{A}_{x}}{{{\mathbf{w}}}_{x}} + {{C}_{{fx}}}{\mathbf{f}}$(1.9)
$\frac{\partial }{{\partial y}}\left\| \begin{gathered} u_{1}^{{(1)}} \\ \frac{{\partial u_{1}^{{(2)}}}}{{\partial y}} \\ \frac{{\partial u_{2}^{{(3)}}}}{{\partial x}} \\ {v}_{2}^{{(2)}} \\ \frac{{\partial {v}_{2}^{{(2)}}}}{{\partial y}} \\ W_{3}^{{(2)}} \\ \frac{{\partial w_{3}^{{(2)}}}}{{\partial y}} \\ \frac{{{{\partial }^{2}}w_{3}^{{(2)}}}}{{\partial {{y}^{2}}}} \\ \frac{{{{\partial }^{3}}w_{3}^{{(2)}}}}{{\partial {{y}^{3}}}} \\ \end{gathered} \right\| = \left\| {\begin{array}{*{20}{c}} 0&1&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0 \\ 0&0&0&0&0&0&{{{a}_{{y57}}}}&0&0 \\ 0&0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&0&1 \\ 0&0&0&0&{{{a}_{{y95}}}}&0&0&0&0 \end{array}} \right\|\left\| \begin{gathered} u_{1}^{{(1)}} \\ \frac{{\partial u_{1}^{2}}}{{\partial y}} \\ \frac{{\partial u_{2}^{{(3)}}}}{{\partial x}} \\ {v}_{2}^{{(2)}} \\ \frac{{\partial {v}_{2}^{{(2)}}}}{{\partial y}} \\ W_{3}^{{(2)}} \\ \frac{{\partial w_{3}^{{(2)}}}}{{\partial y}} \\ \frac{{{{\partial }^{2}}w_{3}^{{(2)}}}}{{\partial {{y}^{2}}}} \\ \frac{{{{\partial }^{3}}w_{3}^{{(2)}}}}{{\partial {{y}^{3}}}} \\ \end{gathered} \right\| + \left\| {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0&0 \\ 0&{{{c}_{{y22}}}}&0&0&0&0&0&0&0 \\ 0&0&0&0&0&{{{c}_{{y36}}}}&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&1&0 \end{array}} \right\|\left\| \begin{gathered} f_{1}^{{(1)}} \\ f_{1}^{{(2)}} \\ f_{1}^{{(3)}} \\ f_{2}^{{(1)}} \\ f_{2}^{{(2)}} \\ f_{2}^{{(3)}} \\ f_{3}^{{(1)}} \\ f_{3}^{{(2)}} \\ f_{3}^{{(3)}} \\ \end{gathered} \right\|$(1.10)
$\frac{\partial }{{\partial y}}{{{\mathbf{w}}}_{y}} = {{A}_{y}}{{{\mathbf{w}}}_{y}} + {{C}_{{fy}}}{\mathbf{f}}$Для каждой из точек 11, 12, 21, …, mn запишем в матричной форме уравнения связи:
(1.11)
$\left\| {\begin{array}{*{20}{c}} 1&1&1&0&0&0&0&0&0 \\ 0&0&0&1&1&1&0&0&0 \\ 0&0&0&0&0&0&1&1&1 \end{array}} \right\|\left\| {\begin{array}{*{20}{c}} {f_{{1ij}}^{{\left( 1 \right)}}} \\ {f_{{1ij}}^{{\left( 2 \right)}}} \\ {f_{{1ij}}^{{\left( 3 \right)}}} \\ {f_{{2ij}}^{{\left( 1 \right)}}} \\ {f_{{2ij}}^{{\left( 2 \right)}}} \\ {f_{{2ij}}^{{\left( 3 \right)}}} \\ {f_{{3ij}}^{{\left( 1 \right)}}} \\ {f_{{3ij}}^{{\left( 2 \right)}}} \\ {f_{{3ij}}^{{\left( 3 \right)}}} \end{array}} \right\| = \left\| {\begin{array}{*{20}{c}} {\frac{{{{q}_{1}}}}{{\bar {B}}}} \\ {\frac{{{{q}_{2}}}}{{\bar {B}}}} \\ {\frac{{{{q}_{3}}}}{D}} \end{array}} \right\|$(1.12)
$\left\| {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&1&0 \end{array}} \right\|\left\| \begin{gathered} u_{{3ij}}^{{(1)}} \\ {{\frac{{\partial u_{3}^{{(1)}}}}{{\partial x}}}_{{ij}}} \\ {v}_{{2ij}}^{{(1)}} \\ {{\frac{{\partial {v}_{2}^{{(1)}}}}{{\partial x}}}_{{ij}}} \\ {{\frac{{\partial {v}_{1}^{{(3)}}}}{{\partial y}}}_{{ij}}} \\ w_{{3ij}}^{{(1)}} \\ {{\frac{{\partial w_{3}^{{(1)}}}}{{\partial x}}}_{{ij}}} \\ {{\frac{{{{\partial }^{2}}w_{3}^{{(1)}}}}{{\partial {{x}^{2}}}}}_{{ij}}} \\ {{\frac{{{{\partial }^{3}}w_{3}^{{(1)}}}}{{\partial {{x}^{3}}}}}_{{ij}}} \\ {{\frac{{{{\partial }^{2}}w_{3}^{{(3)}}}}{{\partial {{y}^{2}}}}}_{{ij}}} \\ {{\frac{{{{\partial }^{3}}w_{3}^{{(3)}}}}{{\partial {{y}^{2}}\partial x}}}_{{ij}}} \\ \end{gathered} \right\| = \left\| {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&0&0&1&0 \end{array}} \right\|\left\| \begin{gathered} u_{{1ij}}^{{(1)}} \\ {{\frac{{\partial u_{1}^{{(2)}}}}{{\partial y}}}_{{ij}}} \\ {{\frac{{\partial u_{2}^{{(3)}}}}{{\partial x}}}_{{ij}}} \\ {v}_{{2ij}}^{{(2)}} \\ {{\frac{{\partial {v}_{2}^{{(2)}}}}{{\partial y}}}_{{ij}}} \\ w_{{3ij}}^{{(2)}} \\ {{\frac{{\partial w_{3}^{{(2)}}}}{{\partial y}}}_{{ij}}} \\ {{\frac{{{{\partial }^{2}}w_{3}^{{(2)}}}}{{\partial {{y}^{2}}}}}_{{ij}}} \\ {{\frac{{{{\partial }^{3}}w_{3}^{{(2)}}}}{{\partial {{y}^{3}}}}}_{{ij}}} \\ \end{gathered} \right\|$Решения ОДУ (1.8), (1.10) определяются аналитически по формулам [9–11]. Вдоль меридиана y = y0j между любыми соседними точками i, j и i, j – 1:
(1.13)
${{{\mathbf{w}}}_{{xij}}} = {\mathbf{K}}_{{i,j - 1}}^{{ij}}{{{\mathbf{w}}}_{{xi,j - 1}}} + {{{\mathbf{T}}}_{{i,j - 1}}}{{{\mathbf{C}}}_{{fx}}}{{{\mathbf{f}}}_{{i,j - 1}}}\frac{{\Delta x}}{2} + {{{\mathbf{T}}}_{{ij}}}{{{\mathbf{C}}}_{{fx}}}{{{\mathbf{f}}}_{{ij}}}\frac{{\Delta x}}{2}$Вдоль параллели $x = {{x}_{{i0}}}$ между любыми соседними точками i, j и $i - 1,j$:
(1.14)
${{{\mathbf{w}}}_{{yij}}} = {\mathbf{K}}_{{i - 1,j}}^{{ij}}{{{\mathbf{w}}}_{{yi - 1,j}}} + {{{\mathbf{T}}}_{{i - 1,j}}}{{{\mathbf{C}}}_{{fy}}}{{{\mathbf{f}}}_{{i - 1,j}}}\frac{{\Delta y}}{2} + {{{\mathbf{T}}}_{{i - 1,j}}}{{{\mathbf{C}}}_{{fy}}}{{{\mathbf{f}}}_{{i - 1,j}}}\frac{{\Delta y}}{2}$Записав решения (1.13), (1.14) между всеми соседними точками в направлениях x и y и мы получим неопределенную систему алгебраических уравнений (СЛАУ). Чтобы полученную СЛАУ сделать определенной, необходимо дополнить ее краевыми условиями и уравнениями связи. Краевые условия устанавливаются следующим образом. Для каждой из точек на контуре x10, x20, …, xm0 (рис. 1) записываются матричные уравнения вида
где Bx – прямоугольная матрица, выбирающая элементы столбца производных, wx0j – столбец производных (1.4), vx0j – столбец задаваемых значений выбранных производных.Например, для постановки краевого условия защемления, уравнение (1.15) в развернутом виде запишется как:
(1.16)
$\left\| {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&0&1&0&0 \end{array}} \right\|\left\| {\begin{array}{*{20}{c}} {u_{1}^{{\left( 1 \right)}}} \\ {\frac{{\partial u_{1}^{{\left( 2 \right)}}}}{{\partial y}}} \\ {\frac{{\partial u_{2}^{{\left( 3 \right)}}}}{{\partial x}}} \\ {{v}_{2}^{{\left( 2 \right)}}} \\ {\frac{{\partial {v}_{2}^{{\left( 2 \right)}}}}{{\partial y}}} \\ {w_{3}^{{\left( 2 \right)}}} \\ {\frac{{\partial w_{3}^{{\left( 2 \right)}}}}{{\partial y}}} \\ {\frac{{{{\partial }^{2}}w_{3}^{{\left( 2 \right)}}}}{{\partial {{y}^{2}}}}} \\ {\frac{{{{\partial }^{3}}w_{3}^{{\left( 2 \right)}}}}{{\partial {{y}^{3}}}}} \end{array}} \right\| = \left\| {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}} \right\|$Для постановки других видов краевых условий следует изменять элементы матрицы Bx. Если же на краю нужно задать не нулевое значение, а, например, приложить силу или изгибающий момент, то следует в столбце vx0j заменить 0 на необходимое значение. Краевые условия для точек y01, y02, …, y0n ставятся аналогично.
Дополнив СЛАУ уравнениями связи (1.11), (1.12) для точек пересечения, мы тем получим определенную систему. Для задания поверхностных нагрузок следует использовать одно из уравнений уравнение связи – уравнение (1.11). Заданием в правой части уравнения (1.11) числовых значений величин q1, q2, q3 будут нагружаться соответствующие области вокруг точек пересечения меридианов (рис. 2).
Решив определенную СЛАУ, получаем значения элементов столбцов (1.4), (1.5), а так же значения функций $f_{1}^{{\left( 1 \right)}}(x,y)$ … $f_{3}^{{\left( 3 \right)}}(x,y)$. Решение носит приближенный характер. При сгущении сетки меридианов и параллелей, т.е при увеличении числа точек выполнения уравнений связи и уменьшения областей осреднения функций $f_{1}^{{\left( 1 \right)}}(x,y)$ … $f_{3}^{{\left( 3 \right)}}(x,y)$ решение стремится к аналитическому, то есть с контролируемой погрешностью.
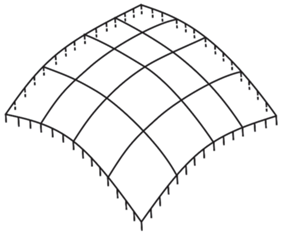
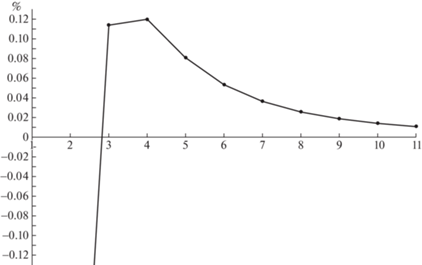
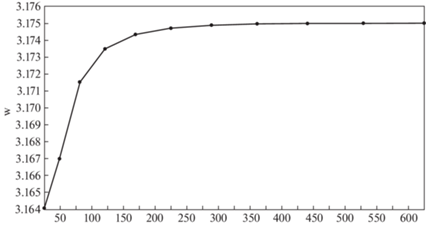
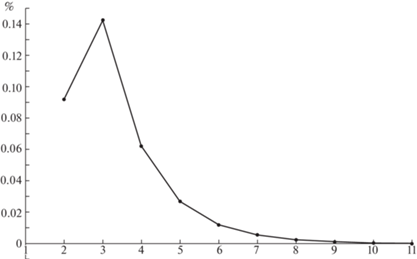
2. Результаты вычислений. Решена краевая задача механики деформирования пологой защемленной по краям оболочки, нагруженной внешним давлением. Расчетная схема представлена на рис. 3. Вычислены перемещения – w – и изгибающие моменты – M – в полюсе пологой оболочки двоякой кривизны. Внешнее давление 10 МПа. Параметры оболочки: размеры в плане – 1 × 1 м, радиусы кривизны – 10 м, толщина – 5 мм. Материал панели – алюминий с характеристиками: модуль Юнга – 0.7 × 1011 Па, коэффициент Пуассона – 0.3. На оболочку накладывалась сетка меридианов и параллелей при разбиении сторон оболочки от 5 × 5 интервалов до 25 × 25 интервалов. Результаты представлены в таблице 1 и в виде графиков. Помимо величин прогибов и моментов (рис. 4, 6) для определения сходимости решения и определения погрешности вычислялась разность их значений полученных на двух соседних итерациях, отнесенная к величине вычисленного значения на данной итерации. В таблице 1 и на графиках (рис. 5, 7) эта величина названа “относительная разность”.
Рис. 4.
Зависимость величины вычисленного изгибающего момента М в полюсе оболочки от плотности сетки.
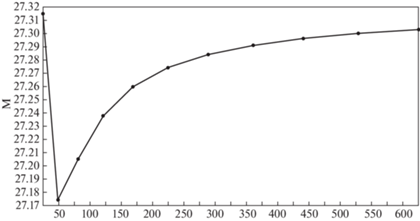
Таблица 1.
Результаты расчетов
| Номер итерации | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|
| Плотность сетки, меридианов × параллелей | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 17 × 17 | 19 × 19 | 21 × 21 | 23 × 23 | 25 × 25 |
| Прогиб, мм | 3.16409 | 3.16700 | 3.17151 | 3.17349 | 3.17433 | 3.17471 | 3.17488 | 3.17496 | 3.17499 | 3.17500 |
| Относительная разность, % | 0.0919 | 0.1424 | 0.0621 | 0.0267 | 0.0119 | 0.0054 | 0.0025 | 0.0010 | 0.0003 | 0.0000 |
| Изгибающий момент, Н | 27.315 | 27.174 | 27.205 | 27.238 | 27.260 | 27.274 | 27.284 | 27.291 | 27.296 | 27.300 |
| Относительная разность, % | –0.5187 | 0.1140 | 0.1196 | 0.0808 | 0.0534 | 0.0364 | 0.0257 | 0.0187 | 0.0140 | 0.0108 |
Выводы. Предложенный автором подход к решению задач механики деформирования элемента пологой оболочки и построенный алгоритм решения краевой задачи на ЭВМ показывает быструю сходимость решения с контролем погрешности при увеличении плотности сетки декомпозиции.
Список литературы
Ломакин Е.В., Юргенсон С.А., Федулов Б.Н., Федоренко А.Н. Механические характеристики подкрепленной и трехслойной оболочек на основе метаматериалов с учетом эксплуатационных повреждений // Изв. РАН. МТТ. 2021. № 6. С. 45–54. https://doi.org/10.31857/S0572329921060064
Васильев В.В., Салов В.А. Устойчивость бесконечно длинной цилиндрической оболочки, нагруженной наружным давлением, создаваемым жесткой внешней средой // Изв. РАН. МТТ. 2021. № 4. С. 98–108. https://doi.org/10.31857/S0572329921040127
Виноградов Ю.И. Анализ концентрации напряжений с контролируемой погрешностью в тонкостенных конструкциях (транспортно-пусковой стакан) // Изв. РАН. МТТ. 2021. № 2. С. 110–123. https://doi.org/10.31857/S0572329921020173
Кириллова И.В., Коссович Л.Ю. Асимптотические методы исследования эллиптического погранслоя в оболочках вращения при ударных торцевых воздействиях нормального типа // Изв. РАН. МТТ. 2020. № 5. С. 131–137. https://doi.org/10.31857/S0572329920050104
Образцов И.Ф. Строительная механика летательных аппаратов: Учебник для авиационных специальностей вузов. М.: Машиностроение, 1986. 536 с.
Власов В.З. Избранные труды. Том 1. М.: Изд-во АН СССР, 1962. 528 с.
Крылов А.Н. О расчете балок, лежащих на упругом основании. Л.: АН СССР, 1931. 154 с.
Пшеничнов Г.И. Решение некоторых задач строительной механики методом декомпозиции // Строит. мех. и расчет сооруж. 1986. № 4. С. 12–17.
Крылов А.Н. Лекции о приближенных вычислениях. М.: Гос. издательство технико-теоретической литературы, 1954. 398 с.
Peano G. Integration par series des equations differentielles lineaires // Math. Ann. 1888. Bd. 32. S. 450–456.
Гантмахер Ф.Р. Теория матриц. М.: Наука. 1988. 548 с.
Беллман Р. Введение в теорию матриц. М.: Наука. 1976. 351 с.
Виноградов Ю.И. Методы решения линейных обыкновенных дифференциальных уравнений // Докл. РАН. 2006. Т. 409. № 1. С. 15–18.
Виноградов Ю.И., Молчанов Д.Б. Основы модифицированного метода конечных элементов решения краевых задач строительной механики тонкостенных конструкций // ПММ. 2018. Т. 82. № 4. С. 498–510.
Vinogradov Y.I., Molchanov D.B., Bakulin V.N. Analytical matrix solutions of linear ordinary differential equations with constant coefficients // J. Phys.: Conf. Ser. 2019. V. 1392. P. 012077. https://doi.org/10.1088/1742-6596/1392/1/012077
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела