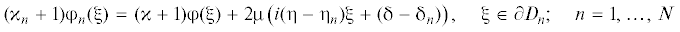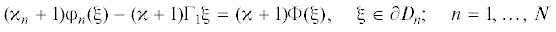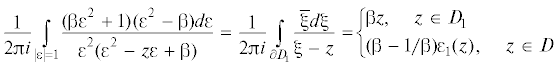Известия РАН. Механика твердого тела, 2022, № 1, стр. 41-58

1. Введение. Задачам теории упругости для бесконечной или полубесконечной кусочно-однородной изотропной среды ввиду их практической важности посвящена обширная литература; настолько обширная, что авторы сочли целесообразным при обсуждении текущего состояния вопроса ограничиться, в основном, изотропным двумерным случаем. Правда, пик интереса к данной проблематике, в частности, к двумерной задаче, миновал – он приходится на 50-е–70-е годы прошлого века. Поэтому самая “свежая” работа, на которую мы сошлемся, датирована 2010 г.

Здесь уместно сказать, что под включением (это слово фигурирует в названии статьи) мы будем по умолчанию понимать конечную область с измененными упругими свойствами; скачок вектора смещений при переходе через границу области отсутствует. Наша терминология отличается от общепринятой, согласно которой область с измененными свойствами называется неоднородностью, а включением – область, на границе которой смещение претерпевает разрыв [1]. Впрочем, разделение упругих дефектов на эти два типа является до некоторой степени условным. Так, в геофизике (авторы имеют к ней непосредственное отношение), а точнее – в современной геодинамике, существенную роль играют дефекты земной коры, т.н. разломы. Их деформационную активизацию можно интерпретировать и как скачок смещений (включение в традиционном смысле слова), и как временное изменение неоднородности. Оба подхода дают идентичные результаты [2].

Двумерная постановка не только уменьшает количество уравнений, – она дает возможность применить метод комплексных потенциалов Колосова–Мусхелишвили [3, 4], который основан на том, что компоненты двумерного тензора напряжений являются вторыми производными некоторой бигармонической функции, т.н. функции Эри. В свою очередь, бигармоническая функция выражается через две функции комплексного переменного (это и есть потенциалы Колосова), аналитические в той области, где упругие модули постоянны. Задача теории упругости сводится, таким образом, к краевой задаче ТФКП. На бесконечности задается однородное напряженное состояние. Условий на границе два: одно следует из третьего закона Ньютона, второе выражает непрерывность вектора смещений.

Но если не накладывать ограничений на соотношение между упругими модулями матрицы и включений, даже этот мощный аппарат позволяет получить точное решение, только если матрица (т.е. вмещающая среда) – вся плоскость, включение одно, и это – эллипс. Предположим, что в бесконечно удаленной точке задано одноосное напряженное состояние; тогда напряженное состояние внутри эллипса будет однородным [5]. Здесь мы имеем полную аналогию с трехмерной задачей об эллипсоидальном включении [1]. Примечательно, что напряженное состояние внутри эллипсоида или эллипса будет однородным даже при анизотропии упругих свойств и включения, и матрицы [6, 7].

Возникает вопрос: верно ли обратное утверждение? То есть: если на бесконечности действует одноосное напряженное состояние, и поле напряжений во включении однородно, означает ли это, что включение представляет собой эллипс? Положительный ответ дал Г. Сендецкий в работе [8].

Задачу, рассмотренную Г. Сендецким, можно назвать обратной задачей о включении: известен общий вид поля напряжений во включении и на бесконечности, а искомой является геометрия включения. Решение основано на том, что внешность единичного круга можно конформно отобразить на внешность любой односвязной области, а функция z(w), осуществляющая это отображение, представима в виде степенного ряда:

Конформные отображения являются основным инструментом при решении “прямой”, классической задачи о плоскости с полостью. Если z(w) – рациональная функция (в частности, если ряд (1.1) конечен), метод Колосова–Мусхелишвили дает точное решение [4]. Но внутри круга у этой функции есть особенность, поэтому в прямой задаче о включении с конечными модулями упругости конформные отображения “не работают”, по крайней мере, столь же эффективно.

Метод комплексных потенциалов, тем не менее, полезен: он позволяет свести задачу о включении к системе сингулярных интегральных уравнений (с ядром Коши). Ее можно регуляризовать, превратив в систему интегральных уравнений Фредгольма. Это сделал Д.И. Шерман в работе [9]. В ней вмещающая область предполагается конечной, но предложенный автором подход почти без изменений переносится на случай, когда матрица – вся плоскость, или даже полуплоскость [10]. Однако решать полученные интегральные уравнения приходится численно. По-видимому, наиболее эффективный алгоритм численного решения предложен в [11]: авторы решают не уравнение Фредгольма, а “исходное”, сингулярное уравнение, заменяя искомую непрерывную функцию ступенчатой. Работоспособность алгоритма они проверяют на эллиптическом включении, сравнивая приближенное решение с решением Хардимана [5]. Но доказательство корректности своей численной процедуры авторы не приводят. Неизвестно, будет ли их алгоритм работать, если граница включения содержит угловые точки.

Альтернативным является метод возмущений – он позволяет свести задачу о неоднородности к последовательности (бесконечной) “однородных” задач. Этот метод подробно описан в [12]. Доказательство сходимости итераций использует предположение о том, что упругие модули меняются от точки к точке непрерывно, более того – достаточно гладко. Но его, по-видимому, можно модифицировать таким образом, что это предположение станет лишним. Основная трудность в другом: метод возмущений тоже не позволяет получить точные квадратурные формулы; довольствоваться, в конечном итоге, приходится некоторым приближением.

Все вышесказанное относится к ситуации, когда упругие модули включений могут произвольным образом отличаться от упругих модулей вмещающей среды. Если же модули сдвига включений одинаковы и совпадают с модулем сдвига матрицы (плоскости), получить точные формулы для потенциалов Колосова, а значит, и для напряжений и деформаций, не составляет труда. При этом включений может быть несколько, их форма принципиального значения не имеет; на модули сжатия никаких ограничений нет.

Данная статья посвящена разбору именно этого частного случая. По непонятным причинам, он остался вне поля зрения исследователей, занимавшихся данной проблематикой. Правда, В.А. Ломакин рассматривает в [12] задачу теории упругости для неоднородно-упругого тела с постоянным модулем сдвига. При этом модуль сжатия предполагается гладкой функцией координат. В.А. Ломакин сводит эту задачу к уравнению в частных производных четвертого порядка относительно вспомогательной функции, которую тоже можно назвать потенциалом: напряжения и смещения выражаются через производные этой функции.

Но о возможности решения в квадратурах речь не идет: во-первых, задача трехмерная. Во-вторых, между непрерывным и скачкообразным изменением модуля сжатия в данном случае есть принципиальная разница. И, в-третьих, автор не конкретизирует геометрию вмещающего тела. Мы же будем рассматривать случай неограниченной двумерной среды (плоскости), и только его.

Предлагаемое решение основано на элементарных свойствах интегралов типа Коши. “Образцом” послужила работа Д.И. Шермана [13], где решена другая, хотя и близкая задача: включение “сделано” из того же материала, что и матрица, но на границе раздела задан скачок смещений. Эту задачу естественно было бы назвать задачей Шермана, или, используя инженерную терминологию, задачей о вставке. Д.И. Шерман, используя интегралы типа Коши, сводит ее к первой основной задаче для вмещающей области, которую он предполагает конечной.

Но для нас гораздо больший интерес представляет случай, когда это – полуплоскость или вся плоскость. Ему посвящена работа [14]. Автор называет задачу о вставке двумерной задачей Эшелби. Работу Шермана [13] он не упоминает. Его подход основан на следующем факте: пусть $D$ – ограниченная область в плоскости комплексного переменного z, которую занимает включение; $\partial D$ – граница этой области и ${{\xi }} \in \partial D$. Тогда функция $F({{\xi }}) = {{\bar {\xi }}}({{\xi }})$ может быть аналитически продолжена на внешность области $D$. Это следует из существования отображения (1.1).

Обрывая ряд (1.1), т.е. рассматривая вместо $D$ близкую к ней, “более регулярную” область, автор добивается того, что точка $z = \infty $ оказывается полюсом конечного порядка для функции F(z). Если включение одно, его идею можно применить к нашей задаче. Но решение будет приближенным; кроме того, сконструировать функцию F(z) не так просто – сначала нужно построить отображение (1.1).

Интереснее и ближе нам работа [15], тоже посвященная задаче о вставке. Авторы идут вслед за Д.И. Шерманом. Они рассматривают частный пример, когда включение представляет собой квадрат, который извлекли из плоскости, увеличили в размерах (скажем, нагрели), затем обжали и с помощью жесткой оправки поместили обратно. Для компонент напряжения в [15] получены явные формулы. Оказывается, что в окрестности вершин квадрата след тензора напряжений остается конечным, а сдвиговая составляющая стремится к бесконечности.

Авторы [15] могли выписать решение для нескольких вставок произвольной формы, и – более того – распространить его на случай, когда только модули сдвига вставок и плоскости совпадают, а модули сжатия различаются. Тогда бы необходимости в данной статье не было – наши формулы были бы частным случаем их результатов. Но они мимо этой возможности прошли.

2. Метод Колосова–Мусхелишвили. Этот метод является основой для дальнейших рассмотрений. С исчерпывающей полнотой он изложен в [4], см. также [16]. Мы только напомним, в чем он состоит, и приведем (без вывода) факты, которые нам понадобятся в дальнейшем.

Метод комплексных потенциалов (Колосова–Мусхелишвили) основан на том, что компоненты ${{{{\sigma }}}_{{xx}}}$, ${{{{\sigma }}}_{{xy}}}$, ${{{{\sigma }}}_{{yy}}}$ двумерного тензора напряжений в однородной изотропной упругой среде являются производными бигармонической функции, т.н. функции напряжений Эри $U(x,y)$:

и на теореме Гурса, в силу которой функцию, бигармоническую в области D можно представить в виде: где ${{\varphi (}}z{\text{)}}$ и ${{\psi }}(z)$ – аналитические функции комплексной переменной $z = x + iy$. Это и есть потенциалы Колосова. Иногда мы будем называть ${{\varphi }}(z)$ и ${{\psi }}(z)$ первым и вторым потенциалом Колосова соответственно.

В силу (2.1), функция Эри определена с точностью до слагаемого вида $ax + by + c$. Следовательно, потенциал φ определен с точностью до слагаемого вида $i{{\alpha }}\,z + {{\beta }}$, где α – действительная, ${{\beta }}$ – комплексная константа, а ${{\psi }}(z)$ – с точностью до аддитивной комплексной константы:

Компоненты тензора напряжений определяются потенциалами Колосова однозначно:

Введем в рассмотрение функцию f(z), “комплексный градиент” бигармонической функции $U(x,y)$:

Пусть сначала конечная область D ограничена кусочно-гладким контуром $\partial D$. Сужение (2.4) на $\partial D$, функцию $f({{\xi }})$, где ${{\xi }} \in \partial D$, можно выразить через компоненты ${{F}_{x}}$ и ${{F}_{y}}$ вектора напряжений, действующих извне:

где ds – элемент дуги контура $\partial D$ (при интегрировании контур обходится в положительном направлении по отношению к области D – так, что эта область остается слева); ${{{{\xi }}}_{0}} \in \partial D$ – произвольно выбранная точка на контуре; $C$ – произвольная константа. По этой причине f(z) мы будем называть силовой функцией для области D. В [4] показано, что граничные значения ${{\varphi }}(\xi )$ и ${{\psi }}(\xi )$ связаны друг с другом и с $f({{\xi }})$ соотношением

Найти потенциалы Колосова по заданной функции $f({{\xi }})$ – значит решить т.н. первую основную задачу плоской теории упругости. По поводу условий, при которых это заведомо можно сделать, см. [4]. Заметим, что функция $f({{\xi }})$ определена с точностью до аддитивной константы. С такой же точностью в силу (2.2) определена и левая часть (2.6).

Пусть теперь граница $\partial D$ области D состоит из одного или нескольких кусочно-гладких контуров:

а потенциалы Колосова ${{\varphi }}(z)$ и ${{\psi }}(z)$ заданы. Этим функция Эри в D определена с точностью до аддитивной константы, а силовая функция (2.4) – однозначно. Зададим функцию ${{f}_{n}}({{\xi }})$, ${{\xi }} \in \partial {{D}_{n}}$ формулой

Функцию ${{f}_{n}}({{\xi }})$, которая есть не что иное, как сужение (2.4) на $\partial {{D}_{n}}$, можно представить в виде, аналогичном (2.5). А именно: пусть $F_{x}^{{(n)}}$ и $F_{y}^{{(n)}}$ – компоненты вектора напряжений, действующих на контур $\partial {{D}_{n}}$ извне. Зафиксируем точку ${{\xi }}_{0}^{{(n)}} \in \partial {{D}_{n}}$. Утверждается, что существует комплексная константа C_n, зависящая от ${{\xi }}_{0}^{{(n)}}$, такая, что

Приведем также формулу (Г.В. Колосова) для смещений. Пусть u и ${v}$ – горизонтальная и вертикальная составляющие вектора смещений. Формула Колосова:

Здесь ${{\mu }}$ – модуль сдвига; ${{\kappa }}$ – константа Колосова, которая выражается через модуль сдвига ${{\mu }}$ и модуль сжатия ${{\lambda }}$:

В силу (2.2), формула (2.8) определяет вектор смещений с точностью до слагаемого вида

где ${{\eta }}$ – действительная, ${{\delta }}$ – комплексная константа. Но оно не влияет на симметризованный тензор деформации, от которого зависят упругие напряжения.

3. Постановка двумерной задачи. Пусть D₀ – изотропная, но не однородная по упругим свойствам плоскость; она же – плоскость комплексного переменного $z$. Пусть ${{D}_{1}} \subset {{D}_{0}}$, ${{D}_{2}} \subset {{D}_{0}}\; \ldots ,\;{{D}_{N}} \subset {{D}_{0}}$ – односвязные области, ограниченные замкнутыми кусочно-гладкими кривыми ${{{{\varphi }}}_{n}}(z)$; предполагается, что каждая гладкая компонента каждого контура является дугой Ляпунова.

Модуль сдвига во всей плоскости D₀ один и тот же; его мы обозначим через ${{\mu }}$.

Модуль сжатия в D₁ равен ${{{{\lambda }}}_{1}}$, и т.д.; в ${{D}_{N}}$ – ${{\lambda }_{n}}(z)$. Модуль сжатия в области D, внешней по отношению к D₁ ∪ ... ∪ D_N, обозначим через ${{\lambda }}$.

Компоненты тензора напряжений D_n, ${{\sigma }}_{{yy}}^{\infty }$ и ${{\sigma }}_{{xy}}^{\infty }$ в бесконечно удаленной точке плоскости заданы, требуется найти напряжения во всех точках D₀ при условии, что вектор смещений при переходе через границы $\partial {{D}_{n}}$ изменяется непрерывно.

Сведем эту задачу к краевой задаче теории функций. Пусть ${{{{\varphi }}}_{n}}(z)$ и ${{{{\psi }}}_{n}}(z)$ – потенциалы Колосова, которые определяют напряженное состояние в области D_n, n = 1, ..., N; а ${{\varphi }}(z)$ и ${{\psi }}(z)$ – потенциалы Колосова в области D. Мы будем искать функции ${{\varphi }}(z)$ и ${{\psi }}(z)$ в виде:

где $\Phi (z)$, $\Psi (z)$ – голоморфные в области $D$ функции такие, что

Константы ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$ задают поле напряжений в бесконечно удаленной точке. Поскольку мнимая часть $\varphi (z)$ на напряжения не влияет, будем считать, что

Из (2.3) следует, что

Если поле в $D$ задано, требования (3.1), (3.2) и (3.3) к потенциалам $\varphi (z)$ и ${{\psi }}(z)$ определяют эти функции однозначно. Поэтому функции ${{f}_{n}}({{\xi }})$, ${{\xi }} \in \partial {{D}_{n}}$, $n = 1,\; \ldots ,\;N$:

тоже определены однозначно. В терминах предыдущего раздела, ${{f}_{n}}({{\xi }})$ – это сужение силовой функции для области D на контур $\partial {{D}_{n}}$. ${{f}_{n}}({{\xi }})$ можно представить в виде (2.7), где $F_{x}^{{(n)}}$ и $F_{y}^{{(n)}}$ – компоненты вектора напряжений, действующих со стороны включения D_n; ${{\xi }}_{0}^{{(n)}}$ – произвольно выбранная точка контура $\partial {{D}_{n}}$; C_n – константа, которая зависит от ${{\xi }}_{0}^{{(n)}}$.

Подчеркнем, что интегрирование идет в положительном направлении по отношению к области D – так, что она остается слева, то есть по часовой стрелке.

Еще рассмотрим силовую функцию для области D_n (точнее, ее сужение на $\partial {{D}_{n}}$), ${{\tilde {f}}_{n}}({{\xi }})$. Эта функция определена с точностью до константы (см. раздел 1). Воспользуемся этим, и выберем такую нормировку:

где ${{\xi }}_{0}^{{(n)}}$ – та же точка на контуре $\partial {{D}_{n}}$, что и раньше; C_n – та же, зависящая от ${{\xi }}_{0}^{{(n)}}$ константа; $\tilde {F}_{x}^{{(n)}}$ и $\tilde {F}_{y}^{{(n)}}$ – компоненты вектора напряжений, действующих со стороны области D. Интегрирование идет в положительном направлении по отношению к области D_n, т.е. против часовой стрелки. Но по третьему закону Ньютона, $\tilde {F}_{x}^{{(n)}} = - F_{x}^{{(n)}}$, $\tilde {F}_{y}^{{(n)}} = - F_{y}^{{(n)}}$. Следовательно, поэтому граничные значения потенциалов ${{{{\varphi }}}_{n}}(z)$ и ${{{{\psi }}}_{n}}(z)$ мы можем подчинить условию:

Исключив ${{f}_{n}}({{\xi }})$ из (3.4) и (3.5), получим N граничных условий для функций ${{{{\varphi }}}_{1}}(z)$, ${{{{\psi }}}_{1}}(z)$; $ \ldots $, ${{{{\varphi }}}_{N}}(z)$, ${{{{\psi }}}_{N}}(z)$; $\Phi (z)$, $\Psi (z)$:

Еще $N$ условий даст непрерывность смещений, ее мы пока не учитывали. Напомним, что мы считали заданным поле напряжений в $D$, т.е. потенциалы $\Phi (z)$ и $\Psi (z)$. С этой точки зрения, (3.6) – граничное условие первой основной задачи (см. пред. раздел), оставляющее произвол в выборе нормировок: ${{{{\varphi }}}_{n}}(z)$ можно заменить на ${{{{\varphi }}}_{n}}(z) + i{{{{\alpha }}}_{n}}z + {{{{\beta }}}_{n}}$, а ${{{{\psi }}}_{n}}(z)$ – на ${{{{\psi }}}_{n}}(z) - \overline {{{{{\beta }}}_{n}}} $. Здесь ${{{{\alpha }}}_{n}}$ – произвольная действительная, ${{{{\beta }}}_{n}}$ – любая комплексная константа. Условия на смещения, как мы увидим, определят “естественную” нормировку для ${{{{\varphi }}}_{n}}(z)$. Тогда и нормировка ${{{{\psi }}}_{n}}(z)$ определится однозначно.

Пусть $u(z)$ – горизонтальная, ${v}(z)$ – вертикальная компонента смещений в D, ${{u}_{n}}(z)$, ${{{v}}_{n}}(z)$ – горизонтальная и вертикальная компонента смещений в D_n. При переходе через границу включения компоненты смещения изменяются непрерывно. Следовательно,

Согласно формуле Колосова (2.8),

Здесь ${{\kappa }}$ и ${{{{\kappa }}}_{n}}$ – коэффициенты, характеризующие упругие свойства матрицы $D$ и включения D_n:

Мы учли, что модуль сдвига всюду один и тот же и что формула (2.8) определяет смещения с точностью до слагаемого вида (2.9). В силу (3.7) и (3.8),

Варьируя нормировку ${{{{\varphi }}}_{n}}$, мы можем добиться того, что второе слагаемое в правой части (3.9) исчезнет. Это и есть та естественная нормировка, о которой говорилось выше. С учетом (3.1), будем иметь:

Равенства (3.6) и (3.10) составляют полную систему граничных условий. Задача теории упругости будет решена, если мы найдем функции, голоморфные в D_n, где $n = 1, \ldots ,N$, а также функции $\Phi (z)$, $\Psi (z)$, регулярные в D, которые этим условиям удовлетворяют. Ниже будет показано, что такие функции определяются однозначно.

4. Решение в квадратурах и его свойства. Начнем с анализа соотношений (3.10): рассмотрим вспомогательную функцию ${{\chi }}(z)$

В силу (3.10), она голоморфна на $D \cup {{D}_{1}} \cup \ldots \cup {{D}_{N}}$, т.е. на всей плоскости D₀. Следовательно, ${{\chi }}(z) = {\text{const}}$. А поскольку на бесконечности эта функция равна нулю (в силу того, что $\Phi (\infty ) = 0$), она равна нулю везде. Отсюда,

Далее: подставим (4.1) в (3.6). После элементарных преобразований получим:

Введем в рассмотрение еще одну вспомогательную кусочно-голоморфную функцию ${{\omega }}(z)$:

Обозначим через $\partial D$ границу области D:

Пусть ${{{{\omega }}}_{ + }}({{\xi }})$ и ${{{{\omega }}}_{ - }}({{\xi }})$ – предельные значения функции ω(z) при стремлении к точке ${{\xi }} \in \partial D$ слева и справа (то есть, изнутри или снаружи одного из контуров $\partial {{D}_{n}}$) соответственно. Из (4.3) и (4.2) следует формула для скачка ${{{{\omega }}}_{ + }}({{\xi }}) - {{{{\omega }}}_{ - }}({{\xi }})$:

Поскольку значение функции ω(z) в бесконечно удаленной точке задано (а именно, ${{\omega }}\,(\infty ) = 0$, так как $\Psi (\infty ) = 0$), эта функция определяется однозначно. По общим правилам, она равна сумме интегралов типа Коши:

Из (4.4) и (4.3) следуют формулы для $\Psi (z)$ и ${{{{\psi }}}_{n}}(z)$, $n = 1, \ldots ,N$:

Эти формулы вместе с (4.1) решают задачу (3.6), (3.10). Если N = 1 (включение одно), то

Ниже полученные результаты (формулы (4.1) и (4.5)) будут проанализированы.

Начнем с рассмотрения тривиального случая, когда на бесконечности задан чистый сдвиг, то есть ${{\Gamma }_{1}} = 0$. Из (4.1) и (4.5) имеем:

Элементарно проверяется, что (4.7) – это, действительно, решение задачи (3.6), (3.10), если ${{\Gamma }_{1}} = 0$. Из (4.7) следует, что тензор напряжений всюду будет таким же, как на бесконечности. Его компоненты, в силу (2.3),

Теперь, в предположении ${{\Gamma }_{1}} \ne 0$, исследуем формулы (4.1) и (4.5) “на регулярность”. Величина ${{\bar {\xi }}}$, если ее рассматривать как функцию точки, принадлежащей границе включения, удовлетворяет условию Гельдера. Поэтому определяемые посредством (4.5) функции ${{{{\psi }}}_{n}}(z)$ и $\Psi (z)$ ограничены. Ограничены также функции ${{{{\varphi }}}_{n}}(z)$, линейные по $z$; а функция $\Phi (z)$ просто равна нулю.

Но напряжения определяются производными потенциалов Колосова. Первые две производные ${{{{\varphi }}}_{n}}$ и φ ограничены: в силу (4.1),

Здесь учтено, что ${{\varphi }}(z) = {{\Gamma }_{1}}z + \Phi (z)$. Для того чтобы прояснить ситуацию с ${{\psi }}_{n}^{'}(z)$ и $\Psi {\text{'}}(z)$, рассмотрим интеграл типа Коши от ${{\bar {\xi }}}$ по кусочно-гладкому контуру $\partial {{D}_{n}}$, границе одной из областей ${{D}_{n}}$. Обозначим этот интеграл через I:

Вычислим производную $I{\text{'}}(z)$, и применим к ней интегрирование по частям:

Проинтегрированный член исчезает, поскольку функция ${{\bar {\xi }}}({{\xi }})$ непрерывна. Производную ${{\bar {\xi }}}$ по ${{\xi }}$ следует понимать как отношение:

где s – длина дуги, отсчитываемая в положительном направлении от произвольной точки ${{a}_{0}} \in \partial {{D}_{n}}$. Очевидно, где ${{\theta }}({{\xi }})$ – угол между касательной l, инцидентной точке ${{\xi }} \in \partial {{D}_{n}}$, и положительным направлением действительной оси, см. рис. 1 .

Следовательно,

и

По предположению, контур $\partial {{D}_{n}}$ состоит из дуг Ляпунова, – дуг, во внутренних точках которых угол ${{\theta }}$ – непрерывная функция ${{\xi }}$, удовлетворяющая, к тому же, условию Гельдера H. Классу H, очевидно, принадлежит и экспонента $\exp ( - 2i{{\theta }})$, поэтому вблизи неугловых точек $\partial {{D}_{n}}$ функция $I{\text{'}}(z)$ ограничена.

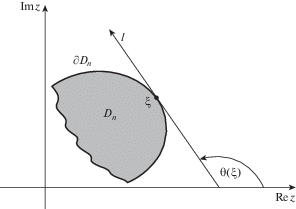
Выясним, что происходит вблизи угловых точек, где функция ${{\theta }}({{\xi }})$ претерпевает разрыв. При этом мы воспользуемся одной важной теоремой из [17]. В упрощенном варианте она формулируется следующим образом: пусть ${{L}_{1}},\;{{L}_{2}},\; \ldots ,\;{{L}_{K}}$ – гладкие дуги, инцидентные точке a; на каждой из дуг ${{L}_{k}}$ задана своя функция ${{q}_{k}}({{\xi }})$, принадлежащая классу H, и направление интегрирования. Обозначим через $Q(z)$ сумму интегралов типа Коши:

Тогда в достаточно малой окрестности точки a

Знак “+” перед слагаемым ${{q}_{k}}(a)$ выбирается, если интегрирование по ${{L}_{k}}$ идет по направлению к точке $a$, знак “–” – если в противоположном направлении.

Применим эту теорему к нашему случаю. Пусть a – угловая точка контура $\partial {{D}_{n}}$; она инцидентна двум дугам (т.е. K = 2). На этих дугах задана функция $\exp ( - 2i{{\theta }})$, принадлежащая классу H. Задано и направление интегрирования (против часовой стрелки). Пусть ${{L}_{1}}$ – дуга, которая заканчивается точкой a, ${{L}_{2}}$ – дуга, которая с нее начинается. Таким образом, ${{q}_{1}}({{\xi }}) = \exp \left( { - 2i{{\theta }}({{\xi }})} \right)$, ${{\xi }} \in {{L}_{1}}$; ${{q}_{2}}({{\xi }}) = \exp \left( { - 2i{{\theta }}({{\xi }})} \right)$, ${{\xi }} \in {{L}_{2}}$, а ${{q}_{1}}(a)$ и ${{q}_{2}}(a)$ – предельные значения ${{q}_{1}}({{\xi }})$ и ${{q}_{2}}({{\xi }})$ при ${{\xi }} \to a$.

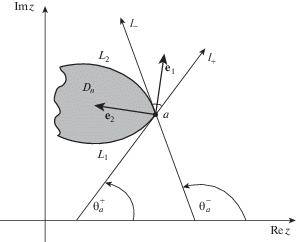
Пусть ${{\theta }}_{a}^{ + }$ и ${{\theta }}_{a}^{ - }$ – предельные значения угла ${{\theta }}$, см. рис. 2:

(пределы односторонние). Тогда

В силу (4.9) и следующего за (4.9) замечания относительно выбора знаков,

Притом неважно, слева или справа (изнутри или извне контура $\partial {{D}_{n}}$) приближаемся мы к угловой точке. Поэтому для ${{\psi }}_{n}^{'}(z)$ и $\Psi {\text{'}}(z)$ мы имеем одну асимптотику: при $z \to a$

Заметим, что (4.11) – асимптотика еще и для ${{\psi '}}(z)$, так как ${{\psi '}}(z) = \Psi {\text{'}}(z) + {{\Gamma }_{2}}$. Итак, производные второго потенциала Колосова при приближении к угловым точкам границы стремятся к бесконечности по логарифмическому закону (исключение составляет случай ${\kern 1pt} {{\Gamma }_{1}} = 0$, – он был рассмотрен выше). Но след тензора напряжений ${\mathbf{\sigma }}$ – величина ограниченная: по первой из формул (4.1), след равен $4{\kern 1pt} {{\Gamma }_{1}}$ в $D$ и $4{{\Gamma }_{1}}({{\kappa }} + 1){\text{/}}({{{{\kappa }}}_{n}} + 1)$ в – ${{D}_{n}}$. Учитывая это и пользуясь (4.11), находим с помощью (2.3) асимптотику для компонент ${\mathbf{\sigma }}$

Здесь ${\mathbf{O}}(1)$ – симметричная матрица, компоненты которой при $z \to a$ остаются конечными. Напряженное состояние вблизи угловой точки определяется, в основном, первым слагаемым в правой части (4.12) и представляет собой практически чистый сдвиг. Собственные значения ${\mathbf{\sigma }}$ (главные напряжения):

Главные оси тензора напряжений в пределе при $z \to a$ коллинеарны векторам e₁ = = $\left( {\cos \frac{{{{\theta }}_{a}^{ + } + {{\theta }}_{a}^{ - }}}{2},\sin \frac{{{{\theta }}_{a}^{ + } + {{\theta }}_{a}^{ - }}}{2}} \right)$ и ${{{\mathbf{e}}}_{2}} = \left( {\sin \frac{{{{\theta }}_{a}^{ + } + {{\theta }}_{a}^{ - }}}{2}, - \cos \frac{{{{\theta }}_{a}^{ + } + {{\theta }}_{a}^{ - }}}{2}} \right)$ – собственным векторам матрицы

Вектор ${{{\mathbf{e}}}_{{\mathbf{1}}}}$ отвечает собственному числу ${{{{\sigma }}}_{1}}$, и, очевидно, коллинеарен биссектрисе угла между предельными касательными ${{l}_{ + }}$ и ${{l}_{ - }}$; рис. 2. Вектор ${{{\mathbf{e}}}_{2}}$ ему ортогонален.

Итак, независимо от условий на бесконечности, предельное положение одной из главных осей тензора напряжений – это биссектриса угла, который образован касательными, инцидентными угловой точке.

Замечание 1. Если a – не просто угловая точка, а точка заострения:

то, согласно (4.12), напряжения в окрестности a ограничены. Этот результат согласуется со следующим фактом (и является, в некотором смысле, его обобщением): пусть включение D_n – трещина (то есть, бесконечно узкая щель) произвольной конфигурации. Тогда, очевидно, и производная $I{\text{'}}$ этого интеграла – тоже 0. Иными словами, трещину, заполненную материалом с “общим” модулем сдвига, поле напряжений во внешней области “не замечает”. Поэтому в окрестности трещины, а значит, и вблизи точки заострения – ее устья напряжения будут конечными.

5. Примеры. 5.1. Эллиптическое включение. Полное решение задачи теории упругости для изотропного эллиптического включения дано в [5]. Здесь мы только убедимся в том, что формулы (4.6) дают правильный ответ для случая, когда модули сдвига включения и плоскости совпадают.

Итак, единственное включение занимает область $D{{{\kern 1pt} }_{1}}$, граница которой $\partial {{D}_{1}}$ – эллипс. Будем считать, что сумма полуосей эллипса равна 2: большая полуось равна $1 + {{\beta }}$, малая – $1 - {{\beta }}$, где ${{\beta }} \in (0,\;1)$; центр совпадает с началом координат; большая полуось ориентирована вдоль действительной оси. Константа Колосова, характеризующая свойства включения, равна ${{\kappa }_{1}}$; константа Колосова для области D (т.е. для плоскости с исключенным из нее эллипсом) равна $\kappa $. Это соответствует обозначениям, принятым в разделах 2 и 3.

Искомые потенциалы Колосова: в области $D{{{\kern 1pt} }_{1}}$ – ${{{{\varphi }}}_{1}}(z)$ и ${{{{\psi }}}_{1}}(z)$, в $D{\kern 1pt} $ – ${{\varphi }}(z) = {{\Gamma }_{1}}z$ + + Φ(z) и ${{\psi }}(z) = {{\Gamma }_{2}}z + \Psi (z)$, где $\Phi (\infty ) = \Psi (\infty ) = 0$. Граничные условия, которым эти функции удовлетворяют – частный случай (3.6) и (3.10) при N = 1:

Функции $\Phi (z)$ и ${{{{\varphi }}}_{1}}(z)$ находятся просто: из (4.6),

Для того, чтобы найти с помощью (4.6) функции ${{{{\psi }}}_{1}}(z)$ и $\Psi (z)$, мы должны вычислить интеграл по эллипсу $\partial {{D}_{1}}$

Произведем замену: ${{\xi }} = {{\varepsilon }} + \frac{{{\beta }}}{{{\varepsilon }}}$; тогда (5.3) сведется к интегралу по окружности $\left| {{\varepsilon }} \right| = 1$:

Здесь учтено, что $d{{\xi }} = (1 - {{\beta /}}{{{{\varepsilon }}}^{2}})d{{\varepsilon }}$ и 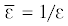. Особые точки подынтегральной функции: начало координат и два (в общем случае) корня уравнения

Обозначим через ε₁ корень, наименьший по абсолютной величине. Поскольку $\left| {{\beta }} \right|$ < 1, при любом z он находится внутри единичной окружности. Второй корень, ${{{{\varepsilon }}}_{2}} = {{\beta /}}{{{{\varepsilon }}}_{1}}$, находится внутри этой окружности, если $z \in {{D}_{1}}$, и вне ее, если $z \notin {{D}_{1}}$. В последнем случае можем написать:

Здесь имеется в виду ветвь квадратного корня, для которой

Вне эллипса ${{{{\varepsilon }}}_{1}}(z)$ – однозначная функция. Действительно, точки ветвления функции $\sqrt {{{z}^{2}} - 4{{\beta }}} $ – это фокусы эллипса. При обходе контура, охватывающего оба фокуса, а тем более весь эллипс, квадратный корень не испытывает приращения.

Теперь вычислить интеграл (5.4) (используя теорию вычетов), не составляет труда:

Легко проверить, что в соответствии с теоремой Племеля,

Подставляя (5.6) в (4.6), получаем формулы для $\Psi (z)$ и ${{\psi }_{1}}(z)$:

где ${{{{\varepsilon }}}_{1}}(z)$ вычисляется по формуле (5.5). Формулы (5.2) и (5.8) решают краевую задачу (5.1): то, что удовлетворяется второе граничное условие (5.1), очевидно. С помощью (5.7) можно убедиться в том, что первое граничное условие (5.1) тоже выполнено.

Обратим внимание на тот факт, что функции ${{{{\varphi }}}_{1}}(z)$ и ${{{{\psi }}}_{1}}(z)$ линейны по z. Так и должно быть: это значит, что напряженное состояние внутри эллиптического включения однородно.

Заметим также, что при β = 1 (когда эллиптическое включение вырождается в прямолинейную щель), из (5.8) имеем:

т.е. поле напряжений во внешней области тоже будет однородным, таким же, каким оно было бы в отсутствие включения. Это – частный случай ситуации, рассмотренной в конце предыдущего раздела, см. Замечание 1.

5.2. Набор из N кругов. Пусть области D_n, $n = 1,\; \ldots ,\;N$ – попарно не пересекающиеся круги. Центр круга D_n находится в точке z_n, радиус равен r_n. Требуется решить краевую задачу (3.6), (3.10).

Ответ для функций $\Phi (z)$ и ${{{{\varphi }}}_{n}}(z)$ готов – это формулы (4.1). Для того, чтобы найти, пользуясь (4.5), функции $\Psi (z)$ и ${{{{\psi }}}_{n}}(z)$, необходимо вычислить интеграл (4.8) по каждой окружности. Это нетрудно:

Подставляем (5.9) в (4.5):

Формулы (4.1) и (5.10) решают краевую задачу (3.6), (3.10). Это легко проверить непосредственной подстановкой, если учесть, что поскольку $\partial {{D}_{n}}$ – окружность радиуса r_n, а z_n – ее центр,

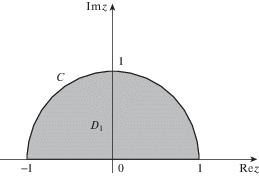
5.2. Полукруг. Пусть включение снова одно, и это – полукруг D₁ (рис. 3.), ограниченный дугой C – верхней полуокружностью единичной окружности и отрезком действительной оси [–1, 1]:

Требуется решить задачу (5.1).

Функции $\Phi (z)$ и ${{{{\varphi }}}_{1}}(z)$ определяются, как и в случае эллиптического включения, формулами (5.2). Для того, чтобы найти с помощью (4.6) функции ${{{{\psi }}}_{1}}(z)$ и $\Psi (z)$, мы должны взять интеграл по границе полукруга:

Переходя от средней части (5.11) к правой, мы учли, что 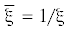, если ${{\xi }} \in C$; и ${{\bar {\xi }}} = {{\xi }}$, если ${{\xi }} \in [ - 1,\;1]$. Дальнейшие вычисления интереса не представляют, – они основаны на элементарной теории вычетов. Приведем ответ:

Под ln(…) в правой части (5.12) можно понимать, например, ветвь логарифма: $\ln z = \ln \left| z \right| + i\arg z$, где $\arg z \in \left( { - {{\pi }},{{\pi }}} \right)$.

Пусть ${{I}_{ + }}(z)$, ${{I}_{ - }}(z)$ – сужение функции $I(z)$ соответственно на ${{D}_{1}}$ и D:

Заметим, что ${{I}_{ + }}(z)$ и ${{I}_{ - }}(z)$ – однозначные функции, каждая в своей области определения. Действительно: внутри контура, расположенного в ${{D}_{1}}$, не содержится ни одной из двух точек ветвления логарифма ($z = \pm 1$); внутри контура, расположенного в $D$, лежат обе эти точки, поэтому в обоих случаях аргумент комплексной величины $(z - 1){\text{/}}(z + 1)$ при обходе по контуру не изменяется. Важно, что при $z \to 0$

При $z \to \pm 1$:

Легко проверить, что согласно теореме Племеля,

Далее: вычислим производные $I_{ + }^{'}(z)$ и $I_{ - }^{'}(z)$. Дифференцирование (5.13) дает:

При стремлении $z$ к любой неугловой точке контура, производные стремятся к конечным пределам. В частности,

Из (5.16) заключаем, что вблизи угловой точки $z = 1$

а окрестности точки z = –1,

Итак, при $z \to \pm 1$ производная интеграла (5.11) стремится к бесконечности по логарифмическому закону.

Сравним (5.17) и (5.18) с результатами, которые были получены в разделе 4, а именно – с асимптотикой (4.10). Напомним, что в разделе 4 через ${{\theta }}_{a}^{ + }\;$ и ${{\theta }}_{a}^{ - }$ обозначены углы, которые образуют левая и правая касательные, инцидентные угловой точке a, с действительной осью, см. рис. 2. В данном случае, угловых точек две: 1 и –1. Для первой точки:

Подставив значения (5. 19) в (4.10), получим правую часть (5.17). Если же $a = - 1$, будем иметь:

Подставив (5.20) в (4.10), придем к (5.18). Таким образом, асимптотики (5.17) и (5.18) – это частные случаи (4.10); так и должно быть.

Согласно (4.6),

Формулы (5.21) и (5.2) дают решение краевой задачи (5.1). То, что функции (5.2) удовлетворяют второму условию (5.1), очевидно. Используя (5.15), убеждаемся в том, что первое граничное условие тоже выполнено. Обратим внимание, что в силу (5.14) функции $\Psi (z)$ и ${{\psi }_{1}}(z)$ вблизи угловых точек ограничены; следовательно, смещения всюду конечны.

Приведем также явные выражения для $\Psi (z)$ и ${{{{\psi }}}_{1}}(z)$:

Формулы (5.22) и (5.2) позволяют найти компоненты тензора напряжений ${\mathbf{\sigma }}$ во всей плоскости. Но мы ограничимся асимптотиками при $z \to \pm 1$, которые проще всего получить из общей формулы (4.12):

и

Здесь ${\mathbf{O}}(1)$ – ограниченная симметричная матрица. Главные напряжения ${{\sigma }_{1}}$ и ${{\sigma }_{2}}$ вблизи угловых точек, согласно (4.13),

где $a = \pm 1$.

6. Сводка результатов. В статье рассмотрена двумерная задача теории упругости для плоскости с одним или несколькими включениями, модули сдвига которых совпадают с модулями сдвига плоскости. Никаких ограничений на модули сжатия нет. Границы включений предполагаются кусочно-гладкими, состоящими из конечного числа дуг Ляпунова. Условия на бесконечности задаются в терминах напряжений. Использован метод Колосова–Мусхелишвили. Основные результаты:

1. Для потенциалов Колосова получено общее решение в квадратурах.

2. Показано, что вблизи угловых точек границы включения напряженное состояние представляет собой практически чистый сдвиг и что напряжения растут по логарифмическому закону. Получены соответствующие асимптотики. Найдено предельное положение главных осей тензора напряжений. Показано, что оно определяется локальной геометрией границы и не зависит от условий на бесконечности.

3. Показано, что вблизи точек заострения напряжения остаются ограниченными и что трещина (бесконечно узкая щель), заполненная материалом с “общим” модулем сдвига, не влияет на поле напряжений во внешней области.

4. Вычислены потенциалы Колосова для нескольких конкретных случаев: когда включение представляет собой эллипс; полукруг; а также когда включений несколько, и это – круги разных радиусов с разными модулями сжатия.