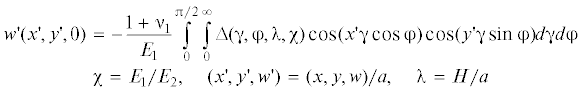Известия РАН. Механика твердого тела, 2022, № 1, стр. 59-67
КОНТАКТ ГЛАДКОГО ИНДЕНТОРА И ДВУХСЛОЙНОГО УПРУГОГО ПОЛУПРОСТРАНСТВА С УСЛОЖНЕННЫМИ УСЛОВИЯМИ НА ПОВЕРХНОСТИ
Ф. И. Степанов a, *, Е. В. Торская a, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: stepanov_ipm@mail.ru
** E-mail: torskaya@mail.ru
Поступила в редакцию 26.02.2021
После доработки 15.03.2021
Принята к публикации 13.05.2021
- EDN: YZLOML
- DOI: 10.31857/S0572329921060131
Аннотация
Рассмотрена задача о нагружении текстурированного двухслойного упругого основания жестким гладким индентором. На границе раздела текстурированного слоя и полупространства заданы условия полного сцепления. Элементами рельефа являются упругие цилиндры, характеризующиеся высотой и радиусом, располагающиеся на поверхности основания с заданным периодом. Для описания механических свойств элементов рельефа используется одномерная модель Винклера. Решение контактной задачи осуществляется с помощью метода граничных элементов. Давление, перемещения, а также форма индентора аппроксимируются кусочно-постоянными функциями. Коэффициенты взаимного влияния строятся с помощью метода, основанного на двойных интегральных преобразованиях Фурье. Проведен анализ влияния плотности расположения элементов текстуры и их податливости на распределение контактного давления. Получено, что в большинстве случаев контакт осуществляется только с элементами текстуры. Для относительно жесткого текстурированного слоя важно комбинированное влияние изгиба слоя и дополнительной податливости, сообщаемой элементами текстуры. Для относительно жестких и податливых текстурированных слоев получены кривые нагрузка–внедрение в зависимости от периода текстуры. В рамках предложенной постановки также рассмотрен предельный случай контакта индентора со слоем Винклера, полностью покрывающим поверхность двухслойного упругого полупространства. Получены и проанализированы кривые нагрузка–внедрение для индентора, имеющего форму пирамиды Берковича.
1. Введение. Создание на поверхности определенного рельефа (текстуры) является распространенным технологическим приемом, преследующим разные цели, такие как создание объемов для удержания смазки и вывода продуктов износа в условиях фрикционного контакта, управления коэффициентом трения и жесткостью контакта путем варьирования геометрии и взаимного расположения элементов текстуры и т.д. При решении задач о контакте текстурированных поверхностей принято пользоваться методами и подходами, разработанными для механики дискретного контакта. Для однородных упругих тел периодические задачи были рассмотрены в ряде работ, таких как [1–5]. Контактные задачи для покрытий переменной толщины, возникающей из-за наличия текстуры, можно рассматривать с помощью приближенных методов, как, например, в работе [6], где рассматривалась соответствующая плоская задача. Пространственная задача о нагружении текстурированного слоя, сцепленного с жестким полупространством, рассмотрена в работе [7]. Приближенный метод решения пространственной задачи для покрытия, масштаб неровностей на поверхности которого существенно уступает толщине покрытия, разработан в [8].
В данной работе предложена постановка и метод решения задачи о контакте гладкого индентора и двухслойного упругого полупространства, на поверхности которого находится периодическая система одинаковых элементов текстуры.
Также на поверхности покрытий могут существовать тонкие слои, как правило достаточно податливые, возникающие в процессе эксплуатации. Типичным примером является слой, возникающий в процессе трения (так называемый трибослой). Определение свойств этого слоя позволяет получить важную информацию о процессах, происходящих при фрикционном взаимодействии. Механические свойства слоя можно определить с помощью наноиндентирования. Существуют экспериментальные работы по индентированию поверхностей трения [10–12], но для корректной идентификации механических свойств поверхностных пленок при интерпретации результатов необходимо учитывать деформацию покрытия и подложки, особенно в случае относительно жестких покрытий. В [12] приведены результаты определения механических свойств трибопленки на поверхности углеродного покрытия при индентировании шариком (осесимметричная задача). В данной работе показано, что в рамках предложенной модели для решения задачи о контакте текстурированной поверхности можно в качестве предельного случая рассмотреть пространственную задачу о контакте гладкого индентора произвольной формы и двухслойного упругого полупространства с относительно податливым слоем на поверхности.
2. Постановка задачи. Рассматривается нагружение жестким индентором двухслойного упругого основания, на поверхность которого нанесен периодический рельеф (рис. 1). Нижняя часть основания представляет из себя упругое полупространство с модулем упругости E2 и коэффициентом Пуассона ${{{{\nu }}}_{2}}$. Верхний слой также является упругим и описывается конечной толщиной H, а также модулем упругости E1 и коэффициентом Пуассона ${{{{\nu }}}_{1}}$. Условия на границе полупространства и верхнего слоя соответствуют полному сцеплению:
(2.1)
$\begin{gathered} {{w}^{{(1)}}} = {{w}^{{(2)}}},\quad u_{x}^{{(1)}} = u_{x}^{{(2)}},\quad u_{y}^{{(1)}} = u_{y}^{{(2)}} \\ {{\sigma }}_{z}^{{(1)}} = {{\sigma }}_{z}^{{(2)}},\quad {{\tau }}_{{xz}}^{{(1)}} = {{\tau }}_{{xz}}^{{(2)}},\quad {{\tau }}_{{yz}}^{{(1)}} = {{\tau }}_{{yz}}^{{(2)}} \\ \end{gathered} $Здесь ${{{{\sigma }}}_{z}}$, ${{{{\tau }}}_{{xz}}}$, ${{{{\tau }}}_{{yz}}}$ – нормальное и касательные напряжения, $w$, ${{u}_{x}}$, ${{u}_{y}}$ – нормальные и касательные перемещения в материале слоя (1) и полупространства (2).
Элементами рельефа являются упругие цилиндры высотой $h$ и радиусом r, располагающиеся на поверхности основания с периодом T. Для описания механических свойств элементов рельефа используется одномерная модель упругого материала, характеризуемая податливостью ${{\eta }} = h{\text{/}}{{E}_{a}}$. Правосторонняя декартова система координат $XYZ$ располагается таким образом, что ее центр находится в плоскости, проходящей через вершины элементов рельефа в недеформированном состоянии, а ось аппликат направлена по нормали к указанной плоскости в сторону, противоположную основанию. Форма индентора описывается гладкой функцией $f(x,y)$. Индентор нагружен вертикальной силой Q. Граничные условия в плоскости z = 0:
(2.2)
$\begin{gathered} {\text{ }}f{\text{*}}(x,y) + {{w}^{{(1)}}}(x,y) + w{\text{*}}(x,y) = f(x,y) - D,\quad (x,y) \in {\text{ }}\Omega \\ {\text{ }}{{{{\sigma }}}_{z}} = 0,\quad (x,y) \notin \Omega \\ {\text{ }}{{{{\tau }}}_{{xz}}} = 0,\quad {{{{\tau }}}_{{{\text{yz}}}}} = 0 \\ \end{gathered} $Здесь $\Omega $ – номинальная область контакта, $f{\text{*}}(x,y)$ – форма поверхности в недеформированном состоянии, ${{w}^{{(1)}}}(x,y)$ – вертикальные перемещения верхней границы двуслойного основания, на котором находятся элементы текстуры, $w{\text{*}}(x,y)$ – вертикальные перемещения верхних точек элементов текстуры относительно поверхности двуслойного основания (вне элементов текстуры $w{\text{*}}(x,y) = 0$), D – внедрение индентора. При этом контактное давление $p(x,y) = - {{{{\sigma }}}_{z}}(x,y)$, номинальная область контакта $\Omega $ и внедрение D – неизвестны.
Также выполняется условие равновесия:
3. Метод решения. Решение контактной задачи осуществляется с помощью метода граничных элементов. Прямоугольная область $\Omega {\text{*}}$, включающая в себя искомую область контакта, разбивается на $N$ квадратных элементов ${{\Omega }_{i}}$, $i = 1..N$. Давление, перемещения, а также форма индентора внутри этой области аппроксимируются кусочно-постоянными функциями (${{p}_{i}}$, ${{\tilde {w}}_{i}}$, $w_{i}^{*}$, ${{f}_{i}}$, $f_{i}^{*}$, ${\text{ }}i = 1..N$). Для определения зависимости вертикальных перемещений границы двуслойного основания от приложенного давления используется решение задачи о действии нагрузки q, равномерно распределенной внутри квадрата со стороной 2a на поверхности двухслойного упругого основания [9]:
Функция $\Delta ({{\gamma }},{{\varphi }},{{\lambda }},{{\chi }})$ определяется из решения системы линейных функциональных уравнений, полученных из граничных условий в результате использования бигармонических функций для определения напряжений и перемещений, а также примененного к постоянной нагрузке двойного интегрального преобразования Фурье. Функция $\Delta ({{\gamma }},{{\varphi }},{{\lambda }},{{\chi }})$ линейно зависит от результата применения двойного преобразования Фурье к постоянному давлению:
(3.2)
$\bar {q} = q\frac{4}{{{{{{\pi }}}^{2}}}}\frac{{\sin ({{\gamma }}\cos {{\varphi }})\sin ({{\gamma }}\sin {{\varphi }})}}{{{{{{\gamma }}}^{2}}\sin {{\varphi }}\cos {{\varphi }}}}$Благодаря тому, что вертикальные перемещения границы линейно зависят от приложенного давления внутри каждого элемента, вертикальные перемещения границы двуслойного основания, а также перемещения элементов рельефа могут быть выражены через давление следующим образом:
(3.3)
$\left( {\begin{array}{*{20}{c}} {{\text{k}}_{1}^{1}}& \cdots &{{\text{k}}_{N}^{1}} \\ \vdots & \ddots & \vdots \\ {{\text{k}}_{1}^{N}}& \cdots &{{\text{k}}_{N}^{N}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ \vdots \\ {{{p}_{N}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{\tilde {w}}}_{1}}} \\ \vdots \\ {{{{\tilde {w}}}_{N}}} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {{{{{\eta }}}_{1}}}& \cdots &0 \\ \vdots & \ddots & \vdots \\ 0& \cdots &{{{{{\eta }}}_{N}}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ \vdots \\ {{{p}_{N}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {w_{1}^{*}} \\ \vdots \\ {w_{N}^{*}} \end{array}} \right)$(3.4)
${\text{k}}_{i}^{j} = - \frac{{1 + {{{{\nu }}}_{1}}}}{{{{E}_{1}}}}\int\limits_0^{{{\pi }}/2} {\int\limits_0^\infty {\Delta {\text{'}}({{\gamma }},{{\chi }},{{\varphi }},{{\lambda }})\cos ({{y}_{{ij}}}{{\gamma }}\sin {{\varphi }})\cos ({{x}_{{ij}}}{{\gamma }}\cos {{\varphi }})} } d{{\gamma }}d{{\varphi }}$Здесь ${{(x_{{ij}}^{2} + y_{{ij}}^{2})}^{{1/2}}}$ – расстояние между центрами элементов-квадратов.
Граничные условия (2.2) и условие равновесия (2.3) могут быть выражены с помощью введенных кусочно-постоянных функций:
(3.5)
$\left( {\begin{array}{*{20}{c}} {4{{a}^{2}}}& \cdots &{4{{a}^{2}}}&0 \\ {{\text{k}}_{1}^{1} + {{{{\eta }}}_{1}}}& \cdots &{{\text{k}}_{N}^{1}}&1 \\ \vdots & \ddots & \vdots & \vdots \\ {{\text{k}}_{1}^{N}}& \cdots &{{\text{k}}_{N}^{N} + {{{{\eta }}}_{N}}}&1 \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ \vdots \\ {{{p}_{N}}} \\ D \end{array}} \right) = \left( {\begin{array}{*{20}{c}} Q \\ {{{f}_{1}} - f_{1}^{*}} \\ \vdots \\ {{{f}_{N}} - f_{N}^{*}} \end{array}} \right)$Поскольку область $\Omega {\text{*}}$ заведомо больше области контакта, при решении системы (3.5) давления pi, $i = 1..N$ могут принимать положительные, отрицательные и нулевые значения, что противоречит граничным условиям. Поскольку элементы с отрицательным давлением не являются частью площадки контакта, им присваивается нулевое значение, ранг матрицы системы уравнений (3.5) сокращается, затем система решается заново. Процесс продолжается до тех пор, пока в решении не окажется элементов с отрицательным давлением. В результате приближенно определяется область контакта, контактное давление и внедрение индентора. Следует отметить, что условие контакта только по поверхности элементов текстуры не ставится заранее, более того, при некоторых комбинациях входных параметров возможен контакт индентора с деформированной поверхностью упругого слоя вне элементов текстуры.
4. Результаты расчетов (текстурированный слой). Расчеты проводились для индентора имеющего форму параболоида $f(x,y) = ({{x}^{2}} + {{y}^{2}}){\text{/}}2R$, где $R$ – радиус. При расчетах рассматривались элементы рельефа, имеющие форму цилиндра радиусом ${{r}_{a}}$ и высотой ${{H}_{a}}$ и расположенные периодически с периодом T, при этом модуль упругости элементов рельефа равен модулю упругости слоя (${{E}_{a}} = {{E}_{1}}$). Результаты получены для полупространства, покрытого относительно жестким слоем и для полупространства, покрытого относительно мягким слоем. Результаты представлены в безразмерном виде, при этом безразмерные параметры получены следующим образом: $(x{\text{'}},y{\text{'}},z{\text{'}}) = (x,y,z){\text{/}}R$, $p{\text{'}}$ = = p/E1, $Q{\text{'}} = Q{\text{/}}{{E}_{1}}{{R}^{2}}$.
На рис. 2 представлено распределение контактного давления при внедрении сферического индентора в различные типы оснований под действием различных усилий. На рис. 2 a, b наблюдается неполный контакт основания и индентора: в контакт с индентором вступают только поверхности элементов рельефа. В случаях, изображенных на рис. 2 c, d имеем полный контакт вблизи центра индентора и неполный на краях. Пики давлений концентрируются на краях элементов неровностей. Во всех рассмотренных случаях максимальное контактное давление находится на краю элемента неровности, центр которой совпадает с осью симметрии индентора.
Рис. 2.
Распределение контактного давления для относительно жестких (b, d) и относительно податливых текстурированных покрытий (a, c) при разных значениях силы: $Q{\text{'}} = {\text{0}}{\text{.3571}} \times {{10}^{{ - 4}}}$ (a), $Q{\text{'}} = {\text{0}}{\text{.3571}} \times {{10}^{{ - 5}}}$ (b), $Q{\text{'}} = 2.1426 \times {{10}^{{ - 4}}}$ (c), $Q{\text{'}} = 2.1426 \times {{10}^{{ - 5}}}$ (d); ${{E}_{1}}{\text{/}}{{E}_{2}}$ = 10, ${{\nu }_{1}} = 0.3$, ${{\nu }_{2}} = 0.4$ (b, d); ${{E}_{1}}{\text{/}}{{E}_{2}}$ = 0.1, ${{\nu }_{1}} = 0.4$, ${{\nu }_{2}} = 0.3$ (a, c); $r_{a}^{'} = 5 \times {{10}^{{ - 3}}}$; $H_{a}^{'} = H' = {{10}^{{ - 4}}}$, ${{E}_{a}} = {{E}_{1}};$ $T{\text{'}} = 1{\text{/}}80$.
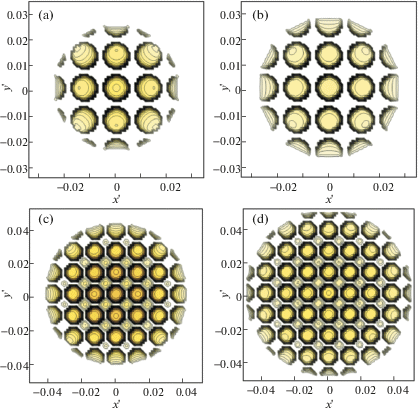
Деформированная поверхность слоя и элементов текстуры изображена на рис. 3 для тех же параметров задачи, что рассматривались на рис. 2. В случае неполного контакта поверхность между инденторами имеет кривизну, при этом максимальные вертикальные смещения находятся вблизи границ элементов неровности, что обусловлено концентрацией контактного давления на краях неровностей.
Рис. 3.
Форма поверхности слоя под элементами текстуры для относительно податливого (а) и относительно жесткого (b) слоя: ${{E}_{1}}{\text{/}}{{E}_{2}} = 0.1$, ${{\nu }_{1}} = 0.4$, ${{\nu }_{2}} = 0.3$ (a); ${{E}_{1}}{\text{/}}{{E}_{2}}$ = 10, ${{\nu }_{1}} = 0.3$, ${{\nu }_{2}} = 0.4$ (b); $Q{\text{'}} = {\text{0}}{\text{.3571}}$ × × 10–5 (а, кривая 1), $Q{\text{'}} = {\text{0}}{\text{.3571}} \times {{10}^{{ - 4}}}$ (a, кривая 2), $Q{\text{'}} = 2.1426 \times {{10}^{{ - 5}}}$ (b, кривая 1), $Q{\text{'}} = 2.1426 \times {{10}^{{ - 4}}}$ (b, кривая 2); $r_{a}^{'} = 5 \times {{10}^{{ - 3}}}$, $H_{a}^{'} = H{\text{'}} = {{10}^{{ - 4}}}$, ${{E}_{a}} = {{E}_{1}};$ $T{\text{'}} = 1{\text{/}}80$.
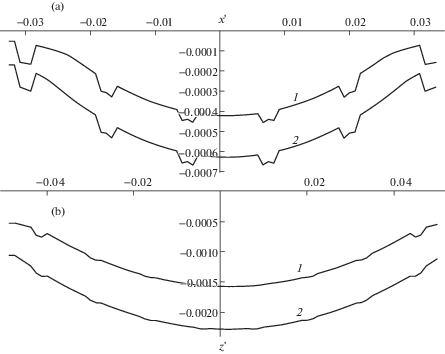
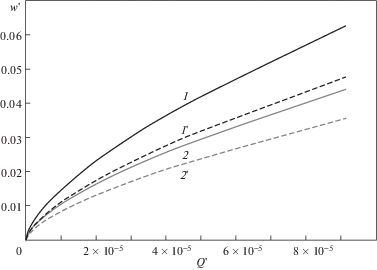
Была исследована зависимость внедрения индентора от нагрузки для двух различных случаев относительной жесткости слоя и двух периодов, характеризующих взаимное расположение неровностей (рис. 4). При этом безразмерная нагрузка $Q{\text{'}} = Q{\text{/}}{{E}_{1}}{{R}^{2}}$ в обоих случаях получена относительно модуля упругости ${{E}_{1}}$ жесткого покрытия, чтобы иметь возможность сравнить результаты для одинаковой абсолютной. Во всех случаях наблюдается нелинейная зависимость между внедрением и нагрузкой. Наибольший рост внедрения при увеличении нагрузки наблюдается вблизи нуля. При увеличении нагрузки, значение $\partial D{\text{/}}\partial Q$ постепенно снижается до некоторого постоянного значения. Ожидаемо, меньшему значению периода взаимного расположения неровностей соответствует меньшее внедрение индентора. Характер зависимости внедрения от нагрузки схож для случаев относительно жестких и относительно мягких текстурированных покрытий.
Рис. 4.
Кривые нагрузка-внедрение для относительно жесткого (кривые 1 и 1') и относительно податливого (кривые 2 и 2') слоев при периодах $T{\text{'}} = 1{\text{/}}60$ (кривые 1 и 2) и $T{\text{'}} = 1{\text{/}}80$ (кривые 1' и 2'); ${{E}_{1}}{\text{/}}{{E}_{2}}{\text{ = 10}}$, ${{\nu }_{1}} = 0.3$, ${{\nu }_{2}} = 0.4$ (кривые 1 и 1'); ${{E}_{1}}{\text{/}}{{E}_{2}} = 0.1$, ${{\nu }_{1}} = 0.4$, ${{\nu }_{2}} = 0.3$ (кривые 2 и 2'); $r_{a}^{'} = 5 \times {{10}^{{ - 3}}}$; $H_{a}^{'} = H{\text{'}} = {{10}^{{ - 4}}}$; ${{E}_{a}} = {{E}_{1}}$.
5. Результаты расчетов (однородный слой). Разработанный метод решения для случая $w{\text{*}}(x,y) \ne 0$ во всех внутренних точках области $\Omega $, был использован для исследования контакта двухслойного упругого полупространства, на поверхности которого находится слой постоянной толщины Hw, описываемый моделью Винклера с податливостью ${{{{\eta }}}_{w}} = {{H}_{w}}{\text{/}}{{E}_{w}}$, и гладкого индентора произвольной формы. С практической точки зрения наиболее востребованной является задача о вдавливании пирамиды Берковича, поскольку она может быть использована при интерпретации результатов индентирования поверхностей покрытий с тонкими пленками. Этот тип головок представляет собой трехгранную пирамиду с закругленным концом (по ГОСТ Р. 8.904-2015 радиус закругления ${{R}_{b}}$ может быть от 20 до 50 нм, в ходе эксплуатации увеличивается). При исследовании тонких пленок все чаще индентирование происходит в упругом режиме, что не позволяет определять твердость исследуемых материалов, но может дать информацию об их упругих свойствах.
Для демонстрации возможностей метода было исследовано вдавливание индентора, геометрия которого определяется ГОСТ Р. 8.904-2015, в относительно жесткое покрытие с модулем Юнга 70 ГПа, нанесенное на подложку с модулем 7 ГПа; на поверхности покрытия находится податливая пленка (0.14 ГПа). В работе [13] показано, что в случае относительно жестких покрытий деформация подложки оказывает существенное влияние на кривую нагрузка–внедрение даже при малых значениях нагрузки.
Полученные результаты представлены на рис. 5 и рис. 6 в размерных величинах (координаты в метрах, нагрузка и давление в Ньютонах и Паскалях соответственно). По рис. 5 можно сравнить распределения контактного давления под индентором при наличии либо отсутствии поверхностной пленки. Помимо ожидаемого результата – увеличения области контакта и уменьшения максимального давления, следует отметить, что форма распределения при наличии пленки ближе к пирамидальной.
Рис. 5.
Распределение контактного давления под пирамидой при наличии пленки (а) и без пленки (b). ${{E}_{1}} = 70$ ГПа, ${{E}_{2}} = 7$ ГПа, ${{E}_{w}} = 0.14$ ГПа, ${{\nu }_{1}} = 0.3$, ${{\nu }_{2}} = 0.4$, ${{H}_{w}} = 5$ нм, $H = 10$ нм, ${{R}_{b}} = 400$ нм, $Q = 2.3$ мН.
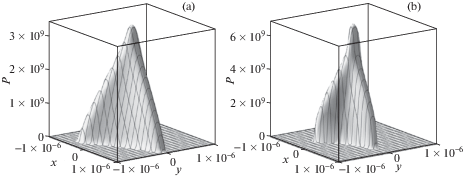
Рис. 6.
Зависимость максимального контактного давления (a) и внедрения (b) от нагрузки при наличии пленки на поверхности покрытия (кривая 2) и без нее (кривая 1). ${{E}_{1}} = 70$ ГПа, ${{E}_{2}} = 7$ ГПа, ${{E}_{w}} = 0.14$ ГПа, ${{\nu }_{1}} = 0.3$, ${{\nu }_{2}} = 0.4$, ${{H}_{w}} = 5$ нм, $H = 10$ нм, ${{R}_{b}} = 400$ нм.
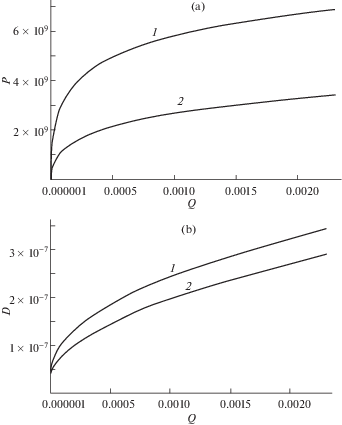
Важным аспектом является влияние пленки на внедрение и максимальное значение контактного давления при индентировании. На рис. 6 представлены соответствующие результаты для выбранного диапазона нагрузки, нижняя граница которого обусловлена чувствительностью численного метода решения. Кривые, иллюстрирующие результаты, полученные для случаев покрытия с поверхностной пленкой и без нее, имеют существенно разные градиенты в области, близкой к нулю (на ранних стадиях нагружения), затем влияние пленки уменьшается. Вопрос о правомерности использования модели Винклера для интерпретации результатов индентирования податливых тонких пленок на жестком основании рассматривался в работе [14], где также представлена экспериментальная верификация модели.
6. Заключение. В рамках данной работы был предложен эффективный способ моделирования контакта жесткого индентора с упругим телом, покрытым текстурированным слоем. Расчеты выполнены для индентора параболической формы, а также относительно мягкого и относительно жесткого покрытия с цилиндрическими неровностями на его поверхности. Результаты показывают, что податливость покрытия существенно зависит от периода расположения неровностей. Выбранная часто используемая форма неровностей (цилиндрическая) вызывает концентрацию контактного давления на краях неровностей, что потенциально может вызвать неравномерный износ такого покрытия.
Предельным случаем предложенной постановки задачи является контакт гладкого индентора с двухслойным упругим полупространством, на поверхности которого находится тонкая пленка (одномерная модель упругого материала). Получены результаты, которые показывают, что при индентировании пирамидой Берковича с малыми нагрузками влияние пленки на кривую нагрузка–внедрение является существенным. Из этого следует, что предложенная модель может быть использована для интерпретации результатов индентирования, диагностирования наличия поверхностных пленок различной природы и оценки их механических свойств.
Работа выполнена при поддержке РФФИ, грант 19-01-00231 (контакт текстурированных поверхностей) и грант 20-58-00007 (индентирование тонких пленок).
Список литературы
Кузнецов Е.А., Гороховский Г.А. О фактическом контактном давлении // Проблемы трения и изнашивания. 1977. № 12. С. 10–15.
Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.
Barber J.R. Contact mechanics. Springer, 2017. 581 p.
Goryacheva I.G., Malanchuk N.I., Martynyak R.M. Contact interaction of bodies with a periodic relief during partial slip // J. Appl. Math. Mech. 2012. V. 76. № 5. P. 695–709.
Tsukanov I.Y. Effects of shape and scale in mechanics of elastic interaction of regular wavy surfaces // Proc. Inst. Mech. Eng., Part J. 2017. V. 231. № 3. P. 332–340.
Soldatenkov I.A. Contact deformation of an elastic composition of a half-plane and a strip of variable width // J. Appl. Math. Mech. 2001. V. 65. № 1. P. 145–153.
Горячева И.Г., Торская Е.В., Степанов Ф.И., Мышкин Н.К., Купреев А.В. Моделирование деформации текстурированного слоя в условиях контактного взаимодействия // Трение и износ. 2017. Т. 38. № 6. С. 526–531.
Torskaya E. Study of roughness effect on elastic indentation of coated bodies // Proc. Inst. Mech. Eng., Part C. 2016. V. 230. № 9. P. 1392–1397.
Никишин B.C., Шапиро Г.С. Пространственные задачи теории упругости для многослойных сред. М.: Вычислительный центр АН СССР, 1970. 260 с.
Liskiewicz T., Kubiak K., Comyn T. Nano-indentation mapping of fretting-induced surface layers // Tribol. Int. 2017. V. 108. P. 186–193.
Губенко М.М., Мезрин А.М., Щербакова О.О., Торская Е.В. Исследование изменения механических свойств поверхностных слоев алюминиевых сплавов в условиях трения скольжения // Трение и износ. 2017. Т. 38. № 5. С. 483–487.
Torskaya E.V., Muravyeva T.I., Sánchez-López J.C. Study of TiC/a-C(:H) Coatings before and after friction by nanoindentation // Proceedings of the 4th International Conference on Industrial Engineering. ICIE 2018. Lecture Notes in Mechanical Engineering. Cham: Springer, 2019. P. 1011–1018.
Степанов Ф.И., Торская Е.В. Моделирование индентирования относительно жестких покрытий индентором произвольной формы // Трение и износ. 2019. Т. 40. № 4. С. 417–423.
Torskaya E., Siroezkin S., Chizhik S. The Method of Elastic Coatings Diagnostics from Indentation Data. Advanced Tribology. Berlin: Springer, 2009. P. 705–706.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела