Известия РАН. Механика твердого тела, 2021, № 6, стр. 23-32
НОВОЕ РЕШЕНИЕ ЗАДАЧИ О ТРЕЩИНЕ В РАСТЯГИВАЕМОЙ ОРТОТРОПНОЙ ПЛАСТИНЕ
В. В. Васильев a, *, С. А. Лурье a, b, В. А. Салов a
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
b Институт прикладной механики РАН
Москва, Россия
* E-mail: vvvas@dol.ru
Поступила в редакцию 17.03.2021
После доработки 22.03.2021
Принята к публикации 29.03.2021
Аннотация
Рассматривается классическая плоская задача теории упругости о трещине в растягиваемой ортотропной упругой неограниченной плоскости, приводящая к сингулярному решению для напряжений в окрестности края трещины. Приводятся соотношения обобщенной теории упругости, включающие малый масштабный параметр. Уравнения обобщенной теории имеют более высокий порядок чем уравнения классической теории и позволяют устранить сингулярность классического решения. Масштабный параметр определяется экспериментально. Полученные результаты определяют влияние длины трещины на несущую способность пластины и сравниваются с результатами эксперимента для пластин из стеклотекстолита и углепластика.
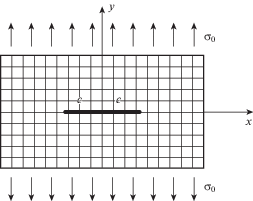
1. Введение – классическое решение задачи о трещине. Рассмотрим неограниченную ортотропную пластину с трещиной длиной 2c, находящуюся в условиях одноосного растяжения напряжением σ0 (рис. 1). Напряженно-деформированное состояние пластины определяется классическим решением, полученным методом комплексных потенциалов [1]. Напряжения определяются равенствами
(1.1)
${{\sigma }_{x}} = - {{p}^{2}}\operatorname{Re} \frac{{A{{w}_{1}}}}{{\sqrt {w_{1}^{2} - {{c}^{2}}} }} - {{q}^{2}}\operatorname{Re} \frac{{B{{w}_{2}}}}{{\sqrt {w_{2}^{2} - {{c}^{2}}} }}$(1.2)
${{\sigma }_{y}} = \operatorname{Re} \frac{{A{{w}_{1}}}}{{\sqrt {w_{1}^{2} - {{c}^{2}}} }} + \operatorname{Re} \frac{{B{{w}_{2}}}}{{\sqrt {w_{2}^{2} - {{c}^{2}}} }}$(1.3)
${{\tau }_{{xy}}} = - p\operatorname{Im} \frac{{A{{w}_{1}}}}{{\sqrt {w_{1}^{2} - {{c}^{2}}} }} - q\operatorname{Im} \frac{{B{{w}_{2}}}}{{\sqrt {w_{2}^{2} - {{c}^{2}}} }}$Здесь A и B – некоторые постоянные коэффициенты, ${{w}_{1}} = x + ipy$, ${{w}_{2}} = x + iqy$, $p = 1{\text{/}}\sqrt {{{k}_{1}}} $, $q = 1{\text{/}}\sqrt {{{k}_{2}}} $ и k1, 2 связаны с корнями характеристического уравнения, соответствующего обобщенному бигармоническому уравнению плоской задачи, и выражаются через упругие постоянные ортотропного материала следующим образом:
Примем y = 0 и рассмотрим интервал $ - с < x < c$, соответствующий границам трещины (рис. 1). Из равенств (1.1), (1.2) следует, что на этом интервале ${{\sigma }_{x}} = {{\sigma }_{y}} = 0$. Выражение (1.3) позволяет заключить, что условие ${{\tau }_{{xy}}} = 0$ на границе трещины выполняется если
При $\left| x \right| \to \infty $ напряжение ${{\sigma }_{у}}$ должно стремиться к ${{\sigma }_{0}}$ (рис. 1). Можно показать, что в пределе для любого луча $y = kx$ имеют место предельные соотношения
В результате из условия ${{\sigma }_{y}}\left( {\left| x \right| \to \infty } \right) \to {{\sigma }_{0}}$ получим $А + В = {{\sigma }_{0}}$. Это условие совместно с уравнением (1.4) дает
Однако из равенства (1.1) следует, что при этих значениях коэффициентов σx также стремится не к нулю, а к σ0 при $\left| x \right| \to \infty .$ Для устранения этого эффекта на напряженное состояние пластины, соответствующее рис. 1, следует наложить сжатие в направлении оси x напряжением σ0 [1]. Окончательно, из равенств (1.1)–(1.3) и (1.5) получим
(1.6)
${{\sigma }_{y}} = - \frac{{{{\sigma }_{0}}}}{{p - q}}\operatorname{Re} \left( {\frac{{q{{w}_{1}}}}{{\sqrt {w_{1}^{2} - {{c}^{2}}} }} - \frac{{p{{w}_{2}}}}{{\sqrt {w_{2}^{2} - {{c}^{2}}} }}} \right)$На действительной оси при $y = 0$ и $x > c$ имеем
(1.7)
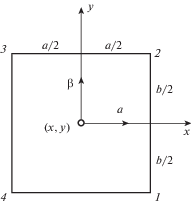
${{\sigma }_{x}} = \sqrt {\frac{{{{E}_{x}}}}{{{{E}_{y}}}}} {{\sigma }_{0}}\left( {\frac{x}{{\sqrt {{{x}^{2}} - {{c}^{2}}} }} - 1} \right)$2. Уравнения плоской задачи обобщенной теории упругости. Обобщенная теория упругости позволяет получить регулярное решение задач, имеющих в рамках классической упругости сингулярное решение [2]. Для вывода соответствующих уравнений рассмотрим показанный на рис. 2 элемент, обладающий малыми, но конечными размерами a и b. Введем локальные координаты $\alpha $ и $\beta $ такие, что $ - a{\text{/}}2 \leqslant \alpha \leqslant a{\text{/}}2$, $ - b{\text{/}}2 \leqslant \beta \leqslant b{\text{/}}2$. Симметричный тензор напряжений $t({{t}_{x}},{{t}_{y}},{{t}_{{xy}}} = {{t}_{{yx}}})$ представим рядом Тейлора в окрестности точки (x, y), т.е.
(2.1)
$\begin{gathered} t(x,y;\alpha ,\beta ) = t(x,y) + \alpha \frac{{\partial t}}{{\partial x}} + \beta \frac{{\partial t}}{{\partial y}} + \frac{1}{{2!}}\left( {{{\alpha }^{2}}\frac{{{{\partial }^{2}}t}}{{\partial {{x}^{2}}}} + 2\alpha \beta \frac{{{{\partial }^{2}}t}}{{\partial x\partial y}} + {{\beta }^{2}}\frac{{{{\partial }^{2}}t}}{{\partial {{y}^{2}}}}} \right) + \\ + \;\frac{1}{{3!}}\left( {{{\alpha }^{3}}\frac{{{{\partial }^{3}}t}}{{\partial {{x}^{3}}}} + 3{{\alpha }^{2}}\beta \frac{{{{\partial }^{3}}t}}{{\partial {{x}^{2}}\partial y}} + 3\alpha {{\beta }^{2}}\frac{{{{\partial }^{3}}t}}{{\partial x\partial {{y}^{2}}}} + {{\beta }^{3}}\frac{{{{\partial }^{3}}t}}{{\partial {{y}^{3}}}}} \right) \\ \end{gathered} $Ограничимся членами представленными в равенстве (2.1) и найдем равнодействующие напряжений, действующих на гранях 1-2 и 3-4 элемента, показанного на рис. 2. Принимая $\alpha = \pm a{\text{/}}2$ и подставляя разложение (2.1), получим
Здесь $t = t({{t}_{x}},{{t}_{{xy}}})$ и символ $(x,y)$ означает, что равнодействующие сил, действующих по граням 2-3 и 1-4 элемента получаются если взаимно заменить x, y; $\alpha $, $\beta $ и a, b. Уравнения равновесия элемента имеют вид
Подставляя сюда равнодействующие R, можно получить дифференциальные уравнения равновесия плоской задачи. Опуская дальнейшие преобразования, описанные в работе [2] для случая a = b, запишем уравнения равновесия в окончательной форме
(2.2)
$\frac{{\partial {{T}_{x}}}}{{\partial x}} + \frac{{\partial {{T}_{{yx}}}}}{{\partial y}} = 0,\quad \frac{{\partial {{T}_{y}}}}{{\partial y}} + \frac{{\partial {{T}_{{xy}}}}}{{\partial x}} = 0$(2.3)
$T({{T}_{x}},{{T}_{y}},T{}_{{xy}}) = t - L(t),\quad L(f) = {{s}^{2}}\frac{{{{\partial }^{2}}f}}{{\partial {{x}^{2}}}} + {{r}^{2}}\frac{{{{\partial }^{2}}f}}{{\partial {{y}^{2}}}}$Здесь $T$ – обобщенное напряжение, выражающееся через традиционное напряжение по формулам (2.3), а s и r – структурные параметры выражающиеся через размеры элемента a и b [2].
По аналогии с обобщенными напряжениями введем обобщенные деформации (рис. 2)
(2.4)
${{\gamma }_{x}} = \frac{1}{{ab}}\int\limits_{ - a/2}^{a/2} {\left[ {{{u}_{x}}(x,y;\alpha ,\beta = b{\text{/}}2) - {{u}_{x}}(x,y;\alpha ,\beta = - b{\text{/}}2)} \right]} d\alpha \,\,\,(x,y)$Здесь $u$ – перемещение точки (x, y) (рис. 2). Предположим, что перемещения можно представить в окрестности точки (x, y) разложениями аналогичными равенству (2.1). Тогда обобщенные деформации (2.4) принимают следующую окончательную форму:
(2.5)
${{E}_{x}}_{x} = \frac{{\partial {{U}_{x}}}}{{\partial x}},\quad {{E}_{{yy}}} = \frac{{\partial {{U}_{y}}}}{{\partial y}},\quad {{E}_{{xy}}} = \frac{{\partial {{U}_{x}}}}{{\partial y}} + \frac{{\partial {{U}_{y}}}}{{\partial x}}$Для ортотропного материала обобщенные напряжения связаны с обобщенными деформациями следующим образом:
(2.7)
${{T}_{x}} = \frac{{{{E}_{x}}}}{{1 - {{\nu }_{{xy}}}{{\nu }_{{yx}}}}}\left( {{{E}_{{xx}}} + {{\nu }_{{xy}}}{{E}_{{yy}}}} \right)\quad (x,y),\quad {{T}_{{xy}}} = {{G}_{{xy}}}{{E}_{{xy}}}$При r = s = 0 соотношения (2.7) вырождаются в традиционный закон Гука. Упругие постоянные E, $\nu $, G определятся из опытов, в которых напряженно-деформированное состояние материала является однородным. В этом случае оператор $L(f) = 0$ и обобщенные напряжения и деформации совпадают с традиционными. Таким образом, соотношения упругости (2.7) включают традиционные упругие постоянные. Кроме этого полученные соотношения содержат два структурных параметра s и r, которые определяются экспериментально применительно к рассматриваемой задаче.
Уравнения (2.2), (2.5) и (2.7) по форме совпадают с соответствующими уравнениями классической теории упругости, только вместо традиционных напряжений и перемещений $t$ и $u$ включают обобщенные характеристики T и $U.$ В качестве решения системы (2.2), (2.5) и (2.7) можно использовать решение, соответствующее классической теории упругости, определяющее обобщенные напряжения и перемещения T, U. Традиционные напряжения и перемещения t, u находятся в результате интегрирования уравнений Гельмгольца (2.3) и (2.6). Если классическое решение не имеет особенностей и согласуется с экспериментом, то s = r = 0 и обобщенное решение вырождается в классическое. Если классическое решение имеет особенность, то решение дополнительного уравнения Гельмгольца позволяет ее устранить.
3. Обобщенное решение задачи о трещине. Как следует из равенств (1.6), сингулярность решения проявляется на оси трещины при x = c. В связи с этим воспользуемся частной формой уравнений обобщенной теории упругости, полученных в предыдущем разделе, приняв $b = dy$, т.е. предположим, что размер элемента, показанного на рис. 2, является конечным в направлении оси $x$ и бесконечно малым – в направлении оси y. Тогда в полученных выше соотношениях необходимо принять r = 0. Как показано в работе [3] для изотропного материала, такой подход обладает удовлетворительной точностью по отношению к эксперименту и решению двумерной задачи [4]. Таким образом, уравнение (2.3) для напряжений ${{t}_{x}} = {{\sigma }_{x}}$ и ${{t}_{y}} = {{\sigma }_{y}}$ принимает вид
(3.1)
${{\sigma }_{x}} - {{s}^{2}}\frac{{{{\partial }^{2}}{{\sigma }_{x}}}}{{\partial {{x}^{2}}}} = {{T}_{x}},\quad {{\sigma }_{y}} - {{s}^{2}}\frac{{{{\partial }^{2}}{{\sigma }_{y}}}}{{\partial {{x}^{2}}}} = {{T}_{y}}$(3.2)
${{T}_{x}} = \sqrt {\frac{{{{E}_{x}}}}{{{{E}_{y}}}}} {{\sigma }_{0}}\left( {\frac{x}{{\sqrt {{{x}^{2}} - {{c}^{2}}} }} - 1} \right),\quad {{T}_{y}} = \frac{{{{\sigma }_{0}}x}}{{\sqrt {{{x}^{2}} - {{c}^{2}}} }}$Рассмотрим напряжение ${{\sigma }_{y}}.$ Это напряжение не включает упругих постоянных, поэтому уравнение
Здесь $\bar {\sigma } = \sigma {\text{/}}{{\sigma }_{0}},$ $\lambda = c{\text{/}}s$ и $\bar {x} = x{\text{/}}c.$ Условие регулярности решения при $\bar {x} \to \infty $ выполняется если принять
Определяя постоянную C1 из условия на конце трещины ${{\bar {\sigma }}_{у}}(\bar {x} = 1) = 0$, окончательно получим следующее выражение для напряжения на оси $\bar {x}$ при $\bar {x} \geqslant 1:$
(3.3)
${{\bar {\sigma }}_{у}}(\bar {x}) = \frac{1}{2}\lambda \left( {{{e}^{{ - \lambda \bar {x}}}}\int\limits_1^{\bar {x}} {\frac{{\bar {x}{{e}^{{\lambda \bar {x}}}}d\bar {x}}}{{\sqrt {{{{\bar {x}}}^{2}} - 1} }} + {{e}^{{\lambda \bar {x}}}}\int\limits_{\bar {x}}^\infty {\frac{{\bar {x}{{e}^{{ - \lambda \bar {x}}}}d\bar {x}}}{{\sqrt {{{{\bar {x}}}^{2}} - 1} }} - {{e}^{{\lambda (2 - \bar {x})}}}\int\limits_1^\infty {\frac{{\bar {x}{{e}^{{ - \lambda \bar {x}}}}d\bar {x}}}{{\sqrt {{{{\bar {x}}}^{2}} - 1} }}} } } } \right)$Решение первого уравнения (3.1) для ${{\sigma }_{x}}$ имеет вид
(3.4)
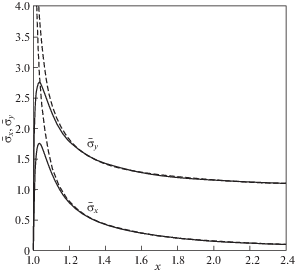
${{\bar {\sigma }}_{x}} = \sqrt {\frac{{{{E}_{x}}}}{{{{E}_{y}}}}} \left[ {{{{\bar {\sigma }}}_{y}}(\bar {x}) - {{\sigma }_{0}}} \right]$Решения (3.3) и (3.4), в отличие от классических решений (1.7) и (1.8), не являются сингулярными. Зависимости напряжений ${{\bar {\sigma }}_{{x,y}}}$от координаты $\bar {x} \geqslant 1$ при λ = 50 и показаны на рис. 3 сплошными линиями. Штриховые линии соответствуют классическому решению (1.7) и (1.8).
4. Экспериментальное исследование. Эксперимент проводился на пластинах из стеклотекстолита и углепластика, в которых направления армирования совпадают с осями x и y (рис. 1).
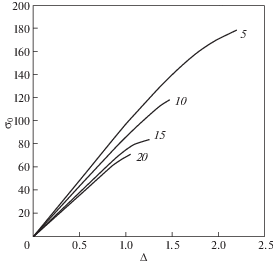
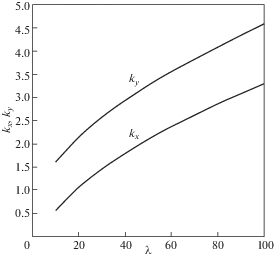
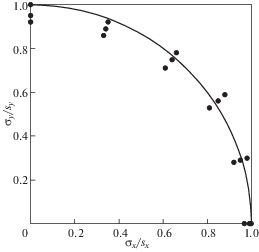
Упругие постоянные стеклотекстолита – ${{E}_{x}} = 23.6$ ГПа, ${{E}_{y}} = 27.5$ ГПа, ${{G}_{{xy}}}$ = 5.8 ГПа, ${{\nu }_{{xy}}}\, = \,0.1$, ${{\nu }_{{yx}}}\, = \,0.116$. Пределы прочности при растяжении – ${{s}_{x}}\, = \,340$ МПа и ${{s}_{у}}$ = 416 МПа. Испытываемые пластины имели длину 250 мм, ширину 40 мм и толщину 1.12 мм. В середине продольного края растягиваемых пластин прорезались трещины с длиной 5, 10, 15 и 20 мм. Следует отметить, что эксперимент с боковой трещиной описывается здесь с помощью решения задачи о центральной трещине (рис. 1). Возможность такого подхода основана на асимптотическом анализе напряженного состояния вблизи конца трещины [5], согласно которому это состояние слабо зависит от условий нагружения вдали от трещины и формы трещины. На рис. 4 представлены диаграммы деформирования при растяжении пластин с трещинами различной длины в направлении оси $у$. Номера на кривых соответствуют длинам трещин в мм. Напряжение σ0 измеряется в МПа, а величина $\Delta $ на горизонтальной оси определяет взаимное смещение в мм захватов испытательной машины на базе 175 мм. Максимальные напряжения, действующие в пластине вблизи трещины, представим следующим образом: $\sigma _{x}^{m} = {{k}_{x}}{{\sigma }_{o}}$ и $\sigma _{y}^{m}$ = kyσ0, где kx и ky – коэффициенты концентрации напряжений в окрестности трещины. Используя решение (3.3) и (3.4) для экспериментальной пластины, можно построить зависимости kx и ky от параметра $\lambda ,$ показанные на рис. 5. Для оценки прочности пластины с трещиной используем квадратичный критерий прочности [6]
(4.1)
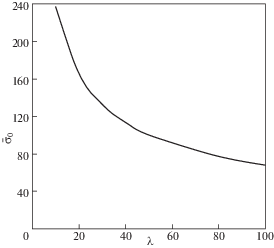
${{\left( {\frac{{\sigma _{x}^{m}}}{{{{s}_{x}}}}} \right)}^{2}} + {{\left( {\frac{{\sigma _{y}^{m}}}{{{{s}_{y}}}}} \right)}^{2}} = 1$Зависимость ${{\bar {\sigma }}_{0}}$, измеряемого в МПа, от параметра $\lambda ,$ построенная с помощью кривых, показанных на рис. 5, представлена на рис. 7.
Определение разрушающего напряжения ${{\bar {\sigma }}_{0}}$ осуществляется следующим образом. Для пластины с трещиной длиной 5 мм (кривая 5 на рис. 4) экспериментальное разрушающее напряжение составляет ${{\bar {\sigma }}_{0}} = 179$ МПа. По графику на рис. 7 находим соответствующее значение параметра $\lambda = 20$ и масштабный коэффициент $s = c{\text{/}}\lambda = 0.25$ мм. Основная идея дальнейшего расчета заключается в том, что параметр s считается не зависящем от длины трещины. Тогда для пластины с трещиной длиной 10 мм получим $\lambda = c{\text{/}}s = 40$ и из рис. 7 следует ${{\bar {\sigma }}_{0}} = 114$ МПа. Соответствующий экспериментальный результат (кривая 10 на рис. 4) – ${{\bar {\sigma }}_{0}} = 118$ МПа. Результаты расчета представлены в табл. 1.
Таблица 1.
Расчетные и экспериментальные значения напряжений для пластин из стеклотекстолита с трещинами различной длины
| Длина трещины c, мм | Параметр s, мм | Параметр $\lambda $ | Расчетное предельное напряжение, МПа | Эксперим. предельное напряжение, МПа | Погрешность, % |
|---|---|---|---|---|---|
| 10 | 0.25 | 40 | 114 | 118 | 3.4 |
| 15 | 0.25 | 60 | 90 | 84 | 7.1 |
| 20 | 0.25 | 80 | 78 | 71 | 9.8 |
Как следует из табл. 1, предлагаемый метод удовлетворительно предсказывает разрушающее напряжение для пластин с трещинами. Следует заметить, что в последней пластине, для которой погрешность достигает 10%, длина трещины составляет половину ширины пластины.
Пластины из углепластика имели специальную гибридную структуру – они были образованы из однонаправленного углепластика, прошитого в поперечном направлении стеклянными нитями. Упругие постоянные материала необходимые для расчета – ${{E}_{x}} = 14$ ГПа, ${{E}_{y}} = 75.2$ ГПа. Пределы прочности при растяжении – ${{s}_{x}} = 170.5$ МПа, ${{s}_{y}} = 1150$ МПа. Ширина образцов – 30 мм, толщина – 1.5 мм. На продольных кромках растягиваемых образцов наносились трещины длиной 3, 6, 9 и 12 мм. Поскольку прочность и жесткость пластин при растяжении в продольном направлении (y, рис. 1) намного больше соответствующих характеристик для поперечного направления (x), для оценки прочности пластин из рассматриваемого материала может быть использован критерий максимальных напряжений. В этом случае для определения коэффициента концентрации напряжения может быть использована кривая для ky на рис. 5. Расчет осуществляется методом, описанным выше. Для пластины с трещиной длиной 3 мм экспериментально получено предельное напряжение ${{\bar {\sigma }}_{0}} = 690$ МПа, что соответствует коэффициенту концентрации напряжения ${{k}_{y}} = {{s}_{y}}{\text{/}}{{\bar {\sigma }}_{0}} = 1.67$. По графику на рис. 5 находим λ = 11 и параметр $s = c{\text{/}}\lambda = 0.27$. Для пластины с длиной трещины 6 мм при найденной величине параметра $s$ имеем $\lambda = c{\text{/}}s = 22.2$, что соответствует ${{k}_{y}} = 2.2$ и предельному напряжению ${{\bar {\sigma }}_{0}} = 523$ МПа. Соответствующее экспериментальное значение – ${{\bar {\sigma }}_{0}} = 549$ МПа. Результаты расчетов представлены в табл. 2.
Таблица 2.
Расчетные и экспериментальные значения предельного напряжения для пластин из углепластика с трещинами различной длины
| Длина трещины c, мм | Параметр s, мм | Параметр $\lambda $ | Расчетное предельное напряжение, МПа | Эксперим. предельное напряжение, МПа | Погрешность, % |
|---|---|---|---|---|---|
| 6 | 0.27 | 22.2 | 523 | 549 | 4.7 |
| 9 | 0.27 | 33.3 | 432 | 441 | 2 |
| 12 | 0.27 | 44.4 | 370 | 353 | 4.8 |
Таблица 2 подтверждает удовлетворительную точность метода.
5. Заключение. Таким образом, согласно предлагаемому методу, задача расчета пластины с трещиной сводится к традиционной задаче о концентрации напряжений. Для пластины с заданными упругими характеристиками и длиной трещины экспериментально определяется масштабный параметр s, который считается независимым от длины трещины и определяет коэффициент концентрации напряжений в окрестности конца трещины.
Работа выполнена при поддержке РФФИ, грант 19-01-00355.
Список литературы
Работнов Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1979. 744 с.
Васильев В.В., Лурье С.А. Обобщенная теория упругости // Изв. РАН. Механика твердого тела. 2015. № 4. С. 16–27.
Васильев В.В., Лурье С.А. Новое решение плоской задачи о равновесной трещине // Изв. РАН. Механика твердого тела. 2016. № 5. С. 61–67.
Васильев В.В., Лурье С.А. Новый метод исследования хрупких тел с трещинами // Деформация и разрушение материалов. 2019. № 9. С. 12–19.
Васильев В.В., Лурье С.А., Салов В.А. Исследование прочности пластин с трещинами на основе критерия максимальных напряжений в масштабно-зависимой обобщенной теории упругости // Физическая мезомеханика. 2018. Т. 21. № 4. С. 5–12.
Гольденблат И.И., Копнов В.А. Критерии прочности и пластичности конструкционных материалов. М.: Машиностроение, 1988. 192 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела