Известия РАН. Механика твердого тела, 2021, № 6, стр. 156-164
РАСЧЕТ КИНЕТИКИ РОСТА/ИЗНАШИВАНИЯ ТВЕРДО-СМАЗОЧНОЙ ПЛЕНКИ В УПОРНОМ ПОДШИПНИКЕ СКОЛЬЖЕНИЯ
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: iasoldat@hotmail.com
Поступила в редакцию 12.03.2021
После доработки 20.04.2021
Принята к публикации 13.05.2021
Аннотация
Описывается модель роста и одновременного изнашивания твердо-смазочной пленки на поверхности композитного покрытия упорного подшипника скольжения. Получены уравнения кинетики изменения толщины твердо-смазочной пленки. Приводятся результаты численного решения этих уравнений. Описываются эффекты формы пяты подшипника и нагрузки на него. Даются оценки долговечности твердо-смазочной пленки по критерию износа.
Введение. В современной технике находят широкое применение самосмазывающиеся композиты, содержащие твердую смазку в виде мягкой фазы. При трении такого композита происходит выделение смазки и образование поверхностной твердо-смазочной пленки [1, 2]. К настоящему времени разработан ряд теоретических моделей образования такой пленки, использующих концепцию пластического выдавливания смазки из композита в результате деформирования его матрицы [3–5]. В работе [6] с использованием такой концепции выполнен расчет кинетики роста и одновременного изнашивания твердо-смазочной пленки, при этом в качестве механизма изнашивания рассматривалось пластическое оттеснение (пропахивания) материала микронеровностями контртела.
Ниже описывается теоретическая модель роста и одновременного изнашивания твердо-смазочной пленки на поверхности покрытия из самосмазывающегося композита в упорном подшипнике скольжения. Упругое поведение пленки и покрытия описывается упрощенной моделью Винклера [7, 8]. На основе феноменологических законов роста и изнашивания твердо-смазочной пленки выводятся уравнения, позволяющие рассчитывать кинетику изменения ее толщины, контактного давления, момента трения, а также оценивать ее долговечность по критерию износа.
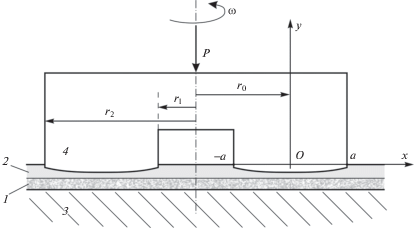
1. Постановка задачи. Рассмотрим двухслойное покрытие 1+2, сцепленное с абсолютно жестким основанием 3 и контактирующее с пятой 4 упорного подшипника скольжения, которая вращается с постоянной угловой скоростью $\omega $ и находится под действием заданной нагрузки $P$ (рис. 1). Пользуясь осевой симметрией задачи, расположим начало O системы координат посередине кольцевой области контакта, при этом совместим координатную ось x с поверхностью покрытия вне области контакта, направив ее вдоль некоторого радиуса пяты (рис. 1). Область контакта пяты с покрытием будем считать неизменной и представлять отрезком [–a, a] оси x, причем a = = $({{r}_{2}} - {{r}_{1}}){\text{/}}2 = {{r}_{0}} - {{r}_{1}}$. Форму подошвы пяты в выбранной системе координат зададим уравнением
где $\delta $ – внедрение в покрытие точки поверхности пяты с координатой x = 0. Скорость $V$ скольжения пяты по покрытию определяется по формуле а нагрузка $P$ связана с контактным давлением p условием равновесияПоказанное на рис. 1 двухслойное покрытие состоит из композитного покрытия (КП) 1 и твердо-смазочной пленки (ТСП) 2, которая с течением времени $t$ растет за счет выделения из КП твердой смазки и одновременно изнашивается в результате контактного взаимодействия с пятой. Подобный процесс можно описать следующими равенствами:
(1.4)
$\begin{gathered} {{h}_{1}}(x,t) = {{h}_{{10}}} - \chi q(x,t),\quad {{h}_{1}}(x,0) = {{h}_{{10}}} \\ {{h}_{2}}(x,t) = {{h}_{{20}}} + q(x,t) - W(x,t),\quad {{h}_{2}}(x,0) = {{h}_{{20}}} \\ \end{gathered} $Основываясь на полученных ранее результатах [3–5, 9], будем использовать феноменологические законы роста и изнашивания ТСП:
определяющие скорости изменения величин q и $W$ по пути трения $l$ в зависимости от контактного давления p и скорости скольжения $V$ для каждой точки контакта. Функция $D(p,V)$ параметрически зависит от структурных и физико-механических характеристик КП, а функция $F(p,V)$ определяется износостойкими свойствами ТСП. Параметр ${{q}_{m}}$ задает максимально возможный прирост толщины ТСП, обусловленный ограниченным количеством твердой смазки в КП, так что $q \in [0,{{q}_{m}})$. Множитель $(1 - q{\text{/}}{{q}_{m}})$ в первом выражении (1.5) отвечает линейной зависимости количества выделяемой твердой смазки от ее текущей концентрации в КП, что подтверждается расчетами [4, 5]. В качестве возможного варианта, функции $D(p,V)$ и $F(p,V)$ могут быть линейными по аргументу $p$ и не зависеть от скорости скольжения $V$: где ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ – некоторые параметры.Существование максимальной величины ${{q}_{m}}$ прироста толщины ТСП, при том, что износ ТСП монотонно увеличивается, означает возможность полного изнашивания ТСП в некоторый момент ${{t}_{ * }}$ времени в некотором месте с координатой ${{x}_{ * }}$, так что
В дальнейшем величина ${{t}_{ * }}$ будет использоваться в качестве характеристики долговечности ТСП по критерию износа.
Допустим, что под действием контактного давления $p$ КП и ТСП деформируются упруго, при этом упругие свойства КП описываются усредненными значениями модуля Юнга ${{E}_{{{\kern 1pt} 1}}}$ и коэффициента Пуассона ${{\nu }_{1}}$ [4]. Кроме того, примем концепцию асимптотически тонкого слоя, согласно которой напряженно-деформированное состояние слоя толщины $h$ в продольном направлении на расстояниях ∼$h$ изменяется незначительно [7]. Все это позволяет воспользоваться упрощенной моделью Винклера для определения упругой осадки $\hat {w}$ поверхности ТСП, связанного с КП [8]:
Здесь $A(x,t) = {{B}_{1}}(x,t){{h}_{1}}(x,t) + {{B}_{2}}(x,t){{h}_{2}}(x,t)$ – коэффициент податливости двухслойного покрытия КП+ТСП, причем слагаемые ${{B}_{i}}{{h}_{i}}$ определяют податливость отдельно КП (i = 1) и ТСП (i = 2), ${{B}_{i}} = (1 - 2{{\nu }_{i}})(1 + {{\nu }_{i}}){{[(1 - {{\nu }_{i}}){{E}_{i}}]}^{{ - 1}}}$. Учитывая, что в процессе контактного взаимодействия с пятой состав КП изменяется, следует положить B1(x, t) = = ${{\beta }_{1}}(q(x,t))$, где ${{\beta }_{1}}(q)$ – функция, определяющая изменение податливости КП при выделении из него твердой смазки. Допуская однородность материала ТСП, коэффициент ${{B}_{2}}$ будем считать постоянным. С учетом равенств (1.4) вышесказанное позволяет записать следующее выражение для коэффициента податливости:
(1.9)
$A(x,t) = \Omega \left( {q(x,t),W(x,t)} \right),\quad \Omega (q,W) = {{\beta }_{1}}(q)({{h}_{{10}}} - \chi q) + {{B}_{2}}({{h}_{{20}}} + q - W)$Имеет место условие контакта:
в котором $h = {{h}_{1}} + {{h}_{2}}$ – текущая толщина двухслойного покрытия КП+ТСП, h0 = ${{h}_{{10}}} + {{h}_{{20}}}$.Ставится задача: основываясь на записанных выше соотношениях, по заданной нагрузке $P(t)$ рассчитать кинетику изменения во времени толщин ${{h}_{1}}(x,t)$ КП и ${{h}_{2}}(x,t)$ ТСП, а также контактного давления $p(x,t)$.
2. Система определяющих уравнений. Прежде всего, выразим контактное давление $p(x,t)$ через функции $q(x,t)$, $W(x,t)$ и $\delta (t)$. Для этого подставим в равенство (1.10) выражения (1.4) и (1.8) для толщин ${{h}_{1}}$, ${{h}_{2}}$ и упругой осадки $\hat {w}$ при учете формулы (1.9) для коэффициента $A(x,t)$. В результате можно прийти к искомому выражению
(2.1)
$\begin{gathered} p(x,t) = \Pi \left( {x,q(x,t),W(x,t),\delta (t)} \right), \\ \Pi (x,q,W,\delta ) = \frac{{\delta - g(x) - (\chi - 1)q - W}}{{\Omega (q,W)}} \\ \end{gathered} $Согласно полученному выражению, начальное распределение ${{p}_{0}}(x) = p(x,0)$ контактного давления определяется по формуле
где ${{\delta }_{0}} = \delta (0)$, ${{A}_{0}} = {{B}_{{10}}}{{h}_{{10}}} + {{B}_{2}}{{h}_{{20}}}$, ${{B}_{{10}}} = {{\beta }_{1}}(0)$. Если положить в условии равновесия (1.3) $t = 0$ и подставить в него правую часть равенства (2.2), то можно получить следующее выражение начального внедрения ${{\delta }_{0}}$ через известную нагрузку ${{P}_{0}} = P(0)$:(2.3)
${{\delta }_{0}} = \frac{{{{A}_{0}}}}{{4\pi a{{r}_{0}}}}({{P}_{0}} + P_{0}^{g}),\quad P_{0}^{g} = \frac{{2\pi }}{{{{A}_{0}}}}\int\limits_{ - a}^a {({{r}_{0}} + x)g(x)dx} $Перейдем теперь в законах (1.5) роста и изнашивания ТСП от производной по пути $l$ трения к производной по времени $t$, используя соотношение $dl = Vdt$. Тогда при учете выражения (2.1) для контактного давления p можно получить следующие уравнения относительно функций $q(x,t)$ и $W(x,t)$:
(2.4)
$\begin{gathered} \dot {q}(x,t) = {{F}_{1}}\left( {x,q(x,t),W(x,t),\delta (t)} \right) \\ \dot {W}(x,t) = {{F}_{2}}\left( {x,q(x,t),W(x,t),\delta (t)} \right) \\ \end{gathered} $Уравнения (2.4) кроме функций $q(x,t)$ и $W(x,t)$ содержат еще одну неизвестную функцию $\delta (t)$, дополнительное уравнение для которой может быть построено на основе условия равновесия (1.3). А именно, следуя известной процедуре [10], продифференцируем по $t$ это условие с внесением операции дифференцирования под знак интеграла. Полученную таким образом производную $\dot {p}(x,t)$ заменим правой частью выражения (2.1), предварительно продифференцированной по $t$ с заменой производных $\dot {q}(x,t)$ и $\dot {W}(x,t)$ правыми частями уравнений (2.4). Выделяя из полученного равенства производную $\dot {\delta }(t)$, придем к искомому уравнению
(2.5)
$\dot {\delta }(t) = \frac{{\dot {P}(t) + {{{\mathbf{E}}}_{1}}\left[ {x,q(x,t),W(x,t),\delta (t)} \right](t)}}{{{{{\mathbf{E}}}_{2}}\left[ {x,q(x,t),W(x,t),\delta (t)} \right](t)}}$Равенства (2.4) и (2.5) образуют систему уравнений, определяющих функции $q(x,t)$, $W(x,t)$ и $\delta (t)$. Эта система решается при начальных условиях
причем ${{\delta }_{0}}$ определяется по формуле (2.3). Найденные функции $q(x,t)$, $W(x,t)$ и $\delta (t)$ позволяют по формулам (1.4) и (2.1) рассчитать кинетику изменения во времени толщин ${{h}_{1}}$ КП и ${{h}_{2}}$ ТСП, а также контактного давления $p$ и, тем самым, решить поставленную выше задачу.Замечание. Система уравнений (2.4), (2.5) является нелинейной и ее решение возможно только численно, даже в случае (1.6) линейных законов роста и изнашивания ТСП. Однако в этом случае можно установить аналитическую связь функций $q(x,t)$ и $W(x,t)$ между собой. Для этого следует исключить из правых частей уравнений (2.4) комплекс $V(x)\Pi \left( {x,q(x,t),W(x,t),\delta (t)} \right)$ и для каждого $x$ получить дифференциальное уравнение относительно $q$ с независимой переменной W. Это уравнение имеет аналитическое решение, которое определяет искомую связь
Укажем ряд ограничений, которым должны удовлетворять используемые величины. Прежде всего, отметим, что толщина ${{h}_{1}}$ КП принимает только положительные значения, поэтому, в силу первого равенства (1.4), величина $q$ ограничена неравенством: $q(x,t) < {{h}_{{10}}}{\text{/}}\chi $. Это неравенство выполняется, если ${{q}_{m}} \leqslant {{h}_{{10}}}{\text{/}}\chi $, так как согласно данному выше определению параметра ${{q}_{m}}$: $q(x,t) \in [0,{{q}_{m}})$.
Положительные значения также принимает контактное давление $p$, а осадка ${{\hat {w}}_{i}}$ = = Bihip каждого слоя двухслойного покрытия КП+ТСП по физическому смыслу должна быть меньше толщины ${{h}_{{{\kern 1pt} i}}}$ соответствующего слоя. Подобные ограничения представляются следующими неравенствами
В случае, когда ТСП изначально отсутствует (${{h}_{{20}}} = 0$) и появляется в результате взаимодействия пяты с КП, необходимо наложить ограничение $0 < {{\dot {h}}_{2}}(x,0)$. В силу соотношений (1.4), (2.1) и (2.4), это ограничение эквивалентно неравенству
которое имеет простой физический смысл – в начальный момент ТСП растет быстрее, чем изнашивается.3. Численный анализ взаимодействия пяты с двухслойным покрытием КП+ТСП выполнялся на основе решения системы дифференциальных уравнений (2.4) и (2.5) относительно функции $q(x,t)$, $W(x,t)$ и $\delta (t)$ с использованием численного метода Рунге–Кутты четвертого порядка точности. Целью расчетов было выявление характерных особенностей процесса роста ТСП при его одновременном изнашивании. Рассматривался случай постоянной во времени нагрузки $P(t)$ и использовались линейные законы (1.6) роста и изнашивания ТСП. Упругие свойства КП считались неизменными во времени, поэтому функция ${{\beta }_{1}}(q)$ принималась постоянной и равной ${{B}_{1}}$. При расчетах контролировалось выполнение неравенств (2.6).
Расчеты проводились при следующих значениях параметров задачи: ${{r}_{1}} = $ 2 мм, ${{r}_{2}} = $ = 22 мм, $a = $ 10 мм, ${{h}_{{10}}} = $ 1 мм, ${{h}_{{20}}} = 0$, $\omega = $ 100 с–1, ${{q}_{m}} = 0.2{{h}_{{10}}}$, $\chi = 0.1$, ${{E}_{{{\kern 1pt} 1}}} = 100$ МПа, ${{E}_{{{\kern 1pt} 2}}} = 25$ МПа, ${{\nu }_{{{\kern 1pt} 1}}} = {{\nu }_{{{\kern 1pt} 2}}} = 0.25$, ${{\alpha }_{1}} = 4 \times {{10}^{{ - 16}}}$ Па–1, ${{\alpha }_{2}} = {{10}^{{ - 16}}}$ Па–1. Форма пяты описывалась линейной функцией
где $k$ – коэффициент, характеризующий угол наклона профиля пяты, причем значение k = 0 отвечает случаю плоской пяты, а значения $k \ne 0$ – случаю конической пяты. Значения коэффициента k, а также нагрузки $P$ указываются ниже отдельно для каждого численного примера.Для графического представления результатов расчетов используются безразмерные величины, $\tilde {x} = x{\text{/}}a$, $\tilde {t} = t{\text{/}}{{t}_{c}}$, $\tilde {p} = p{\text{/}}{{p}_{a}}$, ${{\tilde {h}}_{2}} = {{h}_{2}}{\text{/}}{{h}_{{10}}}$, $\tilde {P} = P{\text{/}}{{P}_{a}}$, где ${{t}_{c}} = {{10}^{5}}$ с, ${{p}_{a}} = P{\text{/}}S$, ${{P}_{a}} = ({{E}_{1}} + {{E}_{2}})S{\text{/}}2$, $S = \pi (r_{2}^{2} - r_{1}^{2})$ – площадь контакта.
Отметим, что выбранные коэффициенты ${{\alpha }_{1}}$, ${{\alpha }_{2}}$ удовлетворяют неравенству ${{\alpha }_{2}} < {{\alpha }_{1}}$, которое эквивалентно неравенству (2.7) в рассматриваемом случае (1.6) линейных законов роста и изнашивания ТСП. Как указывалось выше, выполнение неравенства (2.7) необходимо при выбранном нулевом значении начальной толщины ${{h}_{{20}}}$ ТСП.
Кинетика изменения толщины ${{h}_{2}}(x,t)$ ТСП и контактного давления $p(x,t)$ показана на рис. 2 и 3, соответственно, при k = 0 (случай плоской пяты) и $k = 6.25 \times {{10}^{{ - 3}}}$ (случай конической пяты). Представленные на этих рисунках кривые отвечают следующим моментам времени: $\tilde {t} = $ 0 (1); 0.0345 (2); 0.1799 (3); 0.3616 (4); 0.8158 (5); 1.0884 (6); 1.4517 (7). Значение нагрузки в обоих случаях составляет $\tilde {P} = 0.144$ ($P = 13.57$ кН).
Рис. 2.
Распределения толщины ${{h}_{2}}$ ТСП (а) и контактного давления $p$ (b) в различные моменты времени при k = 0 (плоская пята) и $\tilde {P} = 0.144$
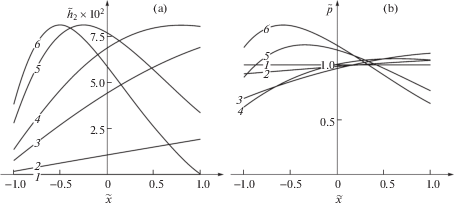
Рис. 3.
Распределения толщины ${{h}_{2}}$ ТСП (a) и контактного давления p (b) в различные моменты времени при $k = 6.25 \times {{10}^{{ - 3}}}$ (коническая пята) и $\tilde {P} = 0.144$
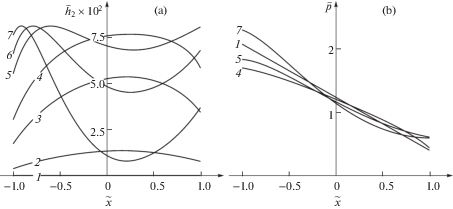
Представленные графики свидетельствуют о существенном влиянии формы пяты на кинетику роста/изнашивания ТСП. В частности, видно, что коническая пята обеспечивает большую долговечность ${{t}_{ * }}$ ТСП. Кроме того, расчеты свидетельствуют о том, что коническая пята обеспечивает режим трения с более низким и стабильным моментом трения M, рассчитанным по формуле
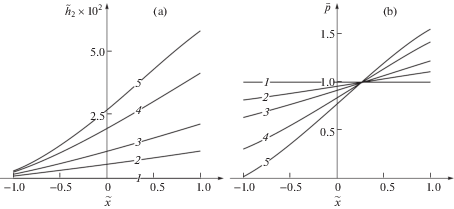
где $\mu $ – коэффициент трения скольжения. Например, при $\mu = 0.2$ значения ${{M}_{{\min }}}\, = \,\mathop {\min }\limits_{t \in [0,{{t}_{ * }}]} M(t)$ и ${{M}_{{\max }}} = \mathop {\max }\limits_{t \in [0,{{t}_{ * }}]} M(t)$ для плоской пяты составляют 37.08 и 41.44 Н ⋅ м, соответственно, тогда как для конической пяты: 34.07 и 35.74 Н ⋅ м.При пониженных нагрузках $P$ возможно протекание процесса, когда на его начальной стадии наблюдается значительная неоднородность по $x$ роста толщины ${{h}_{2}}(x,t)$ ТСП, т.е. проявляется эффект выпячивания ТСП. Это может приводить к локальному нарушению контакта пяты и ТСП. Подобное протекание процесса роста/изнашивания ТСП в случае k = 0 (плоская пята) и $\tilde {P} = 0.048$ ($P = 4.524$ кН) иллюстрирует рис. 4, на котором кривые отвечают следующим моментам времени: $\tilde {t} = $ 0 (1); 0.0540 (2); 0.1085 (3); 0.2175 (4); 0.3265 (5). Представленные графики демонстрируют интенсивный рост толщины ТСП на периферии области контакта (окрестность $x = a$), что приводит к снижению контактного давления до нуля и нарушению контакта пяты и ТСП на внутренней границе $x = - a$ области контакта.
Рис. 4.
Распределения толщины ${{h}_{2}}$ ТСП (a) и контактного давления p (b) в различные моменты времени при k = 0 (плоская пята) и $\tilde {P} = 0.048$
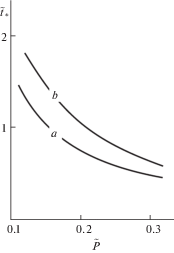
На рис. 5 показаны зависимости долговечности ${{t}_{ * }}$ ТСП, определяемой условием (1.7), от нагрузки $P$ при k = 0 (плоская пята) (a) и $k = 6.25 \times {{10}^{{ - 3}}}$ (коническая пята) (b). Как и следовало ожидать, долговечность ТСП снижается с ростом нагрузки, причем коническая пята обеспечивает большую долговечность.
Рис. 5.
Зависимости долговечности ${{t}_{ * }}$ ТСП от нагрузки $P$ при a) k = 0 (плоская пята); b) $k = 6.25 \times {{10}^{{ - 3}}}$ (коническая пята)
4. Выводы. 1. Предложена математическая модель процесса одновременного роста и изнашивания ТСП в упорном подшипнике скольжения в предположении, что ТСП образуется на поверхности КП за счет выделения из него твердой смазки.
2. Расчетным путем выявлены характерные особенности рассматриваемого процесса. Показано, что кинетика изменения толщины ТСП и контактного давления существенно зависит от формы пяты. В частности, использование конической пяты приводит к повышению долговечности ТСП по критерию износа и обеспечивает режим трения с более низким и стабильным моментом трения.
3. Выявлен эффект выпячивания ТСП при пониженных нагрузках, приводящий к локальному нарушению контакта пяты и ТСП.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (20-58-00007).
Список литературы
Self-Lubricating Composites / Ed. by Menezes P.L., Rohatgi P.K., Omrani E. Berlin: Springer-Verlag GmbH, 2018. 286 p.
Губенко М.М., Мезрин А.М., Щербакова О.О., Торская Е.В. Исследование изменения механических свойств поверхностных слоев алюминиевых сплавов в условиях трения скольжения // Трение и износ. 2017. Т. 38. № 5. С. 483–487. https://doi.org/10.3103/S1068366617050038
Alexeyev N., Jahanmir S. Mechanics of friction in self-lubricating composite materials I: Mechanics of second-phase deformation and motion // Wear. 1993. V. 166. P. 41–48. https://doi.org/10.1016/0043-1648(93)90277-S
Bushe N.A., Goryacheva I.G., Makhovskaya Yu.Yu. Effect of aluminum-alloy composition on self-lubrication of frictional surfaces // Wear. 2003. V. 254. P. 1276–1280. https://doi.org/10.1016/S0043-1648(03)00110-8
Song J. et al. A mechanical model for surface layer formation on self-lubricating ceramic composites // Wear. 2010. V. 268. P. 1072–1079. https://doi.org/10.1016/j.wear.2010.01.012
Valefi M. et al. Modelling of a thin soft layer on a self-lubricating ceramic composite // Wear. 2013. V. 303. P. 178–184. https://doi.org/10.1016/j.wear.2013.02.017
Александров В.М., Мхитарян С.М. Контактные задачи для тел с тонкими покрытиями и прослойками. М.: Наука, 1983. 487 с.
Солдатенков И.А. К анализу процесса изнашивания многослойного покрытия // Трение и износ. 1991. Т. 12. № 2. С. 204–209.
Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ. М.: Машиностроение, 1977. 526 с.
Солдатенков И.А. Трибомеханические эффекты неоднородности упругого покрытия (упрощенная деформационная модель) // Изв. РАН. МТТ. 2020. № 3. С. 134–145. https://doi.org/10.31857/S0572329920030150
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела