Известия РАН. Механика твердого тела, 2021, № 6, стр. 57-72

Введение. При изложении комплексного подхода в истолковании движения тела, имеющего неподвижную точку, целесообразно показать его место в истолкованиях движения тела, которые применялись другими авторами. В связи с этим, автор данной статьи уделил достаточно большое внимание анализу результатов, полученных ранее, приняв во внимание обширную литературу по данной проблеме. Данный метод позволил показать не только роль модифицированного метода Пуансо в комплексном истолковании движения тела, но и его преимущество в визуальном восприятии движения в различных решениях уравнений динамики твердого тела.

Исследование свойств движения твердого тела, имеющего неподвижную точку, проводилось на заключительном этапе изучения задач механики. Остановимся на некоторых проблемах исторического развития геометрических методов в динамике твердого тела.

Начало разработки геометрических методов в аналитической механике положил Л. Пуансо [1]. Приведем его высказывание: “Надо согласиться с тем, что во всех этих решениях (имеются ввиду аналитические решения) мы видим только вычисления без какой-либо ясной картины вращения тела. Конечно, эти вычисления, более или менее длинные и сложные, позволяют определить, где окажется тело к заданному времени, но мы не видим, как оно туда попало, мы его полностью теряем из вида, тогда как хотелось бы наблюдать его и следить за ним, так сказать, взглядом в течение всего вращения. И я старался открыть именно это отчетливое представление вращательного движения, чтобы сделать доступным обозрению то, что пока еще никем не было изображено”.

Л. Пуансо ввел понятие эллипсоида инерции, мгновенной оси вращения. Им приведено геометрическое истолкование движения тела в решении Эйлера: “Эллипсоид инерции во время движения тела катится без скольжения по одной из своих касательных плоскостей, эта плоскость перпендикулярна к главному моменту количества движения тела и остается неподвижной в пространстве”.

Он доказал, что любое движение тела, имеющего неподвижную точку, можно истолковать качением подвижного аксоида угловой скорости по неподвижному аксоиду. Большой вклад в развитие геометрических методов динамики твердого тела внесли Ж. Сильвестр [2], Ж. Мак-Куллаг [3], Г. Дарбу [4, 5], К. Якоби [6, 7], В. Гесс [8, 9], Э. Раус [10, 11], Н.Е. Жуковский [12–14]. Обзор результатов, полученных в данном направлении, изложен в [15, 16].

Особую важность геометрических методов отмечал Н.Е. Жуковский:

“Можно говорить, что математическая истина только тогда должна считаться вполне обработанной, когда она может быть объяснена всякому из публики, желающему ее усвоить. Я думаю, что если возможно приближение к этому идеалу, то только со стороны геометрического толкования или моделирования”.

Заслуживает внимания информация о том, что многие ученые не ограничивались теоретическими исследованиями, а предлагали некоторые конкретные конструкции. Приведем пример Н.Б. Делоне, предложенный им для гироскопа Ковалевской. Его утверждение таково: “Примером такого движения служит движение прямоугольного параллелепипеда размером $2a < 2b < 2c$, подчиненного условию $c = b\sqrt 3 $ и подпертого в точке, лежащей на прямой, проходящей через центр тяжести параллельно ребру 2a и отстоящей от центра тяжести на расстоянии $x_{0}^{{}} = \sqrt {\frac{{b_{{}}^{2} - a_{{}}^{2}}}{3}} $. Данная опора может быть сделана посредством спицы, пропущенной сквозь параллелепипед” (1892 год).

Н.И. Мерцалов построил гироскоп, удовлетворяющий приближенно условиям Н.Б. Делоне, и сфотографировал движение светящейся точки, помещенной на оси Oz.

Результаты этих ученых, как отмечено ранее, в полной мере отражены в монографии Г.К. Суслова [15] и книге [16]. Следует отметить, что для истолкования движения тела применялись различные подходы. Например, Ж. Мак-Куллаг [3] установил, что при движении свободного твердого тела гирационный эллипсоид, соответствующий точке опоры, проходит во все время движения через точку пространства, лежащую на неизменном главном моменте количества движения. Ж. Сильвестр [2] изучал движение главных осей инерции в неподвижном пространстве. Г. Дарбу [5], используя полярную систему координат, исследовал герполодии (неподвижный годограф угловой скорости) в решении Л. Эйлера. Уравнения Г. Дарбу [5] обобщил П.В. Харламов [17] на случай произвольного решения уравнений Эйлера–Пуассона. В последние годы метод Пуансо был развит в работах автора данной статьи [18, 19], в которых предложен модифицированный метод Пуансо и получена алгебраическая связь между углом прецессии и полярным углом, входящим в уравнения Г. Дарбу–П.В. Харламова. Ж. Сильвестр [2] и К. Якоби [6, 7] исследовали вращения Пуансо в решении Л. Эйлера.

Н.Б. Делоне [20] исследовал подвижный годограф угловой скорости в частном случае С.В. Ковалевской и указал метод получения поверхности вращения, несущей неподвижный годограф. Классификацию меридиана поверхности, на которой лежит неподвижный годограф, указали П.В. Харламов, В.И. Коваль [21].

Б.К. Млодзеевский [22] изучал неподвижный годограф вектора угловой скорости в частном случае С.В. Ковалевской [23].

П.В. Харламов применил метод Пуансо для исследования решения с двумя инвариантными соотношениями [24, 25], изучил [26] случай Б.К. Млодзеевского.

Геометрическое истолкование движения тела проводилось не только в классической задаче о движении тяжелого твердого тела, но и в обобщенных задачах. Например, истолкование С.А. Чаплыгина [27] было посвящено задаче о движении тела в жидкости.

Кроме указанных подходов, в геометрическом истолковании движения тела с помощью свойств вектора угловой скорости известен и подход Н.Е. Жуковского (см. обзор [16]), в основе которого лежат свойства момента количества движения тела.

В монографии И.Н. Гашененко, Г.В. Горра, А.М. Ковалева [28] приведено большинство результатов по кинематическому истолкованию движения тяжелого твердого тела, имеющего неподвижную точку.

1. Истолкование движения тела с помощью углов Эйлера. 1.1. Уравнения динамики твердого тела. Движение тяжелого твердого тела, имеющего неподвижную точку, описывается уравнениями

где введены обозначения: ${\mathbf{\omega }} = {\text{(}}\omega _{1}^{{}}{\text{,}}\omega _{2}^{{}}{\text{,}}\omega _{3}^{{}}{\text{)}}$ – вектор угловой скорости тела; ν = (ν₁, ν₂, $\nu _{3}^{{}}{\text{)}}$ – единичный вектор, указывающий направление силы тяжести; $A$ – тензор инерции в неподвижной точке; s – произведение веса тела и расстояния от неподвижной точки $O$ до центра тяжести тела $C$; ${\mathbf{e}} = {\text{(}}e_{1}^{{}}{\text{,}}e_{2}^{{}}{\text{,}}e_{3}^{{}}{\text{)}}$ – единичный вектор, направленный из точки $O$ в точку $C$. Точка над переменными обозначает относительную производную по времени $t$.

Уравнения (1.1) имеют интегралы

где E и k – произвольные постоянные.

Уравнения (1.1) и (1.2) обобщены Д. Гриоли в задаче о движении твердого тела под действием потенциальных и гироскопических сил (см., например, [29]):

которые допускают три первых интеграла где E и k – произвольные постоянные. В уравнении (1.3) через $\frac{{\partial L{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}}}{{\partial {\mathbf{\nu }}}}$, $\frac{{\partial U{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}}}{{\partial {\mathbf{\nu }}}}$ обозначены градиенты функций $L{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}$ и $U{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}$. В уравнениях (1.3), (1.5) $U{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}$ – силовая функция, $L{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}$ – функция, характеризующая гироскопические силы. Если в (1.3), (1.5) положить $L{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}} = {\text{0}}$, то получим уравнения (см., например, [30, 31]) движения тела в потенциальном поле сил

Когда $L{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}\, = \,{\mathbf{\lambda }} \cdot {\mathbf{\nu }}\, - \,\frac{1}{2}\left( {B{\mathbf{\nu }} \cdot {\mathbf{\nu }}} \right)$, $U{\text{(}}\nu _{1}^{{}}{\text{,}}\nu _{2}^{{}}{\text{,}}\nu _{3}^{{}}{\text{)}}\, = \,{\mathbf{s}} \cdot {\mathbf{\nu }} - \frac{1}{2}\left( {C{\mathbf{\nu }} \cdot {\mathbf{\nu }}} \right)$, где $B = (B_{{ij}}^{{}}{\text{)}}$, C = $(C_{{ij}}^{{}}{\text{)}}$ – симметричные матрицы, то уравнения (1.3), (1.4) будут описывать либо движение гиростата в силовом поле, которое является суперпозицией ньютоновского и кулоновского полей и движется дополнительно под действием сил Лоренца, либо уравнения движения тела в идеальной жидкости (см. обзорные монографии [29, 32]).

1.2. Метод апекса. Пусть $Oxyz$ – подвижная система координат с единичными векторами ${\mathbf{i}}_{1}^{{}}$, ${\mathbf{i}}_{2}^{{}}$, ${\mathbf{i}}_{3}^{{}}$; $O\xi \eta \zeta $ – неподвижная система координат с единичными векторами υ₁, υ₂, υ₃. Полагаем, что в результате интегрирования уравнений (1.1) (либо (1.3), (1.4), (1.6)) найдено решение

где через ${\mathbf{\omega }}_{\Pi }^{{}}{\text{(}}t{\text{)}}$ обозначен подвижный годограф вектора ${\mathbf{\omega }}$. Введем углы Эйлера $\theta $, $\varphi $, $\psi $ таким образом, что угол нутации $\theta $ – угол между векторами ${\mathbf{i}}_{3}^{{}}$ и ${\mathbf{\upsilon }}_{3}^{{}} = {\mathbf{\nu }}$. Тогда компоненты $\nu _{i}^{{}}$, $\omega _{i}^{{}}$ ${\text{(}}i = \overline {1,\;3} {\text{)}}$ имеют значения [33]

Используя векторную форму записи, из (1.9), (1.10) получим [19]

Следовательно, после интегрирования уравнений динамики соотношения (1.11), (1.12) позволяют определить положение тела в неподвижном пространстве [33]:

а также компоненты $\omega _{\xi }^{{}}$, $\omega _{\eta }^{{}}$, $\omega _{\zeta }^{{}}$ вектора угловой скорости ${\mathbf{\omega }}$ в неподвижном базисе где [33]

Отметим, что соотношения для ${\mathbf{\omega }}_{\Pi }^{{}}$ и ${\mathbf{\omega }}_{{\rm H}}^{{}}$ из формул (1.8), (1.16) позволяют применить для кинематического истолкования движения тела теорему Пуансо о представлении движения тела путем качения без скольжения подвижного аксоида вектора угловой скорости по неподвижному аксоиду этого вектора. Данный прием представляет значительные вычислительные трудности, поэтому, как правило, для использования теоремы Пуансо применяются уравнения неподвижного годографа Г. Дарбу–П.В. Харламова.

В динамике твердого тела наибольшее применение углов Эйлера осуществляется либо в методе апекса (исследование характерной оси тела в пространстве), либо в изучении программных движений, которые описываются наглядными соотношениями для углов Эйлера. Так, широко известными результатами использования первого метода являются исследования оси симметрии тела в решении Ж. Лагранжа [34] (см. [33, 35]), а также результаты Ж. Сильвестра [2], который рассматривал движение главных осей инерции в решении Л. Эйлера. Одной из последних статей, в которой изучается движение собственной оси тела в решении Д.Н. Горячева, является статья Х.М. Яхьи [36]. Роль исследований данной проблемы для прецессий тела отмечена в статье [37].

1.3. Первый пример применения метода апекса. Рассмотрим исследования движения собственной оси тела в пространстве для решения [30, 31] уравнений (1.6). В [30] показано, что при выполнении условий

уравнения (1.6) допускают решение где $\nu _{3}^{{}}{\text{(t)}}$ удовлетворяет интегральному соотношению

В формулах (1.19). (1.20) $\beta _{1}^{{}}$, $\beta _{2}^{{}}$, $\mu _{1}^{{}}$, $\mu _{2}^{{}}$ – постоянные параметры, $\kappa _{0}^{{}} = \sqrt {\beta _{1}^{{\text{2}}} + \beta _{2}^{2}} $, μ₂ = = $\frac{{\mu _{1}^{{}}n}}{{\kappa _{0}^{{}}{\text{(}}n + 2{\text{)}}}}$. Переменная $\nu _{3}^{{}}{\text{(t)}}$ при $n > 1$ изменяется в промежутках

Параметр $\lambda _{0}^{{}}$, входящий в (1.19)–(1.22), имеет значение

В силу (1.19). (1.20), из (1.11), (1.12) получим

Из равенств (1.24) следует, что годографом вектора (1.24) является окружность с радиусом λ₀, лежащая в плоскости $O\xi \eta $; при $t \to \infty $ конец вектора (1.24) стремится к точке $\left( {\lambda _{0}^{{}}{\text{, }}\; - \frac{1}{{n + 1}},\;0} \right)$. То есть поведение годографа (1.24) носит асимптотический характер. Данный пример показывает эффективность применения метода апекса. Интерес представляют условия (1.18), которые можно отнести к обобщенным условиям Горячева–Чаплыгина в классической задаче о движении тяжелого твердого тела.

1.4. Второй пример применения метода апекса. Рассмотрим второй пример изучения движения главных осей инерции тела в неподвижном пространстве. Вначале дадим характеристику программных движений твердого тела, основанную на углах Эйлера, и полученным в динамике твердого тела результатам. Наиболее распространенными программными движениями являются прецессионные движения тела [38, 39]. Пусть вектор ${\mathbf{a}} = {\text{(}}a_{1}^{{}}{\text{,}}a_{2}^{{}}{\text{,}}a_{3}^{{}}{\text{)}}$ – единичный вектор, неизменно связанный с телом, а подвижная система координат $Oxyz$ является главной системой координат, то есть A = ${\text{diag(}}A_{1}^{{}},A_{2}^{{}},A_{3}^{{}}{\text{)}}$. Введем постоянные параметры μ₀, σ₀ и запишем a₁, a₂a₃ через эти параметры:

Движение тела называют прецессией относительно вертикали, если выполняется инариантное соотношение [39]

где $a_{0}^{{}} = {\text{cos}}\theta _{0}^{{}}$ ($\theta _{0}^{{}} = \angle {\text{(}}{\mathbf{a}}{\text{,}}{\mathbf{\nu }}{\text{)}}$). Все уравнения динамики твердого тела, указанные выше (см. (1.1), (1.3), (1.4), (1.6)), содержат уравнение Пуассона которое имеет первый инетграл ${\mathbf{\nu }} \cdot {\mathbf{\nu }} = 1$. Производная от левой части (1.26), в силу (1.27), ${\mathbf{a}} \cdot {\mathbf{\dot {\nu }}} = {\mathbf{a}} \cdot {\text{(}}{\mathbf{\nu }} \times {\mathbf{\omega }}{\text{)}} = {\text{0}}$. То есть ${\mathbf{\omega }}$ при том, что ${\mathbf{a}}$ не параллелен ${\mathbf{\nu }}$, имеет вид [39]

Запишем решение уравнения (1.27) в случае (1.28); используя обозначения (1.25) и интеграл ${\mathbf{\nu }} \cdot {\mathbf{\nu }} = 1$, получим

Следовательно, в силу (1.29), компоненты $\omega _{i}^{{}}$ ($i = \overline {1,\;3} $) зависят от переменной ${{\varphi }_{*}}$ и скоростей ${{\dot {\varphi }}_{*}}$ и $\dot {\psi }_{*}^{{}}$, которые можно интерпретировать, как скорости собственного вращения и прецессии тела в прецессионной системе координат [37]. В общем случае они не совпадают с $\dot {\varphi }$ и $\dot {\psi }$ из (1.11)–(1.17).

Согласно принятой терминологии [38, 39], прецессии тела подразделяются на классы:

1: ${{\dot {\varphi }}_{*}} = n_{0}^{{}}$, $\dot {\psi }_{*}^{{}} = m_{0}^{{}}$ – регулярные прецессии;

2: ${{\dot {\varphi }}_{*}} \ne n_{0}^{{}}$, $\dot {\psi }_{*}^{{}} = m_{0}^{{}}$ – полурегулярные прецессии первого типа;

3: ${{\dot {\varphi }}_{*}} = n_{0}^{{}}$, $\dot {\psi }_{*}^{{}} \ne m_{0}^{{}}$ – полурегулярные прецессии второго типа;

4: ${{\dot {\varphi }}_{*}} \ne n_{0}^{{}}$, $\dot {\psi }_{*}^{{}} \ne m_{0}^{{}}$ – прецессии общего вида,

где $n_{0}^{{}}$ и $m_{0}^{{}}$ – постоянные параметры. В классической задаче о движении тяжелого твердого тела, согласно результатам [39], регулярные прецессии имеют место только в частном случае решения Ж. Лагранжа [34], полурегулярные прецессии – в частном случае решения В. Гесса [40], прецессии общего вида – в решении А.И. Докшевича [41] (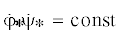), в частном случае решения Ж. Лагранжа ($\dot {\psi }_{*}^{{}} = {{\dot {\varphi }}_{*}}{{_{*}}_{*}}$) и в частном случае решения В. Гесса, установленном А. Брессаном [42]. В обобщенных задачах динамики твердого тела классов прецессий тела с неподвижной точкой значительно больше (см. обзор [43]).

Замечание 1. Применение в истолковании движении тела углов Эйлера в форме (1.10), (1.17) позволяет очевидным способом получить класс изоконических движений тела. Действительно, положив в (1.10), (1.17) $\dot {\psi } = \dot {\varphi }$, устанавливаем, что подвижный и неподвижный годографы угловой скорости симметричны друг другу относительно касательной к ним плоскости, которая содержит неподвижную точку O.

Рассмотрим движение одной из главных осей инерции тела в случае регулярных прецессий: ${{\dot {\varphi }}_{*}} = n_{0}^{{}}$, $\dot {\psi }_{*}^{{}} = m_{0}^{{}}$. Из соотношений (1.29), в силу ${{\varphi }_{*}} = n_{0}^{{}}t$, имеем

Компоненты угловой скорости ${\mathbf{\omega }}$ из (1.28) таковы

где a_i ($i = \overline {1,\;3} $) имеют значения (1.25), а функции $\nu _{i}^{{}}{\text{(}}t{\text{)}}$ ($i = \overline {1,\;3} $) указаны в (1.30). Тогда, на основании (1.30), (1.31), углы Эйлера определим из (1.11), (1.12): где $a_{0}^{'} = \sqrt {1 - a_{0}^{2}} $. Изучим годограф вектора (1.15) при наличии равенств (1.32):

Для наглядности рассмотрим случай ${\text{cos}}\mu _{0}^{{}} = 0$, $m_{0}^{{}} = n_{0}^{{}}$, a₀ = 0. Тогда, обозначая $n_{0}^{{}} = \tau $, из (1.34) получим

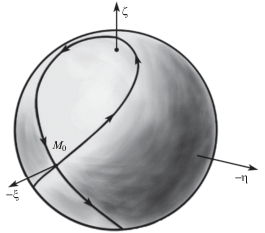
Из формул (1.33), (1.35) следует, что проекцией годографа (1.35) на плоскость $O\xi \eta $ является окружность радиуса 0.5. Движение изображающей точки проеции является периодическим с периодом по $\tau $, равным π. Годограф (1.33) изображен на рис. 1.

Движение конца вектора (1.33) указано стрелкой. Очевидно, что в силу (1.35) движение главной оси Oz в неподвижном пространстве будет иметь периодический характер (период ее движения по $\tau $ равен $2\pi $).

Аналогично изучаются и другие регулярные прецессии тела в случае резонансных значений $m_{0}^{{}} = kn_{0}^{{}}$ ($k \in N)$, а также случай $a_{0}^{{}} \ne 0$. Предварительный анализ показывает, что аналоги годографов вектора (1.33) имеют вид “роз Клелилии”, открытых Брандом.

Отметим, что в обобщенных задачах динамики открыты многочисленные классы прецессий не только в случае постоянного гиростатического момента, но и в случае переменного гиростатического момента [43].

Важным свойством углов Эйлера является применение их в теории ориентации и управления механическими системами. Если известны функции φ(t), ψ(t), θ(t), то параметры Родрига–Гамильтона находятся из соотношений [33, 44]

Они находят широкое применение в разработке ориентации технических объектов (см., например, [45]).

2. Модифицированный метод Пуансо. Обозначим через ${\mathbf{x}} = A{\mathbf{\omega }}$ момент количества движения тяжелого твердого тела, имеющего неподвижную точку. Тогда уравнения (1.1) запишутся в виде

где a – гирационный тензор. При s = 0 из (2.1) имеем случай Л. Эйлера то есть $\frac{{d{\mathbf{x}}}}{{dt}} = {\mathbf{0}}$, вектор ${\mathbf{x}} = {\mathbf{x}}_{0}^{{}} = {\mathbf{const}}$. Решение Эйлера изучали Ж. Сильвестр [2], Г. Дарбу [5], К. Якоби [7], В. Гесс [9], Ж. Мак-Куллаг [3], Э. Раус [10] и многие другие ученые. Результаты их исследований изложены в монографиях (Э. Раус [10], К. Магнус [35], Г.К. Суслов [15]) и во многих учебниках по теоретической механике. Здесь отметим, что герполодии (неподвижный годограф вектора угловой скорости) исследовал Г. Дарбу [5]. Для изучения уравнений этой кривой Г. Дарбу в плоскости герполодии вводил полярные координаты $\rho {\text{,}}\,\alpha $ и получил уравнения [46, стр. 176] где ${\mathbf{\omega }}$ – угловая скорость, $E_{*}^{{}}$ – постоянный параметр. Уравнения Г. Дарбу (2.3) были обобщены П.В. Харламовым [17] на случай произвольного решения (1.7), (1.8) уравнений (1.1), (1.2). В цилиндрической системе координат $O\xi \eta \zeta $ он получил уравнения

В формулах (2.3), (2.6) ${\mathbf{\dot {\omega }}}{\text{(}}t{\text{)}}$ – относительная производная угловой скорости тела. Логично полагать, что исследование уравнений неподвижного годографа вектора угловой скорости в общем случае проводится с помощью метода Г. Дарбу–П.В. Харламова.

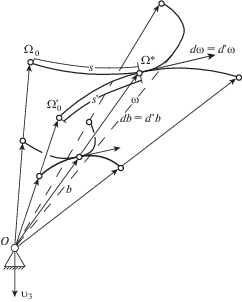
Остановимся на модифицированном методе Пуансо, предложенном в статье [18]. На рис. 2 изображены подвижный и неподвижный годографы вектора угловой скорости ω.

Из равенства абсолютной и относительной производной этого вектора следует $d{\mathbf{\omega }}{\text{(}}t{\text{)}} = d{\text{'}}{\mathbf{\omega }}{\text{(}}t{\text{)}}$. Это означает, что длины годографов $\tilde {s}$ и $\tilde {s}{\text{'}}$ равны, т.е. $ \cup \Omega _{0}^{{}}\Omega * = \cup \Omega _{0}^{'}\Omega {\text{*}}$. Здесь $\Omega _{0}^{{}}$ – начальная точка (при $t = t_{0}^{{}}$) на неподвижном годографе, $\Omega _{0}^{'}$ – начальная точка (при $t = t_{0}^{{}}$) на подвижном годографе, Ω* – точка касания годографов в момент $t$. Из указанных свойств и следует теорема Л. Пуансо о представлении движения тела качением без скольжения подвижного аксоида вектора угловой скорости по неподвижному.

Определенную сложность в применении формулы для полярного угла из (2.6) представляет зависимость от производной ${\mathbf{\dot {\omega }}}$. В статье [18] получена более простая формула

где в силу (1.12)

Равенство (2.7) и функция $\psi {\text{(}}t{\text{)}}$ из (2.8) позволяют не только получить функцию $\alpha {\text{(}}t{\text{)}}$ без использования производной ${\mathbf{\dot {\omega }}}$, но и связать две кинематические переменные: α и $\psi $. При этом, если ${\mathbf{\nu }}{\text{(}}t{\text{)}} \cdot {\mathbf{i}}_{3}^{{}} = {\text{const}}$, то $\delta = 0$, в противном случае δ = 1. Данное обстоятельство имеет важное значение в комплексном подходе истолкования движения тела.

Введем вектор

На рис. 2 указаны подвижный и неподвижный годографы вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$. Очевидно, что, как и в случае годографов угловой скорости, подвижный и неподвижный годографы вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ имеют общую касательную и в силу $db{\text{(}}t{\text{)}}{\mathbf{\omega }}{\text{(}}t{\text{)}} = d{\text{'}}b{\text{(}}t{\text{)}}{\mathbf{\omega }}{\text{(}}t{\text{)}}$ длины дуг, описанных за одинаковый промежуток времени концом вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ на подвижном и неподвижном годографе, равны [25]. Следовательно, за основу кинематического истолкования можно взять годографы вектора b(t) и движение тела, имеющего неподвижную точку, представить качением без скольжения подвижного годографа вектора b(t) по неподвижному. При этом вращать тело необходимо с угловой скоростью

Это обстоятельство можно учесть на заключительном этапе кинематического истолкования, то есть при качении аксоидов годографов вектора b(t). При этом функция b(t) – произвольная дифференцируемая функция.

2.1. Первый метод в истолковании движения тела. Покажем, что функцию b(t) при определенных условиях можно выбрать так, чтобы неподвижный годограф вектора b(t) находился в некоторой, неподвижной в пространстве, плоскости.

Рассмотрим вектор-функцию (2.4). Предположим, что $\omega _{\zeta }^{{}}{\text{(}}t{\text{)}}$ не изменяет своего знака при $t \in {\text{[0;}}\infty {\text{)}}$. Тогда в качестве вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ можно взять вектор ${\mathbf{\omega }}{\text{(}}t{\text{)/}}\omega _{\zeta }^{{}}{\text{(}}t{\text{)}}$ и из (2.4) получить

Следовательно, функция $b{\text{(}}t{\text{)}} = \frac{{\text{1}}}{{\omega _{\zeta }^{{}}{\text{(}}t{\text{)}}}}$ и подвижный годограф вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ определим из формулы

Из (2.10) получаем, что неподвижный годограф ${\mathbf{b}}{\text{(}}t{\text{)}}$ лежит в плоскости ζ = 1. Поскольку касательные векторы к ${\mathbf{b}}_{{\rm H}}^{{}}{\text{(}}t{\text{)}}$ тоже лежат в этой плоскости, то движение тела можно представить качением без скольжения кривой (2.11) по плоской кривой (2.10). Таким образом, получили некоторый аналог истолкования Л. Пуансо о представлении движения свободного тела.

Выбор вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ зависит от свойств вектор-функции (2.4). Например, если одна из функций $\omega _{\xi }^{{}}{\text{(}}t{\text{)}}$, $\omega _{\eta }^{{}}{\text{(}}t{\text{)}}$ не обращается в нуль, то в качестве функции b(t) можно выбрать или $\frac{1}{{\omega _{\xi }^{{}}{\text{(}}t{\text{)}}}}$, или $\frac{{\text{1}}}{{\omega _{\eta }^{{}}{\text{(}}t{\text{)}}}}$.

2.2. Второй метод в истолковании движения тела. Рассмотрим вектор-функцию (1.8). Пусть $\omega _{3}^{{}}{\text{(t)}} \ne 0$ при $t \in {\text{[0;}}\infty {\text{)}}$. Тогда вектор ${\mathbf{b}}{\text{(}}t{\text{)}}$ будем выбирать так

Следовательно, в силу (2.4), имеем

Движение тела можно истолковать как качение аксоида с направляющей линией (2.12) по аксоиду с направляющей линией (2.13). Очевидно, что подвижный годограф вектора (2.12) является плоской кривой, что в ряде случаев может упростить истолкование движения тела.

2.3. Третий метод в истолковании движения тела. Представляется актуальным получение такого метода в истолковании движения, который бы не содержал субъективных факторов конкретного подхода, а был бы универсальным для любых решений уравнений динамики твердого тела. Так как при истолковании движения тела не используется его конструктивное строение, то вполне естественно применить объективный фактор в истолковании движения (как это осуществил Л. Пуансо), а именно свойство движения эллипсоида инерции. Положим, что конец вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ принадлежит эллипсоиду инерции в неподвижной точке. Обозначим через ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ главные моменты инерции тела. Тогда уравнение эллипсоида инерции таково:

где x, y, z – координаты точек, принадлежащих эллипсоиду $\sigma _{0}^{2}$ – постоянная. Потребуем, чтобы конец вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ из формулы (2.9) принадлежал эллипсоиду (2.14). Для нахождения функции b(t) подставим в (2.14) вместо x, y, z величины $b_{i}^{{}} = b{\text{(}}t{\text{)}}\omega _{i}^{{}}{\text{(}}t{\text{)}}$. Тогда

В силу (1.8), (2.4) подвижный и неподвижный годографы вектора ${\mathbf{b}}{\text{(}}t{\text{)}}$ запишем в виде

Функция b(t) определена выражением (2.15).

Движение тела будем воспроизводить качением годографа (2.16) по годографу (2.17). Выражение (2.15) упрощается, например, для уравнений (1.1) с интегралами (1.2). В главной системе координат интеграл энергии из (1.2) можно записать следующим образом:

Используя равенство (2.18), из (2.15) получим

В формулу (2.19) входит лишь скалярное произведение векторов ${\mathbf{e}}$, ${\mathbf{\nu }}$, что в ряде задач имеет преимущество в использовании (2.15).

Замечание 2. Э. Раус применил [11] методы сферической тригонометрии для изучения конусов, которые описывают ось l момента количества движения в подвижном пространстве, и ось $l_{*}^{{}}$ вращения тела в случае Эйлера. Приведем цитату [11, том 2, стр. 123]: “Но можно использовать также сферу с центром в неподвижной точке, считая ее связанной с телом или неподвижной в пространстве. Этот способ особенно полезен в случае, когда нужно изучить движение какой-либо прямой в пространстве или в теле. Измеряя соответствующие углы дугами, приведенными на сфере, можно упростить процесс вычислений с помощью соответствующих формул сферической тригонометрии”. Очевидно, что в общем случае оси l  и $l_{*}^{{}}$ пересекают сферу по сфероконическим кривым.

Сказанное выше означает, что подход Рауса можно условно отнести к частному случаю, изложенному выше.

2.4. Пример применения модифицированного метода Пуансо. Рассмотрим решение (1.19)–(1.21), которое получено в [30] и имеет место при условиях (1.18) для уравнений (1.6) с силовой функцией

Представляет интерес результат, что уравнения Пуассона на инвариантных соотношениях (ИС) (1.19), (1.20) имеют ИС

которое, в силу метода обратных задач динамики, нельзя использовать в выражении (2.20). Для применения прямого метода Пуансо, в силу того, что функция $\psi {\text{(}}\nu _{3}^{{}}{\text{)}}$ найдена (она указана в системе (1.24)), целесообразно использовать формулу (2.7). Тогда на решении (1.19), (1.20) получим

Запишем уравнения неподвижного годографа вектора угловой скорости, используя соотношения (2.4), (2.5), (2.22):

Для подвижного годографа вектора угловой скорости обратимся к равенствам (1.19). Исключая в них переменную $\nu _{3}^{{}}$, получим

Из системы (2.24) следует, что подвижный годограф ${\mathbf{\omega }}$ – линия пересечения конуса второго порядка и алгебраической поверхности n-го порядка.

Применим к исследованию решения (1.19), (1.20) модифицированный метод [18]. Пусть ${\mathbf{b}}{\text{(}}\nu _{3}^{{}}{\text{) }} = b{\text{(}}\nu _{3}^{{}}{\text{)}}\omega {\text{(}}\nu _{3}^{{}}{\text{)}}$, где

Функция (2.25) определена в промежутках (1.22). Тогда из (1.19), (2.9), (2.22), (2.23), (2.25) имеем

где

Подвижный и неподвижный годографы (2.26) и (2.27) – конгруэнтные плоские кривые; в алгебраической форме, в силу (2.28) и (2.29), их координаты определяются уравнениями

Таким образом, применение модифицированного метода [18] позволяет представить движение тела качением без скольжения двух конусов (2.30). В силу структуры (2.26), (2.27), данный подход имеет несомненные преимущества перед прямым методом Пуансо, так как уравнения подвижного и неподвижного годографов (2.24) содержат одно алгебраическое уравнение, степень которого зависит от параметра n. Это обстоятельство существенно скажется на построении годографов. В отличие от этого свойства, годографы (2.30) для любых n являются плоскими кривыми (уравнение плоскости не зависит от n) и только радиусы окружностей зависят от n.

Рассмотрим движение эллипсоида инерции в решении (1.19), (1.20). Данная задача решается следующим образом. Запишем уравнение эллипсоида инерции тела, используя равенства из (1.18):

где $x$, $y$, $z$ – координаты точек эллипсоида (2.31), $\sigma _{0}^{2}$ – постоянная. Непосредственной подстановкой значений $b_{i}^{{}}$ ($i = \overline {1,\;3} $) из (2.28) в уравнение (2.31) убеждаемся в том, что конец подвижного годографа вектора ${\mathbf{b}}_{\Pi }^{{}}$ из (2.26) принадлежит поверхности и (2.31) при $\sigma _{0}^{2} = \mu _{1}^{{\text{2}}}{\text{(}}n + {\text{1)}}$. То есть при обкатывании поверхностей с направляющими ${\mathbf{b}}_{\Pi }^{{}}$, ${\mathbf{b}}_{{\rm H}}^{{}}$ получим движение эллипсоида инерции. Остается выяснить свойство расположения эллипсоида инерции в неподвижном пространстве. Покажем, что эллипсоид инерции тела на кривой (2.28) и (2.29) касается неподвижной плоскости $b_{\eta }^{{}}{\text{(}}\nu _{3}^{{}}{\text{)}} = \mu _{1}^{{}}$.

Запишем уравнение (2.31) в переменных $b_{i}^{{}}$ ($i = \overline {1,\;3} $):

Положение вектора, неизменно связанного с телом, можно найти, используя формулы (1.13)–(1.15), в которых на исследуемом решении имеют место равенства

Вычислим градиент к поверхности (2.32) на кривой ${\mathbf{b}}_{\Pi }^{{}}{\text{(}}\nu _{3}^{{}}{\text{)}}$:

Используя формулы (1.13)–(1.15), (2.33), (2.34), вычислим значение вектора (2.34) в неподвижной системе координат [19]

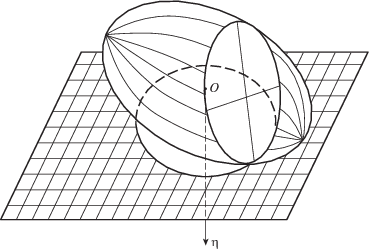
Равенство (2.35) показывает, что при движении эллипсоида инерции в неподвижном пространстве он катается по плоскости $b_{\eta }^{{}}{\text{(}}\nu _{3}^{{}}{\text{)}} = \mu _{1}^{{}}$ по кривым (2.28) и (2.29). Эскиз движения эллипсоида показан на рис. 3. Поскольку при $t \to \infty $ $\nu _{3}^{{}} \to 0$, а точка $\nu _{3}^{{}} = 0$ исключена из рассмотрения, то по непрерывности можно сделать заключение, что при $t \to \infty $ эллипсоид инерции в неподвижном пространстве стремится к состоянию покоя.

Для наглядности на рис. 3 ось $O\eta $ направлена вниз, так как рассматривается задача о движении тела в потенциальном поле, для которой вектор ${\mathbf{\nu }}$ в неподвижном пространстве может быть выбран произвольно.

Замечание 3. И.Н. Гашененко [47] при исследовании случая А. Брессана [42] установил, что движение гироскопа Гесса в этом варианте можно представить качением без скольжения эллипсоида инерции по плоскости. Однако он использовал метод, отличный от представленного выше модифицированного метода, который можно применять для любого решения уравнений динамики.

Заключение. В статье предложен комплексный подход в истолковании движения твердого тела, имеющего неподвижную точку, основанный на применении углов Эйлера, метода апекса, классического метода Пуансо и модифицированного автором статьи метода Пуансо. Показано, что кинематическая формула, полученная автором статьи, имеет большое значение в истолковании движения твердого тела с неподвижной точкой с помощью уравнений Г. Дарбу–П.В. Харламова. Особое внимание уделено результатам Э. Рауса, Ж. Сильвестра и других ученых, исследующих качественные свойства в движении тела.

Данная статья может быть отнесена к первой части в комплексном подходе истолкования движения. Вторая часть будет посвящена исследованию частных решений уравнений движения тяжелого твердого тела (Л. Эйлера, Д.К. Бобылева–В.А. Стеклова, В.А. Стеклова, А.И. Докшевича) и других решений.