Известия РАН. Механика твердого тела, 2021, № 6, стр. 111-129

1. Введение. Динамическая задача теории упругости для длинной упругой полосы традиционно интуитивно разделяется на две независимые задачи: задачу поперечных колебаний балки и задачу продольных колебаний стержня. При этом вторая задача может быть сформулирована как волновая. В силу этого низкочастотные (преимущественно изгибные) и высокочастотные колебания (преимущественно растяжения–сжатия) рассматриваются отдельно. Общим в этих задачах является то, что они формулируются, как это принято в сопротивлении материалов, в усилиях и моментах и описываются обыкновенными дифференциальными уравнениями. Следствием такого подхода является невыполнение всех граничных условий соответствующей задачи теории упругости для полосы. Поэтому решения дифференциальных уравнений в усилиях и моментах обладают решениями, в которых могут наблюдаться разрывы в напряжениях, быстрые переходы, неоднородности, невыполненные граничные условия и т.п. Понижение порядка размерности дифференциальных уравнений в усилиях и моментах в сочетании с потерей некоторых граничных условий является основной чертой таких теорий и сопровождается возникновением асимптотических явлений [1]. Цель уточненного анализа заключается в дополнительном описании асимптотики решения граничной задачи внутри переходных слоев в областях разрывов. Потребность в таких уточненных теориях связана с необходимостью более полного понимания классической теории после того, как становятся видны ее обобщения и они позволяют лучше охарактеризовать погрешность классических теорий [2]. Однако построение теорий последовательных, в смысле учёта всех малых одного порядка крайне трудно осуществить, не располагая регулярными методами [3].

С.П. Тимошенко [4, 5] вывел уравнение влияния эффектов более высокого порядка по сравнению с классической теорией балок и оно в настоящее время представляет большой интерес. Уточненные теории типа Тимошенко получили большое развитие и отражены во многих работах, например [6–14]. В этих и других работах традиционно используются уравнения в усилиях и моментах, граничные условия на длинных сторонах балки или на лицевых сторонах пластины (оболочки) не выполняются, на концах ставятся условия типа балочных. В связи с этим в настоящей работе ставится задача решения динамических уравнений теории упругой полосы в перемещениях и напряжениях для низкочастотных колебаний без каких-либо априорных гипотез с помощью регулярного метода Сен-Венана–Пикара–Банаха (SVPB) [15, 16].

Для решения трехмерной задачи кручения тонкого длинного стержня Сен-Венан предложил в исходных уравнениях задать часть неизвестных и вычислить с помощью преобразованных таким образом уравнений остальные неизвестные [2]. Продолжим этот метод так, чтобы по вычисленным остальным неизвестным можно было найти заданные величины начального приближения в первом приближении и затем остальные неизвестные, представив полуобратный метод как итерационный [15, 16]. Делается это так. В соответствии с идеей Сен-Венана задаются величины начального (нулевого) приближения. Затем по ним вычисляются остальные неизвестные. Для этого система уравнений теории упругости переписывается так, чтобы неизвестные вычислялись (в нулевом приближении) последовательно путем прямого интегрирования через уравнения первого порядка и величины начального приближения в первом. Если поправка к заданным величинам и вычисленным по ним остальным, полученная в следующем приближении, будет малой, то в силу принципа сжатых отображений Банаха полученные в итерационном процессе последовательности Коши для неизвестных будут асимптотически сходящимися. При этом выполняются все граничные условия.

Будем считать, что вопросы, связанные с существованием и единственностью решений уравнений теории упругости формулируются так же как в функциональном анализе в виде вопроса о существовании и единственности неподвижной точки при некотором отображении соответствующего метрического пространства в себя. Среди различных критериев существования и единственности неподвижной точки наиболее общим является принцип сжатых отображений [17–21]. Отображение y = Ay метрического пространства M в себя называется сжимающим отображением, если существует такое число ${{\varepsilon }} < 1$, что для любых двух точек $x,y \in M$ выполняется неравенство $\rho \left( {Ax,Ay} \right) \leqslant \varepsilon \rho \left( {x,y} \right)$, где $\rho $ – метрика пространства M. Точка $y$ называется неподвижной точкой отображения, если y = Ay. Иначе говоря, неподвижные точки – это решения уравнения y = Ay. Итерационный процесс начинается, исходя из некоторого начального приближения ${{y}_{{\left( 0 \right)}}} = {{y}_{0}}$. Если оператор A является сжимающим, процедура сходится к некоторому решению $y$ независимо от выбора величины начального приближения. Последовательные приближения ${{y}_{{\left( 1 \right)}}},\;{{y}_{{\left( 2 \right)}}},\;{{y}_{{\left( 3 \right)}}}\;...$ находятся с помощью формулы ${{y}_{{\left( {n + 1} \right)}}} = A{{y}_{{\left( n \right)}}}$ [17].

Хотя полуобратный метод применялся к линейным и нелинейным задачам для сред с усложненными характеристиками [22–26], его рассмотрение, как итерационного и связанного с оператором Пикара и принципом сжатых отображений Банаха, за исключением работ [15, 16, 27–30] в литературе отсутствует. Также отсутствуют работы по исследованию уточненных граничных условий в сравнении с классическими балочными.

В работе метод простых итераций, с помощью которого решен ряд задач теории упругости тонкостенных тел [15, 16, 27–30], описывается как общий метод SVPB на примере наиболее простой задачи для прямоугольника – вынужденных колебаний с частотами, соизмеримыми с частотами поперечных колебаний балки, длинной тонкой упругой полосы, уравнения которой содержат малый параметр, обеспечивающий асимптотическую сходимость разложений неизвестных в ряды по малому параметру в соответствии с принципом сжатых отображений. Колебания с высокими частотами, соизмеримыми с частотами продольных колебаний балки, в настоящей статье не рассматриваются.

Еще один важный вопрос, разрешаемый уточненной теорией, связан с тем, что в практических расчетах возникают проблемы, связанные с плохой сходимостью рядов полученных путем разложения решений о вынужденных колебаниях балки в ряды по собственным функциям. Отмечается, что выделение частного решения как статического существенно улучшает сходимость [31, 32]. Это положение подтверждается в настоящем исследовании тем, что при нахождении частного решения инерционные члены пренебрежимо малы по сравнению с главными и оно действительно может быть найдено из статических уравнений. Кроме того, инерционные члены могут быть отброшены и в уточненных граничных условиях.

2. Произвольно нагруженная по длинным сторонам полоса. Длинная прямоугольная полоса помещается в декартовой системе координат $х{\kern 1pt} *,z{\kern 1pt} *$ так, что $0 \leqslant x{\kern 1pt} * \leqslant l,$ $ - h \leqslant z{\kern 1pt} * \leqslant h$. Уравнения движения запишем в следующем виде

Здесь приняты традиционные обозначения величин теории упругости. Звездочкой отмечены размерные искомые величины и координаты. В уравнениях E, $\nu $, $\rho $ – модуль упругости, коэффициент Пуассона, удельная плотность материала, $t{\kern 1pt} *$ – время.

Уравнения, описывающие состояние такой полосы в безразмерных координатах $x = x{\kern 1pt} {\text{*/}}l$, $z = z{\kern 1pt} {\text{*/}}h,$ перемещениях $u = u{\kern 1pt} {\text{*/}}h$, $w = w{\kern 1pt} {\text{*/}}h$ вдоль осей $х{\kern 1pt} *,z{\kern 1pt} *$, соответственно, нормальных ${{\sigma }_{x}} = \sigma _{x}^{*}{\text{/}}E$, ${{\sigma }_{z}} = \sigma _{z}^{*}{\text{/}}E$ и касательных $\tau = \tau {\kern 1pt} {\text{*/}}E$ напряжениях принимают вид

Введены обозначения: $\varepsilon = {h \mathord{\left/ {\vphantom {h l}} \right. \kern-0em} l}$ – малый параметр, ${{\varepsilon }^{2}}a_{l}^{2} = {{\rho {{h}^{2}}\omega _{l}^{2}} \mathord{\left/ {\vphantom {{\rho {{h}^{2}}\omega _{l}^{2}} E}} \right. \kern-0em} E}$, ${{\varepsilon }^{4}}a_{c}^{2} = {{\rho {{h}^{2}}\omega _{c}^{2}} \mathord{\left/ {\vphantom {{\rho {{h}^{2}}\omega _{c}^{2}} E}} \right. \kern-0em} E}$. В качестве времени, по которому осуществляется дифференцирование в первом уравнении, выбрано безразмерное время ${{t}_{l}} = {{\omega }_{l}}t{\kern 1pt} *$ и во втором уравнении ${{t}_{c}} = {{\omega }_{с}}t{\kern 1pt} *$. Под величинами ${{\omega }_{l}}$ и ${{\omega }_{c}}$ подразумеваются первые собственные частоты продольных и поперечных колебаний полосы как стержня, соответственно. Между безразмерными временами имеют место соотношения

Коэффициенты ${{\varepsilon }^{2}}a_{l}^{2}$ и ${{\varepsilon }^{4}}a_{c}^{2}$ выбраны так, чтобы на основании известных, записанных в безразмерных координатах, уравнений продольных и поперечных колебаний стержня

имели место оценки $a_{l}^{2},a_{c}^{2} \sim {{\varepsilon }^{0}}$. Здесь $\upsilon $ и y продольные и поперечные перемещения точек поперечного сечения стержня соответственно.

Длинные стороны полосы $z{\kern 1pt} * = \pm h$ несут некоторую произвольную динамическую нагрузку, изменение которой по времени задается в зависимости от времени ${{t}_{c}}$, короткие стороны полосы могут быть закреплены или нагружены.

Расположим уравнения первого порядка относительно координаты z системы (2.1) в такой последовательности, чтобы неизвестные в правой части рассматриваемого уравнения вычислялись через известные величины в правой части путем интегрирования по z и умножения на малый параметр ε. Задав в соответствии с идеей полуобратного метода Сен-Венана в качестве известных величин некоторые начальные значения $w = {{w}_{0}}\left( {x,z,t} \right)$ и $\tau = {{\tau }_{0}}\left( {x,z,t} \right)$, сведем интегрирование системы уравнений к методу последовательных приближений по следующей схеме вычислений

Здесь и далее нижним индексом в скобках обозначен номер приближения.

Легко видеть, что при заданных функциях $w = {{w}_{0}}(x,z,t)$ и $\tau = {{\tau }_{0}}(x,z,t)$ остальные величины вычисляются последовательно путем прямого интегрирования по z

Индексом в скобках обозначен номер приближения, индексом 0 обозначены не зависящие от z произволы интегрирования.

Будем рассматривать уравнения нулевого и первого приближений при выборе величин начального приближения ${{w}_{{\left( 0 \right)}}} = {{w}_{0}}\left( {x,\;t} \right)$ и $\;{{\tau }_{{\left( 0 \right)}}} = {{\tau }_{0}}\left( {x,\;t} \right)$. В силу независимости величин начального приближения от $z$, все интегралы вычисляются в явном виде

в виде полиномов по степеням z. Заданные величины начального приближения ${{w}_{0}}\left( {x,t} \right)$ и ${{\tau }_{0}}\left( {x,t} \right)$ вычислены также в первом приближении ${{w}_{{\left( 1 \right)}}}\left( {x,z,t} \right)$ и ${{\tau }_{{\left( 1 \right)}}}\left( {x,z,t} \right)$ для того, чтобы определить величину поправки с учетом координаты z. Величины $\tau $, ${{\sigma }_{z}}$, $w$, $u$ записаны в первом приближении: с их помощью будут выполняться граничные условия, остальные – в нулевом. При этом все неизвестные выражены в зависимости от произвольных функций интегрирования ${{\tau }_{0}}\left( {x,t} \right)$, ${{\sigma }_{{z0}}}\left( {x,t} \right)$, ${{w}_{0}}\left( {x,t} \right)$, ${{u}_{0}}\left( {x,t} \right)$, относительные порядки которых между собой по $\varepsilon $ будут определены из граничных условий на длинных и коротких сторонах полосы.

Видно, что формулы (2.3) могут быть записаны в виде последовательности Коши по степеням $\varepsilon $ с коэффициентами, зависящими от $\nu $ и z.

Можно заметить, что ${{\ddot {w}}_{0}}{{,}_{c}}$ всегда имеет индекс c после запятой, а индекс l находится при величинах $\ddot {\tau }_{0}^{'}{{,}_{l}}$ и ${{\ddot {u}}_{0}}{{,}_{l}}$. Поэтому в дальнейшем эти индексы отбросим, считая их приписанными к указанным величинам с двумя точками соответствующим образом “по умолчанию”.

3. Выполнение граничных условий на длинных сторонах полосы. Уравнение Тимошенко. На лицевых поверхностях полосы $z{\kern 1pt} * = \pm h$ должны удовлетворяться граничные условия, соответствующие условиям нагружения. В безразмерном виде эти условия записываются так

Безразмерные нагрузки ${{Z}_{ + }}$, ${{X}_{ + }}$, ${{Z}_{ - }}$, ${{X}_{ - }}$ получены путем деления размерных на жесткость E.

Условия (3.1) будем удовлетворять величинами первого приближения из соотношений (2.3) в предположении, что они с достаточной точностью аппроксимируют искомые величины. Получим четыре уравнения для определения неизвестных ${{\tau }_{0}}$, ${{\sigma }_{{z0}}}$, ${{w}_{0}}$, ${{u}_{0}}$

Складывая и вычитая попарно первые два уравнения и последние два, получим четыре уравнения относительно неизвестных w₀, τ₀, определяющих задачу изгиба,

и относительно ${{u}_{0}},\;{{\sigma }_{{z0}}}$, определяющих задачу растяжения–сжатия,

Формулы для поперечных напряжений ${{\sigma }_{z}}$ и $\tau $ из (2.3) c учетом соотношений (3.2), (3.3) приводятся к простому виду

Замечание 1. Продифференцируем первое однородное уравнение из (3.2) по x, умножим на $\varepsilon $ и сложим с однородным вторым. Получим выражение неизвестной $\tau _{0}^{'}$ через ${{w}_{0}}$

Исключив неизвестную $\varepsilon \tau _{0}^{'}$ и ее производные из второго уравнения в (3.2) и пренебрегая различием в дифференцировании по ${{t}_{l}}$ и ${{t}_{с}}$, получим уравнение

Уравнение Тимошенко имеет вид [4]

Здесь $k{\kern 1pt} '$ – коэффициент, зависящий от формы поперечного сечения, F – площадь поперечного сечения, $y{\kern 1pt} *$ – прогиб, $x{\kern 1pt} *$ – координата оси балки, I – момент инерции поперечного сечения.

Приведенное к безразмерному виду это уравнение в случае прямоугольного сечения балки высотой $2h$ ($I = {{2b{{h}^{3}}} \mathord{\left/ {\vphantom {{2b{{h}^{3}}} 3}} \right. \kern-0em} 3}$, $F = 2bh$) при $k{\kern 1pt} ' = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ и $b = 1$ ($b$ – ширина сечения) записывается так

Здесь $y = {{y{\kern 1pt} *} \mathord{\left/ {\vphantom {{y{\kern 1pt} *} h}} \right. \kern-0em} h}$ – безразмерный прогиб и считается, что ${{a}_{c}} = {{a}_{l}} = a$.

Видно, что выведенные разными методами уравнение (3.8) и уравнение (3.6) практически совпадают. Уравнение (3.6), полученное с помощью соотношения (3.5), нельзя считать правильным, поскольку при получении последнего из уравнений (3.2) при вычитании произошло уничтожение главных частей уравнений: исчезли высшие производные и, соответственно, быстро меняющиеся решения. Затем только медленно меняющаяся величина $\varepsilon \tau _{0}^{'}$ подставляется во второе уравнение системы (3.2), содержащее и быстро меняющиеся, и медленно меняющиеся величины $\varepsilon \tau _{0}^{'}$, вместо быстро меняющихся и медленно меняющихся величин¹¹. В силу этого уравнение (3.6) и совпадающее с ним уравнение Тимошенко (3.8), приходится признать некорректными.

4. Уравнения низкочастотных колебаний. Рассмотрим поведение решений уравнений (3.2) и (3.3) при действии только поперечной нагрузки, медленно меняющейся вдоль длинных сторон полосы и изменяющейся во времени по гармоническому закону $\sin \omega {{t}_{c}}$. Этот случай отвечает приложению нагрузки с частотами, соизмеримыми с низшими частотами поперечных колебаний полосы, рассматриваемой как балка.

Положим для определенности, что на границу полосы z = 1 действует только распределенная нагрузка ${{Z}_{ + }} = p\left( x \right)\sin \omega {{t}_{c}}$, p(x) – функция малой изменяемости, $\omega \sim {{\varepsilon }^{0}}$. Остальные нагрузки отсутствуют. Частные решения для $w_{0}^{{\left( p \right)}}$ и $\tau _{0}^{{\left( p \right)}}$ находятся из уравнений (3.2) после отбрасывания членов с высшими производными от ${{\tau }_{0}}$ по $x$ и ${{t}_{l}}$ вследствие малой изменяемости и членов $\left( {1 + \nu } \right){{\varepsilon }^{5}}a_{c}^{2}\ddot {w}_{0}^{'}$ в первом уравнении и $\left( {1 + \nu } \right){{\varepsilon }^{6}}a_{c}^{2}\ddot {w}_{0}^{{''}}$ во втором уравнении, имеющих порядок ε² по сравнению с находящимися в этом же уравнении одноименными величинами

Эти два уравнения сводятся к одному классического вида относительно ${{w}_{0}}$

Его решение является медленно меняющейся функцией и из первого уравнения системы (4.1) следует оценка для частного решения $w_{0}^{{\left( p \right)}}$ относительно нагрузки

и для частного $\tau _{0}^{{\left( p \right)}}$ и общего $\tau _{0}^{{\left( g \right)}}$

Частные решения для ${{u}_{0}}$ и ${{\sigma }_{{z0}}}$ находятся из уравнений (3.3) при ${{Z}_{ + }} = p\sin \omega {{t}_{c}}$

Продифференцируем первое уравнение по x, умножим на $\varepsilon $ и сложим со вторым. Получим

Подставив теперь известную величину $\sigma _{{z0}}^{{\left( p \right)}}$ в первое уравнение системы (4.5) получим уравнение для определения решения u₀

из которого, учитывая малую изменяемость функций u₀ и p, получаем оценку

Будем считать, что частные решения $w_{0}^{{\left( p \right)}}$, $\tau _{0}^{{\left( p \right)}}$, $u_{0}^{{\left( p \right)}}$, $\sigma _{{z0}}^{{\left( p \right)}}$ найдены. Общие решения для величин $w_{0}^{{\left( g \right)}}$ и $\tau _{0}^{{\left( g \right)}}$ будем искать из однородных уравнений (3.2)

Общие решения для величин $u_{0}^{{\left( g \right)}}$, $\sigma _{{z0}}^{{\left( g \right)}}$ следуют из уравнений (4.6) и (4.7) при p = 0.

Представим решения ${{w}_{0}},{{\tau }_{0}}$ в виде сумм

обозначив верхним индексом s медленно меняющуюся часть решения, а индексом q быстро меняющуюся, что может быть записано так

В первом уравнении системы (4.9) член $\left( {2 + \nu } \right){{\varepsilon }^{2}}\tau {{_{0}^{s}}^{{\prime \prime }}}$ имеет порядок ε² по сравнению с последним и может быть отброшен. Аналогичное отбрасывание можно сделать и во втором уравнении. Соответственно, однородные уравнения системы (4.9) в медленно меняющихся зависящих от координат $x$ и $t$ неизвестных записываются в виде

Исключив $\tau _{0}^{{s'}}$ из второго уравнения с помощью первого, получим (однородное) уравнение собственных колебаний балки с учетом инерции вращения

Второй член в уравнении в силу малой изменяемости по $x$ и времени ${{t}_{c}}$ имеет порядок ε² по сравнению с последним и может быть также отброшен. Решение $w_{0}^{s}$ имеет малую изменяемость и только малую, при которой асимптотический порядок дифференцируемых функций меняется в ε⁰ раз. В соответствии с этим верхний индекс s у $w_{0}^{s}$ и член $w_{0}^{q}$ в (4.11) можно отбросить. Уравнение принимает классический вид

Вычитая из уравнений (4.9) попарно уравнения (4.12) и учитывая предположения (4.11), получим уравнения

решения которых зависят от аргументов ${x \mathord{\left/ {\vphantom {x \varepsilon }} \right. \kern-0em} \varepsilon }$ и ${{{t \mathord{\left/ {\vphantom {t {\varepsilon a}}} \right. \kern-0em} {\varepsilon a}}}_{l}}$.

Замечание 2. Продифференцируем уравнение (4.14) по x, умножим на $\varepsilon $ и сложим с уравнением (4.15). Получим соотношение $4\varepsilon \tau _{0}^{{q'}} = 0$, которое показывает, что уравнения (4.14) и (4.15) различаются на постоянную величину $4\varepsilon \tau _{0}^{q} = {{С}_{0}}$, и, поскольку все медленно меняющиеся решения учтены в решении для ${{w}_{0}}$, постоянная ${{С}_{0}}$ может быть отброшена. Вычитая уравнение $4\varepsilon \tau _{0}^{{q'}} = 0$ из (4.15) и интегрируя по $x$, получим два совпадающих уравнения

Его решение можно использовать для удовлетворения потерянных граничных условий и сглаживания разрывов в медленно меняющихся классических решениях [2].

Примем $\tau _{0}^{q} = X\left( x \right)T\left( t \right)$. Подставим это выражение в уравнение (4.16). Получим соотношение

Поскольку первый член в левой части уравнения зависит только от x, а второй только от $t$, оба отношения не зависят ни от x, ни от $t$ и равны некоторым константам ${{\lambda }^{2}} - 2$ и $ - {{\lambda }^{2}}$ соответственно, получаем обыкновенные дифференциальные уравнения для определения функций $X$ и $T$

решения которых запишем так

Здесь введены обозначения

Первый член в выражении для X при ${{\lambda }^{2}} < 2$ описывает решение, затухающее от конца x = 0, второй от конца x = 1.

Замечание 3. В случае вынужденных колебаний функция $T\left( t \right)$ может быть задана, изменяющейся, например, по закону $\sin \omega {{t}_{c}}$. В этом случае из последней формулы (4.17) вытекает равенство $\frac{c}{{\varepsilon {{a}_{l}}}}{{t}_{l}} = \omega {{t}_{c}}$ и тогда из последней формулы (4.18) с учетом соотношения (2.2) определяется размерность и характер поведения величины λ²

По мере возрастания частоты вынужденных колебаний величина λ² растет и при ${{\lambda }^{2}} \geqslant 2$ величина k² в формуле (4.17) становится неположительной: решение X в (4.17) при ${{\lambda }^{2}} > 2$ меняет свое поведение из затухающего на осциллирующее.

5. Граничные условия на коротких сторонах полосы для низкочастотных колебаний. В инженерной практике существует зависящее от вида конструкции многообразие способов закрепления концов балок. В сопротивлении материалов и строительной механике основные условия определяются как жесткое защемление, свободное опирание, свободный конец. В рассматриваемой здесь уточненной теории необходимо сформулировать условия на коротких сторонах для неизвестных ${{w}_{0}},{{u}_{0}},{{\sigma }_{{z0}}},{{\tau }_{0}}$ в представлениях теории упругости. Рассмотрим два примера выполнения граничных условий на коротких сторонах полосы для условий отсутствия на них перемещений при действии на верхний край полосы (1) распределенной медленно меняющейся нагрузки $p(x)\sin \omega {{t}_{c}}$ и (2) сосредоточенной нагрузки $P\delta \left( {x - c} \right)\sin \omega {{t}_{c}}$.

Пример 1. Пусть на концах полосы x = 0 и x = 1 выполняются для перемещений равенства $w = u = 0$, что соответствует в классической теории сопротивления материалов случаю жесткого защемления.

Частные и общие решения для нахождения решений, разыскиваемых как медленно меняющиеся по координате x, определены уравнениями классического вида (4.1) и (4.3), (4.5)–(4.7). Быстро меняющиеся решения определены дополнительным уравнением (4.16), решение которого дается выражениями (4.17).

Граничные условия $w = u = 0$ на коротких сторонах при $x = 0;\;1$ будем выполнять величинами первого приближения из выражений (2.3)

Потребовав в этих уравнениях обращения в ноль коэффициентов при каждой степени $z$, получим 14 условий на концах $x = 0;\;1$

Условие (5.5) можно переписать так $\varepsilon w_{0}^{'} - 2(1 + \nu )(\tau _{0}^{s} + \tau _{0}^{q}) = 0$. Из оценок (4.4) видно, что $\tau _{0}^{s}\sim {{\varepsilon }^{3}}{{w}_{0}}$ и оно может быть отброшено по сравнению с первым членом. Условие $w_{0}^{'} = 0$ вместе с условием (5.1) может быть выполнено решением классического уравнения (4.2), и, следовательно, $\tau _{0}^{q}$ для устранения возможных разрывов в силу их отсутствия следует положить равным нулю. Решение однородных классических уравнений вынужденных колебаний балки при граничных условиях ${{w}_{0}} = w_{0}^{'} = 0$ на концах x = 0; 1 известно и здесь не выписывается.

Механический смысл условия (5.2) заключается в равенстве нулю суммы поперечной деформации полосы от напряжения ${{\sigma }_{{0z}}}$ и поперечной деформации из-за эффекта Пуассона от продольной деформации $u_{0}^{'}$. Из оценок (4.6), (4.8) видно, что $({{\sigma }_{{0z}}},\varepsilon u_{0}^{'})$ ~ p и пренебрежение этим условием в уточненной и тем более в классической теории оправданно. То же самое справедливо относительно условия (5.6).

Условие (5.3) отражает тот факт, что при изгибе полосы, например, вниз, верхние слои сжимаются, а нижние растягиваются. Из-за эффекта Пуассона имеют место поперечные перемещения $[(1 - {{\nu }^{2}}){{\varepsilon }^{4}}{{a}_{c}}^{2}{{\ddot {w}}_{0}} + \nu {{\varepsilon }^{2}}w_{0}^{{''}}]\frac{{{{z}^{2}}}}{2}$, достигающие наибольших значений в угловых точках при $z = \pm 1$. На рис. 1 деформированные положения границ показаны пунктирной линией, недеформированные – сплошными линиями.

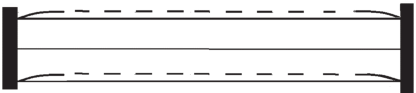
В заделке точки вертикальной границы полосы остаются неподвижными. Отсюда заключаем, что быстро меняющееся решение ${{(1 + \nu )}^{2}}\varepsilon \tau _{0}^{'}$ в (5.3) устраняет получившийся разрыв решения на границе. Поскольку инерционный член имеет порядок ${{\varepsilon }^{2}}$ по сравнению с упругим членом, его можно отбросить и получить условие ${{(1 + \nu )}^{2}}\varepsilon \tau _{0}^{'} = \nu {{\varepsilon }^{2}}w_{0}^{{''}}$ для вычисления $\tau {\kern 1pt} '$ при $x = 0;\;1$. Это дает перемещения $w$ и напряжения σ_x с учетом краевого эффекта

В первой формуле второй член $O({{\varepsilon }^{{ - 2}}})$ и может быть отброшен по сравнению с первым. Вычисленный по классической теории прогиб w₀ является достаточно точным и не нуждается в уточнении на коротких сторонах. В формуле для напряжения σ_x из (2.3) второй член в квадратной скобке $O({{\varepsilon }^{4}})$ и может быть отброшен. Также на основании ранее приведенных оценок (4.6), (4.8) могут быть отброшены первые два члена. Член в квадратных скобках описывает концентрацию напряжений в углах полосы, которые соизмеримы с напряжениями, определяемыми первым членом по классической теории в середине балки.

В условии (5.7) первый член имеет множитель ε⁵ и может быть отброшен по сравнению со вторым с множителем ε³. Последний член имеет множитель ε⁴ в силу соотношения (2.2), т.к. ${{\ddot {\tau }}_{0}}{{,}_{l}} = {{\varepsilon }^{2}}{{\ddot {\tau }}_{0}}{{,}_{c}}$, в то время как в силу условия (4.10) ${{\varepsilon }^{2}}\tau _{0}^{{''}} = {{\varepsilon }^{2}}\tau _{0}^{{s''}} + {{\varepsilon }^{2}}\tau _{0}^{{q''}}$: в последнем выражении первый член при дифференцировании сохраняет свой порядок ε², тогда как второй, быстро меняющийся имеет порядок ε⁰. Оставшиеся члены образуют условие

выражающие требование, чтобы искривляющаяся нормаль в пролете на величину $\left( {2 + \nu } \right){{\varepsilon }^{3}}w_{0}^{{'''}}$ в заделке была подправлена до прямой с помощью быстро меняющегося решения (4.16). Здесь $\tau _{0}^{{q''}} \sim {{\varepsilon }^{3}}{{w}_{0}}$, т.е. на порядок меньше, чем в условии (5.3). Поэтому вклад этой поправки в напряжение σ_x имеет порядок $\varepsilon $ по сравнению с главной частью медленно меняющейся компоненты напряжения ${{\varepsilon }^{2}}w_{0}^{{''}}z$.

Условие (5.4) позволяет решить граничную задачу для уравнения (4.7). Учитывая оценку (4.8) инерционные члены в этом уравнении можно отбросить.

Пример 2. Рассмотрим низкочастотные колебания полосы, возникающие под действием приложенной в точке x = c сосредоточенной силы. Поперечные колебания опишем уравнениями (3.2) при нагрузке ${{X}_{ + }} = {{X}_{ - }} = 0$, ${{Z}_{ - }} = 0$ и ${{Z}_{ + }} = P\delta \left( {x - c} \right)\sin \omega {{t}_{c}}$, моделирующей приложение сосредоточенной силы в точке x = c, z = 1 интенсивностью P, $\omega \sim {{\varepsilon }^{0}}$. Перепишем уравнения (3.2) с заданной правой частью

Заменим $\delta $ – функцию Дирака ее асимптотическим представлением ${{\delta }_{\varepsilon }}$ [15]

где $\kappa \sim {{\varepsilon }^{0}}$ и $\mathop {\lim }\limits_{\varepsilon \to 0} {{\delta }_{\varepsilon }}\left[ {\kappa \left( {x - c} \right)} \right] = \delta \left( {x - c} \right)$.

Частное решение системы уравнений (5.8) будем разыскивать в следующем виде

Эти функции при каждом дифференцировании увеличиваются в асимптотическом смысле в ε^–1 раз. Подставив их в уравнения (5.8), получим уравнения для определения ${{W}_{0}}$ и ${{{\rm T}}_{0}}$:

${\text{при}}\;0 \leqslant x \leqslant c$

${\text{при}}\;c \leqslant x \leqslant 1$

После отбрасывания малых членов с множителями ε⁴ и ε² по сравнению с одноименными уравнения сводятся к виду

при $0 \leqslant x \leqslant c$

при $c \leqslant x \leqslant 1$

Откуда получаем для коэффициентов в формуле (5.10) выражения:

В соответствии с этим запишем решение для w₀ и ${{\tau }_{0}}$

при $0 \leqslant x \leqslant c$

при $c \leqslant x \leqslant 1$

Коэффициент k_c определен формулой в выражении (4.13), A_i и B_i при $i = 1 \div 4$ – постоянные интегрирования уравнения (4.13).

Для упрощения дальнейших вычислений и сокращения записи при выполнении четырех граничных условий и четырех условий непрерывности примем, что ${{\kappa }^{2}} = {2 \mathord{\left/ {\vphantom {2 {(2 + \nu )}}} \right. \kern-0em} {(2 + \nu )}}$. Это дает W₀ = 0. Дополнительно положим c = 1/2, считая силу приложенной в середине пролета полосы.

Теперь надо потребовать выполнения условий непрерывности в точке $c$ для продольного перемещения $u$, продольного напряжения ${{\sigma }_{x}}$, поперечного перемещения $w$ и касательного напряжения $\tau $. Формулы (2.3) и (3.4) позволят их записать так

Здесь надо подставить верхнее значение $x = c - 0$ в выражение в фигурных скобках и вычесть из него это же выражение при $x = c + 0$.

Условия распадаются на восемь соотношений непрерывности. Шесть из них с отброшенными инерционными членами как пренебрежимо малыми записываются относительно неизвестных w₀ и ${{\tau }_{0}} = \tau _{0}^{{\left( p \right)}} + \tau _{0}^{s} + \tau _{0}^{q}$

Поскольку из первого уравнения (4.1) для решения однородного уравнения имеем

оно везде кроме последнего уравнения может быть отброшено как величина $O({{\varepsilon }^{2}})$ по сравнению с одноименной и условия принимают вид

В них везде входит сумма $\tau _{0}^{{\left( p \right)}} + \tau _{0}^{q}$ и поскольку из последнего уравнения следует, что

она также может быть отброшена во втором уравнении как величина O(ε²) по сравнению с $\varepsilon w_{0}^{'}$, а в третьем и четвертом уравнениях как величина O(ε) по сравнению с ${{\varepsilon }^{2}}w_{0}^{{''}}$. После этого третье и четвертое условия совпадут и в результате останутся четыре условия непрерывности, аналогичные классическим для балки за исключением члена $\tau _{0}^{q}$ в последнем уравнении, который следует отбросить, поскольку все четыре условия непрерывности и четыре граничных условия на концах могут быть удовлетворены за счет восьми постоянных интегрирования классического решения ${{A}_{i}}$ и ${{B}_{i}}$ при $i = 1 \div 4$.

После подстановки решений (5.11) получим алгебраические уравнения для определения постоянных интегрирования ${{A}_{i}}$ и ${{B}_{i}}$ при $i = 1 \div 4$

Из первых двух уравнений получаем

и затем из последних двух

Отсюда имеем

Заметим, что если нагрузка приложена не посредине верхнего края полосы, процедура решения остается такой же, но окончательные формулы записываются длиннее.

Поскольку величины ${{\sigma }_{{z0}}},\;u_{0}^{{\left( g \right)}},\;u_{0}^{{\left( p \right)}},w_{0}^{{\left( p \right)}},\;w_{0}^{{\left( g \right)}},\;\tau _{0}^{{\left( p \right)}},\;\tau _{0}^{{\left( g \right)}},\;\tau _{0}^{q}$ имеют различные асимптотические порядки их вклад в каждой формуле (2.3) в искомые неизвестные будет различным. Поэтому в общих выражениях для неизвестных (2.3) надо оставить только главные члены. Во-первых, во все выражения входят величины ${{\sigma }_{{z0}}},\;u_{0}^{{\left( g \right)}},\;u_{0}^{{\left( p \right)}}$, для которых необходимо произвести асимптотические оценки. Выражение (4.6), переписанное для сосредоточенной нагрузки имеет вид

и имеет соответствующую асимптотическую оценку

В уравнении продольных колебаний (4.7) с сосредоточенной нагрузкой

при поиске частного решения $u_{0}^{{\left( p \right)}}$ можно отбросить инерционный член как малый O(ε²) по сравнению с первым, т.к. первый при дифференцировании увеличивается в ε^–2 раз

После интегрирования получим

с оценкой

Формулы (2.3) с учетом записи (3.4) для неизвестных теперь можно переписать с учетом структуры полученных решений

Воспользовавшись соотношениями (5.13)–(5.16), оставим в каждом выражении только главные члены

Здесь справа в каждой формуле указаны относительные порядки отброшенных величин по сравнению с главными. Видно, что перемещения определяются с меньшей погрешностью, чем напряжения.

7. Обсуждение результатов. Предложенный Сен-Венаном полуобратный метод решения уравнений теории упругости расширен до итерационного, совпадающего с методом простых итераций. Для этого оператор исходных уравнений преобразован так, чтобы он позволял вычислять неизвестные величины последовательно: вычисленные в одном уравнении величины входят в следующее уравнение как известные, умноженные на малый параметр. Решение получается в виде асимптотического ряда по малому параметру, обеспечивающему асимптотическую сходимость удовлетворяющую теореме Банаха о неподвижной точке (принципу сжатых отображений). Такая последовательность обеспечивается операторами Пикара и выбором величин начального приближения независящими от поперечной координаты, совпадающими по смыслу к гипотезам Кирхгоффа недеформируемой нормали. В течение одной итерации вычисляются путем прямого интегрирования все неизвестные задачи, содержащие четыре произвольные функции интегрирования, зависящие от продольной координаты и играющие роль коэффициентов в полиномах по степеням поперечной координаты. Построение интеграла исходных уравнений теории упругости в виде последовательности Коши сводится к последовательному применению операторов Пикара для решения дифференциального уравнения первого порядка, разрешенного относительно производной и часто встречающегося в учебной литературе.

Предположим, что любое приближенное решение может быть рассмотрено как нулевое приближение некоторого итерационного процесса. Поэтому, если строить такой процесс, необходимо, чтобы он был сходящимся. Показано, что необходимым условием сходимости является построение такой последовательности вычислений неизвестных, когда вычисляемая через предыдущую величина, не должна быть умножаемой на малый параметр в отрицательной степени. Метод SVPB позволяет написать аналитические выражения с заданной точностью для всех неизвестных задачи и соответственно выполнить любые граничные условия и условия непрерывности напряжений и перемещений, возникающие в классических решениях. Наличие полного решения позволяет формулировать задачи сопряжения элементов.

В процессе последовательного вычисления неизвестных в течение нулевой итерации имеет место четырехкратное интегрирование по поперечной координате и четырехкратное дифференцирование по продольной. Однако это дифференцирование имеет символический характер, т.к. при выполнении граничных условий на длинных сторонах производные приравниваются к нагрузке, которую можно принять за единицу измерения искомых величин, и соответствующие уравнения интегрируются, обеспечивая вместе с однородными сингулярно возмущенными уравнениями непрерывность и ограниченность решения в любом случае. Процесс вычисления можно трактовать как расщепление сложного оператора на четыре последовательных оператора Пикара относительно поперечной координаты и четыре – относительно продольной. Близость полученного решения к точному решению оценивается порядком первого отброшенного члена по $\varepsilon $ для медленно меняющихся величин и оценкой, данной в [4], для быстроменяющихся.

Показана ошибка, совершаемая при выводе уравнения Тимошенко, порожденная уничтожением главных членов при вычитании.

Обнаруженное уменьшение скорости затухания быстро меняющихся компонент решения по мере увеличения частоты колебаний позволяет сделать заключение об отсутствии затухания разрывов на концах полосы при частотах возбуждения, соизмеримых с собственными частотами продольных колебаний стержня.