Известия РАН. Механика твердого тела, 2021, № 6, стр. 88-110

1. Введение. В настоящее время актуальной задачей является повышение точности навигационных приборов, включая волновые твердотельные гироскопы (ВТГ), с помощью построения более точных математических моделей динамики их чувствительных элементов [1]. Учет нелинейности колебаний в математических моделях динамики резонаторов ВТГ позволяет не только оценить погрешности и повысить точность прибора методами компенсации, но и исследовать ряд нелинейных эффектов, которые имеют место в динамике ВТГ и не могут быть исследованы в рамках линейных математических моделей.

Основы теории ВТГ заложены в работах Д.М. Климова и В.Ф. Журавлёва [2–6]. В [3, 6] показано, что погрешность, вызванная нелинейными свойствами колебательной системы, присуща всем ВТГ, а исследование динамики может проводиться в рамках одних и тех же уравнений, аналогичных уравнениям классического маятника Фуко. При этом указано, что для исследования нелинейности требуется учет специфики конкретной колебательной системы. В работах [7–9] отмечено, что при экспериментальных исследованиях динамики вибрационных гироскопов с электростатическими датчиками управления были обнаружены явления, характерные для нелинейных систем, например, срыв колебаний резонатора. Однако исследованию специфики нелинейности, вызванной электростатическими датчиками управления уделяется очень мало внимания.

В данной статье исследуются нелинейные колебания, вызванные электростатическими датчиками управления, выводится ряд нелинейных математических моделей, уточняются и обобщаются результаты предшествующих работ [10–14]. В статье рассматривается только ВТГ с цилиндрическим резонатором. Данный выбор сделан на основе обзора литературы [10], показавшего малое число исследований данного типа резонаторов и его возможные перспективы в связи с простотой изготовления и достаточно высокой добротностью [15]. Результаты, полученные для ВТГ с цилиндрическим резонатором могут быть обобщены на ВТГ с другими типами резонаторов: кольцевым и полусферическим.

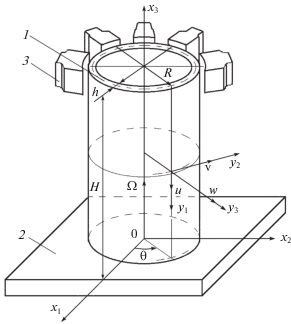
2. Определение собственных форм колебаний цилиндрического резонатора. Рассмотрим резонатор волнового твердотельного гироскопа (рис. 1), представленный упругой осесимметричной цилиндрической оболочкой 1 толщины h, высоты H и кругового сечения радиуса R. Один край резонатора свободен, а другой жестко прикреплен к основанию 2. Предполагается, что упругие свойства материала резонатора изотропны, инструментальные погрешности изготовления не учитываются.

С основанием прибора свяжем ортогональную систему координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Ось ${{x}_{3}}$ направим по оси симметрии резонатора. В качестве криволинейных координат примем нормализованную (отнесенную к радиусу резонатора) длину образующей α, $0 \leqslant \alpha \leqslant {{\alpha }_{1}}$ = H/R, и угол в окружном направлении θ, который отсчитывается от координатной оси $O{{x}_{1}}$, $0 \leqslant \theta \leqslant 2\pi $. Введем правый ортогональный трехгранник ${{y}_{1}}{{y}_{2}}{{y}_{3}}$, жестко связанный с срединной поверхностью резонатора. Пусть ${\mathbf{u}} = {{\left( {u,{v},w} \right)}^{T}}$ – вектор упругого смещения произвольной точки срединной поверхности резонатора в осях ${{y}_{1}}{{y}_{2}}{{y}_{3}}$.

Потенциальную энергию деформации цилиндрической оболочки определим по формуле [16], которая является результатом использования гипотезы Кирхгофа–Лява:

где ${{D}_{1}} = \frac{{E{{h}^{3}}}}{{12(1 - \nu _{p}^{2})}}$ – жесткость цилиндрической оболочки при изгибе (цилиндрическая жесткость); ${{D}_{2}} = \frac{{Eh}}{{1 - \nu _{p}^{2}}}$ – жесткость цилиндрической оболочки при растяжении (сжатии); Е – модуль Юнга; ${{\nu }_{p}}$ – коэффициент Пуассона. Для цилиндрической оболочки компоненты тангенциальной и изгибной деформаций задаются формулами [17]:

Для определения вектора перемещения воспользуемся условиями нерастяжимости срединной поверхности, которые получаются приравниванием нулю всех трех компонент тангенциальной деформации ${{\varepsilon }_{{11}}} = {{\varepsilon }_{{22}}} = {{\varepsilon }_{{12}}} = 0$:

Для рассматриваемого цилиндрического резонатора, у которого один край свободен, а другой закреплен, система уравнений (2.3) не допускает решений кроме тривиального, а приближение к решению может быть получено при выполнении двух условий: ${{\varepsilon }_{{12}}} = 0$ и ${{\varepsilon }_{{22}}} = 0$ [18]. Из данных условий следует существование разрешающей функции $~\Psi (\alpha ,\theta ,t)$:

Учитывая формулы (2.2), (2.3), (2.4), запишем выражения для компонент изгибной деформации через разрешающую функцию:

Для составления функции Лагранжа запишем кинетическую энергию резонатора. По теореме о сложении скоростей определяем вектор абсолютной скорости произвольной точки срединной поверхности резонатора:

где вектор угловой скорости резонатора ${\mathbf{\Omega }}~~ = ~{{( - \Omega ,0,0)}^{T}}$ и радиус вектор ${\mathbf{r}} = {{(0,0,R)}^{T}}$ заданы в проекциях на оси ${{y}_{1}}{{y}_{2}}{{y}_{3}}$. В (2.6) и далее точкой обозначаем дифференцирование по времени t. Учитывая (2.6), выражение кинетической энергии цилиндрической оболочки принимает вид: где ρ – плотность материала резонатора. Формула (2.7) задает в общем виде кинетическую энергию резонатора ВТГ на вращающемся основании.

Подставляя (2.4), (2.5) в (2.7), (2.1), выражаем кинетическую и потенциальную энергию деформации цилиндрического резонатора на неподвижном основании через разрешающую функцию $~\Psi (\alpha ,\theta ,t)$:

С помощью полученных выражений потенциальной и кинетической энергии резонатора, записанных через разрешающую функцию, можно записать функцию Лагранжа в следующем виде:

где введены обозначения ${{x}_{1}} = \frac{{\partial{ \dot {\Psi }}}}{{\partial \alpha }},$ ${{x}_{2}} = \frac{{\partial{ \dot {\Psi }}}}{{\partial \theta }},$ ${{x}_{3}} = \frac{{{{\partial }^{2}}\dot {\Psi }}}{{\partial {{\theta }^{2}}}},$ ${{x}_{4}} = \frac{{{{\partial }^{4}}\Psi }}{{\partial {{\theta }^{4}}}},$ ${{x}_{5}} = \frac{{{{\partial }^{2}}\Psi }}{{\partial {{\theta }^{2}}}}$, x₆ = = $\frac{{{{\partial }^{4}}\Psi }}{{\partial {{\alpha }^{2}}\partial {{\theta }^{2}}}},$ ${{x}_{7}} = \frac{{{{\partial }^{4}}\Psi }}{{\partial \alpha \partial {{\theta }^{3}}}},$ ${{x}_{8}} = \frac{{{{\partial }^{2}}\Psi }}{{\partial \alpha \partial \theta }}$.

В соответствии с вариационным принципом Гамильтона–Остроградского на прямом пути вариация действия по Гамильтону равна нулю:

где ${{t}_{1}},~{{t}_{2}}$ – фиксированные моменты времени. Используя интегрирование по частям, равенство вариаций нулю в фиксированных граничных точках, произвольность вариации δΨ, получим уравнение динамики резонатора ВТГ, записанное через разрешающую функцию $~\Psi (\alpha ,\theta ,t)$:

В силу линейности и специальной структуры уравнения (2.8), для свободных колебаний цилиндрического резонатора гироскопа разрешающая функция ищется в виде:

где для удобства дальнейших преобразований введена величина зазора d между недеформированным резонатором и датчиками управления и произвольная безразмерная константа C; ${{\psi }_{k}}(\alpha )$ – безразмерная функция, определяющая форму колебаний образующей цилиндра; ${{\mu }_{k}}$ – собственная частота, k – номер формы колебаний резонатора по окружной координате, $k = 1,2,...~$.

После подстановки (2.9) в (2.8) получим обыкновенное дифференциальное уравнение четвертого порядка для определения частот ${{\mu }_{k}}$ и функций ${{\psi }_{k}}(\alpha )$:

где введено обозначение безразмерного параметра, характеризующего собственную частоту:

Для постановки краевой задачи накладываются краевые условия на функцию нормального прогиба $~w(\alpha ,\theta ,t)$. Так как один край цилиндрического резонатора свободен, а другой жестко закреплен на основании, имеем:

С учетом формул (2.4) и (2.9) аналогичные краевые условия получаем для функции ${{\psi }_{k}}(\alpha )$:

Дифференциальному уравнению (2.10) соответствует характеристическое уравнение

имеющие корни:

Для нахождения решения краевой задачи (2.10)–(2.11) записываем общее решение дифференциального уравнения (2.10)

и определяем константы ${{C}_{1}},\;{{C}_{2}},\;{{C}_{3}},\;{{C}_{4}}$ из граничных условий (2.11). В результате получаем функцию, определяющую формы колебаний образующей цилиндра: где ${{\zeta }_{n}} = {{\lambda }_{{1n}}}\frac{{{{\lambda }_{{1n}}}{\text{sh}}\left( {{{\alpha }_{1}}{{\lambda }_{{1n}}}} \right) + {{\lambda }_{{2n}}}\sin \left( {{{\alpha }_{1}}{{\lambda }_{{2n}}}} \right)}}{{\lambda _{{1n}}^{2}{\text{ch}}\left( {{{\alpha }_{1}}{{\lambda }_{{1n}}}} \right) + \lambda _{{2n}}^{2}\cos \left( {{{\alpha }_{1}}{{\lambda }_{{2n}}}} \right)}},$ ${{\lambda }_{{1n}}},~~{{\lambda }_{{2n}}}$, $n = 1,2,...$, соответствуют фиксированному k и определяются в результате нахождения нормализованных собственных частот ${{\tilde {\mu }}_{{kn}}}$ при решении трансцендентного уравнения:

Заметим, что при решении (2.14) для фиксированного k определяются корни трансцендентного уравнения ${{\mu }_{{kn}}}$ $n = 1,2,...$. В дальнейшем, при подстановке в (2.9), полагается n = 1, а индекс n в записи выражений опускается.

Таким образом, для номера формы колебаний резонатора по окружной координате k найдены соответствующие ей собственные частоты ${{\mu }_{k}}$ и собственные формы колебаний образующей цилиндра ${{\psi }_{k}}(\alpha )$.

3. Вывод уравнений движения цилиндрического резонатора ВТГ с электростатическими датчиками управления. Резонатор ВТГ изготавливается из кварцевого стекла с нанесением на его поверхность металлического покрытия. Предполагается, что металлическое покрытие не влияет на упругие свойства резонатора. Колебания цилиндрического резонатора возбуждаются системой электростатических датчиков управления, которые представляют собой конденсаторы, образованные металлизированной поверхностью резонатора и электродами управления, расположенными вблизи свободной кромки резонатора.

Для вывода уравнений движения цилиндрического резонатора составим функцию Лагранжа электромеханической системы [19], включающей, помимо кинетической и потенциальной энергию резонатора, потенциальную энергию электрического поля, создаваемого электростатическими датчиками управления.

Так как в волновых твердотельных гироскопах для возбуждения колебаний используется вторая форма колебаний резонатора по окружной координате, то запишем разрешающую функцию (2.9) в следующем виде:

где введены неизвестные функций ${{f}_{*}}(t),\;{{g}_{*}}(t)$, а функция ${{\psi }_{2}}(\alpha )$ определяются при решении задачи (2.10)–(2.11) по алгоритму (2.13)–(2.14).

Используя формулы (2.4) и функцию (3.1), запишем вектор смещения произвольной точки срединной поверхности резонатора в одномодовом приближении по второй форме колебаний (k = 2):

Примем в качестве обобщенных координат второй формы колебаний резонатора функции ${{f}_{*}}(t),{{g}_{*}}(t)$ и положим константу $C = 1{\text{/}}\left( {4{{\psi }_{2}}({{\alpha }_{1}})} \right)$, чтобы прогиб свободной кромки резонатора имел вид $w({{\alpha }_{1}},\theta ,t) = - {{f}_{*}}(t)\cos 2\theta + {{g}_{*}}(t)\sin 2\theta $.

Подставляя (3.2) в (2.2), а (2.2), (2.3) в (2.1), получим выражение для потенциальной энергии деформации цилиндрического резонатора:

где приведенная жесткость резонатора

Подставляя (3.2) в (2.7), определяем кинетическую энергию резонатора:

где приведенная масса коэффициент ${{\zeta }_{*}} = \frac{{\pi \rho h{{R}^{2}}}}{{\psi _{2}^{2}({{\alpha }_{1}})}}\int_0^{{{\alpha }_{1}}} {\psi _{2}^{2}(\alpha ){\text{d}}\alpha } ~$. В связи с малостью Ω, в (3.5) пренебрегались слагаемые, содержащие Ω².

Вычислим энергию n конденсаторов, образованных управляющими электродами и резонатором. Потенциальная энергия электрического поля, локализованного между обкладками заряженных конденсаторов, определяется выражением

где ${{q}_{j}}$ – заряд  j-го конденсатора, образованного резонатором и j-м электродом, центр которого расположен под углом ${{\theta }_{j}} = 2\pi (j - 1){\text{/}}n$ к оси $O{{x}_{1}}$ (рис. 1), $j = 1...n,$ n – число электродов; C_j – емкость. Будем предполагать, что перекрестное влияние конденсаторов отсутствует. Для вычисления емкости используем формулу где ε₀ = 8.85 × 10^–12 Ф/м – электрическая постоянная; S – площадь электрода; d – зазор между недеформированным резонатором и электродами; ${{C}_{0}} = {{\varepsilon }_{0}}S{\text{/}}d$ – емкость конденсатора, образованного электродом управления и недеформированным резонатором; нормальный прогиб свободной кромки резонатора ${{w}_{j}}(t) = w({{\alpha }_{1}},{{\theta }_{j}},t),$ $j = 1...n$. Подставляя (3.8) в (3.7), получаем выражение для энергии

Для составления уравнений Лагранжа–Максвелла электромеханической системы применяем методику, предложенную в [19]:

Внутренние потери при колебаниях будем описывать моделью Кельвина–Фойгта. Внешними потерями пренебрегаем, считая объем корпуса прибора ваккумированным. Введем диссипативную функцию, учитывающую внутреннее трение материала резонатора:

где ${{c}_{*}}$ – коэффициент, характеризующий вязкоупругие свойства материала резонатора. Рассматриваемый материал обладает малыми потерями на внутреннее трение.

Введем электрическую диссипативную функцию

где ${{R}_{e}}$ – электрическое сопротивление цепи между электродом управления и источником питания.

Используя уравнения Лагранжа–Максвелла, учитывая (3.10), (3.11), (3.12), получим

где $\zeta = {{\zeta }_{*}}{\text{/}}m,$ ${{\omega }^{2}} = c{\text{/}}m,$ $\gamma = {{c}_{*}}{\text{/}}m$; ${{U}_{j}}$ – напряжение на  j-м электроде.

Запишем выражение для емкости (3.8) следующим образом:

где $f(t) = - {{f}_{*}}(t){\text{/}}d,$ $g(t) = {{g}_{*}}(t){\text{/}}d$ – безразмерные обобщенные координаты, задающие нормализованные по отношению к величине зазора d радиальные смещения резонатора в двух фиксированных точках, отстоящих друг от друга под углом 45°.

Используя формулу (3.15) и переходя в уравнениях (3.13)–(3.14) к нормализованным обобщенным координатам$f(t)$ и $g(t)$, получим систему уравнений

Поставим начальные условия для системы (3.16)–(3.17):

Перейдем в задаче (3.16)–(3.18) к безразмерному времени $\tau = \omega t$ и запишем ее в векторно-матричном виде

где ${\mathbf{x}} = {{\left( {f,\frac{{{\text{d}}f}}{{{\text{d}}\tau }},g,\frac{{{\text{d}}g}}{{{\text{d}}\tau }}} \right)}^{T}}$, ${\mathbf{q}} = {{\left( {{{q}_{1}},...,{{q}_{n}}} \right)}^{T}}$, $\varepsilon = {{R}_{e}}{{C}_{0}}\omega $ – безразмерный малый параметр (например, $\varepsilon \sim {{10}^{{ - 8}}},$ ${{R}_{e}} \approx 1$ Ом, ${{C}_{0}} \approx {{10}^{{ - 12}}}\Phi $, $\omega \approx {{10}^{4}}$ с^–1).

Установим, что для задачи (3.19)–(3.21) выполняются условия теоремы Тихонова о предельном переходе [21]. Поскольку при работе ВТГ амплитуда прогиба меньше величины зазора между недеформированным резонатором и электродами управления (исключается пробой конденсаторов), при исследовании задачи (3.19)–(3.21) будем использовать ограничение

где β – константа, $0 < \beta < 1$. Используя (3.22), введем область

Правые части уравнений (3.19), (3.20) непрерывны вместе с частными производными по компонентам векторов ${\mathbf{x}}$ и ${\mathbf{q}}$ в области H. Полагая в (3.20) ε = 0, имеем вырожденную задачу:

Система алгебраических уравнений (3.24) представляет n независимых уравнений с единственными решениями

которые вместе с производными по $\bar {f}$ и $\bar {g}$ непрерывны в области $\bar {D}$. Условие устойчивости полученных корней справедливо в результате выполнения (3.22):

Решением задачи (3.23)–(3.25) будем называть непрерывно дифференцируемую вектор-функцию ${\mathbf{\bar {x}}}(\tau )$, удовлетворяющую условиям (3.22), (3.25) и обращающую уравнение (3.23) в тождество. В области $\bar {D}$ решение задачи (3.23)–(3.25) существует и единственно.

Таким образом, согласно теореме Тихонова о предельном переходе [21], решение задачи (3.19)–(3.21) существует на $[0,T]$ и имеет место предельный переход к решению вырожденной задачи (3.23)–(3.25) при стремлении малого параметра к нулю:

Основываясь на теореме Тихонова о предельном переходе и учитывая малость параметра ε, можем использовать решение вырожденной задачи (3.23)–(3.25) в качестве нулевого приближения к решению задачи (3.19)–(3.21).

Опуская обозначение “–” решения вырожденной задачи, перепишем (3.23)–(3.25) в размерном времени t в соответствующем (3.16)–(3.18) виде:

В [19] для исследования влияния электродов управления на динамику резонатора при составлении уравнений учитывались малые электрические сопротивления с помощью асимптотического разложения решения и рассматривались только линейные колебания. В уравнениях (3.36) учтены нелинейные колебания при пренебрежении малым электрическим сопротивлением.

Таким образом, выведены и обоснованы математические модели (3.16)–(3.18) и (3.26)–(3.27). Задачу (3.16)–(3.18) будем называть исходной математической моделью, объединяющей обобщенный вид нелинейности колебаний резонатора, вызванной датчиками управления, и сингулярно возмущенные уравнения электрических колебаний в цепи управления. Задачу (3.36)–(3.27) будем называть базовой математической моделью для исследования нелинейности колебаний, вызванной датчиками управления.

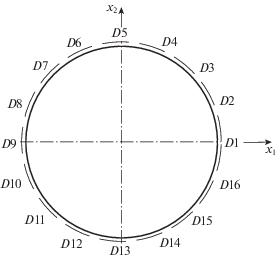
Рассмотрим наиболее распространенный случай, при котором напряжения U_j между j-м электродом датчика управления и резонатором, $j = 1,...,n$, подаются на n = 16 датчиков управления, неизменно ориентированных относительно основания ВТГ (рис. 2):

где ${{\omega }_{0}}$ – частота внешнего гармонического возбуждения колебаний резонатора близкая к резонансной частоте второй формы колебаний, $\left| {{{\omega }_{0}} - \omega } \right| \ll \omega $; U₀ – постоянное опорное напряжение; ${{u}_{1}},\;{{u}_{2}},\;{{u}_{3}},\;{{u}_{4}}$ – нормализованные по отношению к U₀ амплитуды управляющих напряжений, ${{u}_{i}} < 1$, $i = 1,..,4$; ${{u}_{A}}(t),\;{{u}_{B}}(t)$ – нормализованные управляющие напряжения, подаваемые, соответственно, на группу электродов № 1, 5, 9, 13, и смещенную относительно них на угол 45° группу электродов № 3, 7, 11, 15 (рис. 2). На остальных электродах (с четными номерами) разность потенциалов задается равной опорному напряжению U₀.

Сигналы управления (3.28) реализуют для 16 электродов широко применяемую в ВТГ “пуш-пульную” (“push–pull”) схему управления [3]. Данная схема основана на подаче разности потенциалов ${{U}_{0}}(1 + u)$ и ${{U}_{0}}(1 - u)$, $\left| u \right| < 1$, на датчики, расположенные ортогонально, и применяется для линеаризации силы электростатического датчика, которая пропорциональна квадрату напряжения на электроде:

Полученное выражение (3.29) линейно относительно нормализованного управляющего напряжения $u~$. В случае 16 электродов управления линеаризации “push–pull” реализуется благодаря известным тригонометрическим соотношениям.

Поскольку электростатическая сила обратно пропорциональна квадрату величины зазора между электродом управления и металлизированной поверхностью резонатора, покажем, что при учете конечного отношения прогиба резонатора к зазору электростатического датчика, нарушается линеаризация “push–pull”. Несмотря на конечность отношения прогиба к зазору, величина прогиба является малой, что обосновывает одновременное использование при выводе уравнений динамики резонатора линейной теории оболочек и учет нелинейности силового воздействия датчика управления. Силовое воздействие двух ортогонально расположенных датчиков управления пропорционально выражению, которое может быть разложено в ряд по нормализованному величиной зазора прогибу $\left| {\tilde {w}} \right| = \left| {\frac{w}{d}} \right| < 1$:

Таким образом, при учете прогиба $\tilde {w}$, схема линеаризации “push–pull” нарушается. Пренебрегая прогибом в случае его малости, получим из (3.30) линейное выражение относительно управляющего напряжения, соответствующее линеаризации “push-pull” (3.29).

Упростим выражения для сумм в (3.26) при возбуждении колебаний по закону (3.28) с помощью разложения (3.30) и преобразований тригонометрических выражений:

Суммирование (3.31), (3.32) учитывает во взаимосвязанной форме дискретную зависимость от окружного угла управляющего напряжения (3.28) и разложенные в ряд нелинейные по прогибу выражения.

Амплитуды нормализованных величин имеют одинаковый порядок малости,  f ~ ~ 0.1, g ~ 0.1, ${{u}_{\kappa }} \sim 0.1.$ Поэтому в (3.31) и (3.32) слагаемыми, содержащими ${{f}^{\alpha }}{{g}^{\beta }}u_{\kappa }^{\delta }$, $\kappa = A,B$, пренебрегаем при выполнении условия $\alpha + \beta + \delta > 3$ в связи с высоким порядком малости. Подставляя (3.31) и (3.32) в (3.26), получаем следующие уравнения:

где введены обозначения $v = 2\zeta \Omega $, $\eta = \frac{{4U_{0}^{2}{{C}_{0}}}}{{m{{d}^{2}}}}$.

Заметим, что для уточнения нелинейных уравнений динамики (3.33), при подстановке выражений (3.31), (3.32) в (3.26), можно выделить нелинейные слагаемые пятой степени ${{({{f}^{2}} + {{g}^{2}})}^{2}}f,$ ${{({{f}^{2}} + {{g}^{2}})}^{2}}g$, которые по своей структуре аналогичны кубической нелинейности $({{f}^{2}} + {{g}^{2}})f,$ $({{f}^{2}} + {{g}^{2}})g$. С учетом нелинейности пятой степени уравнения принимают вид:

В работе [14] показано, что учет нелинейных слагаемых пятой степени в математической модели динамики резонаторов повышает точность идентификации параметров ВТГ, поэтому, несмотря на высокий порядок малости, в некоторых случаях будем их удерживать.

Рассмотрим нелинейные слагаемые, выведенные в уравнениях (3.33), (3.34) и их связь со слагаемыми разложения (3.30). В (3.30) можно выделить часть разложения, которая определяется управляющим напряжением следующим образом:

и указывает на увеличение абсолютной величины силового воздействия за счет учета прогиба. Выражению (3.35), ограниченному третьим порядком по $\tilde {w},$ u, соответствуют слагаемые $\eta (1 + 3{{f}^{2}}){{u}_{A}},$ $\eta (1 + 3{{g}^{2}}){{u}_{B}}$ в уравнениях (3.33). Слагаемые $\eta {{u}_{A}},$ $\eta {{u}_{B}}$ в (3.30) характеризуют управление вынужденными колебаниями резонатора, а добавление к ним неотрицательных слагаемых с квадратичной нелинейностью $3\eta {{f}^{2}}{{u}_{A}},$ $3\eta {{g}^{2}}{{u}_{B}}$, указывает малое усиление управляющего воздействия:

Другая часть разложения (3.30):

дает в первом приближении по $\tilde {w}$, u выражение $4\tilde {w}U_{0}^{2}$, которому в уравнениях (3.33) соответствуют линейные слагаемые $2\eta f,$ $2\eta g,$ указывающие на малое изменение характерной частоты собственных колебаний и представляющие известный эффект “отрицательной электростатической жесткости”. Электростатическая компонента жесткости приводит к изменению квадрата характерной частоты собственных колебаний ${{\omega }^{2}}$ на величину равную $2\eta = 2{{\eta }_{e}}{{\omega }^{2}}$, где ${{\eta }_{e}} = \frac{{4U_{0}^{2}{{C}_{0}}}}{{c{{d}^{2}}}}$ – безразмерный коэффициент, характеризующий малость электростатических сил. Из разложения (3.36) следует, что в уравнениях (3.34) кубическая нелинейность, нелинейность пятой степени и нелинейное управление представляют нелинейное уточнение электростатической компоненты жесткости, причем имеет место незначительное усиление эффекта “отрицательной электростатической жесткости”:

Заметим, что слагаемые с кубической нелинейностью $({{f}^{2}} + {{g}^{2}})f,$ $({{f}^{2}} + {{g}^{2}})g$ свойственны уравнениям динамики резонаторов гироскопов класса обобщенного маятника Фуко, в том числе и ВТГ [6]. Слагаемые такой структуры получены в [6] для классического маятника Фуко, а в [20] для ВТГ в предположении о том, что для материала резонатора справедлив нелинейный закон упругости. В уравнениях (3.33), (3.34) слагаемые с кубической нелинейностью выведены из нелинейных свойств электростатических датчиков управления, коэффициент при кубической нелинейности η зависит от квадрата постоянного опорного напряжения и параметров датчиков управления.

Согласно рассматриваемому закону управления колебаниями (3.28), $u_{A}^{2}(t)$ и $u_{B}^{2}(t)$ могут быть записаны в виде

Подстановка (3.37) в (3.33) указывает на смещение характерной частоты собственных колебаний – дополнительное малое увеличение “отрицательной электростатической жесткости”, заданное слагаемыми $\eta (u_{1}^{2} + u_{2}^{2}){\text{/}}2$ и $\eta (u_{3}^{2} + u_{4}^{2}){\text{/}}2$. Из-за отличия друг от друга величин ${{u}_{1}},\;{{u}_{2}},\;{{u}_{3}},\;{{u}_{4}},$ данные слагаемые задают разночастотность, вызванную электростатическими датчиками управления. В дальнейшем будем пренебрегать описанными слагаемыми в силу их малости. Слагаемые, содержащие $\cos 2{{\omega }_{0}}t$ и $\sin 2{{\omega }_{0}}t$, характеризуют параметрическое возбуждение колебаний резонатора, сопутствующее вынужденным колебаниям. Устойчивость колебаний при данном сопутствующем параметрическом возбуждении в линейной постановке задачи исследована в [11].

Учитывая (3.37) и сделанные упрощения, запишем уравнения (3.33) в виде

где, путем введения ${{\tilde {\omega }}^{2}} = {{\omega }^{2}} - 2\eta $ и обозначения $\omega = \tilde {\omega }$, учтено уменьшение квадрата характерной частоты собственных колебаний на величину постоянной составляющей электростатической компоненты жесткости 2η.

Уравнения (3.38), которые учитывают все рассмотренные нелинейности до третьего порядка, примем основными при исследовании нелинейной динамики рассматриваемого ВТГ и будем называть нелинейной математической моделью, учитывающей кубическую нелинейность, квадратичную нелинейность при управлении и параметрическое возбуждение, сопутствующее возбуждению колебаний электростатическими датчиками.

4. Осреднение нелинейных уравнений движения резонатора. Для исследования динамики резонатора проведем осреднение [22] системы уравнений (3.38). Перейдем к безразмерному времени $\tau = \omega t$ и с помощью замены переменных

сведем (3.38) к нормальной системе дифференциальных уравнений: где $\mu = {{\omega }_{0}}{\text{/}}\omega = (\omega + \lambda ){\text{/}}\omega ,$ $\lambda = {{\omega }_{0}} - \omega $ – частотная настройка, $\left| \lambda \right| \ll \omega $.

Используя замену переменных

выводим из (4.2) разрешенную относительно производных систему дифференциальных уравнений, которую сокращенно записываем в векторно-матричной форме где ${\mathbf{z}}(\tau ) = {{({{q}_{1}}(\tau ),{{p}_{1}}(\tau ),{{q}_{2}}(\tau ),{{p}_{2}}(\tau ))}^{T}}.$ Проводя осреднение (4.4) по явно входящему безразмерному времени τ, придем к системе, решение которой дает приближение к решению (4.4), обоснованное методом осреднения Крылова–Боголюбова:

Далее опустим обозначение осредненного решения ${\mathbf{\bar {z}}}$ и, переходя от безразмерного времени τ к времени t, запишем осредненную систему (4.5) в виде

где введены обозначения нелинейных слагаемых аналогично [20]: а также нелинейностей при управляющих напряжениях:

Систему уравнений (4.6), которая учитывает все рассмотренные нелинейности до третьего порядка малости, будем называть нелинейной математической моделью в медленных переменных.

5. Влияние опорного напряжения на дрейф гироскопа. Рассмотрим динамику резонатора ВТГ с электростатическими датчиками управления при наличии только постоянного опорного напряжения. Уравнения (3.38) в случае подачи только опорного напряжения (${{U}_{0}} \ne 0$, ${{u}_{1}} = {{u}_{2}} = {{u}_{3}} = {{u}_{4}} = 0$) принимают вид

Исследование дрейфа ВТГ будем проводить с помощью переменных, называемых элементами орбиты [6]: r(t) и k(t) – амплитуды основной и квадратурной волн колебаний, $\theta (t)$ – угол прецессии, $\chi (t)$ – временная фаза,

Уравнения, полученные в результате осреднения (5.1), следуют из системы (4.6) при подстановке $\lambda = 0$, ${{u}_{1}} = {{u}_{2}} = {{u}_{3}} = {{u}_{4}} = 0$. Чтобы перейти в них от ${{q}_{1}}(t),$ ${{p}_{1}}(t),$ ${{q}_{2}}(t),$ ${{p}_{2}}(t)$ к r(t), $k(t)$, $\theta (t)$, $\chi (t)$, будем использовать замену переменных:

В результате выполненных преобразований получаем систему

Первые два уравнения системы (5.4) указывают на то, что амплитуда колебаний уменьшается в результате демпфирования. Из третьей формулы (5.4) следует, что угловая скорость дрейфа ВТГ задается формулой:

где безразмерный параметр ${{\eta }_{e}} = 4U_{0}^{2}{{C}_{0}}{\text{/}}(c{{d}^{2}})$ характеризует малость электростатических сил. Четвертое уравнение системы (5.4) указывает на незначительное изменение частоты колебаний.

Согласно (5.5), угловая скорость дрейфа ВТГ изменяется прямо пропорционально амплитудам основной и квадратурной волн колебаний r, k, что согласуется с [6], а также коэффициенту ${{\eta }_{e}}$. Таким образом, через коэффициент ${{\eta }_{e}}$ видим прямо пропорциональную зависимость угловой скорости дрейфа ВТГ от квадрата опорного напряжения $U_{0}^{2}$ и обратно пропорциональную зависимость от квадрата рабочего зазора d².

Для устранения погрешности, вызываемой нелинейностью, в гироскопах данного класса амплитуду колебаний r поддерживают постоянной, а квадратуру k стремятся уменьшить до нуля [6].

Числовой пример. Вычислим угловую скорость дрейфа ВТГ с цилиндрическим кварцевым резонатором, которая вызвана опорным напряжением при использовании электростатических датчиков управления. Резонатор имеет размеры R = 20 мм, H = R, h = 1 мм, сделан из кварцевого стекла с параметрами ρ = 2210 кг/м³, E = 73.6 ГПа, ν_p = 0.17. Данные значения позволяют рассчитать характерную частоту собственных колебаний ω = 20890 с^–1 (3325 Гц). Пусть опорное напряжение U₀ = 100 В, а емкость C₀ = 1.05 × × 10^–12 Ф (площадь пластины 12 мм², расстояние между пластинами d = 0.1 мм), тогда получаем значение параметра ${{\eta }_{e}} = 8.95 \times {{10}^{{ - 6}}}$. Примем относительные амплитуды основной и квадратурной волн колебаний r = 0.1 и k = 0.001 (соответственно 10 мкм и 0.1 мкм). Абсолютная величина угловой скорости дрейфа, вычисляемая по формуле (5.5), равна 1.45°/час. Полученное значение является существенным для гироскопов, применяемых в навигационных системах.

6. Режим вынужденных нелинейных колебаний резонатора. Для исследования вынужденных колебаний рассмотрим следующий режим подачи управляющего напряжения: ${{u}_{1}} = {{u}_{3}} = {{u}_{4}} = 0$, ${{u}_{2}} = u$, а также будем пренебрегать в силу малости слагаемыми, пропорциональными квадрату амплитуд управляющих сигналов. Поэтому запишем (3.38) в виде:

Вынужденные колебания резонатора исследуем в медленных переменных $A(t),$ $B(t),$ $\varphi (t)$, $\psi (t)$, которые являются амплитудами и фазами колебаний:

поэтому будем использовать замену переменных в осредненной системе с медленными переменными ${{q}_{1}}(t),$ ${{p}_{1}}(t),$ ${{q}_{2}}(t),$ ${{p}_{2}}(t)$.

Сравним результаты описания вынужденных колебаний тремя математическими моделями: линейной; нелинейной, учитывающей свойственную ВТГ кубическую нелинейность; предложенной нелинейной математической моделью, учитывающей не только кубическую нелинейность, но и квадратичную нелинейность при управлении. Чтобы увидеть отличие, рассмотрим сначала уравнения с коэффициентом ξ при кубической нелинейности:

Соответствующая система осредненных уравнений следует из (4.6):

и с помощью замены переменных (6.3) преобразуется в

Одним из стационарных режимов колебаний является режим [20] с нулевой амплитудой B = 0. Тогда из (6.6) следуют уравнения для определения амплитуды А и фазы колебаний φ:

Избавляясь от тригонометрических функций в уравнениях (6.7), получим выражение

Применяя к (6.8) формулу дифференцирования неявной функции, записываем условие экстремума A(λ):

из которого следует, что A(λ) имеет экстремум в точке

Подставляя (6.9) в выражение (6.8), определяем максимальное значение амплитуды

учитывая которое в (6.9), получаем значение

Если рассматривать исследуемый в данной работе случай, когда коэффициент нелинейности определяется только свойствами датчиков управления, $\xi = 3\eta = 3{{\eta }_{e}}{{\omega }^{2}}$, то выражение (6.8), описывающее амплитудно-частотные характеристики, примет вид

а частота, соответствующая максимальной амплитуде, примет значение

Заметим, что для линейной математической модели справедливы преобразования, выполненные в (6.4)–(6.8) с подстановкой ξ = 0. Следовательно, в данном случае амплитуду можно задать в явном виде формулой, которая следует из (6.8):

Из (6.14) следует, что ${{A}_{{\max }}} = \frac{{{{\eta }_{e}}\omega u}}{\gamma }$ при ${{\lambda }_{{\max }}} = 0$.

Рассмотрим теперь нелинейную математическую модель, учитывающую не только кубическую нелинейность, но и квадратичную нелинейность при управлении. В данном случае исследуем уравнения (6.1), содержащие только нелинейности, вызванные датчиками управления. Аналогично описанному выше, из (4.6) при принятых допущениях с заменой переменных (6.3) получаем

Рассмотрим стационарный режим колебаний с B = 0 и получим выражение для резонансной кривой

Таким образом, полученное аналитическое выражение (6.16) описывает амплитудно-частотные характеристики колебаний, учитывая, помимо кубической нелинейности, квадратичную нелинейность при управлении.

Применяя к (6.16) формулу дифференцирования неявной функции, получаем условие экстремума A(λ), из которого следует, что A(λ) имеет экстремум в точке λ = $ - \tfrac{{9{{\eta }_{e}}\omega }}{8}{{A}^{2}},$ что соответствует (6.9). Подставляя полученное значение частотной настройки в выражение (6.16), определяем максимальное значение амплитуды

Если в полученной формуле использовать разложение в ряд Тейлора, принимая ограничение ${{A}_{{\max }}} = \frac{{{{\eta }_{e}}\omega u}}{\gamma } < 1$, вызванное функционированием без пробоев электростатических датчиков, то придем к уточненному значению максимальной амплитуды (6.10):

Полученный результат указывает на увеличение амплитуды колебаний в результате учета квадратичной нелинейности при управлении.

Учитывая уточненное значение максимальной амплитуды, рассчитываем значение

Чтобы увидеть уточнение резонансной частоты, вызванное учетом квадратичной нелинейности при управлении, и сравнить с (6.13), разложим (6.18) в ряд

Получено дополнительное уменьшение резонансной частоты, которое вызвано увеличением амплитуды колебаний в результате учета квадратичной нелинейности при управлении.

Таким образом, при описании колебаний резонатора ВТГ линейной математической моделью и нелинейной математической моделью, учитывающей только кубическую нелинейность, максимальная амплитуда колебаний одинакова, задается формулой (6.10), а разница описания вынужденных колебаний двумя моделями заключается в малом изменении резонансной частоты собственных колебаний. При учете нелинейности на амплитудно-частотных характеристиках наблюдается сдвиг резонансного пика колебаний влево, что соответствует описанию колебаний с мягкой характеристикой. Также из построения амплитудно-частотных характеристик по уравнению (6.8) следует, что при увеличении амплитуды колебаний появляется интервал по оси частотной настройки, при значениях из которого амплитудно-частотная характеристика становится многозначной, что соответствует экспериментально обнаруженному эффекту срыва колебаний ВТГ [7–9], который характерен для нелинейных колебательных систем. Дополнительный учет квадратичной нелинейности при управлении показывает увеличение амплитуды колебаний, следствием которого является увеличение сдвига резонансного пика колебаний влево и расширение области частот срыва колебаний.

Для вывода частот срыва колебаний по математической модели, учитывающей только кубическую нелинейность, определяется экстремум функции λ(A), заданной неявно выражением (6.8). Получаем условие для нахождения амплитуды А, при котором функция λ(A) имеет экстремум:

Из полученного условия определяем точки экстремума, то есть амплитуды, при которых происходит срыв колебаний (выбираем действительные корни многочлена при λ < 0):

где $\xi \ne 0$, так как рассматриваются нелинейные колебания.

Подставляя (6.19) в (6.8), получаем уравнение для определения частот срыва колебаний (при $\xi = 3\eta $):

Корни уравнения (6.20) определяются численно при подстановке известных коэффициентов демпфирования и нелинейности, силового воздействия. Частотам срыва колебаний соответствуют действительные корни уравнения (6.20).

Для определения частот срыва колебаний по математической модели, учитывающей кубическую нелинейность и квадратичную нелинейность при управлении, определяется экстремум функции λ(A), заданной неявно выражением (6.16). Получаем условие для нахождения амплитуды А, при которой функция λ(A) имеет экстремум:

Определение из выражения (6.21) точек экстремума А, которые зависят от λ, и подстановка их в уравнение (6.16) для определения частот срыва колебаний представляет для данной задачи значительную сложность аналитических преобразований. Поэтому воспользуемся следующим итерационным методом. В качестве начального приближения к частотам срыва колебаний, возьмем значения, полученные численно из уравнения (6.20), дающего точные значения частот срыва при использовании математической модели, учитывающей только кубическую нелинейность. Данные частоты подставим в условие (6.21) и найдем первое приближение для амплитуды срыва колебаний, которое подставим в уравнение (6.16). Полученное уравнение решим численно относительно частот и, таким образом, получим очередное приближение к частотам срыва колебаний. Далее итерационно продолжим процесс: полученные частоты подставим в условие (6.21), которое решим численно, полученные приближения для амплитуд подставим в (6.16) и численно определим очередное приближение для частот срыва колебаний. Сходимость итерационного процесса будем контролировать по уменьшению модуля разности соответствующих частот, взятых на последовательных итерациях.

Числовой пример. Построим амплитудно-частотные характеристики колебаний цилиндрического резонатора ВТГ с электростатическими датчиками управления. Как и в предыдущем числовом примере, берем данные ω = 20890 с^–1, ${{\eta }_{e}} = 8.95 \times {{10}^{{ - 6}}}$, u = 0.1, принимаем добротность Q = 5 × 10⁵, а значит $\gamma = 0.042$ с^–1. Расчеты проводим по трем формулам (6.14), (6.12), (6.16), соответствующим трем математическим моделям: линейной; нелинейной, учитывающей только кубическую нелинейность; нелинейной, учитывающей не только кубическую нелинейность, но и квадратичную нелинейность при управлении. Построены расчетные АЧХ, по вертикальной оси откладывается нормализованная амплитуда колебаний A, по горизонтальной оси – частотная настройка λ (рис. 3).

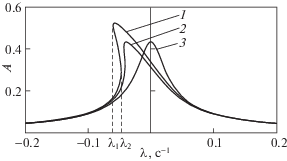
Амплитудно-частотная характеристика в малой окрестности резонанса, вычисленная по формуле (6.14), соответствующей линейной математической модели, симметрична относительно λ = 0 (кривая 3, рис. 3). АЧХ, рассчитанная по формуле (6.12), полученная при учете только кубической нелинейности, имеет сдвиг резонансного пика, максимальная амплитуда при этом не изменяется (кривая 2, рис. 3). Учет квадратичной нелинейности при управлении в расчетах по формуле (6.16) показывает увеличение амплитуды колебаний и еще больший сдвиг резонансной частоты (кривая 1, рис. 3), чем при учете только кубической нелинейности (кривая 2, рис. 3).

По нелинейной математической модели, учитывающей только кубическую нелинейность, получаем с помощью формул (6.10), (6.11): ${{\lambda }_{{\max }}} = - 0.0417$ с^–1, ${{A}_{{\max }}} = 0.442$; из уравнения (6.20) находим ${{\lambda }_{1}} = - 0.0445$ с^–1, ${{\lambda }_{2}} = - 0.0419$ с^–1, и по (6.8) получаем соответствующие им амплитуды ${{A}_{1}} = 0.407,$ ${{A}_{2}} = 0.317.$

При расчетах по нелинейной математической модели, учитывающей оба типа нелинейностей, вызванных датчиками управления, получаем по формулам (6.17) и (6.18) ${{A}_{{\max }}} = 0.544$ и ${{\lambda }_{{\max }}} = - 0.0623$ с^–1. В качестве начальных приближений для итерационного процесса определения частот срыва колебаний используем полученные по другой математической модели, из (6.20), значения $\lambda _{1}^{{(0)}} = - 0.0445$ с^–1, $\lambda _{2}^{{(0)}} = - 0.0419$ с^–1, и, подставляя их в (6.21), определяем приближения амплитуд $A_{1}^{{(1)}} = 0.439,$ $A_{2}^{{(1)}} = 0.273.$ Подставляя $A_{1}^{{(1)}},$ $A_{2}^{{(1)}}$ в (6.16), находим следующее приближение $\lambda _{1}^{{(1)}} = - 0.0560$ с^–1, $\lambda _{2}^{{(1)}} = - 0.0482$ с^–1, и продолжаем итерационный процесс до получения погрешности меньшей 10^–4 с^–1 между последовательными значениями частоты. На пятой итерации получаем удовлетворяющие заданной точности значения ${{\lambda }_{1}} = - 0.0644$ с^–1, λ₂ = –0.0480 с^–1 и соответствующие им нормализованные амплитуды колебаний ${{A}_{1}} = 0.534,$ ${{A}_{2}} = 0.294.$ По полученным значениям λ определяются значения частот с учетом постоянной составляющей электростатической компоненты жесткости: резонансная частота ω_max = = $\omega \sqrt {1 - 2{{\eta }_{e}}} + {{\lambda }_{{\max }}} = 20889.751$ с^–1, и аналогично частоты срыва колебаний ω₁ = = $\omega \sqrt {1 - 2{{\eta }_{e}}} + {{\lambda }_{1}} = 20889.749$ с^–1, ${{\omega }_{2}} = \omega \sqrt {1 - 2{{\eta }_{e}}} + {{\lambda }_{2}} = 20889.765$ с^–1. Полученные результаты представлены на АЧХ (кривая 1, рис. 3). На отрезке между значениями ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$ возможно существование трех значений амплитуд, из которых устойчивым колебаниям соответствуют наибольшие и наименьшие значения. Это означает, что при незначительном изменении частотной настройки в точках ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$ происходит срыв колебаний, то есть скачкообразное изменение амплитуды колебаний.

7. Заключение. Показано, что нелинейность колебаний резонатора ВТГ, вызванную применением электростатических датчиков управления, необходимо учитывать даже при малом прогибе резонатора, так как конечным является отношение малого прогиба к малому зазору электростатического датчика. Учет конечного отношения прогиба к зазору нарушает линеаризацию силового воздействия принятой схемы подачи управляющих напряжений и приводит к нелинейному уточнению электростатической компоненты жесткости и нелинейным слагаемым при управлении в математической модели динамики резонатора. Полученное нелинейное уточнение электростатической жесткости представляет кубическую нелинейность, приводящую к дрейфу гироскопа. Угловая скорость дрейфа ВТГ, вызванная электростатическими датчиками управления, пропорциональна квадрату опорного напряжения и является существенной для приборов навигационной точности. Квадратичная нелинейность при управлении приводит к увеличению амплитуды колебаний, что в свою очередь усиливает нелинейные свойства колебательной системы и должно учитываться при расчете максимальной амплитуды, резонансной частоты и частот срыва колебаний.