1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 2, 2021

Известия РАН. Механика твердого тела, 2021, № 2, стр. 98-109

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ АМПЛИТУДЫ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ ОДНОРОДНЫХ СТЕРЖНЕЙ ПРИ ПРОДОЛЬНОМ УДАРЕ

А. А. Битюрин *

Ульяновский государственный технический университет
Ульяновск, Россия

* E-mail: sntk_2015@maul.ru

Поступила в редакцию 01.01.2020
После доработки 14.01.2020
Принята к публикации 17.01.2020

Полный текст (PDF)

Аннотация

Решение динамических задач продольного удара системы однородных стержней в нелинейной постановке представляет, как известно, существенные математические трудности. Существующие подходы имеют довольно ограниченное применение главным образом из-за существенной приближенности решения поставленной задачи. Помимо этого такие подходы затрагивают обширный математический аппарат, что затрудняет их использование в инженерных расчетах. На практике немалый интерес представляет моделирование амплитуды поперечных колебаний системы однородных стержней при продольном ударе, имеющих различную длину и толщину. Решение поставленной задачи осложняется хаотичностью интерференционной картины продольных волн при их переходе через ударное сечение стержней, являющееся границей однородных участков рассматриваемой стержневой системы. В этой связи деформации и продольные силы по длине стержней быстро меняются во времени. Настоящая работа посвящена математическому моделированию амплитуды поперечных колебаний физически и геометрически однородных стержней, один из которых неподвижен и взаимодействует с абсолютно жесткой преградой, а другой, двигаясь с предударной скоростью, соударяется с первым стержнем. В первом случае соударение рассматривается с учетом эксцентриситета в ударном сечении стержней. Во втором случае учитывается начальная кривизна одного из стержней. Моделирование осуществляется с применением метода начальных параметров и волновой модели продольного удара. Получены результаты моделирования максимального прогиба при различных величинах начальной кривизны и эксцентриситета в зависимости от предударной скорости. При анализе результатов выявлена так называемая “зона максимальных прогибов” – интервал изменения предударной скорости, на котором наблюдается максимальная амплитуда поперечных колебаний однородных стержней. Дополнительно отмечается ряд закономерностей, выявленных при сравнении результатов для обоих случаев. Подчеркивается актуальность применения данной методики расчета в решении динамических задач, возникающих при проектировании инженерных сооружений, имеющих динамически нагруженные стержневые системы.

Ключевые слова: поперечные колебания, прогиб, продольный удар, волновая модель, метод начальных параметров, предударная скорость, стержень

Введение. Задачи расчета на устойчивость и динамический прогиб при поперечных колебаниях в работах [1–6] реализовывались в основном для идеальных стержней с прямолинейной осью при отсутствии каких либо посторонних внешних воздействий. В реальной ситуации очень часто необходимо учитывать различные дополнительные факторы, такие как ударное взаимодействие с эксцентриситетом или с начальной кривизной стержня. В этом случае решение поставленной задачи усложняется. Особую важность представляет учет динамического характера продольного нагружения стержней, что приводит к дальнейшему усложнению поставленной задачи, как это было справедливо отмечено в работах [7–10].

Как показал проведенный обзор литературы, проблема продольного изгиба стержня при динамической нагрузке известна довольно широко. Основную сложность решения динамических задач представляет их нелинейность. Исследователями предлагаются различные подходы к решению поставленной задачи, каждый из которых имеет свои преимущества и недостатки.

Необходимо отметить, что если рассматривать продольный удар нескольких стержней различной длины и толщины, составляющих единую стержневую систему с несколькими однородными участками, то решение задачи известными методами [1–10] может оказаться невозможным из-за хаотичности интерференционной картины продольных волн при их переходе через границы таких участков.

Ранее были рассмотрены задачи поперечных колебаний однородного стержня при продольном ударе о жесткую преграду с учетом собственного веса [11] и продольного удара ступенчатого стержня, имеющего начальную кривизну одного из участков [12]. Был реализован подход, заключавшийся в совместном применении метода начальных параметров [13] и волновой модели продольного удара [14–17]. В настоящей работе этот подход реализуется для решения задачи ударного взаимодействия системы двух однородных стержней.

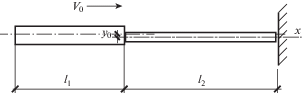
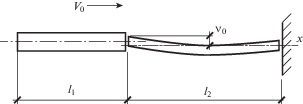
1. Постановка задачи. Ниже приводится модель расчета максимального прогиба однородных стержней 1 и 2 при их продольном ударе о жесткую преграду. Первый стержень длиной l1 и площадью поперечных сечений ${{A}_{1}}$ движется с предударной скоростью V0 и соударяется со стержнем 2, длина которого l2 площадь поперечных сечений A2, соприкасающимся с абсолютно жесткой преградой. Учитывается эксцентриситет ударного взаимодействия y0 (рис. 1 ) и начальная кривизна одного из стержней (рис. 2 ). Cуммарная длина обоих стержней l равна ${{l}_{1}} + {{l}_{2}}$.

Разработанная математическая модель расчета позволяет учесть силы инерции, действующие на рассматриваемую стержневую систему и вызванные кратковременностью действия ударной силы. Методом начальных параметров рассчитываются максимальные поперечные смещения и скорость сечений стержней, сжатых постоянной продольной силой. Далее с применением волновой модели продольного удара и метода характеристик [14–17] вычисляется продольная сила, возникающая в стержнях при продольном ударе, и рассчитывается время ее воздействия. После прекращения действия продольной силы оба стержня представляют из себя колебательную систему, выведенную из положения равновесия и совершающую затухающие поперечные колебания, имея вначале процесса приобретенную скорость и начальное смещение поперечных сечений.

2. Применение метода начальных параметров. Для определения максимальной амплитуды поперечных колебаний или максимального прогиба, которые будут иметь место вначале колебательного процесса стержней после соударения, можно воспользоваться дифференциальным уравнением изогнутой оси стержня постоянного поперечного сечения, несущего равномерно распределенную массу [1, 13]:

(2.1)
$({{d{{y}^{4}}} \mathord{\left/ {\vphantom {{d{{y}^{4}}} {d{{\xi }^{4}}}}} \right. \kern-0em} {d{{\xi }^{4}}}}) + {{\nu }^{2}}({{{{d}^{2}}y} \mathord{\left/ {\vphantom {{{{d}^{2}}y} {d{{\xi }^{2}}}}} \right. \kern-0em} {d{{\xi }^{2}}}}) - {{u}^{4}}y = 0$
где $y$ – прогиб оси стержня, ξ = x/l относительная координата, ${{\nu }_{2}} = {{N{{l}^{2}}} \mathord{\left/ {\vphantom {{N{{l}^{2}}} {EI}}} \right. \kern-0em} {EI}}$; u4 = = $({{m{{\omega }^{2}}{{l}^{4}}} \mathord{\left/ {\vphantom {{m{{\omega }^{2}}{{l}^{4}}} {EI}}} \right. \kern-0em} {EI}})$, N – продольная сила (положительная, если стержень сжат), l – длина стержня или его однородного участка, EI – жесткость стержня при изгибе, m – интенсивность массы, ω – частота свободных колебаний.

При решении поставленной задачи, уравнение (2.1) решается для каждого стержня в отдельности.

Составим характеристическое уравнение, соответствующее уравнению (2.1)

(2.2)
${{\lambda }^{4}} + {{\nu }^{2}}{{\lambda }^{2}}--{{u}^{4}} = 0~$
и его корни будут [13]

(2.3)
$\lambda _{1}^{2} = - ({{\nu }^{2}}{\text{/}}2) - \sqrt {({{\nu }^{4}}{\text{/}}4) + {{u}^{4}}} ;\quad \lambda _{2}^{2} = - ({{\nu }^{2}}{\text{/}}2) + \sqrt {({{\nu }^{4}}{\text{/}}4) + {{u}^{4}}} $

В зависимости от направления продольной силы (сжатие или растяжение) u4 и ν2 принимают как положительные, так и отрицательные значения, поэтому корни (2.3) могут быть вещественными, чисто мнимыми или комплексными сопряженными числами.

Общий интеграл уравнения (2.1) при отсутствии кратных корней можно записать в виде ряда

(2.4)
$y = \sum\limits_{j = 1,2} {({{A}_{j}}{\text{sh}}{{\lambda }_{j}}\xi + {{B}_{j}}{\text{ch}}{{\lambda }_{j}}\xi )} $
где Aj, Bj – постоянные интегрирования, λj – корни характеристического уравнения (2.2).

Выражение (2.4) для прогибов стержня дает возможность составить формулы усилий и углов поворота сечений стержней, если воспользоваться дифференциальными зависимостями [13]

$\varphi = \left( {{{dy} \mathord{\left/ {\vphantom {{dy} {dx}}} \right. \kern-0em} {dx}}} \right)$
(2.5)
$M = - EI({{{{d}^{2}}y} \mathord{\left/ {\vphantom {{{{d}^{2}}y} {d{{x}^{2}}}}} \right. \kern-0em} {d{{x}^{2}}}}),\quad {{Q}^{N}} = - EI({{{{d}^{3}}y} \mathord{\left/ {\vphantom {{{{d}^{3}}y} {d{{x}^{3}}}}} \right. \kern-0em} {d{{x}^{3}}}})$

Здесь φ, M – амплитуды угла поворота и изгибающего момента в сечениях, QN амплитуда поперечной силы, перпендикулярной к изогнутой оси стержня [13].

Для удобства обозначения примем

(2.6)
$\tilde {\varphi } = l\varphi ,\quad \tilde {M} = {{M{{l}^{2}}} \mathord{\left/ {\vphantom {{M{{l}^{2}}} {EI}}} \right. \kern-0em} {EI}},\quad {{\tilde {Q}}^{N}} = {{{{Q}^{N}}{{l}^{3}}} \mathord{\left/ {\vphantom {{{{Q}^{N}}{{l}^{3}}} {EI}}} \right. \kern-0em} {EI}}$

Тогда искомые зависимости запишутся в более простой форме

(2.7)
$\tilde {\varphi } = {{dy} \mathord{\left/ {\vphantom {{dy} {d\xi }}} \right. \kern-0em} {d\xi }},\quad \tilde {M} = - {{{{d}^{2}}y} \mathord{\left/ {\vphantom {{{{d}^{2}}y} {d{{\xi }^{2}}}}} \right. \kern-0em} {d{{\xi }^{2}}}},\quad {{\tilde {Q}}^{N}} = - {{{{d}^{3}}y} \mathord{\left/ {\vphantom {{{{d}^{3}}y} {d{{\xi }^{3}}}}} \right. \kern-0em} {d{{\xi }^{3}}}}$
или в рядах:

(2.8)
$\tilde {\varphi } = \sum\limits_{j = 1,2} {{{\lambda }_{j}}\left( {{{A}_{l}}{\text{ch}}{{\lambda }_{j}}\xi + {{B}_{j}}{\text{sh}}{{\lambda }_{j}}\xi } \right)} $
(2.9)
$\tilde {M} = - \sum\limits_{j = 1,2} {\lambda _{j}^{2}\left( {{{A}_{j}}{\text{sh}}{{\lambda }_{j}}\xi + {{B}_{j}}{\text{ch}}{{\lambda }_{j}}\xi } \right)} $
(2.10)
${{\tilde {Q}}^{N}} = - \sum\limits_{j = 1,2} {\lambda _{j}^{3}\left( {{{A}_{j}}{\text{ch}}{{\lambda }_{j}}\xi + {{B}_{j}}{\text{sh}}{{\lambda }_{j}}\xi } \right)} $

В дальнейшем поставленную задачу удобнее решать методом начальных параметров, как это предлагалось В.Г. Чудновским [13]. Для получения формул метода начальных параметров необходимо постоянные интегрирования Aj и Bj выразить через усилия и перемещения сечения стержня, совпадающего с началом координат. Эти усилия и перемещения и будут называться начальными параметрами: ${{y}_{0}}$, ${{\varphi }_{0}}$, M0 и Q0. Или введем их приведенные величины: ${{\tilde {\varphi }}_{0}}$, ${{\tilde {M}}_{0}}$, ${{\tilde {Q}}_{0}}$, определяемые (2.6).

Подчинив (2.5), (2.8)–(2.10) условиям при ξ = 0, $y = y{}_{0}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\varphi } = {{\tilde {\varphi }}_{0}}$, $\tilde {M} = {{\tilde {M}}_{0}}$, $\tilde {Q} = \tilde {Q}{}_{0}$, получим следующую систему уравнений для определения постоянных ${{A}_{1}}$, ${{A}_{2}}$, B1, B2:

(2.11)
$\begin{gathered} {{B}_{1}} + {{B}_{2}} = {{y}_{0}},\quad {{A}_{1}}{{\lambda }_{1}} + {{A}_{2}}{{\lambda }_{2}} = {{{\tilde {\varphi }}}_{0}},\quad - {{B}_{1}}{{\lambda }^{2}} - {{B}_{2}}\lambda _{2}^{2} = {{{\tilde {M}}}_{0}}, \\ \lambda _{1}^{2}\lambda _{2}^{2}(\left( {{{A{}_{1}} \mathord{\left/ {\vphantom {{A{}_{1}} {{{\lambda }_{1}}}}} \right. \kern-0em} {{{\lambda }_{1}}}}} \right) + ({{A_{2}^{{}}} \mathord{\left/ {\vphantom {{A_{2}^{{}}} {\lambda _{2}^{{}}}}} \right. \kern-0em} {\lambda _{2}^{{}}}})) = {{{\tilde {Q}}}_{0}} \\ \end{gathered} $

Если значения постоянных ${{A}_{1}}$, ${{A}_{2}}$, B1, B2, найденные из системы (2.11) подставить в зависимости (2.5), (2.8)–(2.10), получим формулы метода начальных параметров [13]:

(2.12)
$y = - {{y}_{0}}\lambda _{1}^{2}\lambda _{2}^{2}F{{_{\xi }^{'}}_{{}}} + {{\tilde {\varphi }}_{0}}F_{\xi }^{{{\text{IV}}}} - {{\tilde {M}}_{0}}F_{\xi }^{{{\text{III}}}} - {{\tilde {Q}}_{0}}F{{_{\xi }^{{''}}}_{{}}}$
(2.13)
$\tilde {\varphi } = - {{y}_{0}}\lambda _{1}^{2}\lambda _{2}^{2}F{{_{\xi }^{{''}}}_{{}}} + {{\tilde {\varphi }}_{0}}F_{\xi }^{{\text{V}}} - {{\tilde {M}}_{0}}F_{\xi }^{{{\text{IV}}}} - {{\tilde {Q}}_{0}}F_{\xi }^{{'''}}$
(2.14)
$\tilde {M} = {{y}_{0}}\lambda _{1}^{2}\lambda _{2}^{2}F_{\xi }^{{'''}} + {{\tilde {\varphi }}_{0}}F_{\xi }^{{{\text{VI}}}} - {{\tilde {M}}_{0}}F_{\xi }^{{\text{V}}} - {{\tilde {Q}}_{0}}F_{\xi }^{{{\text{IV}}}}$
(2.15)
$\tilde {Q} = - {{y}_{0}}\lambda _{1}^{4}\lambda _{2}^{4}{{F}_{\xi }} + {{\tilde {\varphi }}_{0}}\lambda _{1}^{2}\lambda _{2}^{2}F_{\xi }^{{{\text{III}}}} - {{\tilde {M}}_{0}}\lambda _{1}^{2}\lambda _{2}^{2}F_{\xi }^{{''}} - {{Q}_{0}}\lambda _{1}^{2}\lambda _{2}^{2}F{{_{\xi }^{'}}_{{}}}$
где

(2.16)
${{F}_{\xi }} = [1{\text{/}}(\lambda _{2}^{2} - \lambda _{1}^{2})]({{{\text{sh}}\lambda {}_{2}\xi } \mathord{\left/ {\vphantom {{{\text{sh}}\lambda {}_{2}\xi } {\lambda _{2}^{3} - {{{\text{sh}}\lambda _{1}^{{}}\xi } \mathord{\left/ {\vphantom {{{\text{sh}}\lambda _{1}^{{}}\xi } {\lambda _{1}^{3}}}} \right. \kern-0em} {\lambda _{1}^{3}}}}}} \right. \kern-0em} {\lambda _{2}^{3} - {{{\text{sh}}\lambda _{1}^{{}}\xi } \mathord{\left/ {\vphantom {{{\text{sh}}\lambda _{1}^{{}}\xi } {\lambda _{1}^{3}}}} \right. \kern-0em} {\lambda _{1}^{3}}}}})$
(2.17)
$F_{\xi }^{'} = ({{dF{}_{\xi }^{{}}} \mathord{\left/ {\vphantom {{dF{}_{\xi }^{{}}} {d\xi }}} \right. \kern-0em} {d\xi }}) = [1{\text{/}}(\lambda _{2}^{2} - \lambda _{1}^{2})]({{{\text{ch}}\lambda {}_{2}\xi } \mathord{\left/ {\vphantom {{{\text{ch}}\lambda {}_{2}\xi } {\lambda _{2}^{2} - {{{\text{ch}}\lambda _{1}^{{}}\xi } \mathord{\left/ {\vphantom {{{\text{ch}}\lambda _{1}^{{}}\xi } {\lambda _{1}^{2}}}} \right. \kern-0em} {\lambda _{1}^{2}}}}}} \right. \kern-0em} {\lambda _{2}^{2} - {{{\text{ch}}\lambda _{1}^{{}}\xi } \mathord{\left/ {\vphantom {{{\text{ch}}\lambda _{1}^{{}}\xi } {\lambda _{1}^{2}}}} \right. \kern-0em} {\lambda _{1}^{2}}}}})$
(2.18)
$F_{\xi }^{{''}} = ({{{{d}^{2}}F{}_{\xi }^{{}}} \mathord{\left/ {\vphantom {{{{d}^{2}}F{}_{\xi }^{{}}} {d{{\xi }^{2}}}}} \right. \kern-0em} {d{{\xi }^{2}}}}) = [1{\text{/}}(\lambda _{2}^{2} - \lambda _{1}^{2})]({{{\text{sh}}\lambda {}_{2}\xi } \mathord{\left/ {\vphantom {{{\text{sh}}\lambda {}_{2}\xi } {\lambda _{2}^{{}} - {{{\text{sh}}\lambda _{1}^{{}}\xi } \mathord{\left/ {\vphantom {{{\text{sh}}\lambda _{1}^{{}}\xi } {\lambda _{1}^{{}}}}} \right. \kern-0em} {\lambda _{1}^{{}}}}}}} \right. \kern-0em} {\lambda _{2}^{{}} - {{{\text{sh}}\lambda _{1}^{{}}\xi } \mathord{\left/ {\vphantom {{{\text{sh}}\lambda _{1}^{{}}\xi } {\lambda _{1}^{{}}}}} \right. \kern-0em} {\lambda _{1}^{{}}}}}})$
(2.19)
$F_{\xi }^{{'''}} = ({{{{d}^{3}}F{}_{\xi }^{{}}} \mathord{\left/ {\vphantom {{{{d}^{3}}F{}_{\xi }^{{}}} {d{{\xi }^{3}}}}} \right. \kern-0em} {d{{\xi }^{3}}}}) = [1{\text{/}}(\lambda _{2}^{2} - \lambda _{1}^{2})]\left( {{\text{ch}}\lambda {}_{2}\xi - {\text{ch}}{{\lambda }_{1}}\xi } \right)$
(2.20)
$F_{\xi }^{{{\text{IV}}}} = ({{{{d}^{4}}F{}_{\xi }^{{}}} \mathord{\left/ {\vphantom {{{{d}^{4}}F{}_{\xi }^{{}}} {d{{\xi }^{4}}}}} \right. \kern-0em} {d{{\xi }^{4}}}}) = [1{\text{/}}(\lambda _{2}^{2} - \lambda _{1}^{2})]\left( {{{\lambda }_{2}}{\text{sh}}\lambda {}_{2}\xi - {{\lambda }_{1}}{\text{sh}}{{\lambda }_{1}}\xi } \right)$
(2.21)
$F_{\xi }^{{\text{V}}} = ({{{{d}^{5}}F{}_{\xi }^{{}}} \mathord{\left/ {\vphantom {{{{d}^{5}}F{}_{\xi }^{{}}} {d{{\xi }^{5}}}}} \right. \kern-0em} {d{{\xi }^{5}}}}) = [1{\text{/}}(\lambda _{2}^{2} - \lambda _{1}^{2})](\lambda _{2}^{2}{\text{ch}}\lambda {}_{2}\xi - \lambda _{1}^{2}{\text{ch}}{{\lambda }_{1}}\xi )$
(2.22)
$F_{\xi }^{{{\text{VI}}}} = ({{{{d}^{6}}F{}_{\xi }^{{}}} \mathord{\left/ {\vphantom {{{{d}^{6}}F{}_{\xi }^{{}}} {d{{\xi }^{6}}}}} \right. \kern-0em} {d{{\xi }^{6}}}}) = [1{\text{/}}(\lambda _{2}^{2} - \lambda _{1}^{2})](\lambda _{2}^{3}{\text{sh}}\lambda {}_{2}\xi - \lambda _{1}^{3}{\text{sh}}{{\lambda }_{1}}\xi )$

Здесь λ1 и λ2 – корни характеристического уравнения, которые могут быть вещественными, мнимыми или комплексными числами в зависимости от величины и знака начальных параметров.

Формулы (2.12)–(2.15), полученные Чудновским В.Г., выражают перемещения и усилия в любом сечении колеблющихся стержней в зависимости от начальных параметров. Таким образом, данный подход дает возможность ответить на интересующие нас вопросы, касающиеся поперечных колебаний соударяющихся стержней с учетом эксцентриситета ударного взаимодействия или начальной кривизны.

При горизонтальном соударении однородных стержней с учетом эксцентриситета ударного взаимодействия (рис. 1 ), используя метод начальных параметров, выражение для максимальных прогибов сечений стержней с учетом (2.12), запишется в виде

(2.23)
${{y}_{{\max }}} = - {{\tilde {M}}_{0}}F_{\xi }^{{{\text{III}}}}$

Здесь ${{\tilde {M}}_{0}} = {{{{M}_{0}}l{}^{2}} \mathord{\left/ {\vphantom {{{{M}_{0}}l{}^{2}} {a{{d}^{2}}}}} \right. \kern-0em} {a{{d}^{2}}}}$, где M0 – начальный изгибающий момент равный произведению возникающей продольной силы N на плечо, равное эксцентриситету $y{}_{0}$ в ударном сечении. Поскольку, при данных условиях начальные угловое и линейное перемещения ударных сечений стержней отсутствуют, то следовательно, начальные угол поворота ${{\varphi }_{0}}$ и вертикальное перемещение ${{y}_{0}}$ равны нулю. Коэффициент $F_{\xi }^{{{\text{III}}}}$ зависит от величины продольной силы N, возникающей в стержнях в процессе удара.

Если при ударе учитывать начальную кривизну одного из стержней (рис. 2 ), то помимо начального изгибающего момента M0 появится дополнительный параметр – начальный угол поворота ударного сечения искривленного стержня ${{\varphi }_{0}}$. В этом случае выражение для максимальных прогибов запишется в виде

(2.24)
${{y}_{{\max }}} = {{\tilde {\varphi }}_{0}}F_{\xi }^{{{\text{IV}}}} - {{\tilde {M}}_{0}}F_{\xi }^{{{\text{III}}}}$

Здесь ${{\tilde {\varphi }}_{0}}$ – относительный угол поворота ударного сечения, связанный с начальной кривизной стержня, $F_{\xi }^{{{\text{IV}}}}$ – коэффициент, зависящий от возникающей продольной силы, и определяемый по формуле (2.20).

Рис. 1
Рис. 2
Рис. 3
Рис. 4
Рис. 5

3. Определение продольной силы. Для определения продольной силы N используется волновая модель продольного удара однородного стержня о жесткую преграду [14–17]. Решается волновое уравнение для первого и второго стержней:

(3.1)
${{{{\partial }^{2}}{{u}_{1}}(x,t)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{u}_{1}}(x,t)} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} - ({1 \mathord{\left/ {\vphantom {1 {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}})({{{{\partial }^{2}}{{u}_{1}}(x,t)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{u}_{1}}(x,t)} {\partial {{t}^{2}}}}} \right. \kern-0em} {\partial {{t}^{2}}}}) = 0,\quad 0 \leqslant x \leqslant l_{1}^{{}}$
(3.2)
${{{{\partial }^{2}}{{u}_{2}}(x,t)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{u}_{2}}(x,t)} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} - (1{\text{/}}{{a}^{2}})({{{{\partial }^{2}}{{u}_{2}}(x,t)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{u}_{2}}(x,t)} {\partial {{t}^{2}}}}} \right. \kern-0em} {\partial {{t}^{2}}}}) = 0,\quad {{l}_{1}} \leqslant x \leqslant l_{1}^{{}} + {{l}_{2}}$
где ${{u}_{1}}(x,t)$ и ${{u}_{2}}(x,t)$ – продольное перемещение поперечного сечения первого и второго стержней, x – координата сечения, $t$ – время, a – скорость распространения продольной волны деформации.

Начальные условия определяют состояние стержней перед их соударением [14, 15]: при $t = {{t}_{0}} = 0$

(3.3)
${{\partial {{u}_{1}}(x,{{t}_{0}})} \mathord{\left/ {\vphantom {{\partial {{u}_{1}}(x,{{t}_{0}})} {\partial t}}} \right. \kern-0em} {\partial t}} = {{V}_{0}},\quad {{\partial u{}_{1}(x,{{t}_{0}})} \mathord{\left/ {\vphantom {{\partial u{}_{1}(x,{{t}_{0}})} {\partial x}}} \right. \kern-0em} {\partial x}} = 0,\quad {{\partial {{u}_{2}}(x,t)} \mathord{\left/ {\vphantom {{\partial {{u}_{2}}(x,t)} {\partial t}}} \right. \kern-0em} {\partial t}} = 0,\quad {{\partial u{}_{2}(x,{{t}_{0}})} \mathord{\left/ {\vphantom {{\partial u{}_{2}(x,{{t}_{0}})} {\partial x}}} \right. \kern-0em} {\partial x}} = 0$

Граничные условия определяют отсутствие силы в сечении x = 0 и равенство нулю скорости сечения $x = {{l}_{1}} + {{l}_{2}}$ при взаимодействии второго стержня с жесткой преградой

(3.4)
${{\partial {{u}_{1}}(0,t)} \mathord{\left/ {\vphantom {{\partial {{u}_{1}}(0,t)} {\partial x}}} \right. \kern-0em} {\partial x}} = 0,\quad {{\partial {{u}_{2}}({{l}_{1}} + l{}_{2}^{{}},t)} \mathord{\left/ {\vphantom {{\partial {{u}_{2}}({{l}_{1}} + l{}_{2}^{{}},t)} {\partial t}}} \right. \kern-0em} {\partial t}} = 0,\quad {\text{если}}\quad {{\partial {{u}_{2}}({{l}_{1}} + l{}_{2}^{{}},t)} \mathord{\left/ {\vphantom {{\partial {{u}_{2}}({{l}_{1}} + l{}_{2}^{{}},t)} {\partial x}}} \right. \kern-0em} {\partial x}} < 0$
а также определяют равенство сил и условия сопряжения стержней в сечении $x = {{l}_{1}}$ при непосредственном их взаимодействии
(3.5)
$E{{A}_{1}}{{\partial u{}_{1}(l{}_{1},t)} \mathord{\left/ {\vphantom {{\partial u{}_{1}(l{}_{1},t)} {\partial x}}} \right. \kern-0em} {\partial x}} = E{{A}_{2}}{{\partial u{}_{2}(l{}_{1},t)} \mathord{\left/ {\vphantom {{\partial u{}_{2}(l{}_{1},t)} {\partial x}}} \right. \kern-0em} {\partial x}},\quad {\text{если}}\quad {{\partial u{}_{1}^{{}}(l{}_{1},t)} \mathord{\left/ {\vphantom {{\partial u{}_{1}^{{}}(l{}_{1},t)} {\partial x}}} \right. \kern-0em} {\partial x}} < 0$
(3.6)
${{\partial u{}_{1}({{l}_{1}},t)} \mathord{\left/ {\vphantom {{\partial u{}_{1}({{l}_{1}},t)} {\partial t}}} \right. \kern-0em} {\partial t}} = {{\partial u{}_{2}({{l}_{1}},t)} \mathord{\left/ {\vphantom {{\partial u{}_{2}({{l}_{1}},t)} {\partial t}}} \right. \kern-0em} {\partial t}},\quad {\text{если}}\quad {{\partial u{}_{1}^{{}}({{l}_{1}},t)} \mathord{\left/ {\vphantom {{\partial u{}_{1}^{{}}({{l}_{1}},t)} {\partial x}}} \right. \kern-0em} {\partial x}} < 0$
либо отсутствие сил в ударных сечениях стержней, если их взаимодействие отсутствует:

(3.7)
${{\partial u{}_{1}({{l}_{1}},t)} \mathord{\left/ {\vphantom {{\partial u{}_{1}({{l}_{1}},t)} {\partial x}}} \right. \kern-0em} {\partial x}} = 0,\quad {{\partial {{u}_{2}}({{l}_{1}},t)} \mathord{\left/ {\vphantom {{\partial {{u}_{2}}({{l}_{1}},t)} {\partial x}}} \right. \kern-0em} {\partial x}} = 0.$

Для решения волновых уравнений (3.1), (3.2) применяется метод Даламбера [14, 15]:

(3.8)
${{u}_{1}}(x,t) = {{f}_{1}}(at - x) + {{\varphi }_{1}}(at + x),\quad 0 \leqslant x \leqslant {{l}_{1}}$
(3.9)
${{u}_{2}}(x,t) = {{f}_{2}}(at - x) + {{\varphi }_{2}}(at + x),\quad {{l}_{1}} \leqslant x \leqslant {{l}_{1}} + l{}_{2}^{{}}$
(3.10)
${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-0em} {\partial x}} = - f'(at - x) + \varphi {\text{'}}(at + x),\quad {{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial t}}} \right. \kern-0em} {\partial t}} = a[f{\text{'}}(at - x) + \varphi {\text{'}}(at + x)]$
где ${{f}_{1}}(at - x)$, ${{f}_{2}}(at - x)$, – функции, описывающие прямую волну, распространяющиеся соответственно по первому и второму стержням в направлении оси x; ${{\varphi }_{1}}(at + x)$ и ${{\varphi }_{2}}(at + x)$ – функции, описывающие обратные волны, распространяющиеся по первому и второму стержням в противоположном направлении; $f_{1}^{'}(at - x)$, $f_{2}^{'}(at$ – x), $\varphi _{1}^{'}(at$ + x), $\varphi _{2}^{'}(at + x)$ − производные функций.

Целесообразно перейти к относительным величинам, определяющим прямые и обратные волны: $\bar {f}{\text{'}}(at - x) = af{\text{'}}(at - x){\text{/}}{{V}_{0}}$; $\bar {\varphi }{\text{'}}(at + x) = a\varphi {\text{'}}(at + x){\text{/}}{{V}_{0}}$

(3.11)
$\bar {\varepsilon }(x,t) = - \bar {f}{\text{'}}(at - x) + \bar {\varphi }{\text{'}}(at + x)$
(3.12)
$\bar {\nu }(x,t) = {{\nu \left( {x,t} \right)} \mathord{\left/ {\vphantom {{\nu \left( {x,t} \right)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}} = \bar {f}{\text{'}}(at - x) + \bar {\varphi }{\text{'}}(at + x)$

В дальнейшем, для удобства определения продольной силы N в сечениях стержней, методом характеристик строим поле волновых состояний [14–17]. Наклонные линии определяют прямые и обратные волны деформаций. Относительная продольная деформация $\bar {\varepsilon }(x,t)$, позволяющая в дальнейшем рассчитать продольную сжимающую силу N, возникающую в рассматриваемых стержнях, связана c параметрами прямых и обратных волн зависимостью (3.11). При известной величине $\bar {\varepsilon }(x,t)$ можно определить продольную силу:

(3.13)
$N = EA\bar {\varepsilon }\left( {{{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} a}} \right. \kern-0em} a}} \right)$

В дальнейшем, используя метод начальных параметров, можно рассчитать прогиб $y$ и скорость $y{\text{'}} = {{dy} \mathord{\left/ {\vphantom {{dy} {dt}}} \right. \kern-0em} {dt}}$ в момент прекращения действия продольной силы N. Далее сечения рассматриваемого стержня, имея приобретенную поперечную скорость $y{\text{'}}$ и двигаясь по инерции до некоторого максимального отклонения $y_{{\max }}^{*}$ от положения равновесия, начинают совершать свободные поперечные колебания.

4. Вычисление максимального прогиба. Максимальное отклонение сечений стержней от положения равновесия, которые и будут максимальными прогибами, легко определится по известной формуле [1]:

(4.1)
$y_{{\max }}^{ * } = \sqrt {{{y}^{2}} + y{\kern 1pt} {{'}^{2}}{\kern 1pt} {\text{/}}{{\omega }^{2}}} $
где y – максимальный прогиб, равный максимальной координате рассматриваемого сечения в момент прекращения действия продольной силы N, $\omega $ – циклическая частота свободных поперечных колебаний стержней при отсутствии продольной силы. Учитывая формы связей рассматриваемых стержней, устанавливаем для первого стержня ξ = 1, для второго ξ = 0.5. Для первой формы поперечных колебаний (n = 1), как наиболее часто встречающейся на практике, а также с учетом зависимости (3.13), имеем для каждого стержня круглого поперечного сечения выражение циклической частоты поперечных колебаний:

(4.2)
$\vartheta = \omega \sqrt {1 - 64V{}_{0}\tilde {\varepsilon }{{l}^{2}}{\text{/(}}{{\pi }^{2}}{{d}^{2}}a)} $

Анализируя формулу (4.2) можно заключить, что с ростом предударной скорости частота поперечных колебаний сжатого стержня $\vartheta $ будет уменьшаться и будет равна нулю при достижении продольной силы величины ${{P}_{{cr}}}$ по Эйлеру, что отмечено в [1, 13].

Частоту свободных поперечных колебаний первого стержня $\omega {}_{1}$, имеющего свободный торец, по первой форме n = 1 можно рассчитать по формуле [1, 13]

(4.3)
${{\omega }_{1}} = ({{\wp _{1}^{2}} \mathord{\left/ {\vphantom {{\wp _{1}^{2}} {l_{1}^{2}}}} \right. \kern-0em} {l_{1}^{2}}})\sqrt {{{E{{I}_{1}}} \mathord{\left/ {\vphantom {{E{{I}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} $
и для второго стержня

(4.4)
${{\omega }_{2}} = {{({{\wp _{2}^{{}}} \mathord{\left/ {\vphantom {{\wp _{2}^{{}}} {l{}_{2}}}} \right. \kern-0em} {l{}_{2}}})}^{2}}\sqrt[{}]{{{{EI_{2}^{{}}} \mathord{\left/ {\vphantom {{EI_{2}^{{}}} {m{}_{2}}}} \right. \kern-0em} {m{}_{2}}}}}$

Параметр $\wp $ выбирается с учетом сопряжения первого и второго стержней, а также сопряжения второго стержня с жесткой преградой [1].

Предполагая гармонический закон колебательного процесса обоих стержней, имеем

(4.5)
$y = {{y}_{{\max }}}\sin (\vartheta t)\quad {\text{и}}\quad y{\text{'}} = {{y}_{{\max }}}\omega {\text{*}}\cos (\vartheta t)$

При малых значениях $t$ максимальная скорость сечений будет

(4.6)
$y{\text{'}} \approx {{y}_{{\max }}}\vartheta $

Подставляя значения частоты свободных колебаний первого и второго стержней ω1 и ω2 и скорость $y{\text{'}}$ в формулу (4.1), получим искомый максимальный прогиб стержней, равный максимальному перемещению его сечений $y_{{\max }}^{ * }$. В этом случае имеет место учет сил инерции, действующих на стержни при динамической нагрузке, что представляло в традиционных моделях расчета довольно сложную задачу.

5. Пример. Рассмотрим продольный удар однородного стержня 1 о покоящийся однородный стержень 2, соприкасающийся с жесткой преградой одним из торцевых сечений. Длина первого стержня выбрана ${{l}_{1}} = 1.6$ м, длина второго ${{l}_{2}} = 2.4$ м. Диаметры первого и второго соответственно: ${{d}_{1}} = 0.2$ м и ${{d}_{2}} = 0.12$ м. Предударная скорость первого стержня о второй ${{V}_{0}} = 1$ м/с. Материал обоих стержней – сталь СТ 5. Массы первого и второго стержней 588 и 212 кг соответственно, погонные массы $m$ на единицу длины стержней 367 и 88 кг на метр. Циклическая частота ω1 собственных поперечных колебаний первого стержня, рассчитанная по (4.3) будет равна 214 р/с. Для второго стержня ω2, рассчитанная по (4.4), будет равна 605 р/с.

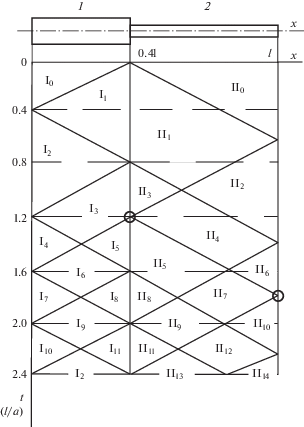
Применим метод характеристик [14–17] для построения поля состояний (рис. 3 ). Области состояний I1 – I12, II0 – II14 с соответствующими значениями $\bar {f}{\text{'}}(at - x)$, $\bar {\varphi }{\text{'}}(at$ + x), $\bar {\varepsilon }(x,t)$, $\bar {\nu }(x,t)$ определяют параметры прямых и обратных волн деформаций, относительную продольную деформацию и относительную скорость поперечных сечений. Длительность состояния для произвольного сечения определяется разностью ординат t, которые имеют точки наклонных линий для этого сечения. Метод характеристик позволяет определить моменты отрыва стержней в ударном сечении в процессе удара (кружок 3 на рис. 2 ) и отскок второго стержня от жесткой преграды (кружок 4 на рис. 3 ).

Из анализа поля состояний (рис. 3 ) выделяем максимальные по модулю значения относительной продольной деформации для первого и второго стержня в рассматриваемом ударном процессе. Для стержня 1 максимальное значение $\bar {\varepsilon }{}_{1}(x,t) = - 0.5$ в области состояний I2 при длительности действия $\Delta {{t}_{1}} = 0.4\left( {{l \mathord{\left/ {\vphantom {l a}} \right. \kern-0em} a}} \right)$; для стержня 2 максимальные значения $\bar {\varepsilon }{}_{2}(x,t) = - 1.5$ в области состояний II2 при длительности $\Delta {{t}_{2}}$ = = 0.4(l/a) и $\bar {\varepsilon }{}_{2}(x,t) = - 1.125$ в области II3 при длительности $\Delta t_{3}^{{}} = 0.2$(l/a). При t = = 1.2(l/a) происходит отрыв стержней в ударном сечении (кружок на рис. 3 ) и деформация в первом стержне становится равной нулю. После разрыва стержней в областях волновых состояний II5–II7 второго стержня, его деформации становятся незначительными и не оказывают влияние на колебательный процесс. При $t = 1.8\left( {{l \mathord{\left/ {\vphantom {l a}} \right. \kern-0em} a}} \right)$ происходит отрыв второго стержня от жесткой преграды (кружок на рис. 3 ) и ударный процесс завершается.

Из анализа поля состояний с учетом конфигурации рассматриваемой системы заключаем, что наибольший прогиб будет иметь место для второго стержня. В этой связи расчет амплитуды поперечных колебаний первого стержня опускаем.

По формуле (3.13) определяем максимальную продольную силу для второго стержня: ${{(N{}_{2})}_{{\max }}} = 712.5$ кН. При учете эксцентриситета ударного взаимодействия стержней, начальным параметром является момент M0, равный произведению эксцентриситета ${{y}_{0}} = 1$ мм на значение возникающей продольной силы N. Для удобства ведения расчета преобразуем выражения для ν2 и u4 относительно ${{V}_{0}}$, d и l; $\nu _{2}^{2}$ =  ${{16\bar {\varepsilon }{{V}_{0}}l_{2}^{2}} \mathord{\left/ {\vphantom {{16\bar {\varepsilon }{{V}_{0}}l_{2}^{2}} {ad_{2}^{2}}}} \right. \kern-0em} {ad_{2}^{2}}}$ = = 1.92; $u_{2}^{4} = {{{{m}_{2}}\omega _{2}^{2}l_{2}^{4}} \mathord{\left/ {\vphantom {{{{m}_{2}}\omega _{2}^{2}l_{2}^{4}} {E{{I}_{2}}}}} \right. \kern-0em} {E{{I}_{2}}}} = 501$. Правильность составленных выражений проверена методом размерностей.

Для второго стержня вычисляем корни характеристического уравнения по формулам (2.3): $\lambda _{1}^{2} = - 23.36$; $\lambda _{2}^{2} = 21.44$.

Подставляя полученные значения ${{\lambda }_{{1,2}}}$ в формулу (2.19) и, учитывая ${{\bar {\lambda }}_{1}} = i{{\lambda }_{1}}$, получим значение коэффициента $F{{_{\xi }^{{{\text{III}}}}}^{{}}} = - 0.012$. После подстановки этих значений в выражение (2.23) для ymax, получим ${{y}_{{\max }}} = 0.023$ мм. Такое значение прогиба возникает при постоянной продольной силе N. При кратковременном ее действии стержень будет только выведен из положения равновесия и далее предоставлен самому себе. Для гармонического закона изменения координаты торцевого сечения стержня имеем (4.5):

(5.1)
$y = 0.023\sin \vartheta t$

Циклическая частота колебаний кратковременно сжатого стержня, рассчитанная по (4.2), будет равна $\vartheta = 284.46$ р/с. С учетом длительностей состояний II2 и II3 и соответствующих им величинах $\bar {\varepsilon }{}_{2}(x,t)$, максимальное отклонение сечения, имеющего координату $x = 0.5{{l}_{2}}$, в течение промежутка времени $\Delta t = \Delta {{t}_{2}} + \Delta {{t}_{3}} = 0.6{l \mathord{\left/ {\vphantom {l a}} \right. \kern-0em} a}$, в соответствии с (4.5) будет равно 0.0039 мм. В соответствии с (4.6) поперечная скорость рассматриваемого сечения будет равна 0.082 м/с. Тогда получаем максимальное его отклонение от положения равновесия при свободных колебаниях в соответствии с (4.1): $y_{{\max }}^{ * } = 0.011$ мм.

Аналогично рассчитываем $y_{{\max }}^{ * }$ второго стержня с учетом его начальной кривизны, используя те же параметры ν2, u4, $\lambda $ и поле состояний (рис. 3 ). Коэффициент $F_{\xi }^{{{\text{IV}}}}$ вычисляем в соответствии с (2.20). Относительный угол поворота ударного сечения второго стержня ${{\tilde {\varphi }}_{0}} = {{0.5y{}_{0}l{}_{2}^{{}}} \mathord{\left/ {\vphantom {{0.5y{}_{0}l{}_{2}^{{}}} {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}$ (рис. 2 ), равен 0.002. В соответствии с (4.1) $y_{{\max }}^{ * }$ составит 0.094 мм, что примерно в 9 раз больше по сравнению с предыдущим случаем.

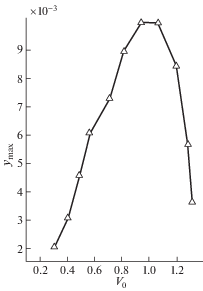
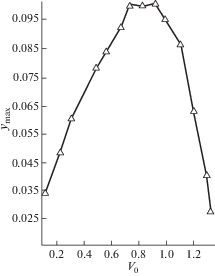
6. Анализ результатов и выводы. Используя для расчета представленную математическую модель, в работе были получены значения амплитуд поперечных колебаний второго стержня при различных значениях предударной скорости V0 с учетом эксцентриситета ударного взаимодействия 1 мм и с учетом начальной кривизны 1 мм. Результаты моделирования $y_{{\max }}^{ * }$ для первого и второго случаев представлены соответственно на графиках (рис. 4 и 5 ).

Полученные результаты позволяют сформулировать следующие выводы:

1. На обоих графиках максимальные значения амплитуд поперечных колебаний второго стержня наблюдаются на интервале изменения предударной скорости V0 примерно 0.75 м/с до 1 м/с с небольшим смещением влево на графике (рис. 5 ) по сравнению с графиком (рис. 4 ). При дальнейшем увеличении предударной скорости, несмотря на ожидаемый рост $y_{{\max }}^{ * }$, наблюдается его довольно резкое снижение вплоть до нуля, что отмечалось ранее при анализе результатов в работе [12].

2. Величины амплитуд поперечных колебаний второго стержня, изначально искривленного (рис. 5 ) примерно в 9–10 раз превышают соответствующие величины амплитуд при эксцентричном ударе этого же стержня (рис. 4 ) несмотря на равные величины кривизны и эксцентриситета.

3. Анализируя зависимости (2.23) и (2.24), можно сделать вывод, что при возрастании величин эксцентриситета ударного взаимодействия стержней и начальной кривизны, амплитуда поперечных колебаний увеличивается.

Заключение. Метод расчета величины максимального прогиба однородного стержня при продольном ударе с учетом эксцентриситета и начальной кривизны, описанный выше, позволил эффективно совместно применить метод начальных параметров и волновую модель продольного удара. Как уже отмечалось во введении, описанный подход можно использовать для моделирования поперечных колебаний системы однородных стержней с различной конфигурацией и предударным состоянием. Примененный подход позволяет учесть инерционные силы при расчете прогиба, что представляло в традиционных методах довольно непростую задачу. Дальнейшее развитие данного подхода будет представлять интерес для решения целого ряда прикладных задач механики.

В выводах, сделанных в ходе анализа результатов моделирования, отмечается различие величин амплитуд поперечных колебаний искривленного стержня и стержня прямолинейного, но воспринимающего продольную нагрузку с эксцентриситетом. Это подчеркивает большее влияние неровности стержня на его состояние при восприятии продольных динамических нагрузок, что необходимо учитывать на практике.

При анализе результатов обращается внимание на уменьшение величины максимального прогиба рассматриваемого стержня с увеличением предударной скорости. Это связано с уменьшением частоты поперечных колебаний сжатого стержня при увеличении сжимающей нагрузки, пропорциональной скорости соударения. При достижении продольной силы критической величины по Эйлеру частота поперечных колебаний стержня стремится к нулю, что означает потерю устойчивости [1].

Подход, описанный в работе, актуален в расчетах системы однородных и ступенчатых стержней, совершающих поперечные колебания при продольном ударе, которые часто встречаются в современных ударных механизмах. В строительной сфере важен учет амплитуд поперечных колебаний жестко закрепленных стержней, являющихся элементами ферм, рамных конструкций, а также колонн, стоек и прочее.

Список литературы

  1. Филиппов А.П. Колебания деформируемых систем. М.: Машиностроение. 1970. – 734 с.

  2. Лаврентьев М.А., Ишлинский А.Ю. Динамические формы потери устойчивости упругих систем // Доклады АН СССР, 1949. Т. 65. № 6.

  3. Малый В.И. Длинноволновое приближение в задачах о потере устойчивости при ударе // Известия АН СССР. МТТ. 1972. № 4. С. 138–144.

  4. Малый В.И. Выпучивание стержня при продольном ударе. Малые прогибы // Известия АН СССР. МТТ. 1973. № 4. C. 181–186.

  5. Малый В.И. Выпучивание стержня при продольном ударе. Большие прогибы // Известия АН СССР. МТТ. 1975. № 1. С. 52–61.

  6. Малышев Б.М. Устойчивость стержня при ударном сжатии // Известия АН СССР. МТТ. 1966. № 4. С. 137–142.

  7. Морозов Н.Ф., Товстик П.Е. Динамика стержня при кратковременном продольном ударе // Вестник С.-Петерб. ун-та. Сер. 1. 2013. Вып. 3. С. 131–141.

  8. Беляев А.К., Ильин Д.Н., Морозов Н.Ф. Динамический подход к задаче Ишлинского–Лаврентьева // Изв. РАН. МТТ. 2013. № 5. С. 28–33.

  9. Беляев А.К., Морозов Н.Ф., Товстик П.Е. О статической и динамической неустойчивости тонких стержней // Тр. 7 Всерос. конф. “Механика деформируемого твердого тела”. Ростов н/Д.: Изд. ЮФУ, 2013. С. 80–84.

  10. Морозов Н.Ф., Товстик П.Е. О динамической потере устойчивости стержня при продольной нагрузке, меньшей Эйлеровой // Докл. АН. 2013. Т. 453. № 3. С. 282–285.

  11. Битюрин А.А. Моделирование амплитуды поперечных колебаний однородного стержня при ударе о жесткую преграду с учетом собственного веса // Вестник ПНИПУ. Механика. 2018. № 2. С. 16–23.

  12. Битюрин А.А. Моделирование максимального прогиба ступенчатого стержня, имеющего начальную кривизну при ударе о жесткую преграду // Известия РАН. МТТ. 2019. № 5. С. 131–141.

  13. Чудновский В.Г. Методы расчета колебаний стержневых систем. Киев: Изд-во АН УССР, 1952. 403 с.

  14. Битюрин А.А., Манжосов В.К. Моделирование продольного удара однородных стержней при неудерживающих связях // Вестник УлГТУ. 2005. № 3. С. 23–25.

  15. Битюрин А.А., Манжосов В.К. Моделирование продольного удара однородного и неоднородного стержней о жесткую преграду при неудерживающих связях // Вестник УлГТУ. 2006. № 1. С. 20–23.

  16. Алимов О.Д., Манжосов В.К., Еремьянц В.Э. Распространение волн деформаций в ударных системах. М.: Наука, 1985. 354 с.

  17. Битюрин А.А., Манжосов В.К. Продольный удар неоднородного стержня о жесткую преграду. Ульяновск, 2009. – 164 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал