Известия РАН. Механика твердого тела, 2021, № 2, стр. 17-30

1. Введение. Будем описывать конечную деформацию с помощью тензора градиента деформации F, задаваемого выражением

Здесь ${\mathbf{r}}$ и ${\mathbf{R}}$ – векторы места точек тела в деформированной и недеформированной (отсчетной) конфигурациях соответственно. Точка означает скалярное произведение (свертку по одному тензорному индексу). В чисто механической теории нелинейной гиперупругости однородного изотропного материала выделяется класс несжимаемых материалов, для которых

а тензор напряжений Коши ${\mathbf{S}}$ определяется выражением [1, 2] где 1 – единичный тензор; ${\mathbf{B}} = {\mathbf{F}} \cdot {{{\mathbf{F}}}^{T}}$ – левый тензор деформации Коши–Грина [2] (в [1] это мера деформации Фингера), значок $^{T}$ обозначает транспонирование; W = = $W({{I}_{1}},{{I}_{2}})$ – удельная энергия упругой деформации (потенциал энергии деформации), отнесенная к единице объема отсчетной конфигурации; ${{I}_{1}} = {\mathbf{1}} \cdot \cdot {\mathbf{B}}$, I₂ = = $1{\text{/}}2(I_{1}^{2} - {\mathbf{1}} \cdot \cdot \,{{{\mathbf{B}}}^{2}})$ – главные алгебраические инварианты тензора B; $\gamma $ – функция гидростатического давления (аддитивная часть напряжения, неопределяемая деформацией).

При изменении температуры все тела, независимо от того сжимаемые они или несжимаемые изотермически, подвергаются тепловому расширению, и для несжимаемых тел уравнения (1.2) и (1.3) не имеют места. Необходимо выражения (1.2) и (1.3) модифицировать так, чтобы учесть тепловое расширение, а в случае отсутствия теплового воздействия новые выражения должны редуцироваться к старым.

Существует довольно обширный список работ, в которых эта задача решалась тем или иным способом. В первой серии работ тепловое расширение выделяется из общей деформации. В работах [3–5] предлагается мультипликативное разложение тензора градиента деформации

причем ${{\Phi }_{\theta }} = g\left( \theta \right){\mathbf{1}}$ – шаровой тензор, описывающий тепловое расширение в термически изотропных телах, а ${{\Phi }_{E}}$ – тензор, описывающий упругую составляющую деформации, и для несжимаемых тел $\det {{\Phi }_{E}} = 1.$ Здесь $g\left( \theta \right)$ некоторая монотонная функция приращения температуры $\theta = T - {{T}_{0}}$, где T – абсолютная температура деформированной конфигурации, а ${{T}_{0}}$ – однородная абсолютная температура отсчетной конфигурации и $g\left( 0 \right) = 1$. Существенным недостатком такого представления является то, что в общем случае неоднородного распределения температуры T тензор ${{\Phi }_{E}}$ не является градиентом упругой деформации. Действительно, введем материальную систему координат $({{q}^{1}},{{q}^{2}},{{q}^{3}})$ тогда основной ${{{\mathbf{R}}}_{k}}$ и сопряженный ${{{\mathbf{R}}}^{k}}$ базисы этой системы в отсчетной конфигурации вычисляется по формулам

Крестик означает векторное произведение. Введем в отсчетной конфигурации оператор Гамильтона $\mathop \nabla \limits^0 = {{{\mathbf{R}}}^{k}}\partial {\text{/}}\partial {{q}^{k}}$, тогда из выражения (1.1) следует связь тензора градиента деформации с тензором градиентом вектора места ${{{\mathbf{F}}}^{T}} = \mathop \nabla \limits^0 {\mathbf{r}}$ [1] и необходимым условием интегрируемости (1.1) является выражение

В развернутом виде это уравнение выглядит так

Поскольку g(θ) монотонно возрастает и отлична от нуля, а ${{\Phi }_{E}}$ произвольный тензор с $\det {{\Phi }_{E}} = 1$, то для выполнения условия $\mathop \nabla \limits^0 \; \times \Phi _{E}^{T} = 0$ требуется чтобы $\mathop \nabla \limits^0 \theta = 0$. То есть тензор Φ_E является градиентом деформации только в случае однородного температурного поля. В работе [7] предполагается аддитивное разбиение массовой плотности свободной энергии Гельмгольца $\Psi = W{\text{/}}{{\rho }_{0}}$ на слагаемое, описывающее дисторсию, слагаемое, описывающие дилатацию и слагаемое, связанное с теплоемкостью

Здесь c(T) – удельная теплоемкость, ${{\rho }_{0}}$ – плотность массы, $\mu $ – модуль сдвига, κ – изотермический объемный модуль и $\bar {\alpha }$ – коэффициент объемного теплового расширения, отнесенные к недеформированной конфигурации, f, l и h – функции отклика. Но приложение этой гипотезы рассмотрено только для однородного температурного поля. В работе [8] дилатация и дисторсия разделяются путем введения модифицированных главных кратностей удлинения

далее вся работа выдержана в терминах главных удлинений и главных напряжений, а в качестве приложения рассмотрена задача об одноосном растяжении. В работе [9] оба предыдущих подхода объединяются, то есть удельная свободная энергия представляется в виде суммы энергии дилатации и энергии дисторсии, выраженной через $I_{1}^{*},I_{2}^{*}$ – модифицированные главные алгебраические инварианты тензора ${\mathbf{B}}$

Здесь $A(I_{1}^{*},I_{2}^{*})$ – функция отклика. Кроме общих рассуждений никаких приложений в работе не приводится. Попутно следует отметить [5], что поскольку ${{I}_{1}} = {{J}^{{2/3}}}I_{1}^{*},$ I₂ = = ${{J}^{{2/3}}}I_{2}^{*}$, то первое слагаемое в (1.5) не описывает чистую дисторсию. Более четкое разделение дилатации и дисторсии проведено в [5]

Здесь c_e постоянная теплоемкость, а ${{\varphi }_{0}} = {{c}_{e}}{{T}_{0}}$, но как было отмечено, это выражение получено в предположении (1.4).

Во второй серии работ модификация уравнений (1.2) и (1.3) либо полностью, либо частично не проводится. Так в работах [10–13] уравнения (1.2) и (1.3) не меняются, при этом полагается, что такая модель несжимаемости является грубым, но важным приближением к точной теории термоупругости. В работах [14–17] уравнение (1.2) модифицируется в ${\text{det}}{\mathbf{F}} = g\left( \theta \right)$, а (1.3) остается неизменным. Список приведенных работ неисчерпывающий, обозначены основные направления. В нашей работе мы не делаем предположений о структуре термоупругой деформации, кроме того, что изменение объема происходит исключительно вследствие теплового расширения.

2. Основные соотношения. Термоупругую деформацию однородного и изотропного материала будем представлять с помощью тензора градиента деформации ${\mathbf{F}}$ определенного выражением (1.1). Положим, что изменение объема происходит только за счет теплового расширения (материал изотермически несжимаемый), то есть

где по [3, 4, 9, 14]

Здесь $\alpha $ – коэффициент линейного расширения. Ниже будем пользоваться первой формулой из (2.2).

Согласно [1, 2] для простого однородного материала с массовой плотностью свободной энергии $\Psi = \Psi ({\mathbf{F}},\,T,\,\mathop \nabla \limits^0 T)$ уравнения состояния принимают вид

Здесь P – тензор напряжений Пиолы [1] (по [2] это транспонированный первый тензор Пиолы – Кирхгофа), $\hat {\eta }$ – массовая плотность энтропии. Из последнего уравнения следует, что для простого однородного материала $\Psi = \Psi \left( {{\mathbf{F}},\,T} \right)$, а если он изотропен, то $\Psi = \Psi \left( {{{I}_{1}},{{I}_{2}},{{I}_{3}},T} \right)$. Здесь ${{I}_{3}} = \det {\mathbf{B}} = {{J}^{2}}$. Вспоминая, что $W = {{\rho }_{0}}\Psi $, по [1] получим

Здесь ${\mathbf{C}} = {{{\mathbf{F}}}^{{Tr}}} \cdot {\mathbf{F}}$ – правый тензор деформации Коши–Грина [2] (по [1] это мера деформации Коши). Использована формула Гамильтона–Келли ${{I}_{1}}{\mathbf{B}} - {{{\mathbf{B}}}^{2}} = {{I}_{2}}{\mathbf{1}} - {{I}_{3}}{{{\mathbf{B}}}^{{ - 1}}}$ [1].

Для несжимаемого материала (${{I}_{3}} = {{J}^{2}} = {{e}^{{6\alpha \theta }}}$) вводится множитель Лагранжа h₁, зависящий от координат точек и температуры, так что удельная энергия деформации представляется выражением $W = W\left( {{{I}_{1}},{{I}_{2}},T} \right) + {{h}_{1}}({{I}_{3}} - {{e}^{{6\alpha \theta }}})$. Используя последнее выражение в (2.3) получим

Введем обозначение $h = {{I}_{2}}\partial W{\text{/}}\partial {{I}_{2}} + {{e}^{{6\alpha \theta }}}{{h}_{1}}$, тогда

Вспоминая связь тензора напряжений Коши с тензором Пиолы ${\mathbf{P}} = J\,{{{\mathbf{F}}}^{{ - 1}}} \cdot {\mathbf{S}}$ [1] из (2.4) будем иметь

где $\gamma = {{e}^{{ - 3\alpha \theta }}}h$. Следовательно,

Выражения (2.1), (2.5) и есть предлагаемая модификация выражений (1.2) и (1.3).

Среди простых, однородных и изотропных материалов будем рассматривать материалы, подчиняющиеся закону Фурье

Здесь q – удельный тепловой поток, рассчитанный на единицу площади поверхности в отсчетной конфигурации, λ – коэффициент теплопроводности, тоже отнесенный к отсчетной конфигурации.

В отсутствие массовых сил и внутренних источников теплоты уравнения равновесия и теплового баланса имеют вид [1]

Из второго уравнения (2.7) и выражения (2.6) следует стационарное уравнение теплопроводности

Первое уравнение в (2.7) можно переписать в виде [1]

Здесь $\nabla = {{{\mathbf{r}}}^{k}}\partial {\text{/}}\partial {{q}^{k}}$ – оператор Гамильтона в деформированной конфигурации, r^k – базис взаимный с базисом r_k, то есть

Согласно (2.5) из (2.9) получим

Исключая в (2.10) функцию γ, будем иметь

Уравнение (2.11) совместно с уравнением (2.1) служат для нахождения деформированного состояния, а уравнение (2.10) совместно с выражением (2.5) или (2.4) используются для нахождения напряженного состояния. Эти уравнения дополняются силовыми и кинематическими граничными условиями. Для нахождения температурного поля используется уравнение (2.8) так же дополненное граничными условиями.

3. Приложение предложенной модели к случаю неоднородного температурного поля и неоднородного напряженно-деформированного состояния. Рассматривается свободное тепловое расширение цилиндрической эластомерной втулки, подвергнутой на внутренней и внешней боковых поверхностях действию уравновешенной системы продольных сдвигающих сил с модулем $Q$. На внутренней боковой поверхности поддерживается температура ${{T}_{1}}$, а на внешней ${{T}_{2}}$. Через ${{R}_{1}}$ и ${{R}_{2}}$ обозначаются внутренний и внешний радиусы втулки, а через $H$ ее длина. В чисто механической постановке в рамках геометрической нелинейности эта задача решалась в [18], а в нелинейной постановке с потенциалом Муни–Ривлина в [20].

3.1. Постановка задачи в рамках полуобратного метода. Материальная система координат выбрана совпадающей в отсчетной конфигурации с цилиндрической системой $\left( {R,\Phi ,Z} \right)$, причем ось $OZ$ совпадает с осью симметрии втулки. Втулка считается достаточно длинной, чтобы пренебречь торцевыми эффектами и считать напряженно-деформированное состояние независящим от $Z$. В этих условиях можно использовать кинематическую гипотезу коаксиальных сечений, то есть сечения цилиндрические и коаксиальные до деформации остаются таковыми и после деформации (ось единая для всех таких сечений совпадает с осью симметрии втулки). В цилиндрической системе координат в силу осевой симметрии вектор места в деформированной конфигурации задается соотношением

Здесь $w\left( R \right)$ и $f\left( R \right)$ подлежащие определению функции, $\left\{ {{{{\mathbf{e}}}_{R}},{{{\mathbf{e}}}_{\Phi }},{\mathbf{k}}} \right\}$ – единичный базис цилиндрической системы координат. Температурное поле так же полагается осесимметричным $\theta = \theta \left( R \right)$. Оператор Гамильтона материальной системы координат в отсчетной конфигурации записывается в форме

Тензор градиента вектора места по (3.1) и (3.2) получается в виде

Так, что условие несжимаемости $(J = \det \mathop \nabla \limits^0 {\mathbf{r}} = {{e}^{{3\alpha \theta \left( R \right)}}})$ принимает форму дифференциального уравнения

Штрих означает производную по R.

Решение краевой задачи с уравнением (2.8) в цилиндрической системе координат

известно и имеет вид

Используя это решение, получим

Подставим это выражение в (3.4) и решим его. Выбирая из двух решений положительное, получим

Здесь η – безразмерная константа интегрирования, в дальнейшем играющая роль параметра.

Используя (3.4) из (3.3) будем иметь

По этим выражениям вычисляются

Дальнейшее продвижение требует некоторых соглашений насчет удельной энергии деформации $W$. Имея ввиду учет влияния теплового расширения, будем считать в первом приближении, что удельная энергия деформации зависит от температуры неявно, только через главные инварианты тензора деформации B. В литературе описано множество конститутивных моделей (выражений для удельной энергии деформации) несжимаемого материала, зависящих как от одного, так и от двух главных инвариантов. В [19–21] показано, что более простые, конститутивные модели, не включающие зависимость от второго инварианта, не в состоянии охватить некоторые физические эффекты. Поэтому будем использовать модель, зависящую от двух инвариантов. Простейшей конститутивной моделью, зависящей от двух главных инвариантов, является модель Муни–Ривлина

Здесь $\mu $ – модуль сдвига линейной теории, отнесенный к отсчетной конфигурации, $\beta \in [ - 1,1]$ безразмерный коэффициент. Полагаем, что $p = 4\gamma {\text{/}}\mu $ является осесимметричным p = p(R). Используя (2.5), (3.7), (3.8) и (3.9) получим

Поскольку ${{{\mathbf{r}}}_{k}} = {\mathbf{F}} \cdot {{{\mathbf{R}}}_{k}}$, то используя (3.6), получим

Вычисляя сопряженный базис

будем иметь оператор Гамильтона в деформированной конфигурации

Здесь $r = f\left( R \right),$ $\varphi = \Phi ,$ $z = Z + w{\kern 1pt} '\left( R \right)$ координаты точек в деформированной конфигурации в цилиндрической системе координат. Теперь вычислим уравнение равновесия (2.10). Используя обозначения ${\mathbf{S}} = {{S}_{{RR}}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}}$ + ${{S}_{{\Phi \Phi }}}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} + {{S}_{{RZ}}}({{{\mathbf{e}}}_{R}}{\mathbf{k}} + {\mathbf{k}}{{{\mathbf{e}}}_{R}})$ + S_ZZkk, в компонентой форме будем иметь

Уравнение (2.11) приводится к виду

и является следствием (3.12).

Первый интеграл уравнения (3.12) записывается в форме

или

Константа интегрирования c находится из силовых граничных условий на боковой поверхности. Вектор единичной нормали к боковой поверхности не меняется в процессе деформации и совпадает с ${{{\mathbf{e}}}_{R}}$. Главный вектор на боковой поверхности получим, используя (3.10) и (3.14), в виде

То есть $c = Q{\text{/}}(\pi \mu H)$. Теперь имеем выражение для касательных напряжений

и уравнение для нахождения продольного смещения

Для предотвращения жесткого смещения втулки вдоль оси $OZ$ положим, что внутренняя боковая поверхность продольно не смещается, а смещается внешняя боковая поверхность. Тогда

В выражения (3.15)–(3.17) входит параметр $\eta $. Для его определения обратимся к плоской части напряженного состояния. Из (3.11) следует выражение

используя которое перепишем уравнение (3.13) в виде или

Из этого уравнения, получаем выражение для p

Здесь ${{p}_{0}}$ – константа интегрирования. Для нахождения η и ${{p}_{0}}$ служат уравнения, полученные из силовых граничных условий на боковой поверхности

Перейдем к безразмерным величинам, переменным и параметрам.

Здесь $\Delta $ – продольное смещение внешней боковой поверхности втулки относительно внутренней. Используя эти соотношения и выражения (3.17), (3.18), получим

Из (3.20) имеем

Уравнения (3.19) для определения ${{p}_{0}}$ и $\eta $ получаются в форме

Таким образом, напряженно-деформированное состояние полностью определено. Относительные продольное и радиальное смещения, а так же зависимость продольного смещения внешней обоймы от приложенной нагрузки (жесткостная характеристика) имеют вид

Относительные касательное, радиальное и тангенциальное напряжения записываются в форме

3.2. Вычисления. В качестве значения коэффициента линейного расширения для эластомеров примем $\alpha = 2 \times {{10}^{{ - 4}}}$°C [22]. Недеформированной конфигурации соответствует однородная температура ${{T}_{0}} = 293$ К. Значение разностной температуры на внутренней поверхности ${{\theta }_{1}} = {{T}_{1}} - {{T}_{0}}$ возьмем равным нулю. Значение разностной температуры на внешней поверхности ${{\theta }_{2}} = {{T}_{2}} - {{T}_{0}}$ возьмем равным 60°С. Отсутствию дополнительного температурного поля соответствует разностная температура на внешней поверхности ${{\theta }_{2}} = 0$°С.

Следует отметить влияние параметра $\beta $. При $\beta = 1$ потенциал энергии деформации Муни–Ривлина переходит в потенциал Трелоара $W = 0.5\,\mu \left( {{{I}_{1}} - 3} \right)$, зависящий только от первого инварианта. Для такой модели материала при θ = 0 поля напряжений и перемещений в поперечной плоскости не выявляются, и напряженно-деформированное состояние является антиплоским. С ростом $\theta $ проявляются поля напряжений и перемещений в поперечной плоскости, связанные с тепловым расширением, и напряженно-деформированное состояние является цилиндрическим (то есть комплексом из плоской и антиплоской деформации [21]). С уменьшением $\beta $ от 1 до –1 появляется зависимость от ${{I}_{2}}$ и при $\beta = - 1$ потенциал энергии деформации зависит только от ${{I}_{2}}$. Поля напряжений и перемещений в поперечной плоскости проявляются даже при θ = 0, то есть поле в поперечной плоскости порождается продольным сдвигом, и плоская и антиплоская составляющие цилиндрической деформации связаны. Рост температуры усиливает этот эффект.

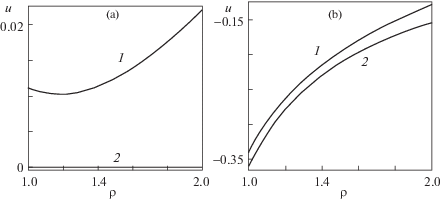
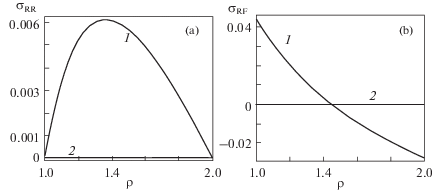
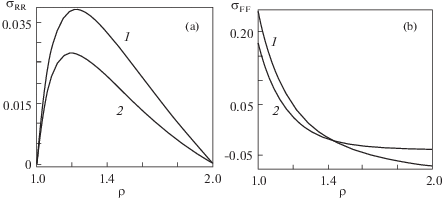
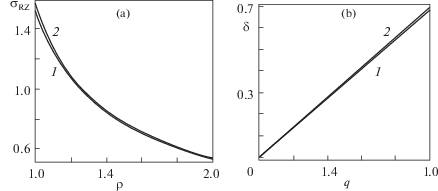
Для $[q = 1,\kappa = 2]$ на рис. 1 представлено удельное радиальное смещение $u = \upsilon \left( \rho \right) - \rho $ для $\beta = 1$ (а) и $\beta = - 0.95$ (b). Кривая 1 соответствует θ = 60°C, а кривая 2 – θ = 0°C. Для $[q = 1,\beta = 1,\kappa = 2]$ на рис. 2 представлены распределения относительных радиальных (а) и тангенциальных (b) напряжений. Кривая 1 соответствует θ = 60°C, а кривая 2 – θ = 0°C Для $[q = 1,\beta = - 0.95,\kappa = 2]$ на рис. 3 представлены распределения относительных радиальных (а) и тангенциальных (b) напряжений. Кривая 1 соответствует θ = 60°С, а кривая 2 – θ = 0°С. На рис. 4 представлены распределения касательного напряжения сдвига для $[q = 1,\beta = - 0.95,\kappa = 2]$ (а) и кривые жесткости для $[\beta = - 0.95$, κ = 2] (b). Кривая 1 соответствует θ = 60°С, а кривая 2 – θ = 0°С.

4. Заключение. Предложена модификация постановки задачи статики однородного изотропного несжимаемого материала при конечных деформациях, учитывающая тепловое расширение. Рассмотрено влияние теплового расширения в неоднородном стационарном температурном поле на неоднородное напряженно-деформированное состояние тела на примере цилиндрической втулки, подвергнутой конечному продольному сдвигу. Исследовано влияние неоднородного поля температур на напряженно-деформированное состояние в поперечной плоскости, порожденное как конечным продольным сдвигом, так и тепловым расширением.