Химическая физика, 2023, T. 42, № 4, стр. 31-46
Ударное уширение спектральных линий при медленных атомных столкновениях
С. Я. Уманский 1, *, С. О. Адамсон 1, А. С. Ветчинкин 1, М. А. Деминский 2, О. А. Ольхов 1, Ю. А. Чайкина 1, А. И. Шушин 1, М. Г. Голубков 1
1 Федеральный исследовательский центр химической физики им. Н.Н. Семёнова Российской академии наук
Москва, Россия
2 ООО “Кинтех Лаб”
Москва, Россия
* E-mail: unan43@mail.ru
Поступила в редакцию 04.10.2022
После доработки 10.11.2022
Принята к публикации 21.11.2022
- EDN: MXJCSX
- DOI: 10.31857/S0207401X23040143
Аннотация
В настоящее время большое внимание исследователей уделяется многоуровневому моделированию сложных газофазных физико-химических процессов, протекающих в атмосфере, при горении и в плазмохимических установках. Одним из важнейших микроскопических процессов, определяющих перенос излучения в указанных системах, является уширение спектральных линий при столкновениях излучающих атомов с атомами в основном состоянии. В данной работе предложена формулировка единой франк-кондоновской теории уширения спектральных линий в газах в терминах теории медленных атомных столкновений и неадиабатических переходов. Это позволяет по виду адиабатических потенциальных кривых сталкивающихся атомов выбирать наиболее эффективные каналы приводящих к уширению столкновений и на этой основе применять достаточно простые модели, разработанные в теории неадиабатических переходов. В качестве примера использования такого подхода проведены расчеты центра и крыльев контура спектральной линии излучения Ar(3P1) → Ar(1S0) возбужденных атомов аргона в собственном газе.
1. ВВЕДЕНИЕ
В последнее время все больший интерес привлекает многоуровневое теоретическое моделирование сложных газофазных физико-химических процессов, протекающих в атмосфере, при горении и в плазмохимических приборах [1–9]. Оно позволяет существенно ускорить и удешевить разработку и практическую реализацию диагностических схем и технологических установок. Это моделирование включает:
1) построение схемы микроскопических процессов (химических реакций, процессов ионизации и передачи энергии при столкновениях, излучения и поглощения света, уширения спектральных линий);
2) квантовохимические расчеты взаимодействий атомов и молекул между собой и с электронами и фотонами;
3) расчеты сечений и констант скорости этих процессов;
4) решение задачи о макроскопической эволюции плазмохимической системы при заданных внешних воздействиях (например, внешнее электрическое поле) и геометрических параметрах системы.
Важнейшим микроскопическим процессом в плазмохимической системе является уширение спектральных линий при столкновениях излучающих атомов с входящими в систему атомами в основном состоянии. Теория уширения спектральных линий при столкновениях между тяжелыми частицами весьма сложна. Это утверждение справедливо даже для низких плотностей газа, когда можно учитывать только парные соударения. В этом простейшем случае существуют различные теоретические подходы, модели и приближения. Для установления соотношений между ними были предприняты значительные усилия [10–17].
В настоящее время можно считать, что только единая франк-кондоновская теория (ЕФКТ) уширения спектральных линий при не очень высоких давлениях прошла достаточно надежную практическую проверку и стала общепринятой [18–25]. Эта теория единым образом описывает и ударный центр линии, и ее крылья, определяемые так называемым статистическим механизмом. Последний термин имеет историческое происхождение и обязан ранним приближенным подходом к расчету крыльев линии [10]. Следует отметить, что ЕФКТ получила дополнительное обоснование в рамках формализма, использующего тетрадный оператор рассеяния [26–28]. Этот формализм применим для описания процессов рассеяния и релаксации с участием микроскопических систем как в стационарных состояниях, описываемых волновыми функциями, так и в нестационарных состояниях, описываемых матрицей плотности.
Ударный центр линии традиционно описывается лоренцевским контуром. При этом его ширина определяется параметрами, характеризующими силу взаимодействия между сталкивающимися атомами при больших межъядерных расстояниях. Подробное обсуждение способов оценки этих параметров с явным учетом вырождения излучающего состояния можно найти в работах [29, 30].
Характеристики крыльев спектральных линий определяются межатомными взаимодействиями на межъядерных расстояниях порядка “радиуса” атома, где поведение потенциальных кривых может быть достаточно сложным. Оно описывается набором параметров, характеризующих электронные состояния излучающих атомов и атомов среды. Поэтому возможны различные варианты поведения крыльев спектральных линий. В работах [29, 30] было проведено качественное обсуждение этого вопроса в рамках полуклассического приближения и даны некоторые оценки, касающиеся значений отклонений частот излучения от центра линии, при которых начинается резкое уменьшение интенсивности излучения. В данной работе обсуждается связь этих оценок с характером электронных состояний излучающих атомов квазимолекулы.
Цель данного исследования состоит в формулировке ЕФКТ уширения линии в терминах хорошо развитой квазиклассической теории неадиабатических переходов при медленных атомных столкновениях [31, 32]. Такая формулировка позволяет по виду потенциалов взаимодействия атомов определить характерные области межъядерных расстояний, вносящих основной вклад в константу скорости уширения линии, и без трудоемких расчетов выделить наиболее важные каналы процесса. В качестве иллюстрации рассмотрен процесс уширения линий излучения Ar в собственном газе.
2. КОНТУР СПЕКТРАЛЬНОЙ ЛИНИИ В РАМКАХ ЕФКТ
Во всех последующих рассуждениях предполагается, что физические условия (плотность газа и температура) таковы, что можно пренебречь радиационным и доплеровским механизмами уширения спектральных линий. Условия, при которых эти механизмы могут быть существенны, подробно обсуждаются в работе [10]. В общих формулах далее, если не оговорено особо, используется система единиц СГС.
2.1. Предположения, на которых основывается ЕФКТ
Основная идея ЕФКТ заключается в том, что ударный контур линии излучения определяется частотным распределением вероятностей спонтанных свободно-свободных радиационных переходов при столкновениях излучающего атома с атомами среды. Переходы происходят в газовой системе S, состоящей из излучающих атомов A* и инертных атомов X. В частном случае атом X может быть самим атомом A в основном состоянии.
Эта теория базируется на следующих предположениях:
1. Поступательные степени свободы газовой системы S находятся в термодинамическом равновесии с температурой T. Это равновесие поддерживается столкновениями между составляющими систему S атомами.
2. Важны только парные соударения.
Для справедливости второго предположения необходимо, чтобы время ${{\tau }_{{coll}}}$ нахождения атомов A* и X в области их сильного взаимодействия при столкновении было много меньше времени ${{\tau }_{{gk}}}$ между столкновениями пары атомов A* и X, находящихся в этой области с другими атомами X. Столкновениями с другими атомами А* можно пренебречь вследствие их малой концентрации. Когда газ находится в термических условиях,
(1)
${{\tau }_{{coll}}} \approx {{10}^{{ - 13}}}{{L}_{{coll}}}{{\left( {\frac{\mu }{T}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$(2)
${{\tau }_{{gk}}} \approx {{10}^{{ - 11}}}\frac{{{{{\left( {{{\mu }_{{AX,X}}}T} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{pL_{{coll}}^{2}}}.$3. Вырожденные состояния излучающих атомов A* заселены равновероятно.
Это предположение основывается на том, что при не слишком низких давлениях газа характерные времена между столкновениями атома A* с атомами X, приводящими к переходам между вырожденными состояниями, существенно меньше характерных излучательных времен жизни A*.
4. Переходы между различными участвующими в радиационном переходе адиабатическими электронными состояниями квазимолекулы, обусловленные относительным движением атомов, можно не учитывать.
Влияние неадиабатических эффектов ранее довольно активно обсуждалось в литературе [33–36]. В отличие от предположений 1 и 2 проведенные исследования показали, что нельзя дать какого-либо общего критерия обоснованности пренебрежения неадиабатическими эффектами. Однако детальные расчеты столкновительного уширения спектральных линий для ряда конкретных систем с явным учетом этих эффектов показали, что они практически не влияют на форму контура спектральных линий в процессах излучения. При этом оказывается, что индуцированные столкновениями переходы между компонентами тонкой структуры и деполяризация являются существенными при поглощении поляризованного света [31, 32].
5. Полное излучение практически полностью определяется лоренцевским ударным центром. Детальное обсуждение этого предположения можно найти в работе [10].
2.2. Адиабатические электронные состояния и потенциальные кривые квазимолекул
Как следует из сказанного выше, для практического применения ЕФКТ прежде всего необходима информация об адиабатических электронных состояниях и потенциальных кривых квазимолекулы AX.
Изолированный возбужденный атом A* в начальном состоянии $\left| i \right\rangle $ c энергией ${{\varepsilon }_{i}}$ в результате дипольного взаимодействия с вакуумом электромагнитного поля переходит из этого состояния в конечное состояние $\left| f \right\rangle $ с энергией ${{\varepsilon }_{f}} < {{\varepsilon }_{i}}.$ За нуль отсчета энергии атома A* принимается энергия его основного состояния. Здесь i и f – наборы квантовых чисел, характеризующих начальное и конечное состояния атома. Уровни энергии ${{\varepsilon }_{i}}$ и ${{\varepsilon }_{f}},$ вообще говоря, вырождены. Кратности вырождения ${{g}_{i}}$ и ${{g}_{f}}$ определяются соответствующими квантовыми числами полного углового момента ${{j}_{i}}$ и ${{j}_{f}}{\text{:}}$ ${{g}_{i}} = 2{{j}_{i}} + 1,$ ${{g}_{f}} = 2{{j}_{f}} + 1.$ В дальнейшем для простоты будем предполагать, что ${{j}_{f}} = 0.$ В процессе этого перехода происходит излучение фотона с циклической частотой ${{\omega }_{{if}}} = {{{{\varepsilon }_{i}} - {{\varepsilon }_{f}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{i}} - {{\varepsilon }_{f}}} \hbar }} \right. \kern-0em} \hbar }$ в оптической или ультрафиолетовой областях спектра.
Атом A* взаимодействует с атомом X, находящимся в невырожденном состоянии $\left| g \right\rangle ,$ энергия которого принимается за нуль отсчета. Это приводит к возникновению набора адиабатических электронных волновых функций ${{\Psi }_{{i{\kern 1pt} \alpha }}}({{{\mathbf{r}}}_{{el}}},R)$ и ${{\Psi }_{f}}({{{\mathbf{r}}}_{{el}}},R),$ коррелирующих при межъядерном расстоянии $R \to \infty $ c электронными состояниями $\left| i \right\rangle \times \left| g \right\rangle $ и $\left| f \right\rangle \times \left| g \right\rangle $ пары невзаимодействующих атомов A* и X. Здесь ${{{\mathbf{r}}}_{{el}}}$ – совокупность координат электронов квазимолекулы A*X. Набор квантовых чисел α характеризует адиабатические электронные состояния квазимолекулы A*X, коррелирующие с состояниями $\left| i \right\rangle \times \left| g \right\rangle .$ В этот набор входит Ω – абсолютное значение проекции полного электронного углового момента квазимолекулы на ее ось. Если Ω > 0, то соответствующее адиабатические электронные состояния квазимолекулы двукратно вырождены, а если Ω = 0, то это состояние невырождено. Подробное описание правил корреляции адиабатических электронных состояний с состояниями разделенных атомов можно найти в работе [32]. Адиабатическим электронным состояниям с волновыми функциями ${{\Psi }_{{i{\kern 1pt} \alpha }}}({{{\mathbf{r}}}_{{el}}},R)$ и ${{\Psi }_{f}}({{{\mathbf{r}}}_{{el}}},R)$ отвечают потенциальные кривые ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ и ${{U}_{f}}(R),$ которые в дальнейшем удобно представить в следующем виде:
(3)
${{U}_{{i\alpha }}}(R) = {{u}_{{i{\kern 1pt} \alpha }}}(R) + {{\varepsilon }_{i}},\,\,\,\,{{U}_{f}}(R) = {{u}_{f}}(R) + {{\varepsilon }_{f}},$Адиабатические потенциальные кривые могут быть двух типов (см. рис. 1):
Рис. 1.
Характерные потенциальные кривые и схема формирования крыльев спектра излучения: а – красное крыло, б – голубое крыло.
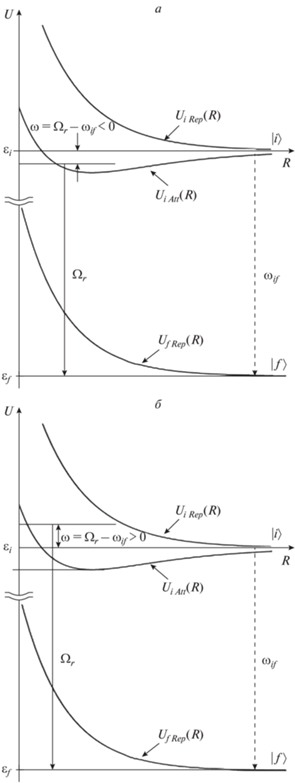
1. притягивающая потенциальная кривая ${{U}_{{i{\kern 1pt} Att}}}(R).$ При $R = {{R}_{{Att}}} \approx 1$ Ǻ на этой кривой есть потенциальная яма с глубиной, существенно превышающей глубину ван-дер-ваальсовой потенциальной ямы, присутствующей, например, в случае взаимодействия атомов инертных газов.
2. отталкивательная потенциальная кривая (кривые ${{U}_{{i{\kern 1pt} Rep}}}\left( R \right)$ и ${{U}_{{f{\kern 1pt} Rep}}}\left( R \right)$ на рис. 1). Потенциальные кривые ${{U}_{f}}(R)$ в случае атома X в невырожденном основном состоянии имеют, как правило, отталкивательный
характер. В случае, когда атомы A и X различны, при межъядерных расстояниях, существенно
превышающих их размеры, всегда имеет место притягивающее  ${{R}^{{ - 6}}}$ дисперсионное взаимодействие. Если атом X – это атом A в основном состоянии, то между
атомами X и A* имеет место
${{R}^{{ - 6}}}$ дисперсионное взаимодействие. Если атом X – это атом A в основном состоянии, то между
атомами X и A* имеет место  ${{R}^{{ - 3}}}$ диполь-дипольное взаимодействие. Подробное обсуждение характера потенциальных кривых
двухатомных квазимолекул можно найти в работе [32].
${{R}^{{ - 3}}}$ диполь-дипольное взаимодействие. Подробное обсуждение характера потенциальных кривых
двухатомных квазимолекул можно найти в работе [32].
2.3. Общее выражение для контура спектральной линии в рамках ЕФКТ
С учетом предположений, выдвинутых в п.2.1, выражение для контура линии перехода ${{F}_{{if}}}(\omega ,t)$ в ЕФКТ [18–25] можно представить в следующем виде:
(4)
${{F}_{{if}}}(\omega ,T) = \frac{1}{\pi }\frac{{{{Q}_{{if}}}(\omega ,T)}}{{{{\omega }^{2}} + {{Q}_{{if}}}{{{(0,T)}}^{2}}}},$(5)
${{Q}_{{if}}}(\omega ,T) = {{n}_{\operatorname{X} }}\sum\limits_\alpha {G(i\alpha \to f){{K}_{{i{\kern 1pt} \alpha \to f}}}} (\omega ,T),$(6)
${{K}_{{i{\kern 1pt} \alpha \to f}}}(\omega ,T) = \left\langle w \right\rangle \int\limits_0^\infty {\frac{{{{e}_{i}}{\kern 1pt} d{{e}_{i}}}}{{{{{({{k}_{B}}T)}}^{2}}}}} \exp {\kern 1pt} \left( { - \frac{{{{e}_{i}}}}{{{{k}_{B}}T}}} \right){{\sigma }_{{i{\kern 1pt} \alpha \to f}}}(\omega ,{{e}_{i}}),$Определяющая контур линии функция ${{Q}_{{if}}}(\omega ,t)$ может быть интерпретирована как полная скорость свободно-свободных радиационных переходов на частоте $\Omega {{{\kern 1pt} }_{r}}\,\, = {{\omega }_{{if}}} + \omega $ при столкновениях излучающего атома с атомами среды. Входящая в выражение (5) для ${{Q}_{{if}}}(\omega ,t)$ величина $G(i\alpha \to f)$ – статистический вес, который приписывается каждой паре потенциальных кривых ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ и ${{U}_{f}}(R).$ Явное выражение для $G(i\alpha \to f)$ выводится с использованием приведенных выше предположений 3 и 4 и имеет следующий вид:
Здесь $N(i \to f)$ – полное число разрешенных дипольных переходов из состояний свободного атома A c энергией ${{\varepsilon }_{i}}$ в состояние с энергией ${{\varepsilon }_{f}}$ в свободном атоме A, а $N{{(i\alpha \to f)}_{{\operatorname{AX} }}}$ – число разрешенных дипольных переходов с Ω = 0, ±1 между адиабатическими электронными состояниями квазимолекулы c потенциальными кривыми ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ и ${{U}_{f}}(R).$В газовой системе S атомы A* излучают в широком спектре частот ${{\Omega }_{r}}.$ Ту часть спектра, в которой $\omega = \Omega {{{\kern 1pt} }_{r}}\, - {{\omega }_{{{\kern 1pt} if}}} < 0,$ называют красным крылом спектральной линии, а где $\omega = \Omega {{{\kern 1pt} }_{r}}\, - {{\omega }_{{if}}} > 0$ – голубым (см. рис. 1). Согласно закону сохранения энергии излучение с частотой ${{\Omega }_{r}},$ отличающейся от частоты излучения ${{\omega }_{{if}}}$ изолированного атома A*, может иметь место, только если в процессе излучения происходит обмен энергией между электронными и ядерными степенями свободы при столкновениях атома A* с атомами среды X. В свою очередь, эти степени свободы связаны между собой слабым взаимодействием с вакуумом электромагнитного поля. При этом следует отметить, что расчет константы скорости уширения ${{K}_{{i{\kern 1pt} \alpha \to f}}}(\omega ,T)$ сводится к расчету факторов Франка–Кондона в непрерывном спектре.
Развитый в работе [25] подход к расчету факторов Франка–Кондона позволяет сделать метод ЕФКТ физически наглядным, поскольку в рамках этого подхода сечение уширения ${{\sigma }_{{i{\kern 1pt} \alpha \to f}}}(\omega ,{{e}_{i}})$ и константа скорости уширения ${{K}_{{i{\kern 1pt} \alpha \to f}}}(\omega )$ совпадают с рассчитанными в первом порядке метода искаженных волн сечением и константой скорости неадиабатического перехода в модельной двухуровневой задаче рассеяния (см. [31, 32]).
Отвечающая этой задаче пара связанных радиальных уравнений имеет следующий вид:
(8)
$\begin{gathered} \left[ { - \frac{{{{\hbar }^{2}}}}{{2\mu }}\frac{{{{d}^{2}}}}{{d{{R}^{2}}}} + \frac{{{{\hbar }^{2}}\ell (\ell + 1)}}{{2\mu {{R}^{2}}}} + {{U}_{{i\alpha }}}(R) - {{e}_{i}}} \right]{{\Phi }_{{i\alpha }}}(R,\ell ) = \\ = - {{V}_{{i\alpha ,f}}}(R){{\Phi }_{f}}(R,\ell ), \\ \end{gathered} $(9)
$\begin{gathered} \left[ { - \frac{{{{\hbar }^{2}}}}{{2\mu }}\frac{{{{d}^{2}}}}{{d{{R}^{2}}}} + \frac{{{{\hbar }^{2}}\ell (\ell + 1)}}{{2\mu {{R}^{2}}}} + {{U}_{{f,\omega }}}(R) - {{e}_{i}}} \right]{{\Phi }_{f}}(R,\ell ) = \\ = - {{V}_{{f,i\alpha }}}(R){{\Phi }_{{i\alpha }}}(R,\ell ), \\ \end{gathered} $(10)
${{V}_{{i\alpha ,f}}}(R) = \frac{{{{D}_{{i\alpha ,f}}}(R)}}{{\sqrt 2 {{D}_{{i\alpha ,f}}}(\infty )}}\Delta {{U}_{{i\alpha ,f}}}(R),$(11)
${{D}_{{i\alpha ,f}}}(R) = \int {\Psi _{{i\alpha }}^{*}} ({{{\mathbf{r}}}_{{el}}},R){\mathbf{D}}{{\Psi }_{f}}({{{\mathbf{r}}}_{{el}}},R)d{{{\mathbf{r}}}_{{el}}},$Сечение уширения в (6) имеет вид
(14)
${{\sigma }_{{i{\kern 1pt} \alpha \to f}}}(\omega ,{{e}_{i}}) = \sum\limits_{\ell = 0}^\infty {\frac{{\pi (2\ell + 1)}}{{k_{i}^{2}}}} {{P}_{{i\alpha \to f}}}(\ell ,\omega ,{{e}_{i}}),$(15)
${{P}_{{i\alpha \to f}}}(\ell ,\omega ,{{e}_{i}}) = {{\left| {{{S}_{{i\alpha \to f}}}(\ell ,\omega ,{{e}_{i}})} \right|}^{2}}.$В первом порядке метода искаженных волн (см., например, [32])
(16)
$\begin{gathered} {{S}_{{i{\kern 1pt} \alpha \to f}}}(\ell ,\omega ,{{e}_{i}}) = \\ = \frac{4}{\hbar }\exp \left[ {i{{\delta }_{{i\alpha }}}({{e}_{i}},\ell ) + i{{\delta }_{f}}({{e}_{f}}({{e}_{i}},\omega ),\ell ) - i{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right] \times \,\,\,\, \\ \times \,\,\Theta \left[ {{{e}_{f}}({{e}_{{i\alpha }}},\omega )} \right]\int\limits_0^\infty {{{\varphi }_{{i{\kern 1pt} \alpha }}}(R,{{e}_{i}},\ell ){{V}_{{i\alpha ,f}}}(R){{\varphi }_{f}}(R,{{e}_{f}}({{e}_{i}},\omega )} ,\ell )dR. \\ \end{gathered} $(17)
$\Theta \left[ x \right] = \left\{ {\begin{array}{*{20}{c}} {1,}&{x \geqslant 0,} \\ {0,}&{x < 0.} \end{array}} \right.$Принадлежащие континууму радиальные волновые функции ${{\varphi }_{{i{\kern 1pt} a}}}(R,{{e}_{i}},\ell )$ и ${{\varphi }_{f}}(R,{{e}_{f}}({{e}_{i}},\omega ),\ell )$ относительного движения атомов A* и X в поле потенциалов ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ и ${{U}_{{f,\omega }}}(R)$ (см. (3), (13) и рис. 1) удовлетворяют уравнениям (8) и (9), в которых матричный элемент ${{V}_{{i{\kern 1pt} \alpha ,f}}}(R)$ связи между каналами положен равным нулю. Функции ${{\varphi }_{{i{\kern 1pt} a}}}(R,{{e}_{i}},\ell )$ и ${{\varphi }_{f}}(R,{{e}_{f}}({{e}_{i}},\omega ),\ell )$ нормированы следующим образом:
(18)
$\begin{gathered} {{\varphi }_{{i{\kern 1pt} \alpha }}}{{({{e}_{i}},\ell ,R)}_{{R \to \infty }}} \to \\ \to \,\,{{\left( {\frac{\mu }{{\hbar {{k}_{i}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sin \left\{ {{{k}_{i}}R - \frac{{\pi \ell }}{2} + {{\delta }_{{i{\kern 1pt} \alpha }}}({{e}_{i}},\ell )} \right\}, \\ \end{gathered} $(19)
$\begin{gathered} {{\varphi }_{f}}{{\left[ {{{e}_{f}}({{e}_{i}},\omega ),\ell ,R} \right]}_{{R \to \infty }}} \to \\ \to {{\left( {\frac{\mu }{{\hbar {{k}_{f}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sin \left\{ {{{k}_{f}}R - \frac{{\pi \ell }}{2} + {{\delta }_{f}}\left[ {{{e}_{f}}({{e}_{i}},\omega ),\ell } \right]} \right\}, \\ \end{gathered} $(20)
${{k}_{i}} = {{{{{\left( {2\mu {{e}_{i}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{\left( {2\mu {{e}_{i}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \hbar }} \right. \kern-0em} \hbar },\,\,\,\,{{k}_{f}} = {{{{{\left[ {2\mu {{e}_{f}}({{e}_{i}},\omega )} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{\left[ {2\mu {{e}_{f}}({{e}_{i}},\omega )} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \hbar }} \right. \kern-0em} \hbar }.$Если не рассматривать слишком низкие температуры, то вычисление ${{\sigma }_{{i{\kern 1pt} \alpha \to f}}}(\omega ,{{e}_{i}})$ можно существенно упростить. В этом случае столкновения между атомами газа происходят в квазиклассических условиях и в сумму (14) вносит вклад большое число волн, причем величина ${{\left| {{{S}_{{i\alpha \to f}}}(\ell ,\omega ,{{e}_{i}})} \right|}^{2}}$ плавно зависит от 𝓁. Поэтому ${{S}_{{i{\kern 1pt} \alpha \to f}}}(\ell ,\omega ,{{e}_{i}})$ и ${{P}_{{i\alpha \to f}}}(\ell ,\omega ,{{e}_{i}})$ можно заменить на ${{S}_{{i\alpha \to f}}}(b,\omega ,{{e}_{i}})$ и ${{P}_{{i\alpha \to f}}}(b,\omega ,{{e}_{i}}),$ где $b = {{(\ell + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})} \mathord{\left/ {\vphantom {{(\ell + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$ – прицельный параметр. Соответственно, суммирование по 𝓁 в (14) можно заменить интегрированием по b, т.е.
(21)
$\sum\limits_{\ell = 0}^\infty {\frac{{\pi (2\ell + 1)}}{{k_{i}^{2}}}} \to \int\limits_0^\infty {2\pi bdb} .$Этот вопрос подробно обсуждается в работах [31, 32]. Ниже всюду будет использоваться описанная замена.
Заканчивая обсуждение общей формулировки ЕФКТ, отметим следующее. Из выражения (4) следует, что ${{Q}_{{if}}}(0,T)$ имеет смысл полуширины $\Delta \omega _{{{{{\kern 1pt} {\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} {\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}$ лоренцевского центра спектрального контура (см., например, [10]). С другой стороны, в работах [25, 37] получены общие формулы для спектральной интенсивности спонтанного свободно-свободного излучения при парных столкновениях в рассматриваемой здесь газовой системе S при ${{\omega }^{2}} \gg {{Q}_{{if}}}{{(0,T)}^{2}}.$ Оказывается, что эта интенсивность пропорциональна $\frac{1}{\pi }\frac{{{{Q}_{{if}}}(\omega ,T)}}{{{{\omega }^{2}}}}$ (см. (4)), где ${{Q}_{{if}}}(\omega ,T)$ дается формулами (5), (6) и (14), и представляет собой крылья спектрального контура (4). Учитывая этот факт и предположение 5 можно интерпретировать основную формулу ЕФКТ (4) как интерполяцию между ударным лоренцевским центром спектрального контура и его крыльями.
3. КОНТУР СПЕКТРАЛЬНОЙ ЛИНИИ ИЗЛУЧЕНИЯ Ar(3P1) → Ar(1S0) В СОБСТВЕННОМ ГАЗЕ
3.1. Адиабатические электронные состояния, потенциальные кривые, дипольные моменты перехода
Излучающие атомы Ar(3P1) составляют малую примесь в газе, состоящем из атомов Ar(1S0) в основном состоянии. Уровни энергии Ar(3P1) и Ar(1S0) и характеристики радиационного перехода Ar(3P1) → Ar(1S0) приведены в табл. 1 [38]. Уширение линии этого перехода происходит в результате столкновений атома Ar(3P1) с атомами Ar(1S0).
Таблица 1.
Уровни энергии Ar и параметры радиационного перехода [38]
| Канал | Состояние | Энергия, см–1 | ${{\lambda }_{{{\kern 1pt} if}}}$, Å | $A{{{\kern 1pt} }_{{if}}}$, 108 с–1 |
|---|---|---|---|---|
| i | 3p54s(3P1) | 93 751 | 1067 | 1.32 |
| f | 3p6(1S0) | 0 |
Контур линии перехода определяется адиабатическими потенциальными кривыми, коррелирующими при $R \to \infty $ c уровнем энергии пар невзаимодействующих атомов Ar(1)(3P1) + Ar(2)(1S0) и Ar(1)(1S0) + Ar(2)(1S0); здесь Ar(1) и Ar(2) – разные атомы Ar. При сближении Ar(1)(3P1) и Ar(2)(1S0) формируются два оптически активных адиабатических электронных состояния. Это невырожденное нечетное эксимерное состояние $\left| {0_{u}^{ + }} \right\rangle $ с Ω = 0, обладающее довольно глубокой потенциальной ямой на соответствующей потенциальной кривой ${{U}_{{i0}}}(R)$ и двукратно вырожденное состояние $\left| {{{1}_{u}}} \right\rangle $ с Ω = 1, обладающее отталкивательной потенциальной кривой ${{U}_{{i1}}}(R).$ При сближении Ar(1)(1S0) с Ar(2)(1S0) возникает невырожденное четное состояние $\left| {0_{g}^{ + }} \right\rangle $ с отталкивательной потенциальной кривой ${{U}_{f}}(R).$
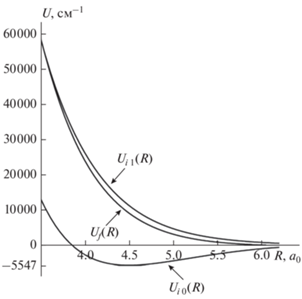
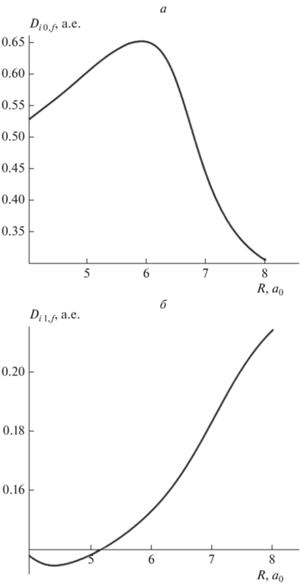
Потенциальные кривые ${{U}_{{i0}}}(R),$ ${{U}_{{i1}}}(R)$ и ${{U}_{f}}(R),$ а также дипольные матричные элементы ${{D}_{{i0,f}}}(R)$ и ${{D}_{{i1,f}}}(R)$ были рассчитаны ab initio с использованием квантовохимического пакета Firefly [39], который частично базируется на исходном коде GAMESS (US) [40]. Результаты этих расчетов приведены на рис. 2 и 3, где потенциальные кривые и дипольные матричные элементы относятся к той области межъядерных расстояний, которая определяет крылья спектрального контура. Из рис. 3 видно, что дипольные моменты перехода в этой области имеют сильную зависимость от R.
Как будет показано ниже, ударный центр контура определяется поведением потенциальных кривых ${{U}_{{i0}}}(R),$ ${{U}_{{i\,1}}}(R)$ и ${{U}_{f}}(R)$ при больших R (см. подробное обсуждение этого вопроса в [10]), где матричные элементы ${{D}_{{i0,f}}}(R)$ и ${{D}_{{i1,f}}}(R)$ с большой точностью можно считать независимыми от R и равными ${{D}_{{i0,f}}}(\infty )$ и ${{D}_{{i1,f}}}(\infty ).$ Последние же полностью определяются дипольным моментом перехода в свободном атоме Ar. Этими же дипольными моментами перехода определяется и диполь-дипольное взаимодействие $ \propto {{R}^{{ - 3}}},$ которое является основным при больших R в состояниях $0_{u}^{ + }\left( {{}^{3}{{P}_{1}}} \right)$ и ${{1}_{u}}\left( {{}^{3}{{P}_{1}}} \right).$
Дипольный момент перехода связан с приведенным в табл. 1 коэффициентом Эйнштейна ${{A}_{{if}}}$ соотношением
(22)
${{A}_{{{\kern 1pt} if}}} = \frac{{4{{\omega }_{{if}}}}}{{3\hbar {{c}^{3}}}}\frac{1}{{2{{j}_{i}} + 1}}{{\left| {\left\langle i \right|\left| {\mathbf{D}} \right|\left| f \right\rangle } \right|}^{2}},$При больших межъядерных расстояниях R нечетные электронные волновые функции квазимолекулы Ar2, отвечающие уровню энергии пары невзаимодействующих атомов Ar(1)(3P1) + Ar(2)(1S0), имеют следующий вид:
(23)
$\begin{gathered} \left| {0_{u}^{ + }} \right\rangle = \\ = \frac{1}{{\sqrt 2 }}\left[ {{{{\left| {{}^{3}{{P}_{{1,0}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(1)}}}}}}}}{{{\left| {{}^{1}{{S}_{{0,0}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(2)}}}}}}}} + {{{\left| {{}^{1}{{S}_{{0,0}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(1)}}}}}}}}{{{\left| {{}^{3}{{P}_{{1,0}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(2)}}}}}}}}} \right], \\ \end{gathered} $(24)
$\begin{gathered} \left| {{{1}_{u}}} \right\rangle = \\ = \frac{1}{{\sqrt 2 }}\left[ {{{{\left| {{}^{3}{{P}_{{1,1}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(1)}}}}}}}}{{{\left| {{}^{1}{{S}_{{0,0}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(2)}}}}}}}} + {{{\left| {{}^{1}{{S}_{{0,0}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(1)}}}}}}}}{{{\left| {{}^{3}{{P}_{{1,1}}}} \right\rangle }}_{{{\text{A}}{{{\text{r}}}^{{{\text{(2)}}}}}}}}} \right]. \\ \end{gathered} $В системе координат с осью z, направленной по межъядерной оси, оператор диполь-дипольного взаимодействия имеет вид [29, 32]
(25)
${{{\mathbf{V}}}_{{d - d}}} = - \frac{2}{{{{R}^{3}}}}\sum\limits_{q = - 1}^1 {\frac{1}{{(1 - q)!(1 + q)!}}{\mathbf{D}}_{q}^{{{\text{A}}{{{\text{r}}}^{{(1)}}}}}{\mathbf{D}}_{{ - q}}^{{{\text{A}}{{{\text{r}}}^{{(2)}}}}}} ,$(26)
$\begin{gathered} U_{{i0}}^{{(d - d)}}(R) = \left\langle {0_{u}^{ + }\left| {{{{\mathbf{V}}}_{{d - d}}}} \right|0_{u}^{ + }} \right\rangle = \\ = - \frac{2}{{3{{R}^{3}}}}{{\left| {\left\langle i \right|\left| {\mathbf{D}} \right|\left| f \right\rangle } \right|}^{2}} = \frac{{C_{{i0}}^{{(d - d)}}}}{{{{R}^{3}}}}, \\ \end{gathered} $(27)
$U_{{i1}}^{{(d - d)}}(R) = \left\langle {{{1}_{u}}\left| {{{{\mathbf{V}}}_{{d - d}}}} \right|{{1}_{u}}} \right\rangle = \frac{1}{{3{{R}^{3}}}}{{\left| {\left\langle i \right|\left| {\mathbf{D}} \right|\left| f \right\rangle } \right|}^{2}} = \frac{{C_{{i1}}^{{(d - d)}}}}{{{{R}^{3}}}}.$Подстановка приведенного выше значения ${{\left| {\left\langle i \right|\left| {\mathbf{D}} \right|\left| f \right\rangle } \right|}^{2}}$ дает, что
(28)
$C_{{i0}}^{{(d - d)}} = - 0.16\,{\text{а}}{\text{.е}}{\text{. и}}\,\,C_{{i1}}^{{(d - d)}} = 0.08\,\,{\text{а}}{\text{.е}}{\text{.}}$При получении выражений (26) и (27) использовались теорема Вигнера–Эккарта и определения приведенных матричных элементов в соответствии с изложенным в [10]. Согласно [41], потенциальная кривая ${{U}_{f}}(R)$ основного электронного состояния квазимолекулы Ar2 при больших межъядерных расстояниях имеет вид
где ${{C}_{{f,6}}}$ = 64.3 а.е.3.2. Лоренцевский центр контура спектральной линии излучения Ar(3P1) → Ar(X1S0) в собственном газе
Согласно изложенному в книге [10], лоренцевский центр контура спектральной линии излучения полностью определяется полушириной $\Delta \omega {\kern 1pt} _{{{{{\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}(T)$ и имеет вид
(30)
${{F}_{{if,L}}}(\omega ,T) = \frac{1}{\pi }\frac{{\Delta \omega _{{{{{\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}(T)}}{{{{\omega }^{2}} + {{{\left( {\Delta \omega _{{{{{\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}(T)} \right)}}^{2}}}},$При взаимодействии двух атомов Ar в основном состоянии формируется единственное основное $0_{g}^{ + }$-состояние квазимолекулы ${\text{A}}{{{\text{r}}}_{2}}.$ При взаимодействии атома Ar в основном состоянии с ${{j}_{f}} = 0$ с атомом Ar в возбужденном состоянии с ${{j}_{i}} = 1$ формируются невырожденное $0_{u}^{ + }$-состояние и двукратно вырожденное ${{1}_{u}}$-состояние квазимолекулы ${\text{Ar}}{{{\kern 1pt} }_{2}}$ (см. (23) и (24)), из которых разрешен дипольный переход в основное $0_{g}^{ + }$-состояние. Соответственно, $N(i0 \to f) = 1,$ $N(i1 \to f) = 2,$ и поэтому, согласно (7), имеем
(31)
$G(i0 \to f) = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},\,\,\,\,G(i1 \to f) = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}.$Принимая во внимание (5) и (31), для $\Delta \omega {\kern 1pt} _{{{{{\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}(T)$ получим следующее выражение:
(32)
$\Delta \omega _{{{{{\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}(T) = {{n}_{{{\text{Ar}}}}}\left( {\frac{1}{3}{{K}_{{i0 \to f}}}(0,T) + \frac{2}{3}{{K}_{{i1 \to f}}}(0,T)} \right).$Сравнение (30) с (4) показывает, что лоренцевский вид контура излучения является приближением в некоторой небольшой области $\delta {{\omega }_{L}}$ значений $\omega ,$ где ${{Q}_{{if}}}(\omega ,T) \approx {{Q}_{{if}}}(0,T).$ Очевидно, что в этой области энергия $\hbar \omega ,$ которая передается между электронными и ядерными степенями свободы, должна быть достаточно мала. Для того чтобы оценить $\delta {{\omega }_{L}},$ удобно перейти к полуклассическому описанию неупругого столкновения, описываемого двухуровневой моделью (8), (9), (14) и (15). В монографии [32] приведены подробности вывода уравнений неупругого рассеяния в полуклассическом приближении, в котором относительное движение атомов описывается единой классической траекторией в поле некоторого среднего потенциала ${{U}_{0}}(R).$ Отметим, что в теории атомных столкновений показано (см. [31, 32]), что процессы с малой передачей энергии между электронными и ядерными степенями свободы определяются большими прицельными параметрами b. Это означает, что ${{K}_{{i0 \to f}}}(\omega ,T)$ и ${{K}_{{i1 \to f}}}(\omega ,T)$ определяются потенциалами ${{U}_{{i0}}}(R),$ ${{U}_{{i1}}}(R)$ и ${{U}_{f}}(R)$ при больших $R.$ В такой ситуации выполняются следующие условия применимости полуклассического приближения:
1) движение в поле обоих потенциалов, ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ и ${{U}_{f}}(R),$ квазиклассично везде, кроме хорошо локализованных областей вблизи точек поворота;
2) траектории относительного движения в поле обоих потенциалов различаются мало. Это позволяет ввести единую классическую траекторию относительного движения для обоих потенциалов в классически разрешенной области в поле некоего среднего потенциала ${{U}_{0}}(R);$
3) вклад областей вблизи точек поворота в определяющие недиагональные элементы матрицы рассеяния ${{S}_{{i{\kern 1pt} \alpha \to f}}}(b,\omega ,{{e}_{i}})$ интегралы (см. (16)) несуществен.
При выполнении вышеприведенных условий
(33)
$\begin{gathered} \left| {{{S}_{{i\alpha \to f}}}(b,\omega ,{{e}_{i}})} \right| = \\ = \left| {\int\limits_0^\infty {\frac{{\sqrt 2 {{\Delta }}{{U}_{{i\alpha ,f}}}[R(t,b,{{e}_{i}})]}}{\hbar }\cos \left[ {\omega t - {{\eta }_{{i\alpha ,f}}}(t)} \right]dt} } \right|, \\ \end{gathered} $(34)
${{\eta }_{{i{\kern 1pt} \alpha ,f}}}(t,b,{{e}_{i}}) = \int\limits_0^t {\frac{{{{\Delta }}{{U}_{{i{\kern 1pt} \alpha ,f}}}[R(t{\kern 1pt} ',b,{{e}_{i}})]}}{\hbar }} dt{\kern 1pt} '.$В выражениях (33) и (34) начало отсчета времени t отвечает началу радиального движения с энергией ${{e}_{i}}$ и прицельным параметром b в поле ${{U}_{0}}(R)$ в точке поворота.
Учитывая, что
(35)
$\frac{{{{\Delta }}{{U}_{{i\alpha ,f}}}[R(t{\kern 1pt} ',b,{{e}_{i}})]}}{\hbar }dt{\kern 1pt} ' = d{{\eta }_{{i\alpha ,f}}},$(36)
$\left| {{{S}_{{i\alpha \to f}}}(b,0,{{e}_{i}})} \right| = \sqrt 2 \left| {\sin {{\eta }_{{i\alpha ,f}}}(\infty ,b,{{e}_{i}})} \right|.$С учетом выражений (6) и (14), константы скорости уширения даются выражением
(37)
$\begin{gathered} {{K}_{{i{\kern 1pt} \alpha \to f}}}(0,T) = \\ = 2\left\langle u \right\rangle \int\limits_0^\infty {\frac{{{{e}_{i}}d{{e}_{i}}}}{{{{{({{k}_{B}}{\kern 1pt} T)}}^{2}}}}\exp \left( { - \frac{{{{e}_{i}}}}{{{{k}_{B}}T}}} \right)} \int\limits_0^\infty {2\pi bdb{{{\sin }}^{2}}{{\eta }_{{i\alpha ,f}}}} (\infty ,b,{{e}_{i}}). \\ \end{gathered} $Оценки показывают, что в рассматриваемой задаче при температурах не ниже комнатной можно положить ${{U}_{0}}(R) = 0$ и считать единую траекторию относительного движения прямолинейной, т.е.
(38)
${{R}_{{str}}}(t,b,{{e}_{i}}) = {{\left( {{{b}^{2}} + \frac{{2{{e}_{i}}}}{\mu }{{t}^{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$В качестве потенциалов ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ в (33) следует использовать потенциалы (26) и (27), обусловленные диполь-дипольным взаимодействием, а в качестве ${{U}_{f}}(R)$ – дисперсионное взаимодействие. Простая оценка относительной роли этих взаимодействий получается в терминах радиусов Вайскопфа [10]:
(39)
$R{{{\kern 1pt} }_{{3W,i{\kern 1pt} \alpha }}} = {{\left( {\frac{{2\left| {C_{{i1}}^{{(d - d)}}} \right|}}{{\hbar \left\langle w \right\rangle }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$(40)
${{R}_{{{\kern 1pt} 6W,{\kern 1pt} f}}} = {{\left( {\frac{{3\pi {{C}_{{f,6}}}}}{{8\hbar \left\langle w \right\rangle }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}}}}$Расчеты по формулам (5), (26), (27), (32)–34), (37), (38) показывают, что при ${{\Delta }}{{U}_{{i\alpha ,f}}}(R) \propto \frac{1}{{{{R}^{3}}}}$ величина $\Delta \omega _{{{{{\kern 1pt} {\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} {\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}$ не зависит от T, и дают для нее выражение
(41)
$\Delta \omega _{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{(imp)}} = \frac{{{{\pi }^{2}}}}{{3\hbar }}\left( {\left| {C_{{i0}}^{{(d - d)}}} \right| + 2\left| {C_{{i1}}^{{(d - d)}}} \right|} \right){{n}_{{\operatorname{Ar} }}} = \Gamma {{n}_{{\operatorname{Ar} }}}.$Подстановка приведенных выше значений $C_{{i0}}^{{{\kern 1pt} (d - d)}}$ и $C_{{i1}}^{{{\kern 1pt} (d - d)}}$ дает $\Gamma = 3.4 \cdot {{10}^{{ - 20}}}$ см–1 · см3.
Оценим теперь область $\delta {{\omega }_{L}},$ в которой применима формула (30). Оценка основывается на том факте, что функция $\left| {{{S}_{{i\alpha \to f}}}(b,\omega ,{{e}_{i}})} \right|,$ определенная в (33), является интегралом суммы произведений гладких функций времени
Для оценки $\xi (\omega ,b,{{e}_{i}})$ в термических условиях естественно взять $\tau (b,{{e}_{i}}) = {{R{{{\kern 1pt} }_{{3W,i{\kern 1pt} \alpha }}}} \mathord{\left/ {\vphantom {{R{{{\kern 1pt} }_{{3W,i{\kern 1pt} \alpha }}}} {\left\langle w \right\rangle }}} \right. \kern-0em} {\left\langle w \right\rangle }}.$
Лоренцевский центр контура отвечает достаточно малым значениям |ω|, при которых
Соответственно, формула (30) применима при
(44)
$\left| \omega \right| < {{\left\langle w \right\rangle } \mathord{\left/ {\vphantom {{\left\langle w \right\rangle } {{{R}_{{3W,i\alpha }}}}}} \right. \kern-0em} {{{R}_{{3W,i\alpha }}}}}.$Подстановка в выражение (42) приведенных выше значений $C_{{i0}}^{{(d - d)}},$ $C_{{i1}}^{{(d - d)}}$ и характерных значений температуры газа показывает, что |ω| принимает значение в несколько см–1. При этом в области частот, где допустимо описание контура линии формулой (30), сосредоточено более половины полного излучения.
3.3. Дальние крылья контура спектральной линии излучения Ar(3P1) → Ar(1S0) в собственном газе
Из приведенных выше оценок следует, что уже при |ω|, превышающем 10 см–1, формула (30) неприменима для описания контура рассматриваемой спектральной линии. При этом в довольно
широкой области роста |ω| основной вклад в константу скорости уширения вносят достаточно
большие прицельные параметры (и, соответственно, межъядерные расстояния), при которых
потенциалы ${{U}_{{i{\kern 1pt} 0}}}(R)$  $\frac{1}{{{{R}^{3}}}}$ и ${{U}_{{i{\kern 1pt} 1}}}(R)$
$\frac{1}{{{{R}^{3}}}}$ и ${{U}_{{i{\kern 1pt} 1}}}(R)$  $\frac{1}{{{{R}^{3}}}}.$ В этой области значений |ω| ЕФКТ дает аналитическое описание как квазистатического
(статистического) крыла линии [10, 17, 23], так и антистатического крыла [17, 23]. Однако рассматриваемая здесь линия излучения Ar обладает очень высокой интенсивностью.
Поэтому в плазмохимических системах высокого давления (${{p}_{{{\text{Ar}}}}} \geqslant 1$ атм) крылья этой линии вносят заметный вклад в непрерывный спектр излучения системы
даже при очень больших значениях |ω|. Экспериментальное исследование далеких крыльев
спектральных линий весьма затруднительно. В то же время информация о них представляет
большой интерес при моделировании мощных непрерывных источников света, в которых используется
поддерживаемая лазером плазма инертных газов [43, 44].
$\frac{1}{{{{R}^{3}}}}.$ В этой области значений |ω| ЕФКТ дает аналитическое описание как квазистатического
(статистического) крыла линии [10, 17, 23], так и антистатического крыла [17, 23]. Однако рассматриваемая здесь линия излучения Ar обладает очень высокой интенсивностью.
Поэтому в плазмохимических системах высокого давления (${{p}_{{{\text{Ar}}}}} \geqslant 1$ атм) крылья этой линии вносят заметный вклад в непрерывный спектр излучения системы
даже при очень больших значениях |ω|. Экспериментальное исследование далеких крыльев
спектральных линий весьма затруднительно. В то же время информация о них представляет
большой интерес при моделировании мощных непрерывных источников света, в которых используется
поддерживаемая лазером плазма инертных газов [43, 44].
3.3.1. Метод модифицированного волнового числа для крыльев контура линии излучения
Рассмотренный выше лоренцевский центр контура спектральной линии полностью определяется его полушириной $\Delta \omega _{{{{{\kern 1pt} {\kern 1pt} 1} \mathord{\left/ {\vphantom {{{\kern 1pt} {\kern 1pt} 1} 2}} \right. \kern-0em} 2}}}^{{(imp)}}$ (см. (30)). Во всех практически интересных ситуациях $\hbar {\kern 1pt} \Delta \omega _{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{(imp)}} \ll {{k}_{B}}T.$ Поэтому он определяется большими межъядерными расстояниями, и при расчете можно считать, что относительное движение атомов происходит по единой классической прямолинейной траектории (см. (38)). Для дальних крыльев спектральной линии $\hbar \left| \omega \right| \geqslant {{k}_{B}}T.$ Как показано в теории атомных столкновений [31, 32], неадиабатические переходы при таких дефектах резонанса определяются межъядерными расстояниями R порядка атомного радиуса. В этом случае потенциальные кривые ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ и ${{U}_{{f}}}(R)$ различаются сильно, поэтому при рассмотрении относительного движения атомов в поле этих потенциалов, вообще говоря, необходимо учитывать квантовые эффекты.
Указанные обстоятельства усложняют расчет крыльев спектральных линий. Однако при межатомных расстояниях порядка атомных размеров центробежный потенциал ${{{{e}_{i}}{{b}^{2}}} \mathord{\left/ {\vphantom {{{{e}_{i}}{{b}^{2}}} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$ зависит от R гораздо слабее, чем ${{U}_{{i{\kern 1pt} \alpha }}}(R),$ ${{U}_{f}}(R)$ и ${{V}_{{i\alpha ,f}}}(R).$ В работе [45] было предложено учесть это обстоятельство, заменив центробежный потенциал на постоянную величину ${{{{e}_{i}}{{b}^{2}}} \mathord{\left/ {\vphantom {{{{e}_{i}}{{b}^{2}}} {R_{0}^{2}}}} \right. \kern-0em} {R_{0}^{2}}},$ где ${{R}_{0}}$ – некоторое среднее межъядерное расстояние, отвечающее максимуму неадиабатической связи. Для достаточно сильно зависящих от R взаимодействий результат расчета слабо зависит от ${{R}_{0}}.$ Конкретный пример такого выбора будет приведен ниже, а подробное обсуждение приближения модифицированного волнового числа (МВЧ) можно найти в монографии [46].
После указанной выше замены уравнения рассеяния принимают вид уравнений (8) и (9) с $\ell = b = 0$ и модифицированной кинетической энергией
Аналогичная замена проводится в асимптотических выражениях (18) и (19) для волновых функций с $\ell = b = 0$ непрерывного спектра, входящих в выражение (16) для недиагонального элемента амплитуды рассеяния. Соответственно, в приближении МВЧ вероятность перехода имеет вид
(46)
$P_{{i\alpha \to f}}^{{{\kern 1pt} {\text{МВЧ}}}}(\omega ,{{e}_{{Ri}}}) = {{\left| {S_{{i\alpha \to f}}^{{{\kern 1pt} {\text{МВЧ}}}}(\omega ,{{e}_{{Ri}}})} \right|}^{2}},$(47)
$S_{{i{\kern 1pt} \alpha \to f}}^{{{\kern 1pt} {\text{МВЧ}}}}(\omega ,{{e}_{{Ri}}}) = {{S}_{{i\alpha \to f}}}(0,\omega ,{{e}_{{Ri}}}).$В приближении МВЧ интегрирование по b в выражении для сечения уширения фактически проводится по ${{e}_{{Ri}}}.$ Поэтому для интегрирования по b (см. обсуждение после формулы (20)) проведем замену переменной интегрирования, воспользовавшись выражением (45). Тогда
Если ${{U}_{{i{\kern 1pt} \alpha }}}({{R}_{{0}}}) < 0,$ то при квазиклассических условиях(49)
$\sigma _{{i{\kern 1pt} \alpha \to f}}^{{{\kern 1pt} {\text{МВЧ}}}}(\omega ,{{e}_{{Ri}}}) = \frac{{\pi R_{0}^{2}}}{{{{e}_{i}}}}{{\mathbb{Z}}_{{i{\kern 1pt} \alpha \to f}}}(\omega ,{{e}_{i}}),$(50)
${{\mathbb{Z}}_{{i{\kern 1pt} \alpha \to f}}}(\omega ,{{e}_{i}}) = \int\limits_{ - \left| {{{U}_{{i\alpha }}}({{R}_{0}})} \right|}^{{{e}_{i}}} {P_{{{\kern 1pt} \alpha \to f}}^{{{\text{МВЧ}}}}(\omega ,{{e}_{{Ri}}})} .$Подставляя (49) и (50) в (6) и проводя интегрирование по частям, для константы скорости уширения получаем
(51)
$\begin{gathered} K_{{i{\kern 1pt} \alpha \to f, - }}^{{{\text{МВЧ}}}}(\omega ,T) = \\ = \frac{{\left\langle w \right\rangle \pi R_{0}^{2}}}{{{{k}_{B}}{\kern 1pt} T}}{{\mathbb{Z}}_{{i\alpha \to f}}}(\omega ,0) + \left\langle w \right\rangle \pi R_{0}^{2}\left\langle {P_{{i\alpha \to f, - }}^{{{\text{МВЧ}}}}} \right\rangle (\omega ,T). \\ \end{gathered} $(52)
$\left\langle {P_{{i\alpha \to f, - }}^{{{\text{МВЧ}}}}} \right\rangle (\omega ,T) = \int\limits_0^\infty {P_{{i\alpha \to f}}^{{{\text{МВЧ}}}}(\omega ,{{e}_{i}})\exp \left( { - \frac{{{{e}_{i}}}}{{{{k}_{B}}{\kern 1pt} T}}} \right)} \frac{{d{{e}_{i}}}}{{{{k}_{B}}T}}$Если ${{U}_{{i\alpha }}}({{R}_{0}}) > 0,$ то аналогичное предыдущему рассмотрение дает, что соответствующая константа скорости уширения имеет вид
(53)
$K_{{i{\kern 1pt} \alpha \to f, + }}^{{{\text{МВЧ}}}}(\omega ,T) = \left\langle w \right\rangle \pi R_{0}^{2}\left\langle {P_{{i{\kern 1pt} \alpha \to f, + }}^{{{\text{МВЧ}}}}} \right\rangle (\omega ,T),$(54)
$\begin{gathered} \left\langle {P_{{i\alpha \to f, + }}^{{{\text{МВЧ}}}}} \right\rangle (\omega ,T) = \\ = \int\limits_{{{U}_{{i\alpha }}}({{R}_{0}})}^\infty {P_{{i{\kern 1pt} \alpha \to f}}^{{{\text{МВЧ}}}}(\omega ,{{e}_{i}})\exp \left( { - \frac{{{{e}_{i}}}}{{{{k}_{B}}T}}} \right)} \frac{{d{{e}_{i}}}}{{{{k}_{B}}{\kern 1pt} T}}. \\ \end{gathered} $Рис. 4.
Адиабатические потенциальные кривые квазимолекулы Ar–Ar: сплошные линии отвечают потенциальным кривым ${{U}_{f}}(R)$ и ${{U}_{{i{\kern 1pt} {\kern 1pt} 0}}}(R)$ основного и возбужденного $0_{u}^{ + }$(3P1) состояний (см. (3)); штриховые линии – сдвинутым потенциальным кривым основного состояния ${{U}_{{f,\omega }}}(R),$ определяемым в (13). Вертикальными линиями отмечены межъядерные расстояния ${{R}_{c}}(\omega ),$ соответствующие точкам пересечения кривых ${{U}_{{i0}}}(R)$ и ${{U}_{{f,\omega }}}(R).$

Проблема неадиабатического перехода между молекулярными состояниями, которым отвечают пересекающиеся потенциальные кривые, и ее обобщения подробно обсуждаются в работах [31, 32]. В рассматриваемом здесь случае для расчета вероятности перехода (46) может быть использована полуклассическая модель Ландау, предполагающая слабую связь между состояниями, отвечающими пересекающимся потенциальным кривым [47]. В модели Ландау явное выражение $P_{{i\alpha \to f}}^{{\text{Л}}}(\omega ,{{e}_{{Ri}}})$ для этой вероятности имеет следующий вид:
(55)
$\begin{gathered} P_{{i\alpha \to f}}^{{{\text{Л}}}}(\omega ,{{e}_{{Ri}}}) = \\ = {{\mho }_{{i{\kern 1pt} \alpha \to f}}}\left( \omega \right)\left\{ {\begin{array}{*{20}{c}} {\frac{{\Theta \{ {{e}_{{Ri}}} - {{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]\} }}{{{{{\left\{ {{{e}_{{Ri}}} - {{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]} \right\}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}},}&{{{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]\, > \,0,} \\ {\frac{1}{{{{{\left\{ {{{e}_{{Ri}}} + \left| {{{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]} \right|} \right\}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}},}&{{{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]\, < \,0.} \end{array}} \right. \\ \end{gathered} $(56)
${{\mho }_{{i\alpha \to f}}}(\omega ) = \frac{{2\pi \sqrt {2\mu } {{V}_{{i\alpha ,{\kern 1pt} f}}}{{{[{{R}_{c}}(\omega )]}}^{2}}}}{{\hbar \Delta {{F}_{{i\alpha ,f}}}[{{R}_{c}}(\omega )]}},$Соответствующая константа скорости уширения записывается как
(58)
$K_{{i\alpha \to f}}^{{\text{Л}}}(\omega ,T) = \left\langle w \right\rangle \pi {{R}_{c}}{{(\omega )}^{2}}\left\langle {P_{{i\alpha \to f}}^{{\text{Л}}}} \right\rangle (\omega ,T),$(59)
$\begin{gathered} \left\langle {P_{{i\alpha \to f}}^{{{\text{Л}}}}} \right\rangle (\omega ,{\kern 1pt} T) = \frac{{{{\mho }_{{i\alpha \to f}}}(\omega )}}{{\sqrt {{{k}_{B}}T} }} \times \\ \times \,\,\left\{ {\begin{array}{*{20}{c}} {\sqrt \pi \exp \left\{ { - \frac{{{{U}_{{i{\kern 1pt} \alpha }}}[{{R}_{c}}(\omega )]}}{{{{k}_{B}}{\kern 1pt} T}}} \right\},\,\,\,{{U}_{{i{\kern 1pt} \alpha }}}[{{R}_{c}}(\omega )] > 0,} \\ {2{{{\left\{ {\frac{{\left| {{{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]} \right|}}{{{{k}_{B}}T}}} \right\}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \sqrt \pi \exp \left\{ {\frac{{{{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]}}{{{{k}_{B}}{\kern 1pt} T}}} \right\} \times } \\ { \times \,\,{\text{erfc}}\left\{ {{{{\left[ {\frac{{\left| {{{U}_{{i\alpha }}}[{{R}_{c}}(\omega )]} \right|}}{{{{k}_{B}}T}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\},\,\,\,\,{{U}_{{i\alpha }}}[{{R}_{c}}(\omega )] < 0.} \end{array}} \right. \\ \end{gathered} $3.3.2. Красное крыло контура спектральной линии излучения Ar(3P1) → Ar(1S0) в собственном газе
Энергетическая схема формирования красного крыла контура линии излучения представлена на рис. 1а. Частота излучения в красном крыле, ${{\Omega }_{r}},$ ниже, чем частота ${{\omega }_{{\,if}}}$ атомного радиационного перехода. Однако радиационный переход 3P1 → 1S0 может произойти только во время столкновения атомов Ar(3P1) и Ar(1S0), когда в поле потенциала ${{U}_{{i{\kern 1pt} \alpha }}}(R)$ $(\alpha = 0,1)$ часть энергии возбуждения атома уносится излучаемым фотоном. При этом энергия $\hbar \left| {\omega {\kern 1pt} } \right|$ в случае ω < 0 переходит в энергию относительного движения тяжелых атомов Аr. В рамках описанной выше двухуровневой модели (см. (8)–(20)) сечения уширения ${{\sigma }_{{i{\kern 1pt} \alpha \to f}}}(\omega ,{{e}_{i}})$ равны сечениям неадиабатического перехода $\left| {i{\kern 1pt} \alpha } \right\rangle \to \left| f \right\rangle .$ Вероятности таких переходов, константы скорости уширения ${{K}_{{i{\kern 1pt} \alpha \to f}}}(\omega )$ и крыло контура линии перехода ${{F}_{{if}}}(\omega )$ сильно зависят от поведения ${{U}_{{f,\omega }}}(R)$ и ${{U}_{{i{\kern 1pt} \alpha }}}(R).$
Две принципиально различные ситуации имеют место в случаях состояний квазимолекулы $0_{u}^{ + }$(3P1) и ${{1}_{u}}$(3P1). Из рис. 4 видно, что в случае $0_{u}^{ + }$(3P1) потенциальные кривые ${{U}_{{i{\kern 1pt} {\kern 1pt} 0}}}(R)$ и ${{U}_{{f,{\kern 1pt} {\kern 1pt} \omega }}}(R)$ пересекаются на расстояниях ${{R}_{c}}(\omega ).$ Поэтому неадиабатический переход $\left| {i0} \right\rangle \to \left| f \right\rangle $ при прохождении расстояния ${{R}_{c}}(\omega )$ во время относительного движения ядер сопровождается достаточно малой передачей энергии. Соответственно, вероятность такого перехода высока [31, 32]. Как следует из рис. 4, такие пересечения имеют место в широком интервале изменения $\omega .$ Поэтому константы скорости уширения ${{K}_{{i0 \to f}}}(\omega )$ довольно велики и медленно меняются на этом интервале.
Совершенно иная ситуация имеет место в случае состояния ${{1}_{u}}$(3P1) квазимолекулы Ar–Ar (см. рис. 5). Здесь потенциальные кривые ${{U}_{{i1}}}(R)$ и ${{U}_{{f,\omega }}}(R)$ не пересекаются, и переходы между электронными состояниями сопровождаются большим обменом энергией между быстрыми (электроны) и медленными (ядра) степенями свободы при всех R. В теории атомных столкновений показано [31, 32], что здесь вероятности электронных переходов малы при всех значениях $\omega < 0,$ поэтому ${{K}_{{i1 \to f}}}(\omega )$ всегда существенно меньше, чем ${{K}_{{i0 \to f}}}(\omega ,T).$
Рис. 5.
Адиабатические потенциальные кривые квазимолекулы Ar–Ar: сплошные линии отвечают потенциальным кривым ${{U}_{f}}(R)$ и ${{U}_{{i1}}}(R)$ основного и возбужденного ${{1}_{u}}$(3P1) состояний; пунктирная линия – сдвинутая потенциальная кривая основного состояния ${{U}_{{f,\omega }}}(R).$
Для подтверждения этого качественного заключения были проведены численные расчеты ${{K}_{{i1 \to f}}}(\omega )$ методом МВЧ с использованием формул (6), (14)–(16). При этом при расчете $P_{{i1 \to f}}^{{{\text{МВЧ}}}}(\omega ,{{e}_{{Ri}}})$ по формулам (15)–(20) использовалось равномерное квазиклассическое приближение [48, 49]. Поскольку ${{U}_{{i1}}}(R)$ и ${{U}_{{f}}}(R)$ хорошо аппроксимируются экспонентами в широком интервале изменения R, это приближение дает практически точное аналитическое выражение для волновых функций ${{\varphi }_{{i{\kern 1pt} \alpha }}}({{e}_{{Ri}}},0,R)$ и ${{\varphi }_{f}}\left[ {{{e}_{f}}({{e}_{{Ri}}},\omega ),0,R} \right].$
В связи со сказанным выше при детальных расчетах был учтен только вклад ${{K}_{{i0 \to f}}}(\omega ,T)$ в красное крыло контура спектральной линии ${{F}_{{if,rw}}}(\omega ,{\kern 1pt} T).$ Метод расчета константы скорости неадиабатического перехода между пересекающимися потенциальными кривыми описан формулами (55)–(59). Из теории следует, что в присутствии пересечений потенциальных кривых полная вероятность неадиабатических переходов ${{P}_{{i0 \to f}}}(b,\omega ,{{e}_{i}})$ определяется вкладом этих пересечений.
Положение точки пересечения ${{R}_{{{\kern 1pt} c}}}(\omega )$ является корнем уравнения
Разностный потенциал $\Delta {{U}_{{i0,f}}}(R)$ при ${{R}_{c}} = 2.55{{a}_{0}}$ имеет минимум $\hbar {{\omega }_{с}} = - 87450$ см–1. Это означает, что при $\omega < {{\omega }_{c}}$ уравнение (44) не имеет действительных корней. В интервале $0 > \omega > {{\omega }_{c}}$ оно имеет два действительных положительных корня. На рис. 6 показаны три типа таких корней. При $R = {{R}_{c}}(\omega {{{\kern 1pt} }_{0}}) = 3.86{{a}_{0}}$ (${{\omega }_{{\,0}}} = - 31372$ см–1) ${{U}_{{i0}}}(R)$ принимает нулевое значение. Для частот типа $\omega = {{\omega }_{{Rep}}} < {{\omega }_{0}}$ корни ${{R}_{c}}(\omega ) < {{R}_{c}}(\omega {{{\kern 1pt} }_{0}}).$ При этом ${{U}_{{i0}}}[{{R}_{c}}(\omega )] > 0$ и быстро растет с уменьшением частоты $\omega .$ В этом случае для достижения точки пересечения потенциальных кривых требуется энергия относительного движения атомов ${{\varepsilon }_{i}} \geqslant {{U}_{{i0}}}\left( {{{R}_{c}}(\omega )} \right)$ и при не слишком высоких температурах ${{K}_{{i0 \to f}}}(\omega ,T)$ экспоненциально спадает при уменьшении $\omega .$ Поэтому практический интерес представляют пересечения потенциальных кривых при отрицательных $\omega $ вплоть до ${{\omega }_{0}} - j{{k}_{B}}{T \mathord{\left/ {\vphantom {T \hbar }} \right. \kern-0em} \hbar }$ с величиной $j = 0,1,2,3.$
Рис. 6.
Адиабатические потенциальные кривые квазимолекулы Ar–Ar: ${{U}_{{i0}}}(R)$ соответствует возбужденному состоянию $0_{u}^{ + }$(3P1); $\Delta {{U}_{{i0,f}}}(R)$ – разностный потенциал, рассчитанный по формуле (12).
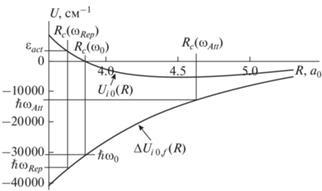
Для частот типа $\omega = {{\omega }_{{Att}}} > {{\omega }_{0}}$ корни ${{R}_{c}}(\omega ) > {{R}_{c}}(\omega {{{\kern 1pt} }_{0}})$ и ${{U}_{{i0}}}[{{R}_{c}}(\omega )] < 0.$ В этом случае точка пересечения потенциальных кривых достигается при любых ${{\varepsilon }_{i}},$ и поэтому ${{K}_{{i0 \to f}}}(\omega ,T)$ слабо зависят от $\omega $. Константы скорости уширения ${{K}_{{i0 \to f}}}(\omega ,T)$ вычислялись по формулам (55)–(59) с использованием результатов квантовохимических расчетов [39, 40], представленных на рис. 2–4 и 6.
На рис. 7 приведены результаты расчетов для красного крыла контура спектральной линии ($\omega < 0$):
(61)
${{F}_{{i,f,rw}}}(\omega ,T) = \frac{1}{3}\frac{{{{n}_{{{\text{Ar}}}}}{{K}_{{i{\kern 1pt} 0 \to f}}}(\omega ,T)}}{{\pi {{\omega }^{2}}}},$Рис. 7.
Зависимости красного крыла контура спектральной линии излучения ${{F}_{{i,f,rw}}}(\omega ,\,\,T)$ квазимолекулы Ar–Ar, рассчитанные по формулам (37), (55)–(59), (61) для различных значений температуры T: кривая 1 – $T = 600$ K; 2 – 1000 K; 3 – 2000 K. Расчет проводился при концентрации аргона ${{n}_{{\operatorname{Ar} }}} = {{10}^{{20}}}$ см–3.
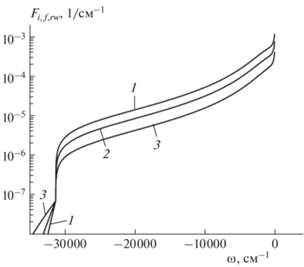
3.3.3. Голубое крыло контура спектральной линии излучения Ar(3P1) → Ar(1S0) в собственном газе
Энергетическая схема формирования голубого крыла контура линии излучения показана на рис. 1б. Частота излучения ${{\Omega }_{r}}$ в голубом крыле выше, чем частота ${{\omega }_{{if}}}$ атомного радиационного перехода ($\omega > 0$), однако, как и в случае красного крыла, радиационный переход 3P1 → 1S0 происходит только во время столкновения атомов Ar(3P1) и Ar(1S0). В этом случае недостающая энергия $\hbar \omega \;(\omega > 0)$ для излучения фотона с энергией $\hbar {{\Omega }_{r}}$ берется из энергии относительного движения тяжелых атомов Аr. При этом в рамках описанной выше двухуровневой модели (см. (8)–(20)) сечения уширения ${{\sigma }_{{i\alpha \to f}}}(\omega ,{{e}_{i}})$ равны сечениям неадиабатического перехода $\left| {i\alpha } \right\rangle \to \left| f \right\rangle .$ Вероятности таких переходов, константы скорости уширения ${{K}_{{i\alpha \to f}}}(\omega )$ и крыло контура линии излучения ${{F}_{{i,f,rw}}}(\omega ,T)$ сильно зависят от поведения потенциальных кривых ${{U}_{{f,\omega }}}(R)$ и ${{U}_{{i{\kern 1pt} \alpha }}}(R).$
Аналогично случаю красного крыла принципиально различные ситуации имеют место для состояний квазимолекулы $0_{u}^{ + }$(3P1) и ${{1}_{u}}$(3P1). Из рис. 8 видно, что в случае возбужденного состояния ${{1}_{u}}$(3P1) квазимолекулы потенциальные кривые ${{U}_{{i{\kern 1pt} {\kern 1pt} 1}}}(R)$ и ${{U}_{{f,\omega }}}(R)$ пересекаются в точке ${{R}_{c}}(\omega ).$ Переход между ними при прохождении точки ${{R}_{c}}$ во время относительного движения ядер сопровождается малой передачей энергии. Соответственно, вероятность такого перехода высока.
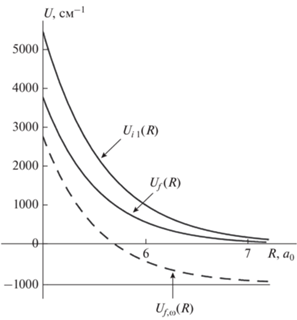
Рис. 8.
Адиабатические потенциальные кривые квазимолекулы Ar–Ar: сплошные линии отвечают потенциальным кривым ${{U}_{f}}(R)$ и ${{U}_{{i\,1}}}(R)$ основного и возбужденного ${{1}_{u}}$(3P1) состояний; щтриховая линия – сдвинутая потенциальная кривая основного состояния ${{U}_{{f,\omega }}}(R).$ Вертикальной линией отмечено межъядерное расстояние ${{R}_{c}}(\omega ),$ соответствующее точке пересечения кривых ${{U}_{{i1}}}(R)$ и ${{U}_{{f,\omega }}}(R).$
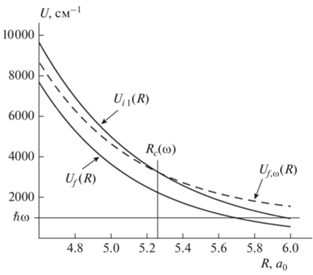
В случае возбужденного состояния $0_{u}^{ + }$(3P1) квазимолекулы потенциальные кривые ${{U}_{{i{\kern 1pt} 0}}}(R)$ и ${{U}_{{f,\omega }}}(R)$ не пересекаются (см. рис. 9) и переходы между электронными состояниями сопровождаются передачей большой порции энергии между быстрыми (электроны) и медленными (ядра) степенями свободы при всех R. В такой ситуации вероятности электронных переходов малы при всех $\omega > 0,$ и поэтому константа скорости ${{K}_{{i{\kern 1pt} 1 \to f}}}(\omega )$ всегда существенно больше, чем ${{K}_{{i{\kern 1pt} 0 \to f}}}(\omega ,T).$ Это подтверждается конкретными численными расчетами с использованием метода МВЧ, поэтому всюду ниже рассматривается только вклад ${{K}_{{i{\kern 1pt} 1 \to f}}}(\omega )$ в голубое крыло контура линии излучения ${{F}_{{i,\,f,bw}}}(\omega ,{\kern 1pt} T).$
Рис. 9.
Адиабатические потенциальные кривые квазимолекулы Ar–Ar: сплошные линии отвечают потенциальным кривым ${{U}_{f}}(R)$ и ${{U}_{{i0}}}(R)$ основного и возбужденного $0_{u}^{ + }$(3P1) состояний; штриховая линия – сдвинутая потенциальная кривая основного состояния ${{U}_{{f,\omega }}}(R).$

Разностный потенциал $\Delta {{U}_{{i{\kern 1pt} 1,f}}}(R)$ имеет максимум $\hbar {{\omega }_{с}} = 2462$ см–1 при ${{R}_{c}} = 4.13{{a}_{0}}.$ Следует подчеркнуть, что в этом случае ${{U}_{{i1}}}[{{R}_{c}}(\omega )] > 0$ и константа скорости ${{K}_{{i1 \to f}}}(\omega )$ начинает заметно уменьшаться на интервале $\omega $ от 100 до 2400 см–1. С ростом $\omega $ при $\omega > {{\omega }_{c}}$ потенциальные кривые квазимолекулы ${{U}_{{i{\kern 1pt} 1}}}(R)$ и ${{U}_{{f,\omega }}}(R)$ не пересекаются, и падение ${{K}_{{i1 \to f}}}(\omega )$ становится резким. На рис. 10 представлены результаты расчетов голубого крыла контура линии
(62)
${{F}_{{i,f,bw}}}(\omega ,T) = \frac{2}{3}\frac{{{{n}_{{{\text{Ar}}}}}{{K}_{{i1 \to f}}}(\omega ,T)}}{{\pi {{\omega }^{2}}}},$Рис. 10.
Зависимости голубого крыла контура спектральной линии излучения ${{F}_{{i,f,bw}}}(\omega ,\,\,T)$ квазимолекулы Ar–Ar, рассчитанные по формулам (55)–(59), (62) для различных значений температуры T: кривая 1 – $T = 600$ K; 2 – 1000 K; 3 – 2000 K. Расчет проводился при концентрации аргона ${{n}_{{\operatorname{Ar} }}} = {{10}^{{20}}}$ см–3.
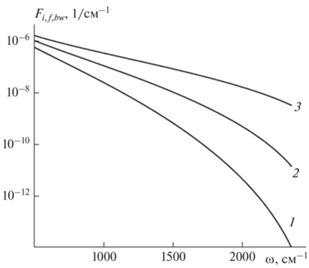
4. ЗАКЛЮЧЕНИЕ
В настоящей работе предложена формулировка единой франк-кондоновской теории уширения спектральных линий в газах в терминах теории медленных атомных столкновений, которая оказывается достаточно эффективной при качественном анализе механизмов уширения и построения соответствующих простых динамических моделей. В первую очередь это относится к центру и крыльям контура спектральной линии. Так, в случае крыльев, которые определяются межъядерными расстояниями порядка характерных размеров атомов, предложен простой и эффективный метод модифицированного волнового числа. Работа метода продемонстрирована на примере расчета красного и голубого крыльев контура линии излучения Ar(3P1) → Ar(1S0) возбужденных атомов аргона в собственном газе.
Тем не менее до сих пор имеются проблемы с развитием простых количественных методов расчета частей контура линии между центром и крыльями контура. Отсутствуют достаточно надежные простые подходы к оценке влияния столкновительных неадиабатических эффектов на уширение спектральных линий. Такие эффекты являются существенными в случае столкновения атомов с незаполненными внешними электронными оболочками.
Работа выполнена в рамках госзадания Министерства науки и высшего образования Российской Федерации (регистрационный номер темы 122040500060-4).
Список литературы
Родионов А.И., Родионов И.Д, Родионова И.П. и др. // Хим. физика. 2021. Т. 40. № 10. С. 61; https://doi.org/10.31857/S0207401X21100113
Harde H. // Intern. J. Atmos. Sci. 2013. V. 2013. P. 1; https://doi.org/10.1155/2013/503727
Chu H., Liu F., Zhou H. // Intern. J. Heat Mass Transf. 2011. V. 54. № 21–22. P. 4736; https://doi.org/10.1016/j.ijheatmasstransfer.2011.06.002
Голубков Г.В., Шапочкин М.Б. // Хим. физика. 2019. Т. 38. № 7. С. 19; https://doi.org/10.1134/S0207401X19070033
Yang S., Nagaraja S., Sun W. et al. // J. Phys. D. Appl. Phys. 2017. V. 50. № 43. 433001; https://doi.org/10.1088/1361-6463/aa87ee
Левашов В.Ю., Козлов П.В., Быкова Н.Г. и др. // Хим. физика. 2021. Т. 40. № 1. С. 16; https://doi.org/10.31857/S0207401X2101009X
Забелинский И.Е., Козлов П.В., Акимов Ю.В. и др. // Хим. физика. 2021. Т. 40. № 11. С. 22; https://doi.org/10.31857/S0207401X2111011X
Козлов П.В., Забелинский И.Е., Быкова Н.Г. и др. // Хим. физика. 2021. Т. 40. № 12. С. 23; https://doi.org/10.31857/S0207401X21120104
Deminsky M., Adamson S., Chernysheva I. et al. // J. Phys. D: Appl. Phys. 2015. V. 48. № 20. 205202; https://doi.org/10.1088/0022-3727/48/20/205202
Собельман И.И. Введение в теорию атомных спектров. М.: Физматгиз, 1963.
Schuller F., Behmenburg W. // Phys. Rep. 1974. V. 12. № 4. P. 273; https://doi.org/10.1016/0370-1573(74)90018-0
Ben-Reuven A. // Adv. Chem. Phys. 1975. V. 33. P. 235; https://doi.org/10.1002/9780470142523.ch5
Lewis E.L. // Phys. Rep. 1980. V. 58. № 1. P. 1; https://doi.org/10.1016/0370-1573(80)90056-3
Peach G. // Adv. Phys. 1981. V. 30. № 3. P. 367; https://doi.org/10.1080/00018738100101467
Allard N., Kielkopf J. // Rev. Mod. Phys. 1982. V. 54. № 4. P. 1103; https://doi.org/10.1103/RevModPhys.54.1103
Sando K.M., Chu S.I. // Adv. At. Mol. Phys. 1989. V. 25. P. 133; https://doi.org/10.1016/S0065-2199(08)60085-8
Szudy J., Baylis W.E. // Phys. Rep. 1996. V. 266. № 3–4. P. 127; https://doi.org/10.1016/0370-1573(95)00054-2
Jabloński A. // Phys. Rev. 1945. V. 68. № 3–4. P. 78; https://doi.org/10.1103/PhysRev.68.78
Jabloński A. // Phys. Rev. 1946. V. 69. № 1–2. P. 31; https://doi.org/10.1103/PhysRev.69.31
Baranger M. // Phys. Rev. 1958. V. 111. № 2. P. 481; https://doi.org/10.1103/PhysRev.111.481
Baranger M. // Phys. Rev. 1958. V. 112. № 3. P. 855; https://doi.org/10.1103/PhysRev.112.855
Royer A. // Can. J. Phys. 1974. V. 52. № 18. P. 1816; https://doi.org/10.1139/p74-238
Szudy J., Baylis W.E. // J. Quant. Spectr. Radiat. Transf. 1975. V. 15. № 7–8. P. 641; https://doi.org/10.1016/0022-4073(75)90032-1
Szudy J. // Acta Phys. Pol. A. 1978. V. 54. № 6. P. 841.
Herman P.S., Sando K.M. // J. Chem. Phys. 1978. V. 68. № 3. P. 1153; https://doi.org/10.1063/1.435804
Fano U. // Phys. Rev. 1963. V. 131. № 1. P. 259; https://doi.org/10.1103/PhysRev.131.259
Ben-Reuven A., Mukamel S. // J. Phys. A: Math. Gen. 1975. V. 8. № 8. P. 1313; https://doi.org/10.1088/0305-4470/8/8/016
Rabin Y., Mukamel S. // J. Phys. B: At. Mol. Phys. 1980. V. 13. № 11. P. L331; https://doi.org/10.1088/0022-3700/13/11/002
Demura A.V., Umanskii S.Y., Scherbinin A.V. et al. // Intern. Rev. At. Mol. Phys. 2011. V. 2. № 2. P. 109.
Demura A.V., Umanskii S.Y., Scherbinin A.V. et al. // J. Phys.: Conf. Ser. 2012. V. 397. № 1. 012033; https://doi.org/10.1088/1742-6596/397/1/012033
Никитин Е.Е., Уманский С.Я. Неадиабатические переходы при медленных атомных столкновениях. М.: Атомиздат, 1979.
Nikitin E.E., Umanskii S.Y. Theory of slow atomic collisions / Eds. Goldanskii V.I., Gomer R., Schäfer F.P., Toennies J.P. Berlin, Heidelberg: Springer, 1984; https://doi.org/10.1007/978-3-642-82045-8
Lewis E.L., Harris M., Alford W.J. et al. // J. Phys. B: At. Mol. Phys. 1983. V. 16. № 4. P. 553; https://doi.org/10.1088/0022-3700/16/4/009
Julienne P.S. // Spectral line shapes. V. 2. Berlin, New York: Walter de Gruyter & Co., 1983. P. 770.
Julienne P.S., Mies F.H. // Phys. Rev. A. 1984. V. 30. № 2. P. 831; https://doi.org/10.1103/PhysRevA.30.831
Julienne P.S., Mies F.H. // Phys. Rev. A. 1986. V. 34. № 5. P. 3792; https://doi.org/10.1103/PhysRevA.34.3792
Mies F.H., Smith A.L. // J. Chem. Phys. 1966. V. 45. № 3. P. 994; https://doi.org/10.1063/1.1727717
Sansonetti J.E., Martin W.C. // J. Phys. Chem. Ref. Data. 2005. V. 34. № 4. P. 1559; https://doi.org/10.1063/1.1800011
Granovsky A.A. // J. Chem. Phys. 2011. V. 134. № 21. 214 113; https://doi.org/10.1063/1.3596699
Schmidt M.W., Baldridge K.K., Boatz J.A. et al. // J. Comput. Chem. 1993. V. 14. № 11. P. 1347; https://doi.org/10.1002/jcc.540141112
Tang K.T., Toennies J.P. // J. Chem. Phys. 2003. V. 118. № 11. P. 4976; https://doi.org/10.1063/1.1543944
Lewis E.L. // Proc. Phys. Soc. 1967. V. 92. № 3. P. 817; https://doi.org/10.1088/0370-1328/92/3/334
Laporte P., Damany N., Damany H. // Opt. Lett. 1987. V. 12. № 12. P. 987; https://doi.org/10.1364/OL.12.000987
Hu Y., Wang X., Zuo D. // Vacuum. 2022. V. 203. 111 229; https://doi.org/10.1016/j.vacuum.2022.111229
Takayanagi K. // Prog. Theor. Phys. 1952. V. 8. № 1. P. 111; https://doi.org/10.1143/ptp/8.1.111
Никитин Е.Е. Теория элементарных атомно-молекулярных процессов в газах. М.: Химия, 1970.
Ландау Л.Д., Лифшиц Е.М. Курс теоретической физики: Т. 3. Квантовая механика (нерелятивистская теория). М.: Физматлит, 2004.
Langer R.E. // Phys. Rev. 1937. V. 51. № 8. P. 669; https://doi.org/10.1103/PhysRev.51.669
Найфэ А.Х. Методы возмущений. М.: Мир, 1976.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика