Химическая физика, 2023, T. 42, № 4, стр. 73-80
Распространение в атмосфере импульсов акустико-гравитационных волн и прохождение их через слои с заданным распределением температуры
Н. В. Бахметьева 1, *, Г. И. Григорьев 1, **, Е. Е. Калинина 1
1 Научно-исследовательский радиофизический институт Нижегородского государственного университета
им. Н.И. Лобачевского
Нижний Новгород, Россия
* E-mail: nv_bakhm@nirfi.unn.ru
** E-mail: grigorev@nirfi.unn.ru
Поступила в редакцию 09.09.2022
После доработки 17.09.2022
Принята к публикации 20.09.2022
- EDN: MVCJAY
- DOI: 10.31857/S0207401X23040039
Аннотация
В применении к экспериментальным измерениям параметров нейтральной компоненты в ионосфере Земли проанализировано распространение квазигармонических импульсов акустико-гравитационных волн (АГВ) ограниченной длительности в изотермической атмосфере. Получен критерий слабых искажений импульсных сигналов при их распространении на значительные расстояния. Рассмотрены также отражение и преломление таких импульсов атмосферными слоями с параболической зависимостью равновесной температуры в них от высоты. Показано, что при выполнении определенных условий импульсы АГВ могут распространяться без искажений на большие расстояния.
1. ВВЕДЕНИЕ
Значимость проблемы экспериментального и теоретического исследования распространения волновых возмущений в различных средах во многом определяется той ролью, которую они играют во взаимодействии между нижней и верхней атмосферой и, в целом, в околоземном пространстве. Существует огромное количество публикаций, посвященных изучению атмосферных волн. Среди уже ставших классическими можно указать работы [1–10]. Например, в работе [8] рассмотрены теория акустико-гравитационных волн (АГВ) и взаимодействие таких волн с ионосферой, приведено экспериментальное подтверждение их существования в верхних слоях атмосферы и обсуждается роль АГВ в динамике термосферы. Обсуждаются эффекты, вызываемые горизонтальными ветрами, резкими разрывами границ и диссипативными процессами; рассматривается генерация этих волн стационарными или движущимися источниками; обсуждается их роль в атмосферной динамике.
В работах [11–16] представлена обширная библиография по экспериментальным и теоретическим вопросам распространения атмосферных волн. В монографии [15] обсуждаются вопросы комплексных (экспериментальных и теоретических) исследований атмосферных волн различной природы и разных масштабов. Использование данных большого набора различных инструментов, традиционных и оригинальных подходов к описанию состояния нейтральной атмосферы и ионосферы позволило авторам этих работ получить новые сведения о динамических процессах на высотах 20–1000 км.
В последнее десятилетие большое внимание уделяется экспериментальным исследованиям генерации атмосферных волн при возмущении ионосферы мощным радиоизлучением нагревных стендов. В работах [17, 18] приведены результаты исследований возможностей генерации (усиления) АГВ, распространяющихся на ионосферных высотах, мощным периодическим высокочастотным излучением нагревного стенда СУРА. Исследовались вариации доплеровского смещения частоты отраженных от ионосферы сигналов высокочастотного радара вертикального зондирования ионосферы, расположенного вблизи г. Харькова на расстоянии 960 км от нагревного стенда. Проводился спектральный анализ временны́х вариаций доплеровского сдвига частоты. В эксперименте было установлено, что спектральные характеристики квазипериодических вариаций в доплеровском сдвиге частоты в диапазоне периодов 10–60 мин в дни работы стенда и в контрольный день существенно различались. Авторы работы [17] считают это доказательством генерации (усиления) АГВ мощным периодическим высокочастотным излучением нагревного стенда СУРА. Колебания в спектре с периодами 8–12 мин и 13–17 мин и амплитудами 60–100 мГц обнаруживались почти во всех сеансах и запаздывали по отношению к моменту включения стенда СУРА на 100 мин – первые периоды и на 40–50 мин – вторые [18]. Это объяснялось возбуждением искусственных АГВ (или усилением естественных волн) при воздействии на ионосферу. В работе [19] сообщается о генерации АГВ в F-области ионосферы по данным спутников CHAMP и GRACE при работе аврорального нагревного стенда HAARP.
В теоретических исследованиях распространения акустических и других типов волн в разных средах развиты методы анализа, позволяющие рассмотреть многие аспекты генерации и распространения волн. Например, в монографии [10] проанализирована проблема распространения звука в воде, решены многие задачи вычисления акустических полей в горизонтально стратифицированной среде, даны различные представления полей гармонического источника, их взаимосвязь и обосновано применение метода параболического уравнения к решению поставленных задач. Метод параболического уравнения использовался также авторами работы [20] для расчета инфразвуковых сигналов, генерированных наземным взрывом. Полученные формы сигналов хорошо согласуются с сейсмическими записями на трассах протяженностью до 800 км от источника взрыва. В монографии [21] найден класс решений волнового уравнения, описывающих “безотражательные” волны в сильно неоднородной сжимаемой атмосфере применительно к геофизическим и астрофизическим объектам. Анализ проблемы возбуждения импульсными источниками упругих волновых полей, их пространственно-временных структур применительно к модели земной среды – полупространству с заданными характеристиками – с описанием натурных экспериментальных данных содержится в монографии [22].
Для понимания особенностей распространения АГВ в океане, атмосфере и ионосфере необходимо численное моделирование в конкретных условиях окружающей среды. Численные исследования атмосферных возмущений от импульсных источников различной природы представлены в работе [23]. Среди возможных источников в этой работе были рассмотрены взрывы, землетрясения, волны цунами, температурные импульсные возмущения. Отмечено “достаточно хорошее совпадение характеристик ионосферных возмущений, наблюдаемых после крупных землетрясений, химических и ядерных взрывов и после прохождения волн цунами, с результатами численных расчетов откликов верхней атмосферы от соответствующих модельных источников”.
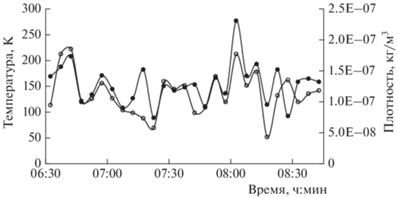
Данная статья является логическим продолжением работы [11], в которой решена задача о распространении монохроматических плоских АГВ через слои атмосферы с параболической и линейной зависимостью равновесной температуры от высоты, найдены коэффициенты отражения и прохождения волн через такие слои и выполнен численный анализ вертикальной структуры мод АГВ внутри слоев атмосферы с меняющейся температурой. Показано, в частности, что при наличии таких структур в принципе может быть реализован волноводный режим распространения АГВ в горизонтальном направлении. На рис. 1 показаны высотные профили температуры нейтральной компоненты, а на рис. 2 – зависимости от времени температуры и плотности, полученные методом резонансного рассеяния радиоволн на искусственных периодических неоднородностях (ИПН) ионосферной плазмы. На этих рисунках видны ярко выраженные высотно-временные вариации температуры с периодами, характерными для АГВ.
Рис. 1.
Высотные профили температуры нейтральной компоненты на высотах нижней термосферы за несколько последовательных сеансов измерений методом создания ИПН 24.09.2007 (левая панель) и 04.04.2006 (правая панель) [11].
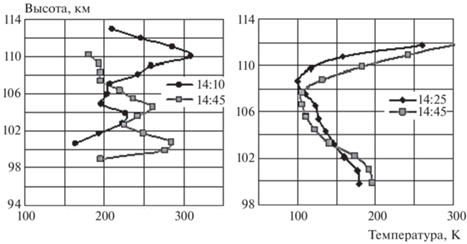
Рис. 2.
Временны́е вариации температуры (⚫) и плотности (⚪) нейтральной атмосферы на высоте 105 км после восхода Солнца 13 июня 2015 г., полученные методом создания ИПН.
Метод, основанный на создании ИПН, подробно описан [24, 25]. Он является одним из эффективных экспериментальных методов исследования атмосферных волн по их влиянию на параметры нейтральной компоненты на высотах мезосферы и нижней термосферы. Методом, основанным на создании ИПН, получен большой объем сведений о высотных профилях и временны́х вариациях температуры и плотности нейтральной компоненты в интервале высот 90–120 км. В результате на основе этих данных достоверно обнаружены волновые движения на высотах 60–130 км с периодами от 10–15 мин до нескольких часов, характерными для атмосферных волн. Подчеркнем, что, несмотря на применение для создания неоднородностей метода воздействия на ионосферу мощным высокочастотным радиоизлучением, данные о параметрах нейтральной компоненты относятся к невозмущенному (фоновому) состоянию среды, что обусловлено методикой их определения [24].
2. ПОСТАНОВКА ЗАДАЧИ
В работе рассмотрена задача по распространению импульса АГВ в слое с параболическим профилем температуры, в том числе проанализировано искажение импульсных сигналов АГВ при их распространении на большие расстояния.
Воспользуемся известной системой линейных гидродинамических уравнений, описывающих малые отклонения параметров атмосферы от их равновесных значений (помечены индексом “0”):
(1)
$\begin{gathered} {{\rho }_{0}}\frac{{dv}}{{dt}} + \nabla p - \rho g = 0,\,\,\,\,{{d\rho } \mathord{\left/ {\vphantom {{d\rho } {dt}}} \right. \kern-0em} {dt}} + {{\rho }_{0}}{\text{div}}v = 0, \\ \frac{{dp}}{{dt}} - {{c}^{2}}\frac{{d\rho }}{{dt}} = 0, \\ \end{gathered} $(2)
$\begin{gathered} \frac{{{{\partial }^{4}}\chi }}{{\partial {{t}^{4}}}} - {{c}^{2}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\Delta \chi - \left( {\frac{{d{{c}^{2}}}}{{dz}} - \gamma g} \right)\frac{{{{\partial }^{3}}\chi }}{{\partial {{t}^{2}}\partial z}} - \\ - \,\,g\left[ {\frac{{d{{c}^{2}}}}{{dz}} + \left( {\gamma - 1} \right)g} \right]\left( {\frac{{{{\partial }^{2}}\chi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\chi }}{{\partial {{y}^{2}}}}} \right) = 0, \\ \end{gathered} $(3)
${{p}_{0}}\left( z \right) = {{p}_{0}}\left( {z = 0} \right){\text{exp}}\left( { - \frac{{mg}}{{{{k}_{В}}}}\int\limits_0^z {\frac{{dz}}{{{{T}_{0}}\left( z \right)}}} } \right),$(4)
${{{{\rho }}}_{0}}\left( z \right) = \frac{{{{{{\rho }}}_{0}}\left( {z = 0} \right){{T}_{0}}\left( {z = 0} \right)}}{{{{T}_{0}}\left( z \right)}}{\text{\;exp}}\left( { - \frac{{mg}}{{{{k}_{В}}}}\int\limits_0^z {\frac{{dz}}{{{{T}_{0}}\left( z \right)}}} } \right),$(5)
$\frac{{{{p}_{0}}\left( z \right)}}{{{{p}_{0}}\left( {z = 0} \right)}} = \frac{{{{\rho }_{0}}\left( z \right)}}{{{{\rho }_{0}}\left( {z = 0} \right)}} = {\text{exp}}\left( { - \frac{z}{H}} \right).$(6)
$\chi \left( {r,t} \right)~\sim ~{\text{exp}}\left( { - i\omega t + ikx + i\sigma z + {z \mathord{\left/ {\vphantom {z {2H}}} \right. \kern-0em} {2H}}} \right).$Частота ω и компоненты волнового вектора по горизонтали, k, и вертикали, σ, связаны дисперсионным уравнением [6]:
(7)
${{\omega }^{4}} - {{\omega }^{2}}{{c}^{2}}\left( {{{k}^{2}} + {{\sigma }^{2}} + k_{0}^{2}} \right) + \omega _{g}^{2}{{c}^{2}}{{k}^{2}} = 0.$Уравнение (7) определяет два типа волн: быстрые при $\omega > {{\omega }_{A}} = с{{k}_{0}} = {c \mathord{\left/ {\vphantom {c {2H}}} \right. \kern-0em} {2H}}$ и медленные на частотах ω, меньших частоты Бранта–Вяйсяля ${{\omega }_{g}} = {{\left( {\gamma - 1} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{g \mathord{\left/ {\vphantom {g c}} \right. \kern-0em} c}.$ Уравнение (7) записано без учета потерь из-за вязкости и теплопроводности. Учет теплообмена и политропичности возмущений оставляет справедливым уравнение (7) с заменой $\gamma $ на показатель политропы n, который, как показывают расчеты, сделанные на основе измерений нейтральных температуры и плотности, может достигать значений n = 2 [27].
Влияние вязкости и теплопроводности на характер распространения АГВ оценивалось, например, в работах [28–30]. Из уравнения (7) легко найти групповые, ${{v}_{{grz}}},$ и фазовые, ${{v}_{{ph}}},$ скорости АГВ:
(8)
${{v}_{{grz}}} = \frac{{{{c}^{2}}\omega \sigma }}{{{{\omega }^{2}} - {{\omega _{g}^{2}{{k}^{2}}{{c}^{2}}} \mathord{\left/ {\vphantom {{\omega _{g}^{2}{{k}^{2}}{{c}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}}},\,\,\,\,{{v}_{{grz}}}\sigma = \frac{{{{c}^{2}}\omega {{\sigma }^{2}}}}{{{{\omega }^{2}} - {{\omega _{g}^{2}{{k}^{2}}{{c}^{2}}} \mathord{\left/ {\vphantom {{\omega _{g}^{2}{{k}^{2}}{{c}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}}}.$Как следует из этих формул, групповая скорость по вертикали и вертикальная фазовая скорость имеют противоположные знаки на частотах, меньших частоты Бранта–Вяисяля в силу того, что произведение ${{v}_{{grz}}}\sigma < 0.$ Этот факт необходимо учитывать при анализе распространения сигналов АГВ.
3. МОДЕЛЬ СРЕДЫ РАСПРОСТРАНЕНИЯ СИГНАЛА
В работе [11] решалась модельная задача о падении плоских монохроматических АГВ на слой атмосферы, в котором температура изменяется с высотой по параболическому или линейному законам. Для слоя с параболическим профилем температуры:
(9)
${{T}_{0}}\left( z \right) = {{T}_{S}}\left[ {1 + {{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}} {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}} \right],$(10)
${{p}_{0}}\left( z \right) = {{p}_{0}}\left( {{{z}_{0}}} \right){\text{exp}}\left( { - \frac{h}{{{{H}_{S}}}}{\text{arctg}}\frac{{z - {{z}_{0}}}}{h}} \right),$(11)
$\begin{gathered} {{\rho }_{0}}\left( z \right) = {{\rho }_{0}}\left( {{{z}_{0}}} \right) \times \\ \times \,\,{\text{exp}}\left( { - \frac{h}{{{{H}_{S}}}}{\text{arctg}}\frac{{z - {{z}_{0}}}}{h}} \right){{\left[ {1 + \frac{{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}}}{{{{h}^{2}}}}} \right]}^{{ - 1}}}. \\ \end{gathered} $(12)
${{c}^{2}} = c_{S}^{2}\left[ {1 + {{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}} {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}} \right],$4. РАСПРОСТРАНЕНИЕ ИМПУЛЬСОВ АГВ В АТМОСФЕРЕ
Проанализируем распространение импульса АГВ в слое с параболическим профилем, а также оценим дисперсионное искажение прошедшего и отраженного сигналов. Предположим, что на нижнюю границу слоя при z = z1 под углом $\theta $ к вертикали падает квазимонохроматический импульс АГВ в виде набора плоских волн:
(13)
$\begin{gathered} \chi \left( t \right) = A\left( t \right) \times \\ \times \,\,{\text{exp}}\left\{ { - i{{\omega }_{0}}t + ik\left( {{{\omega }_{0}}} \right)x \pm i\sigma \left( {{{\omega }_{0}}} \right)z + {z \mathord{\left/ {\vphantom {z {2H}}} \right. \kern-0em} {2H}}} \right\}. \\ \end{gathered} $Предполагается, что амплитуда A(t) медленно изменяется со временем, т.е. импульс является узкополосным квазимонохроматическим. Выбор знака в формуле (13) для медленных волн в соответствии с указанным выше определяется направлением групповой скорости (к границе или от нее). Спектр сигнала найдем по формуле [31]
(14)
$f\left( \omega \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {A\left( t \right){\text{exp}}\left( { - i{{\omega }_{0}}t + i\omega t} \right)dt} .$Если длительность импульса $\tau $ велика по сравнению с периодом волн, заполняющих этот импульс, то существенный диапазон частотного спектра мал по сравнению с частотой ${{\omega }_{0}}$ и $\tau \gg {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}.$ Приведем для примера частотные спектры двух сигналов: ${{A}_{1}}\left( t \right) = {\text{exp}}\left( {{{ - {{t}^{2}}} \mathord{\left/ {\vphantom {{ - {{t}^{2}}} {{{\tau }^{2}}}}} \right. \kern-0em} {{{\tau }^{2}}}}} \right)$ и ${{A}_{2}}\left( t \right) = 1~~$ при $~{{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2} \leqslant t \leqslant {\tau \mathord{\left/ {\vphantom {\tau 2}} \right. \kern-0em} 2}$ и ${{A}_{2}}\left( t \right) = 0$ при $~{\tau \mathord{\left/ {\vphantom {\tau 2}} \right. \kern-0em} 2}~ < t < {{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2}.$ Для первого из них получаем гауссов спектр, а для второго – синусоидальный:
(15)
${{f}_{1}}\left( \omega \right) = \frac{\tau }{{2\sqrt \pi }}{\text{exp}}\left\{ {{{ - {{{\left( {\omega - {{\omega }_{0}}} \right)}}^{2}}{{\tau }^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {\omega - {{\omega }_{0}}} \right)}}^{2}}{{\tau }^{2}}} 4}} \right. \kern-0em} 4}} \right\},$(16)
${{f}_{2}}\left( \omega \right) = \frac{\tau }{{2\pi }}\frac{{{\text{sin}}u}}{u},\,\,\,\,u = {{\left( {\omega - {{\omega }_{0}}} \right)\tau } \mathord{\left/ {\vphantom {{\left( {\omega - {{\omega }_{0}}} \right)\tau } 2}} \right. \kern-0em} 2}.$Таким образом, исходный импульс АГВ представлен набором плоских волн с амплитудой $f\left( \omega \right)$ каждой составляющей в спектре. Легко проверить, что при $\tau \to \infty $ оба спектра, (15) и (16), превращаются в дельта-функцию Дирака $\delta \left( {\omega - {{\omega }_{0}}} \right)$ и обратная свертка по частотам дает выражение
5. ЧИСЛЕННЫЙ АНАЛИЗ РАСПРОСТРАНЕНИЯ АГВ В ВИДЕ ИМПУЛЬСОВ
В работе [11] нами были найдены коэффициенты отражения и прохождения плоских монохроматических АГВ для атмосферных слоев с линейным и параболическим высотными профилями равновесной температуры, а также выполнен численный расчет вертикальной структуры мод АГВ внутри таких слоев. В данной же работе мы рассмотрим прохождение и отражение сигналов АГВ конечной длительности от слоя атмосферы, в котором температура изменяется по параболическому закону. Алгоритм решения сформулированной задачи состоит из следующих этапов. Исходный импульс представляется совокупностью плоских волн, каждая из которых имеет соответствующую амплитуду в спектре – $f\left( \omega \right).$ Для каждой составляющей спектра численно решается уравнение (2) с граничными условиями, сформулированными в [11], для которых требуется непрерывность дивергенции скорости и ее производной ${{\chi }_{1}} = {{\chi }_{2}},$ ${{d{{\chi }_{1}}} \mathord{\left/ {\vphantom {{d{{\chi }_{1}}} {dz}}} \right. \kern-0em} {dz}} = {{d{{\chi }_{2}}} \mathord{\left/ {\vphantom {{d{{\chi }_{2}}} {dz}}} \right. \kern-0em} {dz}},$ и определяются коэффициенты отражения и прохождения волны через слой – $~R\left( \omega \right)$ и $~D\left( \omega \right).$ Таким образом, отраженный, ${{\chi }_{{ref}}},$ и прошедший, ${{\chi }_{{pas}}},$ импульсы АГВ представляются следующими выражениями [4]:
(17)
$\begin{gathered} {{\chi }_{{ref}}} = \int\limits_{ - \infty }^{ + \infty } {f\left( \omega \right)R\left( \omega \right)} \times \\ \times \,\,{\text{exp}}\left\{ { - i\omega t + ik\left( \omega \right)x \pm i\sigma \left( {z - {{z}_{1}}} \right)} \right\}d\omega + {\text{к}}{\text{.с}}{\text{.}}, \\ \end{gathered} $(18)
$\begin{gathered} {{\chi }_{{pas}}} = \int\limits_{ - \infty }^{ + \infty } {f\left( \omega \right)D\left( \omega \right)} \times \\ \times \,\,{\text{exp}}\left\{ { - i\omega t + ik\left( \omega \right)x \pm i\sigma \left( {z - {{z}_{2}}} \right)} \right\}d\omega + {\text{к}}{\text{.с}}{\text{.}}, \\ \end{gathered} $Анализ коэффициентов отражения, $R\left( \omega \right),$ и прохождения, $D\left( \omega \right),$ волны также выполнен нами в работе [11]. Отметим, что с ростом угла падения волны на слой коэффициент отражения растет, а коэффициент прохождения падает, в то время как с ростом частоты ω падает доля отраженной от слоя волны и растет доля волны, проходящей через слой.
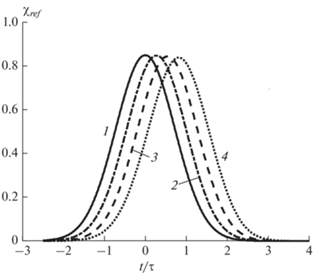
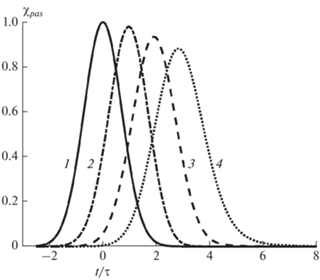
На рис. 3 и 4 приведены рассчитанные формы импульсов АГВ, отраженных и прошедших через указанный выше слой атмосферы при следующих значениях параметров: угол падения волны на слой $\theta = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4},$ частота ${{\omega }_{0}} = 1.7{{\omega }_{g}},$ длительность $~\tau = 673\,{\text{с}},$ частота Вяйсяля–Бранта ${{\omega }_{g}} = 0.0274\,{{{\text{с}}}^{{ - 1}}}$ (соответствующий период равен ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\omega }_{g}}}}} \right. \kern-0em} {{{\omega }_{g}}}} = 3.82\,{\text{мин}}$). При этом групповые скорости импульса по вертикали и горизонтали равны 0.5 с, а отношения волновых чисел ${k \mathord{\left/ {\vphantom {k {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}} = {\sigma \mathord{\left/ {\vphantom {\sigma {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}} = 0.824$ (при длине волны $\lambda = 15.25H$).
Рис. 3.
Огибающие отраженных импульсов АГВ на разных расстояниях от поверхности земли при угле падения θ = π/4 и несущей частоте ω0 = 1.7ωg: z = 95 (1), 66.5 (2), 38 (3) и 9.5 км (4).
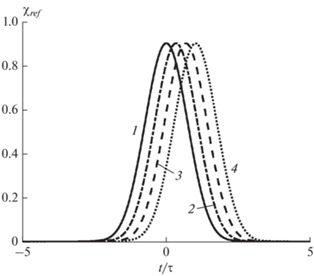
Рис. 4.
Огибающие прошедших через слой импульсов АГВ на разных расстояниях от поверхности земли при угле падения θ = π/4 и несущей частоте ω0 = = 1.7ωg: z = 105 (1), 300 (2), 600 (3) и 900 км (4).
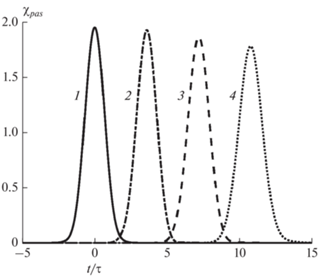
На рис. 5 и 6 показаны рассчитанные формы импульсов для частоты заполнения ${{\omega }_{0}} = 0.55~{{\omega }_{g}}$ и угла падения $\theta = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ Для них задана длительность $\tau = 2300\,{\text{с}}$ (34.6 мин). Из этих рисунков видно, что отраженные импульсы практически не меняют своей формы вследствие ограниченных расстояний распространения и больших длин волн, в то время как деформация прошедших импульсов растет с удалением от слоя и ростом пройденного расстояния, а их амплитуда уменьшается. Полученный результат может быть важен при идентификации искусственных АГВ, возбуждаемых в ионосфере при воздействием на нее излучения нагревного стенда или других источников с известными характеристиками.
6. ДИСПЕРСИОННОЕ ИСКАЖЕНИЕ ИМПУЛЬСОВ АГВ
Определим условия, при выполнении которых дисперсионное искажение сигналов АГВ является слабым. Такая оценка также является важной для решения задачи отличия естественных волновых возмущений от генерируемых искусственно. Если известны параметры искусственно возбуждаемых сигналов АГВ, то их регистрация в удаленных приемных пунктах возможна с сохранением ими первоначальных параметров в том случае, если выполнены условия слабого искажения сигнала. На расстоянии $r = {{\left( {{{x}^{2}} + {{z}^{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ от места возбуждения волн (например, от пункта воздействия на ионосферу излучения мощных нагревных стендов или других источников) квазимонохроматический сигнал можно представить в виде [9]
(19)
$\begin{gathered} u\left( {t,x,z} \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {A\left( \zeta \right)} {\text{exp}}\left( { - i{{\omega }_{0}}\zeta + i\omega \zeta } \right)d\zeta \times \\ \times \,\,\int\limits_{ - \infty }^{ + \infty } {{\text{exp}}\left\{ { - i\omega t + ixk\left( {{{\omega }_{0}}} \right) + iz\sigma \left( {{{\omega }_{0}}} \right)} \right\}d\omega } . \\ \end{gathered} $Если амплитуда $A\left( \zeta \right)$ является медленной функцией времени и длительность импульса велика по сравнению с периодом заполнения и, значит, ширина его спектра мала, то компоненты волнового вектора по горизонтали, k, и вертикали, σ, можно представить в виде рядов, ограничиваясь вторыми членами разложения:
(20)
$k(\omega ) = k\left( {{{\omega }_{0}}} \right) + {{\left( {\frac{{\partial k}}{{\partial \omega }}} \right)}_{{{{\omega }_{0}}}}}\left( {\omega - {{\omega }_{0}}} \right) + {{\delta }_{1}}{{\left( {\omega - {{\omega }_{0}}} \right)}^{2}}~,$(21)
$\sigma \left( \omega \right) = \sigma \left( {{{\omega }_{0}}} \right) + {{\left( {\frac{{\partial \sigma }}{{\partial \omega }}} \right)}_{{{{\omega }_{0}}}}}\left( {\omega - {{\omega }_{0}}} \right) + {{\delta }_{2}}{{\left( {\omega - {{\omega }_{0}}} \right)}^{2}},$В общем случае выражения для ${{\delta }_{1}}~$ и ${{\delta }_{2}}~$ представляются громоздкими формулами и здесь не приводятся. Приведем их только для упрощенных выражений ветвей дисперсионного уравнения. Для быстрых волн хорошей является аппроксимация ω+ = $ = c{{\left( {{{k}^{2}} + {{\sigma }^{2}} + k_{0}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ и ${{\omega }_{ - }} = {{\omega }_{g}}k{{\left( {{{k}^{2}} + {{\sigma }^{2}} + k_{0}^{2}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$ – для медленных. Для этих приближенных дисперсионных уравнений получим выражения
(22)
$\delta _{1}^{ - } = \frac{{\omega _{g}^{2}{{k}^{3}}}}{{2{{\omega }^{4}}\left( {{{k}^{2}} + k_{0}^{2}} \right)}}\left( {\frac{{5{{k}^{2}}}}{{{{k}^{2}} + k_{0}^{2}}} - 1} \right),$(23)
$\delta _{2}^{ - } = - \frac{{\omega _{g}^{2}{{k}^{4}}}}{{2\sigma {{\omega }^{4}}}}\left[ {\frac{{\omega _{g}^{2}k_{0}^{2}}}{{{{\omega }^{2}}{{\sigma }^{2}}\left( {{{\sigma }^{2}} + k_{0}^{2}} \right)}} + 3\left( {\frac{1}{{{{\sigma }^{2}} + k_{0}^{2}}} - \frac{1}{{{{k}^{2}}}}} \right)} \right],$(24)
$\delta _{1}^{ + } = \frac{{{{k}^{2}} - \left( {{{\sigma }^{2}} + k_{0}^{2}} \right)}}{{2{{c}^{2}}{{k}^{3}}}},\,\,\,\,\delta _{2}^{ + } = \frac{{{{\sigma }^{2}} - \left( {{{k}^{2}} + k_{0}^{2}} \right)}}{{2{{c}^{2}}{{\sigma }^{3}}}}.$Подставляя выражения (20) и (21) в интегральное представление для импульса (19), получим
(25)
$\begin{gathered} u\left( {t,x,z} \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {A\left( \zeta \right)} {\text{exp}}\left( { - i{{\omega }_{0}}\zeta + i\omega \zeta } \right)d\zeta \times \\ \times \,\,\int\limits_{ - \infty }^{ + \infty } {{\text{exp}}\left\{ { - i\omega t + ix\left[ {k\left( {{{\omega }_{0}}} \right) + {{{\left( {\frac{{dk}}{{d\omega }}} \right)}}_{{{{\omega }_{0}}}}} \times } \right.} \right.} \\ \left. { \times \,\,\left( {\omega - {{\omega }_{0}}} \right) + {{\delta }_{1}}{{{\left( {\omega - {{\omega }_{0}}} \right)}}^{2}}} \right] + \\ + \,\,\left. {iz\left[ {\sigma \left( {{{\omega }_{0}}} \right) + {{{\left( {\frac{{d\sigma }}{{d\omega }}} \right)}}_{{{{\omega }_{0}}}}}\left( {\omega - {{\omega }_{0}}} \right) + {{\delta }_{2}}{{{\left( {\omega - {{\omega }_{0}}} \right)}}^{2}}} \right]} \right\}d\omega . \\ \end{gathered} $Если в формуле (25) не учитывать вклад слагаемых с параметрами дисперсии δ1 и δ2, то на расстоянии r получим неискаженную форму импульса [4, 9]:
(26)
$\begin{gathered} u\left( {t,x,.z} \right) = A\left( {t - x\left( {\frac{{\partial \omega }}{{\partial k}}} \right){{{_{{{{\omega }_{0}}}}^{{ - 1}}}}_{{}}} - z\left( {\frac{{\partial \omega }}{{\partial \sigma }}} \right){{{_{{{{\omega }_{0}}}}^{{ - 1}}}}_{{}}}} \right) \times \\ \times \,\,{\text{exp}}\left\{ { - i{{\omega }_{0}}t + ik\left( {{{\omega }_{0}}} \right)x + i\sigma \left( {{{\omega }_{0}}} \right)z} \right\}. \\ \end{gathered} $Больший интерес представляет форма импульса с учетом в его интегральном представлении квадратичных по частоте слагаемых. Если за исходную форму импульса ${{A}_{1}}\left( t \right)$ принять гауссову форму, то интегрирование в (25) для него при использовании параметров дисперсии для АГВ в (20)–(24) выполняется до конца. Из-за громоздкости получающихся выражений для произвольного момента времени итоговый вид сигнала мы здесь не приводим, но отметим, что полученный результат позволяет найти ограничения на дальность распространения импульсов АГВ, при которых искажения импульсов АГВ являются незначительными. Запишем эти условия в виде
(27)
$x \ll {{{{x}_{0}} = {{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{x}_{0}} = {{\tau }^{2}}} {4{{\delta }_{1}}}}} \right. \kern-0em} {4{{\delta }_{1}}}},\,\,\,\,z \ll {{{{z}_{0}} = {{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{z}_{0}} = {{\tau }^{2}}} {4{{\delta }_{2}}}}} \right. \kern-0em} {4{{\delta }_{2}}}}.$При выполнении этих условий огибающая исходного импульса имеет вид
(28)
$u\left( {t,x,z} \right) = {\text{exp}}\left\{ {{{ - {{{\left( {t - {x \mathord{\left/ {\vphantom {x {{{V}_{{grx}}}}}} \right. \kern-0em} {{{V}_{{grx}}}}} - {z \mathord{\left/ {\vphantom {z {{{V}_{{grz}}}}}} \right. \kern-0em} {{{V}_{{grz}}}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {t - {x \mathord{\left/ {\vphantom {x {{{V}_{{grx}}}}}} \right. \kern-0em} {{{V}_{{grx}}}}} - {z \mathord{\left/ {\vphantom {z {{{V}_{{grz}}}}}} \right. \kern-0em} {{{V}_{{grz}}}}}} \right)}}^{2}}} {{{\tau }^{2}}}}} \right. \kern-0em} {{{\tau }^{2}}}}} \right\}.$Приведем численные оценки дальности распространения импульсов АГВ при следующих значениях параметров: угол θ между вертикалью и вектором k равен ${\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4},$ частота ${{\omega }_{0}} = 1.7{{\omega }_{g}}.$ При этом оказывается, что k = σ = 0.824k0 и $\delta _{1}^{ + } = \delta _{2}^{ + }~$ = = 0.127 с2/м. При длительности импульса τ = = ${{10\pi } \mathord{\left/ {\vphantom {{10\pi } {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ (около 670 с) получаем x0 = z0 ≈ 1700 км. В этом случае дисперсионное искажение сигналов с указанными параметрами является незначительным вплоть до расстояний порядка 600 км. В случае низких частот (для примера ${{\omega }_{0}} = 0.55{{\omega }_{g}}$) с периодом порядка 7 мин и при угле падения $\theta = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ имеем $\delta _{1}^{ - } = 0.2$ с2/м и $\delta _{2}^{ - } = 0.66\,{{{{{\text{с}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\text{с}}}^{2}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}.{\text{\;}}$ Это означает, что при $\tau = 5{{T}_{0}}$ (что составляет примерно 2100 с) импульс внутренних гравитационных волн (ВГВ) должен сохранять свою первоначальную форму вплоть до расстояний порядка 1000 км. Такие сравнительно большие значения расстояний неискаженного распространения импульсов ВГВ обусловлены большими длительностями $\tau $ и квадратичной зависимостью оцениваемых расстояний от длительности сигнала ВГВ. Напомним, что приведенные оценки являются справедливыми для узкополосных квазигармонических импульсов при $\tau \gg {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}.$ Отсюда следует важный вывод о том, что при выполнении определенных условий импульсы АГВ, создаваемые, например, искусственным источником, могут быть зарегистрированы неискаженными на очень больших расстояниях от него.
7. ЗАКЛЮЧЕНИЕ
В работе сформулирована и решена задача о распространении импульсов акустико-гравитационных волн через слои атмосферы с параболической зависимостью равновесной температуры от высоты. Получен критерий слабых дисперсионных искажений импульсов АГВ при их распространении на значительные расстояния. Приведенные выше аналитические оценки являются приближенными в связи с использованием упрощенных выражений для дисперсионного уравнения и разложения компонент волнового вектора в ряд по частоте. Численно рассчитаны формы импульсов АГВ без введения указанных упрощений с учетом коэффициентов отражения и прохождения волн через параболический слой температуры. Показано удовлетворительное соответствие результатов, полученных обоими методами. Отметим, что в рассмотренных случаях метод геометрической оптики не пригоден вследствие низких частот и больших по сравнению с масштабами слоя длин волн. Другой задачей, представляющей практический интерес, является анализ распространения широкополосных импульсов АГВ в атмосфере Земли с учетом влияния ветра на их дисперсионное искажение.
Экспериментальные данные по температуре атмосферы были получены на нагревном стенде СУРА, который в 2020–2022 гг. поддерживался в рабочем состоянии в рамках выполнения проекта Минобрнауки № 0729-2020-0057 по базовой части госзадания.
Работа выполнена при финансовой поддержке Российским научным фондом по гранту № 20-17-00050.
Список литературы
Ламб Г. Гидродинамика. М.: ОГИЗ, 1947.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1956.
Fritts D.C., Alexander M.J. // Rev. Geophys. 2003. V. 41. № 1. P. 1003.
Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1973.
Hines C.O. // Can. J. Phys. 1960. V. 38. № 11. C. 1441.
Госсард Э., Хук У. Волны в атмосфере. М.: Мир, 1978.
Morse P.M., Ingard K.U. Theoretical acoustics. New York, London: McGrow Hill Book Company, 1968.
Yeh K.C., Liu C.H. // Rev. Geophys. 1974. V. 12. № 2. P. 193; https://doi.org/10.1029/RG012i002p00193
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Физматгиз, 1979.
Келлер Дж.Б., Пападакис Дж.С. Распространение волн и подводная акустика. М.: Мир, 1980.
Бахметьева Н.В., Григорьев Г.И., Калинина Е.Е. // Хим. физика. 2022. Т. 41. № 5. С. 44.
Kshevetski S.P., Kurdyaeva Y.A., Gavrilov N.M. // Atmosphere. 2021. V. 12. № 7. P. 818; https://doi.org/10.3390/atmos12070818
Голубков Г.В., Адамсон С.О., Борчевкина О.П. и др. // Хим. физика. 2022. Т. 41. № 5. С. 531.
Карпов И.В., Борчевкина О.П., Васильев П.А. // Хим. физика. 2020. Т. 39. № 4. С. 63.
Волновые процессы в атмосфере Земли и их влияние на ионосферу / Под ред. акад. Г.А. Жеребцова. М.: ГЕОС, 2020.
Бахметьева Н.В., Жемяков И.Н. // Хим. физика. 2022. Т. 41. № 10. С. 65.
Черногор Л.Ф., Фролов В.Л., Комраков Г.П., Пушин В.Ф. // Изв. вузов. Радиофизика. 2011. Т. 54. № 2. С. 81.
Черногор Л.Ф., Фролов В.Л. // Изв. вузов. Радиофизика. 2013. Т. 56. № 4. С. 219.
Mishin E., Sutton E., Milikh G. et al. // Geophys. Res. Let. 2012. V. 39. L11101; https://doi.org/10.1029/2012GL052004
Chunchuzov I., Kulichkov S., Popov O., Hedlin M. // J. Acoust. Soc. Amer. 2014. V. 135. № 1. P. 38.
Бацына Е.К., Петрухин Н.С., Пелиновский Е.Н. Безотражательное распространение волн в неоднородной сжимаемой атмосфере Земли и Солнца. Нижний Новгород: РАСТР–НН, 2014.
Заславский Ю.М. Излучение сейсмических волн вибрационными источниками. Нижний Новгород: ИПФ, 2007.
Куницын В.Е., Воронцов А.М., Крысанов Б.Ю. // Вестн. МГУ. Сер. 3, Физика, астрономия. 2015. № 6. С. 112.
Беликович В.В., Бенедиктов Е.А., Толмачёва А.В., Бахметьева Н.В. Исследование ионосферы с помощью искусственных периодических неоднородностей. Н. Новгород: Изд-во ИПФ РАН, 1999.
Bakhmetieva N.V., Grigoriev G.I., Tolmacheva A.V., Zhemyakov I.N. // Atmosphere. 2019. V. 10. № 8. P. 450.
Митра С.К. Верхняя атмосфера. М.: Изд-во иностр. лит., 1955.
Григорьев Г.И., Толмачева А.В. // Хим. физика. 2021. Т. 40. № 5. С. 91.
Голицын Г.С. // Изв. АН СССР. Физика атмосферы и океана. 1965. Т. 1. С. 82.
Pitteway M.L.V., Hines C.O. // Can. J. Phys. 1963. V. 41. P. 1935.
Godin O.A. // J. Acoust. Soc. Amer. 2014. V. 136. № 6. P. EL411.
Харкевич А.А. Спектры и анализ. М.: Физматлит, 1962.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика