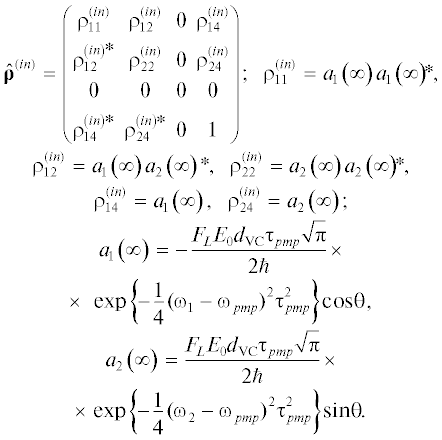Химическая физика, 2022, T. 41, № 9, стр. 72-82
Возбуждение и стимулированное излучение Mn2+(3d5) в допированных марганцем квантовых точках ZnCdS в фемтосекундном эксперименте накачка–зондирование
А. С. Ветчинкин 1, С. Я. Уманский 1, *, Ю. А. Чайкина 1, А. И. Шушин 1
1 Федеральный исследовательский центр химической физики им. Н.Н. Семёнова Российской академии наук
Москва, Россия
* E-mail: unan43@mail.ru
Поступила в редакцию 25.08.2021
После доработки 09.09.2021
Принята к публикации 20.09.2021
- EDN: FADZFP
- DOI: 10.31857/S0207401X22090102
Аннотация
Построена модель возбуждения ${\text{M}}{{{\text{n}}}^{{2 + }}}$(6A) в допированных марганцем квантовых точках (КТ) ZnCdS фемтосекундным лазерным импульсом с несущей частотой, близкой к частоте радиационного перехода между краем валентной зоны и краем зоны проводимости. Модель базируется на том, что возбужденное состояние 4T иона, локализованного вблизи ловушки электрона с энергией в запрещенной зоне, перемешивается обменным взаимодействием с состояниями электронов в зоне проводимости КТ. Модель описывает экспериментально наблюдаемое при очень малых временах задержки между накачивающим и зондирующим лазерными импульсами растущее с ростом времени задержки стимулированное зондирующим импульсом излучение на частоте, отвечающей переходу 4T → 6A в ${\text{M}}{{{\text{n}}}^{{2 + }}}.$
ВВЕДЕНИЕ
В последние годы большой интерес исследователей вызывают полупроводниковые квантовые точки (КТ). Это связано с их уникальными электронными и оптическими свойствами, которые обусловлены эффектом размерного квантования. Простота в управлении размерами нанокристаллов и их яркая люминесценция являются хорошей платформой для использования в фотовольтаике и оптоэлектронике [1–3].
Одним из типов полупроводниковых КТ, привлекающих внимание исследователей, являются КТ, допированные ${\text{M}}{{{\text{n}}}^{{2 + }}}$ [4–15]. Дело в том, что многие полупроводники имеют широкую запрещенную зону, что ограничивает возможности поглощения видимого света соответствующими КТ. В то же время ${\text{M}}{{{\text{n}}}^{{2 + }}}$ может излучать оранжевый свет с длиной волны около 590 нм, отвечающий запрещенному по спину переходу 4T1 → 6A1.
Для того чтобы использовать это свойство допанта ${\text{M}}{{{\text{n}}}^{{2 + }}},$ необходима безызлучательная передача электронного возбуждения кристалла-хозяина допанту [15–25]. Практически во всех экспериментах наблюдалось время такой передачи в пикосекундном диапазоне. Исключение представляет работа [25], в которой проводились фемтосекундные эксперименты накачка–зондирование с допированными Mn2+(3d5) квантовых точках ZnxCd1 –xS и ZnxCd1 –xS/ZnS в коллоидном растворе в циклогексане. Накачивающий лазерный импульс имел несущую частоту ωpmp, несколько меньшую, чем частота ωCBEX радиационного перехода между краем валентной зоны и краем зоны проводимости (см. рис. 1).
Рис. 1.
Система электронных состояний и энергий в квантовых точках ZnCdS, допированных ${\text{M}}{{{\text{n}}}^{{2 + }}}(3{{d}^{5}}){\text{:}}$ VB – валентная зона, CB – зона проводимости, ${\text{E}}{{{\text{l}}}_{{{\text{Tr}}}}}{{{\text{H}}}_{{{\text{VB}}}}}$ – электрон в ловушке с дыркой в VB, $~{\text{E}}{{{\text{l}}}_{{{\text{CB}}}}}{{{\text{H}}}_{{{\text{VB}}}}}$ – электрон на краю CB с дыркой в VB, ${{E}_{{{\text{Tr}}}}}$ – энергия электрона в ловушке, ${{\Delta }}{{E}_{{{\text{Mn}}}}}$ – энергия перехода ${\text{M}}{{{\text{n}}}^{{2 + }}}$(4T) → ${\text{M}}{{{\text{n}}}^{{2 + }}}$(6A), $~{{E}_{{{\text{CB}}}}}~$ – энергия края зоны проводимости, SE – стимулированное зондирующим лазерным импульсом излучение, CBEX – возбуждение квантовой точки накачивающим лазерным импульсом.
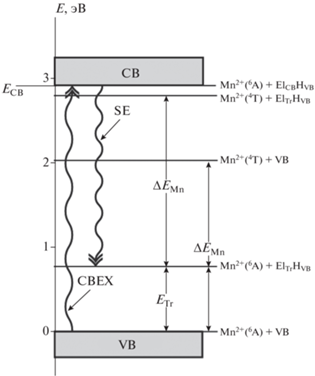
В этих экспериментах уже при временах задержки (τdel) между накачивающим и зондирующим импульсами τdel ≥ 120 фс наблюдалось медленно растущее с ростом τdel стимулированное зондирующим импульсом излучение (SE) в области длин волн ~590 нм, отвечающей полосе длин волн излучения при переходе 4T1 → 6A1 в Mn2+(3d5). Дефект резонанса при передаче энергии возбуждаемого накачивающим импульсом экситона допанту Mn2+(6A1) в основном электронном состоянии 6A1 с образованием Mn2+(4T1) в возбужденном состоянии 4T1 довольно велик (>5 · 103 см–1). Такую энергию надо передать фононам. Это многофононный процесс, и поэтому его время существенно превышает 120 фс. В настоящей работе предлагается простая модель, позволяющая качественно объяснить наблюдаемый в работе [25] эффект.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Модель электронной подсистемы
Предлагаемая модель, объясняющая быстрое появление стимулированного излучения в экспериментах накачка–зондирование в работе [25] тем, что в полупроводниковых КТ имеется весьма высокая концентрация ловушек электронов с энергиями в запрещенной зоне [26–36].
Предполагается, что в рассматриваемом коллоидном растворе имеется некоторая заметная концентрация $N{\text{*}}$ наночастиц, в которых присутствуют “комплексы” Mn2+(6A1)/Tr. В этих комплексах Mn2+(6A1) локализован вблизи ловушки Tr, электронный уровень которой ${{E}_{{{\text{Tr}}}}}$ (см. рис. 1) удовлетворяет следующему условию:
(1)
$\left| {{{\Delta }}{{E}_{{{\text{Mn}}}}} + {{E}_{{{\text{Tr}}}}} - {{E}_{{{\text{CB}}}}}} \right| \ll {{E}_{{{\text{CB}}}}} - {{\Delta }}{{E}_{{{\text{Mn}}}}}.$В пренебрежении взаимодействием между электронами, принадлежащими ZnxCd1 –xS и Mn2+ волновые функции “комплексов” Mn2+(6A1) + + ElСВHVB, Mn2+(4T) + ElTrHVB, Mn2+(6A1) + ElTrHVB и Mn2+(6A1) + VB (см. рис. 2) могут быть представлены в следующем виде:
(2)
$\begin{gathered} {{\Phi }_{1}}({{{\mathbf{r}}}_{e}},{{{\mathbf{r}}}_{{e,{\text{Mn}}}}}) = {{\Theta }_{{{\text{CB}}}}}({{{\mathbf{r}}}_{e}}){{\Phi }_{{{\text{Mn}}}}}({{{\mathbf{r}}}_{{e,{\text{Mn}}}}}), \\ {{\Phi }_{2}}({{{\mathbf{r}}}_{e}},{{{\mathbf{r}}}_{{e,{\text{Mn}}}}}){\text{ }} = {{\Theta }_{{{\text{Tr}}}}}({{{\mathbf{r}}}_{e}}){{\Phi }_{{{\text{Mn*}}}}}({{{\mathbf{r}}}_{{e,{\text{Mn}}}}}), \\ {{\Phi }_{3}}({{{\mathbf{r}}}_{e}},{{{\mathbf{r}}}_{{e,{\text{Mn}}}}}){\text{ }} = {{\Theta }_{{{\text{Tr}}}}}({{{\mathbf{r}}}_{e}}){{\Phi }_{{{\text{Mn}}}}}({{{\mathbf{r}}}_{{e,{\text{Mn}}}}}), \\ {{\Phi }_{4}}({{{\mathbf{r}}}_{e}},{{{\mathbf{r}}}_{{e,{\text{Mn}}}}}){\text{ }} = {{\Theta }_{{{\text{VB}}}}}{{\Phi }_{{{\text{Mn}}}}}({{{\mathbf{r}}}_{{e,{\text{Mn}}}}}). \\ \end{gathered} $Рис. 2.
Четырехуровневая модель электронных состояний, описывающая показанную на рис. 1 электронную подсистему квантовой точки ZnxCd1 –xS/Mn2+(3d5).
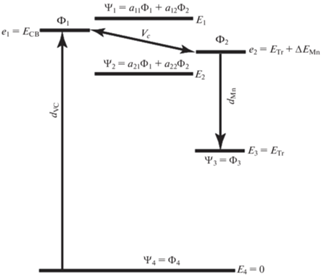
Следует подчеркнуть, что все это относится к качественной модели, не учитывающей спины электронов и спин-орбитальное взаимодействие. При этом в рамках более детального рассмотрения можно показать, что сохранение полного спина может быть обеспечено для всех представляющих интерес радиационных переходов в системе ZnxCd1 – xS/Mn2+ обменным взаимодействием между электронными подсистемами ZnxCd1 –xS и Mn2+ (см. [37–39]). Соответственно, в предлагаемой модели вводятся эффективные дипольные моменты перехода
(3)
$\begin{gathered} {{d}_{{{\text{VC}}}}} = \left\langle {{{\Phi }_{4}}\left| {{\mathbf{\hat {D}}}} \right|{{\Phi }_{1}}} \right\rangle , \hfill \\ {{d}_{{{\text{Mn}}}}} = \left\langle {{{\Phi }_{2}}\left| {{\mathbf{\hat {D}}}} \right|{{\Phi }_{3}}} \right\rangle , \hfill \\ \end{gathered} $В рассматриваемой здесь модели особенно важно, что не равен нулю матричный элемент Vc = 〈Φ1|${{\hat {V}}_{{ex}}}$|Φ2〉, где ${{\hat {V}}_{{ex}}}$ – оператор обменного взаи модействия. Всюду ниже для простоты будем предполагать, что матричный элемент Vc действителен. Как показывают расчеты, проведенные в работах [37–39], |Vc| имеет порядок величины 101–102 см–1. Это приводит к тому, что состояния Φ1(${{r}_{e}},$ ${{r}_{{e,{\text{Mn}}}}}$) и Φ2(${{r}_{e}},$ ${{r}_{{e,{\text{Mn}}}}}$) перемешиваются, а соответствующие им уровни энергии расталкиваются (см. рис. 2). Что касается изолированных по энергии состояний Φ3 и Φ4, то влияние обменного взаимодействия на эти состояния не существенно и учитываться здесь не будет.
Волновые функции и уровни энергии перемешанных состояний Ψ1 и Ψ2
Базис модельных электронных состояний, не учитывающий слабую связь между электронной системой квантовой точки ZnCdS и допанта Mn2+(3d5), включает четыре состояния (см. (2) и рис. 2). В соответствии c рис. 2 матрица ${{{\mathbf{\hat {H}}}}^{{(d)}}}$ электронного гамильтониан на ${\mathbf{\hat {H}}}$ в базисе состояний Φ1, Φ2,Φ3, Φ4 имеет следующий вид (здесь и всюду ниже электронная энергия отсчитывается от уровня энергии $E$4 = 0 основного состояния Φ4):
(4)
${{{\mathbf{\hat {H}}}}^{{(d)}}} = \left( {\begin{array}{*{20}{c}} {{{e}_{1}}}&{{{V}_{c}}}&0&0 \\ {{{V}_{c}}}&{{{e}_{2}}}&0&0 \\ 0&0&{{{E}_{3}}}&0 \\ 0&0&0&{{{E}_{4}}} \end{array}} \right).$При этом перемешанные функции Ψ1 и Ψ2 имеют следующий вид:
(5)
$\begin{gathered} {{\Psi }_{1}} = \cos \theta {{\Phi }_{1}} + \sin \theta {{\Phi }_{2}}, \\ {{\Psi }_{2}} = - \sin \theta {{\Phi }_{1}} + \cos \theta {{\Phi }_{2}}, \\ \end{gathered} $(6)
${{\theta }} = \frac{1}{2}{\text{arctan}}\left( {\frac{{2{{V}_{c}}}}{{{{e}_{1}} - {{e}_{2}}}}} \right).$Соответствующие же уровни энергии E1 и E2 определяются следующими формулами:
(7)
${{E}_{{1,2}}} = \frac{1}{2}({{e}_{1}} + {{e}_{2}}) \pm \frac{1}{2}{{\left[ {{{{({{e}_{1}} - {{e}_{2}})}}^{2}} + 4V_{c}^{2}} \right]}^{{1{\text{/}}2}}}.$В рассматриваемой модели электронных состояний (см. (4)–(7)и рис. 2) состояния Φ3 и Φ4, далеко отстоящие по энергии от состояний Φ1 и Φ2 и друг от друга, и соответствующие им уровни энергии не модифицируются обменным взаимодействием. Ниже для единообразия для них будут использоваться обозначения Ψ3 и Ψ4 и E3 и E4. Матрица ${{{\mathbf{\hat {H}}}}^{{(ad)}}}$ электронного гамильтониана H в базисе состояний Ψ1, Ψ2,Ψ3 и Ψ4 имеет следующий диагональный вид:
Схема эксперимента
Прежде чем переходить к рассмотрению интерпретации результатов экспериментов, полученных в работе [25] в рамках описанной выше модели электронной подсистемы наночастиц с ионами Mn2+(6A1), локализованными вблизи ловушки электрона с энергией в запрещенной зоне, представляется полезным описать схему этих экспериментов. Следует отметить, что в этих экспериментах использовался метод накачка–зондирование, в котором накачка осуществлялась спектрально ограниченным импульсом, но зондирование проводилось импульсом-суперконтинуумом с аномально широким спектром (см. [40]). Импульс-суперконтинуум имеет ту же длительность: ~10 фс, что и обычно используемые спектрально ограниченные импульсы. Однако этот импульс имеет очень большую спектральную ширину: ~104 см–1. Характерная же спектральная ширина спектрально ограниченных импульсов имеет величину ~103 см–1. Импульсы-суперконтинуумы с указанными свойствами необходимы при исследовании очень быстрых (с характерным временем ~10–13–10–12 с) процессов передачи энергии между различными электронными состояниями, дефект резонанса которых часто превышает 5 · 103 см–1 (в рассматриваемом здесь случае его величина составляет примерно 6 · 103 см–1).
На рис. 3 представлена схема экспериментов, проведенных в работе [25]. Мощный спектрально ограниченный фемтосекундный импульс 2 разделяется на два импульса. Импульс 21 проходит через линию задержки 6 и кювету 7 со взвесью квантовых точек в циклогексане и осуществляет их возбуждение. Импульс 22 поступает в элемент 4, преобразующий спектрально-ограниченный фемтосекундный импульс в фемтосекундный импульс-суперконтинуум 5.
Рис. 3.
Схема эксперимента накачка-зондирование с зондирующим импульсом-суперконтинуумом: 1 – основной блок экспериментальной установки; 2 – исходный мощный спектрально ограниченный фемтосекундный импульс, который полупрозрачным зеркалом разделяется на импульсы 21 и 22; 3 – блок сравнения; 4 – элемент преобразования спектральноограниченного фемтосекундного импульса в фемтосекундный импульс суперконтинуум; 5 – фемтосекундный импульс-суперконтинуум; который полупрозрачным зеркалом разделяется на импульсы 51 и 52; 6 – линия задержки; 7 – кювета со взвесью квантовых точек в циклогексане; 8 – полихроматор, позволяющий получить спектр коэффициента поглощения.
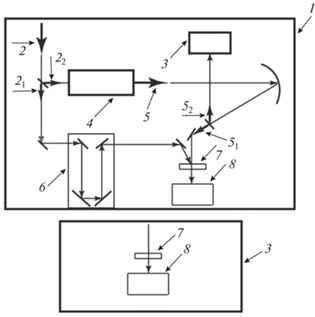
Импульс 5 также разделяется на два. Импульс 51 поступает в кювету 7 через время задержки ${{\tau }_{{del}}}$ после импульса 21 и зондирует временнýю эволюцию возбужденных электронных состояний квантовых точек. Эта эволюция регистрируется полихроматором, позволяющим получить спектр коэффициента поглощения ${{A}_{{ex}}}\left( {\omega ,{{\tau }_{{del}}}} \right).$ Функция ${{A}_{{ex}}}\left( {\omega ,{{\tau }_{{del}}}} \right)$ описывает не только возбуждение квантовых точек накачивающим импульсом 21 и временнýю эволюцию соответствующих возбужденных состояний, но и поглощение импульса суперконтинуума 51 на электронных переходах из основных состояний, которые не были индуцированы импульсом 21. Поэтому импульс-суперконтинуум 52 поступает в блок сравнения, который дает спектр коэффициента поглощения ${{A}_{{gr}}}\left( \omega \right)$ квантовых точек в основных электронных состояниях. Эволюцию возбужденных состояний в чистом виде описывает величина ${{\Delta }}A\left( {\omega ,{{\tau }_{{del}}}} \right) = {{A}_{{ex}}}\left( {\omega ,{{\tau }_{{{\text{del}}}}}} \right) - {{A}_{{gr}}}\left( \omega \right),$ которая измерялась в [25]. Система уровней, использованная при интерпретации экспериментальных данных, и соответствующие электронные волновые функции показаны на рис. 4.
Функции Ψ1–Ψ4 определены формулами (2) и (5). Соответствующие электронные уровни энергии определены формулами (4) и (7). Волновая функция Ψ5(re, re,Mn) = ΘVBΦMn*(re,Mn) и соответствующий уровень энергии E5 отвечает ионам Mn2+(4T), не локализованным вблизи ловушек. Волнистые стрелки отвечают индуцированным импульсом-суперконтинуумом 51 переходам в возбужденные электронные состояния допированных Mn2+ квантовых точек из их основных состояний. Эффект этих переходов исключается при формировании описанной выше величины ${{\Delta }}A\left( {\omega ,{{\tau }_{{del}}}} \right).$ Прямые стрелки – стимулированному импульсом-суперконтинуумом 51 излучению заселенных накачивающим спектрально ограниченным импульсом в незаселенное при комнатной температуре состояние Ψ3. Именно этот процесс определяет измеренную в работе [25] величину ${{\Delta }}A\left( {\omega ,{{\tau }_{{del}}}} \right),$ которая рассчитывается в настоящей работе в рамках модели электронных состояний, показанной на рис. 2.
Формирование электронного волнового пакета накачивающим спектрально ограниченным импульсом
Эксперименты в работе [25] проводились в коллоидном растворе квантовых точек ZnCdS в циклогексане при температуре 278 K. Поэтому эволюция электронного волнового пакета, сформированного накачивающим спектрально ограниченным лазерным импульсом, определяется не только внутренней динамикой КТ, но и диссипативными процессами, обязанными взаимодействию со средой. Строго говоря, в такой ситуации эту эволюцию следует описывать в терминах эволюции матрицы плотности $\hat {\rho }(t)$ (см, например, [41–44]). Формирование включающего возбужденные состояния Ψ1 и Ψ2 электронного волнового пакета при моделировании реального эксперимента в [25] определяется следующим:
1. Поскольку частота повторяемости накачивающих импульсов в экспериментах составляет примерно 102 Гц, начальные условия для $\hat {\rho }(t)$ можно задать при t → –∞.
2. Энергия состояний Ψ1, Ψ2 и Ψ3 по отношению к энергии основного состояния Ψ4 превышает $5 \cdot {{10}^{3}}\,\,{\text{с}}{{{\text{м}}}^{{ - 1}}}(7 \cdot {{10}^{3}}\,\,{\text{K}}).$ Поэтому начальное состояние может считаться чистым и описываться волновой функцией Ψ4 = Φ4, а заселенности состояний Ψ1, Ψ2 и Ψ3 до прихода накачивающего импульса могут считаться равными нулю.
3. Как следует из (1) и рис. 1, несущая частота накачивающего лазерного импульса ωpmp и наблюдаемая частота ωSE, отвечающая стимулированным зондирующим импульсом переходам Ψ1 → Ψ3 и Ψ2 → Ψ3, значительно превосходят частоту ωTr = ETr/ћ. Поэтому возможная индуцированная внешним полем излучения связь Ψ4 с Ψ3 не существенна в рассматриваемом случае и ею можно пренебречь. Состояние Ψ4 связывается внешним полем излучения только с состоянием Φ1, а состояние Ψ3 – только с состоянием Φ2. Соответственно матрицу электронного дипольного момента квантовой точки в базисе Ψ1, Ψ2, Ψ3 и Ψ4 можно взять в следующем виде (см. (3), (5) и рис. 2):
(9)
${\mathbf{\hat {D}}} = \left( {\begin{array}{*{20}{c}} 0&0&{{{d}_{{13}}}}&{{{d}_{{14}}}} \\ 0&0&{{{d}_{{23}}}}&{{{d}_{{24}}}} \\ {{{d}_{{13}}}}&{{{d}_{{23}}}}&0&0 \\ {{{d}_{{14}}}}&{{{d}_{{24}}}}&0&0 \end{array}} \right),$где
(10)
$\begin{gathered} {{d}_{{13}}} = {{d}_{{{\text{Mn}}}}}\sin \theta ,\,\,\,\,{{d}_{{14}}} = {{d}_{{{\text{VC}}}}}\cos \theta , \\ {{d}_{{23}}} = {{d}_{{{\text{Mn}}}}}\cos \theta ,\,\,\,\,{{d}_{{24}}} = - {{d}_{{{\text{VC}}}}}\sin \theta . \\ \end{gathered} $4. Эволюция $\hat {\rho }(t)$ с момента прихода накачивающего импульса определяется следующими временны́ми параметрами: длительность накачивающего импульса τpmp; временем фазовой релаксации τph, характеризующим скорость затухания недиагональных элементов матрицы плотности; временем τpt переноса заселенности между лежащими близко по энергии перемешанными состояниями Ψ1 и Ψ2. Эти характерные времена определяются следующими соотношениями:
(11)
$\begin{gathered} {{\tau }_{{pmp}}}\sim {{10}^{{ - 14}}}{\text{с}},\,\,\,\,{{\tau }_{{ph}}}\sim {{10}^{{ - 13}}}{\text{с}} > {{\tau }_{{pmp}}}, \\ {{\tau }_{{pt}}} > {{10}^{{ - 13}}}{\text{c}} \gg {{\tau }_{{pmp}}}_{.} \\ \end{gathered} $Порядки величин τpmp и τpt следуют из данных работы [25]. Что касается фазовой релаксации, то прежде всего следует отметить, что, как будет показано в дальнейшем при обсуждении формирования сигнала SE, именно она определяет спектральную ширину стимулированного зондирующим импульсом излучения в [25]. Хорошо известно (см., например, [41, 45]), что фазовая релаксация включает две компоненты – однородную и неоднородную. Однородная фазовая релаксация обязана, как и перенос заселенности, динамическому взаимодействию электронных степеней свободы КТ с ее колебательными степенями свободы и средой. Неоднородная релаксация обязана статистическому разбросу параметров КТ. Ширины полос выцветания и SE, наблюдаемых в [25], составляют $\sim {\kern 1pt} {{10}^{3}}$ см–1. Формально эта величина соответствует времени релаксации $\sim {\kern 1pt} {{10}^{{ - 15}}}$ с и (ср. с (11)), практически полностью определяется неоднородным уширением. Однако в работе [25] имеются количественные результаты, касающиеся временнóй эволюции максимума гауссовского распределения абсолютной величины дифференциального коэффициента стимулированного излучения (отрицательного поглощения). Именно эта величина в компактном виде особенно ярко описывает отмеченное выше очень раннее появление сигнала SE и его роста с ростом ${{\tau }_{{del}}}.$ Поэтому в рассматриваемой здесь модели учитываются только узкие полосы вблизи максимумов полос CBEX и SE с шириной порядка ширины, обязанной однородному уширению с характерным временем τph из соотношений (11).
Накачивающий спектрально ограниченный лазерный импульс
(12)
${{E}_{{pmp}}}(t) = {{E}_{0}}\exp ( - {{t}^{2}}/\tau _{{pmp}}^{2})\cos \left( {{{\omega }_{{pmp}}}t} \right)$(13)
$\begin{gathered} \Psi \left( t \right) = {{a}_{1}}\left( t \right){{\Psi }_{1}}\exp \left( { - i{{\omega }_{1}}t} \right) + {{a}_{2}}\left( t \right){{\Psi }_{2}}\exp \left( { - i{{\omega }_{2}}t} \right){\text{ + }} \\ + \,\,{{a}_{3}}\left( t \right)\exp \left( { - i{{\omega }_{3}}t} \right){{\Psi }_{3}} + {{a}_{4}}\left( t \right)\exp \left( { - i{{\omega }_{4}}t} \right){{\Psi }_{4}}. \\ \end{gathered} $Здесь
(14)
$\begin{gathered} {{\omega }_{1}} = {{E}_{1}}/\hbar ,\,\,\,{{\omega }_{2}} = {{E}_{2}}/\hbar , \\ {{\omega }_{3}} = {{E}_{3}}/\hbar ,\,\,\,{{\omega }_{4}} = {{E}_{4}}/\hbar = 0. \\ \end{gathered} $Решение временнóго уравнения Шредингера в первом порядке теории возмущений по взаимодействию ${{\hat {V}}_{{pmp}}}(t)$ накачивающего поля Epmp(t) с дипольным моментом ${\mathbf{\hat {D}}}$ (см. (9)) квантовой точки при начальных условиях
(15)
$\begin{gathered} {{a}_{1}}\left( { - \infty } \right) = 0,\,\,\,\,{{a}_{2}}\left( { - \infty } \right) = 0, \\ {{a}_{3}}\left( { - \infty } \right) = 0,\,\,\,\,{{a}_{4}}\left( { - \infty } \right) = 1 \\ \end{gathered} $(16)
$\begin{gathered} {{a}_{1}}\left( t \right) = \frac{1}{\hbar }\int\limits_{ - \infty }^t {\left\langle {1\left| {{{{\hat {V}}}_{{pmp}}}\left( {t{\kern 1pt} '} \right)} \right|4} \right\rangle } \exp (i{{\omega }_{1}}t{\kern 1pt} ')dt{\kern 1pt} ', \\ {{a}_{2}}\left( t \right) = \frac{1}{\hbar }\int\limits_{ - \infty }^t {\left\langle {2\left| {{{{\hat {V}}}_{{pmp}}}\left( {t{\kern 1pt} '} \right)} \right|4} \right\rangle } \exp (i{{\omega }_{2}}t{\kern 1pt} ')dt{\kern 1pt} ', \\ {{a}_{3}}\left( t \right) = 0,\,\,\,\,{{a}_{4}}\left( t \right) = 1. \\ \end{gathered} $Здесь (см. [46])
(17)
$\begin{gathered} \left\langle {1\left| {{{{\hat {V}}}_{{pmp}}}\left( t \right)} \right|4} \right\rangle = - {{F}_{L}}{{E}_{{pmp}}}\left( t \right){{d}_{{14}}}, \\ \left\langle {2\left| {{{{\hat {V}}}_{{pmp}}}\left( t \right)} \right|4} \right\rangle = - {{F}_{L}}{{E}_{{pmp}}}\left( t \right){{d}_{{24}}}, \\ \end{gathered} $– лоренцева поправка, учитывающая поляризацию среды (n – показатель преломления). Для использованного в работе [25] в качестве растворителя циклогексана n2 ≈ 2 в представляющем интерес интервале частот $3 \cdot {{10}^{{15}}} - 4.5 \cdot {{10}^{{15}}}$ с–1.
Зондирующий импульс длительностью τpr воздействует на возбужденную накачивающим импульсом квантовую точку через время задержки
Поэтому хорошим начальным условием ${{\hat {\rho }}^{{(in)}}}$ для матрицы плотности $\hat {\rho }(t),$ которая затем эволюционирует вследствие внутренней динамики и релаксации и зондируется пробным импульсом, является матрица плотности, отвечающая сформированному накачивающим лазерным импульсом электронному волновому пакету. В базисе состояний Ψ1, Ψ2, Ψ3, Ψ4 эта матрица имеет следующий вид:
Временнáя эволюция сформированного накачивающим импульсом электронного волнового пакета
Временнáя эволюция сформированной накачивающим импульсом электронной матрицы плотности ${{\hat {\rho }}^{{(in)}}}$ определяется управляющим уравнением
Здесь $\mathfrak{L}$ – супероператор Лиувилля, описывающий внутреннюю динамику рассматриваемой модельной электронной системы. Он действует на матрицу плотности следующим образом:(22)
$\mathfrak{L}\hat {\rho }(t) = - \frac{i}{\hbar }\left[ {{{{{\mathbf{\hat {H}}}}}^{{\left( {ad} \right)}}}\hat {\rho }(t) - \hat {\rho }(t){{{{\mathbf{\hat {H}}}}}^{{\left( {ad} \right)}}}} \right],$Процессы релаксации описываются в рамках простейшего подхода с использованием марковского и секулярного приближений [41, 42, 44]. В этом подходе входящий в (21) релаксационный член $\Re \hat {\rho }(t)$ имеет следующий вид:
(23)
$\begin{gathered} \Re \hat {\rho }(t) = \left( {\begin{array}{*{20}{c}} {\Re {{{\hat {\rho }}}_{{ex}}}(t)}&{\Re {{{\hat {\rho }}}_{{eg}}}(t)} \\ {\Re \hat {\rho }_{{eg}}^{ + }(t)}&{\Re {{{\hat {\rho }}}_{{gr}}}(t)} \end{array}} \right), \\ \Re {{{\hat {\rho }}}_{{ex}}}(t) = \left( {\begin{array}{*{20}{c}} { - {{k}_{1}}{{\rho }_{{11}}}(t{\text{) + }}{{k}_{2}}{{\rho }_{{22}}}(t)}&{ - {{k}_{d}}{{\rho }_{{12}}}(t)} \\ { - {{k}_{d}}\rho _{{12}}^{*}}&{ - {{k}_{2}}{{\rho }_{{22}}}(t{\text{) + }}{{k}_{1}}{{\rho }_{{11}}}(t)} \end{array}} \right), \\ \Re {{{\hat {\rho }}}_{{eg}}}(t) = \left( {\begin{array}{*{20}{c}} { - {{k}_{d}}{{\rho }_{{13}}}(t)}&{ - {{k}_{d}}{{\rho }_{{14}}}(t)} \\ { - {{k}_{d}}{{\rho }_{{23}}}(t)}&{ - {{k}_{d}}{{\rho }_{{24}}}(t)} \end{array}} \right), \\ \Re {{{\hat {\rho }}}_{{gr}}}(t) = \left( {\begin{array}{*{20}{c}} 0&{ - {{k}_{d}}{{\rho }_{{34}}}(t)} \\ { - {{k}_{d}}\rho _{{34}}^{*}}&0 \end{array}} \right). \\ \end{gathered} $(24)
${{k}_{1}} = {{k}_{p}}\exp \left( { - \frac{{{{E}_{2}} - {{E}_{1}}}}{{2{{k}_{B}}T}}} \right),\,\,\,\,{{k}_{2}} = {{k}_{p}}\exp \left( {\frac{{{{E}_{2}} - {{E}_{1}}}}{{2{{k}_{B}}T}}} \right).$Уравнения (21) должны решаться со следующими начальными условиями:
где ${{\hat {\rho }}^{{(in)}}}$ дается формулой (20). Это решение в базисе состояний Ψ1, Ψ2, Ψ3, Ψ4 имеет следующий вид:(26)
$\begin{gathered} \hat {\rho }(t) = \left( {\begin{array}{*{20}{c}} {{{{\hat {\rho }}}_{{ex}}}(t)}&{{{{\hat {\rho }}}_{{eg}}}(t)} \\ {\hat {\rho }_{{eg}}^{ + }(t)}&{{{{\hat {\rho }}}_{{gr}}}(t)} \end{array}} \right), \\ {{{\hat {\rho }}}_{{ex}}}(t) = \left( {\begin{array}{*{20}{c}} {{{\rho }_{{11}}}(t)}&{\exp [ - {{k}_{d}}t - i({{\omega }_{1}} - {{\omega }_{2}})t]\rho _{{12}}^{{(in)}}} \\ {\exp [ - {{k}_{d}}t + i({{\omega }_{1}} - {{\omega }_{2}})t]\rho _{{12}}^{{(in)*}}}&{{{\rho }_{{22}}}(t)} \end{array}} \right), \\ {{{\hat {\rho }}}_{{eg}}}(t) = \left( {\begin{array}{*{20}{c}} {\exp [ - {{k}_{d}}t - i({{\omega }_{1}} - {{\omega }_{3}})t]\rho _{{13}}^{{(in)}}}&{\exp [ - {{k}_{d}}t - i{{\omega }_{1}}t]\rho _{{14}}^{{(in)}}} \\ {\exp [ - {{k}_{d}}t - i({{\omega }_{2}} - {{\omega }_{3}})t]\rho _{{23}}^{{(in)}}}&{\exp [ - {{k}_{d}}t - i{{\omega }_{2}}t]\rho _{{24}}^{{(in)}}} \end{array}} \right), \\ {{{\hat {\rho }}}_{{gr}}}\left( t \right) = \left( {\begin{array}{*{20}{c}} 0&{\exp [ - {{k}_{d}}t - i{{\omega }_{3}}t]\rho _{{34}}^{{(in)}}} \\ {\exp [ - {{k}_{d}}t + i{{\omega }_{3}}t]\rho _{{34}}^{{(in)*}}}&1 \end{array}} \right); \\ \end{gathered} $(27)
$\begin{gathered} {{\rho }_{{11}}}(t{\text{)}} = \frac{{\left[ {{{k}_{2}} + \exp ( - {{k}_{{pt}}}t){{k}_{1}}} \right]\rho _{{11}}^{{(in)}}}}{{{{k}_{{pt}}}}} - \\ - \,\,\frac{{\left[ { - 1 + \exp ( - {{k}_{{pt}}}t)} \right]{{k}_{2}}\rho _{{22}}^{{(in)}}}}{{{{k}_{{pt}}}}}, \\ {{\rho }_{{22}}}(t{\text{)}} = \frac{{\left[ {{{k}_{1}} + \exp ( - {{k}_{{pt}}}t)} \right]{{k}_{2}}\rho _{{22}}^{{(in)}}}}{{{{k}_{{pt}}}}} - \\ - \,\,\frac{{\left[ { - 1 + \exp ( - {{k}_{{pt}}}t)} \right]{{k}_{1}}\rho _{{11}}^{{(in)}}}}{{{{k}_{{pt}}}}}, \\ {{k}_{{pt}}} = {{k}_{1}} + {{k}_{2}}. \\ \end{gathered} $Простая модель спектра отрицательного поглощения (SE)
Модель спектра отрицательного времяразрешенного поглощения базируется на соотношениях различных временны́х масштабов (см. (11) и (19)). Самое существенное упрощение основывается на том, что ${{\tau }_{{del}}}$ $ \gg $ τph, τpr и τpt $ \gg $ τpr. Это позволяет сделать два существенных упрощения:
1) к моменту прихода зондирующего импульса когерентность сформированного накачивающим импульсом волнового пакета теряется (исчезают все недиагональные элементы $\hat {\rho }(t)$);
2) в течение всего действия зондирующего импульса на квантовую точку матрицу плотности $\hat {\rho }(t)$ может считаться постоянной и равной
(28)
$\hat {\rho }({{\tau }_{{del}}}) = \left( {\begin{array}{*{20}{c}} {{{\rho }_{{11}}}({{\tau }_{{del}}})}&0&0&0 \\ 0&{{{\rho }_{{22}}}({{\tau }_{{del}}})}&0&0 \\ 0&0&0&0 \\ 0&0&0&1 \end{array}} \right).$Поскольку все недиагональные элементы $\hat {\rho }({{\tau }_{{del}}})$ равны нулю, средний дипольный момент квантовой точки ${{P}_{{av}}}({{\tau }_{{del}}}{\text{)}} = {\text{Sp}}(\hat {\rho }({{\tau }_{{del}}}{\text{)}}{\mathbf{\hat {D}}})$ равен нулю. Ненулевой средний дипольный момент наводится в результате взаимодействия квантовой точки с зондирующим лазерным импульсом.
В рассматриваемом приближении задача о расчете индуцированного зондирующим импульсом дипольного момента квантовой точки ставится следующим образом. За начало отсчета времени принимается t = τdel, и начальное условие для соответствующей модельной матрицы плотности ${{\hat {\rho }}_{{pr}}}(t,{{\tau }_{{del}}})$ принимает вид ${{\hat {\rho }}_{{pr}}}(t = - \infty ,{{\tau }_{{del}}}) = \hat {\rho }({{\tau }_{{del}}}{\text{)}}{\text{.}}$ Взаимодействие между электрическим полем зондирующего импульса Epr(t) и квантовой точкой описывается оператором ${{{\mathbf{\hat {V}}}}_{{pr}}}\left( t \right) = - {{F}_{L}}{{E}_{{pr}}}(t){\mathbf{\hat {D}}},$ где ${{E}_{{pr}}}(t)$ – быстро спадающий при $t \to \pm \infty ~$ фемтосекундный импульс-суперконтинуум. Соответственно, уравнение для матрицы плотности принимает вид
(29)
$\begin{gathered} \frac{{d{{{\hat {\rho }}}_{{pr}}}(t,{{\tau }_{{del}}})}}{{dt}} = \mathfrak{L}{{{\hat {\rho }}}_{{pr}}}(t,{{\tau }_{{del}}}) + \Re {{{\hat {\rho }}}_{{pr}}}(t,{{\tau }_{{del}}}) + \\ + \,\,{{\mathfrak{L}}_{{pr}}}{{{\hat {\rho }}}_{{pr}}}(t,{{\tau }_{{del}}}), \\ \end{gathered} $(30)
$\begin{gathered} {{\mathfrak{L}}_{{pr}}}(t){{{\hat {\rho }}}_{{pr}}}(t,{{\tau }_{{del}}}) = \\ = - \frac{i}{\hbar }\left( {{{{{\mathbf{\hat {V}}}}}_{{pr}}}\left( t \right){{{\hat {\rho }}}_{{pr}}}(t,{{\tau }_{{del}}}) - {{{\hat {\rho }}}_{{pr}}}(t,{{\tau }_{{del}}}){{{{\mathbf{\hat {V}}}}}_{{pr}}}\left( t \right)} \right), \\ \end{gathered} $Уравнение (29) решается с точностью до первого порядка по ${{\mathfrak{L}}_{{pr}}}{\text{:}}$
(31)
${{\hat {\rho }}_{{pr}}}(t,{{\tau }_{{del}}}) = \hat {\rho }({{\tau }_{{del}}}{\text{)}} + \hat {\rho }_{{pr}}^{{(1)}}(t,{{\tau }_{{del}}})$(32)
$\begin{gathered} \frac{{d\hat {\rho }_{{pr}}^{{(1)}}(t,{{\tau }_{{del}}})}}{{dt}} = \mathfrak{L}\hat {\rho }_{{pr}}^{{(1)}}(t,{{\tau }_{{del}}}) + \Re \hat {\rho }_{{pr}}^{{(1)}}(t,{{\tau }_{{del}}}) + \\ + \,\,{{\mathfrak{L}}_{{pr}}}{{{\hat {\rho }}}_{{pr}}}({{\tau }_{{del}}}). \\ \end{gathered} $Это уравнение удобно решать с использованием преобразования Фурье:
(33)
$\begin{gathered} \rho _{{pr}}^{{\left( 1 \right)}}\left( {t,{{\tau }_{{del}}}} \right) = \int\limits_{ - \infty }^\infty {\widehat {F\rho }_{{pr}}^{{(1)}}\left( {\omega ,{{\tau }_{{del}}}} \right){{e}^{{ - i\omega t}}}d\omega } , \\ \widehat {F\rho }_{{pr}}^{{(1)}}\left( {\omega ,{{\tau }_{{del}}}} \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\hat {\rho }_{{pr}}^{{(1)}}\left( {t,{{\tau }_{{del}}}} \right){{e}^{{i\omega t}}}dt} , \\ {{\mathfrak{L}}_{{pr}}}(t) = \int\limits_{ - \infty }^\infty {\mathcal{F}{{\mathfrak{L}}_{{pr}}}\left( \omega \right){{e}^{{ - i\omega t}}}d\omega } , \\ \mathcal{F}{{\mathfrak{L}}_{{pr}}}\left( \omega \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {{{\mathfrak{L}}_{{pr}}}(t){{e}^{{i\omega t}}}dt.} \\ \end{gathered} $Подстановка (33) в (32) дает, что фурье-компоненты $\widehat {F\rho }_{{pr}}^{{(1)}}\left( {\omega ,{{\tau }_{{del}}}} \right)$ поправки первого порядка $\hat {\rho }_{{pr}}^{{\left( 1 \right)}}\left( {t,{{\tau }_{{del}}}} \right)$ к матрице плотности $\hat {\rho }({{\tau }_{{del}}})$ удовлетворяют следующему алгебраическому уравнению:
(34)
$( - i\omega - \mathfrak{L} - \Re )\widehat {F\hat {\rho }}_{{pr}}^{{(1)}}\left( {\omega ,{{\tau }_{{del}}}} \right) = \mathcal{F}{{\mathfrak{L}}_{{pr}}}\left( \omega \right)\hat {\rho }({{\tau }_{{del}}}).$Решение уравнения (34) с учетом (28) дает, что в полосе SE c частотами ω вблизи ωSE = $ = {{\left( {{{\omega }_{1}} + {{\omega }_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\omega }_{1}} + {{\omega }_{2}}} \right)} 2}} \right. \kern-0em} 2} - {{\omega }_{3}}$ (см. (14), рис. 1 и 2) средний наведенный зондирующим импульсом дипольный момент КТ при времени задержки τdel имеет вид
(35)
$\begin{gathered} {{P}_{{av}}}\left( {\omega ,{{\tau }_{{del}}}} \right) = {\text{Sp}}\left( {\widehat {F\hat {\rho }}_{{pr}}^{{\left( 1 \right)}}\left( {\omega ,{{\tau }_{{del}}}} \right){\mathbf{\hat {D}}}} \right) = \\ = \alpha \left( {\omega ,{{\tau }_{{del}}}} \right){\mathbf{F}}{{E}_{{pr}}}\left( \omega \right), \\ F{{E}_{{pr}}}\left( \omega \right) = \frac{1}{2}\int\limits_{ - \infty }^\infty {{{E}_{{pr}}}(t){{e}^{{i\omega t}}}dt} , \\ \alpha \left( {\omega ,{{\tau }_{{del}}}} \right) = - \left[ {\frac{{{{F}_{L}}d_{{13}}^{{~2}}{{\rho }_{{11}}}({{\tau }_{{del}}})}}{{\hbar \left( {{{\omega }_{1}} - {{\omega }_{3}} - \omega - i{{k}_{d}}} \right)}}} \right] - \\ - \left[ {\frac{{{{F}_{L}}d_{{~23}}^{{~2}}{{\rho }_{{22}}}({{\tau }_{{del}}})}}{{\hbar \left( {{{\omega }_{2}} - {{\omega }_{3}} - \omega - i{{k}_{d}}} \right)}}} \right]. \\ \end{gathered} $При этом (см. [47]), интенсивность стимулированного излучения (отрицательного поглощения) пропорциональна мнимой части поляризуемости α$\left( {\omega ,{{\tau }_{{del}}}} \right){\text{:}}$
(36)
$\begin{gathered} {\text{Im}}\left( {\omega ,{{\tau }_{{del}}}} \right) = - \left\{ {\frac{{{{F}_{L}}d_{{13}}^{{~2}}{{k}_{d}}{{\rho }_{{11}}}({{\tau }_{{del}}})}}{{\left[ {\hbar {{{\left( {{{\omega }_{1}} - {{\omega }_{3}} - \omega } \right)}}^{2}} + k_{d}^{2}} \right]}}} \right\} - \\ - \left\{ {\frac{{{{F}_{L}}d_{{23}}^{{~2}}{{k}_{d}}{{\rho }_{{22}}}({{\tau }_{{del}}})}}{{\hbar \left[ {{{{\left( {{{\omega }_{2}} - {{\omega }_{3}} - \omega } \right)}}^{2}} + k_{d}^{2}} \right]}}} \right\}, \\ \end{gathered} $(37)
${{\sigma }_{{{\text{SE}}}}}\left( {\omega ,{{\tau }_{{del}}}} \right) = - \frac{{4{{\pi \omega }}}}{c}{\text{Im}}\alpha \left( {\omega ,{{\tau }_{{del}}}} \right).$При этом коэффициент усиления пробного импульса в указанной области частот
(38)
$K\left( {\omega ,{{\tau }_{{del}}}} \right) = N{\text{*}}{{\sigma }_{{{\text{SE}}}}}\left( {\omega ,{{\tau }_{{del}}}} \right),$(39)
$\begin{gathered} {{\Delta }}A\left( {\omega ,{{\tau }_{{del}}}} \right) = - N{\text{*}}\ell \frac{{4{{\pi \omega }}}}{{c\hbar {{k}_{d}}}}\,\, \times \\ \times \,\,\left[ {\frac{{{{F}_{L}}d_{{13}}^{{~2}}k_{d}^{2}{{\rho }_{{11}}}({{\tau }_{{del}}})}}{{{{{\left( {{{\omega }_{1}} - {{\omega }_{3}} - \omega } \right)}}^{2}} + k_{d}^{2}}} + \frac{{{{F}_{L}}d_{{23}}^{{~2}}k_{d}^{2}{{\rho }_{{22}}}({{\tau }_{{del}}})}}{{{{{\left( {{{\omega }_{2}} - {{\omega }_{3}} - \omega } \right)}}^{2}} + k_{d}^{2}}}} \right]. \\ \end{gathered} $В работе [25] по экспериментальным данным определялась функция ${{\left| {{{\Delta }}{{A}_{{rel}}}\left( {{{\tau }_{{del}}}} \right)} \right|}_{{max}}}$ – максимум распределения абсолютной величины дифференциального коэффициента отрицательного поглощения в относительных единицах. В рассматриваемой модели эта функция следующим образом выражается через детализированное общее выражение (39):
(40)
$\begin{gathered} {{{{\Phi }}}_{1}}\left( {\omega ,{{\tau }_{{del}}}} \right) = \frac{{k_{d}^{2}{\text{si}}{{{\text{n}}}^{2}}{{\theta }}}}{{{{{\left( {{{\omega }_{1}} - {{\omega }_{3}} - \omega } \right)}}^{2}} + k_{d}^{2}}} \times \\ \times \,\,\left[ {{{B}_{{11}}} - {{B}_{{12}}}{\text{exp}}\left( { - {{k}_{{pt}}}{{\tau }_{{del}}}} \right)} \right], \\ \end{gathered} $Здесь
(41)
$\begin{gathered} {{B}_{{12}}} = {\text{sin}}{{{{\theta }}}^{2}}\exp \left[ { - \frac{1}{2}{{{\left( {{{\omega }_{2}} - {{\omega }_{{pmp}}}} \right)}}^{2}}\tau _{{pmp}}^{2}} \right] \times \\ \times \,\,{\text{exp}}\left( { - \frac{{{{E}_{1}} - {{E}_{2}}}}{{2{{k}_{B}}T}}} \right) - {\text{co}}{{{\text{s}}}^{2}}{{\theta }} \times \\ \times \,\,{\text{exp}}\left[ { - \frac{1}{2}{{{({{\omega }_{1}} - {{\omega }_{{pmp}}})}}^{2}}\tau _{{pmp}}^{2}} \right]{\text{exp}}\left( {\frac{{{{E}_{1}} - {{E}_{2}}}}{{2{{k}_{B}}T}}} \right), \\ {{B}_{{21}}} = {\text{co}}{{{\text{s}}}^{2}}{{\theta exp}}\left[ { - \frac{1}{2}{{{\left( {{{\omega }_{1}} - {{\omega }_{{pmp}}}} \right)}}^{2}}\tau _{{pmp}}^{2}} \right]{\text{exp}}\left( {\frac{{{{E}_{1}} - {{E}_{2}}}}{{2{{k}_{B}}T}}} \right) + \\ + \,\,{\text{si}}{{{\text{n}}}^{2}}{{\theta exp}}\left[ { - \frac{1}{2}{{{\left( {{{\omega }_{2}} - {{\omega }_{{pmp}}}} \right)}}^{2}}\tau _{{pmp}}^{2}} \right]{\text{exp}}\left( {\frac{{{{E}_{1}} - {{E}_{2}}}}{{2{{k}_{B}}T}}} \right), \\ \end{gathered} $Выражения для коэффициентов ${{B}_{{ij}}}$ получены с использованием формул (27) для ${{\rho }_{{11}}}({{\tau }_{{del}}})$ и ${{\rho }_{{22}}}({{\tau }_{{del}}})$ и (20) для $\rho _{{11}}^{{(in)}}$ и $\rho _{{22}}^{{(in)}}.$
СОПОСТАВЛЕНИЕ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ
Прежде всего отметим, что общее выражение (39) для ${{\Delta }}A\left( {\omega ,{{\tau }_{{del}}}} \right)$ позволяет качественно объяснить очень большое (три порядка) различие величин сигналов в экспериментах (см. рис. 2 в [25]) в областях длин волн порядка 450 нм (выцветание) и 550–600 нм (SE). Дело, видимо, в том, что определяющая SE концентрация $N{\text{*}}$ много меньше определяющей выцветание полной концентрации $N$ квантовых точек в растворе.
Количественное сопоставление развитой в настоящей работе теории с экспериментом можно провести для ${{\left| {{{\Delta }}{{A}_{{rel}}}\left( {{{\tau }_{{del}}}} \right)} \right|}_{{max}}}.$ Измеренная в [25] для квантовых точек QD2 величина $\left| {{{\Delta }}{{A}_{{rel}}}\left( {{{\tau }_{{del}}}} \right)} \right|_{{max}}^{{(exp)}}$ при ${{\tau }_{{del}}}$ в интервале 10–13–2 · 10–12 сможет быть аппроксимирована функцией
(42)
$\begin{gathered} \left| {{{\Delta }}{{A}_{{rel}}}\left( {{{\tau }_{{del}}}} \right)} \right|_{{max}}^{{(exp)}} = 1 - 0.15{\text{exp}}\left( {{{ - {{\tau }_{{del}}}} \mathord{\left/ {\vphantom {{ - {{\tau }_{{del}}}} {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}}} \right), \\ {{\tau }_{1}} = 6.25 \cdot {{10}^{{ - 13}}}\,\,{\text{c}}. \\ \end{gathered} $Прежде всего отметим, что (см. (40)), зависимость функции ${{\left| {{{\Delta }}{{A}_{{rel}}}\left( {{{\tau }_{{del}}}} \right)} \right|}_{{max}}}$от ${{\tau }_{{del}}}$ определяется константой скорости ${{k}_{{pt}}}.$ Из (27) же следует, что этой константой определяется скорость переноса заселенности между близколежащими по энергии перемешанными состояниями Ψ1 и Ψ2. Поэтому, учитывая то, что время ${{\tau }_{1}}$ имеет характерный для переноса заселенности между близколежащими электронными состояниями порядок величины (см. (11)), естественно отождествить ${{k}_{{pt}}}$ ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}}.$ Если не обращать внимание на зависимость от ${{\tau }_{{del}}},$ то ${{\left| {{{\Delta }}A\left( {{{\tau }_{{del}}}} \right)} \right|}_{{max}}}$ зависит отвеличин ${{E}_{1}},~{{E}_{2}},~{{\theta }}$ и константы скорости фазовой релаксации ${{k}_{d}}.$ Что касается ${{E}_{1}},~{{E}_{2}}$ и ${{\theta ,}}$ то их величина определяется энергетическими параметрами ${{e}_{1}} = {{E}_{{{\text{CB}}}}},$ ${{e}_{2}} = {{\Delta }}{{E}_{{{\text{Mn}}}}} + {{E}_{{{\text{Tr}}}}}$ и ${{V}_{c}}$ (см. рис. 1, 2). При расчетах были использованы приведенные в [25] значения ${{E}_{{{\text{CB}}}}} = 23{\kern 1pt} 256~$ см–1, ${{\Delta }}{{E}_{{{\text{Mn}}}}} = 16{\kern 1pt} 938$ см–1. Энергия электрона в ловушке, ${{E}_{{{\text{Tr}}}}},$ и матричный элемент Vc обменного взаимодействия подбирались из условия согласия результатов расчета с (42). При этом учитывалось, что энергия ${{E}_{{{\text{Tr}}}}}$ должна удовлетворять неравенству (1), а значение |Vc| должно лежать в пределах, полученных в работах [37–39]. Было установлено, что воспроизвести $\left| {{{\Delta }}{{A}_{{rel}}}\left( {{{\tau }_{{del}}}} \right)} \right|_{{max}}^{{(exp)}}$ удается, приняв, что ${{E}_{{{\text{Tr}}}}} = 6133$ см–1 и ${{V}_{c}} = 59$ см–1. При этих значениях ${{E}_{{{\text{Tr}}}}}$ и ${{V}_{c}}$ функция ${{{{\Phi }}}_{1}}\left( {\omega ,{{\tau }_{{del}}}} \right) \ll {{{{\Phi }}}_{2}}\left( {\omega ,{{\tau }_{{del}}}} \right)$ и поэтому${{\left| {{{\Delta }}{{A}_{{rel}}}\left( {{{\tau }_{{del}}}} \right)} \right|}_{{max}}}$ не зависит от ${{k}_{d}}.$ Кроме того, при этих значениях параметров в шкале длин волн положение ${{\lambda }_{{max}}}$ максимума распределения абсолютной величины дифференциального коэффициента отрицательного поглощения не зависит от ${{\tau }_{{del}}}$ и равно 590 нм. В работе [25] наблюдалось, что в рассматриваемом интервале времен задержки ${{\lambda }_{{max}}}$ практически не зависит от ${{\tau }_{{del}}}$ и равно примерно 580 нм. Следует отметить, что обе величины лежат в центре полосы SE, ширина которой составляет примерно 60 нм.
ЗАКЛЮЧЕНИЕ
Предложенная в настоящей работе простая аналитическая модель дает качественное и даже в некоторых аспектах количественное описание следующих основных особенностей наблюдавшегося в работе [25] сигнала фемтосекундного эксперимента накачка–зондирование с допированными марганцем квантовыми точками ZnCdS:
1) наблюдение уже при τdel = 120 фс сигнала стимулированного зондирующим импульсом излучения в полосе длин перехода 4T1 → 6A1 в Mn2+(3d5);
2) медленный рост интенсивности этого излучения с ростом τdel.
Первая особенность объясняется тем, что возбужденное состояние 4T иона ${\text{M}}{{{\text{n}}}^{{2 + }}},$ локализованного вблизи ловушки электрона с энергией в запрещенной зоне, может лежать близко по энергии к краю зоны проводимости. Это состояние перемешивается обменным взаимодействием с состояниями электронов в зоне проводимости КТ и может возбуждаться накачивающим фемтосекундным импульсом. Поэтому SE появляется сразу после прохождения накачивающего импульса с длительностью порядка 10–14 с.
Вторая особенность обязана перераспределению заселенности между двумя отмеченными выше перемешанными состояниями, вызванному релаксационными процессами.
Авторы выражают благодарность В.А. Надточенко за плодотворные обсуждения.
Работа выполнена при финансовой поддержке Министерством науки и высшего образования Российской Федерации в рамках госзадания (регистрационный номер AAAA-A19-119012890064-7).
Список литературы
Nozik A.J., Beard M.C., Luther J.M. et al. // Chem. Rev. 2010. V. 110. P. 6873; https://doi.org/10.1021/cr900289f
Николенко Л.М., Разумов В.Ф. // Успехи химии. 2013. Т. 82. № 5. С. 429.
Lodahl P., Mahmoodian S., Stobbe S. // Rev. Mod. Phys. 2015. V. 87. P. 347; https://doi.org/10.1103/RevModPhys.87.347
Gumlich H.E. // J. Lumin. 1981. V. 23. P. 73; https://doi.org/10.1016/0022-2313(81)90191-5
Bhargava R.N., Gallagher D. // Phys. Rev. Lett. l994. V. 72. P. 416.
Sooklal K., Cullum B.S., Angel S.M. et al. // J. Phys. Chem. 1996. V. 100. P. 4551.
Dinsmore A.D., Hsu D.S., Gray H.F. // Appl. Phys. Lett. 1999. V. 75. P. 802.
Song Wei Lua, Burtrand I.L., Zhong Lin Wang // J. Lumin. 2001. V. 92. P. 73.
Li-Yu Lin, Teng-Ming Chen // Tamkang J. Sci. Eng. 2002. V. 5. № 3. P. 187.
de Mello Donega C., Bol A.A., Meijerink A. // J. Lumin. 2002. V. 96. P. 87.
Yang H., Holloway P.H., Ratna B.B. // J. Appl. Phys. 2003. V. 93. P. 586; https://doi.org/10.1063/1.1529316
Peng W.Q., Qua S.C., Conga G.W. et al. // J. Cryst. Gr. 2005. V. 282. P. 179; https://doi.org/10.1016/j.jcrysgro.2005.05.005
Sapra S., Prakash A., Ghangrekar A. et al. // J. Phys. Chem. B. 2005. V. 109. P. 1663; https://doi.org/10.1021/jp049976e
Hao Ying Lu, Sheng Yuan Chu, Soon Seng Tan // Jap. J. Appl. Phys. 2005. V. 44. P. 5282.
Zhen-Qian Chen, Chao Lian, Dong Zhou et al. // Chem. Phys. Lett. 2010. V. 488. P. 73; https://doi.org/10.1016/j.cplett.2010.02.002
Olano E.M., Grant C.D., Norman T.J. et al. // J. Nanosci. Nanotech. 2005. V. 5. P. 1492; https://doi.org/10.1166/jnn.2005.315
Бендерский В.А., Кац Е.И. // Хим. физика. 2009. Т. 28. С. 6.
Kripal R., Gupta A.K., Mishra S.K. et al. // Spectr. Acta. A. 2010. V. 76. P. 523; https://doi.org/10.1016/j.saa.2010.04.018
Taguchi S., Ishizumi A., Kanemitsu Y. // J. Phys. Soc. Jap. 2010. V. 79. P. 063710; https://doi.org/10.1143/JPSJ.79.063710
Hsiang-Yun Chen, Maiti S., Dong Hee Son // ACS Nano. 2012. V. 6. P. 583; https://doi.org/10.1021/nn204452e
Maiti S., Hsiang-Yun Chen, Park Y. et al. // J. Phys. Chem. C. 2014. V. 118. P. 18226; https://doi.org/10.1021/jp505162c
Horoz S., Dai Q., Maloney F.S. et al. // Phys. Rev. Appl. 2015. V. 3. P. 024011; https://doi.org/10.1103/PhysRevApplied.3.024011
Данилов В.В., Панфутова А.С., Шилов В.Б. и др. // Хим. физика. 2015. Т. 34. С. 58.
Gahlot K., Pradeep K.R., Camellini A. // ACS Energy Lett. 2019. V. 4. P. 729; https://doi.org/10.1021/acsenergylett.9b00064
Nadtochenko V., Kostrov A., Titov A. et al. // Chem. Phys. Lett. 2020. V. 743. A. 137160; https://doi.org/10.1016/j.cplett.2020.137160
Bawendi M.G., Carroll P.J., Wilson W.L. et al. // J. Chem. Phys. 1992. V. 96. P. 946; https://doi.org/10.1063/1.462114
Иванов Г.К., Боднева В.Л. // Хим. физика. 2007. Т. 26. С. 74.
Балашов Е.М., Иванов Г.К., Колченко Н.Н. // Хим. физика. 2008. Т. 27. С. 75.
Lee S.F., Osborne M.A. // ChemPhysChem. 2009. V. 10. P. 2174; https://doi.org/10.1002/cphc.200900200
Jones M., Lo S.S., Scholes G.D. // Proc. Nat. Acad. Sci. 2009. V. 106. P. 3011; https://doi.org/10.1073/pnas.0809316106
Mao Ye, Searson P.C. // Phys. Rev. B. 2011. V. 84. 125 317; https://doi.org/10.1103/PhysRevB.84.125317
Veamatahau A., Bo Jiang, Seifert T. et al. // Phys. Chem. Chem. Phys. 2014. V. 17. P. 2850; https://doi.org/10.1039/c4cp04761c
Boehme S.C., Azpiroz J.M., Aulin Y. et al. // Nano Lett. 2015. V. 15. P. 3056; https://doi.org/10.1021/acs.nanolett.5b00050
Kahmann S., Sytnyk M., Schrenker N. et al. // Adv. Electron. Mater. 2017. 1700348; https://doi.org/10.1002/aelm.201700348
Kushavah D., Mohapatra P.K., Ghosh P. et al. // Mater. Res. Expr. 2017. V. 4. 075007; https://doi.org/10.1088/2053-1591/aa7a4f
Kirkwood N., Monchen J.O.V., Crisp R.W. et al. // J. Amer. Chem. Soc. 2018. V. 140. P. 15712; https://doi.org/10.1021/jacs.8b07783
Beaulac R., Gamelin D.R. // Phys. Rev. B. 2010. V. 82. P. 224401; https://doi.org/10.1103/PhysRevB.82.224401
Beaulac R., YongFeng, May J.W. et al. // Phys. Rev. B. 2011. V. 84. P. 195324; https://doi.org/10.1103/PhysRevB.84.195324
Bo Peng, Liang W., White M.A. et al. // J. Phys. Chem. C. 2012. V. 116. P. 11223; https://doi.org/10.1021/jp2118828
Желтиков А.М. // УФН. 2006. Т. 176. С. 623.
Mukamel S. Nonlinear optical spectroscopy. New York, Oxford: Oxford University Press, 1995.
Domcke W., Stock G. // Adv. Chem. Phys. 1997. V. 100. P. 1.
Gelin M.F., Pisliakov A.V., Egorova D. et al. // J. Chem. Phys. 2003. V. 118. P. 5287; https://doi.org/10.1063/1.1547751
Blum K. Density matrix theory and applications. Berlin, Heidelberg: Springer, 2012.
Allen L., Eberly J.H. Optical resonance and two-level atoms. N.Y., London: John Wiley & Sons, 1975.
Dexter D.L. // Sol. State. Phys. 1958. V. 6. P. 353.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Физматлит, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика