Химическая физика, 2022, T. 41, № 8, стр. 48-58
Характеристический анализ динамики распространения ударной волны в среде с неравномерным распределением плотности
Я. Э. Порошина 1, А. И. Лопато 1, П. С. Уткин 1, *
1 Институт автоматизации проектирования Российской академии наук
Москва, Россия
* E-mail: pavel_utk@mail.ru
Поступила в редакцию 10.01.2022
После доработки 12.02.2022
Принята к публикации 21.02.2022
- EDN: LTTGKD
- DOI: 10.31857/S0207401X22080106
Аннотация
Работа посвящена численному исследованию распространения ударной волны в среде с неравномерным распределением плотности. Математическая модель основывается на уравнениях Эйлера, которые решаются в системе координат, связанной с лидирующим скачком. Подобный подход делает возможным проведение аккуратного характеристического анализа задачи. Сначала рассмотрены задачи о распространении ударной волны в среде с участками конечной длины с линейно увеличивающейся и уменьшающейся плотностью. Проведено сравнение полученных результатов с известными аналитическими решениями. Затем рассмотрен случай непрерывного изменения плотности среды перед ударной волной по синусоидальному закону. Возникающее при этом течение описано и объяснено с использованием результатов для случая линейного градиента плотности.
ВВЕДЕНИЕ
В последние несколько лет наблюдается рост числа работ, посвященных задачам распространения детонационных волн в неоднородных газовых смесях. Такие задачи представляют интерес не только с точки зрения фундаментальных основ теории детонации, но и с практической точки зрения. Одно из конкретных применений – предотвращение случайного возникновения детонации в шахтах, в изолированных частях которой может накапливаться взрывоопасная смесь. В такой смеси по разным причинам возможно образование градиента концентрации топлива, что, в свою очередь, будет влиять на механизм воспламенения смеси, переход горения в детонацию и ее последующее распространение. Однако основной причиной активных исследований особенностей детонационных процессов в неоднородных газовых смесях является разработка двигателей, основанных на непрерывной вращающейся детонации [1–4]. В таких двигателях окислитель и топливо впрыскиваются в установку раздельно, что приводит к распространению детонации по сильно неоднородной смеси.
Для описания сложного процесса, происходящего в реальных установках, проводятся исследования модельных постановок, при рассмотрении которых проясняются механизмы распространения детонации в неоднородных средах. Можно выделить следующие гуппы работ, в которых изучается распространение детонации в плоском канале:
• в среде с переменным продольным [5, 6] и поперечным [7–9] градиентом концентрации топлива;
• в среде c переменной плотностью смеси [10, 11];
• вдоль [12, 13] или поперек [14] инертного слоя газа;
• в рамках уравнений-аналогов [15].
Отдельно стоит отметить недавнюю работу [16], в которой изучаются соотношения вкладов следующих двух составляющих в итоговую нелинейную динамику процесса распространения детонационной волны в неоднородной среде: первая – связана с пульсирующей природой детонационной волны как таковой, проявляющейся и в однородной среде; вторая – обусловлена периодическим изменением параметров перед фронтом лидирующей ударной волны (ЛУВ). Обнаружено, что в зависимости от параметров задачи может происходить как усиление колебаний параметров за фронтом детонационной волны, так и, наоборот, их стабилизация по сравнению со случаем однородной среды.
В наших предыдущих работах [17, 18] были построены вычислительные алгоритмы для моделирования детонации в системе координат, связанной с лидирующим фронтом (СКФ) волны детонации, в рамках одно- [17] и двухстадийной [18] моделей кинетики химических реакций. Суммируем кратко основные достоинства и недостатки расчетов детонации в СКФ [18]. В подобной постановке, с одной стороны, осуществляется переход в неинерциальную систему координат, поскольку скорость лидирующего скачка зависит от времени. Это приводит к преобразованию привычных уравнений Эйлера, составляющих основу математической модели – в них начинает фигурировать априори неизвестная скорость лидирующего скачка, для нахождения которой необходимо использовать те или иные дополнительные соображения [19–21]. Неинерциальность системы координат и необходимость рассмотрения дополнительных уравнений для скорости волны определяют бóльшую сложность подобного подхода с точки зрения его программной реализации по сравнению с численным решением уравнений Эйлера в неподвижной, лабораторной системе координат. С другой стороны, рассмотрение задачи в СКФ имеет три основных достоинства.
Во-первых, данный подход требует существенно меньше вычислительных затрат по сравнению с традиционным рассмотрением задачи инициирования и распространения детонации в лабораторной системе координат (см., например, [22]). Здесь расчетная область физически соответствует на части или полному по длине каналу, в котором рассматривается распространение детонационной волны, а всегда некоторой области непосредственно за фронтом ЛУВ.
Во-вторых, данный подход позволяет точно фиксировать параметры непосредственно за фронтом ЛУВ. Ударная волна является фиксированной границей расчетной области и не испытывает численного “размазывания”, что неизбежно происходит в методах сквозного счета.
В-третьих, СКФ гораздо больше подходит для характеристического анализа поля течения за фронтом детонационной волны [23]. Характеристический анализ, в отличие от анализа только полей давления, плотности, массовой доли реагента, скорости газа, который обычно проводится для иллюстрации динамики распространения детонации, способен дать объяснение наблюдающихся режимов течения. Так, в работе [19] подобный анализ позволил обобщить понятие звуковой точки из теории Чепмена–Жуге для случая нестационарной пульсирующей волны детонации. Более того, реализующиеся пульсирующие режимы течения можно объяснить и с количественной точки зрения, анализируя поведение характеристик, как это сделано в работах [18, 23].
Эти факторы стимулируют расчеты распространения детонационной волны в неоднородной газовой смеси в системе координат фронта лидирующего скачка. При построении такого алгоритма необходимо разработать соответствующие вычислительные алгоритмы расчета распространения ударной волны (УВ) в неоднородной среде.
Целями настоящей работы являются:
• разработка вычислительного алгоритма для моделирования распространения УВ в среде с возмущением плотности в СКФ;
• проведение с использованием разработанного алгоритма характеристического анализа динамики распространения УВ в среде с линейным (задача, рассмотренная в работах Чиснелла и Уизема [24, 25]) и синусоидальным распределениями плотности (задача Шу–Ошера [26]).
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ПОСТАНОВКА ЗАДАЧИ
Математическая модель основывается на уравнениях Эйлера, дополненных уравнением состояния идеального газа и записанных в векторной форме в системе координат $\left( {x,t} \right),$ связанной с фронтом ЛУВ:
(1)
$\begin{gathered} \frac{{\partial {\mathbf{u}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {{\mathbf{f}} - D{\mathbf{u}}} \right) = 0,\,\,\,\,x = {{x}^{l}} - \int\limits_0^t {D\left( \tau \right)d\tau } , \\ {\mathbf{u}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho v} \\ e \end{array}} \right],~\,\,\,{\mathbf{f}} = \left[ {\begin{array}{*{20}{c}} {\rho v} \\ {\rho {{v}^{2}} + p} \\ {\left( {p + e} \right)v} \end{array}} \right], \\ e = \rho \varepsilon + \frac{1}{2}\rho {{v}^{2}},~\,\,\,\,\varepsilon = \frac{p}{{\rho \left( {\gamma - 1} \right)}}. \\ \end{gathered} $(2)
$\frac{{\partial u}}{{\partial t}} + \frac{{\partial D}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} = 0,$Для определения скорости ударной волны в СКФ определяющая система уравнений (1) записывается в характеристической форме вдоль ${{C}_{ + }}$-характеристики:
(3)
$\left\{ {\begin{array}{*{20}{l}} {\frac{{dp}}{{dt}} + \rho c\frac{{dv}}{{dt}} = 0,} \\ {\frac{{dx}}{{dt}} = v + c - D,} \\ {{{\rho }_{0}} = {{\rho }_{0}}\left( t \right),\,\,\,\,{{p}_{0}} = {{p}_{0}}\left( t \right),\,\,\,\,{{v}_{0}} = {{v}_{0}}\left( t \right),} \end{array}} \right.$(4)
${{\rho }_{0}} = {{\rho }_{0}}\left( {{{x}_{0}} + \int\limits_0^t {D\left( \tau \right)d\tau } } \right),\,\,\,{{p}_{0}} = {\text{const}},\,\,\,{{v}_{0}} = {\text{const}}.$Через ${{x}_{0}}$ обозначена начальная координата УВ.
Возможность определения скорости ЛУВ при рассмотрении системы (3) обусловлена результатами работы [19], в которой изучалась динамика распространения детонационной волны в однородной среде, т.е. в случае ${{\rho }_{0}} = {\text{const}}.$ Конкретная разностная реализация, приводящая к выражению для текущей скорости ЛУВ, приведена ниже в разделе с вычислительным алгоритмом.
Определяющая система уравнений решается на фиксированном отрезке $\left[ { - H;0} \right].$ Правая граница соответствует фронту ЛУВ. На ней выставляются граничные условия, определяемые соотношениями Ренкина–Гюгонио (Rankine–Hugoniot) на скачке, движущемся с текущей скоростью $D,$ которая находится в результате решения системы уравнений (3), (4) (см. следующий раздел). Длина расчетной области $H$ выбиралась достаточно большой, чтобы для рассматриваемых задач левая граница области не влияла на динамику движения фронта ЛУВ. Формально левая граница области считалась свободной, использовались граничные условия экстраполяции нулевого порядка.
В качестве начальных условий во всей расчетной области задаются одинаковые параметры за фронтом ударной волны с числом Маха $M,$ которая в начальный момент времени начинает взаимодействовать с пространственной неоднородностью плотности на пути ее распространения:
(5)
$\begin{gathered} {{p}_{s}} = {{p}_{0}} + {{p}_{0}}\frac{{2\gamma \left( {{{M}^{2}} - 1} \right)}}{{\left( {\gamma + 1} \right)}},\,\,\,\,{{\rho }_{s}} = \frac{{{{\rho }_{0}}\left( {{{x}_{0}}} \right)\left( {\gamma + 1} \right){{M}^{2}}}}{{\left( {\gamma - 1} \right){{M}^{2}} + 2}}, \\ {{v}_{s}} = \frac{{2\left( {{{M}^{2}} - 1} \right)}}{{\left( {\gamma + 1} \right)M}}{{\left( {\frac{{\gamma {{p}_{0}}}}{{{{\rho }_{0}}\left( {{{x}_{0}}} \right)}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ
Расчетная область покрывается равномерной расчетной сеткой. Расчетные ячейки нумеруются от 1 до $N.$ Для численного интегрирования системы уравнений (1) используются конечно-объемная дискретизация конвективной части и явная схема Эйлера интегрирования по времени. Параметры на гранях ячеек определяются в результате кусочно-линейной реконструкции вектора консервативных переменных с помощью ограничителя minmod. Шаг интегрирования по времени выбирается динамически для обеспечения устойчивости на выбранной сетке. Численный поток, который рассчитывается по сеточно-характеристическому варианту схемы Куранта–Изаксона–Рис (Courant–Isaakson–Rees) [28] учитывает неявным образом скорость УВ. В этой части решения уравнений газовой динамики без учета протекания химических реакций алгоритм не отличается от методики, подробно описанной в работах [17, 18].
Основное отличие от предыдущих работ в части вычислительного алгоритма связано со способом интегрирования уравнений для нахождения скорости ЛУВ, так как параметры среды перед УВ теперь неоднородны. Дискретизация системы уравнений (3), (4) выглядит следующим образом [19]:
(6)
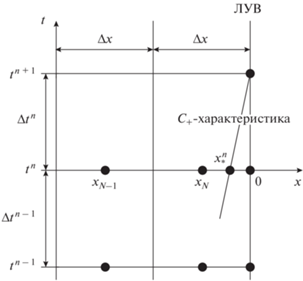
$\left\{ {\begin{array}{*{20}{l}} {p_{s}^{{n + 1}} - p_{{\text{*}}}^{n} + \frac{1}{2}\left( {\left( {\rho c} \right)_{{\text{*}}}^{n} + \left( {\rho c} \right)_{s}^{{n + 1}}} \right)\left( {v_{s}^{{n + 1}} - v_{{\text{*}}}^{n}} \right) = 0,} \\ { - x_{{\text{*}}}^{n} = \left( {c_{{\text{*}}}^{n} + v_{{\text{*}}}^{n} - {{D}^{n}}} \right)\Delta {{t}^{n}},} \\ {\rho _{0}^{{n + 1}} = {{\rho }_{0}}\left[ {{{x}_{0}} + {{L}^{n}} + {{{\left( {\frac{{\gamma p_{0}^{{n + 1}}}}{{\rho _{0}^{{n + 1}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{M}^{{n + 1}}}\Delta {{t}^{n}}} \right].} \end{array}} \right.$Нижним индексом “s” обозначим параметры на скачке при ${{x}_{s}} = 0,$ индексом “*" – параметры в точке пересечения ${{C}_{ + }}$-характеристики с осью x (см. рис. 1). Через ${{L}^{n}}$ обозначен путь, пройденный ЛУВ на момент времени ${{t}^{n}}{\text{:}}$
Параметры с индексом “*” находятся с помощью линейной интерполяции по известным параметрам в точках ${{x}_{N}} = - \Delta x{\text{/}}2$ (центр последней ячейки в расчетной области) и ${{x}_{s}} = 0$ и имеют вид
(7)
$\begin{array}{*{20}{c}} {p_{{\text{*}}}^{n} = p_{s}^{n} + \frac{{x_{{\text{*}}}^{n}}}{{\Delta x{\text{/}}2}}\left( {p_{s}^{n} - p_{N}^{n}} \right){\text{,}}\,\,\,v_{{\text{*}}}^{n} = v_{s}^{n} + \frac{{x_{{\text{*}}}^{n}}}{{\Delta x{\text{/}}2}}\left( {v_{s}^{n} - v_{N}^{n}} \right),} \\ {\rho _{{\text{*}}}^{n} = \rho _{s}^{n} + \frac{{x_{{\text{*}}}^{n}}}{{\Delta x{\text{/}}2}}\left( {\rho _{s}^{n} - \rho _{N}^{n}} \right),\,\,\,\,c_{{\text{*}}}^{n} = {{{\left( {\gamma \frac{{p_{{\text{*}}}^{n}}}{{\rho _{{\text{*}}}^{n}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.} \end{array}$Из второго уравнения системы (6) следует выражение для координаты точки пересечения С+-характеристики с осью x:
(8)
$x_{*}^{n} = - \frac{{\left( {c_{s}^{n} + {v}_{s}^{n} - {{D}^{n}}} \right)\Delta {{t}^{n}}}}{{1 + \frac{{2\Delta {{t}^{n}}}}{{\Delta x}}\left( {c_{s}^{n} - c_{N}^{n} + {v}_{s}^{n} - {v}_{N}^{n}} \right)}}.$Параметры в точке ${{x}_{s}} = 0$ в момент времени $t = {{t}^{{n + 1}}}$ определяются из соотношений Ренкина–Гюгонио, аналогичным параметрам (5) как
(9)
$\begin{gathered} p_{s}^{{n + 1}} = {{p}_{0}}\left( {1 + \frac{{2\gamma \left( {{{{\left( {{{M}^{{n + 1}}}} \right)}}^{2}} - 1} \right)}}{{\gamma + 1}}} \right), \\ \rho _{s}^{{n + 1}} = \rho _{0}^{{n + 1}}\frac{{\left( {\gamma + 1} \right){{{\left( {{{M}^{{n + 1}}}} \right)}}^{2}}}}{{\left( {\gamma - 1} \right){{{\left( {{{M}^{{n + 1}}}} \right)}}^{2}} + 2}}, \\ {v}_{s}^{{n + 1}} = c_{s}^{{n + 1}}\frac{{2\left( {{{{\left( {{{M}^{{n + 1}}}} \right)}}^{2}} - 1} \right)}}{{\left( {\gamma + 1} \right){{{\left( {{{M}^{{n + 1}}}} \right)}}^{2}}}}{\text{,\;}}\,\,\,c_{s}^{{n + 1}} = {{\left( {\gamma \frac{{p_{s}^{{n + 1}}}}{{\rho _{s}^{{n + 1}}}}} \right)}^{{1/2}}}. \\ \end{gathered} $Подстановка выражений (7)–(9) в (6) приводит к системе из двух нелинейных алгебраических уравнений относительно неизвестных параметров ${{M}^{{n + 1}}}$ и $\rho _{0}^{{n + 1}},$ которая решается численно методом Ньютона. Граничные условия реализуются путем задания параметров в фиктивных ячейках. Для расчета потоков через левую и правую грани расчетной области вводятся фиктивные ячейки с индексами “$m = - 1$” и “$m = N$”. На левой границе расчетной области применяется экстраполяция нулевого порядка:
На правой границе параметры в фиктивной ячейке равняются текущим параметрам за фронтом ЛУВ:
РАСПРОСТРАНЕНИЕ УДАРНОЙ ВОЛНЫ В СРЕДЕ С ЛИНЕЙНЫМ ГРАДИЕНТОМ ПЛОТНОСТИ
Перед рассмотрением задачи о распространении УВ в среде с синусоидальным распределением плотности рассмотрим сначала более простую задачу, когда плотность перед УВ меняется линейно – увеличивается или уменьшается. Во-первых, для данной задачи существуют аналитические оценки решения. Во-вторых, можно провести наглядную качественную аналогию между гладким синусоидальным профилем плотности и кусочно-линейным профилем с чередующимися участками увеличения и уменьшения плотности.
Задача о распространении УВ в среде с линейным градиентом плотности изучалась многими авторами. Аналогично задаче о взаимодействии УВ с единичным контактным разрывом [29], при взаимодействии УВ с градиентом плотности формируются контактные разрывы и волны разрежения или сжатия (в зависимости от знака градиента). Волны разрежения или сжатия взаимодействуют с контактными разрывами с образованием переотраженных волн, которые также влияют на динамику движения ЛУВ. В работе [30] с использованием численного анализа проводилось исследование влияния переотраженных волн на фронт ЛУВ в зависимости от различных факторов, таких как: число Маха волны, абсолютное значение и знак градиента плотности, а также вид профиля плотности (линейное изменение или по степенному закону). Выводы были основаны на сравнении численных результатов с аналитическим решением Чиснелла–Уизема [24, 25] (см. Приложение 1). Одно из основных предположений при построении аналитического решения Чиснелла–Уизема – отсутствие влияния переотраженных волн на фронт ЛУВ. Отметим, что аналитические оценки параметров течения в ударно-волновых задачах представляют и самостоятельный интерес, например, в задачах распространения ударных волн в двухфазных средах [31–33] и в каналах сложной формы [34].
Расчетная область – отрезок [–10;0]. Значения начальной плотности, скорости и давления во всей расчетной области соответствуют параметрам за УВ с числом $M = 3.0.$ Перед фронтом ЛУВ находится покоящийся газ при давлении ${{p}_{0}} = 1.0.$ На участке конечной длины, равной 1.0 плотность газа меняется по линейному закону:
(10)
${{\rho }_{0}}\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {a\int\limits_0^t {D\left( \tau \right)d\tau } + b,\,\,{\text{если}}\,\,\int\limits_0^t {D\left( \tau \right)d\tau } < 1.0,~} \\ {a + b,\,\,{\text{иначе}}{\text{.}}} \end{array}} \right.$Для случая линейно растущей плотности газа перед фронтом ЛУВ $a = 7.0,$ $b = 1.0.$ Для случая линейно падающей плотности $a = - 7.0,$ $b = 8.0.$ Числовые параметры постановки взяты из работ [30] (закон изменения плотности (10) и конкретные значения $a$ и $b$) и [26] (интенсивность УВ). Здесь и далее все параметры приведены в безразмерном виде. Расчеты проводились на сетке с числом ячеек $N = 2000.$
Рассмотрим сначала случай линейно растущего градиента плотности. Ударная волна преодолевает участок с неоднородной плотностью за время ${{t}_{A}} \approx 0.43$ (см. рис. 2 и 3). Процедура построения характеристик описана в Приложении 2. В течение этого периода времени за фронтом ЛУВ генерируются волны сжатия и контактные разрывы. При этом скорость ЛУВ падает, а число Маха увеличивается. Как до, так и после момента времени ${{t}_{A}}$ аналитическое решение Чиснелла–Уизема (кривая 4 на рис. 3), не учитывающее влияние переотраженных волн на ЛУВ, сильно отличается от численного решения (кривая 2 на рис. 3). Отметим, что в работе [35] представлена модификация аналитической теории Чиснелла–Уизема для возможности учета влияния переотраженных волн на ЛУВ.
Рис. 2.
Семейство характеристик в задаче о распространении УВ по участку среды конечной длины с линейно возрастающим градиентом плотности.
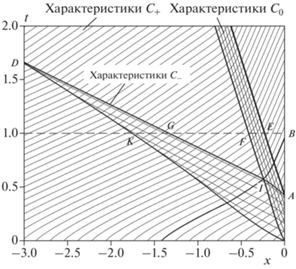
Рис. 3.
Динамика изменения скорости (кривая 1) и числа Маха ЛУВ (кривая 2) в задаче о распространении УВ по участку среды конечной длины с линейно возрастающим градиентом плотности (кривая 3, плотность перед фронтом ЛУВ). Штрих-пунктирная кривая 4 – аналитическое решение Чиснелла–Уизема. Штрих-пунктирная прямая 5 – асимптотическое решение.
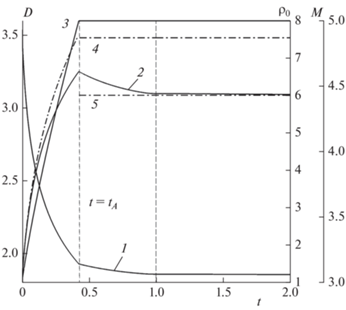
После того как плотность перед волной становится постоянной, скорость волны и число Маха уменьшаются под воздействием волн, отраженных от контактных разрывов за волной и догоняющих ЛУВ. Основные изменения продолжаются до тех пор, пока волна, отраженная от контактного разрыва, следующего вдоль ${{C}_{0}}$-характеристики, выпущенной в начальный момент времени, не догонит ЛУВ при ${{t}_{B}} \approx 1.$ В этот момент времени число Маха ЛУВ выходит на значение, близкое асимптотической величине (прямая 5 на рис. 3). Данная асимптотика определяется решением задачи Римана (Riemann). Параметры по одну сторону от разрыва в этой задаче Римана – параметры за фронтом УВ с числом Маха, равным 3.0, соответствующие начальному моменту времени, когда значение плотности перед УВ равно 1.0. Параметры справа – итоговые параметры перед УВ, соответствующие моменту времени, когда плотность перестает меняться и ее значение становится равным 8.0.
Из рис. 2 видно, что ${{C}_{ - }}$-характеристики, вдоль которых следуют отраженные от ЛУВ волны сжатия, постепенно вливаются в характеристику, следующую из начала координат. По этой причине по мере распространения протяженность волны сжатия уменьшается. Например, в момент времени ${{t}_{B}} \approx 1$ на рис. 2 и 4 границы ее обозначены точками K и G. Контактные разрывы, формирующиеся при прохождении ЛУВ участка переменной плотности, двигаются с постоянной скоростью. Граница области контактных разрывов обозначена на рис. 2 и 4 точками E и F. Давление и скорость в области между ЛУВ и хвостом волны сжатия на промежутке времени от ${{t}_{A}}$ до ${{t}_{B}}$ (например, для момента времени ${{t}_{B}}$ это – область $\left[ {{{x}_{{\text{G}}}};0} \right]$ на рис. 4) не постоянны из-за влияния характеристик из “переотраженного характеристического треугольника”, IAB, на рис. 2. Время, в течение которого переотраженные волны продолжают влиять на ЛУВ, несмотря на то, что плотность перед УВ уже постоянна, коррелирует со временем, которое требуется пройти волне, отраженной от точки A, до точки I, а также волне, переотраженной от точки I, до точки B.
Рис. 4.
Рассчитанные пространственные профили распределения за фронтом ЛУВ в задаче о распространении УВ по участку среды конечной длины с линейно возрастающим градиентом плотности в момент времени t = 1.0. Кривая 1 – распределение плотности, 2 – распределение скорости, 3 – распределение давления.
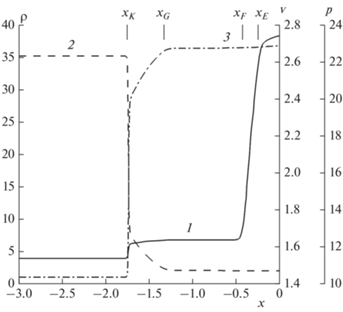
Аналогичное исследование проведено для случая уменьшающейся перед фронтом ЛУВ плотности. В этом случае УВ преодолевает участок с градиентом плотности за время ≈0.66. Вместо волн сжатия за фронтом ЛУВ генерируются волны разрежения. При этом, в отличие от случая с увеличивающейся плотностью перед ЛУВ, скорость ЛУВ увеличивается, а число Маха уменьшается. Также аналитическое решение Чиснелла–Уизема, не учитывающее влияние переотраженных волн на ЛУВ, практически не отличается от численного до момента времени t = 0.66, когда аналитическое решение выходит на стационарный уровень. По предположению, сделанному в работе [30], это свидетельствует о том, что переотраженные волны почти не влияют на итоговое решение в этой области. Данное предположение подкрепляется проведенным характеристическим анализом. Характеристики ${{C}_{ + }},$ вначале отклоняясь от ЛУВ, гораздо позже приходят к правой границе расчетной области, и, соответственно, их влияние на ЛУВ также начинается позже. Характеристики ${{C}_{ - }},$ вдоль которых следуют отраженные от ЛУВ волны разрежения, постепенно расходятся, расстояние между ними увеличивается.
После того как плотность перед волной становится постоянной, ее скорость и число Маха увеличиваются под воздействием волн, отраженных от контактных разрывов за волной и догоняющих ЛУВ. Это продолжается до тех пор, пока последняя переотраженная волна не догонит ЛУВ в момент времени $t \approx 3.69.$ К этому времени число Маха выходит на асимптотический уровень.
РАСПРОСТРАНЕНИЕ УДАРНОЙ ВОЛНЫ В СРЕДЕ С СИНУСОИДАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ ПЛОТНОСТИ
Задача о взаимодействии УВ с синусоидальным возмущением плотности была рассмотрена в статье [26] (отсюда ее название – задача Шу–Ошера) в качестве примера, иллюстрирующего свойства ENO-схем повышенного порядка точности. Со временем данная задача стала распространенным, достаточно жестким тестом для проверки реализации и свойств методов сквозного счета для решения уравнений Эйлера, так как решением задачи является течение, в поле которого содержатся и гладкие структуры, и движущиеся разрывы. По этой же причине задача Шу–Ошера часто используется для проверки методов расчета течений с волнами детонации (см., например [36, 37]), поскольку структура фронта детонационной волны включает и лидирующий скачок, и область гладкого изменения параметров за ней, которая должна очень хорошо разрешаться. Разрешение гладких областей течения возможно при использовании схем повышенного порядка точности, которые в то же время должны быть достаточно устойчивыми и не приводить к возникновению нефизичных осцилляций в окрестностях газодинамических разрывов. Задача Шу–Ошера не имеет точного решения, и в качестве эталонного часто рассматривают решение из работы [26], полученное на сетке с разрешением 6.25 · 10–3 методом сквозного счета третьего порядка точности.
Отметим работы [35, 38, 39], в которых для исследования распространения УВ в среде с неоднородным распределением плотности, в том числе в модельных постановках, близких задаче Шу–Ошера, использовались методы, отслеживающие фронт ЛУВ. Данные методы, в некотором смысле близкие алгоритму, который предлагается в настоящей работе, базировались на аппарате подвижных сеток или представляли собой разновидности метода погруженной границы.
Расчетная область – отрезок [–20;0]. Значения начальной плотности, скорости и давления во всей расчетной области соответствуют параметрам за УВ с числом $M = 3.0.$ Перед фронтом ЛУВ находится покоящийся газ при давлении ${{p}_{0}} = 1.0,$ плотность которого меняется по закону
В начальный момент времени и до момента $t \approx 0.154$ плотность перед УВ увеличивается по синусоидальному закону. Как и в задаче с линейно растущей плотностью перед фронтом ЛУВ, это сопровождается образованием волн сжатия и контактных разрывов (см. рис. 5). При этом число Маха ЛУВ увеличивается, в то время как ее скорость уменьшается. Волны, отраженные от ЛУВ и следующие вдоль характеристик ${{C}_{ - }},$ постепенно сливаются в одну характеристику, догоняя друг друга. Фронт волны сжатия со временем становится более крутым. В итоге этот процесс приводит к формированию внутренних ударных волн. В момент времени $t \approx 0.154$ плотность перед ЛУВ начинает уменьшаться, и, аналогично описанному ранее случаю уменьшающегося линейного градиента плотности, теперь вдоль характеристик ${{C}_{ - }}$ следуют волны разрежения; ЛУВ начинает ускоряться, а число Маха ее уменьшается. Далее процесс циклично повторяется по мере продвижения ударной волны по среде с переменной плотностью.
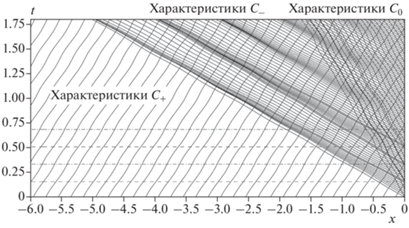
Рис. 5.
Семейство характеристик в задаче Шу–Ошера. Пунктирные горизонтальные прямые обозначают моменты времени, соответствующие максимальным значениям плотности перед ЛУВ, штрих-пунктирные линии – минимальным.
На рис. 6 показано изображение профиля плотности газа за ЛУВ в момент времени $t = 1.8$ в сравнении с профилем из работы [26]. При $ - 1.69 < x < 0$ график плотности имеет вид колеблющейся кривой, что связано с распространением налево контактных разрывов, отраженных от ЛУВ, а также влиянием на эту область характеристик ${{C}_{ + }}$ и ${{C}_{ - }},$ переотраженных внутри зоны контактных разрывов. Видно хорошее соответствие между результатом, полученным при расчете с использованием предложенного алгоритма, и эталонным результатом [26].
Рис. 6.
Пространственные профили плотности газа за фронтом ЛУВ в задаче Шу–Ошера в момент времени t = 1.8. Сплошная линия – расчет авторов, точки – расчет из работы [26].
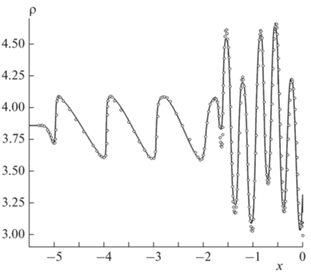
Некоторая неточность в фазе пиков в области контактных разрывов связана с погрешностями оцифровки результатов [26], не полной идентичностью моментов времени сравнения результатов и необходимостью совмещения графиков относительно текущего положения фронта ЛУВ для прямого сравнения результатов. Важными являются различия в амплитудах пиков, отстоящих от фронта ЛУВ. Как показано, например, в работе [40], занижение амплитуды пиков связано с недостаточно высоким порядком точности численного метода. При использовании методов третьего и выше порядков точности соответствие данным [26] в этой части будет лучше. Специфика решения задачи в СКФ может также потребовать использования более точного алгоритма определения скорости ЛУВ. В работе [17] для этих целей использовалась локально-квадратичная аппроксимации характеристики ${{C}_{ + }}$ в окрестности ЛУВ.
ВЫВОДЫ
1. В работе предложен алгоритм для расчета распространения ударной волны в среде с переменной плотностью в системе координат, связанной с ударной волной. С использованием работ [17, 18] описанный алгоритм может быть обобщен на случай химически реагирующих сред в рамках одно- и двухстадийной модели кинетики и применен для исследования механизмов распространения волн детонации в неоднородных средах.
2. Работоспособность вычислительного алгоритма продемонстрирована для двух типов неоднородностей перед ударной волной: участок конечной длины с линейным градиентом плотности и синусоидальное распределение плотности. Для случая линейного градиента проведено сравнение полученных результатов с аналитической теорией Чиснелла–Уизема, не учитывающей влияния переотраженных волн на лидирующую ударную волну. Были получены хорошее согласование для случая уменьшающейся плотности перед ударной волной и расхождение результатов для случая увеличивающейся плотности, что связано с разной степенью влияния переотраженных волн на лидирующий скачок. Решение задачи о взаимодействии ударной волны с синусоидальным распределением плотности (задача Шу–Ошера) сравнивалось с решением, представленным в работе [26]. Получено хорошее согласование за исключением амплитуд некоторых пиков в зоне контактных разрывов. На уровне характеристик показано, что решение задачи Шу–Ошера циклически сочетает в себе элементы решения задачи об уменьшающемся и увеличивающемся линейных градиентах плотности перед волной.
3. Рассмотренные в статье задачи служат не только для валидации вычислительного алгоритма. Они демонстрируют основную идею исследования в системе координат, связанной с лидирующим скачком. Подобный математический аппарат позволяет проводить качественные и количественные исследования течений с ударными и детонационными волнами с точки зрения поведения характеристик, которые раскрывают механику газодинамических процессов.
Список литературы
Wolanski P. // Shock Waves. 2021. V. 31. № 7. P. 623; https://doi.org/10.1007/s00193-021-01038-2
Bykovskii F.A., Zhdan S.A., Vedernikov E.F. et al. // Ibid. Issue 8. P. 829; https://doi.org/10.1007/s00193-021-01044-4
Matsuoka K., Tanaka M., Noda T. et al. // Combust. and Flame. 2020. V. 225. P. 13; https://doi.org/10.1016/j.combustflame.2020.10.048
Фролов С.М., Иванов В.С. // Хим. физика. 2021. Т. 40. № 4. С. 68; https://doi.org/10.31857/S0207401X21040075
Honhar P., Kaplan C.R., Houim R.W. et al. // Combust. and Flame. 2020. V. 222. P. 152; https://doi.org/10.1016/j.combustflame.2020.08.034
Ma W.J., Wang C., Han W.H. // Shock Waves. 2020. V. 30. P. 703; https://doi.org/10.1007/s00193-020-00976-7
Kessler D.A., Gamezo V.N., Oran E.S. // Philos. Trans. R. Soc. B. London, Ser., 2012. V. 370. P. 567; https://doi.org/10.1098/rsta.2011.0342
Boeck L.R., Berger F.M., Hasslberger J. et al. // Shock Waves. 2016. V. 26. P. 181; https://doi.org/10.1007/s00193-015-0598-8
Han W., Wang C., Law C.C. // J. Fluid Mech. 2019. V. 865. P. 602; https://doi.org/10.1017/jfm.2019.37
Chue R.S., Lee J.H., Zhang F. // Shock Waves. 1995. V. 5. P. 159; https://doi.org/10.1007/BF01435523
Kim M., Mi X., Kiyanda C.B. et al. // Proc. Combust. Inst. 2021. V. 38. P. 3701; https://doi.org/10.1016/j.proci.2020.07.138
Mi X.C., Higgins A.J., Kiyanda C.B. et al. // Shock Waves. 2018. V. 28. P. 993; https://doi.org/10.1007/s00193-018-0847-8
Taileb S., Melguizo-Gavilanes J., Chinnayya A. // Combust. and Flame. 2020. V. 218. P. 247; https://doi.org/10.1016/j.combustflame.2020.04.018
Tropin D., Bedarev I. // J. Loss Prev. Process. Ind. 2021. V. 72. P. 104 595; https://doi.org/10.1016/j.jlp.2021.104595
Kasimov A.R., Gonchar A.R. // Proc. Comb. Inst. 2021. V. 38. Issue 3. P. 3725; https://doi.org/10.1016/j.proci.2020.07.149
Kasimov A.R., Goldin A.Yu. // Shock Waves. 2021; https://doi.org/10.1007/s00193-021-01049-z
Lopato A.I., Utkin P.S. // Combust. Sci. Technol. 2016. V. 188. № 11–12. P. 1844; https://doi.org/10.1080/00102202.2016.1212570
Poroshyna Y.E., Lopato A.I., Utkin P.S. // J. Inverse Ill-Posed Probl. 2021. V. 29. № 4. P. 557; https://doi.org/10.1515/jiip-2020-0032
Kasimov A.R., Stewart D.S. // Phys. Fluids. 2004. V. 16. P. 3566; https://doi.org/10.1063/1.1776531
Henrick A.K., Aslam T.D., Powers J.M. // J. Comput. Phys. 2006. V. 213. P. 311; https://doi.org/10.1016/j.jcp.2005.08.013
Romick C.M., Aslam T.D. // Ibid. 2019. V. 395. P. 765; https://doi.org/10.1016/j.jcp.2019.06.011
Киверин А.Д., Смыгалина А.Е., Яковенко И.С. // Хим. физика. 2020. Т. 39. № 8. С. 9; https://doi.org/10.31857/S0207401X2008004X
Leung C., Radulescu M.I., Sharpe G.J. // Phys. Fluids. 2010. V. 22. Paper 126101; https://doi.org/10.1063/1.3520188
Chisnell R.F. // Proc. R. Soc. A. London, Ser., 1955. V. 232. № 1190. P. 350; https://doi.org/10.1098/rspa.1955.0223
Whitham G.B. // J. Fluid Mech. 1958. V. 4. P. 337; https://doi.org/10.1017/S0022112058000495
Shu C.-W., Osher S. // J. Comput. Phys. 1989. V. 83. P. 32; https://doi.org/10.1016/0021-9991(89)90222-2
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. М.: ГИФМЛ, 1963. Ч. 1.
Холодов А.С. // Журн. вычислительной математики и мат. физики. 1978. Т. 18. № 6. С. 1476.
Овсянников Л.В. Лекции по основам газовой динамики. 2-е изд., доп. Москва–Ижевск: Ин-т компьютерных исслед., 2003.
Bird G.A. // J. Fluid Mech. 1961. V. 11. № 2. P. 180; https://doi.org/10.1017/S0022112061000457
Медведев С.П., Фролов С.М., Гельфанд Б.Е. // Инж.-физ. журн. 1990. Т. 58. № 6. С. 924.
Медведев С.П., Андержанов Э.К., Гук И.В. и др. // Хим. физика. 2020. Т. 39. № 12. С. 24; https://doi.org/10.31857/S0207401X20120110
Хомик С.В., Гук И.В., Иванцов А.Н. и др. // Хим. физика. 2021. Т. 40. № 8. С. 63; https://doi.org/10.31857/S0207401X21080045
Шаргатов В.А., Чугайнова А.П., Горкунов С.В. и др. // Тр. МИАН. 2018. Т. 300. С. 216.
Tian Y., Jaberi F.A., Livescu D. // Proc. AIAA SciTech Forum. 2020. Orlando, FL, USA; https://doi.org/10.2514/6.2020-0101
Cole L.K., Karagozian A.R., Cambier J.-L. // Combust. Sci. Technol. 2012. V. 184. P. 1502; https://doi.org/10.1080/00102202.2012.690316
Dong H., Fu L., Zhang F. et al. // Commun. Comput. Phys. 2019. V. 25. P. 1357; https://doi.org/10.4208/cicp.OA-2018-0008
Suresh A. // J. Comput. Phys. 2005. V. 206. P. 6; https://doi.org/10.1016/j.jcp.2004.11.036
Rawat P.S., Zhong X. // Ibid. 2010. V. 229. № 19. P. 6744; https://doi.org/10.1016/j.jcp.2010.05.021
Лопато А.И., Уткин П.С. // Компьютерные исслед. и моделирование (Ижевск). 2014. Т. 6. № 5. С. 643; https://doi.org/10.20537/2076-7633-2014-6-5-643-653
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика