Химическая физика, 2022, T. 41, № 5, стр. 441-52
Акустико-гравитационные волны в условиях неоднородного профиля температуры нейтральной компоненты в атмосфере Земли
Н. В. Бахметьева 1, *, Г. И. Григорьев 1, **, Е. Е. Калинина 1
1 Научно-исследовательский радиофизический институт ННГУ им. Н.И. Лобачевского
Нижний Новгород, Россия
* E-mail: nv_bakhm@nirfi.unn.ru
** E-mail: grigorev@nirfi.unn.ru
Поступила в редакцию 10.11.2021
После доработки 09.12.2021
Принята к публикации 20.12.2021
- EDN: SLLYXK
- DOI: 10.31857/S0207401X22050028
Аннотация
Исследовано влияние неоднородного распределения температуры по высоте в атмосфере на распространяющиеся в ней акустико-гравитационные волны. Найдены коэффициенты отражения и прохождения волн для слоев с линейным и параболическим высотными профилями температуры. Обсуждаются условия волноводного распространения акустико-гравитационных волн в таких слоях. Приведены примеры высотных профилей температуры, полученных в экспериментах по рассеянию радиоволн на искусственных периодических неоднородностях плазмы в нижней термосфере.
1. ВВЕДЕНИЕ
Атмосферные волны изучаются в течение многих десятилетий. Они практически постоянно присутствуют на разных высотах в атмосфере Земли. Одной из разновидностей атмосферных волн являются акустико-гравитационные волны (АГВ). К настоящему времени изучены основные свойства этих волн, механизмы их генерации, особенности распространения, определены основные источники генерации (см. работы [1–6] и содержащиеся в них ссылки). В последние десятилетия большое внимание уделяется численному моделированию распространения акустических волн в разных средах. Влияние неизотермичности и неоднородного по высоте ветра на распространение АГВ в приближении геометрической оптики исследовано в работе [5]. В работе [7] в линейном приближении проанализирован спектр мод АГВ в неизотермической атмосфере, граничащей асимптотически на больших высотах с изотермическим полупространством. Авторы работ [8, 9] рассмотрели механизм формирования крупномасштабных возмущений в верхней атмосфере от источников АГВ на поверхности Земли. В работе [10] представлены результаты анализа численного эксперимента по генерации АГВ в нижней атмосфере и их распространению в верхнюю атмосферу. В качестве источника волн рассмотрены наблюдаемые вариации атмосферного давления в период прохождения солнечного затмения 20 марта 2015 года над Калининградом (54° N, 20° E). В работе [11] представлены результаты наблюдений динамики параметров атмосферы и ионосферы, выполненных в период прохождения метеорологического шторма над Калининградским регионом в декабре 2010 года. Показано, что метеорологические возмущения нижней атмосферы могут проявляться на высотах мезосферы и термосферы. А в работе [12] проведено моделирование ионосферных эффектов, вызванных прохождением метеорологических штормов, в частности рассмотрена модель источника, имитирующего эффект диссипации акустико-гравитационных волн, распространяющихся из области метеорологического шторма на высоты верхней атмосферы.
Фундаментальная проблема подводного распространения звука рассмотрена в монографии [13], где решены задачи вычисления акустических полей в стратифицированной среде. Даны различные представления поля точечного гармонического источника и их взаимосвязь, обосновано применение метода параболического уравнения к решению задач подводной акустики. Рассмотрены некоторые явления, связанные со случайными флуктуациями скорости звука в океане.
С развитием техники эксперимента и разработкой новых методов исследования атмосферных волн появились новые данные о параметрах и особенностях распространения волн в разных средах [14–16]. Одним из эффективных экспериментальных методов исследования атмосферных волн по их влиянию на параметры нейтральной компоненты на высотах мезосферы и нижней термосферы является метод, основанный на создании искусственных периодических неоднородностей (ИПН) ионосферной плазмы, подробно описанный в монографии [17]. Этим методом получен большой объем сведений о высотных профилях и временны́х вариациях температуры и плотности нейтральной компоненты в интервале высот 90–120 км, скорости регулярного вертикального движения среды и параметрах турбулентности на высотах ниже высоты турбопаузы [18–26]. Разработанные авторами этих работ способы регистрации позволили обнаружить волновые движения на высотах 60–130 км с периодами от 10–15 мин до нескольких часов. В работе [18] проведено моделирование характеристик внутренних гравитационных волн (ВГВ) на основе линейной теории их свободного распространения в безграничной изотермической невозмущенной атмосфере. С использованием поляризационных соотношений для низкочастотных волн по измеренным значениям амплитуды вертикальной скорости рассчитаны относительные амплитуды температуры и плотности нейтральной компоненты для периодов от 15 мин до 4-х ч, которые сопоставлены с экспериментально полученными значениями этих параметров на высотах 90–120 км. Для волн с периодами 15–30 мин получено удовлетворительное соответствие. В работе [19] на основе полученных методом ИПН высотных профилей температуры нейтральной компоненты рассмотрено влияние гидродинамической неустойчивости на распространение атмосферных волн на высотах мезосферы и нижней термосферы.
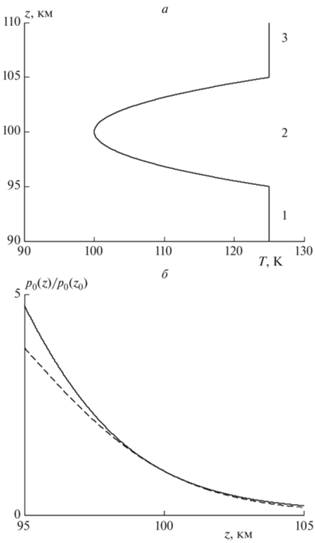
Результаты определения температуры методом создания ИПН показали, что высотные профили температуры на высотах мезосферы и нижней термосферы отличаются большим разнообразием формы. На рис. 1 приведены примеры высотных профилей температуры, полученные нами в разные периоды наблюдений [19, 21]. Часть показанных на рис. 1 профилей температуры имеет форму, близкую к параболической, остальные представлены волнообразными изменениями температуры по высоте. Некоторые профили содержат линейный участок изменения T(z). В работе [27] нами рассмотрено влияние линейного профиля температуры на свойства внутренних гравитационных волн. В данной работе мы рассмотрели задачу о распространении и отражении АГВ в слое атмосферы с подобными неоднородными распределениями температуры с параметрами, близкими к полученным нами в экспериментах.
2. МОДЕЛИ СРЕДЫ РАСПРОСТРАНЕНИЯ АГВ
Вначале рассмотрим некоторые модели среды распространения АГВ. Для аналитических расчетов характеристик волн широко используется изотермическая модель атмосферы [1]. В этой модели при T = const равновесные давление p0(z) и плотность ρ0(z) изменяются по высоте z в соответствии с барометрической формулой
Как показано на рис. 1, реальная зависимость температуры атмосферы от высоты в большинстве случаев отличается от принятой в этой модели. Влияние линейного профиля температуры на свойства ВГВ частично исследованы нами в работах [19, 27]. Здесь мы рассмотрим модельную задачу, в которой слой с параболической зависимостью температуры T от высоты z (среда 2) граничит сверху при z = z2 и снизу при z = z1 с изотермическими средами 1 и 3 при T = T1 = T0(z1):
(1)
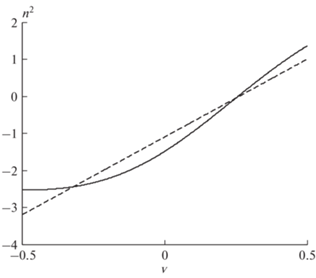
${{T}_{0}}\left( z \right) = {{T}_{s}}\left[ {1 + {{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}} {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}} \right].$Рис. 2.
а – Высотный модельный профиль температуры T(z) – пояснения см. в тексте; б – высотные зависимости давления p0(z) – сплошная кривая и плотности ρ0(z) – штриховая, нормированные на их значения на высоте z0.
Используя уравнение состояния идеального газа и условие его равновесия ${{d{{p}_{0}}} \mathord{\left/ {\vphantom {{d{{p}_{0}}} {dz}}} \right. \kern-0em} {dz}} = - {{\rho }_{0}}g,$ легко определить, что внутри слоя равновесные давление и плотность изменяются по высоте в соответствии с формулами
(2)
${{p}_{0}}\left( z \right) = {{p}_{0}}\left( {{{z}_{0}}} \right){\text{exp}}\left[ { - \frac{h}{{{{H}_{S}}}}{\text{arctg}}\left( {\frac{{z - {{z}_{0}}}}{h}} \right)} \right],$(3)
$\begin{gathered} {{\rho }_{0}}\left( z \right) = {{\rho }_{0}}\left( {{{z}_{0}}} \right){\text{exp}}\left[ { - \frac{h}{{{{H}_{s}}}}{\text{arctg}}\left( {\frac{{z - {{z}_{0}}}}{h}} \right)} \right] \times \\ \times \,\,{{\left[ {1 + {{{\left( {\frac{{z - {{z}_{0}}}}{h}} \right)}}^{2}}} \right]}^{{ - 1}}}~. \\ \end{gathered} $(4)
${{c}^{2}}\left( z \right) = \gamma \frac{{{{p}_{0}}}}{{{{\rho }_{0}}}} = c_{s}^{2}\frac{{1 + {{{\left( {z - {{z}_{0}}} \right)}}^{2}}}}{{{{h}^{2}}}}.$Далее рассмотрим особенности распространения АГВ в такой среде, а также найдем коэффициенты отражения и прохождения волн в слоях с неоднородным по высоте профилем температуры.
3. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ АМПЛИТУДЫ ВОЛНЫ
Волновое уравнение для дивергенции скорости $\chi = {\text{div}}~{\mathbf{v}}$ приведено в монографии [28] для произвольной зависимости c(z) скорости звука от высоты и малых амплитуд возмущений. Предполагая, что свойства равновесной среды не изменяются во времени и по горизонтальной координате x, преобразуем уравнение для дивергенции скорости в уравнение для ее амплитуды F(z), приняв зависимость χ от координат и времени в виде $\chi = F\left( z \right){\text{exp}}\left( { - i\omega t + ikx} \right).$ С учетом соотношения (4) получаем
(5)
$\begin{gathered} {{c}^{2}}\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}} + \left( {\frac{{d{{c}^{2}}}}{{dz}} - \gamma g} \right)\frac{{dF}}{{dz}} + \\ + \,\,\left\{ {{{\omega }^{2}} - {{k}^{2}}{{c}^{2}} + \frac{{g{{k}^{2}}}}{{{{\omega }^{2}}}}\left[ {\frac{{d{{c}^{2}}}}{{dz}} + \left( {\gamma - 1} \right)g} \right]} \right\}F = 0. \\ \end{gathered} $Вводя вместо z новую безразмерную переменную v = (z – z0)/h и представляя F в виде произведения: F = fy, где, согласно [29], y = exp(0.5β arctgv)(1 + + v2)–1/2, а β = h/Hs, для функции f получим уравнение без первой производной:
(7)
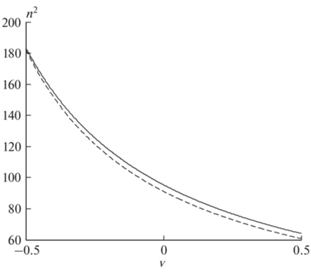
$\begin{gathered} {{n}^{2}}\left( v \right) = - \frac{{1 + 0.25{{\beta }^{2}}}}{{{{{\left( {1 + {{v}^{2}}} \right)}}^{2}}}} - {{k}^{2}}{{h}^{2}} + \\ + \,\,\frac{{{{\omega }^{2}}{{h}^{2}}}}{{c_{s}^{2}\left( {1 + {{v}^{2}}} \right)}} + \frac{{g{{k}^{2}}h\left[ {2v + {{\left( {\gamma - 1} \right)gh} \mathord{\left/ {\vphantom {{\left( {\gamma - 1} \right)gh} {c_{s}^{2}}}} \right. \kern-0em} {c_{s}^{2}}}} \right]}}{{{{\omega }^{2}}\left( {1 + {{v}^{2}}} \right)}}. \\ \end{gathered} $На рис. 3 сплошной линией показана рассчитанная по формуле (7) зависимость n2(v), а штриховой – ее аппроксимация линейной функцией n2 = 4.2v – 1.1 (см. ниже).
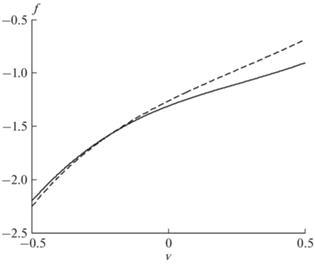
Рис. 3.
Зависимость квадрата коэффициента преломления n2 (сплошая кривая) от величины v = (z – z0)/h в слое с квадратичным высотным профилем температуры при значениях параметров Hs = 2.976.4 м, β = = 3.359, k = 1.365 ⋅ 10–5 м–1, $c_{s}^{2}$ = 4.08648 ⋅ 104 м2 с–2, ω = 2.74 ⋅ 10–3 с–1, θ = 30°. Штриховой кривой показана аппроксимация рассчитанной кривой линейной функцией n2 = 4.2v – 1.1.
4. ГРАНИЧНЫЕ УСЛОВИЯ
Из свойства непрерывности (сплошности) среды следует, что на границе сред 1 и 2 должно выполняться равенство вертикальных смещений: ζ1 = ζ2. В отсутствие горизонтального ветра это означает равенство вертикальных скоростей w1 = w2 при одинаковых частотах возмущений в обеих средах. Если на границе нет скачка плотности, т.е. $~{{\rho }_{{01}}} = {{\rho }_{{02}}},$ то в качестве второго граничного условия выступает равенство давлений p1 = p2. Выразим эти условия через дивергенцию скорости χ. Для этой цели воспользуемся выражением из работы [28]:
(8)
$\left( {{{\omega }^{4}} - {{g}^{2}}{{k}^{2}}} \right)w = - {{\omega }^{2}}{{c}^{2}}\frac{{d\chi }}{{dz}} + g\left( {\gamma {{\omega }^{2}} - {{k}^{2}}{{c}^{2}}} \right)\chi ~.$Учитывая, что на границе неизменными являются величины вертикальной скорости w, частоты ω, ускорения свободного падения g и горизонтального волнового числа k, из формулы (8) получаем
(9)
$\left( {\frac{{d{{\chi }_{1}}}}{{dz}} - \frac{{d{{\chi }_{2}}}}{{dz}}} \right) = g\left( {\frac{\gamma }{{{{c}^{2}}}} - \frac{{{{k}^{2}}}}{{{{\omega }^{2}}}}} \right)\left( {{{\chi }_{1}} - {{\chi }_{2}}} \right).~$Связь давления и плотности в акустико-гравитационных волнах без учета поглощения дается соотношением ${{dp} \mathord{\left/ {\vphantom {{dp} {dt}}} \right. \kern-0em} {dt}} = {{{{c}^{2}}d\rho } \mathord{\left/ {\vphantom {{{{c}^{2}}d\rho } {dt}}} \right. \kern-0em} {dt}}.$ Если воспользоваться уравнением непрерывности ${{dp} \mathord{\left/ {\vphantom {{dp} {dt}}} \right. \kern-0em} {dt}} + {{\rho }_{0}}\chi = 0,$ получим связь давления и дивергенции скорости в виде ${{dp} \mathord{\left/ {\vphantom {{dp} {dt}}} \right. \kern-0em} {dt}} + {{c}^{2}}{{\rho }_{0}}\chi = 0.$ Раскрывая в этом уравнении полную производную по времени и записывая его по обе стороны границы, получим выражение
(10)
$\begin{gathered} i\omega \left( {{{p}_{1}} - {{p}_{2}}} \right) + g\left( {{{\rho }_{{01}}}{{w}_{1}} - {{\rho }_{{02}}}{{w}_{2}}} \right) = \\ = {{c}^{2}}\left( {{{\rho }_{{01}}}{{\chi }_{1}} - {{\rho }_{{02}}}{{\chi }_{2}}} \right). \\ \end{gathered} $Равенство левых частей в (10) по разным сторонам границы приводит к соотношению
Из уравнений (9) и (11) окончательно получаем нужные граничные условия применительно к дивергенции скорости и ее производной:
(12)
${{\chi }_{1}} = {{\chi }_{2}},\,\,\,\,~\frac{{d{{\chi }_{1}}}}{{dz}} = \frac{{d{{\chi }_{2}}}}{{dz}}~.$Далее полагаем, что на слой с параболической зависимостью равновесной температуры и скорости звука от высоты под углом θ к вертикали падает акустико-гравитационная волна с частотой ω = δωg, где δ – безразмерный параметр. Найдем коэффициенты отражения и прохождения АГВ в таком слое.
5. КОЭФФИЦИЕНТЫ ОТРАЖЕНИЯ И ПРОХОЖДЕНИЯ ВОЛНЫ В СЛОЕ С НЕОДНОРОДНЫМ ПРОФИЛЕМ ТЕМПЕРАТУРЫ
Перепишем условия (12) для нижней (z = z1) и верхней (z = z2) границ слоя, учитывая, что снизу на слой падает плоская волна, характеризуемая ${{\chi }_{{inc}}} = A{\text{exp}}\left( { - i\omega t + ikx - i\unicode{230} z} \right),$ c амплитудой A = 1, частотой ω, горизонтальным волновым числом k и вертикальным волновым числом æ. Разумно предположить, что от слоя отразится волна с ${{\chi }_{{ref}}} = R{\text{exp}}\left\{ { - i\omega t + ikx + i\unicode{230} \left( {z - {{z}_{1}}} \right)} \right\}$ и пройдет через него волна с ${{\chi }_{{pas}}} = D{\text{exp}}\left\{ { - i\omega t + ikx - i\unicode{230} \left( {z - {{z}_{2}}} \right)} \right\}.$ Заметим, что частота ω и горизонтальное волновое число k у всех волн одинаковы, так как мы предполагаем, что свойства модельной среды не изменяются со временем и по горизонтали. Вертикальное волновое число æ в средах ниже границы 1 и выше границы 2 будет одним и тем же при условии, что температуры этих сред одинаковы (как в принятой нами модели). Этот вывод следует из дисперсионного уравнения для АГВ, которое получается из (5) при условии c2(z) = const:
(13)
${{\omega }^{4}} - {{\omega }^{2}}{{c}^{2}}\left( {{{k}^{2}} + {{\unicode{230} }^{2}} + k_{0}^{2}} \right) + \omega _{g}^{2}{{c}^{2}}{{k}^{2}} = 0,$Подставляя искомую функцию f и плоские волны χinc, χref и χpas в уравнения (12), найдем коэффициенты отражения R и прохождения D волн для слоя с параболическим профилем температуры, а также определим конкретные условия для функции f. Запишем их при z = z1 и z = z2 в виде
(14)
$\begin{gathered} \frac{{df}}{{dv}} + \left( {a - i{{\alpha }^{{ - 1}}}} \right)f = \\ = 2{{\left( {i\alpha y} \right)}^{{ - 1}}}{\text{exp}}\left( { - i\unicode{230} {{z}_{1}}} \right),\,\,\,\,\alpha = {{\left( {\unicode{230} h} \right)}^{{ - 1}}}, \\ \end{gathered} $(15)
$\frac{{df}}{{dv}} + \left( {a + i{{\alpha }^{{ - 1}}}} \right)f = 0,\,\,\,\,a = {{y}^{{ - 1}}}\frac{{dy}}{{dv}} = \frac{{0.5\beta - v}}{{1 + {{v}^{2}}}}.$Если функция f найдена и известна на границах параболического слоя температуры, то коэффициенты отражения и прохождения волны определяются соответственно формулами:
В этих выражениях коэффициенты отражения и прохождения, а также искомая функция f нормированы на амплитуду волны, падающей на слой. Вертикальное волновое число определяется из дисперсионного уравнения (13) и может быть представлено в виде
(18)
${{\unicode{230} }^{2}} = \left[ {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}} - k_{0}^{2} + {{k}^{2}}\left( {\frac{{\omega _{g}^{2}}}{{{{\omega }^{2}}}} - 1} \right)} \right].$Если ввести обозначения k = Ksin θ, æ = K cos θ, то уравнение (18) запишется в виде
Такая форма записи уравнения позволяет выбрать разумные параметры падающей и прошедшей волн при численном анализе возмущений внутри слоя.
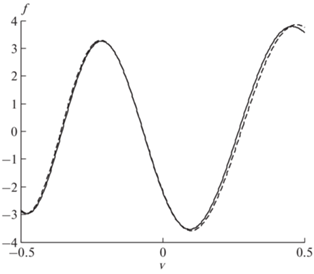
Результаты численного решения уравнений (6) с граничными условиями (14), (15) в виде зависимости функции f(v), которая определяет коэффициенты отражения R и прохождения D плоской акустико-гравитационной волны в слое с параболическим профилем температуры, представлены на рис. 4 при значениях параметров, указанных на рис. 3 (сплошная кривая). Обращаясь к рис. 3, отметим, что для квазилинейной зависимости величины n2(v) из (6), которая описывается уравнением
Рис. 4.
Зависимость функции f(v), которая определяет коэффициенты отражения R и прохождения D плоской акустико-гравитационной волны в слое с параболическим профилем температуры (численное решение, сплошная кривая) и аналитическое решение ${{f}_{1}} = {{C}_{1}}Ai\left( \zeta \right) + {{C}_{2}}Bi\left( \zeta \right)$ (формула (22), штриховая кривая) для линейной аппроксимации n2, приведенной на рис. 3. Здесь ζ = 1.61v – 0.423.
при значениях параметров, указанных на рисунке, можно получить аналитическое решение сформулированной задачи в функциях Эйри.
Вводя новую независимую переменную по формуле
преобразуем уравнения (6), (19) к стандартному виду уравнения Эйри:
Решением этого уравнения являются функции Эйри Ai(ζ), Bi(ζ), так что
(22)
${{f}_{1}} = {{C}_{1}}{\text{Ai}}\left( \zeta \right) + {{C}_{2}}{\text{Bi}}\left( \zeta \right).$Свойства функций Эйри хорошо известны [30–32]. Подставляя формулу (22) в граничные условия (14), (15), в которых переменную v следует заменить на ζ, определяем константы C1, C2 и коэффициенты отражения R и прохождения волны D. Найденное по формуле (22) аналитическое решение для линейной аппроксимации n2, приведенной на рис. 3, показано штриховой кривой на рис. 4. Здесь принято, что ζ = 1.61v – 0.423. Видно, что оба решения близки при изменении величины v = (z – z0)/h в интервале значений (–0.5; 0) и дают удовлетворительное соответствие при v = = (z – z0)/h = 0–0.5. В последнем случае максимальное относительное расхождение кривых вблизи границы интервала изменения переменной v составляет не более 40%.
На рис. 5 показана зависимость функции F(v) = = f(v)y как решения уравнения (5) от высоты z для значений параметра δ = 0.1 при разных углах падения (θ) волны на параболический слой: θ = 30°, 45° и 60° – рис. 5а, и для трех значений параметра δ = 0.1, 0.2 и 0.3 – рис. 5б. В первом случае расчеты проведены при следующих значениях величин: при θ = 30° K = 2.73 ⋅ 10–5 м–1, k = 1.37 ⋅ 10–5 м–1, æ1 = 2.37 ⋅ 10–5 м–1; при θ = 45° K = 1.91 ⋅ 10–5 м–1, k = 1.35 ⋅ 10–5 м–1, æ1 = 1.35 ⋅ 10–5 м–1; при θ = 60° K = = 1.56 ⋅ 10–5 м–1, k = 1.35 ⋅ 10–5 м–1, æ1 = 7.78 ⋅ 10–6 м–1. Были вычислены коэффициенты отражения R и прохождения D акустико-гравитационной волны для параболического слоя, которые при θ = 30° оказались равными R = –0.277 + 0.881i, D = –1.763 + + 0.420i с модулями |R| = 0.924 и |D| = 1.812; при θ = 45° – R = –0.756 + 0.607i, D = –0.978 – 0.628i с модулями |R| = 0.969 и |D| = 1.162; при θ = 60° R = = –0.919 + 0.365i, D = –0.376 – 0.589i с модулями |R| = 0.989 и |D| = 0.699. Из расчета следует, что с ростом угла падения волны на слой с параболическим профилем температуры коэффициент отражения от слоя растет, а коэффициент прохождения падает.
Рис. 5.
а – Зависимость решения уравнения (5) функции F от высоты z для значений параметра δ = 0.1 при разных углах падения волны на параболический слой θ = 30° (сплошная кривая), 45° (штриховая) и 60° (точки); б – зависимость F(z) для значений параметра δ = 0.1 (сплошная кривая), δ = 0.2 (штриховая), δ = 0.3 (точки), т.е. для ω = 0.1ωg, ω = 0.2ωg, ω = 0.3ωg и угла падения θ = 30°.
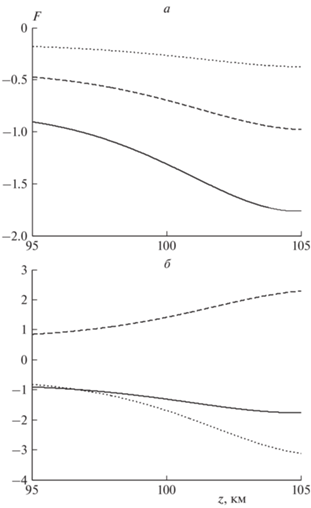
Во втором случае расчеты проведены для δ = 0.1 при K = 2.73 ⋅ 10–5 м–1, k = 1.37 ⋅ 10–5 м–1, æ1 = 2.37 ⋅ ⋅ 10–5 м–1; для δ = 0.2 при K = 5.77 ⋅ 10–5 м–1, k = 2.88 · ⋅ 10–5 м–1, æ1 = 4.99 ⋅ 10–5 м–1, для δ = 0.3 при K = = 9.70 ⋅ 10–5 м–1, k = 4.85 ⋅ 10–5 м–1, æ1 = 8.40 ⋅ 10–5 м–1. Коэффициенты отражения R и прохождения D в этом случае для δ = 0.1 оказались равными R = = ‒0.277 + 0.881i, D = –1.763 + 0.420i с модулями |R| = 0.924 и |D| = 1.812; для δ = 0.2 R = 0.815 – ‒ 0.034i, D = 2.292 + 1.507i с модулями |R| = 0.815 и |D| = 2.743, для δ = 0.3 R = –0.690 – 0.082i, D = = ‒3.113 – 1.391i с модулями |R| = 0.695 и |D| = 3.410. Из этих данных следует, что с ростом величины параметра δ, т.е. с ростом частоты ω, падает доля энергии волны, отраженной от слоя, и растет доля энергии волны, проходящей через слой.
6. РАСПРОСТРАНЕНИЕ АГВ В СЛОЕ С ЛИНЕЙНЫМ ПРОФИЛЕМ ТЕМПЕРАТУРЫ
В качестве следующего примера рассмотрим слой атмосферы с линейно изменяющейся по высоте температурой в интервале ${{z}_{1}} \leqslant z \leqslant {{z}_{2}}{\text{:}}$
Примем следующие значения параметров: z0 = = 100 км, h = 10 км, z1 = 95 км, z2 = 105 км, T1 = 40 К, T2 = 120 К, Ts = 80 К. При таком распределении температуры высота однородной атмосферы H и квадрат скорости звука $c_{s}^{2}$ в слое определяются по формуле
(24)
$\frac{{H\left( z \right)}}{{{{H}_{s}}}} = \frac{{{{c}^{2}}}}{{c_{s}^{2}}} = 1 + \frac{{z - {{z}_{0}}}}{h}.$При этом уравнение (5) для функции F(z) принимает вид
(25)
$\begin{gathered} \frac{{{{d}^{2}}F}}{{d{{v}^{2}}}} + \frac{{1 - \beta }}{{1 + v}}\frac{{dF}}{{dv}} + \\ + \,\,{{h}^{2}}\left\{ {\frac{{{{\omega }^{2}}}}{{c_{S}^{2}\left( {1 + v} \right)}} - {{k}^{2}} + \frac{{g{{k}^{2}}}}{{h{{\omega }^{2}}}}\left[ {1 + \frac{{\left( {\gamma - 1} \right)\beta }}{{\gamma \left( {1 + v} \right)}}} \right]} \right\}F = 0. \\ \end{gathered} $После исключения в (25) слагаемого с первой производной при помощи замены $~F = f{{y}_{1}},$ где ${{y}_{1}} = {{\left( {1 + v} \right)}^{{{{\left( {\beta - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\beta - 1} \right)} 2}} \right. \kern-0em} 2}}}},$ получим
(27)
$\begin{gathered} {{n}^{2}}\left( v \right) = \frac{{1 - {{\beta }^{2}}}}{{4{{{\left( {1 + v} \right)}}^{2}}}} + \frac{{{{\omega }^{2}}{{h}^{2}}}}{{c_{S}^{2}\left( {1 + v} \right)}} - \\ - \,\,{{k}^{2}}{{h}^{2}} + \frac{{gh{{k}^{2}}}}{{{{\omega }^{2}}\left( {1 + v} \right)}}\left( {1 + \frac{{\gamma - 1}}{\gamma }\beta } \right). \\ \end{gathered} $Зависимость n2(v), определяемая формулой (27), показана сплошной кривой на рис. 6 при значениях параметров Hs = 2381.1 м, β = 4.199, $c_{s}^{2} = 32691.9$ м2/с2, ω2 = 2.3533 ⋅ 10–5 с–2, k = 1.04719 ⋅ ⋅ 10–4 м–1. Штриховой кривой на этом рисунке показана зависимость n2(v), полученная по упрощенной формуле:
Рис. 6.
Зависимость квадрата коэффициента преломления среды n2 (сплошная кривая) от величины v = (z – z0)/h по формуле (27) для линейного профиля температуры при значениях параметров β = 4.199, Hs = 2381.1 м, h = = 104 м, $c_{s}^{2}$ = 3.2691 ⋅ 104 м2 с–2, ω2 = 2.3533 ⋅ 10–5 с–2, k = 1.04719 ⋅ 10–4 м–1. Штриховой кривой показана зависимость n2(v), полученная по упрощенной формуле (28).
которая, как видно из рис. 6, в указанном интервале изменения переменной v является хорошей аппроксимацией исходной зависимости (27).
Если подставить выражение (28) для $n_{1}^{2}~$ в уравнение (26), то можно получить его аналитическое решение с помощью функций Бесселя в виде
(29)
$\begin{gathered} f = {{\left( {1 + v} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left[ {{{C}_{1}}{{J}_{1}}\left( t \right) + {{C}_{2}}{{N}_{1}}\left( t \right)} \right], \\ t = 2{{\left[ {91.8\left( {1 + v} \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}~. \\ \end{gathered} $Постоянные ${{C}_{1}},{{C}_{2}}$ и коэффициенты отражения R и прохождения D определяются из граничных условий (12). Как и для случае параболического профиля температуры (см. разд. 4 и 5), при линейной зависимости температуры от частоты в слое приближенное и точное решения задачи (функции f) близки (см. рис. 7).
Рис. 7.
Зависимость функции f от величины v = (z – z0)/h как решения уравнения (26) в слое с линейным профилем температуры для показателя преломления n2 согласно (27) – сплошая кривая и для n2 в виде упрощенного выражения (28) – штриховая. Расчет выполнен с использованием следующих парметров: ω = 0.1ωg, H1 = = 1190.58 м–1, ω2 = 2.35337 ⋅ 10–5 с–2, для среды ниже слоя с линейным профилем температуры θ1 = 6.28°, æ1 = 9.54321 ⋅ 10–4 м–1, $c_{{s1}}^{2}$ = 16345.95 м2 с–2, $\omega _{{g1}}^{2}$ = 2.3533 ⋅ ⋅ 10–3 c–2, для среды выше этого слоя θ1 = 10.2°, æ3 = = 5.79187 ⋅ 10–4 м–1, $c_{{s3}}^{2}$ = 49037.85, $\omega _{{g3}}^{2}$ = 2.35337 ⋅ 10–5 c–2.
На рис. 7 показана зависимость функции f от величины v = (z – z0)/h как решения уравнения (26) в слое с линейным профилем температуры для показателя преломления n2 согласно (27) – сплошая линия и для n2 в виде упрощенного выражения (28) – штриховая. Параметры, использованые при расчетах, указаны в подписи к рис. 7. С использованием граничных условий найдены постоянные коэффициенты в решении с функциями Бесселя: C1 = –7.341 + 12.129i и C2 = 17.677 + 6.297i, и модули коэффициентов отражения |R| = 0.233 и прохождения |D| = 7.240. Это означает, что в данном примере падающая волна преимущественно проходит через слой. Кроме того, пример расчета, приведенный на рис. 7, показывает, что численное решение с точным показателем преломления, выраженным формулой (27), и аналитическое решение с его приближенным значением (28) хорошо соответствуют друг другу, особенно в области высот вблизи z0, т.е. при v = 0. В отличие от случая параболического профиля температуры имеет место волнообразный характер изменения амплитуды F(z) внутри слоя.
Полученные результаты подтверждают физически очевидный факт, что слой с линейно изменяющейся температурой (в отличие от параболического профиля) является преломляющим, т.е. углы падения волны на слой, θ1, и выхода из него, θ3, различаются, в то время как углы падения и отражения являются одинаковыми. Этот факт легко объяснить с помощью дисперсионного уравнения (18) при учете равенства частот ω и горизонтальных компонент волнового вектора падающей и прошедшей волн, разницы температур и определяемых ею величин в средах 1 и 3.
Можно было бы предположить, что при выполнении условия χ = 0, (f = 0) в слоях с неоднородным профилем температуры реализуется волноводный режим распространения АГВ. Но оказывается, что это условие является необходимым, но недостаточным. На самом деле требуется выполнение еще одного условия, а именно ${{d\chi } \mathord{\left/ {\vphantom {{d\chi } {dz}}} \right. \kern-0em} {dz}} = 0\,~\left( {{{df} \mathord{\left/ {\vphantom {{df} {dz}}} \right. \kern-0em} {dz}} = 0} \right).~$ Действительно, поток энергии, переносимой волной в вертикальном направлении, равен ε = pw. Если выразить $\varepsilon $ через дивергенцию скорости и ее производную по вертикали, то поток энергии обращается в нуль при одновременном равенстве нулю и величины χ, и ее производной dχ/dz. При одновременном выполнении этих условий отсутствует поток волновой энергии через узлы (ε = 0) и возникает волноводный режим распространения АГВ, когда волны распространяются только в горизонтальном направлении, а коэффициент их прохождения через слой равен или близок к нулю.
7. ЗАКЛЮЧЕНИЕ
В работе сформулирована и решена задача о распространении акустико-гравитационных волн через слои атмосферы с параболической и линейной зависимостью равновесной температуры от высоты. Найдены коэффициенты отражения и прохождения волн через такие слои. Выполнен численный анализ вертикальной структуры мод АГВ внутри слоев атмосферы с изменяющейся температурой. Показано, что при наличии таких структур в принципе может быть реализован волноводный режим распространения АГВ в горизонтальном направлении. Следовательно, такие слои могут выполнять роль фильтра при распространении волн от нижележащих областей атмосферы в верхние.
Численный анализ распространения АГВ для некоторых частных случаев подтвержден аналитическими расчетами. Показано удовлетворительное соответствие результатов, полученных тем и другим методами. Разработанная методика расчетов также пригодна для анализа распространения АГВ во всем интервале высот от поверхности Земли до высот ионосферы. Для такого анализа требуется обобщение на случай действия различных источников непосредственно в областях атмосферы с изменяющейся по высоте температурой. Отметим, что в рассмотренных случаях не пригоден метод геометрической оптики вследствие низких частот и больших по сравнению с масштабами слоя длин волн.
В заключение заметим, что аналогичным образом решается и задача о взаимодействии АГВ со слоями, в которых зависимость температуры от высоты имеет экспоненциальный характер [33]. Полученные результаты могут быть использованы при анализе распространения атмосферных волн в мезосфере и нижней термосфере с реальными высотными профилями температуры нейтральной компоненты.
Стенд СУРА поддерживался в рабочем состоянии в рамках выполнения проекта № 0729-2020-0057 по базовой части госзадания.
Исследования поддержаны Российским научным фондом в рамках гранта № 20-17-00050.
Список литературы
Госсард Э., Хук У. Волны в атмосфере. М.: Мир, 1978.
Hines C.O. // Can. J. Phys. 1960. V. 38. № 11. C. 1441.
Григорьев Г.И. // Изв. вузов. Радиофизика. 1999. Т. 42. № 1. С. 3.
Fritts D.C., Alexander M.J. // Rev. Geophys. 2003. V.41. № 1. P. 1003.
Ma J.Z.G. // Global J. Sci. Frontier Res.: F Mathem. Decis. Sci.2016. V. 16. № 3. P. 37.
Григорьев Г.И., Савина О.А. // Неустойчивости и волновые явления в системе ионосфера-термосфера. Горький: ИПФ АН СССР, 1989. С. 26.
Kshevetski S.P., Kurdyaeva Y.A., Gavrilov N.M. // Atmosphere. 2021. V. 12. Issue 7. P. 818; https://doi.org/10.3390/atmos12070818
Карпов И.В., Кшевецкий С.П. // Геомагнетизм и аэрономия. 2014. Т. 54. № 4. С. 553.
Карпов И.В., Кшевецкий С.П., Борчевкина О.П., Радиевский A.В., Карпов И.В. // Хим. физика. 2016. Т. 35. № 1. P. 59.
Песков В.Д., Родионов А.И., Родионова И.П. и др. // Хим. физика. 2016. Т. 39. № 4. P. 56.
Карпов И.В., Карпов М.И., Борчевкина О.П., Якимова Г.А., Коренькова Н.А. // Хим. физика. 2019. Т. 38. № 7. С. 79.
Карпов И.В., Борчевкина О.П., Васильев П.А. // Хим. физика. 2020. Т 39. № 4. С. 63.
Келлер Дж.Б., Пападакис Дж.С. Распространение волн и подводная акустика. М.: Мир, 1980.
Брюнелли Б.Е., Намгаладзе А.А. Физика ионосферы. М.: Наука, 1988.
Шефов Н.Н., Семенов А.И., Хомич В.Ю. Излучение верхней атмосферы – индикатор ее структуры и динамики. М.: ГЕОС, 2006.
Шалимов С.Л. Атмосферные волны в плазме ионосферы. М.: ИФЗ РАН, 2018.
Беликович В.В., Бенедиктов Е.А., Толмачёва А.В., Бахметьева Н.В. Исследование ионосферы с помощью искусственных периодических неоднородностей. Н. Новгород: Изд-во ИПФ РАН, 1999.
Бахметьева Н.В., Беликович В.В., Григорьев Г.И., Толмачева А.В. // Изв. вузов. Радиофизика. 2002. Т. 45. № 3. С. 233.
Бахметьева Н.В., Григорьев Г.И., Толмачёва А.В. // Изв. вузов. Радиофизика. 2010. Т. 53. № 11. С. 695.
Толмачева А.В., Григорьев Г.И., Бахметьева Н.В. // Хим. физика. 2013. Т. 32. № 9. С. 89.
Tolmacheva A.V., Bakhmetieva N.V., Grigoriev G.I., Kalinina E.E. // Adv. Space Res. 2015. V. 56. P. 1185.
Бахметьева Н.В., Вяхирев В.Д., Григорьев Г.И. и др. // Геомагнетизм и аэрономия. 2020. Т. 60. № 1. С. 99.
Bakhmetieva N.V., Grigoriev G.I., Tolmacheva A.V., Zhemyakov I.N. // Atmosphere. 2019. V. 10. Issue 8. P. 450; https://doi.org/10.3390/atmos10080450
Григорьев Г.И., Толмачева А.В. // Хим. физика. 2021. Т. 40. № 5. С. 91.
Бахметьева Н.В., Бубукина В.Н., Вяхирев В.Д. и др. // Хим. физика. 2017. Т. 36. № 12. С. 44.
Бахметьева Н.В, Григорьев Г.И., Толмачева А.В., Калинина Е.Е. // Хим. физика. 2018. Т. 37. № 5. С. 1.
Bakhmetieva N.V., Grigoriev G.I., Tolmacheva A.V., Kalinina E.E. // Proc. V Intern. conf. “Atmosphere, Ionosphere, Safety”. Kaliningrad, 2016. P. 110.
Ламб Г. Гидродинамика. М.: ОГИЗ, 1947.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 1961.
Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1957.
Фок В.А. Таблицы функций Эйри. М.: ГТТИ, 1946.
Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979.
Савина О.Н. // Геомагнетизм и аэрономия. 1996. Т. 36. № 2. С. 180.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика