Химическая физика, 2022, T. 41, № 12, стр. 49-55

ВВЕДЕНИЕ

В связи с климатическими и экологическими проблемами, а также с вопросами химической технологии, все большее значение приобретают задачи очистки как газовых, так и жидких сред [1–3]. Реакторы с противотоком на основе гетерогенных систем являются наиболее перспективными для решения этих задач [4–6]. Для реакторов c гетерогенными реагирующими системами газ–жидкость и жидкость–жидкость разработаны математические модели, учитывающие различные типы химических реакций в дисперсионной среде, межфазный тепло- и массообмен и позволившие в ряде случаев исследовать тепловые режимы реактора и влияние на них различных управляющих параметров [7–11].

В работе [7] исследована динамика температурных профилей в зависимости от скорости охлаждения поверхности реактора. В работе [8] для гетерогенной реагирующей системы жидкость–жидкость в реакторе вытеснения проведено исследование колебательной неустойчивости реактора в зависимости от изменения температуры на входе в реактор. Авторами работы [9] на основе теоретической модели для процесса вымывания газа из гидрата в противоточном трубчатом реакторе исследовано влияние давления и начальной температуры на процесс. В работе [10] для двух химически взаимодействующих жидких сред показано, что имеется критическое значение скорости движения дисперсионной среды, при котором существуют два типа стационарных режимов. В работе [11] подробно описано, какой должна быть дисперсная фаза, а именно: пузырьки газа равномерно распределены в жидкой фазе и не взаимодействуют друг с другом. На основании этой формулировки можно было бы сразу сделать вывод, что математическим условием, следующим из этого определения, является минимальное расстояние между соседними пузырьками, при котором можно пренебречь силами взаимодействия между ними. В общем случае структура дисперсной фазы определяется двумя расстояниями между центрами пузырьков: первое расстояние – перпендикулярно к направлению скорости движения дисперсионной среды, второе – параллельно этому направлению (см. [12]).

В настоящей работе сформулирована математическая модель экзотермической реакции превращения в противоточном реакторе вытеснения, учитывающая структуру гетерогенной среды. В математическую модель вводится параметр, характеризующий расположение в дисперсионной среде частиц дисперсной фазы. Цель настоящей работы – исследование тепловых режимов и динамики выхода реактора на установившийся (стационарный или периодический) режим работы и их зависимость от следующих параметров: структура гетерогенной среды, теплообмен с окружающей средой, концентрации исходных веществ. Заметим, что ранее сходная задача решалась для реактора идеального смешения [13].

ПОСТАНОВКА ЗАДАЧИ

В противоточный реактор идеального вытеснения высотой H сверху со скоростью –V подается жидкий раствор двух веществ, A и F (дисперсионная среда L). Концентрации веществ в ней – [A]_L и [F]_L. Снизу в виде пузырьков одного размера и с постоянной скоростью U подается смесь газов (дисперсная фаза G). Один из компонентов газовой смеси B (концентрация [B]_G) экстрагируется дисперсионной средой (концентрация [B]_L), где и вступает в простую химическую реакцию второго порядка с веществом A. При этом образуется вещество C (концентрация [C]_L). Вещество C вступает в реакцию с веществом F (концентрация [F]_L).

Для построения математической модели необходимо сформулировать некоторые главные упрощающие допущения, не изменяющие основных черт процесса. Допущения, относящиеся к дисперсионной (жидкой) среде, означают, что течение последней – “поршневое” и происходит со скоростью V при отсутствии радиальных распределений температур и концентраций.

Для дисперсной фазы, движущейся в виде пузырьков в противоположном направлении со скоростью U, предполагаем, что пузырьки движутся упорядоченно, на фиксированном и равном расстоянии друг от друга. Расстояние между пузырьками l определяется из условия, что на этом расстоянии силы взаимодействия между соседними пузырьками пренебрежимо малы. В этом приближении дисперсную фазу можно представить в виде “кристаллической” структуры, состоящей из кубических ячеек, в узлах которой расположены пузырьки газа. В этих допущениях объемная доля дисперсионной среды m будет определяться выражением

Здесь величина l выражена в долях радиуса пузырька r.

Предполагается, что теплообмен реактора с окружающей средой происходит по закону Ньютона по боковой поверхности S. Заметим, что при изложенных выше допущениях теплоотвод из реактора должен быть достаточно малым, чтобы можно было пренебречь распределениями.

Перед тем как сформулировать математическую модель, рассмотрим выражение для межфазного теплообмена по закону Ньютона. В общем случае оно имеет вид

Здесь α_LG – коэффициент межфазного теплообмена, m – объемная доля дисперсионной среды, S_G – суммарная поверхность пузырьков, v_S – объем реактора, T_L – температура дисперсионной среды, T_G – температура дисперсной фазы.

Поскольку принято, что независимые друг от друга пузырьки расположены на расстоянии l_r, то расстояние между их центрами будет равно

2r + l_r = r(2 + l).

Мы считаем, что реагирующая система состоит из кубических ячеек, в углах которых расположены пузырьки. Поэтому при объеме ячейки r³(2 + l)³ объем жидкой фазы равен

При этом ее доля составляет Число пузырьков в реакторе равно а их общая поверхность

Окончательно выражение для теплообмена с пузырьковой дисперсной фазой приобретает вид

При принятых допущениях система дифференциальных уравнений в частных производных с начальными и граничными условиями может быть представлена в следующем виде:

уравнение теплового баланса для дисперсионной среды L –

уравнение теплового баланса для дисперсной фазы G – уравнение материального баланса для вещества A дисперсионной среды L – уравнение материального баланса для вещества C дисперсионной среды L – уравнение материального баланса для вещества B (дисперсная фаза G) – уравнение материального баланса для вещества B в дисперсионной среде L – уравнение материального баланса для вещества F в дисперсионной среде L –

Начальные условия:

t = 0 T_L = T_L0, T_G = T_G0, [A]_L = [A]_L0, [C]_L = 0, [B]_G = [B]_G0, [B]_L = 0, [F]_L = [F]_L0 при x < 0 < H.

Граничные условия:

T_L = T_L,en, $\frac{{\partial {\kern 1pt} {{T}_{{\text{G}}}}}}{{\partial x}} = 0,$ [A]_L = [A]_L,en, [C]_L = 0, $\frac{{\partial {{{[{\text{B}}]}}_{{\text{G}}}}}}{{\partial x}} = 0,$ [B]_L = 0, [F]_L = [F]_L,en при t > 0, x = H;

$\frac{{\partial {\kern 1pt} {{T}_{{\text{L}}}}}}{{\partial x}} = 0,$ T_G = T_G,en, $\frac{{\partial {{{[{\text{A}}]}}_{{\text{L}}}}}}{{\partial x}} = 0,$ $\frac{{\partial {{{[{\text{C}}]}}_{{\text{L}}}}}}{{\partial x}} = 0,$

[B]_G = [B]_{G, en}, $\frac{{\partial {{{[{\text{B}}]}}_{{\text{L}}}}}}{{\partial x}} = 0,$ $\frac{{\partial {{{[{\text{F}}]}}_{{\text{L}}}}}}{{\partial x}} = 0$ при t > 0, x = 0.

Здесь c_L, c_G – удельные теплоемкости дисперсионной среды и дисперсной фазы; ρ_L, ρ_G – плотности дисперсионной среды и дисперсной фазы; Q₁, Q₂ – тепловые эффекты; k₀₁, k₀₂ – предэкспоненциальные множители; E₁, E₂ – энергии активации; R – универсальная газовая постоянная; λ – коэффициент теплопроводности; D_ef – коэффициент диффузии; β – коэффициент межфазного массобмена; ε – коэффициент распределения, характеризующий концентрацию реагента B на границе раздела фаз; x – координата по высоте реактора; “en” – индекс, соответствующий входным значениям переменных.

Система дифференциальных уравнений с начальными и граничными условиями решалась численно. Алгоритм решения системы уравнений основан на использовании линеаризованной неявной двухслойной разностной схемы. Аппроксимация строилась на подвижной, неравномерной по времени и пространству, адаптирующейся к решению разностной сетке. В зависимости от знака скорости аппроксимация конвективной составляющей осуществлялась с помощью правой или левой трехточечной схемы. Полученные разностные уравнения решались методом прогонки.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Проанализируем влияние некоторых характеристик реактора на стационарное состояние и динамику выхода на него при нулевых начальных значениях активных компонентов и при отсутствии стадии прогрева. Значения переменных, которые не изменялись в процессе численных расчетов, приняты следующими: H = 100 см, U = = 4 см/с, V = 0.2 см/с, r = 0.1 см, c_L = 0.5 кал/(г · K), c_G = 0.3 кал/(г · K), ρ_L = 1 г/см³, ρ_G = 0.001 г/см³, β = 0.009 см/с, ε = 1, α_LG = 0.14 кал/(см² · с · K), Q₁= 100 кал/г, k₀₁ = 10¹⁰ л/(моль · с); E₁ = = 11 000 кал/моль.

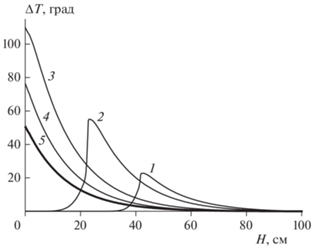
I. Влияние расстояния между пузырьками. На рис. 1 представлены зависимости разогрева реактора ΔT = (T_L – T₀) от пространственной координаты x при выходе реактора на стационарный режим. Из приведенных данных видно, что установление стационарного режима происходит через очень большие разогревы. При этом можно выделить три стадии процесса. В первой стадии наблюдается возникновение максимума разогрева вблизи входа в реактор дисперсионной среды L (кривая 1, рис. 1). Затем этот максимум постепенно смещается к месту входа в реактор дисперсной фазы G (кривая 2) и, наконец, достигает этого места (кривая 3). Возникновение максимума разогрева обусловлено встречей дисперсионной среды, содержащей вещество A, c дисперсной фазой, содержащей вещество B. Координата “места встречи” определяется соотношением скоростей перемещения дисперсной фазы и дисперсионной среды. Кривая 3 соответствует достижению максимального разогрева системы. Эта кривая является пограничной между концом первой и началом второй стадии процесса, в которой наблюдается уменьшение температуры на месте выхода дисперсионной среды из реактора (кривая 4) под влиянием более холодной дисперсной фазы, поступающей в реактор. Вторая стадия процесса завершается переходом к стационарному режиму (третья стадия, кривая 5).

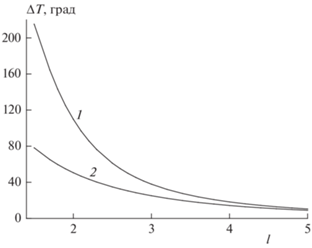
На рис. 2 показано, как при изменении параметра l меняются максимальные разогревы дисперсионной среды L при выходе на стационарный режим (кривая 3 рис. 1) (T_L,max–T₀) и собственно в стационарном режиме (T_ST,max–T₀). Из представленных на этом рисунке данных следует, что с увеличением параметра l различие между максимальным разогревом дисперсионной среды L при выходе на стационарный режим (кривая 1) и в стационарном режиме (кривая 2) уменьшается и при больших значениях l практически исчезает. Это естественно, поскольку при больших значениях l уменьшается концентрация пузырьков в реакторе, что приводит к уменьшению количества вещества B в дисперсионной среде.

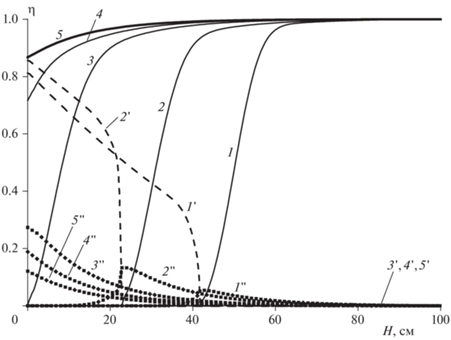
Как ведут себя концентрационные зависимости веществ A, B и C по высоте реактора в дисперсионной среде и вещества B в дисперсной фазе в процессе запуска реактора, следует из данных рис. 3 (дисперсионная среда) и 4 (дисперсная фаза). На рис. 3 в координатах (x, η) представлены пространственные распределения относительных концентраций веществ A (кривые 1–5), B (кривые 1'–5') и C (кривые 1''–5''). Одна и та же цифра без штриха, с одним и двумя штрихами на приведенных кривых соответствует одному тому же моменту времени после запуска реактора. Из приведенных данных следует, что и максимум разогрева (рис. 1), и максимальная концентрация продукта реакции C (рис. 3) достигаются, естественно, в момент “встречи” вещества A и вещества B (рис. 3, кривые 1 и 1'), экстрагированного в дисперсионную среду. Координата “встречи” соответствует выражениям [A]_L/[A]_L, en = 0 и [B]_L/[B]_G, en = 0. Этот факт можно трактовать в том смысле, что экзотермическая химическая реакция протекает в режиме “сжигания”. По мере протекания реакции максимальная концентрация промежуточного продукта C постепенно смещается к выходу дисперсионной среды из реактора. Как и при анализе теплового поведения реактора, здесь также можно наблюдать три стадии процесса, о которых говорилось выше.

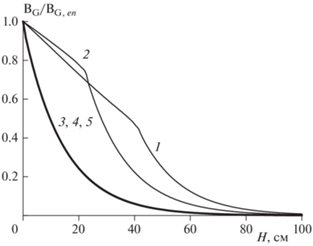
На рис. 4 показано, как ведет себя при тех же временах распределение концентрации вещества B в дисперсной фазе. На кривых 1, 2, соответствующих подходу системы к стационарному режиму, отчетливо видны изломы. Они как раз и соответствуют координате “сжигания” веществ A и B, которая постепенно смещается к входу дисперсной фазы в реактор.

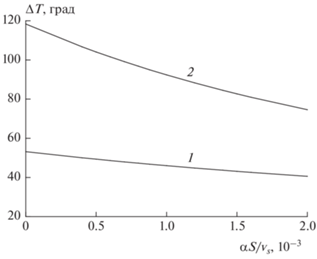
II. Влияние комплекса внешнего теплообмена реактора, ${{\alpha S} \mathord{\left/ {\vphantom {{\alpha S} {{{v}_{S}}}}} \right. \kern-0em} {{{v}_{S}}}}.$ На рис. 5 представлены две зависимости, которые получены при изменении условий теплообмена реактора: первая (практически прямая 1) отображает зависимость максимального разогрева от величины ${{\alpha S} \mathord{\left/ {\vphantom {{\alpha S} {{{v}_{S}}}}} \right. \kern-0em} {{{v}_{S}}}}$ в стационарном режиме, вторая (кривая 2) получена для подхода реактора к стационарному режиму. Как видно из этого рисунка, зависимость максимального разогрева в стационарном режиме от параметра ${{\alpha S} \mathord{\left/ {\vphantom {{\alpha S} {{{v}_{S}}}}} \right. \kern-0em} {{{v}_{S}}}}$ весьма слабая. Это позволяет упростить модель и в дальнейшем проводить анализ динамического поведения реактора в адиабатических условиях

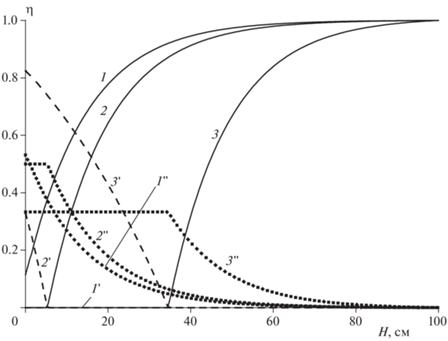
III. Влияние концентрации вещества A. На рис. 6 для трех значений начальной концентрации вещества A в дисперсионной среде для стационарных условий приведены пространственные распределения концентраций [A]_L/[A]_L,en (кривые 1, 2, 3), экстрагированного вещества B [B]_L/[B]_G,en (кривые 1', 2 ', 3') и продукта реакции C [C]_L/([A]_L, en + + [B]_G,en) (кривые 1'', 2 '', 3''). Из этих данных следует, что при достаточно высоких концентрациях вещества А на входе в реактор ([A]_L,en ≥ 0.3 моль/л) на выходе из реактора (x = 0) дисперсионная среда содержит лишь два вещества – A и C. С уменьшением начальной концентрации вещества A распределение [A]_L/[A]_L,en (кривые 2, 3) смещается к входу дисперсионной среды в реактор. При этом возникает стационарный режим с наличием особой точки (изломы на кривых 2 ", 3"), в которой происходит “сжигание” веществ A и B. Кроме того, в дисперсионной среде дополнительно появляется вещество B (кривые 2 ' и 3').

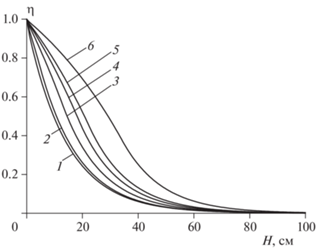
Для иллюстрации на рис. 7 приведены пространственные распределения концентрации вещества B в дисперсной фазе для нескольких значений [A]_L,en. Из этого рисунка видно, что перегиб на кривой возникает при значении [A]_L,en ≈ ≈ 0.15 моль/л. Приведенные данные показывают, что получить высокую степень очистки газовой фазы вполне реально.

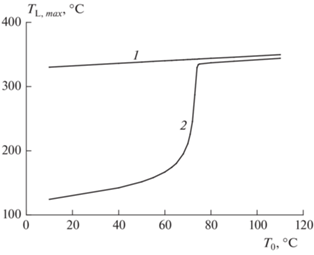
При анализе теплового поведения противоточного реактора вытеснения с учетом второй стадии последовательной реакции при изменении внешней температуры T₀ обнаружены два стационарных режима (рис. 8, кривая 2): низкотемпературный и высокотемпературный. Расчеты проведены для следующих кинетических характеристик второй стадии: E₂ = 22 000 кал/моль, k₀₂ = 10¹⁰ л/(моль · с) и Q = 500 кал/г. Анализ численных результатов показал, что выход на стационарный режим всегда происходит через высокие температуры (рис. 8, линия 1).

ВЫВОДЫ

1. Предложена и исследована математическая модель экзотермического химического превращения гетерогенной среды в противоточном реакторе вытеснения.

2. Предложен алгоритм численного решения системы дифференциальных уравнений, описывающих эту модель. Проведены расчеты динамики процессов и ее зависимости от определяющих параметров, характеризующих конкретную гетерогенную среду.

3. Определены закономерности изменения теплового состояния гетерогенной среды по высоте реактора. Обнаружено существование высокотемпературного поля, превышающего температуру устойчивого стационарного поля. Проведен анализ полей концентраций реагентов, взаимодействующих в гетерогенной среде, и процесс их перехода из начального состояния в стационарное в зависимости от условий теплообмена в реакторе.

Работа выполнена по теме государственного задания (регистрационные номера: AAAA-A19-119022690098-3, АААА-А19-119071190040-5, АААА-А21-121011990037-8).