Журнал высшей нервной деятельности им. И.П. Павлова, 2020, T. 70, № 6, стр. 837-851
Байесовский параллельный факторный анализ для исследования связанных с событиями потенциалов
В. А. Пономарев 1, *, Ю. Д. Кропотов 1
1 Федеральное государственное бюджетное учреждение науки Институт мозга человека им. Н.П. Бехтеревой Российской академии наук
Санкт-Петербург, Россия
* E-mail: valery_ponomarev@mail.ru
Поступила в редакцию 24.04.2020
После доработки 01.06.2020
Принята к публикации 01.06.2020
Аннотация
Целью данной работы являлась разработка байесовской вероятностной модели для параллельного факторного анализа связанных с событиями потенциалов (ПСС) мозга человека. Предложено 12 статистических моделей, учитывающих специфику сигналов источников ПСС. Для этих моделей были разработаны процедуры построения выборки случайных значений их параметров, основанные на методах Монте-Карло с цепями Маркова. Эффективность этих процедур оценивалась, используя как синтезированные данные с различным соотношением сигнал–шум, так и массив записей ПСС, полученных у 351 человека в Go/NoGo тесте. Была выбрана процедура, позволяющая получить оценки параметров модели с наилучшей точностью. Анализ зависимости сигналов модели от вида выполняемой деятельности человеком показал, что байесовский параллельный факторный анализ позволяет выделить функционально различные компоненты ПСС.
ВВЕДЕНИЕ
Потенциалы, связанные с событиями (ПСС), широко используются в исследованиях процессов мозга [Кропотов, 2010; Luck, Kappenman, 2011]. В них отражается протекание различных психических процессов, таких как восприятие стимулов и их категоризация, принятие решения о последующем действии, переключение с одного вида выполняемого задания на другой, подготовка ответа или его подавление, обнаружение несоответствия между доминирующей моделью поведения и текущим контекстом и многие другие. Это позволяет получить объективную информацию о мозговых механизмах, лежащих в основе этих процессов.
Типичная и широко распространенная схема исследования ПСС выглядит следующим образом. Электроэнцефалограмма регистрируется с помощью электродов, расположенных на поверхности кожи головы у человека, который выполняет определенный психологический тест. Причем, как правило, такие исследования выполняются с участием представительного числа испытуемых. В психологическом тесте выполняются несколько видов деятельности, случайным образом чередующейся в зависимости от типа предъявляемых стимулов. Методом усреднения вычисляются ПСС для каждого из видов деятельности отдельно и сравниваются между собой. Среднегрупповые ПСС вычисляются для выявления общих для группы особенностей. Подбирая подходящие виды деятельности, такой подход позволяет выявить составляющие ПСС, связанные с различными психическими процессами, оценить временной интервал, в течение которого они протекают, и определить зоны мозга, которые участвуют в их реализации.
В качестве альтернативного подхода для выявления общих характеристик ПСС может рассматриваться параллельный факторный анализ, использующий тензорное разложение [Cichocki et al., 2015; Cong et al., 2015; Zhou et al., 2015] и позволяющий представить ПСС в виде суммы компонент с различными сигналами и топографиями [Пономарев и др., 2019а]. Применение параллельного факторного анализа может оказаться перспективным, поскольку с его помощью удается выделить функционально различные компоненты ПСС [Пономарев, et al., 2019б].
Чтобы оценить компоненты модели параллельного факторного анализа, часто используется метод наименьших квадратов, а для поиска минимума целевой функции применяются различные итеративные процедуры [Kolda, Bader, 2009; Cichocki et al., 2015]. Такой подход имеет ряд ограничений.
Во-первых, при наличии шума целевая функция может оказаться невыпуклой и иметь несколько локальных минимумов. В таких случаях итеративные процедуры (в частности, метод стохастического градиентного спуска) могут сходиться только к одному из локальных минимумов в зависимости от начального приближения.
Во-вторых, аналогично традиционному подходу, необходимо выполнить сравнение компонент ПСС при разных видах деятельности. Для этого необходимо оценить доверительные интервалы для компонент ПСС. Теоретически эту задачу можно решить с помощью многократной генерации искусственных выборок записей ПСС методом Монте-Карло (бутстрэп), но на практике это приводит к необходимости много раз выполнять тензорное разложение, что требует значительных временных затрат. Кроме того, из-за невыпуклости целевой функции такой метод может давать слишком широкие доверительные интервалы.
Наконец, в-третьих, число компонент в модели неизвестно, но при этом метод наименьших квадратов не подразумевает возможности получить оценку этого параметра.
Для решения перечисленных проблем широко используется байесовское иерархическое моделирование [Gelman et al., 2014], которое, в частности, применялось для решения задач параллельного факторного анализа [Schmidt, Mohamed, 2009; Xiong et al., 2010; Natarajan et al., 2014; Nakatsuji et al., 2016; Chen et al., 2019 a, b]. Однако предложенные статистические модели были разработаны для анализа многомерных данных другой природы и не учитывают специфику сигналов источников ПСС. Простое использование таких известных моделей может приводить к противоречивым или трудно интерпретируемым результатам.
Целью данной работы являлась разработка байесовской модели для параллельного факторного анализа ПСС.
МЕТОДИКА
Пусть матрица ${\mathbf{X}}$ размера $K \times T$, $K$ – число электродов и $T$ – число отсчетов времени, описывает ПСС. Обычно в экспериментах с регистрацией ПСС у человека предъявляется несколько проб ($N$), по которым вычисляются средние значения ПСС. В этом случае имеется возможность получить оценки дисперсии ПСС для каждого канала и каждого отсчета времени в отдельности, которые будем обозначать как ${\mathbf{Z}}$. Если имеется несколько записей ПСС у разных людей, полученных в одинаковых условиях, то они описываются множеством матриц ${{{\mathbf{X}}}^{j}}$ и ${{{\mathbf{Z}}}^{j}}$ размера $K \times T$, с числом проб ${{N}_{j}}$, где $j = 1 \cdots J$ и $J$ – число участников исследования. И в этом случае множества матриц ${{{\mathbf{X}}}^{j}}$ и ${{{\mathbf{Z}}}^{j}}$ удобно объединить в трехмерные массивы данных ${\mathbf{Y}} = \{ {{{\mathbf{X}}}^{1}} \cdots {{{\mathbf{X}}}^{J}}\} {\kern 1pt} '$ и ${\mathbf{V}} = \{ {{{\mathbf{Z}}}^{1}} \cdots {{{\mathbf{Z}}}^{J}}\} {\kern 1pt} '$ размера $J \times K \times T$ с элементами ${{{\text{y}}}_{{j,k,t}}}$ и ${{{\text{v}}}_{{j,k,t}}}$ соответственно.
Допустим, что (в соответствии с квазистационарной аппроксимацией уравнений Максвелла) эти ПСС описываются моделью линейного мгновенного смешивания [Hallez et al., 2007]:
(1)
${{{\text{x}}}_{{k,t}}} = \sum\limits_{d = 1}^D {{{{\text{a}}}_{{d,k}}}{{{\text{s}}}_{{d,t}}}} + {{{\text{e}}}_{{k,t}}}\quad {\text{или}}\quad {\mathbf{X}} = {\mathbf{A}}{\kern 1pt} '{\mathbf{S}} + {\mathbf{E}},$Допустим также, что справедливо приближение, при котором топографии и сигналы источников ПСС одинаковы у всех людей, включая полярность, а изменяется только их величина. Тогда ПСС у всех участников исследования описываются следующей моделью:
(2)
${{{\text{y}}}_{{j,k,t}}} = \sum\limits_{d = 1}^D {{{{\text{u}}}_{{d,j}}}{{{\text{a}}}_{{d,k}}}{{{\text{s}}}_{{d,t}}}} + {{{\text{e}}}_{{j,k,t}}} \equiv {{{\text{r}}}_{{j,k,t}}} + {{{\text{e}}}_{{j,k,t}}},$Исходно матрицы ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$ неизвестны, и необходимо их определить. Причем это возможно сделать только с точностью до произвольных масштабов и перестановок компонент [Kolda, Bader, 2009]. Для оценки матриц ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$ используется метод Монте-Карло [Gelman et al., 2014]. Используя подходы, применяемые в байесовском иерархическом моделировании, в настоящем исследовании была построена статистическая модель сигналов, основанная на следующих предположениях.
1) Шум представляет собой последовательность независимых нормально распределенных величин с нулевым средним и дисперсией ${\sigma }_{{j,k,t}}^{2}$. Тогда функцию максимального правдоподобия можно представить в следующем виде
(3)
$p\left( {{\mathbf{Y}}\,{\text{|}}\,{\mathbf{U}},{\mathbf{A}},{\mathbf{S}},\vartheta } \right) = \prod\limits_{j,k,t} {{{N}_{1}}({{{\text{y}}}_{{j,k,t}}}\,{\text{|}}\,{{{\text{r}}}_{{j,k,t}}},\vartheta _{{j,k,t}}^{{ - 1}})} ,$2) Векторы-столбцы матрицы ${\mathbf{A}}$ взаимно независимы и имеют многомерное нормальное распределение с произвольными средними ${\mathbf{\mu }}_{k}^{A}$ и матрицами точности ${\mathbf{\Lambda }}_{k}^{A}$, где ${\mathbf{\Lambda }}_{k}^{A} = {\mathbf{\Sigma }}{{_{k}^{A}}^{{^{{ - 1}}}}}$, и ${\mathbf{\Sigma }}_{k}^{A}$ – матрица ковариаций [Salakhutdinov, Mnih, 2008; Natarajan et al., 2014; Nakatsuji et al., 2016; Chen et al., 2019 a, b]
(4)
$p({{{\mathbf{a}}}_{k}}\,{\text{|}}\,{\mathbf{\mu }}_{k}^{A},{\mathbf{\Lambda }}_{k}^{A}) = {{N}_{D}}({{{\mathbf{a}}}_{k}}\,{\text{|}}\,{\mathbf{\mu }}_{k}^{A},{\mathbf{\Lambda }}{{_{k}^{A}}^{{^{{ - 1}}}}}),$3) Векторы-столбцы матрицы ${\mathbf{U}}$ взаимно независимы и имеют усеченное в интервале от 0 до $ + \infty $ многомерное нормальное распределение с произвольными ${\mathbf{\mu }}_{j}^{U}$ и ${\mathbf{\Lambda }}_{j}^{U}$ [Alquier, Guedj, 2017]
(5)
$\begin{gathered} p({{{\mathbf{u}}}_{j}}\,{\text{|}}\,{\mathbf{\mu }}_{j}^{U},{\mathbf{\Lambda }}_{j}^{U}) = {{R}_{D}}({{{\mathbf{u}}}_{j}}\,{\text{|}}\,{\mathbf{\mu }}_{j}^{U},{\mathbf{\Lambda }}{{_{j}^{U}}^{{^{{ - 1}}}}}) \equiv \\ \equiv \frac{1}{{{{{\text{c}}}_{j}}}}{{N}_{D}}({{{\mathbf{u}}}_{j}}\,{\text{|}}\,{\mathbf{\mu }}_{j}^{U},{\mathbf{\Lambda }}{{_{j}^{U}}^{{^{{ - 1}}}}})\prod\limits_d {\theta ({{{\mathbf{u}}}_{{d,j}}})} , \\ \end{gathered} $4) Сигналы источников таковы, что их значения в момент времени t зависят только от предыдущих значений (t – 1) и имеют многомерное нормальное распределение с произвольными ${{{\mathbf{\mu }}}^{S}}$ и ${\mathbf{\Lambda }}_{t}^{S}$ [Xiong et al., 2010]
(6)
$p({{{\mathbf{s}}}_{1}}\,{\text{|}}\,{{{\mathbf{\mu }}}^{S}},{\mathbf{\Lambda }}_{1}^{S}) = {{N}_{D}}({{{\mathbf{s}}}_{1}}\,{\text{|}}\,{{{\mathbf{\mu }}}^{S}},{\mathbf{\Lambda }}{{_{1}^{S}}^{{ - 1}}}),\quad t = 1,$(7)
$p({{{\mathbf{s}}}_{t}}\,{\text{|}}\,{{{\mathbf{s}}}_{{t - 1}}},{\mathbf{\Lambda }}_{t}^{S}) = {{N}_{D}}({{{\mathbf{s}}}_{t}}\,{\text{|}}\,{{{\mathbf{s}}}_{{t - 1}}},{\mathbf{\Lambda }}{{_{t}^{S}}^{{ - 1}}}),\quad t = 2 \cdots T.$5) Точность ${{\vartheta }_{{j,k,t}}}$ является случайной величиной с распределением
(8)
$p\left( {{{\vartheta }_{{j,k,t}}}\,{\text{|}}\,{{N}_{j}},{{{\text{v}}}_{{j,k,t}}}} \right) = \Gamma \left( {{{\vartheta }_{{j,k,t}}}\,{\text{|}}\,{{{{N}_{j}}} \mathord{\left/ {\vphantom {{{{N}_{j}}} 2}} \right. \kern-0em} 2},{{{{N}_{j}}{{{\text{v}}}_{{j,k,t}}}} \mathord{\left/ {\vphantom {{{{N}_{j}}{{{\text{v}}}_{{j,k,t}}}} 2}} \right. \kern-0em} 2}} \right),$6) Скрытые параметры модели ${\mathbf{\mu }}_{k}^{A}$, ${\mathbf{\Lambda }}_{k}^{A}$, ${\mathbf{\mu }}_{j}^{U}$, ${\mathbf{\Lambda }}_{j}^{U}$, ${{{\mathbf{\mu }}}^{S}}$ и ${\mathbf{\Lambda }}_{t}^{S}$ являются случайными величинами со следующими распределениями [Xiong et al., 2010; Natarajan et al., 2014; Nakatsuji et al., 2016; Chen et al., 2019 a, b]
(9)
$\begin{gathered} p({\mathbf{\mu }}_{k}^{A},{\mathbf{\Lambda }}_{k}^{A}) = \\ = {{N}_{D}}({\mathbf{\mu }}_{k}^{A}\,{\text{|}}\,{\mathbf{\mu }}_{0}^{A},{{(\beta _{0}^{A}{\mathbf{\Lambda }}_{k}^{A})}^{{ - 1}}}) \cdot {{W}_{D}}({\mathbf{\Lambda }}_{k}^{A}\,{\text{|}}\,{\mathbf{\Lambda }}_{0}^{A},\nu _{0}^{A}), \\ \end{gathered} $(10)
$\begin{gathered} p({\mathbf{\mu }}_{j}^{U},{\mathbf{\Lambda }}_{j}^{U}) = \\ = {{{\text{c}}}_{j}} \cdot {{R}_{D}}({\mathbf{\mu }}_{j}^{U}\,|\,{\mathbf{\mu }}_{0}^{U},{{(\beta _{0}^{U}{\mathbf{\Lambda }}_{j}^{U})}^{{ - 1}}}) \cdot {{W}_{D}}({\mathbf{\Lambda }}_{j}^{U}\,|\,{\mathbf{\Lambda }}_{0}^{U},\nu _{0}^{U}), \\ \end{gathered} $(11)
$p({{{\mathbf{\mu }}}^{S}},{\mathbf{\Lambda }}_{1}^{S})\, = \,{{N}_{D}}({{{\mathbf{\mu }}}^{S}}\,{\text{|}}\,{\mathbf{\mu }}_{0}^{S},{{(\beta _{0}^{S}{\mathbf{\Lambda }}_{1}^{S})}^{{ - 1}}})\, \cdot \,{{W}_{D}}({\mathbf{\Lambda }}_{1}^{S}\,{\text{|}}\,{\mathbf{\Lambda }}_{0}^{S},\nu _{0}^{S}),$(12)
$p({\mathbf{\Lambda }}_{t}^{S}\,{\text{|}}\,{\mathbf{\Lambda }}_{0}^{S},\nu _{0}^{S}) = {{W}_{D}}({\mathbf{\Lambda }}_{t}^{S}\,{\text{|}}\,{\mathbf{\Lambda }}_{0}^{S},\nu _{0}^{S}),$Наконец, допустим, что совместное условное распределение для всех неизвестных параметров модели может быть представлено в следующем виде
(13)
$\begin{gathered} \times \;\prod\limits_k {p({{{\mathbf{a}}}_{k}}\,{\text{|}}\,{\mathbf{\mu }}_{k}^{A},{\mathbf{\Lambda }}_{k}^{A})} p({{{\mathbf{s}}}_{1}}\,{\text{|}}\,{{{\mathbf{\mu }}}^{S}},{\mathbf{\Lambda }}_{1}^{S}) \times \\ \times \;\prod\limits_{t = 2}^T {p({{{\mathbf{s}}}_{t}}\,{\text{|}}\,{\mathbf{s}}_{{t - 1}}^{S},{\mathbf{\Lambda }}_{t}^{S})} \prod\limits_j {p({\mathbf{\mu }}_{j}^{U},{\mathbf{\Lambda }}_{j}^{U})} \times \\ \end{gathered} $Рассматривались различные модификации этой модели, в которых предполагалось, что:
1) Компоненты модели взаимно независимые [Schmidt, Mohamed, 2009]. Тогда формулы (4) и (9) принимают следующий вид: $p({{{\mathbf{a}}}_{k}}\,{\text{|}}\,{\mathbf{\mu }}_{k}^{A},{\mathbf{\Lambda }}_{k}^{A})$ = $\prod\nolimits_d {{{N}_{1}}({{a}_{{d,k}}}\,|\,\mu _{{d,k}}^{A}} $, $\alpha _{{d,k}}^{{{{A}^{{ - 1}}}}})$ и $p({\mathbf{\mu }}_{k}^{A},{\mathbf{\Lambda }}_{k}^{A})$ = = $\prod\nolimits_d {{{N}_{1}}(\mu _{{d,k}}^{A}\,|\,\mu _{0}^{A}} $, ${{(\beta _{0}^{A}\alpha _{{d,k}}^{A})}^{{ - 1}}})\Gamma (\alpha _{{d,k}}^{A}\,|\,a_{0}^{A}$, $b_{0}^{A})$, где ${\mu }_{0}^{A}$, $a_{0}^{A}$ и $b_{0}^{A}$ – скалярные величины. Аналогично для формул (5)–(7) и (10)–(12).
2) Компоненты модели взаимно зависимые, но матрицы ${\mathbf{\Lambda }}_{j}^{U}$, ${\mathbf{\Lambda }}_{k}^{A}$ и ${\mathbf{\Lambda }}_{t}^{S}$ диагональные [Alquier, Guedj, 2017]. В этом случае изменялись только формулы (9–12) аналогично тому, как это описано выше.
3) Сигналы не имеют автокорреляции [Natarajan et al., 2014; Alquier, Guedj, 2017]. В этом случае ${{{\mathbf{\mu }}}^{S}}$ заменяется на ${\mathbf{\mu }}_{t}^{S}$, формулы (6), (7), (11) и (12) – на формулы, аналогичные (4) и (9) соответственно, а произведения $p({{{\mathbf{s}}}_{1}}\,{\text{|}}\,{{{\mathbf{\mu }}}^{S}}$, ${\mathbf{\Lambda }}_{1}^{S})\prod\nolimits_{t = 2}^T {p({{{\mathbf{s}}}_{t}}\,{\text{|}}\,{\mathbf{s}}_{{t - 1}}^{S}} $, ${\mathbf{\Lambda }}_{t}^{S})$ и $p({{{\mathbf{\mu }}}^{S}}$, ${\mathbf{\Lambda }}_{1}^{S})\prod\nolimits_{t = 2}^T {p({\mathbf{\Lambda }}_{t}^{S})} $ в формуле (13) – на $\prod\nolimits_t {p({{{\mathbf{s}}}_{t}}\,{\text{|}}\,{\mathbf{\mu }}_{t}^{S}} $, ${\mathbf{\Lambda }}_{t}^{S})$ и $\prod\nolimits_t {p({\mathbf{\mu }}_{t}^{S}} $, ${\mathbf{\Lambda }}_{t}^{S})$ соответственно.
4) Скрытые параметры ${\mathbf{\mu }}_{j}^{U}$, ${\mathbf{\mu }}_{k}^{A}$, ${\mathbf{\mu }}_{t}^{S}$, ${\mathbf{\Lambda }}_{j}^{U}$, ${\mathbf{\Lambda }}_{k}^{A}$ и ${\mathbf{\Lambda }}_{t}^{S}$ не зависят от индексов k, j и t соответственно [Xiong et al., 2010; Natarajan et al., 2014; Alquier, Guedj, 2017]. При этом в формуле (13) произведения $\prod\nolimits_j {p({\mathbf{\mu }}_{j}^{U}} $, ${\mathbf{\Lambda }}_{j}^{U})$, $\prod\nolimits_k {p({\mathbf{\mu }}_{k}^{A}} $, ${\mathbf{\Lambda }}_{k}^{A})$ и $p({{{\mathbf{\mu }}}^{S}}$, ${\mathbf{\Lambda }}_{1}^{S})\prod\nolimits_{t = 2}^T {p({\mathbf{\Lambda }}_{t}^{S})} $ (или $\prod\nolimits_t {p({\mathbf{\mu }}_{t}^{S}} $, ${\mathbf{\Lambda }}_{t}^{S})$ – см. выше) заменяются на $p({{{\mathbf{\mu }}}^{U}}$, ${{{\mathbf{\Lambda }}}^{U}})$, $p({{{\mathbf{\mu }}}^{A}}$, ${{{\mathbf{\Lambda }}}^{A}})$ и $p({{{\mathbf{\mu }}}^{S}}$, ${{{\mathbf{\Lambda }}}^{S}})$.
Поскольку заранее неизвестно, какие из предположений лучше соответствуют свойствам ПСС, рассматривались 12 различных моделей, перечисленных в табл. 1.
Таблица 1.
Свойства моделей для разных алгоритмов Table 1. Model properties for different algorithm
| Алгоритм | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Компоненты взаимно независимые | + | + | + | + | – | – | – | – | – | – | – | – |
| ${\mathbf{\Lambda }}_{j}^{U}$, ${\mathbf{\Lambda }}_{k}^{A}$ и ${\mathbf{\Lambda }}_{t}^{S}$ диагональные | + | + | + | + | + | + | + | + | – | – | – | – |
| Учитывается автокорреляция сигналов | – | + | – | + | – | + | – | + | – | + | – | + |
| ${\mathbf{\mu }}_{j}^{U}$, ${\mathbf{\mu }}_{k}^{A}$, ${\mathbf{\mu }}_{t}^{S}$, ${\mathbf{\Lambda }}_{j}^{U}$, ${\mathbf{\Lambda }}_{k}^{A}$ и ${\mathbf{\Lambda }}_{t}^{S}$ зависят от индексов k, j и t | + | + | – | – | + | + | – | – | + | + | – | – |
* – в соответствии с формулой (6) для моделей, учитывающих автокорреляцию сигналов, скрытый параметр ${{{\mathbf{\mu }}}^{S}}$ является вектором, и не имеет индекса t. * – in accordance with formula (6) for models that take into account the autocorrelation of signals, the hidden parameter ${{{\mathbf{\mu }}}^{S}}$ is a vector and does not have an index t.
Условное распределение для каждого из неизвестных параметров модели несложно получить, используя формулу (13). Во всех случаях эти условные распределения могут быть приведены к стандартным, таким как гамма-распределение, распределение Уишарта, одномерные или многомерные нормальное и усеченное нормальное распределения, для которых предложены эффективные алгоритмы генерации случайных чисел [Smith, Hocking, 1972; Press et al., 2007; Li, Ghosh, 2015; Koch, Bopp, 2019]. Вывод окончательных формул для 12 моделей можно найти в приложении к Руководству пользователя для программного обеспечения WinEEG (https://mitsar-eeg.com/).
Для построения выборки случайных значений параметров CP-модели использовался метод Гиббса – “Gibbs sampler”, аналогичный тем, которые описаны ранее [Xiong et al., 2010; Natarajan et al., 2014; Nakatsuji et al., 2016; Alquier, Guedj, 2017; Chen et al., 2019a].
В качестве примера рассмотрим алгоритм A10, в основе которого лежат предположения относительно распределений случайных величин, описываемые формулами (3–12), а входными данными являются трехмерные массивы ${\mathbf{Y}}$ и ${\mathbf{V}}$, одномерный массив ${\mathbf{N}}$ и матрицы ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$, элементам которых присвоены случайные значения. На каждом шаге этой итеративной процедуры выполнялись следующие действия.
1) Для всех значений d выполняется перенормировка строк матриц ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$ следующим образом: ${{{\text{u}}}_{{d,j}}}$ = ${{{\text{u}}}_{{d,j}}}\frac{J}{{{{{\left\| {{{{\mathbf{u}}}_{{d, \bullet }}}} \right\|}}_{1}}}}$, ${{{\text{a}}}_{{d,k}}}$ = ${{{\text{a}}}_{{d,k}}}\frac{K}{{\left\| {{{{\mathbf{a}}}_{{d, \bullet }}}} \right\|_{F}^{2}}}$ и ${{{\text{s}}}_{{d,t}}}$ = ${{{\text{s}}}_{{d,t}}}\frac{{{{{\left\| {{{{\mathbf{u}}}_{{d, \bullet }}}} \right\|}}_{1}}\left\| {{{{\mathbf{a}}}_{{d, \bullet }}}} \right\|_{F}^{2}}}{{JK}}$, ${{\left\| {} \right\|}_{1}}$ – сумма абсолютных величин элементов вектора, ${{\left\| {} \right\|}_{F}}$ – норма Фробениуса.
2) Для всех значений k, j и t выбираются ${{\vartheta }_{{j,k,t}}}$ из $\Gamma ({{\vartheta }_{{j,k,t}}}\,{\text{|}}\,\overline {{{a}_{j}}} $, $\overline {{{b}_{{j,k,t}}}} )$, где $\overline {{{a}_{j}}} $ = $\frac{{{{N}_{j}} + 1}}{2}$ и $\overline {{{b}_{{j,k,t}}}} $ = = $\frac{1}{2}[({{{\text{y}}}_{{j,k,t}}}$ – ${{{\text{r}}}_{{j,k,t}}}{{)}^{2}}$ + ${{N}_{j}}{{{\text{v}}}_{{j,k,t}}}]$.
3) Для всех значений j выбираются матрицы ${\mathbf{\Lambda }}_{j}^{U}$ из ${{W}_{D}}({\mathbf{\Lambda }}_{j}^{U}\,{\text{|}}\,{\mathbf{\Lambda }}_{j}^{{*U}}$, $\nu {\kern 1pt} {{*}^{U}})$, где ${{({\mathbf{\Lambda }}_{j}^{{*U}})}^{{ - 1}}}$ = ${{({\mathbf{\Lambda }}_{0}^{U})}^{{ - 1}}}$ + + $\frac{{\beta _{0}^{U}}}{{\beta _{0}^{U} + 1}}({\mathbf{\mu }}_{0}^{U} - {{{\mathbf{u}}}_{j}})({\mathbf{\mu }}_{0}^{U} - {{{\mathbf{u}}}_{j}}){\kern 1pt} '$ и $\nu {\kern 1pt} {{*}^{U}} = \nu _{0}^{U} + 1$, и далее – векторы ${\mathbf{\mu }}_{j}^{U}$ из ${{R}_{D}}({\mathbf{\mu }}_{j}^{U}\,{\text{|}}\,{\mathbf{\mu }}_{j}^{{*U}}$, ${{(\beta {\kern 1pt} {{*}^{U}}{\kern 1pt} {\mathbf{\Lambda }}_{j}^{U})}^{{ - 1}}})$, где ${\mathbf{\mu }}_{j}^{{*U}}$ = = $\frac{{\beta _{0}^{U}{\mathbf{\mu }}_{0}^{U} + {{{\mathbf{u}}}_{j}}}}{{\beta _{0}^{U} + 1}}$ и ${{\beta }^{{*U}}} = \beta _{0}^{U} + 1$.
4) Для всех значений k выбираются матрицы ${\mathbf{\Lambda }}_{k}^{A}$ из ${{W}_{D}}({\mathbf{\Lambda }}_{k}^{A}\,{\text{|}}\,{\mathbf{\Lambda }}_{k}^{{*A}}$, ${{\nu }^{{*A}}})$, где ${{({\mathbf{\Lambda }}_{k}^{{*A}})}^{{ - 1}}}$ = ${{({\mathbf{\Lambda }}_{0}^{A})}^{{ - 1}}}$ + + $\frac{{\beta _{0}^{A}}}{{\beta _{0}^{A} + 1}}({\mathbf{\mu }}_{0}^{A}$ – ${{{\mathbf{a}}}_{k}})({\mathbf{\mu }}_{0}^{A} - {{{\mathbf{a}}}_{k}}){\kern 1pt} '$ и ${{\nu }^{{*A}}} = \nu _{0}^{A} + 1$, и далее – векторы ${\mathbf{\mu }}_{k}^{A}$ из ${{N}_{D}}({\mathbf{\mu }}_{k}^{A}\,{\text{|}}\,{\mathbf{\mu }}_{k}^{{*A}}$, ${{({{\beta }^{{*A}}}{\mathbf{\Lambda }}_{k}^{A})}^{{ - 1}}})$, где ${\mathbf{\mu }}_{k}^{{*A}}$ = = $\frac{{\beta _{0}^{A}{\mathbf{\mu }}_{0}^{A} + {{{\mathbf{a}}}_{k}}}}{{\beta _{0}^{A} + 1}}$ и ${{\beta }^{{*A}}} = \beta _{0}^{A} + 1$.
5) Для t = 1 выбирается матрица ${\mathbf{\Lambda }}_{1}^{S}$ из ${{W}_{D}}({\mathbf{\Lambda }}_{1}^{S}\,{\text{|}}\,{\mathbf{\Lambda }}_{1}^{{*S}}$, ${{\nu }^{{*S}}})$, где ${{({\mathbf{\Lambda }}_{1}^{{*S}})}^{{ - 1}}}$ = ${{({\mathbf{\Lambda }}_{0}^{S})}^{{ - 1}}}$ + $\frac{{\beta _{0}^{S}}}{{\beta _{0}^{S} + 1}}({\mathbf{\mu }}_{0}^{S}$ – – ${{{\mathbf{s}}}_{1}})({\mathbf{\mu }}_{0}^{S} - {{{\mathbf{s}}}_{1}}){\kern 1pt} '$ и ${{\nu }^{{*S}}} = \nu _{0}^{S} + 1$, потом – вектор ${{{\mathbf{\mu }}}^{S}}$ из ${{N}_{D}}({{{\mathbf{\mu }}}^{S}}\,{\text{|}}\,{{{\mathbf{\mu }}}^{{*S}}}$, ${{({{\beta }^{{*S}}}{\mathbf{\Lambda }}_{1}^{{*S}})}^{{ - 1}}})$, где ${{{\mathbf{\mu }}}^{{*S}}}$ = $\frac{{\beta _{0}^{S}{\mathbf{\mu }}_{0}^{S} + {{{\mathbf{s}}}_{1}}}}{{\beta _{0}^{A} + 1}}$ и ${{\beta }^{{*S}}} = \beta _{0}^{S} + 1$, и далее – матрицы ${\mathbf{\Lambda }}_{t}^{S}$ из ${{W}_{D}}({\mathbf{\Lambda }}_{t}^{S}\,{\text{|}}\,{\mathbf{\Lambda }}_{t}^{{*S}}$, ${{\nu }^{{*S}}})$ для всех значений t последовательно, начиная с t = 2, где ${{({\mathbf{\Lambda }}_{t}^{{*S}})}^{{ - 1}}}$ = ${{({\mathbf{\Lambda }}_{0}^{S})}^{{ - 1}}}$ + + $({{{\mathbf{s}}}_{t}}$ – ${{{\mathbf{s}}}_{{t - 1}}})({{{\mathbf{s}}}_{t}}$ – ${{{\mathbf{s}}}_{{t - 1}}}){\kern 1pt} '$.
6) Для всех значений j выбираются ${\mathbf{u}}_{j}^{'}$ из ${{R}_{D}}({\mathbf{u}}_{j}^{'}\,{\text{|}}\,{\mathbf{\mu }}_{j}^{{_{ + }U}}$, ${\mathbf{\Lambda }}_{j}^{{_{ + }{{U}^{{ - 1}}}}})$, где ${\mathbf{\mu }}_{j}^{{ + U}}$ = ${{({\mathbf{\Lambda }}_{j}^{{ + U}})}^{{ - 1}}}({\mathbf{\Lambda }}_{j}^{U}{\mathbf{\mu }}_{j}^{U}$ + ${\mathbf{b}}_{j}^{U})$, ${\mathbf{\Lambda }}_{j}^{{ + U}}$ = ${\mathbf{\Lambda }}_{j}^{U}$ + ${\mathbf{G}}_{j}^{U}$, ${\text{b}}_{{d,j}}^{U}$ = $\sum\nolimits_{k,t} {{{\vartheta }_{{j,k,t}}}} {{{\text{y}}}_{{j,k,t}}}{\text{q}}_{{d,k,t}}^{U}$, ${\text{g}}_{{d1,d2,j}}^{U}$ = = $\sum\nolimits_{k,t} {{{\vartheta }_{{j,k,t}}}{\text{q}}_{{d1,k,t}}^{U}{\text{q}}_{{d2,k,t}}^{U}} $ и ${\text{q}}_{{d,k,t}}^{U}$ = ${{{\text{a}}}_{{d,k}}}{{{\text{s}}}_{{d,t}}}$
7) Для всех значений k выбираются ${\mathbf{a}}_{k}^{'}$ из ${{N}_{D}}({\mathbf{a}}_{k}^{'}\,{\text{|}}\,{\mathbf{\mu }}_{k}^{{_{ + }A}}$, ${\mathbf{\Lambda }}_{k}^{{_{ + }{{A}^{{ - 1}}}}})$, где ${\mathbf{\mu }}_{k}^{{ + A}}$ = ${{({\mathbf{\Lambda }}_{k}^{{ + A}})}^{{ - 1}}}({\mathbf{\Lambda }}_{k}^{A}{\mathbf{\mu }}_{k}^{A}$ + ${\mathbf{b}}_{k}^{A})$, ${\mathbf{\Lambda }}_{k}^{{ + A}}$ = ${\mathbf{\Lambda }}_{k}^{A}$ + ${\mathbf{G}}_{k}^{A}$, ${\text{b}}_{{d,k}}^{A}$ = $\sum\nolimits_{j,t} {{{\vartheta }_{{j,k,t}}}} {{{\text{y}}}_{{j,k,t}}}{\text{q}}_{{d,j,t}}^{A}$, ${\text{g}}_{{d1,d2,k}}^{A}$ = = $\sum\nolimits_{j,t} {{{\vartheta }_{{j,k,t}}}{\text{q}}_{{d1,j,t}}^{A}{\text{q}}_{{d2,j,t}}^{A}} $ и ${\text{q}}_{{d,j,t}}^{A}$ = ${\text{u}}_{{d,j}}^{'}{{{\text{s}}}_{{d,t}}}$.
8) Для всех значений t (последовательно, начиная с t = 1) выбираются ${\mathbf{s}}_{t}^{'}$ из ${{N}_{D}}({\mathbf{s}}_{t}^{'}\,{\text{|}}\,{\mathbf{\mu }}_{t}^{{_{ + }S}}$, ${\mathbf{\Lambda }}_{t}^{{_{ + }{{S}^{{ - 1}}}}})$, где ${\mathbf{\mu }}_{1}^{{ + S}}$ = ${{({\mathbf{\Lambda }}_{1}^{{ + S}})}^{{ - 1}}}({\mathbf{\Lambda }}_{1}^{S}{{{\mathbf{\mu }}}^{S}}$ + ${\mathbf{\Lambda }}_{2}^{S}{{{\mathbf{s}}}_{2}}$ + ${\mathbf{b}}_{1}^{S})$, ${\mathbf{\Lambda }}_{1}^{{ + S}}$ = = ${\mathbf{\Lambda }}_{1}^{S}$ + ${\mathbf{\Lambda }}_{2}^{S}$ + ${\mathbf{G}}_{1}^{S}$, ${\mathbf{\mu }}_{t}^{{ + S}}$ = ${{({\mathbf{\Lambda }}_{t}^{{ + S}})}^{{ - 1}}}({\mathbf{\Lambda }}_{t}^{S}{\mathbf{s}}_{{t - 1}}^{'}$ + ${\mathbf{\Lambda }}_{{t + 1}}^{S}{{{\mathbf{s}}}_{{t + 1}}}$ + + ${\mathbf{b}}_{t}^{S})$, ${\mathbf{\Lambda }}_{t}^{{ + S}}$ = ${\mathbf{\Lambda }}_{t}^{S}$ + ${\mathbf{\Lambda }}_{{t + 1}}^{S}$ + ${\mathbf{G}}_{t}^{S}$, ${\mathbf{\mu }}_{T}^{{ + S}}$ = ${{({\mathbf{\Lambda }}_{T}^{{ + S}})}^{{ - 1}}}({\mathbf{\Lambda }}_{T}^{S}{\mathbf{s}}_{{T - 1}}^{'}$ + + ${\mathbf{b}}_{T}^{S})$, ${\mathbf{\Lambda }}_{T}^{{ + S}}$ = ${\mathbf{\Lambda }}_{T}^{S}$ + ${\mathbf{G}}_{T}^{S}$, для $t = 1$, $1 < t < T$ и $t = T$ соответственно, ${\text{b}}_{{d,t}}^{S}$ = $\sum\nolimits_{j,k} {{{\vartheta }_{{j,k,t}}}} {{{\text{y}}}_{{j,k,t}}}{\text{q}}_{{d,j,k}}^{S}$, ${\text{g}}_{{d1,d2,t}}^{S}$ = = $\sum\nolimits_{j,k} {{{\vartheta }_{{j,k,t}}}{\text{q}}_{{d1,j,k}}^{S}{\text{q}}_{{d2,j,k}}^{S}} $ и ${\text{q}}_{{d,j,k}}^{S}$ = ${\text{u}}_{{d,j}}^{'}{\text{a}}_{{d,k}}^{'}$.
9) Запоминаются вновь полученные значения: ${\mathbf{U}} = {\mathbf{U}}{\kern 1pt} '$, ${\mathbf{A}} = {\mathbf{A}}{\kern 1pt} '$ и ${\mathbf{S}} = {\mathbf{S}}{\kern 1pt} '$.
Постоянные параметры были следующими: ${\mathbf{\mu }}_{0}^{U}$ = $\left[ {1, \cdots ,1} \right]{\kern 1pt} '$, $\beta _{0}^{U} = 1$, ${\mathbf{\Lambda }}_{0}^{U} = {{{\mathbf{{\rm I}}}}_{D}}$, $\nu _{0}^{U} = D$, ${\mathbf{\mu }}_{0}^{A}$ = = $\left[ {0, \cdots ,0} \right]{\kern 1pt} '$, $\beta _{0}^{A} = 1$, ${\mathbf{\Lambda }}_{0}^{A} = {{{\mathbf{{\rm I}}}}_{D}}$, $\nu _{0}^{A} = D$, ${\mathbf{\mu }}_{0}^{S}$ = $\left[ {0, \cdots ,0} \right]{\kern 1pt} '$, $\beta _{0}^{S} = 1$, ${\mathbf{\Lambda }}_{0}^{S} = {{{\mathbf{{\rm I}}}}_{D}}$ и $\nu _{0}^{S} = D$, где ${{{\mathbf{{\rm I}}}}_{D}}$ – единичная матрица размера $D$.
Всего выполнялось 15 000 шагов. Первые 10 000 значений параметров отбрасывались, чтобы избежать влияния начальных условий, а последующие 5000 использовались для оценки средних значений и доверительных интервалов для элементов матриц ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$.
Выборка случайных значений параметров в других алгоритмах выполнялась аналогично.
Типичной задачей исследования ПСС является выявление интервалов времени, в которых наблюдается зависимость ПСС от условий. Однако если матрицы ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$ оцениваются для каждого условия отдельно, то вследствие принципиальной неопределенности масштабов компонент в CP-модели сравнение сигналов при различных условиях становится невозможным. Чтобы преодолеть это ограничение, можно предположить, что топографии компонент (матрица ${\mathbf{A}}$) и величины компонент (матрица ${\mathbf{U}}$) одинаковы для всех условий. Тогда становится возможным объединить ПСС, полученные при различных условиях, в единый временной ряд, и получить оценки ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$ для всей совокупности данных одновременно. Дисперсии ПСС объединялись аналогично, а массив ${\mathbf{N}}$ имел дополнительную размерность, поскольку число проб могло зависеть от условий. Отметим также, что если статистическая модель учитывала автокорреляцию сигналов, то в соответствующих алгоритмах A2, A4, A6, A8, A10 и A12 выборка случайных значений для ${\mathbf{\Lambda }}_{t}^{S}$, ${{{\mathbf{\mu }}}^{S}}$ и ${{{\mathbf{s}}}_{t}}$ (операции 4 и 7) выполнялась для каждого условия отдельно.
Поскольку параметр $D$ – число компонент – в модели неизвестен, его необходимо оценить. Для сравнения байесовских моделей можно использовать коэффициент Байеса, который определяется как
(14)
$\frac{{p\left( {{{D}_{1}}\,{\text{|}}\,{\mathbf{Y}}} \right)}}{{p\left( {{{D}_{2}}\,{\text{|}}\,{\mathbf{Y}}} \right)}} = \frac{{p\left( {{{D}_{1}}} \right)}}{{p\left( {{{D}_{2}}} \right)}}\frac{{p\left( {{\mathbf{Y}}\,{\text{|}}\,{{D}_{1}}} \right)}}{{p\left( {{\mathbf{Y}}\,{\text{|}}\,{{D}_{2}}} \right)}},$(15)
$p\left( {{\mathbf{Y}}\,{\text{|}}\,{{D}_{m}}} \right) = \int {p\left( {{\mathbf{Y}}\,{\text{|}}\,{\mathbf{U}},{\mathbf{A}},{\mathbf{S}},{{D}_{m}}} \right)d\left\{ {{\mathbf{U}},{\mathbf{A}},{\mathbf{S}}} \right\}} .$В том случае, когда $p\left( {{{D}_{m}}} \right)$ неизвестны, предполагается, что все $p\left( {{{D}_{m}}} \right)$ равны, тогда модель с максимальным $p\left( {{\mathbf{Y}}\,{\text{|}}\,{{D}_{m}}} \right)$ считается наиболее вероятной.
Чтобы оценить $p\left( {{\mathbf{Y}}\,{\text{|}}\,{{D}_{m}}} \right)$, необходимо вычислить интеграл в формуле (15), но получить аналитическое решение крайне сложно. Оценку $p\left( {{\mathbf{Y}}\,{\text{|}}\,{{D}_{m}}} \right)$ можно получить, используя метод, предложенный в работе Чиба [Chib, 1995]. В нашем случае при реализации метода Чиба определялись три подмножества параметров CP-модели, соответствующих матрицам ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$, и для каждого из них выполнялось 5000 шагов итеративной процедуры.
Для оценки эффективности 12 алгоритмов использовались массив записей ПСС, полученных в Go/NoGo тесте, и синтезированные данные.
Методика регистрации массива данных ПСС была подробно описана ранее [Пономарев, Кропотов, 2013; Kropotov et al., 2016; Пономарев и др., 2019 а, б]. Поэтому здесь приводится краткое описание. Массив включал в себя 351 записей, полученных у здоровых людей в возрасте от 18 до 55 лет (150 мужчин). Запись ЭЭГ выполнялась с помощью компьютерного электроэнцефалографа “Мицар-ЭЭГ” (полоса пропускания – 0.53–50 Гц, режекторный фильтр 45–55 Гц, частота квантования – 250 Гц). Электроды располагались в соответствии с международной системой 10–20, референт – объединенные электроды, расположенные на мочках ушей, заземляющий – в отведении Fpz. Перед вычислением ПСС выполнялись коррекция артефактов моргания и удаление артефактов [Пономарев и др., 2019а].
Зрительный Go/NoGo тест состоял из 400 проб длительностью 3000 мс, по 100 проб каждого типа. В пробах предъявлялись пары зрительных стимулов (изображения животных – “Ж”, растений – “Р” и людей – “Ч”), для каждого типа проб пары были различные: “Ж–Ж”, “Ж–Р”, “Р–Р” и “Р–Ч”. Длительность предъявления стимула – 100 мс, интервал между стимулами в пробе – 1000 мс. Первый стимул в пробе предъявлялся через 300 мс после ее начала. В пробах “Р–Ч” также предъявлялся звуковой стимул для поддержания уровня внимания. Пробы различного типа предъявлялись в псевдослучайном порядке. Участнику исследования давалось задание нажимать на кнопку только после предъявления пары “Ж–Ж”. ПСС вычислялись отдельно для каждого из типов проб (условий). Пробы, в которых задание выполнялось неправильно, исключались. Для анализа использовались ПСС, полученные в пробах “Ж–Ж”, “Ж–Р” и “Р–Р”, а частота квантования уменьшалась до 125 Гц путем прореживания.
Все исследования проведены в соответствии с принципами биомедицинской этики, сформулированными в Хельсинкской декларации 1964 г. и ее последующих обновлениях, и одобрены Комитетом по этике Института мозга человека им. Н.П. Бехтеревой Российской академии наук (ИМЧ РАН), Санкт-Петербург, Россия, и местным комитетом по этике кантона Граубюнден, округ Гризон, Швейцария. Каждый участник исследования представил добровольное письменное информированное согласие, подписанное им после разъяснения ему потенциальных рисков и преимуществ, а также характера предстоящего исследования.
Синтезированные данные были созданы следующим образом. Было выбрано несколько тестовых CP-моделей с различным числом компонент $D$ от 1 до 8, которые были ранее получены для описанного выше массива записей ПСС. Для каждой из этих моделей вычислялись ${\mathbf{R}}$ (см. формулу 2) и ${\mathbf{Y}}$ (J = 351, K = = 19, T = 1125) в соответствии с формулой ${\mathbf{Y}} = {\mathbf{R}}$ + $w{\mathbf{E}}\frac{{\left\| {\mathbf{R}} \right\|_{F}^{2}}}{{\left\| {\mathbf{E}} \right\|_{F}^{2}}}$, где ${\mathbf{E}}$ – трехмерный массив случайных нормально распределенных чисел, полученных из распределения $N\left( {0,1} \right)$, ${{\left\| {} \right\|}_{F}}$ – норма Фробениуса и $w$ – положительная величина, определяющая соотношение сигнал–шум, которая варьировалась. Для определения массивов ${\mathbf{V}}$ и ${\mathbf{N}}$ также использовались записи ПСС. Были вычислены среднегрупповые значения дисперсии ПСС. Далее, элементам трехмерного массива ${\mathbf{V}}$ присваивались средние значения среднегрупповых дисперсий в интервале, предшествующем первому стимулу в пробе (первые 300 мс), различные для индекса k и одинаковые для индексов j и t. Массив ${\mathbf{N}}$ содержал число проб для каждого условия и индивидуальной записи ПСС отдельно.
Для оценки точности описания исходных данных с помощью CP-модели использовались количественные показатели: относительная ошибка аппроксимации ${{\varepsilon }_{{{\text{app}}}}}$, инвариантное по отношению к произвольному масштабу расстояние между двумя CP-моделями $\hat {\Delta }$ и средние значения относительной ширины доверительного интервала $\overline {C{{I}^{U}}} $, $\overline {C{{I}^{A}}} $ и $\overline {C{{I}^{S}}} $ для элементов каждой из матриц ${\mathbf{U}}$, ${\mathbf{A}}$ и ${\mathbf{S}}$ отдельно. ${{\varepsilon }_{{{\text{app}}}}}$ вычислялась в соответствии с формулой ${{\varepsilon }_{{{\text{app}}}}}$ = ${{\left\| {{\mathbf{Y}} - {\mathbf{R}}} \right\|_{F}^{2}} \mathord{\left/ {\vphantom {{\left\| {{\mathbf{Y}} - {\mathbf{R}}} \right\|_{F}^{2}} {\left\| {\mathbf{Y}} \right\|_{F}^{2}}}} \right. \kern-0em} {\left\| {\mathbf{Y}} \right\|_{F}^{2}}}$. $\hat {\Delta }$ = $\frac{1}{D}\sum\nolimits_{d = 1}^D {{{\Delta }_{{d,d}}}} $, где матрица $\left\{ {{{\Delta }_{{r,q}}}} \right\}$ с элементами ${{\Delta }_{{r,q}}}$ = = $\delta (U_{{r, \bullet }}^{1},U_{{q, \bullet }}^{2})$ + $\delta (A_{{r, \bullet }}^{1},A_{{q, \bullet }}^{2})$ + $\delta (S_{{r, \bullet }}^{1},S_{{q, \bullet }}^{2})$ получена путем перестановок столбцов таким образом, чтобы максимальные значения ${{\Delta }_{{r,q}}}$ были расположены на диагонали, $\delta ({\mathbf{b}}_{{r, \bullet }}^{1},{\mathbf{b}}_{{q, \bullet }}^{2})$ = 1 – ‒ $\frac{{\left\langle {{\mathbf{b}}_{{r, \bullet }}^{1},{\mathbf{b}}_{{q, \bullet }}^{2}} \right\rangle }}{{\left\| {{\mathbf{b}}_{{r, \bullet }}^{1}} \right\|\left\| {{\mathbf{b}}_{{q, \bullet }}^{2}} \right\|}}$, ${{{\mathbf{b}}}_{{r, \bullet }}}$ – строка матрицы ${\mathbf{B}}$ с индексом r, 〈u, v〉 – скалярное произведение векторов u и v, $\left\| {\mathbf{u}} \right\|$ = $\sqrt {\left\langle {{\mathbf{u}},{\mathbf{u}}} \right\rangle } $. $\overline {C{{I}^{U}}} $ = $\frac{1}{D}\sum\nolimits_{d = 1}^D {CI_{d}^{U}} $, где $CI_{d}^{U}$ – отношение суммы разностей верхней и нижней границ доверительного интервала к сумме абсолютных значений элементов строки матрицы ${\mathbf{U}}$ с индексом d, аналогично для $\overline {C{{I}^{A}}} $ и $\overline {C{{I}^{S}}} $.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ
При использовании синтезированных данных, прежде всего, оценивалась способность двенадцати алгоритмов восстановить тестовую CP-модель при выборе соответствующего числа компонент D. Оказалось, что если тестовая CP-модель состоит из небольшого числа компонент ($D \leqslant 3$), то все 12 алгоритмов способны ее восстановить с удовлетворительной точностью ($\hat {\Delta } < 0.02$) независимо от соотношения сигнал–шум. При большем числе компонент для большинства алгоритмов величина $\hat {\Delta }$ была также меньше 0.02, исключая A2 и A4, для которых величина $\hat {\Delta }$ могла быть больше, чем 0.3.
При произвольном выборе числа компонент в CP-модели для большинства алгоритмов независимо от соотношения сигнал–шум типичная картина была следующей: относительная ошибка аппроксимации ${{\varepsilon }_{{app}}}$ монотонно уменьшалась, а функция предельного правдоподобия $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$ монотонно увеличивалась с ростом $D$. Но для алгоритмов A2, A4, A7 и A8 зависимости ${{\varepsilon }_{{app}}}$ и $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$ от $D$ могли быть немонотонные.
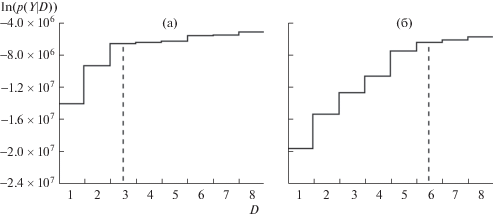
Примеры монотонной зависимости $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$ от $D$ для сильно зашумленных синтезированных данных ($w = 1$), полученные с помощью алгоритма A10, представлены на рис. 1. Видно, что $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$ быстро увеличивалась с ростом $D$, пока оно не достигает числа компонент в тестовой CP-модели, но далее скорость роста $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$ заметно уменьшается. Такое свойство зависимости $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$ от числа компонент подтверждает возможность использования коэффициента Байеса для определения числа компонент. Причем оптимальное число компонент в CP-модели может соответствовать точке излома функции $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$.
Рис. 1.
Результаты оценки числа компонент в CP-модели для синтезированных данных. По оси абсцисс – число компонент ($D$), по оси ординат – логарифм функции предельного правдоподобия. Вертикальная линия показывает правильное $D$: (а) – $D = 3$, (б) – $D = 6$.
Fig. 1. The results of estimating the number of components in the CP-model for the synthetic data. Abscissa, the number of components ($D$); ordinate, the logarithm of marginal likelihood. The vertical line show the true value of $D$: (a) – $D = 3$, (б) – $D = 6$.
Для синтезированных данных величина $\overline {C{{I}^{U}}} $, $\overline {C{{I}^{A}}} $ и $\overline {C{{I}^{S}}} $ относительно мало зависела от соотношения сигнал–шум. При этом показатели $\overline {C{{I}^{U}}} $, $\overline {C{{I}^{A}}} $ и $\overline {C{{I}^{S}}} $ увеличивались с ростом $D$. Иными словами, чем больше параметров имела CP-модель (больше компонент), тем больше была дисперсия их оценки. Несмотря на то что эти наблюдения приводят к тривиальным выводам, тем не менее, они подтверждают адекватность использованных количественных показателей для оценки относительной ширины доверительных интервалов. Не столь очевидным оказался характер их зависимости от используемого алгоритма. В частности, если в статистических моделях предполагается, что скрытые параметры ${\mathbf{\mu }}_{j}^{U}$, ${\mathbf{\mu }}_{k}^{A}$, ${\mathbf{\mu }}_{t}^{S}$, ${\mathbf{\Lambda }}_{j}^{U}$, ${\mathbf{\Lambda }}_{k}^{A}$ и ${\mathbf{\Lambda }}_{t}^{S}$ зависят от индексов k, j и t (алгоритмы A1, A2, A5, A6, A9 и A10), то в этих моделях количество скрытых параметров больше по сравнению с другими соответствующими (см. табл. 1). Тем не менее оказалось, что при использовании этих алгоритмов величина $\overline {C{{I}^{U}}} $, $\overline {C{{I}^{A}}} $ и $\overline {C{{I}^{S}}} $ была в 1.2–1.5 раза меньше по сравнению с алгоритмами A3, A4, A7, A8, A11 и A12 соответственно. Если же статистическая модель учитывала автокорреляцию сигналов (алгоритмы с четными номерами), это мало отражалось на величине $\overline {C{{I}^{U}}} $ и $\overline {C{{I}^{A}}} $, но для алгоритмов A6 и A10 величина $\overline {C{{I}^{S}}} $ была в 1.3–2 раза меньше по сравнению с десятью другими.
Представленные выше результаты указывают на то, что алгоритмы A6 и A10 являются наиболее эффективными. Во-первых, они обеспечивает приемлемую точность восстановления тестовой CP-модели. Во-вторых, дисперсия оценки параметров CP-модели относительно небольшая, по сравнению с другими алгоритмами. В-третьих, зависимость функции предельного правдоподобия от числа компонент является монотонной.
Анализ массива записей ПСС также выполнялся, используя все 12 алгоритмов. В целом результаты оценки эффективности алгоритмов совпадали с описанными выше. Поэтому здесь будут представлены результаты, полученные с помощью алгоритмов A6 и A10.
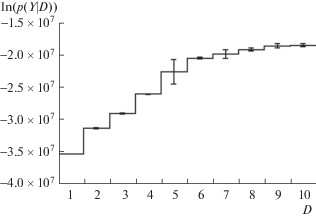
Результаты оценки оптимального числа компонент в CP-модели, полученные с помощью алгоритма A10, показаны на рис. 2. Причем оценка CP-модели выполнялась 8 раз для каждого значения $D$, что позволяло оценить зависимость оценки функции предельного правдоподобия от начального приближения. Видно, что функция предельного правдоподобия монотонно увеличивалась с ростом $D$. Но скорость роста заметно уменьшается, если $D \geqslant 6$. Иными словами, точка излома функции $p\left( {{\mathbf{Y}}\,{\text{|}}\,D} \right)$ соответствует $D = 6$. Аналогичные результаты были получены с помощью алгоритма A6.
Рис. 2.
Результаты оценки числа компонент в CP-модели для ПСС. Отрезки на кривых – плюс-минус два стандартных отклонения. Обозначения те же, что на рис. 1.
Fig. 2. The results of estimating the number of components in the CP-model for the ERPs. Spreads – plus or minus two standard deviations. For other designation, see Fig. 1.
При оптимальном $D$ оценки параметров CP-модели относительно мало зависят от начального приближения. В то же время в результате сравнительного анализа использования алгоритмов A6 и A10 было выявлено, что последний показывает лучшую повторяемость. В частности, среднее значение $\hat {\Delta }$, полученное при попарном сравнении CP-моделей, была равной 0.035 для A10, по сравнению с 0.232 для A6. Тем не менее среднее значение $\hat {\Delta }$ для ПСС больше, чем для синтезированных данных, что показывает необходимость выполнять тензорное разложение несколько раз для его верификации.
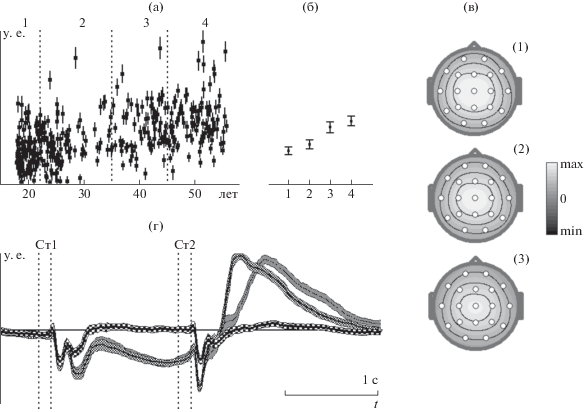
Пример одной компоненты CP-модели с доверительными интервалами (с надежностью 0.95), полученной с помощью алгоритма A10, показан на рис. 3. Отметим, что на графиках и топограммах все величины показаны в условных единицах, поскольку CP-модель может быть оценена только с точностью до произвольного масштаба. Ширина доверительного интервала для элементов матрицы ${\mathbf{U}}$ значительно меньше, чем разброс значений величин компоненты от человека к человеку (рис. 3 (а)). В то же время величина этой компоненты в среднем увеличивается с возрастом (рис. 3 (б)). Ширина доверительного интервала для элементов матрицы ${\mathbf{A}}$ относительно невелика (рис. 3 (в)), т.е. оценка топографии этой компоненты была получена с удовлетворительной точностью. Наконец, ширина доверительного интервала для сигналов (рис. 3 (г)) значительно меньше величины их отклонения от изолинии, и можно выделить интервалы времени, в течение которых эти доверительные интервалы для сигналов, соответствующих различным типам проб, не перекрываются. Таким образом, оценка сигналов была получена с удовлетворительной точностью для того, чтобы выявить различия сигналов при выполнении разных видов деятельности.
Рис. 3.
Доверительные интервалы для параметров компоненты CP-модели. (а) – величина компоненты у разных испытуемых, по оси абсцисс – возраст, по оси ординат – величина компоненты в условных единицах, вертикальные пунктирные линии – границы четырех возрастных групп. (б) – среднее значение величины компоненты в четырех возрастных группах. (в) – топография компоненты (2) и нижняя (3) и верхняя (1) границы доверительных интервалов. (г) – сигналы компоненты в пробах а – “Ж–Ж”, б – “Ж–Р”, в – “P–Р”. По оси абсцисс – время, по оси ординат – величина сигнала в условных единицах. Вертикальные пунктирные линии – моменты включения и выключения стимулов в пробе.
Fig. 3. Confidence intervals for the parameters of the component of the CP- model. (a) – magnitude of the components in different subjects; abscissa, age; ordinate, magnitude in conventional units; vertical dashed lines – borders of four age groups. (б) – average magnitude of the component in four age groups. (в) – topography of components (2) and lower (3) and upper (1) boundaries of confidence intervals. (г) – component signals in trials a – “A–A”, b – “A–P”, c – “P–P”. Abscissa, time; ordinate, signal magnitude in conventional units. The time points when the stimuli were turned on and off in a trial are shown with vertical dashed lines.
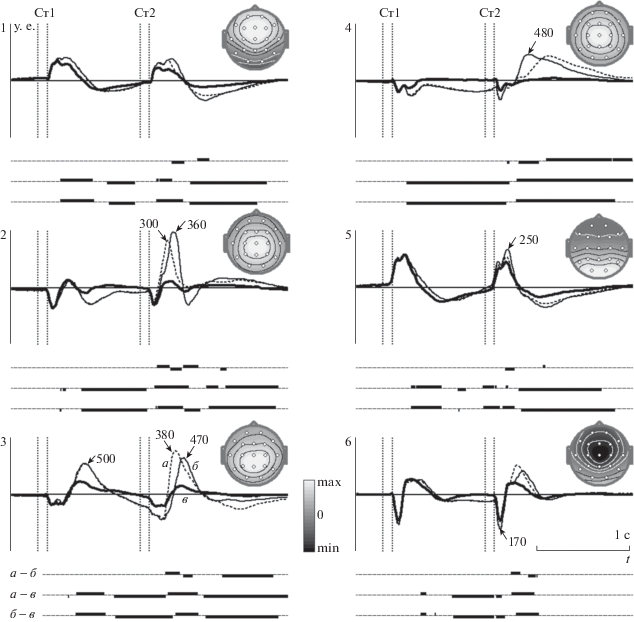
Топографии и сигналы шести компонент CP-модели показаны на рис. 4. Сигналы компонент нормированы так, что среднее значение величины компонент (элементов строк матрицы ${\mathbf{U}}$) и абсолютное значение максимума на топографиях компонент (в строках матрицы ${\mathbf{A}}$) равны 1. Ниже под графиками показаны интервалы времени, в течение которых при парном сравнении эти сигналы различались, т.е. соответствующие доверительные интервалы не перекрывались. Эта модель с хорошей точностью аппроксимирует среднегрупповые ПСС (${{\varepsilon }_{{{\text{app}}}}}$ = 0.014) и описывает 71.8% дисперсии исходных данных.
Рис. 4.
Сигналы и топографии компонент в CP-модели. а – пробы “Ж–Ж” (Go условие), б – пробы “Ж–Р” (NoGo условие), в – пробы “P–Р”. По оси абсцисс – время, по оси ординат – величина сигнала в условных единицах. Вертикальные пунктирные линии – моменты включения и выключения стимулов в пробе. Среднегрупповое время реакции – 400 мс. Латентности пиков, отмеченных стрелками, – в миллисекундах. Интервалы времени, в течение которых доверительные интервалы (с надежностью 0.95) не перекрывались, выделены под графиками с помощью прямоугольников, расположенных в три строки для пар кривых а – б, а – в и б – в соответственно.
Fig. 4. Waveforms and topographies of the components in the CP-model. а – “A–A” trials (Go condition), б – “A–P” (NoGo condition), and в –“P–P” trials. Abscissa, time; ordinate, signal magnitude in conventional units. The time points when the stimuli were turned on and off in a trial are shown with vertical dashed lines. The group average reaction time – 400 ms. The latencies of the peaks indicated with arrows are shown in milliseconds. The time intervals during which the confidence intervals (with level 0.95) did not overlap are highlighted under the graphs using rectangles located in three rows for pairs of waveforms а – б, а – в and б – в, respectively.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Результаты исследования показали, что байесовский параллельный факторный анализ может оказаться эффективным средством для выявления общих характеристик сигналов мозговых источников, отражающихся в ПСС, регистрируемых на поверхности кожи головы. В то же время этот подход имеет ряд ограничений, связанных с тем, что CP-модель является определенным приближением. Рассмотрим особенности этого приближения подробнее.
Во-первых, предполагается, что топографии компонент одинаковы у всех людей. Это, безусловно, является существенным приближением, поскольку, несмотря на то, что анатомическое строение мозга сходно у различных людей, индивидуальные особенности все-таки существуют. Кроме того, положение электродов относительно мозговых источников может варьировать от человека к человеку. Но, во-первых, используя метод независимых компонент, было показано, что для спонтанной ЭЭГ в пределах точности измерения топографии компонент приблизительно одинаковы [Ponomarev et al., 2014]. Во-вторых, считается, что источники электрического потенциала для ЭЭГ и длиннолатентных компонентов ПСС находятся в коре головного мозга [Hallez et al., 2007]. И, наконец, физические законы распространения электрических полей одинаковы для ЭЭГ и ПСС. Все эти факты указывают на то, что, несмотря на то, что индивидуальные отличия топографий компонент ПСС существуют, они, вероятно, относительно невелики, и в первом приближении можно принять, что эти топографии одинаковы.
Во-вторых, предполагается, что сигналы компонент одинаковы у всех людей. Строго говоря, это предположение несправедливо для произвольной группы участников исследования. В частности, хорошо известно, что время реакции человека и пиковая латентность некоторых волн ПСС варьируют от человека к человеку и зависят от возраста. Эти свойства являются косвенным подтверждением того, что сигналы компонент также неодинаковы. С другой стороны, широко используемый метод усреднения ПСС по группе участников исследования позволяет выделить хорошо выраженные волны ПСС. Но это было бы невозможно, если бы индивидуальные различия ПСС были бы большими. Кроме того, анализ зависимости пиковой латентности волн ПСС от возраста показывает, что существует возможность выбрать возрастной диапазон, в котором эта зависимость относительно невелика [Kropotov et al., 2016; Пономарев и др., 2019а]. Эти наблюдения позволяют считать, что при подходящем выборе возрастного диапазона в первом приближении можно принять, что сигналы компонент одинаковы.
В-третьих, предполагается, что топографии и величины компонент не зависят от условий. Такое предположение может показаться слишком строгим. Тем не менее, СР-модель допускает зависимость сигналов компонент от условия исследования. Более того, допустимыми являются даже такие случаи, когда при одном условии сигнал источника существует, а при другом он отсутствует. Эти аргументы указывают на то, что это предположение может оказаться справедливым. И это подтверждается результатами исследований, представленными выше. Тем не менее точность оценки сигналов уменьшается с ростом числа компонент в CP-модели. Поэтому включение в CP-модель большого числа условий, при которых выполняется различная деятельность, может сказываться на точности измерений, поскольку для описания таких ПСС может потребоваться большое число компонент.
Наконец, следует иметь в виду, что не для каждого массива данных и CP-модели с произвольным числом компонент можно получить единственное решение (подробнее см. [Kolda, Bader, 2009]). Это может накладывать ограничения на максимально допустимое число компонент в CP-модели. Тем не менее при анализе достаточно большого массива записей ПСС это ограничение не является слишком строгим.
Следует особо подчеркнуть, что предположения о схожести топографий и сигналов компонент могут быть приняты в первом приближении для здоровых испытуемых в ограниченном возрастном диапазоне и, возможно, для некоторых групп пациентов. Но у людей с различными поражениями мозга топографии и сигналы могут сильно различаться, и это ограничивает использование предложенного подхода.
Результаты сравнительного анализа эффективности работы 12 алгоритмов показали, что лучшую точность оценки параметров CP-моделей можно получить, если, во-первых, в статистических моделях используются многомерные распределения, во-вторых, выборка значений скрытых параметров выполняется для каждой индивидуальной записи ПСС, каждого момента времени и каждого электрода отдельно, и, наконец, статистическая модель учитывает автокорреляцию сигналов. По-видимому, это непосредственно связано со спецификой ПСС, которые, во-первых, довольно сильно варьируют от человека к человеку, во-вторых, представляют собой нестационарный и относительно быстро изменяющийся во времени переходной процесс, имеющий значительную автокорреляцию, и, наконец, пространственное распределение электрического потенциала по скальпу имеет хорошо выраженные экстремумы, положение которых меняется во времени.
Отметим некоторые особенности данной статистической модели. Во-первых, в ней считается, что только элементы матрицы ${\mathbf{U}}$ не могут быть отрицательными. Напротив, в ранее предложенных моделях считалось, что элементы всех матриц могут быть либо произвольными [Xiong et al., 2010; Natarajan et al., 2014; Nakatsuji et al., 2016; Chen et al., 2019a], либо неотрицательными [Schmidt, Mohamed, 2009, Alquier, Guedj, 2017]. Во-вторых, при моделировании автокорреляции сигналов считается, что скрытый параметр точности ${\mathbf{\Lambda }}_{t}^{S}$ зависит от индекса t (времени), тогда как ранее предполагалось, что он постоянный [Xiong et al., 2010]. И, наконец, в данной модели учитывается дисперсия исходных данных.
Сравнивая CP-модель, представленную на рис. 4, с полученной ранее [Пономарев и др., 2019б, рис. 2] для тех же записей ПСС, видно, что большинство сигналов и топографий компонент довольно схожи, несмотря на то, что использовались различные методы оценки. Это косвенно подтверждает адекватность предлагаемого в данной работе подхода.
С другой стороны, использование байесовских статистических моделей предоставляет дополнительные возможности. Во-первых, такой подход позволяет оценить не только параметры CP-модели, но и соответствующие им доверительные интервалы, и, следовательно, выполнить статистические сравнения сигналов при различных условиях. Во-вторых, используя коэффициент Байеса, имеется возможность получить объективную оценку числа компонент в CP-модели. Наконец, сравнивая метод градиентного спуска, использованный ранее [Пономарев и др., 2019 а,б], и предлагаемый в этой работе подход, необходимо отметить еще одно преимущество последнего. В частности, в зависимости от начального приближения метод градиентного спуска сходится к одному из локальных минимумов невыпуклой целевой функции. Поэтому для выбора наилучшей модели было необходимо многократно выполнять тензорное разложение, варьируя начальное приближение. Предложенный в данной работе метод оценки параметров CP-модели, использующий байесовские статистические модели, работает более стабильно. И, несмотря на то, что для верификации необходимо выполнить тензорное разложение несколько раз, использование этого подхода значительно уменьшает объемы вычислений.
Предложенный подход был разработан, прежде всего, для группового анализа ПСС. Он также подходит для анализа индивидуальных данных, но при этом следует учитывать ряд ограничений. Во-первых, соотношение сигнал–шум в единичных пробах меньше, чем у усредненных по пробам ПСС, что может сказаться на точности оценки топографий и сигналов компонент. Во-вторых, вариабельность величины различных компонентов ПСС от пробы к пробе может быть коррелированна, что может приводить к уменьшению ранга матрицы ${\mathbf{U}}$ и, как следствие, ограничивает возможность разделения сигналов этих компонентов. В-третьих, латентность некоторых компонентов ПСС и времени реакции человека коррелированны, причем время реакции варьирует от пробы к пробе. Если в зависимости от задания дисперсия времени реакции окажется слишком большой, то предположение о схожести сигналов в пробах станет несправедливым, и точность оценки сигналов будет снижена. Наконец, сигналы компонент могут быть оценены только с точностью до произвольного масштаба. Если оценки этих сигналов получены при анализе индивидуальных данных, то будет невозможно выполнить их количественное сравнение при последующем групповом анализе.
Хотя исследование функциональной роли компонент CP-модели не входило в задачу данного исследования, кратко остановимся на этом вопросе. Величина ранних пиков в сигналах компонент 1 и 6 после второго стимула больше в пробах “Ж–Ж” и “Ж–Р” по сравнению с “Р–Р”, что, по-видимому, связано с различным уровнем внимания [Kropotov, Ponomarev, 2015]. Величина пика в сигналах компоненты 5 с латентностью 250 мс больше в пробах “Ж–Р” по сравнению с “Ж–Ж” и “Р–Р”. Ранее было показано, что подобный эффект, вероятно, связан с процессом сравнения стимула с образом, хранящимся в рабочей памяти [Kropotov, Ponomarev, 2015]. Особенности сигналов компонент 2, 3 и 4 подробно обсуждались ранее, и был высказан ряд гипотез [Пономарев и др., 2019б]. В частности, возможно, что в сигналах компоненты 2 после второго стимула отражаются процессы, связанные с принятием решения о выполнении ответной реакции или ее подавлении; в сигналах компоненты 3 после первого и второго стимулов – с переключением с одного вида деятельности на другой; а в сигналах компоненты 4 после второго стимула – с восстановлением состояния нейронных сетей после действия. Иными словами, сигналы компонент по-разному зависят от типа проб, и в них отражается протекание различных мозговых процессов. Эти результаты указывают на то, что байесовский параллельный факторный анализ позволяет выделить функционально различные компоненты ПСС.
ЗАКЛЮЧЕНИЕ
Предложена байесовская вероятностная модель для параллельного факторного анализа связанных с событиями потенциалов мозга человека. Для этой модели была разработана процедура построения выборки случайных значений ее параметров, основанная на методах Монте-Карло с цепями Маркова. Использование этой процедуры позволяет, во-первых, получить объективную оценку числа компонент в модели и, во-вторых, выполнить статистические сравнения сигналов при выполнении различных видов деятельности. Результаты использования этой модели показали, что с помощью байесовского параллельного факторного анализа удается выделить функционально различные компоненты ПСС, что, в свою очередь, позволяет рассматривать динамику процессов, протекающих в мозге, с нетрадиционной точки зрения.
Авторы выражают благодарность Dr. Andreas Müller, Детский центр, Кур, Швейцария за предоставленные записи ПСС в Go/NoGo тесте.
Работа выполнена в рамках государственного задания Минобрнауки по теме № АААА-А19-119101890066-2.
Список литературы
Кропотов Ю.Д. Количественная ЭЭГ, когнитивные вызванные потенциалы мозга человека и нейротерапия. Донецк: Издатель Заславский Ю.А., 2010. 512 с.
Пономарев В.А., Кропотов Ю.Д. Уточнение локализации источников вызванных потенциалов в GO/NOGO тесте с помощью моделирования структуры их взаимной ковариации. Физиология человека. 2013. 39 (1): 36–50.
Пономарев В.А., Пронина М.В., Кропотов Ю.Д. Параллельный факторный анализ в исследовании связанных с событиями потенциалов. Физиология человека. 2019а. 45 (3): 5–15.
Пономарев В.А., Пронина М.В., Кропотов Ю.Д. Скрытые компоненты связанных с событиями потенциалов в зрительном Go/NoGo тесте c предупреждающим стимулом. Физиология человека. 2019б. 45 (5): 20–29.
Alquier P., Guedj B. An Oracle Inequality for Quasi-Bayesian Non-Negative Matrix Factorization. Mathematical Methods of Statistics. 2017. 26 (1): 55–67.
Chen X., He Z., Sun L. A Bayesian tensor decomposition approach for spatiotemporal traffic data imputation. Transp. Res. Part C Emerg. Technol. 2019a. 98: 73–84.
Chen X., He Z., Chen Y., Lu Y., Wang J. Missing traffic data imputation and pattern discovery with a Bayesian augmented tensor factorization model. Transp. Res. Part C Emerg. Technol. 2019b. 104: 66–77.
Chib S. Marginal Likelihood from the Gibbs Output. J. Am. Stat. Assoc. 1995. 90 (432): 1313–1321.
Cichocki A., Mandic D., Phan A.-H., Caiafa C.F., Zhou G., Zhao Q., De Lathauwer L. Tensor decompositions for signal processing applications from two-way to multiway component analysis. IEEE Signal Proc. Mag. 2015. 32 (2): 145–163.
Cong F., Lin Q.H., Kuang L.D., Gong X.F., Astikainen P., Ristaniemi T. Tensor decomposition of EEG signals: a brief review. J. Neurosci. Methods. 2015. 248: 59–69.
Gelman A., Carlin J.B., Stern H.S., Dunson D.B., Vehtari A., Rubin D.B. Bayesian Data Analysis, Third Edition. New-York, London: CRC Press, 2014. 675 p.
Hallez H., Vanrumste B., Grech R., Muscat J., De Clercq W., Vergult A., D’Asseler Y., Camilleri K.P., Fabri S.G., Van Huffel S., Lemahieu I. Review on solving the forward problem in EEG source analysis. J. Neuroeng. Rehabil. 2007. 4: 46.
Koch H., Bopp G.P. Fast and Exact Simulation of Multivariate Normal and Wishart Random Variables with Box Constraints. arXiv preprint. 2019. arXiv: 1907.00057.
Kolda T., Bader B. Tensor decompositions and applications. SIAM Review. 2009. 51 (3): 455–500.
Kropotov J.D., Ponomarev V.A. Differentiation of neuronal operations in latent components of event-related potentials in delayed match-to-sample tasks. Psychophysiology. 2015. 52 (6): 826–838.
Kropotov J., Ponomarev V., Tereshchenko E.P., Muller A., Jancke L. Effect of aging on ERP components of cognitive control. Front. Aging Neurosci. 2016. 8: 69.
Li Y., Ghosh S.K. Efficient sampling methods for truncated multivariate normal and student-t distributions subject to linear inequality constraints. J. Stat. Theory Pract. 2015. 9: 712–732.
Luck S.J., Kappenman E.S. (Eds.) The Oxford handbook of event-related potential components. Oxford: Oxford University Press. 2011. 642 p.
Nakatsuji M., Toda H., Sawada H., Zheng J.G., Hendler J.A. Semantic sensitive tensor factorization. Artif. Intell. 2016. 230: 224–245.
Natarajan R., Banerjee A., Shan H. Multiple imputation of missing data in multi-dimensional retail sales data sets via tensor factorization. US Patent: US08818919, Aug. 26, 2014/13/204,237
Ponomarev V.A., Mueller A., Candrian G., Grin-Yatsenko V.A., Kropotov J.D. Group independent component analysis (gICA) and current source density (CSD) in the study of EEG in ADHD adult. Clin. Neurophysiol. 2014. 125 (1): 83–97.
Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. Numerical recipes. The art of scientific computing. Third edition. New York: Cambridge University Press. 2007. 1256 p.
Salakhutdinov R., Mnih A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo. Proc. of 25th Int. Conf. on Machine Learning. 2008. 880–887 pp.
Schmidt M.N., Mohamed S. Probabilistic non-negative tensor factorization using Markov chain Monte Carlo. Proc. of 17th European Signal Proc. Conf. 2009. 1918–1922 pp.
Smith W.B., Hocking R.R. Algorithm AS 53: Wishart variate generator. J. R. Stat. Soc. Ser. C. 1972. 21 (3): 341–345.
Trinh G., Genz A. Bivariate conditioning approximations for multivariate normal probabilities. Stat. Comput. 2015. 25: 989–996.
Xiong L., Chen X., Huang T.K., Schneider J., Carbonell J.G. Temporal collaborative filtering with Bayesian probabilistic tensor factorization. Proc. of 2010 SIAM Int. Conf. on Data Mining. 2010. 211–222 pp.
Zhou G., Zhao Q., Zhang Y., Adalı T., Xie S., Cichocki A. Linked component analysis from matrices to high order tensors: applications to biomedical data. Proc. IEEE. 2016. 104 (2): 310–331.
Дополнительные материалы отсутствуют.
Инструменты
Журнал высшей нервной деятельности им. И.П. Павлова


