Геохимия, 2021, T. 66, № 11, стр. 1050-1066
Совместный расчет химических и изотопных равновесий в программном комплексе GEOCHEQ_Isotope: изотопы кислорода
В. Б. Поляков a, b, М. В. Мироненко a, М. В. Аленина a
a Институт геохимии и аналитической химии им. В.И. Вернадского РАН, ГСП-1
119991 Москва, ул. Косыгина, 19, Россия
b Институт экспериментальной минералогии им. академика Д.С. Коржинского РАН
142432 Московская область, Черноголовка, ул. Академика Осипьяна, 4, Россия
Поступила в редакцию 29.05.2021
После доработки 04.06.2021
Принята к публикации 05.06.2021
Аннотация
Программный комплекс GEOCHEQ_Isotope, раннее разработанный для моделирования химических и изотопных равновесий углерода в гидротермальных и гидрогеохимических системах методом минимизации энергии Гиббса, распространен на одновременный расчет изотопных эффектов углерода и кислорода. Как и в случае углерода при разработке алгоритмов и базы данных для расчета изотопных эффектов кислорода использовали формализм β-фактора. Согласно разработанному алгоритму энергия Гиббса G*(P, T) образования редкого изотополога рассчитывалась через энергию Гиббса образования основного изотополога с учетом величины β18O-фактора этого вещества и соотношения масс редкого (18O) и основного изотопов (16O) химического элемента. Используется приближение идеальности смеси изотопов. Температурная зависимость β-фактора унифицирована в виде полинома по обратным степеням абсолютной температуры. Критически проанализирована необходимая информация по кислородным изотопным равновесиям, включающим важные геохимические соединения, проведены согласование и модификация имеющихся данных. С учетом этого оптимизированы температурные зависимости β18O-факторов. База термодинамических данных пополнена информацией по температурным зависимостям β18O-факторов, заключающейся в введении полиномиальных коэффициентов для каждого из веществ. Практическая реализация программного комплекса и соответствующей базы данных продемонстрирована на примере использования программного комплекса GEOCHEQ_Isotope для моделирования зависимости факторов фракционирования изотопов кислорода и углерода от показателя кислотности раствора (pH) в карбонатной гидротермальной системе. Получено хорошее согласие результатов моделирования с имеющимися литературными экспериментальными данными. При повышении pH системы происходит уменьшение обогащения растворенных карбонатов тяжелым изотопом кислорода 18O относительно воды. В то же время повышение pH приводит к уменьшению отрицательного углеродного изотопного сдвига между кальцитом и растворенными карбонатами. При высоких значениях pH (~11) наблюдается инверсия изотопного сдвига и растворенный карбонат обогащен тяжелым изотопом углерода относительно кальцита.
ВВЕДЕНИЕ
Исследования изотопных эффектов кислорода занимают одно из центральных мест в изотопной геохимии. Подавляющее большинство изотопных геотермометров являются кислородными. Данная статья посвящена совместному расчету химических и кислородных изотопных равновесий на основе программного комплекса GEOCHEQ_Isotope. Основные подходы и методы расчетов кислородных изотопных эффектов в данной работе в целом аналогичны методам и подходам, изложенным нами ранее для изотопных эффектов углерода. Впервые совместное моделирование химических и изотопных равновесий путем минимизации свободной энергии, получившее название: метод изотопно-химической системы (идея принадлежит Б.Н. Рыженко), было выполнено для изотопов серы в работах Д.В. Гричука с соавторами (Банникова и др., 1987; Гричук, 1987, 1988, 2000; Гричук, Лейн, 1991). Этот метод позволяет проводить расчет химических и изотопных равновесий в один этап в отличие от обычных подходов (Ohmoto, 1972), когда на первом этапе проводится расчет химических равновесий, а на втором проводят расчет изотопных равновесий.
Как отмечалось ранее (Mironenko et al., 2018), одной из основных причин, тормозящих распространение совместных расчетов химических и изотопных равновесий, является отсутствие внутренне-согласованных баз термодинамических данных по редким изотопологам. Данное исследование направлено на устранение этого недостатка и создание базы данных для моделирования геохимических процессов с учетом кислородных изотопных эффектов на основе критического анализа имеющейся информации по изотопным равновесиям.
ПОДХОДЫ И МЕТОДЫ
Также, как и в случае углеродных изотопных эффектов (Mironenko et al., 2018), основу для расчетов составляет программный комплекс (Мироненко и др., 2000), использующий базу данных SUPCRT92 (Johnson et al., 1992) c более поздними дополнениями и исправлениями. Минимизация энергии Гиббса в программном комплексе G-EOCHEQ проводится по алгоритму выпуклого симплекса (de Capitani, Brown, 1987). Для учета изотопных эффектов в расширении программного комплекса GEOCHEQ – GEOCHEQ_Isotope вместо химического элемента, для которого рассчитываются изотопные эффекты, введены его изотопы в качестве независимых компонент, a в список веществ добавлены соответствующие изотопологи (Mironenko et al., 2018). В случае кислорода – это изотопы 16O и 18O и их изотопологи.
Все расчеты изотопных эффектов в GE-OCHEQ_Isotope проводятся в приближении идеальности смеси изотопов, в котором замещения ядер изотопов в разных позициях не влияют друг на друга, и изотопные эффекты не зависят от кратности изотопного замещения. Для молекул, содержащих несколько атомов, это приближение обычно формулируют в виде правила геометрического среднего (Галимов, 1973, 1974). Для всех элементов за исключением водорода приближение идеальности смеси изотопов выполняется при температурах, превышающих 100 K (Поляков, 1993). Это приближение по умолчанию считается выполненным в подавляющем большинстве геохимических расчетов, если не проводится специальный расчет перекрестных (или “clumped”) изотопных эффектов (Гричук, 2000; Hill et al., 2014, 2020; Schauble, Young, 2020). Как и в случае изотопных эффектов углерода расчеты кислородных изотопных эффектов опираются на формализм β-фактора. Понятие β-фактора было введено Я.М. Варшавским и С.Э. Вайсбергом (Варшавский, Вайсберг, 1957) на основе предложенного ранее (Bigeleisen, Mayer, 1947) редуцированного по числам симметрии отношения статистических сумм изотопологов (the reduced isotopic partition function ratio). Однако, в практику геохимических исследований понятие β-фактора было внедрено Э.М. Галимовым (Галимов, 1973, 1974, 1982; Galimov, 2006). β-фактор вещества, содержащего атомы рассматриваемого химического элемента в эквивалентных положениях удобно выразить в логарифмической форме в терминах энергии Гиббса
(1)
$\ln \beta = {{\left( {G(P,T) - G{\text{*}}(P,T)} \right)} \mathord{\left/ {\vphantom {{\left( {G(P,T) - G{\text{*}}(P,T)} \right)} {zRT}}} \right. \kern-0em} {zRT}} - 1.5\left( {{{m{\text{*}}} \mathord{\left/ {\vphantom {{m{\text{*}}} m}} \right. \kern-0em} m}} \right),$(2а)
${{\alpha }_{{{\text{A/B}}}}} = {{{{\beta }_{{\text{A}}}}} \mathord{\left/ {\vphantom {{{{\beta }_{{\text{A}}}}} {{{\beta }_{{\text{B}}}}}}} \right. \kern-0em} {{{\beta }_{{\text{B}}}}}},$(2б)
${{\Delta }_{{{{\text{A}} \mathord{\left/ {\vphantom {{\text{A}} {\text{B}}}} \right. \kern-0em} {\text{B}}}}}} \equiv {{\alpha }_{{{{\text{A}} \mathord{\left/ {\vphantom {{\text{A}} {\text{B}}}} \right. \kern-0em} {\text{B}}}}}} - 1 \approx \ln {{\beta }_{{\text{A}}}} - \ln {{\beta }_{{\text{B}}}}.$В последнем равенстве (2б) учтено что |β – 1| $ \ll $ 1.
В том случае, когда атомы элемента, подвергающегося изотопному замещению, находятся в неэквивалентных положениях формулы (1) и (2а) требуют уточнения. Поскольку в природных процессах в изотопном обмене участвуют все изотопологи, то необходимо понимание того каким образом β-фактор соединения в целом связан с β-факторами атомов в определенных неэквивалентных положениях. Развитая Э.М. Галимовым (Галимов, 1973, 1974, 1981, 1982; Galimov, 2006) на примере изотопов углерода теория внутримолекулярных изотопных эффектов носит общий характер и имеет непосредственное применение к фракционированию изотопов кислорода, поскольку в геохимических исследованиях часто приходится иметь дело с веществами, которые содержат несколько атомов кислорода, причем не все они находятся в эквивалентных положениях11. В частности Э.М. Галимовым было показано что для замещения редким изотопом β-фактор соединения в целом связан с β-факторами однозамещенных изотопологов (βi) следующим соотношением (Галимов, 1973, 1981, 1982):
Соотношение (3а) было названо Э.М. Галимовым первым законом аддитивности (Галимов, 1981; 1982)22. Впоследствии было показано, что соотношение (3а) выполняется не только в случае замещения редкими изотопами, но и в том случае, когда βi не сильно отличаются от единицы (Поляков, 1987; Polyakov, Horita, 2021). Кроме того, логарифмическая форма оказывается незначительно точнее (Polyakov, Horita, 2021):
(3б)
$\ln \beta \approx \frac{1}{n}\sum\limits_{i = 1}^n {\ln {{\beta }_{{i\,}}};\,} \,\,\,\left| {\ln {{\beta }_{{i\,}}}} \right| \approx \,\left| {{{\beta }_{i}} - 1} \right| \ll 1.$Поскольку в представленной версии GE-OCHEQ_Isotope внутримолекулярные эффекты кислорода не рассчитываются, использование β-фактора соединения в целом в соответствии с формулой (3б) позволяет избежать излишнего “разбухания” базы данных за счет введения данных по изопологам разной кратности и локализации. Таким образом, при расчете коэффициентов равновесного фракционирования изотопов кислорода в комплексе GEOCHEQ_Isotope достаточно наряду с наиболее распространенным изотопологом, содержащим 16O, рассмотреть 18O изотополог, на один атом кислорода которого приходится изменение энергии Гиббса в соответствии с (1), аналогично тому, как это было сделано ранее для фракционирования изотопов углерода 13C/12C (Mironenko et al., 2018).
Кислородные β-факторы обнаруживают слабую зависимость от давления (Polyakov, Kharlаshina, 1994), поэтому в GEOCHEQ_Isotope учитывается только их температурная зависимость. Температурные зависимости β18O-факторов представлены в виде полинома по обратным температурам, как это сделано для углеродных β-факторов (Mironenko et al., 2018):
(4)
${{10}^{3}}\ln \beta = {{A}_{0}} + {{A}_{1}}{{x}^{1}} + {{A}_{2}}{{x}^{2}} + {{A}_{3}}{{x}^{3}} + {{A}_{4}}{{x}^{4}} + {{A}_{5}}{{x}^{5}},$Таблица 1.
Коэффициенты полинома для расчета температурной зависимости углеродных β-факторов: 103 lnβ = A0 + A1x1 + A2x2 + A3x3 + A4x4 + A5x5
| Наименование | Коэффициенты полинома (4) для расчета β18O-факторов | Литературные источники | |||||
|---|---|---|---|---|---|---|---|
| A5 × 105 | A4 × 103 | A3 × 102 | A2 | A1 | A0 | ||
| Вода (пар, сверхкритический флюид) | 9.4061 | –4.5191 | 9.0272 | –1.0263 | 14.2552 | 0 | Bron et al., 1973; Richet et al., 1977; Hill et al., 2014; 2020; Guo, Zhou, 2019; Schauble, Young, 2021 |
| Вода (жидкость) | 12.5205 | –5.9793 | 11.7997 | –1.2802 | 12.3064 | –0.2719 | Horita, Wesolowky, 1994 |
| CO2 (газ) | 12.5770 | –5.7152 | 10.9758 | –1.2875 | 16.6328 | 0 | Richet et al., 1977; Hill et al., 2014, 2020; Guo, Zhou, 2019; Schauble, Young, 2021 |
| HC${\text{O}}_{3}^{ - }$ | 7.1964 | –3.2198 | 6.1426 | –0.7597 | 13.3181 | 0 | Guo, Zhou, 2019; Beck et al., 2005 |
| C${\text{O}}_{3}^{{2 - }}$ | 2.3089 | –1.1561 | 2.6730 | –0.4529 | 11.5340 | 0 | Guo, Zhou, 2019; Beck et al., 2006 |
| H2CO3 | 11.0249 | –4.8602 | 8.9747 | –1.0256 | 15.2492 | 0 | Guo, Zhou, 2019; Beck et al., 2007 |
| CO (газ) | 32.1713 | –13.5446 | 23.0002 | –2.1794 | 18.5424 | 0 | Bron et al., 1973; Richet et al., 1977; Schauble, Young, 2021 |
| Ca2C${\text{O}}_{3}^{{2 - }}$ ⋅ n(H2O) | 2.8385 | –1.3560 | 2.9337 | –0.4644 | 11.5005 | 0 | Hill et al., 2020 |
| C${\text{a}}_{2}^{ + }$HCO3 ⋅ n(H2O) | 12.3083 | –5.1550 | 8.8026 | –0.9209 | 13.7407 | 0 | Hill et al., 2020 |
| Кальцит CaCO3 | 2.7471 | –1.3188 | 2.9157 | –0.4758 | 11.9672 | 0 | Hill et al., 2014, 2020; Guo, Zhou, 2019; Schauble, Young, 2021; Cayton, Kiffer, 1991; Chacko, Deines, 2008; Chacko et al., 1991; Поляков, 2008 |
| Арагонит CaCO3 | 3.1991 | –1.5106 | 3.2486 | –0.5083 | 12.2459 | 0 | Hill et al., 2014; 2020; Guo, Zhou, 2019; Schauble, Young, 2021; Chacko, Deines, 2008; |
| Ватерит CaCO3 | 3.1214 | –1.4835 | 3.2296 | –0.5156 | 12.5852 | 0 | Chacko, Deines, 2008; |
| Магнезит MgCO3 | 3.1639 | –1.5048 | 3.2836 | –0.5313 | 13.4051 | 0 | Chacko, Deines, 2008; Schauble, Young, 2021; Hill et al., 2020 |
| Доломит CaMg(CO3)2 | 2.8572 | –1.3689 | 3.0184 | –0.4929 | 12.5339 | 0 | Chacko, Deines, 2008; Schauble, Young, 2021; Hill et al., 2020 |
| Церуссит PbCO3 | 2.5060 | –1.2069 | 2.6803 | –0.4396 | 11.0728 | 0 | Chacko, Deines, 2008 |
| Отавит CdCO3 | 2.7787 | –1.3355 | 2.9593 | –0.4852 | 12.2691 | 0 | Chacko, Deines, 2008 |
| Родохрозит MnCO3 | 2.7141 | –1.3070 | 2.9055 | –0.4726 | 12.2243 | 0 | Chacko, Deines, 2008 |
| Сидерит FeCO3 | 2.9128 | –1.3926 | 3.0607 | –0.4956 | 12.2988 | 0 | Chacko, Deines, 2008 |
| Анкерит CaFe(CO3)2 | 2.6661 | –1.2873 | 2.8732 | –0.4752 | 12.0625 | 0 | Chacko, Deines, 2008 |
| Смитсонит ZnCO3 | 2.7726 | –1.3354 | 2.9707 | –0.4903 | 12.4862 | 0 | Chacko, Deines, 2008 |
| Церуссит PbCO3 | 2.5060 | –1.2069 | 2.6803 | –0.4396 | 11.0728 | 0 | Chacko, Deines, 2008 |
| Отавит CdCO3 | 2.7787 | –1.3355 | 2.9593 | –0.4852 | 12.2691 | 0 | Chacko, Deines, 2008 |
| Родохрозит MnCO3 | 2.7141 | –1.3070 | 2.9055 | –0.4726 | 12.2243 | 0 | Chacko, Deines, 2008 |
| Сидерит FeCO3 | 2.9128 | –1.3926 | 3.0607 | –0.4956 | 12.2988 | 0 | Chacko, Deines, 2008 |
| Анкерит CaFe(CO3)2 | 2.6661 | –1.2873 | 2.8732 | –0.4752 | 12.0625 | 0 | Chacko, Deines, 2008 |
| Смитсонит ZnCO3 | 2.7726 | –1.3354 | 2.9707 | –0.4903 | 12.4862 | 0 | Chacko, Deines, 2008 |
| Стронцианит SrCO3 | 2.9762 | –1.4135 | 3.0693 | –0.4874 | 11.9085 | 0 | Chacko, Deines, 2008 |
| Витерит BaCO3 | 2.7424 | –1.3109 | 2.8769 | –0.4638 | 11.4521 | 0 | Chacko, Deines, 2008 |
| Забуелит Li2CO3 | 2.7955 | –1.3436 | 2.9781 | –0.4908 | 12.6321 | 0 | Chacko, Deines, 2008 |
| Натрит Na2CO3 | 2.5863 | –1.2479 | 2.7803 | –0.4574 | 11.4606 | 0 | Chacko, Deines, 2008 |
| α-кварц (SiO2) | 1.7849 | –0.9257 | 2.3197 | –0.4453 | 12.7676 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991 |
| Альбит NaSi3O8 | 1.1491 | 0.6176 | 1.6476 | –0.3506 | 11.5927 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991 |
| Микроклин KAlSi3O8 | 1.1595 | –0.6234 | 1.6630 | –0.3529 | 11.5774 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991 |
| Анортит CaAl2Si2O8 | 0.7420 | –0.4139 | 1.1781 | –0.2782 | 10.5704 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991 |
| Диопсид CaMg(Si2O6) | 0.5267 | –0.3023 | 0.9010 | –0.2289 | 9.8071 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991 |
| Жадеит NaAl(Si2O6) | 0.6909 | –0.3869 | 1.1094 | –0.2669 | 10.7115 | 0 | Schauble, Young, 2021 |
| Форстерит Mg2SiO4 | 0.2832 | –0.1702 | 0.5602 | –0.1691 | 8.9993 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991; Поляков, Кусков, 1994 |
| Циркон ZrSiO4 | 0.4345 | –0.2561 | 0.7951 | –0.2128 | 9.5926 | 0 | Schauble, Young, 2021; Крылов, 2019 |
| Гроссуляр Ca3Al2(SiO4)3 | 0.2130 | –0.1366 | 0.4841 | –0.1581 | 9.0199 | 0 | Schauble, Young, 2021; Крылов, Глебовицкий, 2017; Поляков, Кусков, 1994 |
| Лизардит Mg3Si2O5(OH)4 | 14.4778 | –5.7486 | 8.9051 | –0.7744 | 10.9752 | 0 | Schauble, Young, 2021; |
| Каолинит Al2Si2O5(OH)4 | 14.4249 | –5.7581 | 9.0446 | –0.8215 | 12.3262 | 0 | Schauble, Young, 2021; |
| Флогопит KMg3(Si3Al)O10 (OH)2 | 5.8428 | –2.3759 | 3.9461 | –0.4375 | 10.3503 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991 |
| Тремолит Ca2Mg5(OH)2Si8O22 | 3.3038 | –1.4029 | 2.5845 | –0.3607 | 10.5184 | 0 | Schauble, Young, 2021; Chacko et al., 1996; Clayton, Kiffer, 1991 |
| Глаукофан Na2Mg3Al2(OH)2Si8O22 | 3.4104 | –1.4582 | 2.7186 | –0.3837 | 10.9892 | 0 | Schauble, Young, 2021 |
| Шпинель (нормальная) MgAl2O4 | 0.0495 | –0.0422 | 0.2128 | –0.1041 | 8.3127 | 0 | Schauble, Young, 2021 |
| Диаспор AlО(ОH) | 9.2163 | –3.7200 | 5.9344 | –0.5584 | 10.6488 | 0 | Schauble, Young, 2021 |
| Xenotime YPO4 | 0.6862 | –0.3844 | 1.1007 | –0.2629 | 10.3347 | 0 | Schauble, Young, 2021 |
| Xenotime LuPO4 | 0.7250 | –0.4042 | 1.1484 | –0.2712 | 10.5328 | 0 | Schauble, Young, 2021 |
| Монацит LaPO4 | 0.6350 | 0.3576 | 1.0324 | –0.2491 | 9.8310 | 0 | Schauble, Young, 2021 |
| Фторапатит Ca5(PO4)3F | 0.6895 | –0.3850 | 1.0965 | –0.2595 | 9.9952 | 0 | Schauble, Young, 2021; Chacko et al., 1996 |
| Ангидрит CaSO4 | 1.1221 | –0.5974 | 1.5739 | –0.3324 | 11.0553 | 0 | Schauble, Young, 2021 |
| Барит BaSO4 | 0.9841 | –0.5284 | 1.4137 | –0.3065 | 10.5378 | 0 | Schauble, Young, 2021 |
| Нахколит NaHCO3 | 8.3082 | –3.5920 | 6.5731 | –0.7858 | 13.7585 | 0 | Schauble, Young, 2021 |
| Нитратин NaNO3 | 2.4492 | –1.1958 | 2.7249 | –0.4648 | 11.7580 | 0 | Schauble, Young, 2021 |
| Гематит Fe2O3 | 0 | 0 | 0.0524 | –0.0520 | 5.9923 | 0 | Blanchard et al., 2015; Поляков и др., 2001 |
| Гетит FeOOH | 0 | 0 | 0.5279 | –0.1875 | 7.1664 | 0 | Blanchard et al., 2015 |
| Мусковит KAl2(Si3Al)O10(OH)2 | 2.7471 | –1.3188 | 3.4257 | –0.3958 | 10.9522 | 0 | Chacko et al., 1996 |
| Магнетит Fe3O4 | 69.7674 | –21.3501 | 20.6729 | –0.6777 | 7.0760 | 0 | Cole et al., 2005; Blattner et al., 1999; Zhang et al., 1995; Mandernack et al., 1999 |
| Рутил TiO2 | 0 | 0 | 0.1160 | –0.0816 | 6.9304 | 0 | Clayton, Kieffer, 1991; Крылов, Кузнецов, 2019 |
| Анатаз TiO2 | 0 | 0 | 0.1530 | –0.0991 | 7.3428 | 0 | Крылов, Кузнецов, 2019 |
| Брукит TiO2 | 0 | 0 | 0.1390 | –0.0916 | 7.9088 | 0 | Крылов, Кузнецов, 2019 |
| Касситерит SnO2 | 0 | 0 | 0.0803 | –0.0737 | 7.1760 | 0 | Polyakov et al., 2005 |
| Корунд Al2O3 | 0 | 0 | 0.0360 | –0.0891 | 9.0336 | 0 | Крылов и др., 2017; Krylov, Evarestov, 2018 |
| Кианит Al2SiO5 | 0 | 0 | 0.2820 | –0.1933 | 10.6647 | 0 | Крылов и др., 2020 |
| Силлиманит Al2SiO5 | 0 | 0 | 0.1406 | –0.1749 | 10.5148 | 0 | Крылов и др., 2020 |
| Андалузит Al2SiO5 | 0 | 0 | 0.5500 | –0.0757 | 10.1402 | 0 | Крылов и др., 2020 |
| Андрадит Ca3Fe2(SiO4)3 | 0 | 0 | 0.4020 | –0.1509 | 8.7247 | 0 | Крылов, Глебовицкий, 2017 |
| Пироп Mg3Al2(SiO4)3 | 0 | 0 | 0.56700 | –0.92040 | 9.68511 | 0 | Крылов, Глебовицкий, 2017 |
| Спессартин Mn3Al2(SiO4)3 | 0 | 0 | 0.49900 | –0.17598 | 9.33600 | 0 | Крылов, Глебовицкий, 2017 |
| Альмандин Fe3Al2(SiO4)3 | 0 | 0 | 0.53900 | –0.18465 | 9.45295 | 0 | Крылов, Глебовицкий, 2017 |
| Уваровит Ca3Cr2(SiO4)3 | 0 | 0 | 0.38500 | –0.14749 | 8.71526 | 0 | Крылов, Глебовицкий, 2017 |
Еще одним добавлением к расчету химических и изотопных равновесий в системах, включающих изотоп 18O, является изменение формулы для моляльности растворенных в воде компонентов в связи с присутствием системе изотополога H218O:
где mi – моляльность i-го компонента, ni – количество молей компонента 55.51 – количество молей в 1 кг воды.β18O-ФАКТОРЫ В ТЕРМОДИНАМИЧЕСКОЙ БАЗЕ ДАННЫХ GEOCHEQ_ISOTOPE
Также, как и в случае углеродных изотопных факторов (Mironenko et al., 2018), точность и обоснованность расчетов по кислородным изотопным равновесиям определяется точностью данных по β18O-факторам, которые используются в программном комплексе GEOCHEQ_Isotope. Для оценки кислородных равновесных изотопных факторов фракционирования применяют как экспериментальные, так и теоретические подходы. Для экспериментального определения кислородных равновесных изотопных факторов фракционирования наряду с методом частичного изотопного обмена Нортропа-Клейтона (Northrop, Clayton, 1966) используют также трехизотопный метод (Matsuhisa et al., 1978). Для калибровки кислородных изотопных геотермометров используют и метод эмпирической калибровки (Clayton et al., 1968; Устинов и др., 1978; Macey, Harris, 2006). Обзор этих методов с оценкой их преимуществ и недостатков дан в (Chacko et al., 2001). Теоретические расчеты проводят как с помощью модельных колебательных спектров (Urey, 1947; Bigeleisen, Mayer, 1947; Kieffer, 1982) и межатомных потенциалов (Patel et al., 1991), так и из “первых принципов” на основе метода функционала плотности (Schauble, 2004; Blanchard et al., 2009; Hill et al., 2014; Крылов и др., 2017; Schauble, Young, 2021). В последние годы метод расчета из “первых принципов” стал наиболее употребительным. Кислородные β-факторы многих минералов рассчитаны с помощью полуэмпирического метода инкрементов (Schütze H., 1980; Zheng, 1991; 1999), который представляет собой распространение метода изотопических чисел связей Э.М. Галимова (Галимов, 1973, 1974) на кристаллические тела. Однако к этим результатам надо относится с осторожностью, поскольку они часто противоречат экспериментальным данным и теоретическим расчетам (Horita, Clayton, 2007).
Кислородные факторы фракционирования в системе H2O–CO2 (газ)–растворенный неорганический углерод
Подавляющее большинство экспериментальных исследований по определению равновесных факторов фракционирования изотопов кислорода выполнено при участии воды и углекислого газа (Chacko et al., 2001). Поэтому, корректный выбор β18O-факторов воды и углекислого газа имеет принципиальное значение для калибровки всего массива данных по кислородным изотопным равновесиям.
β18O-факторы H2O. Для расчета кислородных β-факторов водяного пара использовали различные теоретические подходы. Расчеты на основе спектроскопических данных и молекулярных констант были проведены с учетом ангармонизма и взаимодействия колебаний и вращений (Bron et al., 1973; Richet et al., 1977). В последние годы расчеты были сделаны “из первых принципов” на основе функционала плотности (Hill et al., 2014 2020; Guo, Zhou, 2019; Schauble, Young, 2021). Эти расчеты, выполненные различными методами, находятся в разумном согласии с друг другом. Коэффициенты аппроксимирующего полинома (4) использованные в GEOCHEQ_Isotope даны в табл. 1. Для жидкой воды β18O-факторы были получены (табл. 1) путем сложения кислородных значений ln β для водяного пара и экспериментальных величин lnα для равновесного фракционирования изотопов кислорода между жидкой H2O и насыщенным паром (Horita, Wesolowski, 1994).
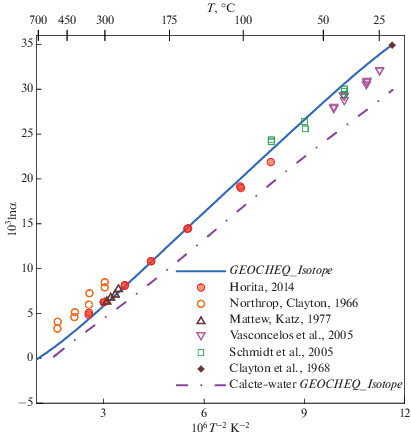
β18O-факторы CO2 и растворенного неорганического углерода. Для углекислого газа β18O-факторы были рассчитаны таким же образом, как и для воды: из спектроскопических данных и молекулярных констант (Richet et al., 1977), из “первых принципов” (Hill et al., 2014, 2020; Guo, Zhou, 2019; Schauble, Young, 2021). По этим данным были рассчитаны коэффициенты полинома (4) для O2(газ) (табл. 1) Имеются также экспериментальные данные по равновесному фракционированию изотопов кислорода CO2(газ) – H2O(жидкость) при 25°C, поскольку это значение используется при определении изотопного состава воды. Многочисленные эксперименты (ссылки приведены в Chacko et al., 2001) позволили IAEA Consultants Group рекомендовать для равновесного коэффициента фракционирования CO2(газ)–H2O(жидкость) значение 1.0412 при 25°C (Hoefs, 2018). Существуют также оценки для температурных диапазонов 5 – 100°C (Brenninkmeijer et al., ) и 130–350°C (Truesdell, 1974). Сравнение рассчитанных по данным G-EOCHEQ_Isotope ( табл. 1) коэффициентов равновесного изотопного фракционирования CO2(газ)–H2O(жидкость) и соответствующих экспериментальных значений проведено на рис. 1. Наблюдается хорошее согласие между экспериментальными и расчетными результатами.
Рис. 1.
Сравнение данных GEOCHEQ_Isotope по равновесным коэффициентам фракционирования изотопов кислорода в системе H2O–CO2 – растворенный неорганический углерод с экспериментальными определениями.
Погрешность определения экспериментальных равновесных коэффициентов фракционирования изотопов кислорода не превышает размеров используемых значков.
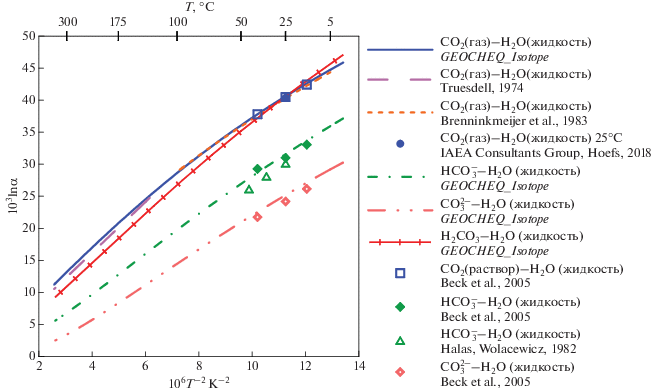
Растворенный неорганический углерод представлен в GEOCHEQ_Isotope растворенными в воде карбонатными частицами: СО2, H2CO3, ${\text{HCO}}_{3}^{ - }$, ${\text{CO}}_{3}^{{2 - }}$. β18O-факторы этих частиц были рассчитаны на основе функционала плотности из “первых принципов” (Hill et al., 2014, 2020; Guo, Zhou, 2019; Schauble, Young, 2021). В базу данных G-EOCHEQ_Isotope (табл. 1) внесены результаты расчетов (Guo, Zhou, 2019), которые наилучшим образом согласуются с экспериментальными данными (Beck et al., 2005). Экспериментальные данные для растворенных карбонатных частиц (Beck et al., 2005) хорошо согласуются с равновесными коэффициентами фракционирования между этими растворенными частицами и водой, рассчитанными по данным базы GEOCHEQ_Isotope (рис. 1). Следует подчеркнуть, что β18O-факторы для растворенной нейтральной частицы СО2 приняты равными таковым в газовой фазе. Как расчетные, так и экспериментальные значения равновесного коэффициента фракционирования изотопов кислорода между углекислотой и водой для растворенной в воде и газофазной СО2 различаются на ~0.1‰, т.е. на величину меньшую погрешности как измерений, так и расчетов (рис. 1).
Кислородные β-факторы карбонатных минералов
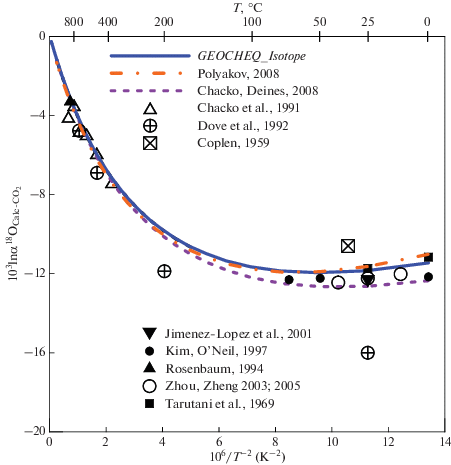
Фракционирование изотопов кислорода в системе кальцит–CO2. С точки зрения изотопной геохимии кальцит является, пожалуй, наиболее важным среди карбонатных минералов. Дело в том, что коэффициенты фракционирования изотопов кислорода, найденные в ходе экспериментов в “сухой” системе (без водного флюида) привязывают к кальциту (Chacko et al., 2001; Clayton, Kiffer, 1991). В этой связи представляется весьма важным оценка равновесного фракционирования в системе кальцит–CO2, поскольку, как было показано в предыдущем разделе, для углекислого газа существует надежная оценка величины β18O‑фактора. Для кальцита, наблюдается хорошее согласие между результатами расчетов из “первых принципов” (Hill et al., 2014, 2020; Guo, Zhou, 2019; Schauble, Young, 2021) и расчетов, основанных на модельных спектрах колебаний решетки типа Киффер (Clayton, Kiffer, 1991; Chacko, Deines, 2008; Поляков, 2008). В GEOCHEQ_Isotope в качестве β18O-фактора приняты результаты расчетов из “первых принципов”. Эти результаты совпадают при температурах выше 400 K с оценкой Р.Клейтона и С. Киффер (Clayton, Kiffer, 1991). Разница в величинах β18O-фактора кальцита, принятых в GEOCHEQ_Isotope, и рассчитанных на основе модельного спектра Киффер в квазигармоническом приближении (Поляков, 2008) также значительно меньше разброса экспериментальных данных (рис. 2). Несколько больше разница между CaCO3/CO2 фракционной кривой, полученной Т. Чако и П. Дейнесом (Chacko, Deines, 2008), и фракционной кривой, рассчитанной по базе данных GEOCHEQ_Isotope. Это связано с занижением значения частоты эйнштейновского осциллятора ν3 = 1460 см–1 (Mironenko et al., 2018), что приводит к занижению β-фактора кальцита. Для β18O-фактора кальцита этот эффект меньше, чем для β13C-фактора. В целом, наблюдается согласие расчетов равновесного фракционирования кальцита в системе кальцит–CO2, с использованием β18O-фактора кальцита из базы данных GEOCHEQ_Isotope с экспериментальными данными по измерению равновесного коэффициента фракционирования изотопов кислорода в этой системе (рис. 2).
Рис. 2.
Сравнение различных оценок равновесного коэффициента фракционирования изотопов кислорода в системе кальцит–CO2.
Кислородные изотопные эффекты между карбонатными минералами. Метод расчета коэффициентов полинома (4) для карбонатных минералов аналогичен методу, который был использован для их β13C-факторов (Mironenko et al., 2018). Поскольку фракционирование между карбонатными минералами хорошо описывается моделью Т. Чако и П. Дейнеса (Chacko, Deines, 2008), но наблюдается занижение β18O-факторов кальцита по сравнению со значениями, принятыми в G-EOCHEQ_Isotope (рис. 2), то к значениям 103lnβ для карбонатных минералов была добавлена разница между значениями 103ln β для кальцита, принятыми в базе данных GEOCHEQ_Isotope, и значениями для кальцита по модели Т. Чако и П. Дейнеса (Chacko, Deines, 2008):
(6)
$\begin{gathered} \ln {{\beta }_{{{\text{carb}}}}} = \ln {{\beta }_{{{\text{calc}}}}} + \left( {\ln \beta _{{{\text{carb}}}}^{{{\text{СD}}}} - \ln \beta _{{{\text{calc}}}}^{{{\text{СD}}}}} \right) = \\ = \ln \beta _{{{\text{carb}}}}^{{{\text{СD}}}} + (ln{{\beta }_{{{\text{calc}}}}} - \ln \beta _{{{\text{calc}}}}^{{{\text{СD}}}}), \\ \end{gathered} $где βcarb и βcalc – β18O-факторы карбонатного минерала и кальцита, использованные в базе данных GEOCHEQ_Isotope, а $\ln \beta _{{{\text{carb}}}}^{{{\text{CD}}}}$ и $\ln \beta _{{{\text{calc}}}}^{{{\text{CD}}}}$ – те же β‑факторы, рассчитанные по модели Т. Чако и П. Дейнеса (Chacko, Deines, 2008). Коэффициенты полинома (4) для β18O-факторов карбонатов, полученные в соответствии с (6), представлены в табл. 1.
На рис. 3 проведено сравнение фракционирования изотопов кислорода в системе доломит – вода по данным GEOCHEQ_Isotope с экспериментальными калибровками других авторов. Наблюдается хорошее согласие между экспериментальными значениями кислородного коэффициента равновесного фракционирования между доломитом и водой и расчетными величинами, найденными по базе данных GEOCHEQ_Isotope (рис. 3).
Кислородные β-факторы в силикатах и оксидах в программном комплексе GEOCHEQ_Isotope
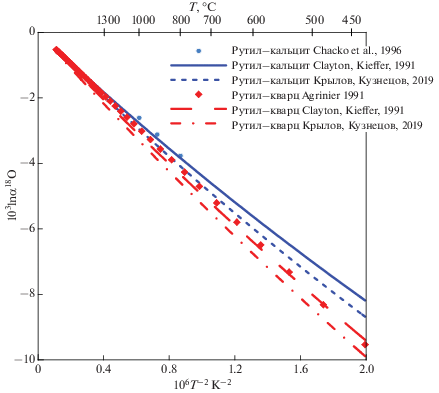
Многие применения геохимии стабильных изотопов связаны с использованием фракционирования изотопов кислорода в силикатах и оксидах. Коэффициенты полинома (4) для расчета β18O-факторов этих минералов, включенных в GEOCHEQ_Isotope, представлены в табл. 1. Большинство из этих данных получено на основе расчетов из “первых принципов”. С одной стороны, результаты этих расчетов хорошо согласуются с экспериментальными и эмпирическими данными, а с другой стороны, позволяют экстраполировать результаты на условия, недоступные в эксперименте. В ряде случаев требуется согласование результатов, полученных разными методами и авторами. Пример такого согласования дают калибровки β18O-факторов полиморфов TiO2: рутила, анатаза и брукита. Расчеты β18O-факторов для этих полиморфов, выполненные из “первых принципов” с применением метода суперячеек (Крылов, Кузнецов, 2019), дают прекрасное согласие с эмпирической калибровкой этих геотермометров (Zack, Kooijman, 2017). Однако, β18O-факторы рутила хуже согласуются с экспериментальными и эмпирическими оценками коэффициентов фракционирования изотопов кислорода для пар рутил–кварц и рутил–кальцит (рис. 4), чем калибровка рутила, рассчитанная на основании модельного спектра Киффер (Clayton, Kieffer, 1991). Для согласования различных калибровок мы применили прием аналогичный тому, который был использован для карбонатов. Мы оценили разницу между β18O-факторами рутила, полученных этими методами, и скорректировали β18O-факторы полиморфов TiO2 на эту величину, сохранив тем самым калибровку геотермометров, основанную на этих полиморфах, и обеспечив удовлетворительное согласие с экспериментальными и эмпирическими оценками изотопных коэффициентов фракционирования рутил–кварц и рутил–кальцит.
При отборе калибровок β18O-факторов для включения их в базу данных GEOCHEQ_Isotope большое внимание уделяли согласованию. Именно согласие в оценках значений β18O-факторов (или возможность их согласования), полученных разными методами является критерием их надежности.
Для определения β18O-факторов оксидов наряду со стандартными методами, упомянутыми выше, используются и новые подходы. В этих случаях особую важность приобретает верификация результатов, полученных новыми методами, за счет использования методов, уже зарекомендовавших себя надежными. Для оксидов, катионы которых имеют “мессбауэровский” изотоп, оказывается возможным оценка β18O-факторов по экспериментальным данным по гамма-резонансному рассеянию и теплоемкости. Таким образом, были измерены β18O-факторы гематита (Поляков и др., 2001) и касситерита (Polyakov et al., 2005). Для касситерита, такая проверка была сделана экспериментально, методом Нортропа–Клейтона (Hu et al., 2005), и методом эмпирической калибровки с использованием других изотопных геотермометров и оценки температуры по газово-жидкостным включениям (Macey, Harris, 2006). Проверка, для гематита может быть сделана из сравнения результатов расчета β18O-факторов гематита, рассчитанного из “первых принципов” (Blanchard et al., 2015) и найденного из экспериментальных данных по температурному сдвигу в мессбауэровских спектрах и теплоемкости (Поляков и др., 2001). Эти оценки β18O-фактора гематита практически совпадают: даже при комнатной температуре разница в значениях 103lnβ составляет ~0.3 (0.4% от величины 103lnβ), а с повышением температуры становится еще меньше.
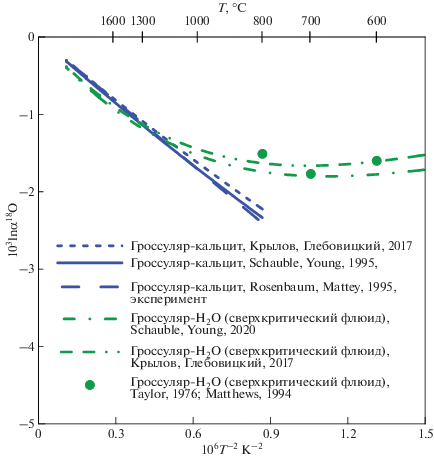
Подобное согласование может быть сделано и в случае гроссуляра, для которого существуют два расчета (Крылов, Глебовицкий, 2017; Schauble, Young, 2020), основанных на функционале плотности состояний, но использующие разные методики. В этом случае согласие несколько хуже (~3.3% от величины 103lnβ), но остается приемлемым (рис. 5). Оба расчета хорошо согласуются с экспериментальным коэффициентом фракционирования гроссуляр–кальцит (Rosenbaum, Mattey, 1995, 1996) и гроссуляр – водный сверхкритический флюид. В GEOCHEQ_Isotope принято усредненное значение β18O-фактора для гроссуляра по двум рассмотренным калибровкам (табл. 1).
Рис. 5.
Сравнение β18O-фактора для гроссуляра, рассчитанного различными методами, с экспериментальными данными.
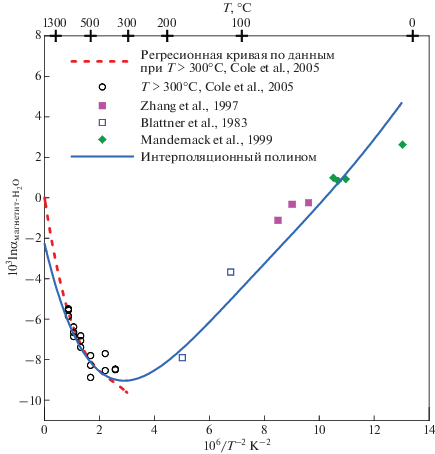
Для использования β-факторов в базах данных необходимо их знание в широком интервале температур. Это чаще всего достигается в расчетных теоретических работах. Но иногда подобные расчетные данные отсутствуют. В этом случае возможно согласование результатов, полученных различными авторами. Для β18O-факторов подобная ситуация имеет место в случае магнетита. Имеются надежные экспериментальные определения равновесных коэффициентов фракционирования изотопов кислорода в системе магнетит-H2O при температурах выше 300°C (Cole et al., 2004) и разрозненные данные по фракционированию изотопов в системе магнетит–вода при низких температурах (Blattner et al., 1999; Zhang et al., 1995; Mandernack et al., 1999). По этим экспериментальным данным мы построили интерполяционный полином вида (4) для фракционной кривой магнетит–H2O (рис. 6). Для получения полинома для β18O-фактора магнетита коэффициенты полинома для H2O (жидкость или свехкритический флюид (T > 647 K)) из табл. 1 сложили с коэффициентами полинома для фракционной кривой. По полученным полиномам построили температурную зависимость β18O-фактора магнетита, которую для получения сглаженной кривой снова аппроксимировали полиномом вида (4). Результат представлен в табл. 1.
Мы рассмотрели основные принципы, методы и приемы согласования и построения базы кислородных изотопных данных в GEOCHEQ_Isotope. Более подробное рассмотрение конкретных случаев выходит за рамки настоящей статьи и относится скорее к инструкциям по применению этого программного комплекса.
СОВМЕСТНЫЙ РАСЧЕТ РАВНОВЕСНЫХ КИСЛОРОДНЫХ И УГЛЕРОДНЫХ ИЗОТОПНЫХ ЭФФЕКТОВ И ХИМИЧЕСКОГО СОСТАВА В ГИДРОТЕРМАЛЬНОЙ СИСТЕМЕ
В настоящее время GEOCHEQ_Isotope позволяет моделировать равновесные химические процессы с учетом кислородных и углеродных изотопных эффектов. В качестве примеров подобного моделирования мы выбрали систему, аналогичную рассмотренной ранее (Mironenko et al., 2018). В целом методика расчета химических равновесий с учетом как углеродных, так и кислородных изотопных равновесий совпадает с той, которая применялась к моделям, включающим оценку только углеродных равновесных изотопных эффектов (Mironenko et al., 2018; Мироненко и др., 2021; Сидкина и др., 2019). Естественным изменением явилось добавление изотопа 18O в качестве независимого компонента и 18O-изотопологов в список веществ, для которых проводится минимизация энергии Гиббса. Кроме того, моляльность компонентов водного раствора рассчитывали по формуле (5).
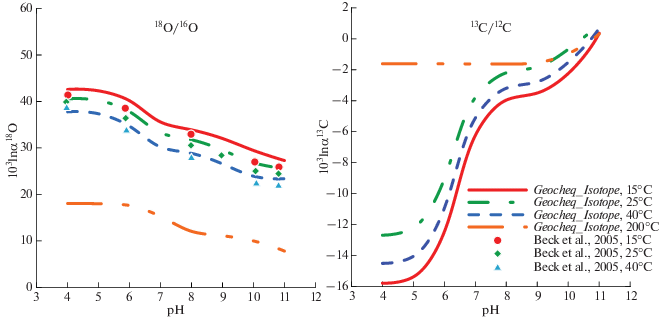
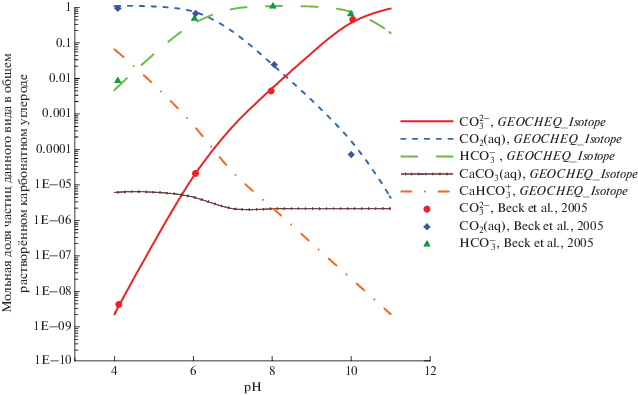
В качестве примера использования G-EOCHEQ_Isotope мы рассчитали химические и изотопные равновесия в углекислой гидротермальной системе валового состава “1 моль СаО + + 1 кг Н2О + 1.4 моля СО2” для температур 15, 25, 40°С и давления 40 бар в зависимости от водородного показателя pH кислотности. Соотношения 18О/16О и 13С/12С в системе отвечали природным распространенностям этих изотопов. Рассматривались 16O-, 18O-, 12C- и 13C-изотопологи кальцита, воды, СО2(aq), ${\text{HCO}}_{3}^{ - }$, ${\text{CO}}_{3}^{{2 - }}$, CaCO3(aq), Ca${\text{HCO}}_{3}^{ - }$, CO2(газ), СН4(газ), H2O(газ). Для подобной системы имеется экспериментально-теоретическое исследование зависимости состава растворенного неорганического (карбонатного) углерода и равновесного фракционирования изотопов кислорода между растворенными карбонатными частицами и водой от pH (Beck et al., 2005). Между этим экспериментальным исследованием и карбонатной системой, которая рассмотрена в настоящей статье, есть очень незначительные отличия. При моделировании с использованием GEOCHEQ_Isotope, мы рассматривали возможность появления растворенных частиц CaCO3(aq), Ca${\text{HCO}}_{3}^{ - }$, в то время, как в работе (Beck et al., 2005) эти частицы не принимали во внимание. С другой стороны, при теоретическом моделировании в работе (Beck et al., 2005) учитывали присутствие в растворе частиц H2CO3. Следует подчеркнуть, что концентрация H2CO3 по результатам моделирования составляла ~0.2–0.3% в общем количестве растворенного карбонатного углерода при pH < 5 и резко уменьшалась при понижении кислотности. Результаты моделирования состава карбонатных частиц средствами GEOCHEQ_Isotope представлены на рис. 7. Наблюдается хорошее согласие между результатами нашего моделирования с предшествующими результатами (Beck et al., 2005).
Рис. 7.
Зависимость состава растворенного карбонатного углерода от рH по результатам моделирования с использованием GEOCHEQ_Isotope. При разных значениях рH наблюдается доминирование частиц разного вида. Кальцийсодержащие частицы дают незначительный вклад в общий карбонатный углерод. Только при низких рH доля CaHC${\text{O}}_{3}^{ + }$ достигает 7%.
Доминирование той или иной формы растворенного карбонатного углерода в зависимости от pH с учетом разницы в значениях β18O- и β13C-факторов растворенных карбонатных частиц (табл. 1, рис. 1) определяет зависимость равновесных коэффициента фракционирования изотопов кислорода и углерода между общим растворенным неорганическим углеродом и сосуществующими фазами. Примеры таких зависимостей по результатам расчетов с использованием GEOCHEQ_Isotope показаны на рис. 8. Для изотопов кислорода имеются надежные экспериментальные данные (Beck et al., 2005) по равновесному фракционированию растворенного карбонатного углерода и воды в интервале температур 15–40°С. Результаты нашего моделирования обнаруживают хорошее согласие с этими экспериментальными данными (рис. 8). Уменьшение обогащения растворенных карбонатов тяжелым изотопом кислорода относительно воды с ростом pH (рис. 8) объясняется последовательной сменой доминирующей карбонатной формы в ряду CO2(aq) → ${\text{HCO}}_{3}^{ - }$ → ${\text{CO}}_{3}^{{2 - }}$ наряду с тем, что равновесные факторы фракционирования этих карбонатных форм с водой (а значит и их β18O-факторы) уменьшаются в той же последовательности (рис. 1). Для изотопов углерода имеет место обратная ситуация: β13С-факторы указанных карбонатных форм имеют обратный порядок (Mironenko et al., 2021) и, поэтому, обеднение растворенного карбонатного углерода тяжелым изотопом 13С уменьшается с ростом pH. Причем углеродный изотопный сдвиг между растворенныч карбонатным углеродом и кальцитом при высоких pH претерпевает инверсию, поскольку значения β13С-фактора для доминирующей карбонатной формы ${\text{CO}}_{3}^{{2 - }}$ больше, чем для кальцита (рис. 8).
ВЫВОДЫ
Представлено расширение базы данных и программного комплекса GEOCHEQ_Isotope, предназначенного для одновременного моделирования химических и изотопных равновесий методом минимизации свободной энергии Гиббса, на расчет изотопных равновесий кислорода. Также, как и в случае изотопов углерода, представленная версия основана на формализме β-фактора в приближении. идеальной смеси изотопов.
Представленная версия GEOCHEQ_Isotope использует базу данных GEOCHEQ (Мироненко и др., 2000) для описания неизотопных термодинамических свойств веществ. Энергия Гиббса для изотопологов рассчитывается по известным значениям β‑факторов в соответствии с уравнением (1). При этом учитывается аддитивная связь между lnβ соединения в целом и lnβi однозамещенных изотопологов.
Проведена адаптация расчетных алгоритмов на случай использования изотопов кислорода и повышения точности расчетов. В частности, в уравнении для расчета моляльности учтено присутствие изотополога H218O.
Проведен критический анализ, оптимизация и согласование имеющейся информации по равновесным факторам фракционирования изотопов кислорода. Температурные зависимости углеродных β-факторов унифицированы в виде полиномов (4) по степеням обратной температуры (табл. 1).
Применение комплекса GEOCHEQ_Isotope к совместному расчету химических кислородных и углеродных изотопных равновесий протестировано на моделировании зависимости состава растворенных карбонатных частиц и коэффициента равновесного фракционирования 18O/16O между растворенным карбонатным углеродом и водой от pH раствора. Получено хорошее согласие с экспериментальными результатами (Beck et al., 2005). С увеличением pH обогащение растворенного карбонатного углерода тяжелым изотопом 18O уменьшается за счет последовательной смены доминирующей карбонатной формы в ряду CO2(aq) → ${\text{HCO}}_{3}^{ - }$ → → ${\text{CO}}_{3}^{{2 - }}$, характеризующейся меньшим значением β18O-фактора (${{\beta }^{{{\text{18}}}}}{{{\text{O}}}_{{{\text{C}}{{{\text{O}}}_{2}}}}} > {{\beta }^{{18}}}{{{\text{O}}}_{{{\text{HCO}}_{3}^{ - }}}} > ~~{{\beta }^{{18}}}{{{\text{O}}}_{{{\text{CO}}_{{\text{3}}}^{{{\text{2 - }}}}}}}$). Для углерода рост pH приводит к увеличению коэффициента фракционирования растворенный карбонатный углерод–кальцит, поскольку ${{\beta }^{{{\text{13}}}}}{{{\text{C}}}_{{{\text{CO}}}}}_{{_{{\text{2}}}}} < {{\beta }^{{13}}}{{{\text{C}}}_{{{\text{HCO}}_{3}^{ - }}}} < ~~{{\beta }^{{13}}}{{{\text{C}}}_{{{\text{CO}}_{{\text{3}}}^{{{\text{2 - }}}}}}}$. При этом при высоких значениях рН (~11) происходит инверсия равновесного изотопного сдвига и растворенный неорганический углерод обогащен изотопом 13С относительно кальцита.
Исследование выполнено в рамках госзадания ГЕОХИ РАН (№ 0137-2019-0015) и частично поддержано РФФИ грант № 19-05-00865a.
Список литературы
Банникова Л.Н., Гричук Д.В., Рыженко Б.Н. (1987) Расчеты химических и изотопных равновесий в системе C–H–O и их использование при изучении окислительно-восстановительных реакций в гидротермальных условиях. Геохимия (3), 416-428.
Варшавский Я.М., Вайсберг С.Э. (1957) Термодинамические и кинетические особенности реакций изотопного обмена. Успехи химии 26,1434-1468.
Галимов Э.М. (1973) Изотопы углерода в нефтегазовой геологии. М.: Недра. 372 с.
Галимов Э.М. (1974) Приближенный способ нахождения термодинамических изотопных факторов соединений углерода. Журнал физической химии. 48, 290-296.
Галимов Э.М. (1981) Природа биологического фракционирования изотопов. М.: Наука. 248 с.
Галимов Э.М. (1982) Принцип аддитивности в изотопной термодинамике. Геохимия (6) 767-779.
Галимов Э.М. (2006) Органическая геохимия изотопов. Becтник PAH 76, 978-988.
Гричук Д.В. (1987) Оценка свободных энергий Гиббса изотопных форм соединений. Геохимия (2), 178-191.
Гричук Д.В. (1988) Изотопно-химическая термодинамическая модель гидротермальной системы. ДАН СССР 298 (5), 1222-1225.
Гричук Д.В. (2000) Термодинамические модели субмаринных гидротермальных систем. М.: Научный мир. 304 с.
Гричук Д.В., Леин А.Ю. (1991) Эволюция океанской гидротермальной системы и изотопный состав серы сульфидов. ДАН СССР, 318(2), 422-425.
Крылов Д.П., (2019) Кислородные и кремниевые β-факторы циркона, определенные из первых принципов. Петрология. 27, 420-430.
Крылов Д.П., Глебовицкий В.А. (2017) Факторы фракционирования 18O/16O гранатов на основе расчетов изотопных сдвигов частот колебаний. ДАН 475(3), 306-309.
Крылов Д.П., Глебовицкий В.А., Акимова Е.Ю. (2017) Факторы фракционирования 18O/16O корунда на основе расчетов изотопных сдвигов частот колебаний. Геохимия (6), 571-576.
Крылов Д.П., Кузнецов А.Б. (2019) Изотопное фракционирование в полиморфах TiO2 (рутил, анатаз, брукит), определенное из “первых принципов”. ДАН 489(1), 62-64.
Крылов Д.П., Кузнецов А.Б., Гаврилова А.А. (2020) Изотопное фракционирование и влияния давления на 18O/16O в полиморфных модификациях кианит-силлиманит-андалузит (Al2SiO5): моделирование из “первых принципов”. ДАН. Науки о Земле 491(2), 56-59.
Мироненко М.В., Акинфиев Н.Н., Мелихова Т.Ю. (2000) GEOCHEQ – комплекс для термодинамического моделирования геохимических процессов. Вестник ОГГГГН РАН. 5(15). (URL: http: //www.scgis.ru/russian/ cp1251/h_dggms/5_000/term10).
Мироненко М.В., Сидкина Е.С., Поляков В.Б., (2021) Равновесно-кинетический расчет серпентинизации оливина. Сопоставление с модельным экспериментом. Геохимия 66(1), 37-44.
Mironenko M.V., Sidkina E.S. and Polyakov V.B. (2021) Equilibrium-Kinetic Calculation of Olivine Serpentinization. A Comparison with the Model Experiment. Geochem. Int. 59(1), 32-39.
Поляков В.Б. (1987) Изотопный фактор соединений, содержащих несколько атомов одного элемента. Геохимия. (7), 104-044.
Поляков В.Б. (1993) Об идеальности смесей изотопов в твердых телах. Журнал физической химии 67,47-73.
Поляков В.Б. (2008) Равновесные факторы фракционирование изотопов кальцита. Экспериментальные исследования эндогенных процессов.: Памяти академика В.А. Жарикова. (Под ред. Рябчикова И.Д., Шаповалова Ю.Б., Осадчего Е.Г.) Черноголовка, Редакционно–издательский отдел ИПХФ РАН, 20-16.
Поляков В.Б., Кусков О.Л. (1994). Самосогласованная модель для расчета термических и калорических свойств минералов. Геохимия (7), 1096-1122.
Поляков В.Б., Минеев С.Д., Гуревич В.М., Храмов Д.А., Гавричев К.С., Горбунов В.Е., Голушина Л.Н. (2001). Использование мессбауэровской спектроскопии и калориметрии для определения равновесных изотопных констант. Гематит. Журнал физической химии 75, 1017-1021.
Устинов В.И., Гриненко В.А., Знаменский В.С. (1988) Генетическое значение интраструктурного распределения изотопов кислорода в алунитах Курильских островов. ДАН СССР, 302(2), 410-412.
Agrinier P. (1991) The natural calibration of 18O/16O geothermometers: Application to the quartz-rutile pair. Chem. Geol. 91, 49-64.
Beck W.C., Grossman E.L., Morse J.W. (2005) Experimental studies of oxygen isotope fractionation in the carbonic acid system at 15, 25 and 40°C. Geochim. Cosmochim. Acta 69, 3493-3503.
Bigeleisen J, Mayer MG (1947) Calculation of equilibrium constants for isotopic exchange reactions. J. Phys. Chem. 13, 261-267.
Blanchard M., Dauphas N., Hu M., Roskosz M., Alp E., Golden D., Sio C., Tissot F., Zhao J., Gao L. (2015) Reduced partition function ratios of iron and oxygen in goethite. Geochim Cosmochim Acta 151, 19-33.
Blanchard M., Poitrasson F., Méheut M., Lazzeri M., Mauri F., Balan E. (2009) Iron isotope fractionation between pyrite (FeS2), hematite (Fe2O3) and siderite (FeCO3): A first-principles density functional theory study. Geochim. Cosmochim. Acta 73, 6565-6578.
Blattner P., Braithwaite W.R., Glover R.B. (1983) New evidence on magnetite oxygen isotope geothermometers at 175°C and 112°C in Wairakei steam pipelines (New Zealand). Isotope Geosci. 1, 195-204.
Brenninkmeijer C.A.M, Kraft P., Mook W.G. (1983) Oxygen isotope fractionation between CO2 and H2O. Isotope Geosci. 1, 181-190.
Bron, J., Chang, C.F., Wolfsberg, M., (1973). Isotopic partition function ratios involving H2, H2O, H2S, HSe and NH3.28a, 129-136.
Chacko T., Cole D.R., Horita J. (2001) Equilibrium oxygen, hydrogen and carbon isotope fractionation factors applicable to geologic systems. Rev. Mineral. Geochem. 43, 1-81.
Chacko T., Deines P. (2008) Theoretical calculation of oxygen isotope fractionation factors in carbonate systems. Geochim. Cosmochim. Acta 72, 3642-3660.
Chacko T., Mayeda T. K., Clayton R. N., Goldsmith J. R. (1991) Oxygen and carbon isotope fractionations between CO2 and calcite. Geochim. Cosmochim. Acta 55, 2867-2882.
Clayton R.N., Jones B.F., Berner R. A. (1968) Isotope studies of dolomite formation under sedimentary conditions. Geochim. Cosmochim. Acta 32, 41-32.
Clayton R.N., Kieffer S.W. (1991) Oxygen isotopic thermometer calibrations. In: Stable Isotope Geochemistry: A Tribute to Samuel Epstein. (eds. Taylor, H.P., Jr., O’Neil J.R. Kaplan I.R.) The Geochemical Society Division of Sciences, Mathematics and Engineering Trinity University, San Antonio, Texas, Lancaster Press. 3-10.
Coplen T.B. (2007) Calibration of the calcite-water oxygen isotope geothermometer at Devils Hole, Nevada, a natural laboratory. Geochim. Cosmochim. Acta 71, 3948-3957.
de Capitani C., Brown T.H. (1987) The computation of chemical equilibrium in complex systems containing nonideal solutions. Geochim. Cosmochim. Acta 51. 2639-2152.
Dove M.T., Winkler B., Leslie M., Harris M.J., Salje E.K.H. (1992) A new interatomic model for calcite: applications to lattice dynamics studies, phase transition, and isotopic fractionation. Am. Mineral. 77, 244-250.
Galimov, E.M. (2006) Isotope organic geochemistry. Organic Geochemistry 37, 1200-1262.
Guo W., Zhou C. (2019) Triple oxygen isotope fractionation in the DIC-H2O-CO2 system: A numerical framework and its implications. Geochim. Cosmochim. Acta 246, 541-564.
Hill P.S., Schauble E.A., Tripati A.K. (2020) Theoretical constraints on the effects of added cations on clumped, oxygen, and carbon isotope signatures of dissolved inorganic carbon species and minerals. Geochim. Cosmochim. Acta 269, 496-539.
Hill P.S., Tripati A.K., Schauble E.A. (2014) Theoretical constraints on the effects of pH, salinity, and temperature on clumped isotope signatures of dissolved inorganic carbon species and precipitating carbonate minerals. Geochim. Cosmochim. Acta 125, 61-52.
Horita J. (2014) Oxygen and carbon isotope fractionation in the system dolomite–water–CO2 to elevated temperatures. Geochim. Cosmochim. Acta. 129, 111-124.
Horita J., Clayton R.N. (2007) Comment on the studies of oxygen isotope fractionation between calcium carbonates and water at low temperatures by Zhou and Zheng (2003; 2005). Geochim. Cosmochim. Acta 71, 3131-3135.
Horita, J., Wesolowski, D.J. (1994). Liquid–vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature. Geochim. Cosmochim. Acta 58, 3425-3437.
Hu G., Clayton R.N., Polyakov V.B., Mineev S.D. (2005) Oxygen isotope fractionation factors involving cassiterite (SnO2): II. Determination by direct isotope exchange between cassiterite and calcite. Geochim. Cosmochim. Acta 69, 1301-1305.
Johnson J.W., Oelkers E.H., Helgeson H.C. (1992) SUPCRT-92: A software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bars and 0° to 1000°C. Comp. Geosci. 18, 899-947.
Kieffer S.W. (1979) Thermodynamic and lattice vibrations of minerals: 3.Lattice dynamics and an approximation for minerals with application to simple substances and framework silicates models. Rev. Geophys. Space Phys. 17, 35-59.
Kim S.-T., O’Neil J.R. (1997) Equilibrium and nonequilibrium oxygen isotope effects in synthetic carbonates. Geochim. Cosmochim. Acta 61, 3461-3475.
Krylov D.P., Evarestov R.A. (2018) Ab initio (DFT) calculations of corundum (α-Al2O3) oxygen isotope fractionation. Eur. J. Minera1. 30, 1063-1070.
Macey P., Harris H. (2006) Stable isotope and fluid inclusion evidence for the origin of the Brandberg West area Sn–W vein deposits, NW Namibia. Miner. Deposita 41, 671-690.
Mandernack K.W., Bazylinski D.A., Shanks W.C. III, Bullen T.D. (1999) Oxygen and iron isotope studies of magnetite produced by magnetotactic bacteria. Science 285, 1892-1896.
Matsuhisa Y, Goldsmith JR, Clayton RN (1978) Mechanisms of hydrothermal crystallization of quartz at 250 єC and 15 kbar. Geochim. Cosmochim. Acta 42, 173-182.
Matthews A., Katz A. (1977) Oxygen isotope fractionation during the dolomitization of calcium carbonate. Geochim. Cosmochim. Acta 41, 1431-1438.
Matthews A. (1994) Oxygen isotope geothermometers for metamorphic rocks. J. Metam. Geol. 12, 211-219.
Mironenko M.V., Polyakov V.B., Alenina M.V. (2018) Simultaneous Calculation of Chemical and Isotope Equilibria Using the GEOCHEQ_Isotope Software: Carbon Isotopes. Geochem. Int. 56(13), 1354-1367.
Northrop D.A., Clayton R.N. (1966) Oxygen–isotope fractionations in systems containing dolomite. J. Geol. 74, 174-196.
Ohmoto H. (1972) Systematics of sulfur and carbon isotopes in hydrothermal ore deposits. Econ. Geol. 67, 551-578.
Patel A., Price G. D., Mendelssohn M. J. (1991) A computer simulation approach to modelling the structure, thermodynamics and oxygen isotope equilibria of silicates. Phys. Chem. Minerals 17, 690-699.
Polyakov V.B., Horita J. (2021) Equilibrium carbon isotope fractionation factors of hydrocarbons: Semi-empirical force-field method. Chem. Geol. 559, 119948.
Polyakov V.B., Kharlashina N.N. (1994) Effect of pressure on the equilibrium isotopic fractionation. Geochim. Cosmochim. Acta 58, 4739-4750.
Polyakov V.B., Mineev S.D., Clayton R. N., Hu G. (2005) Oxygen isotope equilibrium factors involving cassiterite (SnO2). I: Calculation of reduced partition function ratios from heat capacity and X-ray resonant studies. Geochim. Cosmochim. Acta 69, 1287-1300.
Richet P., Bottinga Y., Javoy M. (1977) A review of hydrogen, carbon, nitrogen, oxygen, sulphur and chlorine stable isotope fractionation among gaseous molecules. Ann. Rev. Earth Planet. Sci. 5, 65-110.
Rosenbaum J.M. (1994) Stable isotope exchange between carbon dioxide and calcite at 900oC. Geochim. Cosmochim. Acta 58, 3747-3753.
Rosenbaum J.M., Mattey D.P (1995) Equilibrium garnet-calcite oxygen isotope fractionation. Geochim Cosmochim Acta 59, 2839-2842.
Schauble E.A. (2004) Applying stable isotope fractionation theory to new systems. Rev. Mineral.Geochem. 55, 65-111.
Schauble E.A., Young E.D. (2021) Mass Dependence of Equilibrium Oxygen Isotope Fractionation in Carbonate, Nitrate, Oxide, Perchlorate, Phosphate, Silicate, and Sulfate Minerals. Rev. Mineral. Geochem. 86, 137-178.
Schmidt M., Xeflide S., Botz R., Mann S. (2005) Oxygen isotope fractionation during synthesis of CaMg-carbonate and implications for sedimentary dolomite formation. Geochim. Cosmochim. Acta 69, 4665-4674.
Schütze H. (1980) Der isotopenindex – eine Inkrementenmethode zur nдherungsweisen Berechnung von Isotopenaustauschgleichgewichten zwischen kristallinen Substanzen. Chem. Erde 39, 321-334.
Sidkina E.S., Mironenko M.V., Polyakov V.B. (2020) Calculation of serpentinization of olivin. Verification of the equilibrium-kinetic model. Experiment in Geosciences 26(1), 100-104.
Tarutani T., Clayton R.N., Mayeda T.K. (1969) The effect of polymorphism and magnesium substitution on oxygen isotope fractionation between calcium carbonate and water. Geochim. Cosmochim. Acta 33, 987-996.
Taylor B.E. (1976) Origin and significance of C-O-H fluids in the formation of Ca-Fe-Si skarn, Osgood Mountains, Humboldt County, Nevada. PhD Dissertation, Stanford University, 214 c.
Truesdell A.H. (1974) Oxygen isotope activities and concentrations in aqueous salt solutions at elevated temperatures: Consequences for isotope geochemistry. Earth Planet. Sci. Lett. 23, 387-396.
Urey H.C. (1947) The thermodynamic properties of isotopic substances. J. Chem. Soc. (London) 56-81.
Vasconcelos C., McKenzie J. A. (1997) Microbial mediation of modern dolomite precipitation and diagenesis under anoxic conditions (Lagoa Vermelha, Rio De Janeiro, Brazil). J. Sediment. Res. 67, 378-390.
Zack T., Kooijman E. (2017) Petrology and geochronology of rutile. Rev. Mineral. Geochem. 83, 443-467.
Zhang C., Liu S., Phelps T.J., Cole D.R., Horita J., Fortier S.M., Elless M., Valley J.W. (1997) Physiochemical, mineralogical, and isotopic characterization of magnetite-rich iron oxides formed by thermophilic iron reducing bacteria. Geochim. Cosmochim. Acta 61, 4621-4632.
Zheng Y.-F. (1991) Calculation of oxygen isotope fractionation in anhydrous silicate minerals. Geochim. Cosmochim. Acta 57, 1079-1091.
Zheng Y.-F. (1999) Calculation of oxygen isotope fractionation in minerals. Episodes 22, 99-106.
Zhou G.-T., Zheng Y.-F. (2003) An experimental study of oxygen isotope fractionation between inorganically precipitated aragonite and water at low temperature. Geochim. Cosmochim. Acta 67, 387-399.
Zhou G.-T., Zheng Y.-F. (2005) Effect of polymorphic transition on oxygen isotope fractionation between aragonite, calcite and water. Am. Mineral. 90, 1121-1130.
Дополнительные материалы отсутствуют.