Геохимия, 2021, T. 66, № 11, стр. 1067-1074

ВВЕДЕНИЕ

Настоящая работа выполнена в рамках широкого круга исследований, направленных на объяснение и описание эволюционных процессов и их свойств (Галимов, 2008а, 2013), и является прямым продолжением опубликованных ранее в журнале Геохимия статей (Грибов, 2007; Грибов, Михайлов, 2010; Грибов и др., 2012; Баранов и др., 2013; Грибов, Баранов, 2014; Баранов и др., 2016; Баранов и др., 2016а; Грибов и др., 2018; Baranov, Gribov, 2014). Следует особо отметить, что существенной причиной возросшего интереса к изучению различных аспектов возможности появления и существования наблюдаемых в течение миллиардов лет устойчивых процессов превращения части материи во все более высокоорганизованные формы стало появление концепции устойчивого упорядочения академика РАН Эрика Михайловича Галимова (Галимов, 2001, 2008; Galimov, 2004).

В наших прежних работах показано, что описание важнейших экспериментальных фактов эволюционного развития Вселенной на первых стадиях образования молекулярного мира возможно с помощью математических моделей, в основе которых лежит понятие о причинно-следственных связях, явным образом прослеживающихся в процессах эволюции. Важнейшей особенностью таких моделей, представимых в виде цепочек импликаций разной сложности с количественными характеристиками в виде вероятностей превращений, является их опора на фундаментальный физический закон – второе начало термодинамики. То обстоятельство, что отправляясь от общего положения физики – монотонного возрастания энтропии, – удается прийти к тем же закономерностям, что и наблюдаемые особенности эволюционных процессов окружающего мира, свидетельствует не только о корректности предложенного подхода, но и о том, что законы эволюции не являются случайными, а вполне согласуются с базовыми физическими утверждениями.

Еще одним важнейшим результатом наших исследований является ответ на принципиальный вопрос о вероятностях образования тех или иных молекулярных объектов из сгустка атомов, локализованных в малой области пространства (Баранов и др., 2013). Проблема заключается в том, что молекулы имеют вполне определенные структуры, и такое расположение атомов, в результате которого могут сразу образоваться, например, плоские молекулы бензола, представляется очень маловероятным. Вопрос снимается, если учесть, что уже сравнительно малые молекулы (а в открытом космосе сейчас обнаружены и весьма крупные (Tielens, 2013; Endres et al., 2016; Mcguire et al., 2018)) имеют большое число структурных изомеров. Появление любого такого изомера уже не случайно, а закономерно, и может привести в результате мономолекулярной реакции к появлению структур, сильно отличающихся от начальной. Также было показано, что на ранних стадиях эволюции молекулярного мира образование ациклических (протяженных) структур, является более вероятным, чем циклических (свернутых, объемных) (Баранов и др., 2016).

В настоящей работе рассмотрен важнейший вопрос о причинах, приводящих к малым энергиям активации многих биохимических реакций, и показано, что некоторые разработанные в физической теории строения и свойств молекул положения могут быть с успехом применены для заполнения промежутков в логике общей эволюционной теории развития Вселенной.

НЕКОТОРЫЕ ОБЩИЕ ПОЛОЖЕНИЯ ФИЗИЧЕСКОЙ ТЕОРИИ СТРОЕНИЯ И СВОЙСТВ МОЛЕКУЛ

Все процессы в микромире подчиняются законам не классической, а квантовой теории. Последняя базируется на представлении о дискретных уровнях энергии. В свою очередь, такие дискретные энергетические состояния возникают тогда, когда на понимаемое в широком смысле движение частиц накладываются определенные ограничения. В теории вводится понятие потенциальной ямы и считается, что устойчивый молекулярный объект находится внутри ямы. Принципиально важно, что количество уровней (возможных состояний, в которых может находиться система) в яме зависит от ее глубины, ширины и размерности (числа степеней свободы).

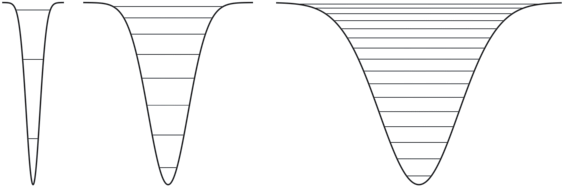
Увеличение плотности уровней в ямах одинаковой глубины, имеющих разную ширину, иллюстрирует рис. 1. Все расчеты, результаты которых приводятся здесь и далее, выполнены в среде MATLAB (https://www.mathworks.com), в том числе с помощью пакета программ Chebfun (http:// www.chebfun.org).

Число уровней (состояний системы) увеличивается также с ростом числа степеней свободы молекулярного объекта, т.е. при его усложнении. На рис. 2 показано как меняется плотность уровней гармонического осциллятора в одном и том же энергетическом промежутке при увеличении размерности осциллятора.

Глубина ямы для молекул определяется энергией электронно-ядерных взаимодействий, которая возрастает при увеличении числа атомов. Получается, что чем сложнее молекулярный объект, тем более плотно (на меньших расстояниях друг от друга) расположены энергетические уровни в ямах. Это очень важный фактор, определяющий, как увидим ниже, увеличение вероятности превращений (химических реакций) с участием крупных молекул по сравнению с малыми.

Каждому уровню энергии (состоянию системы) отвечает своя волновая функция. Квадрат волновой функции определяет вероятность нахождения частицы в единичном объеме в окрестности некоторой точки пространства, и его величина быстро падает до нуля за пределами ямы, что хорошо видно на рис. 3.

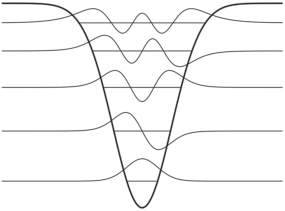
В результате химической реакции одни устойчивые объекты (исходные молекулы) превращаются в другие, тоже устойчивые. В теории такой процесс в простейшем случае мономолекулярной реакции описывается как переход из одной потенциальной ямы в другую. В том случае, когда ямы расположены достаточно близко друг к другу, могут возникнуть уровни с волновыми функциями, отличными от нуля в пределах не одной ямы, а сразу двух. Такая ситуация показана на рис. 4. В центре рисунка изображена двухминимумная потенциальная яма, образующаяся при сближении показанных по краям потенциалов, имеющих две пары состояний с очень близкими (но не равными) энергиями. Первую пару составляют состояние 1 левой ямы и состояние 0 правой ямы, вторую – состояние 2 левой ямы и состояние 1 правой ямы. Хорошо видно, что, если для первой пары состояний каждая их двух волновых функций локализована только в пределах своей ямы, то для второй пары состояний, энергии которых значительно ближе к барьеру, наблюдается размазывание обеих волновых функций по всей области двухминимумного потенциала. Возникающий дублет (резонансный уровень) определяет возможность химического (структурного) превращения – перехода из одной ямы в другую.

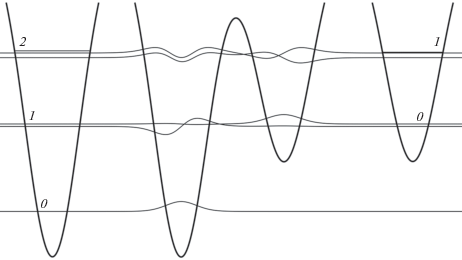
На рис. 4 волновые функции, нулевые значения которых совмещены с энергиями соответствующих состояний, намеренно изображены не только внутри ям, но и далеко за их пределами. Это с одной стороны сделано для иллюстрации близости энергий состояний в упоминавшихся выше парах уровней правой и левой ям, а с другой является попыткой показать уменьшение энергии уровней в двухминимумном потенциале по сравнению с отдельными ямами. Такое уменьшение особенно выражено для второй пары состояний и хорошо видно на рис. 5, который является увеличенным участком рис. 4.

Характеристики потенциалов, показанных на рис. 4 и 5, специально подобраны таким образом, чтобы появлялись пары уровней имеющих очень близкие энергии. Очевидно, что в ямах с небольшим числом уровней достаточная для возникновения резонанса близость энергий состояний является маловероятной. Именно поэтому такую важную роль играет большая плотность уровней в сложных молекулах, которая резко повышает вероятность резонанса. Одновременно уменьшаются и энергия уровня, и энергия активации реакции. Отсюда следует, что для начала того, что принято называть жизнью, эволюция молекулярного мира должна от стадии простых малых молекул перейти в стадию крупных.

В общей физической теории химических реакций показано, что в полном соответствии с экспериментом реакции с участием крупных молекул возможны только тогда, когда имеются так называемые реакционные центры (Баранов и др., 2013; Грибов, Баранов, 2012а; Баранов и др., 2016а). Это малые участки сложных молекулярных объектов, где и происходят перестановки атомов, приводящие к превращению исходных структур в продукты. Реакционные центры с большей вероятностью образуются на концах протяженных (ациклических), т.е. вытянутых в одном направлении молекул (участков молекул), чем в объемных (циклических). А, как уже говорилось во Введении, согласно теории ациклические молекулы образуются на ранних стадиях с большей вероятностью, чем циклические (объемные) (Баранов и др., 2016).

Все биохимические реакции происходят в жидкой конденсированной среде. Для протекания реакции требуется, чтобы, во-первых, до реакции реагирующие частицы были подвижными и в результате хаотического движения они могли встретиться друг с другом, а во-вторых, число реагирующих частиц в объеме было достаточно велико.

На основании всего вышесказанного можно сделать следующие выводы. Во-первых, реакции происходят в ограниченной области пространства в конденсированной среде (жидкости). Во-вторых, в реакциях должны участвовать крупные молекулы протяженной структуры. В-третьих, реакционные центры в таких молекулах должны быть расположены на концах структур. Все это точно соответствует эксперименту. Можно, поэтому, заключить, что для объяснения особенностей биохимических реакций не надо вводить какие-то новые химические силы.

МОДЕЛИРОВАНИЕ МНОГОСТУПЕНЧАТЫХ РЕАКЦИЙ

В предыдущем разделе показано, что общие положения физической теории химических реакций приводят к заключениям общего характера, согласующимся с наблюдаемыми закономерностями эволюции молекулярного мира. Рассмотрим теперь, как современное состояние теории позволяет изучать особенности развития процессов (в том числе и геохимических) любой сложности во времени на примере построения системы кинетических уравнений для описания многоступенчатого превращения, схема которого показана на рис. 6.

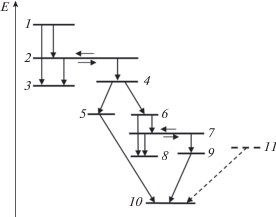
Будем считать, что в результате внешнего воздействия на ансамбль исходных молекул (состояния 1, 2 и 3) заселяется возбужденное состояние 1. Величину этой заселенности удобно принять равной единице. Так как уровень 2 резонансный (общий для двух ям), то в процессе релаксации становятся возможными переходы на уровень 4 второй молекулы – структурного изомера исходной. Этот изомер является неустойчивым (переходная структура) и распадается на две части – одной соответствует состояние 5, другой – состояния 6, 7 и 8. Для последней снова возможен изомерный переход, так как уровень 7 резонансный. Уровни 8 и 9 являются основными состояниями структурных изомеров, имеющих меньшее число атомов, чем первая (исходная) и вторая (неустойчивая) молекулы. Появляющиеся в ходе многоступенчатого процесса структуры с уровнями 5 и 9 способны вступать в реакцию присоединения с образованием молекулы 10 с тем же числом атомов, что и исходная, т.е. структура 10 является изомером первой молекулы (описываемой уровнями 1, 2 и 3). Таким образом, последовательность превращений, показанная сплошными линиями, включает в себя внутримолекулярные переходы между уровнями энергии, две реакции структурной изомеризации (два резонансных уровня), одну реакцию разложения и одну реакцию присоединения. Конечными состояниями являются состояния 3, 8, 10 и одно из состояний 5 или 9 (в зависимости от соотношения вероятностей превращений).

В системе дифференциальных уравнений для описания развития многоступенчатого процесса во времени должны быть учтены все четыре перечисленных выше типа превращений.

Реакция разложения исходного состояния 4 (Ван-дер-Ваальсова комплекса, способного к распаду с вероятностью α), в результате которой появляются компоненты 5 и 6, описывается системой трех уравнений

Вероятность реакции присоединения β определяется вероятностью одновременного нахождения структур 5 и 9 в одном и том же малом объеме V. Последняя равна произведению вероятностей нахождения объеме V частиц 5 и 9 по отдельности: n₅n₉/V ². Тогда процесс появления новой молекулы 10 можно охарактеризовать также системой трех уравнений

Для внутримолекулярного перехода между двумя нерезонансными уровнями, например, 1 и 3 с заселенностями n₁ и n₃, характеризующегося вероятностью p₁₃, изменение заселенностей состояний записывается в виде

Для внутримолекулярных переходов между двумя уровнями, один из которых резонансный, например, 1 → 2, 2 → 3 или 2 → 4 следует учитывать, что резонансный уровень является не просто общим для двух ям (в многоминимумных потенциалах все уровни энергии общие), но и имеет волновую функцию, локализованную (отличную от нуля) в области обеих ям (пример такой функции показан на рис. 5 предыдущего раздела). В результате получается дублет с близкими энергиями, функции которого имеют вид, с хорошей степенью точности отвечающий выражению (φ_i ± φ_j)/√2, где φ_i и φ_j − участки функций, локализованные в левой и правой ямах. При такой форме волновых функций переход из состояния 1 с функцией, локализованной в пространстве только левой ямы, на уровень дублета (состояние 2) создает условия дальнейшего развития процесса в двух направлениях – на нижележащие уровни 3 и 4 с функциями, локализованными только в левой и правой ямах соответственно. Переход 2 → 4 отвечает появлению структурной формы (в нашем случае неустойчивой), являющейся продуктом химической реакции, необходимым условием которой можно считать существование состояния с “размазанной” волновой функцией.

Расстояние между уровнями энергии дублета мало, и вместо дублета можно ввести один дважды вырожденный уровень с энергией E = (E_i + E_j)/2. Для квадрата волновой функции резонансного уровня можно записать

и говорить о безызлучательном переходе из левой ямы в правую (Грибов, Баранов, 2006; Грибов и др., 2019).

Это означает, что вероятности переходов на уровни дублета (1 → 2) и с них (2 → 3 и 2 → 4) будут зависеть от величины частоты квантовых биений ω и определяться квадратами матричных элементов дипольного момента, умноженными на осциллирующие функции cos²ωt или sin²ωt. Выбор конкретного множителя определяется начальными условиями, т.е. направлением химического превращения (Грибов, Баранов, 2006). Для переходов 1 → 2 и 2 → 3 между уровнями энергии исходного вещества (донора) вероятность перехода умножается на cos²ωt, а для перехода 2 → 4 между уровнями продукта реакции (акцептора) – на sin²ωt:

Все вышесказанное позволяет записать систему дифференциальных уравнений первого порядка, описывающую сложный многоступенчатый процесс превращений, в виде

Важно отметить, в общей физической теории химических реакций разработаны методы и алгоритмы расчета вероятностей переходов (p_ij) и частот квантовых биений (ω₂ и ω₇), являющихся параметрами системы (Грибов и др., 2019). Оценки величин других параметров (вероятности α и β) также могут быть получены средствами теории.

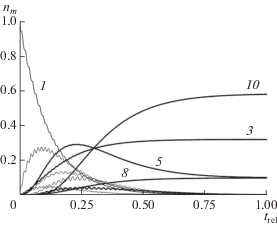
Результат решения системы уравнений будет зависеть от начальных условий. Как уже говорилось выше, в нашем случае естественно принять n₁(0) = 1, n_2,…,10(0) = 0. Полученные временные зависимости заселенностей уровней энергии молекул показаны на рис. 7. Видно, что сохранится определенное число исходных молекул (состояние 3), появятся ее изомерные формы (состояние 10) и одинаковое число еще двух меньших по размеру молекул (состояния 5 и 8). Использован некоторый временной интервал от 0 до t_max, а все результаты представлены для безразмерных величин t_rel = t/t_max.

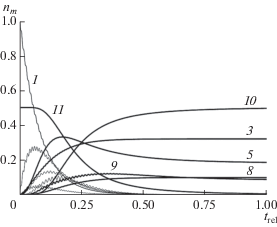
Схему переходов между уровнями энергии, показанную на рис. 6 сплошными линиями, можно распространить на случай, когда изначально присутствуют два типа молекул, причем молекулы второго типа реагируют с продуктами превращений первого соединения. Тогда могут появиться реакции третьего порядка. Дополнительные уровни и превращения для такого процесса показаны на рис. 6 штриховыми линиями. Соответствующая система уравнений по сравнению с записанной выше изменится незначительно – появится одно новое уравнение dn₁₁/dt = −β n₅n₉n₁₁, а в правых частях уравнений для заселенностей n₅, n₉ и n₁₀ слагаемое β n₅n₉ следует заменить на β n₅n₉n₁₁. Результат решения расширенной системы с начальными условиями n₁(0) = 1, n_2,…,10(0) = 0 и n₁₁(0) = 0.5 показан на рис. 8.

ЗАКЛЮЧЕНИЕ

Показано, что общие положения физической теории строения и свойств молекул и химических превращений приводят к выводам, которые согласуются с наблюдаемыми особенностями процессов эволюции молекулярного мира. Высокая плотность энергетических уровней, достижимая только в больших и сложных молекулярных объектах, резко увеличивает вероятность реакций и структурных перестроек и приводит к заметному снижению энергии активации. Отсюда следует, что то, что принято называть жизнью, не могло возникнуть на ранних стадиях эволюции молекулярного мира.

Кроме размера и сложности молекулярных объектов для многих биохимических реакций наблюдаются и другие характерные особенности. Во-первых, такие реакции происходят в ограниченной области пространства в конденсированной среде. Во-вторых, молекулы, участвующие в таких реакциях, обычно имеют в своей структуре протяженные участки. В-третьих, реакционные центры в таких молекулах обычно расположены на концах протяженных участков. Все это хорошо согласуется с выводами теории.

Приведен пример моделирования сложной цепочки превращений, в которой происходят как процессы внутримолекулярные (они приводят к поглощению или излучению электромагнитных волн), так и реакционные – мономолекулярные (изомеризация), синтеза и разложения. Показанная возможность построения математической модели сложного процесса, с помощью которой можно описывать, в том числе и процессы эволюции молекулярного мира на ранних стадиях развития, принципиально важна. Целью любой естественной науки является не только понимание, но, и это главное, прогноз, который невозможен без использования моделей достаточно хорошо описывающих явления в природе. Давно известно, что любая отрасль науки достигает совершенства тогда, когда она начинает пользоваться математикой. Геохимия исключением не является, и перспектива ее развития определяется не только накоплением экспериментальных фактов, но и переходом к построению математических моделей.