Геомагнетизм и аэрономия, 2022, T. 62, № 2, стр. 198-205

1. ВВЕДЕНИЕ

Моделирование процессов, происходящих в плазме околоземного космического пространства, – одна из важнейших задач в современной солнечно-земной физике. Развитие этого направления стало возможным лишь в результате проведения комплексных спутниковых, ракетных и наземных экспериментов. Особое место в физике ионосферы и магнитосферы занимают следующие вопросы: получение морфологических сведений о различных параметрах ионосферы и магнитосферы; выявление экспериментальных факторов, влияющих на поведение волн; теоретическое исследование и моделирование процессов генерации, взаимодействия и распространения волн; сравнение экспериментальных и теоретических результатов.

К настоящему времени ни один из перечисленных вопросов не решен окончательно, однако в ходе исследований накоплен большой теоретический и экспериментальный материал [Кринберг и Тащилин, 1984; Ляцкий и Мальцев, 1983; Сергеев и Цыганенко, 1980; Шафранов, 1983] и сформулированы современные представления о среде и процессе распространения радиоволн [Альперт, 1972; Лихтер, 1974; Сажин, 1972; Budden, 1966], что делает реальной задачу создания на базе этих представлений единой модели процесса распространения.

Модель среды должна описывать все параметры, которые влияют на свойства волн, поэтому в нее должны быть включены: распределения концентраций и температур, определяющие преломление волн; частоты соударений, определяющие столкновительное затухание; распределение магнитного поля, определяющее удержание волн в магнитосфере. Околоземная плазма является единой ионизированной областью пространства, однако при рассмотрении распространения волн в ней удобно выделить две области: ионосферу и магнитосферу. В первой существенное влияние на распространение волн оказывают электроны, во второй ‒ магнитное поле Земли [Ратклифф, 1975].

В настоящей работе ставится задача описать метод и результаты моделирования процесса распространения средних радиоволн (СВ) в магнитосфере Земли. Как известно [Альперт, 1972; Шлионский, 1979], волны различных диапазонов могут распространяться в околоземной плазме. Традиционно низкочастотные волны используются при магнитосферном распространении, а высокочастотные – при ионосферном. Промежуточный средневолновый диапазон (f = 1‒3 МГц) преимущественно также связывается с ионосферой. Хотя имеются доказательства магнитосферного распространения СВ, например [Nagy et al., 2018]. В данном исследовании делается попытка оценить возможности СВ для изучения, в частности, положения главного ионосферного провала и плазмопаузы в магнитосфере.

2. МОДЕЛЬ ОКОЛОЗЕМНОЙ ПЛАЗМЫ

В основу расчетов распространения СВ положены результаты анализа серии экспериментов по наблюдению сигналов передатчика на частоте f = 1.8 МГц, совмещенного с приемником и расположенного вблизи г. Санкт-Петербург (L = 3.2, где L – оболочка является параметром, равным отношению расстояния от центра Земли до силовой линии магнитного поля над экватором R к радиусу Земли R_O, т.е. L = R/R_O), в зимний период 2018 г. В ходе экспериментов были обнаружены эхо-сигналы со средними задержками t_эксп = = 0.28‒0.29 с, с низким уровнем затухания и практическим отсутствием доплеровского сдвига. Пример записи эхо-сигналов показан на рис. 1. На нем представлены три последовательные временны́е отрезка длиной четыре секунды каждый. Интервал между двумя соседними вертикальными штриховыми линиями составляет 200 мс. Каждый интенсивный импульс, например в 57-ую секунду, соответствует сигналу передатчика, каждый слабый импульс, отстоящий от импульса передатчика на t_эксп, есть эхо-сигнал. В середине центрального рисунка после эхо-сигнала зафиксирован третий, невыраженный, импульс, который является помехой_. Объяснить характеристики подобных сигналов можно только с помощью механизма магнитосферного распространения, контролируемого положением провала и плазмопаузы [Благовещенский и Гладкий, 2020].

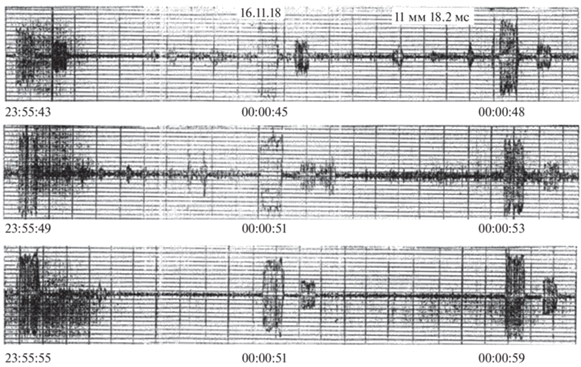
Существуют определенные условия в ионосфере и магнитосфере, при которых наблюдалась канализация средних волн вдоль плазмопаузы. В моменты появления эхо-сигналов в месте приема были получены следующие сведения о геофизической обстановке: а) наблюдения проводились во время магнитосферных суббурь; б) данные вертикального зондирования станции, расположенной рядом с пунктом приема эхо-сигналов, свидетельствуют о том, что пункт наблюдения находился глубоко внутри главного ионосферного провала, ближе к его южной границе; в) критические частоты слоя F 2 для рассматриваемых сеансов лежали в пределах foF 2 = 1.5–2.0 МГц в районе передатчика и в пределах 4.0–6.0 МГц – в магнитосопряженной области [Благовещенский и Добросельский, 1995, 1996]. Эти результаты использовались для построения модели плазмы, максимально приближенной к экспериментальным условиям.

Для описания распределения электронной концентрации Ne(h), так называемого фона, использовались эмпирические модели среднеширотной ионосферы Ne ^mod [Фаткуллин и др., 1981] в диапазоне высот от начальной высоты ионосферы ho до уровня 1000 км, который является базовым для модели диффузионного равновесия [Мальцева и Молчанов, 1984], описывающей распределение Ne в магнитосфере в виде степенного падения концентрации с расстоянием Ne(r) ∼ r^–n [Angerami and Thomas, 1964]. Чтобы варьировать фон, то есть N_emaxF 2 всех моделей в [Фаткуллин и др., 1981], оставляя вид профиля Ne(h) неизменным, введен множитель div, с помощью которого можно подобрать значения foF 2 (или N_emaxF 2), соответствующие экспериментальным значениям foF 2 (или N_emaxF 2). Множитель div равен отношению концентраций в максимуме слоя N_еmaxF 2 для модели и эксперимента

Данный множитель определяет, во сколько раз должны быть изменены значения модельного профиля Ne ^mod для соответствия экспериментальным данным, и варьируется в диапазоне div = = 1.9–7.8 для foF 2 = 1.5–2.6 МГц.

Факт увеличения foF 2 в сопряженном (южном) полушарии относительно foF 2 в полушарии передатчика смоделирован с помощью дополнительных высотных и широтных градиентов, описываемых для простоты двумя параметрами: ah и dr.

Параметр ah равен отношению максимальных концентраций N_e maxF 2 в обоих полушариях

где tr обозначает передатчик (transmitter).

Параметр dr характеризует высотный размер области профиля, в пределах которой концентрация в сопряженном полушарии отличается от концентрации в полушарии передатчика, то есть это как бы масштаб вводимого различия по высоте.

В модель распределения концентрации в магнитосфере включены такие элементы, как главный ионосферный провал (trough) и плазмопауза (plasmapause). Данные элементы учитываются множителями Fth и F pp так, чтобы

Среднеширотный или главный ионосферный провал (ГИП), как известно, представляет собой уменьшение электронной концентрации в области геомагнитных широт Ф_L = 50°‒65° в спокойное время и Ф_L = 35°‒50° – в периоды возмущений, образующихся под действием конвекции, высокоскоростного истечения ионов и электронов, а также вследствие различия положений географического и магнитного полюсов [Гальперин и др., 1980; Колесник и Голиков, 1983; Мизун, 1985]. ГИП является особенностью поведения электронной концентрации в области высот от h_maxF 2 до 2000–3000 км и наиболее четко проявляется в ночное время в годы минимума солнечной активности. Форма провала зависит от долготы, сезона, местного времени, уровня геомагнитной возмущенности и других параметров, как показано на рис. 2 из работы [Карпачев, 2003].

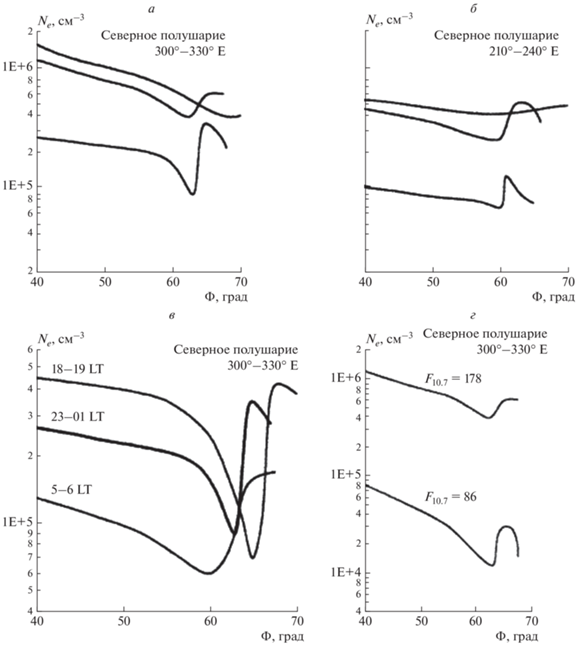
Множитель, описывающий ГИП, вводится в виде [Мальцева и Молчанов, 1984]

где Lth определяет положение центра провала, a_th – падение концентрации в центре провала, d – величина внутренней (din) и внешней (dout) стенок провала. Коэффициент a_th зависит от расстояния r, становясь равным нулю вблизи экваториальной плоскости.

Плазмопауза (ПП) в отличие от ГИП является особенностью распределения концентрации в более высоких областях вплоть до экваториальной плоскости. Отличается и структура: в частности, плазмопауза имеет только одну стенку, а падение концентрации происходит на 1‒2 порядка на расстоянии ΔL = 0.1–0.3. Провал и плазмопауза не находятся на одной L-оболочке, в частности, провал лежит внутри плазмопаузы и движется к экватору быстрее во время возмущений при малых Kр [Гальперин и др., 1990]. Множитель, описывающий изменение концентрации вблизи ПП, имеет вид [Мальцева и Молчанов, 1984]

где L_pp – положение плазмопаузы; параметр w представляет собой полутолщину плазмопаузы, измеряется в единицах L и зависит от Кр (w = w ⁰ – – CKp); n – показатель степени радиального спадания концентрации за плазмопаузой.

Что касается ГИП, то указанная модель провала имеет одинаковую глубину (1 – a_th) вдоль всего канала. И хотя такие случаи не редки [Благовещенский и Жеребцов, 1987], известно, что провал имеет определенную пространственную протяженность [Rodger and Dudeney, 1987; Rodger et al., 1992]. Для учета влияния данного фактора целесообразно ввести пространственную зависимость коэффициента a_th, дающую уменьшение глубины провала к экваториальной плоскости. В этом случае

Варьируя параметр dR, можно изменять протяженность провала, то есть его структуру.

Долготная зависимость Ne здесь не рассматривалась в силу своей малой значимости.

Диапазон изменения каждого указанного выше модельного параметра (div, ah, dr) задавался в соответствии с экспериментальными данными. Так, распределение плазменных частот f_Ne характеризуется значениями foF 2 в полушарии передатчика  foF 2 = 1.5–2.6 МГц, что дает диапазон изменения div = 1.9–7.8. Критические частоты foF 2 = 4.0–6.0 МГц в сопряженном полушарии определяют диапазон изменений ah = 2–10. Статистических данных по распределению Ne вдоль силовых линий между асимметричными полушариями нет, однако в соответствии с некоторыми данными [Berger and Barlier, 1981; Brace et al., 1988; Brace et al., 1967; Strangeways, 1982] параметр dr может изменяться в диапазоне 1000–10 000 км.

Параметры главного ионосферного провала (L-оболочка его центра Lth, коэффициент глубины a_th) и плазмопаузы соответствуют возмущенным условиям (Lth, L_pp = 3.2–3.6, a_th = 0.6–0.9). Кроме того, задавалась величина разности ΔLth = = L_pp – Lth в диапазоне 0 – 0.6, исходя из того, что среднестатистическое значение ΔLth составляет 0.2–0.3 [Rycroft and Burnell, 1970; Rycroft and Thomas, 1970], а во время возмущений эта разность может достигать 0.6 [Titheridge, 1976] и более [Smith et al., 1987].

3. МЕТОД РАСЧЕТА ТРАЕКТОРИЙ РАДИОВОЛН

Для моделирования характеристик волн (L-оболочек точек наблюдения волн L_k, времен распространения t_гр и др.) использовался традиционный метод ray tracing в версии [Мальцева и Молчанов, 1984]. При определении L_k и t_гр необходимо задать положение источника и углы излучения волн. В соответствии с данными эксперимента источник располагался на Ltr = 3.23. Для получения более общих результатов в модельных расчетах использовались и другие значения. Углы “старта” волн δ между волновым вектором k и вертикалью задавались в диапазоне –20° ≤ δ ≤ 60°. Эти углы определяли соответствующие начальные углы ψ между вектором k и вектором магнитного поля Земли B₀, анализ поведения которых играет важную роль при проведении траекторных расчетов. Значения параметров, использованных в расчетах, сведены в табл. 1.

4. МЕХАНИЗМЫ РАСПРОСТРАНЕНИЯ

Значения экспериментальных групповых задержек эхо-сигналов, как указывалось выше, составили порядка 0.28‒0.29 с. Подобным величинам задержек могут соответствовать три физических механизма: распространение средних волн в верхней ионосфере, кругосветное распространение СВ и магнитосферное распространение.

Первый механизм ‒ распространение с отражением волн от верхней ионосферы. Здесь О-мода конвертирует в Х-моду на высотах h < h_maxF 2, затем распространяется в верхней ионосфере (h > > h_maxF 2), отражается в данной области и возвращается назад. Вблизи h_maxF 2 теперь уже Х-мода конвертирует в О-моду и достигает Земли.

Второй механизм ‒ кругосветное распространение. За счет него имеется возможность проникновения волн в сопряженное полушарие. Там волна может отразиться, вернуться к передатчику и, повторив этот процесс несколько раз, набрать большую задержку.

Третий механизм ‒ магнитосферное распространение, т.е. прохождение волн в сопряженное полушарие и обратно через магнитосферу.

В работе [Благовещенский и Гладкий, 2020] было показано, что экспериментальные эхо-сигналы обязаны только распространению СВ в магнитосфере. Здесь это обстоятельство доказывается еще раз путем моделирования. А именно, методом численного моделирования исследовались три механизма:

1) распространение волн в верхней ионосфере полушария, в котором находится передатчик, и возврат к передатчику после отражения; 2) кругосветное распространение волн и 3) магнитосферное распространение.

Выбор наиболее вероятного механизма основан на сравнении измеренных и рассчитанных значений групповых задержек с привлечением информации о поведении других характеристик. Рассмотрим каждый из механизмов отдельно.

Основные данные ‒ задержки τ и локализация точки наблюдения Lk, дополнительные данные ‒ поглощение и доплеровские сдвиги.

Первый механизм дает групповые задержки в широком диапазоне, в том числе и равные экспериментальным, но измеренные значения лежат в узком диапазоне. Кроме того, волна может испытать большое ослабление в результате двух конверсий из О-моды в Х-моду и обратно. Это находится в противоречии с измеренными малыми значениями ослабления.

Второй механизм обеспечивает Lk ≈ L_tr и малое ослабление с постоянной задержкой 0.25 с, но это значение меньше экспериментального. Согласно расчетам, единственный случай мог бы обеспечить необходимое τ при нескольких отражениях от Земли, однако в этом случае должны наблюдаться сигналы с промежуточными задержками, но они отсутствуют.

Третий механизм ‒ магнитосферное распространение – включает два случая: отражение от Земли и от ионосферы. Если выбираем первый случай, то измеренные значения должны сравниваться с величинами 2τ. Расчеты показывают, что величина 2τ для всех минимальных задержек больше измеренных значений. Следовательно, волна должна отражаться от сопряженной ионосферы и только этот второй случай необходимо использовать для объяснения экспериментальных значений.

Все модельные расчеты во втором случае проводились с учетом соответствующей геофизической обстановки. Два обстоятельства здесь являются главными [Бенькова и др., 1985; Гальперин и др., 1990].

1) В условиях длительных умеренных магнитных возмущений (Kр ≥ 2) северная граница провала в максимуме F-слоя ионосферы совпадает с положением плазмопаузы, то есть главный провал ионизации в ночное время располагается внутри плазмопаузы.

2) В стационарных спокойных условиях в вечернем и околополуночном секторах северная граница провала располагается вне L-оболочек плазмопаузы.

Моделирование магнитосферного распространения для всех диапазонов параметров, указанных в табл. 1, показало, что экспериментальные значения τ можно получить в довольно широком диапазоне фоновой плазмы (div = = 3.5‒7.8).

а) Умеренно возмущенные условия (L_pp = 3.6; L_th = 3‒ 3.6; L_tr = 3.2; f = 1.8 МГц). Результат расчетов показан на рис. 3.

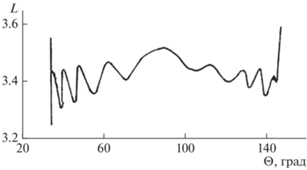
‒ Низкая фоновая плазма дает в основном завышенные значения τ. Здесь центр ГИП не должен находиться много южнее передатчика.

‒ Высокая фоновая плазма требует более глубоких провалов (a_th = 0.8–0.9). Хорошее соответствие τ^эксп и τ^модель дают случаи, когда передатчик расположен несколько южнее центра провала.

‒ Наиболее благоприятные условия для интерпретации данных экспериментов создаются умеренной фоновой плазмой (div = 5), причем для четко ограниченных относительных положений провала и передатчика (ΔL = 0.1) и умеренно глубоких провалов (a_th = 0.6‒0.7).

‒ Волны не канализируются и не проходят в сопряженное полушарие при L_pp = L_th.

б) Значительное возмущение (L_pp = 3.3‒3.5, L_th = 3.0‒3.5, L_tr = 3.2, f = 1.8 МГц).

Здесь результаты расчетов не сильно изменили картину, описанную в пункте (а), но распространение волн в магнито-сопряженную область и их отражение в ней становятся маловероятными для L_pp ‒ L_th ≥ 0.3 и совсем невероятными при L_pp < < L_th. Последнее неравенство физически неосуществимо для L_pp = 3.3‒3.4.

Вышесказанное можно интерпретировать с точки зрения физических представлений. Канал для распространения необразуется и канализация волн вдоль плазмопаузы будет отсутствовать в двух ситуациях:

1) положение провала много южнее плазмопаузы (L_pp ‒ L_th > 0.5), т.е. провал находится внутри плазмосферы почти полностью;

2) центр провала близок к положению плазмопаузы (L_pp ≅ L_th), т.е. провал своей южной частью расположен в плазмосфере, а северной границей ‒ вне плазмосферы, происходит размытие северной границы провала.

Для создания оптимальных условий канализации волн необходимо, чтобы центр ГИП был несколько южнее положения плазмопаузы (L_pp ‒ ‒ L_th ≤ 0.2) и передатчик находился вблизи центра провала (–0.1 ≤ L_th ‒ L_tr ≤ 0.1). Распространение волн происходит вдоль ступеньки ионизации, образованной центром ГИП и плазмопаузой.

5. ВЫВОДЫ

1. Описана модель среды (ионосферы и магнитосферы), включающая распределения концентраций и температур, частот соударений и параметров магнитного поля. Для моделирования параметров СВ в данной среде использован метод ray tracing. Расчет траекторий волн проводится в приближении геометрической оптики. Привлечение этого метода оказалось наиболее оправданным, поскольку он является достаточно развитым и широко распространенным. Создана конкретная программа, с помощью которой, задавая уровень солнечной и геомагнитной активности, местонахождение передатчика и частоту, можно рассчитать параметры траекторий волн.

2. Численное моделирование характеристик сигналов показало, что в условиях эксперимента, описанного в [Благовещенский и Гладкий, 2020], возврат сигналов к передатчику возможен по крайней мере в трех случаях: а) при отражении в верхней ионосфере на высотах как ниже, так и выше h_maxF 2, б) при распространении вокруг земного шара и в) в результате магнитосферного распространения (канализации волн). Сравнение измеренных и рассчитанных значений групповых задержек сигнала совместно с анализом других характеристик позволило отдать предпочтение механизму магнитосферного распространения. В отличие от традиционной канализации волн в дактах в данном случае необычным каналом оказался главный ионосферный провал. Распространение СВ происходит внутри провала вдоль плазмопаузы во время умеренных и сильных возмущений.

3. Канализация средних волн возможна при достаточно четких соотношениях между положениями провала, плазмопаузы и передатчика:

− относительное положение передатчика и провала определяется условием ΔL = L_th – L_tr = = 0.0 ± 0.1;

− ограничение на положение провала и плазмопаузы задается равенством L_pp = L_th + (0.1 – 0.3).

Наиболее благоприятными условиями для существования эхо-сигналов являются следующие:

− критические частоты слоя F ионосферы должны быть близки к частоте зондирования;

− малые высотные градиенты Ne вдоль силовых линий магнитного поля.

4. Рассмотренный эффект канализации средних волн вдоль плазмопаузы дает основание для возможного использования средневолновых сигналов (как случаев наблюдения эхо-сигналов, так и случаев прохождения волн в магнито-сопряженную область) для оперативного определения положения провала и плазмопаузы, а также диагностики явлений, связанных с этими областями.