1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 61, № 2, 2021

Геомагнетизм и аэрономия, 2021, T. 61, № 2, стр. 139-147

Динамика солитонов обобщенного уравнения NLS в неоднородной и нестационарной среде: эволюция и взаимодействие

В. Ю. Белашов 1, *, О. А. Харшиладзе 2, Е. С. Белашова 3

1 Казанский (Приволжский) федеральный университет
г. Казань, Россия

2 Тбилисский государственный университет им. И. Джавахишвили
г. Тбилиси, Грузия

3 Казанский национальный исследовательский технический университет им. А.Н. Туполева
г. Казань, Россия

* E-mail: vybelashov@yahoo.com

Поступила в редакцию 22.06.2020
После доработки 27.07.2020
Принята к публикации 24.09.2020

Полный текст (PDF)

Аннотация

Изучена устойчивость и динамика взаимодействия солитоноподобных решений обобщенного нелинейного уравнения Шредингера, описывающего динамику огибающей модулированных нелинейных волн и импульсов (в том числе явления волнового коллапса и самофокусировки волновых пучков) в плазме (включая космическую), а также в нелинейных оптических системах с учетом неоднородности и нестационарности среды распространения. Уравнение используется и в других областях физики – таких, например, как теория сверхпроводимости и физика низких температур, гравитационные волны малой амплитуды на поверхности глубокой невязкой жидкости и др. Следует отметить, что исследуемое уравнение не является полностью интегрируемым, и его аналитические решения в общем случае не известны (за исключением, пожалуй, гладких решений типа уединенных волн). Однако, используя ранее развитые нами подходы для других уравнений (обобщенное уравнение Кадомцева–Петвиашвили и 3-мерное нелинейное уравнение Шредингера с производной нелинейного члена) системы Белашова–Карпмана, можно аналитически исследовать устойчивость возможных решений данного уравнения, а динамику взаимодействия солитонов изучить численно. Именно такой подход реализован в работе. Аналитически получены достаточные условия устойчивости 2- и 3-мерных солитоноподобных решений и численно изучены случаи устойчивой и неустойчивой (с образованием бризеров) эволюции импульсов различной формы, а также взаимодействие 2- и 3-импульсных структур, приводящее к формированию устойчивых и неустойчивых решений. Полученные результаты могут быть полезны в многочисленных приложениях в физике ионосферной и магнитосферной плазмы и многих других областях физики.

1. ВВЕДЕНИЕ. ОСНОВНЫЕ УРАВНЕНИЯ

Если в системе BK (Belashov-Karpman system) [Belashov and Vladimirov, 2005; Belashov et al., 2018a]

(1)
$\begin{gathered} {{\partial }_{t}}u + \hat {A}(t,u)u = f,\,\,\,\,f = \sigma \int\limits_{ - \infty }^x {{{\Delta }_{ \bot }}u{\text{d}}x} + f{\kern 1pt} ', \\ {{\Delta }_{ \bot }} = \partial _{y}^{2} + \partial _{z}^{2} \\ \end{gathered} $
оператор имеет вид ${\hat {A}}(t,u) = i[\gamma {{\left| u \right|}^{2}} - \beta \partial _{x}^{2}] + {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}$, она представляет собой 3-мерное (3D) обобщенное нелинейное уравнение Шредингера (3-GNLS) [Belashov et al., 2018b]:
(2)
${{\partial }_{t}}u + i\gamma {{\left| u \right|}^{2}}u - i\beta \partial _{x}^{2}u + \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}} \right)u = \sigma \int\limits_{ - \infty }^x {{{\Delta }_{ \bot }}u{\text{d}}x} + f{\kern 1pt} ',$
где $\alpha ,\beta ,\gamma = \varphi (t,x,y,z),$ $f{\kern 1pt} ' = f{\kern 1pt} '(t,x,y,z)$ и $({\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2})u$ описывает диссипативные эффекты, а u есть огибающая волнового пакета (импульса). Уравнение 3-GNLS (2) описывает динамику огибающей модулированных нелинейных волн и импульсов (волновых пакетов) в средах с дисперсией и имеет многочисленные важные приложения в физике плазмы (например, описывает распространение ленгмюровских волн в горячей плазме), нелинейной оптике (распространение световых импульсов в кристаллах, оптоволокне и плоских оптических волноводах), оно описывает, в частности, такие явления, как турбулентность, волновой коллапс и оптическая самофокусировка. Уравнение (2) используется и в других областях физики – таких, например, как теория сверхпроводимости и физика низких температур (в частности, обычное уравнение NLS есть упрощенная 1D форма уравнения Гинзбурга–Ландау [Гинзбург и Ландау, 1950], впервые введенного ими в 1950 г. при описании сверхпроводимости), гравитационные волны малой амплитуды на поверхности глубокой невязкой жидкости и др. Отметим, что 3D-уравнение (2) не является полностью интегрируемым, и его аналитические решения в общем случае не известны (за исключением, пожалуй, гладких решений типа уединенных волн). Однако, с использованием подходов, развитых в работах [Белашов, 1991, 1999] для других уравнений системы BK (обобщенное уравнение Кадомцева–Петвиашвили – уравнение GKP, когда в системе (1) ${\hat {A}}(t,u) = \alpha u{{\partial }_{x}} - \partial _{x}^{2}(\nu - \beta {{\partial }_{x}} - \gamma \partial _{x}^{3})$, и 3-мерное нелинейное уравнение Шредингера с производной нелинейного члена − 3-DNLS, если оператор в (1) ${\hat {A}}(t,u) = 3s{{\left| p \right|}^{2}}{{u}^{2}}{{\partial }_{x}} - \partial _{x}^{2}(i\lambda + \nu )$), мы можем исследовать устойчивость возможных решений уравнения 3-GNLS. При этом динамику взаимодействия солитоноподобных структур уравнения GNLS можно изучить численно с использованием методов, развитых Belashov and Vladimirov [2005]. Решение такой задачи является целью настоящей работы.

1. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ РЕШЕНИЙ

Запишем уравнение (2) с α = 0 (уравнение 3-NLS) в гамильтоновой форме:

(3)
${{\partial }_{t}}u = {{\partial }_{x}}({{\delta H} \mathord{\left/ {\vphantom {{\delta H} {\delta u}}} \right. \kern-0em} {\delta u}}),$
где гамильтониан, имеющий смысл энергии системы, ${\text{H = }}\int_{ - \infty }^\infty {\left[ {\tfrac{\gamma }{2}{{{\left| u \right|}}^{4}} + \beta u{\kern 1pt} u{\kern 1pt} *{\kern 1pt} {{\partial }_{x}}\varphi + \tfrac{1}{2}\sigma {\kern 1pt} {{{\left( {{{\nabla }_{ \bot }}{{\partial }_{x}}w} \right)}}^{2}}} \right]d{\kern 1pt} {\mathbf{r}},} $ $\partial _{x}^{2}w = u,$ $\varphi = \arg (u)$.

Используя метод анализа трансформационных свойств гамильтониана, подробно изложенный для уравнений системы BK в работах [Белашов, 1991, 1999; Belashov and Vladimirov, 2005] и впервые примененный для существенно более простых случаев “классического” уравнения Кадомцева–Петвиашвили в работе [Кузнецов и Мушер, 1986] и уравнения NLS в работе [Захаров и Кузнецов, 2012], исследуем устойчивость 2D- и 3D-решений уравнения (2). При этом задача для уравнения (3) формулируется в виде вариационного уравнения $\delta (H\, + \upsilon {{P}_{x}}) = 0,$ ${{P}_{x}} = \tfrac{1}{2}\int {{{u}^{2}}d{\kern 1pt} {\mathbf{r}}} $, смысл которого состоит в том, что все финитные решения уравнения (3) есть стационарные точки гамильтониана Н при фиксированном значении проекции импульса ${{P}_{x}}$. В соответствии с теоремой Ляпунова об устойчивости, в динамической системе точки, которые соответствуют минимуму или максимуму гамильтониана Н, являются абсолютно устойчивыми. Если же экстремум локальный, ему будут соответствовать локально устойчивые решения.

Рассмотрим деформации Н, сохраняющие проекцию импульса ${{P}_{x}}$:

$u(x,{{r}_{ \bot }}) \to {{\zeta }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{\eta }^{{ - 1}}}u({x \mathord{\left/ {\vphantom {x \zeta }} \right. \kern-0em} \zeta },{{{{{\mathbf{r}}}_{ \bot }}} \mathord{\left/ {\vphantom {{{{{\mathbf{r}}}_{ \bot }}} \eta }} \right. \kern-0em} \eta }),\,\,\,\,\zeta ,\eta \in C.$
Гамильтониан примет вид $H(\zeta ,\eta ) = a{{\zeta }^{{ - 1}}}{{\eta }^{{ - 2}}}$ + $ + \,\,b{{\zeta }^{{ - 1}}} - c{{\zeta }^{2}}{{\eta }^{{ - 2}}}$ с коэффициентами
(4)
$\begin{gathered} a = ({\gamma \mathord{\left/ {\vphantom {\gamma 2}} \right. \kern-0em} 2})\int {{{{\left| u \right|}}^{4}}{\text{d}}{\mathbf{r}}} ,\,\,\,\,b = \beta \int {u{\kern 1pt} u{\kern 1pt} {\text{*}}{{\partial }_{x}}\varphi {\text{d}}{\mathbf{r}}} , \\ c = ({\sigma \mathord{\left/ {\vphantom {\sigma 2}} \right. \kern-0em} 2})\int {{{{({{\nabla }_{ \bot }}{{\partial }_{x}}w)}}^{2}}{\text{d}}{\mathbf{r}}} . \\ \end{gathered} $
Из необходимых условий экстремума ${{\partial }_{\zeta }}{\kern 1pt} H = 0,$ ${{\partial }_{\eta }}{\kern 1pt} H = 0$ сразу же найдем его координаты:
${{\zeta }_{{{\kern 1pt} 0}}} = - a{{c}^{{ - 1}}},\,\,\,\,{{\eta }_{0}} = {{[ - a{{b}^{{ - 1}}}(1 + {{a}^{2}}{{c}^{{ - 2}}})]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$
где b < 0, если η ∈ R ⊂ C, поскольку a > 0, c > 0 по определению, и b > 0, если η ∈ C. Достаточные условия минимума в точке (ζi, ηj):
$\begin{gathered} \left| {\begin{array}{*{20}{c}} {\partial _{\zeta }^{2}H{\text{(}}{{\zeta }_{i}}{\text{,}}{{\eta }_{j}}{\text{) }}}&{\partial _{{\zeta \eta }}^{2}H{\text{(}}{{\zeta }_{i}},{{\eta }_{j}})} \\ {\partial _{{\eta \zeta }}^{2}H{\text{(}}{{\zeta }_{i}},{{\eta }_{j}})}&{\partial _{\eta }^{2}H{\text{(}}{{\zeta }_{i}},{{\eta }_{j}})} \end{array}} \right| > 0, \\ \partial _{\zeta }^{2}H{\kern 1pt} ({{\zeta }_{i}},{{\eta }_{j}}) > 0. \\ \end{gathered} $
Решая данную систему неравенств, получим, что для волн в случае b < 0 (положительная нелинейность) ${a \mathord{\left/ {\vphantom {a c}} \right. \kern-0em} c} < d = {{(2\sqrt 2 )}^{{ - 1}}}\sqrt {13 + \sqrt {185} } $, откуда следует, что $H > {{ - 3bd} \mathord{\left/ {\vphantom {{ - 3bd} {(1 + 2{{d}^{2}})}}} \right. \kern-0em} {(1 + 2{{d}^{2}})}}$, то есть гамильтониан ограничен снизу. При b > 0 (отрицательная нелинейность): замена b → −b эквивалентна замене y → −iy, z → −iz и $H < {{ - 3bd} \mathord{\left/ {\vphantom {{ - 3bd} {(1 + 2{{d}^{2}})}}} \right. \kern-0em} {(1 + 2{{d}^{2}})}}$, то есть гамильтониан снизу не ограничен (ограничен сверху).

Итак, мы доказали возможность существования устойчивых 3D-решений в модели 3-NLS и получили условия их устойчивости, то есть определили области значений коэффициентов уравнения (переменных во времени и пространстве характеристик среды), когда 3D-солитоны будут устойчивыми.

2. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ЭВОЛЮЦИИ И ДИНАМИКИ ВЗАИМОДЕЙСТВИЯ СОЛИТОНОВ GNLS

Численное исследование эволюции и динамики взаимодействия солитоноподобных структур уравнения 3-GNLS проводилось нами с использованием методов, разработанных и детально описанных в работе [Belashov and Vladimirov, 2005]. Результаты моделирования для общего случая неоднородной и нестационарной среды подтверждают сделанные на основе аналитического рассмотрения проблемы заключения. В качестве иллюстрации на рисунках 1 и 2 представлены результаты, полученные при σ = 0 (1D-случай) для начальных условий в виде солитоноподобного импульса огибающей:

$\begin{gathered} u\left( {x,0} \right) = A\exp ({{ - {{x}^{2}}} \mathord{\left/ {\vphantom {{ - {{x}^{2}}} l}} \right. \kern-0em} l}), \\ u\left( {x,0} \right) = A\exp {\kern 1pt} \text{[}{{ - {{{(x - 5)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{(x - 5)}}^{2}}} l}} \right. \kern-0em} l}] + A\exp [{{ - {{{(x + 5)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{(x + 5)}}^{2}}} l}} \right. \kern-0em} l}], \\ \end{gathered} $
соответственно, в простейшем случае уравнения NLS с β, γ = const (стационарная среда); α, f ' = 0 при отрицательной нелинейности, β > 0. При этом b > 0 и гамильтониан H > 3bd/(1 + 2d 2), а значит условие устойчивости для отрицательной нелинейности, H < 3bd/(1 + 2d 2), не выполняется, и, как видно из рисунков, мы наблюдаем рассеяние импульсов огибающей со временем.

Рис. 1.

Эволюция гауссова импульса огибающей при A = 2, l = 2; β = 0.5, γ = 0.

Рис. 2.

Эволюция гауссова 2-импульсного возмущения огибающей при A = 1, l = 4; β = 0.5, γ = 0.

Примеры, когда коэффициент γ ≠ 0 и условие устойчивости для положительной нелинейности H > 3bd/(1 + 2d 2) > 0 не выполняется и когда условие для отрицательной нелинейности H < 0 < < −3bd/(1 + 2d 2) удовлетворено, показаны соответственно на рисунках 3 и 4.

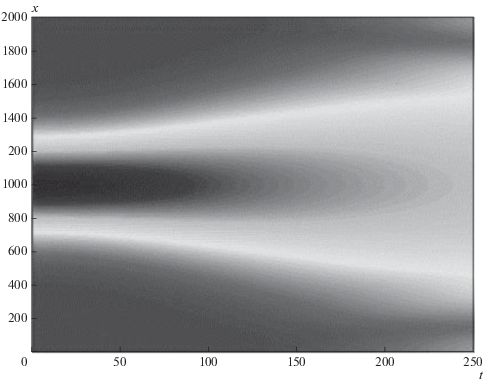
Рис. 3.

Эволюция гауссова импульса огибающей при A = 1, l = 4; β < 0, γ > 0 (положительная нелинейность).

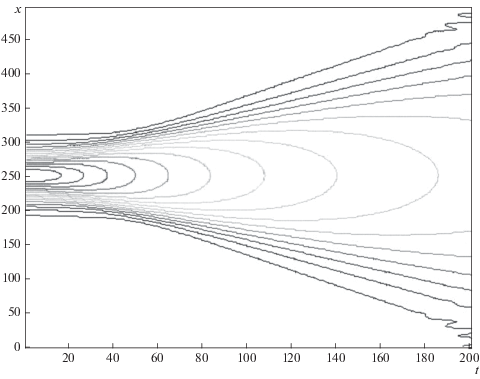
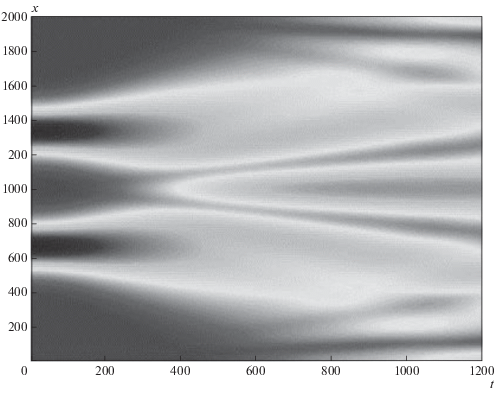
Рис. 4.

Эволюция гауссова импульса огибающей при A = 1, l = 4; β < 0, γ = −0.5 < 0 (отрицательная нелинейность).

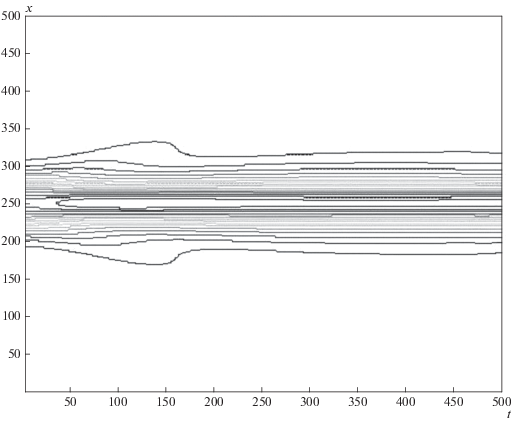
В первом случае мы наблюдаем рассеяние импульса огибающей со временем, а во втором имеет место стабилизация решения и формирование солитона из начального импульса.

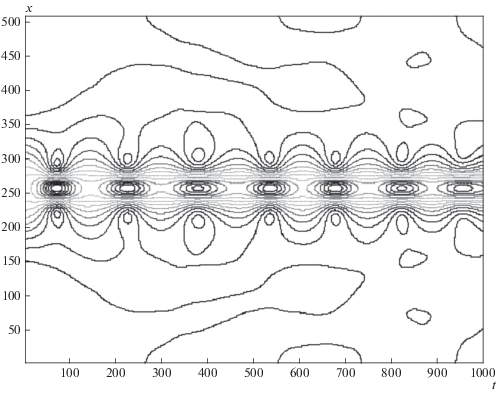
На рисунке 5 показан результат для того же, как и на рис. 4, случая отрицательной нелинейности [β < 0, γ < 0 и a, b < 0 в формулах (4)], однако здесь имеет место случай сильной отрицательной нелинейности, когда γ = −1 и наблюдается появление квазиустойчивых мощных солитоноподобных пульсаций типа бризеров.

Рис. 5.

Эволюция гауссова импульса огибающей при A = 1, l = 4; β < 0, γ = −1.

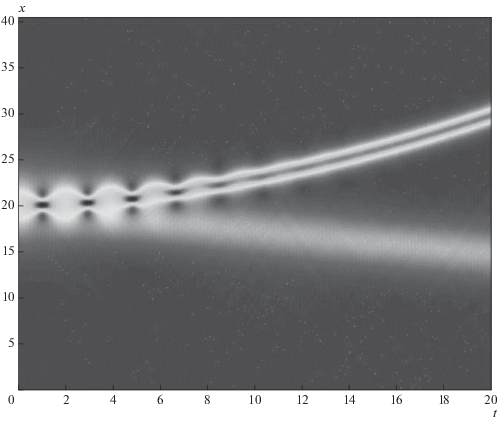
В численных экспериментах для уравнения GNLS (2) с σ = 0 при β, γ = φ(t); α, f ' = 0 нами было установлено, что квазиустойчивая эволюция начального гауссова импульса может наблюдаться, когда в нестационарной среде с отрицательной нелинейностью условие устойчивости H < −3bd/(1 + + 2d 2) удовлетворено. В этом случае можно наблюдать пульсации со сдвигом импульса в процессе его эволюции в x-направлении (рис. 6).

Рис. 6.

Эволюция гауссова импульса огибающей при A = 1, l = 4; β(t) = −0.5(1 + sin 0.1πt), γ = −1.

На рисунке 7 представлены два примера результатов эволюции гауссова импульса в нестационарной среде при отрицательной нелинейности, когда условие устойчивости H < −3bd/(1 + 2d 2) выполняется. В результате эволюции при этом наблюдается возникновение из начального уединенного импульса мощных устойчивых пульсаций типа бризеров.

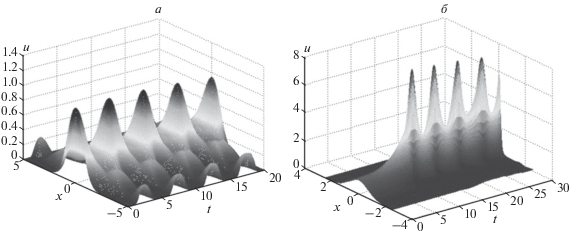
Рис. 7.

Эволюция гауссова импульса огибающей в нестационарной среде при α, f ' = 0: (а) β = 0.5, γ = −1 + 0.01 sin 2πt; (б) γ = −1, β(t) = −0.5 при t ≤ 5 и β(t) = 0.5(1 + 0.2 sin 2πt) при t > 5; случаи отрицательной нелинейности.

Пример взаимодействия солитоноподобных начальных импульсов вида

(5)
$\begin{gathered} u\left( {x,0} \right) = A[sch(x) + sch(x - {s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2}) + sch(x + {s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2})], \\ u\left( {x,0} \right) = A[sch(x - {s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2}) + sch(x + {s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2})] \\ \end{gathered} $
при отрицательной нелинейности в рамках модели GNLS приведен на рис. 8, 9, соответственно. В первом случае условие устойчивости не выполняется, и мы наблюдаем на первом этапе возникновение одного мощного импульса из 3-импульсного начального возмущения и далее, со временем, его распад на два импульса малой амплитуды. Во втором случае, условие устойчивости выполнено, и имеет место устойчивая эволюция 2-импульсного возмущения.

Рис. 8.

Взаимодействие трех импульсов GNLS (стационарная среда) при γ = −1, β = 0.25; случай слабой отрицательной нелинейности.

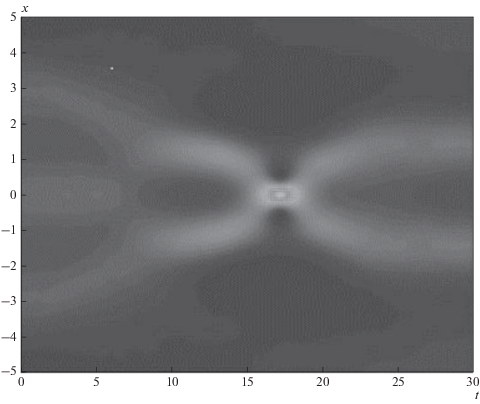
Рис. 9.

Отсутствие взаимодействия импульсов GNLS (стационарная среда) при γ = −1, β = 0.05; случай отрицательной нелинейности.

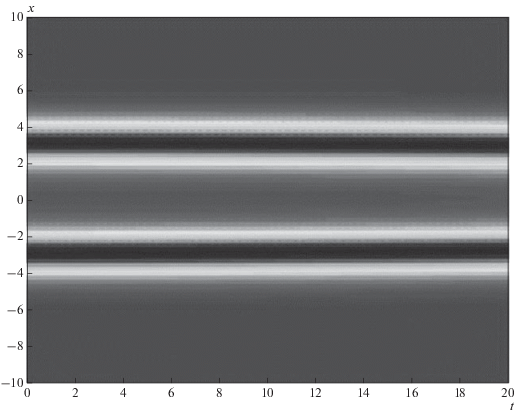
Интересно отметить, что, когда в некоторый момент времени поле становится нестационарным, устойчивость многоимпульсного возмущения может нарушаться и процесс эволюции переходит в неустойчивый с малыми пульсациями. Такой случай можно видеть на рисунке 10 (ср. со случаем, представленным на рис. 9).

Рис. 10.

Эволюция 2-импульсного возмущения в нестационарной среде при γ = −1, β(t) = 0.5 для t ≤ 15 и β(t) = 0.5[1 + + 0.2 sin(2πt/15)] для t >15; отрицательная нелинейность.

В численных экспериментах было также установлено, что при слабой отрицательной нелинейности, когда условие устойчивости выполняется, переход от устойчивой эволюции к режиму устойчивых пульсаций (бризеров) происходит при уменьшении начального расстояния s в начальных условиях (5) между импульсами [Belashov et al., 2019a; Белашов и др., 2019].

Детальному численному исследованию задач эволюции и взаимодействия 2D- и 3D-импульсов в модели 3-GNLS посвящены работы [Belashov et al., 2018b, 2019a, b; Belashov and Kharshiladze, 2019; Белашов и др., 2019, 2020].

3. ЗАКЛЮЧЕНИЕ

Резюмируя результаты, отметим следующее.

1. Мы обсудили проблему эволюции и динамики неодномерных решений обобщенного уравнения NLS (уравнения GNLS), как частного случая системы BK, а именно: устойчивость 3D-решений уравнения 3-GNLS и динамику устойчивых и неустойчивых решений уравнения NLS в стационарных и нестационарных средах.

2. В работе аналитически получены условия, разделяющие классы устойчивых и неустойчивых солитоноподобных решений уравнения GNLS, и найдены достаточные условия устойчивости неодномерных решений.

3. Показано, что даже в простейшем 1D-случае уравнение GNLS имеет широкий класс устойчивых или квазиустойчивых решений типа солитонов и бризеров, а также неустойчивые пульсирующие решения, рассеивающиеся со временем.

4. Полученные аналитические результаты подтверждены численным исследованием случаев устойчивой и неустойчивой (с образованием бризеров) эволюции импульсов различной формы, а также взаимодействия 2- и 3-импульсных структур, приводящего к формированию устойчивых и неустойчивых решений.

Список литературы

  1. − Белашов В.Ю. Об устойчивости двумерных и трехмерных солитонов в слабо диспергирующих средах // ДАН СССР. Т. 320. № 1. С. 85−89. 1991.

  2. − Белашов В.Ю. Проблема устойчивости трехмерных альфвеновских волн, распространяющихся в замагниченной плазме // Докл. АН. Т. 366. № 4. С. 465−467. 1999.

  3. − Белашов В.Ю., Харшиладзе О.А., Рогава Дж.Л. Взаимодействие многомерных NLS-солитонов в неоднородной и нестационарной среде // Тр. XXVI Всеросс. откр. науч. конф. “Распространение радиоволн”, Казань, 1–6 июля 2019 г.: в 2 т. Казань: Изд-во Казан. ун-та. Т. 2. С. 491−494. 2019.

  4. − Белашов В.Ю., Харшиладзе О.А., Белашова Е.С. Динамика солитонов обобщенного уравнения NLS в неоднородной и нестационарной среде: эволюция и взаимодействие // Пятнадцатая ежегодн. конф. “Физика плазмы в солнечной системе”, 10–14 февраля 2020 г. ИКИ РАН. М.: ИКИ РАН. С. 253. 2020.

  5. − Гинзбург В.Л., Ландау Л.Д. К теории сверхпроводимости // ЖЭТФ. Т. 20. С. 1064−1967. 1950.

  6. − Захаров В.Е., Кузнецов Е.А. Солитоны и коллапсы: два сценария эволюции нелинейных волновых систем // УФН. Т. 182. С. 569–592. 2012.

  7. − Кузнецов Е.А., Мушер С.Л. Влияние коллапса звуковых волн на структуру бесстолкновительных ударных волн в замагниченной плазме // ЖЭТФ. Т. 91. Вып. 5(11). С. 1605–1619. 1986.

  8. – Belashov V.Yu., Vladimirov S.V. Solitary waves in dispersive complex media. Theory, simulation, applications. Berlin, Heidelberg, New York, Tokyo: Springer-Verlag GmbH & Co. KG, 303 p. 2005.

  9. − Belashov V.Yu., Belashova E.S., Kharshiladze O.A. Problem of stability of the multidimensional solutions of the BK class equations in space plasma // Adv. Space Res. V. 62. P. 65−70. 2018a.

  10. − Belashov V.Yu., Kharshiladze O.A., Rogava J.L. Interaction of the multidimensional NLS solitons in non-uniform and nonstationary medium: modeling and stability problem // J. Astrophys. Aerospace Tech. V. 6. P. 38. 2018b.

  11. − Belashov V.Yu., Kharshiladze O.A., Rogava J.L. Interaction of multidimensional NLS solitons in nonuniform and nonstationary medium // 2019 Russian Open Conference on Radio Wave Propagation (RWP), Kazan, Russia, July 1–6, 2019, Kazan Federal University. Proc. IEEE Xplore Digital Library. P. 535−538. 2019a.

  12. − Belashov V.Yu., Belashova E.S., Kharshiladze O.A. The BK system: stability and interaction dynamics of the GKP and GNLS solitons // J. Lasers, Optics & Photonics. V. 6. P. 20–21. 2019b.

  13. − Belashov V.Yu., Kharshiladze O.A. Numerical study of evolution and collisional interaction of the GNLS solitons in nonstationary and non-uniform media // J. Lasers, Optics & Photonics. V. 6. P. 33–34. 2019.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал