Геомагнетизм и аэрономия, 2021, T. 61, № 1, стр. 35-45
Формирование экстремальных аномалий полной электронной концентрации по данным линейной теории
1 Институт вычислительной математики РАН (ИВМ РАН)
г. Москва, Россия
2 Институт прикладной геофизики им. Е.К. Федорова (ФГБУ ИПГ)
г. Москва, Россия
* E-mail: asgrit@mail.ru
Поступила в редакцию 03.10.2019
После доработки 11.06.2020
Принята к публикации 24.09.2020
Аннотация
В предположении, что эволюция полной электронной концентрации в спокойной ионосфере может быть описана в рамках динамико-стохастического подхода, была построена и верифицирована соответствующая модель. При вычислениях использовался архив данных TEC SDDIS NASA за 1998–2018 гг. Наблюдаемые экстремальные аномалии поля TEC (с величиной аномалии втрое превышающей величину среднеквадратичного отклонения нормы аномалии) интерпретировались как реакция спокойной ионосферы на внешние воздействия. Такими воздействиями считаются возмущения потока солнечного излучения и геомагнитные аномалии, характеризуемые соответствующими индексами, а также воздействия, имеющие другую физическую природу (влияние обрушения атмосферных гравитационных волн и т.п.). Внешнее воздействие определялось как разница прогнозируемого с помощью линейной модели изменения аномалии TEC и ее реального значения. Линейная динамико-стохастическая модель позволила выделить аномалии начального состояния ионосферы и внешние воздействия, способные произвести наибольшие ее изменения через заданное время. Было показано, что структура экстремальных аномалий TEC определяется формой оптимальных векторов-откликов (левых сингулярных векторов соответствующих операторов). Величина коэффициента корреляции для проекции аномалии на 5 ведущих векторов достигает 0.85, и для проекции на первый вектор составляет 0.7.
1. ВВЕДЕНИЕ
Ионосферные аномалии, особенно экстремальные, критически влияют на работоспособность спутниковых систем, качество дальней радиосвязи и радиолокации [NRC, 2008]. Прогноз таких событий, несомненно, является весьма востребованным и актуальным [NRC, 2008; Baker, 2012; Sharma et al., 2012]. В качестве причин, инициирующих и определяющих динамику экстремальных аномалий, традиционно считаются геомагнитные аномалии, вызванные солнечной активностью и внутренними факторами (например, широко обсуждающимся сейсмическим фактором) [Kellеy, 2009; Sun et al., 2013; Sharma et al., 2012] и характеризуемые соответствующими индикаторами (индексами kp/ap, Dst, F10.7 и т.д.). Обсуждается влияние нижней атмосферы на ионосферные аномалии, проявляющееся в обрушении гравитационных волн и сопутствующих изменениях в ионосфере [Данилов и др., 1987]. Возможно и совместное действие различных факторов [Baker and Allen, 2000]. Очевидно, что данные процессы имеют различное физическое происхождение, зачастую до конца не исследованное, поэтому традиционный подход к созданию прогностических ионосферных систем основан на эмпирическом подходе. Используются различного вида регрессионные схемы, нейронные сети и т.п. [Bilitza et al., 2012, 2016; Лещинская и Михайлов, 2016; Шубин, 2017; Oyeyemi et al., 2005; Hoque and Jakowski, 2012; Jian et al., 2014].
Mодели, основанные на первых принципах (законах природы) хороши тем, что позволяют проводить анализ факторов, ответственных за формирование аномалий в терминах уравнений и позволяют делать строгие выводы относительно причинно-следственных связей, верифицируя эмпирические методики. Отметим, в частности, разработки, осуществляемые в США [Richmond et al., 1992], Великобритании [Fuller-Rowell et al., 1997; Bailey et al., 1997], Германии [Schmidt et al., 2006] и России [Namgaladze et al., 1998; Bessarab et al., 2015; Дымников и др., 2020].
Настоящая работа выполнена с целью формализовать образование экстремальных аномалий полной электронной концентрации в предположении того, что динамика спокойной ионосферы может быть описана в терминах динамико-стохастического подхода. Соответствующая приближенная модель является системой линейных дифференциальных уравнений с матрицей системы, периодически зависящей от времени и дополненной стохастической правой частью, параметризующей нелинейные взаимодействия. В таком случае, и линейный оператор (матрица) системы, и характеристики стохастической части могут быть получены с помощью эмпирического подхода. Анализируя динамические свойства оператора задачи с помощью подходов линейной алгебры (сингулярное разложение, построение собственных векторов) оказывается возможным связать появление экстремальных аномалий со специфическим видом воздействий на систему и начальных условий, оценить возможность наиболее эффективного воздействия на систему. Работа построена следующим образом. В следующей главе (часть 2) описаны используемые данные и дано определение “экстремальности” аномалии TEC, проанализированы их статистические характеристики. В третьей части сформулирована модель, используемая для описания динамики ионосферы. В четвертой части анализируются особенности возникновения экстремальных аномалий в терминах построенной модели.
2. ИСПОЛЬЗУЕМЫЕ ДАННЫЕ
В работе используются данные значений полного электронного содержания (TEC) с сайта архива данных NASA (ftp.cddis.nasa.gov). Данные представляют собой двумерные массивы на географической широтно-долготной сетке с разрешением 5 и 2.5 град. по долготе и широте с временны́м шагом 2 ч начиная с 00GMT каждых суток. Данные доступны с середины 1998 г. по настоящее время, в работе используется 20 полных лет архива, начиная с осени 1998 г. Также используются значения индексов ap и F10.7 за тот же промежуток времени с сайта Goddard Space Flight Center (GSFC, Центр космических полетов им. Годдарда, (https://omniweb.gsfc.nasa.gov/ow.html)). Поскольку в настоящей работе мы интересуемся изменениями состояния ионосферы на временны́х масштабах в несколько часов (определяемой внутренней динамикой ионосферы/верхней атмосферы), нам необходимо выделить компоненту динамики, наименее зависящую от детерминированных периодических факторов (кроме суточного хода солнечной радиации, который учитывается непосредственно). Для этого в работе все вычисления проводятся для высокочастотной компоненты TEC – его аномалии относительно двухнедельной средней ($\Delta = 24\,{\text{hr}}$):
Число возмущенных состояний, а также среднее состояние поля значений TEC и его изменчивость естественным образом зависит от 11-летнего цикла солнечной активности. На рисунке 1 штриховой линией показана среднегодовая величина евклидовой нормы $X{\kern 1pt} '$ (рис. 1а) и ее среднеквадратичного отклонения (рис. 1б) для спокойных условий (в единицах TECU). Жирная штриховая линия – их трехточечное скользящее среднее. Сплошной линией показаны соответствующие величины, вычисленные для всего набора данных.
Рис. 1.
Среднее значение нормы аномалии TEC (в ед. TECU), вычисленное по всем данным (сплошная линия) и для спокойных условий (штриховая линия), в зависимости от года. Трехточечное среднее последней (в ед. TECU) – жирная штриховая линия (а). Аналогично для дисперсии нормы аномалии TEC в случае всех/спокойных дней в единицах TECU (б). Число экстремальных аномалий N (жирная кривая) в зависимости от года (в). Тонкая сплошная линия на рис. 1в – среднее за соответствующий год значение индекса ap (в ед. nT).
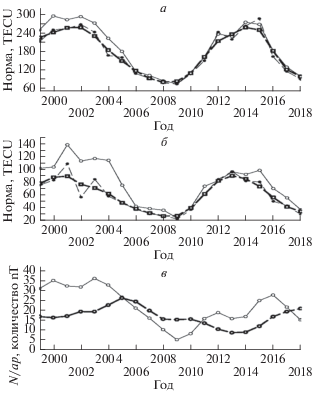
Далее, экстремальной аномалией поля значений полного электронного содержания $X{\kern 1pt} '$ мы будем считать состояние, отклонение $X{\kern 1pt} '$ для которого относительно средней для спокойных условий втрое превышает величину среднеквадратичного отклонения (СКО) в спокойных условиях для данного года и времени суток. При этом, аномалии такой величины не должно быть в предыдущие трое суток. В этом смысле аномалия является изолированной. Такой выбор предполагает необходимость существования внешнего воздействия для образования аномалии (вероятность естественной аномалии, превышающей 3 величины СКО – менее 0.1%).
Всего за 20 лет имело место 355 событий, удовлетворяющих данному выше определению. На рисунке 1в показано распределение числа таких экстремальных аномалий в зависимости от года (рис. 1в). Для справки на рис. 1в тонкой линией также показано среднегодовое значение индекса ap. Очевидна корреляция между двумя кривыми, однако она далека от единицы.
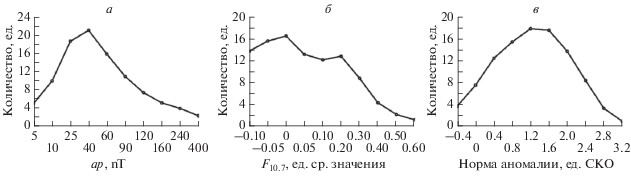
На рисунке 2 (a–в) показано, какие события обычно предшествуют возникновению экстремальной аномалии. Рисунок 2а – распределение числа экстремальных событий относительно значения индекса ap за 1.5 сут до возникновения экстремальной аномалии (при построении распределения используются все 355 случаев экстремальных событий). Рисунок 2б – то же для величины отклонения индекса F10.7 от его годового значения (единица соответствует среднегодовому значению индекса), рис. 2в – то же для нормы аномалии TEC (в единицах величины СКО для спокойных условий). Анализируя распределения, представленные на рис. 2, можно сделать вывод, что для образования экстремальной аномалии, как правило, требуется сочетание нескольких факторов – высокие значения индекса ap или сильные аномалии индекса F10.7, непосредственно предшествующие аномальному событию, а также высокое значение самой аномалии (порядка 1.5 СКО в среднем). Отметим также, что существует порядка 10% экстремальных событий, не имеющих каких-либо значительных аномалий-предвестников. По-видимому, их появление обеспечивается другими факторами, например, атмосферными. В настоящей работе мы попытаемся охарактеризовать структуру экстремальных аномалий в терминах оптимальных воздействий на ионосферу, без привязки к конкретным физическим явлениям, их вызывающим.
Рис. 2.
Распределение числа состояний ионосферы относительно величины индекса ap за 1.5 сут до образования экстремальной аномалии (в ед. nT) (а). Тоже относительно величины отклонения индекса F10.7 от среднего за год значения (в долях от среднегодового значения) (б) и нормы аномалии TEC (в долях от соответствующего СКО) (в).
3. МОДЕЛЬ ЭВОЛЮЦИИ АНОМАЛИИ TEC И ВНЕШНИЙ ФОРСИНГ
Главное предположение, на котором основано все дальнейшее рассмотрение, заключается в том, что исходную нелинейную динамику аномалии поля значений TEC $X{\kern 1pt} '$ в условиях невозмущенной ионосферы (в отсутствии кратковременных солнечных, геомагнитных и других аномалий) можно достаточно точно описать с помощью линейной динамико-стохастической модели вида
здесь ${\mathbf{x}}$ это зависящий от времени двумерный массив значений аномалий поля значений TEC на широтно-долготной сетке, размерности 5183 (71 × 73), матрица $B(t)$ (размерностью 5183 × 5183) зависит от времени суток, т.е. является периодической по времени ($B(t + \Delta ) = B(t)$) с периодом $\Delta $ = 1 сут. Здесь и далее будет предполагаться, что матрица $B(t)$ устойчива по Ляпунову (все действительные части ее собственных значений строго отрицательны) для всех значений времени. Зависящий от времени форсинг в правой части представляет собой белый шум по времени с не зависящей от времени ковариационной матрицей. Среднее состояние исходной системы предполагается нулевым (в случае ненулевого среднего задача рассматривается в отклонениях).В случае, если на ионосферу действуют какие-либо возмущения (например, характеризуемые резким изменением индекса ap), то в уравнении появляется детерминированный, зависящий от времени форсинг (двумерный массив значений воздействий в точках широтно-долготной сетки), который предполагается независимым от текущего состояния ионосферы:
(2)
$\frac{{d{\mathbf{x}}}}{{dt}} = B(t){\kern 1pt} {\mathbf{x}} + \zeta + {\mathbf{f}}\left( t \right).$Решение этого уравнения для начального значения ${\mathbf{x}}\left( {{{t}_{0}}} \right) = {{{\mathbf{x}}}_{0}},$ может быть записано как:
(3)
${\mathbf{x}}(t) = M(t,{{t}_{0}}){{{\mathbf{x}}}_{0}} + \int\limits_{{{t}_{0}}}^t {M\left( {t,\tau } \right)\left( {{\mathbf{\zeta }}(\tau ){\kern 1pt} {\text{dW}} + {\mathbf{f}}(\tau ){\kern 1pt} d\tau } \right)} ,$Еще раз подчеркнем, что описанный выше подход для определения динамического оператора $M\left( {t,{{t}_{0}}} \right)$ предполагает отсутствие внешних воздействий, и периодическая зависимость данных лишь от времени суток. С учетом рис. 1а и рис. 1б понятно, что наилучший интервал времени, удовлетворяющий данным условиям это 2006–2010 гг., когда изменения статистик минимальны во времени и число дней, соответствующих невозмущенному состоянию ионосферы, максимально. Именно этот набор данных (невозмущенные дни 2006–2010 гг. в определении главы 2) и был использован в настоящей работе для определения матриц $M\left( {t,{{t}_{0}}} \right).$ Отметим, что простейшая регрессионная модель
(4)
${\mathbf{x}}\left( {{{t}_{i}}} \right) = M\left( {{{t}_{i}},{{t}_{{i - 1}}}} \right){{{\mathbf{x}}}_{{i - 1}}} = С\left( {{{t}_{i}},{{t}_{{i - 1}}}} \right){{\left\{ {C\left( {{{t}_{{i - 1}}},{{t}_{{i - 1}}}} \right)} \right\}}^{{ - 1}}}{{{\mathbf{x}}}_{{i - 1}}},$(5)
$\begin{gathered} {{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {{{t}_{{i - 1}}}} \right) = {\mathbf{x}}\left( {{{t}_{i}}} \right) - M\left( {{{t}_{i}},{{t}_{{i - 1}}}} \right){{{\mathbf{x}}}_{{i - 1}}} \equiv \\ \equiv {\mathbf{x}}\left( {{{t}_{i}}} \right) - С\left( {{{t}_{i}},{{t}_{{i - 1}}}} \right){{\left\{ {C\left( {{{t}_{{i - 1}}},{{t}_{{i - 1}}}} \right)} \right\}}^{{ - 1}}}{{{\mathbf{x}}}_{{i - 1}}}. \\ \end{gathered} $Рис. 3.
Число геомагнитных аномалий, имеющих значение выше 40 nT по индексу $ap$ относительно их продолжительности (штриховая линия) (а). Тоже, для событий с индексом $ap$ выше 30 nT – сплошная линия, помеченная крестами (а). Тоже для экстремальных аномалий поля TEC – сплошная линия (а). Величина корреляции (безразмерные единицы) с запаздыванием между евклидовой нормой ${{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {t + \delta } \right)$ и индексом $ap\left( t \right)$ (сплошная жирная линия) и между нормой ${{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {t + \delta } \right)$ и индексом $F10.7\left( t \right)$ (прерывистая жирная линия), в зависимости от запаздывания δ (в часах) (б). Тонкая сплошная (прерывистая) линия – корреляция с запаздыванием между нормой аномалии поля TEC и индексом $~ap$ (индексом $~F10.7$) в зависимости от запаздывания (в часах) (б).
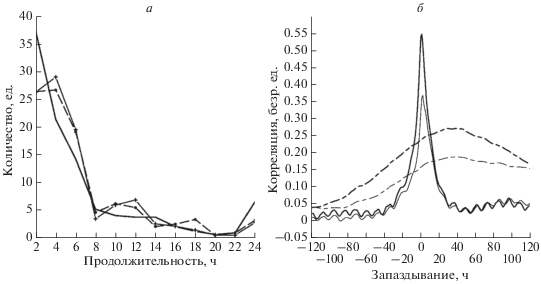
Информацию о среднестатистическом времени действия форсинга дает представление рис. 3а, на котором показано распределение продолжительности (в часах) геомагнитных аномалий, имеющих значение выше 40 единиц индекса $ap$ (штриховая линия) и выше 30 единиц индекса $ap$ (сплошная линия, помеченная крестами). Видно, что в среднем воздействие длится порядка 8 ч. Сплошная линия показывает распределение времени жизни экстремальных аномалий в определении данной статьи, также оцениваемое величиной порядка 8 ч.
4. ОПЕРАТОР ОТКЛИКА И ОПТИМАЛЬНЫЕ ВОЗМУЩЕНИЯ
Рассмотрим тождества (${{{\mathbf{f}}}_{{{\text{eff}}}}}$ рассчитывается согласно (5)):
(6)
$\begin{gathered} {\mathbf{x}}\left( {{{t}_{i}}} \right) = M\left( {{{t}_{i}},{{t}_{{i - k}}}} \right){{{\mathbf{x}}}_{{i - k}}} + {{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {{{t}_{{i - 1}}}} \right) + \\ + \,\,M\left( {{{t}_{i}},{{t}_{{i - 1}}}} \right){{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {{{t}_{{i - 2}}}} \right) + \ldots ~ + \,M\left( {{{t}_{i}},{{t}_{{i - k + 1}}}} \right){{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {{{t}_{{i - k}}}} \right). \\ \end{gathered} $Если в эффективном воздействии в модели (6) преобладает детерминистический форсинг, причем он пространственно слабо зависит от времени, то (6) еще более упрощается:
(7)
$\begin{gathered} {\mathbf{x}}\left( {{{t}_{i}}} \right) = M\left( {{{t}_{i}},{{t}_{{i - k}}}} \right){{{\mathbf{x}}}_{{i - k}}} + \\ + \,\,\left( {E + M\left( {{{t}_{i}},{{t}_{{i - 1}}}} \right) + \ldots ~~ + \,~M\left( {{{t}_{i}},{{t}_{{i - k + 1}}}} \right)} \right){{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {{{t}_{{i - k}}}} \right) \equiv \\ \equiv M\left( {{{t}_{i}},{{t}_{{i - k}}}} \right){{{\mathbf{x}}}_{{i - k}}} + U\left( {{{t}_{i}},{{t}_{{i - k}}}} \right){{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {{{t}_{{i - k}}}} \right). \\ \end{gathered} $Формулы (6) и (7) содержат исключительно корреляционные функции известного решения и могут быть рассчитаны по данным наблюдений.
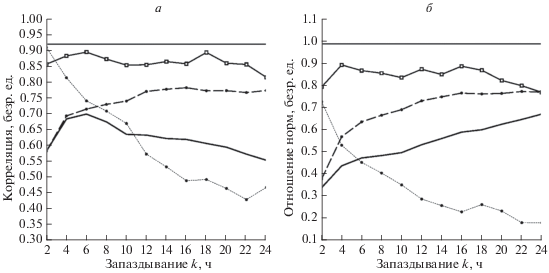
На рисунке 4 представлены прогностические характеристики линейных моделей (6) и (7) в зависимости от $k,$ принимающего значения 1, 2, …, 12 двухчасовых интервалов, при прогнозе экстремальных аномалий поля значений ТЕС. Рисунок 4а – средние значения корреляций прогноза и реальности по всем 355 аномалиям. Рисунок 4б – средняя величина отношения нормы прогноза к норме реальности. Сплошная тонкая постоянная линия на рис. 4а и рис. 4б – средняя по всем экстремальным аномалиям корреляция (отношение норм) ${\mathbf{x}}\left( {{{t}_{i}}} \right)$ и ее прогноза по формуле (6). Как уже отмечалась, прогноз по формуле (6) не зависит от $k.$ Сплошная линия, маркированная квадратами, – прогноз по формуле (7). Тонкая пунктирная убывающая линия – прогноз экстремальной аномалии с помощью первого слагаемого в формуле (6), отвечающего за влияние на прогноз начального условия в момент ${{t}_{{i - k}}}.$ Штриховая возрастающая линия – прогноз по интегральному слагаемому в формуле (6). Жирная линия – прогноз по второму слагаемому в формуле (6) – результат умножения $U{{{\mathbf{f}}}_{{{\text{eff}}}}},$ характеризующий справедливость предположения о постоянстве внешнего воздействия в случае образования сильных аномалий ТЕС (в качестве ${{{\mathbf{f}}}_{{{\text{eff}}}}}$ здесь использовано среднее значение $\sum\nolimits_1^k {{{{\mathbf{f}}}_{{{\text{eff}}}}}\left( {{{t}_{{i - j}}}} \right)} $). Из рисунка можно сделать вывод, что, во-первых, начиная примерно с 8 ч эффект внешних воздействий доминирует. Во-вторых, предположение о постоянстве внешнего воздействия не лишено смысла – слагаемое $U{{{\mathbf{f}}}_{{{\text{eff}}}}}$ обеспечивает среднюю корреляцию реального и прогнозируемого отклика на уровне 0.6, примерно вдвое занижая его норму. При этом, прогноз по формуле (7) не сильно уступает прогнозу (6). Таким образом, имеет смысл анализировать структуру сингулярных векторов операторов $M\left( {{{t}_{i}},{{t}_{{i - k}}}} \right)$ и $U~$ на предмет изучения структуры максимальных откликов, оптимальных воздействий и их реализуемости на практике, что и было сделано при $k = 4$ (что соответствует 8 ч – с учетом рис. 3а – наиболее вероятному времени действия геомагнитного форсинга).
Рис. 4.
Средние значения корреляций прогноза и реальности по всем 355 экстремальным аномалиям в зависимости от времени запаздывания k (часы) (а). Сплошная тонкая постоянная линия – средняя по всем экстремальным аномалиям корреляция ${\mathbf{x}}\left( {{{t}_{i}}} \right)$ и ее прогноза по формуле (6). Сплошная линия, маркированная квадратами – прогноз по формуле (7). Тонкая пунктирная убывающая линия – прогноз с помощью первого слагаемого в формуле (6), тонкая штрихованная возрастающая линия – прогноз по интегральному слагаемому в формуле (6). Жирная линия – прогноз по второму слагаемому в формуле (7). Тоже для средних величин отношения нормы прогноза к норме реальности в зависимости от времени запаздывания k (часы) (б).
Для каждой экстремальной аномалии определялась проекция ${{{\mathbf{f}}}_{{{\text{eff}}}}}$ на соответствующие ведущие правые сингулярные векторы $M$ и $U,$ а также проекция самой аномалии на ведущие левые сингулярные векторы данных операторов. В результате было показано, что средняя проекция ${{{\mathbf{f}}}_{{{\text{eff}}}}}$ на пространство первых 5 правых ведущих векторов, как $M,$ так и $U$ составляет величину порядка 0.35–0.40 для каждого вектора, распределяясь практически равномерно между всеми векторами (со средней корреляцией порядка 0.15–0.18 для каждого вектора и максимальной корреляцией не превосходящей 0.5). Таким образом, оптимальные воздействия не реализуются в природе. Корреляции между экстремальными аномалиями ${\mathbf{x}}\left( {{{t}_{i}}} \right)$ и ведущими левыми векторами (оптимальными откликами) значительно выше, что не удивительно – операторы максимально усиливают возмущения вдоль этих направлений. Средняя проекция аномалии на 5 ведущих откликов – 0.80–0.85, причем отклик концентрируется вдоль наиболее растущего первого вектора с корреляцией 0.65–0.7 как для оператора $M,$ так и для $U.~$
Структура вычисленных левых сингулярных векторов $P$ для $M\left( {{{t}_{i}},{{t}_{{i - k}}}} \right)$ и $U$ при $k = 4$ и времени ${{t}_{i}},$ равном 04:00 GMT, 12:00 GMT и 20:00 GMT показана на рис. 5 (3 ведущих вектора-отклика для $M$) и рис. 6 (3 ведущих вектора-отклика для $U$). В верхнем ряду приведены векторы для случая 04:00 GMT, в среднем и нижнем – для 12:00 GMT и 20:00 GMT соответственно. Видно, что корреляции между сингулярными векторами $M~$ и $U$ значимы. Правые векторы (воздействия) мы не приводим, ввиду их нереализуемости в природе.
Рис. 5.
Три ведущих оптимальных вектора-отклика оператора $U,$ вычисленного для оценки отклика в 04:00 GMT (первая строка – (a–в)), времени 10:00 GMT (вторая строка – (г–е)) и времени 20:00 GMT (третья строка – (ж–и)). Безразмерные единицы.
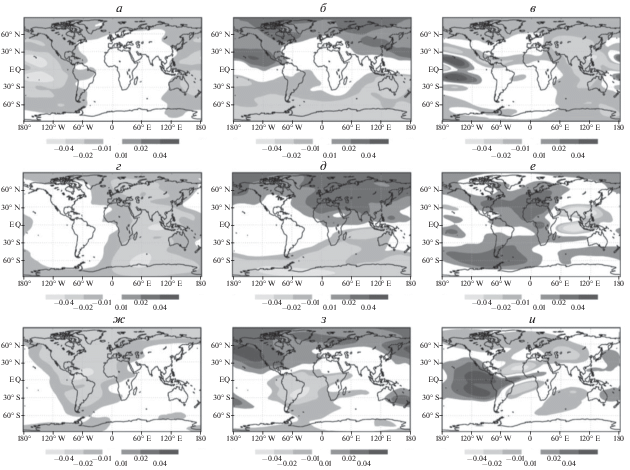
Рис. 6.
Три ведущих оптимальных вектора-отклика оператора $M~$ вычисленного для оценки отклика в 04:00 GMT (первая строка – (a–в)), времени 10:00 GMT (вторая строка – (г–е)) и времени 20:00 GMT (третья строка – (ж–и)). Безразмерные единицы.
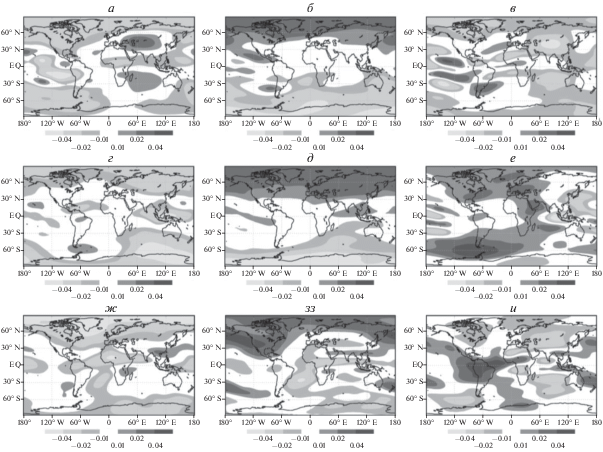
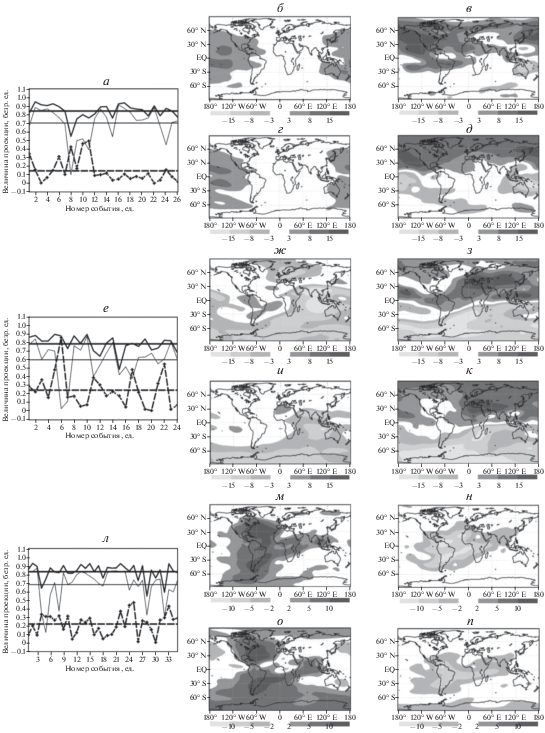
На рисунке 7 продемонстрированы шесть случаев образования экстремальных аномалий. Группа рис. 7а–7д относится к случаю возникновения аномалии в 04:00 GMT. На рисунке 7а представлены значения величины коэффициента корреляции для проекции аномалии на пространство 5 ведущих левых векторов-откликов матрицы $U$ (сплошная жирная линия), на 1-й ведущий вектор (сплошная тонкая линия) и на 2-й ведущий вектор (прерывистая линия) для каждого случая возникновения аномалии (всего 26 случаев). Горизонтальными линиями показаны соответствующие средние по всем 26 событиям. На рисунке 7б и рис. 7в показаны экстремальные аномалии, соответствующие событию m = 16 и m = 10. В первом случае мы имеет отклик вдоль первого вектора (рис. 5а, корреляция 0.91), во втором – второго (рис. 5б, корреляция 0.51). Прогнозы аномалий с помощью $U{{{\mathbf{f}}}_{{{\text{eff}}}}}$ показаны на рис. 7г и рис. 7д (величина отклика умножена на 1.3, поскольку прогноз недооценивает его величину). Полностью аналогичную структуру имеют группы рис. 7е–7к (возникновение аномалии в 12:00 GMT) и рис. 7л–7п (возникновение аномалии в 20:00 GMT). На рисунке 7ж показан случай экстремального события m = 2 (корреляция с ведущим откликом – 0.92, см. рис. 5г), на рис. 7з – случай m = 6 (возбуждается второй оптимальный отклик, рис. 5д). На рисунке 7м–7н приведены экстремальные события m = 14 и m = 25, также проектирующиеся на первый и второй вектор соответствующего оператора (рис. 5ж, рис. 5з).
Рис. 7.
Примеры экстремальных аномалий поля TEC, образующихся в 04:00 GMT (a–д). Величины проекции аномалии TEC (безразмерные единицы) на пространство 5 ведущих левых векторов-откликов матрицы $U$ (сплошная жирная линия), на 1-ый ведущий вектор (сплошная тонкая линия) и на 2-ой ведущий вектор (штриховая линия) в зависимости от номера m экстремального события (всего 26 случаев) (а). Соответствующие горизонтальные линии – их средние значения. Пространственная структура экстремальных аномалий, соответствующая событиям m = 16 и m = 10 (б и в) и ее прогноз (г и д). Аналогичная информация для экстремальных аномалий, образующихся в 12:00 GMT (24 случая, (е)), события m = 2 и m = 6 (ж–к). Аналогично для 20:00 GMT (35 событий (л)), события m = 14 и m = 25 (м–п).
5. ЗАКЛЮЧЕНИЕ
В предположении, что эволюция полной электронной концентрации в спокойной ионосфере может быть описана в рамках динамико-стохастического подхода, был вычислен линейный, зависящий от времени суток, оператор динамико-стохастической модели. При вычислениях использовался метод обратной линейной модели (LIM), применяемый к данным наблюдений – архиву данных TEC SDDIS NASA за 1998–2018 гг.
Наблюдаемые экстремальные аномалии поля значений TEC (с величиной аномалии втрое превышающей величину СКО нормы аномалии) интерпретировались как реакция спокойной ионосферы на внешние воздействия, такие как возмущения потока солнечного излучения и геомагнитные аномалии, характеризуемые соответствующими индексами, а также воздействиями, имеющими другую физическую природу (влияние нижней атмосферы и т.п.). Внешнее воздействие в конкретный момент времени, при этом, определялась как разница прогнозируемого с помощью линейной модели изменения аномалии TEC и ее реального значения. Было показано, что рассчитанный форсинг коррелирует с индексами ap и F10.7, характеризующими величину большей части воздействий на ионосферу.
Формулировка динамики ионосферы в виде линейной динамико-стохастической модели позволяет выделить аномалии начального состояния ионосферы и внешние воздействия, способные произвести наибольшие ее изменения через заданное время. Соответствующие структуры определяются с помощью сингулярного разложения операторов влияния начальных условий и внешнего форсинга соответственно, которые вычисляются по данным наблюдений. Было показано, что при возбуждении экстремальных аномалий влияние начальных условий наблюдается в течение ~8–16 ч, начиная с 6–8 ч эффект внешних воздействий становится определяющим. При 8-часовой заблаговременности прогноза аномалии оба фактора примерно равнозначны. Сравнение (корреляции) наблюдаемых внешних воздействий с результатами сингулярного разложения операторов влияния показывают, что оптимальные воздействия на ионосферу редко реализуются в природе (максимальная корреляция наблюдаемой аномалии и ведущего сингулярного вектора-воздействия не превышает величины 0.5 со средним значением порядка 0.15). В свою очередь, структура самих экстремальных аномалий почти полностью определяется структурой оптимальных векторов-откликов (левых сингулярных векторов соответствующих операторов), с величиной коэффициента корреляции для проекции на 5 ведущих векторов, достигающего 0.85, и проекции на первый вектор порядка 0.7.
Отметим также, что ведущие оптимальные векторы-отклики близки к ведущим низкочастотным (от суток до нескольких дней) модам изменчивости. Это является еще одним свидетельством того, что динамика экстремальных ионосферных аномалий допускает интерпретацию в терминах простой линейной динамико-стохастической модели.
Список литературы
– Грицун А.С. Потенциальная предсказуемость и прогноз состояния поля аномалий полной электронной концентрации по данным наблюдений // Геомагнетизм и аэрономия. Т. 59. № 1. С. 98–109. 2019.
– Данилов А.Д., Казимирский Э.С., Вергасова Г.В., Хачикян Г.Я. Метеорологические эффекты в ионосфере // Л.: Гидрометеоиздат. 268 с. 1987.
– Дымников В.П., Кулямин Д.В., Останин П.А. Совместная модель глобальной динамики термосферы и ионосферы Земли // Изв.РАН. Физика атмосферы и океана. Т. 56. № 3. С. 280–292. 2020.
– Лещинская Т.Ю., Михайлов В.В. Модель SIMP-1: картирование месячных медиан foF2 по северному полушарию // Геомагнетизм и аэрономия. Т. 56. № 6. С. 772–780. 2016.
– Шубин В.Н. Глобальная эмпирическая модель критической частоты F2-слоя ионосферы для спокойных геомагнитных условий // Геомагнетизм и аэрономия. Т. 57. № 4. С. 450–462. 2017.
– Bailey, G. J., Balan N., Su Y. Z. The Sheffield university plasmasphere ionosphere model: A review // J. Atmos. Solar-Terr. Phys. 1997. V. 59. № 13. P. 1541–1552.
– Baker D.N., Allen J.H. Confluence of natural hazards: A possible scenario // Eos Trans. AGU. V. 81. № 23. P. 254–254. 2000.
– Baker D.N. Extreme space weather: a nonlinear dynamical system / Complexity and Extreme Events in Geoscience P. 255–265. Geophys. Monogr. Ser. AGU. Washington, DC. USA. 2012.
– Bessarab F.S., Korenkov Yu.N., Klimenko V.V. et al. E-region ionospheric storm on May 1–3, 2010: GSM TIP model representation and suggestions for IRI improvement // Adv. Space Res. 2015. V. 55. № 8. P. 2124–2130.
– Bilitza D., Altadill D., Zhang Y. et al. The International Reference Ionosphere 2012 – a model of international collaboration // J. Space Weather Space Clim. V. 4. A07. 2014.
– Bilitza D., Altadill D., Reinisch B. et al. The International Reference Ionosphere: Model Update 2016 // Geophysical Research Abstracts. V. 18. EGU2016-9671. 2016.
– Fuller-Rowell T.J., Codrescu M.V., Fejer B.G. et al. Dynamics of the low-latitude thermosphere: Quiet and disturbed conditions // J. Atmos. Terr. Phys. V. 59. P. 1533–1540. 1997.
– Hoque M.M., Jakowski N. A new global model for the ionospheric F2 peak height for radio wave propagation // Ann. Geophysicae. V. 30. № 5. P. 797–809. 2012.
– Jian Lin, Xinan Yue, Zhen Zeng. et al. Empirical orthogonal function analysis and modeling of the ionospheric peak height during the years 2002–2011 // J. Geophys. Res.– Space. V. 119. № 5. P. 3915–3929. 2014.
– Kelley M.C. The Earth’s Ionosphere: Plasma Physics and Electrodynamics. 2nd ed. // San Diego, CA. USA: Academic Publishers, 2009.
– Namgaladze A.A., Martynenko O.V., Volkov M.A. et al. Highlatitude version of the global numerical model of the Earth’s upper atmosphere // Proceedings of the MSTU. V. 1. № 2. P. 23–84. 1998.
– National Research Council (NRC). Severe space weather events: Understanding societal and economic impacts // A Workshop Report. Natl. Acad. Press. Washington, DC. USA. 2008.
– Oyeyemi E.O., Poole A.W.V., McKinnell L A. On the global model for foF2 using neural networks // Radio Sci. V. 40. RS6011. 2005.
– Penland C., Sardeshmukh D. Error and sensitivity of geophysical eigensystems // J. Climate. V. 8. P. 1988–1998. 1995.
– Penland C. A stochastic model of IndoPacific sea surface temperature anomalies // Physica D. V. 98. P. 534–558. 1996.
– Richmond A.D., Ridley E.C., Roble R.G. A Thermosphere/Ionosphere General Circulation Model with coupled electrodynamics // Geophys. Res. Lett. V. 19. P. 601–604. 1992.
– Sharma-A.S., Baker D.N., Bhattacharyya A. et al. Complexity and Extreme Events in Geosciences: An Overview // Complexity and Extreme Events in Geoscience. P. 1–16. Geophys. Monogr. Ser. AGU. Washington, DC. USA. 2012.
– Schmidt, H., Brasseur G.P., Charron M. et al. The HAMMONIA Chemistry Climate Model: Sensitivity of the Mesopause Region to the 11-Year Solar Cycle and CO2 Doubling // J. Climate. V. 19. P. 3903–3931. 2006.
– Sun Y.Y., Matsuo T., Eduardo E.A. et al. Ground-based GPS observation of SED-associated irregularities over CONUS // J. Geophys. Res.–Space. V. 118. P. 2474–2489. 2013.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия


